1 Introduction

In only a decade, techniques that determine the fluid flow pressure based on PIV measurements have come to a degree of maturity that justifies their application in practical problems. These developments have been surveyed in a recent review article by van Oudheusden (2013). Starting from the work of Liu and Katz (2006), who used a dual-PIV system to measure velocity and its material derivative and subsequently applied the momentum equation for pressure evaluation, all following studies dealing with instantaneous pressure from PIV have made use of either time-resolved measurements or followed the dual-PIV approach, in order to experimentally determine the velocity material derivative. It has been shown that an accurate determination of the velocity material derivative in turbulent flows requires full three-dimensional evaluation of the velocity and acceleration field, which is currently possible by high-speed tomographic PIV experiments (Ghaemi et al. 2012). Due to uncorrelated random errors in consecutive PIV snapshots, recent studies have employed a Lagrangian pseudo-tracking approach to obtain the velocity material derivative from a series of consecutive time-resolved velocity measurements. For example, Liu and Katz (2013) employed five consecutive velocity fields and Novara and Scarano (2013) applied a PTV technique to eleven consecutive camera images. Other studies have focused on noise reduction of the PIV velocity measurements using for example a POD-based filtering approach (Charonko et al. 2010) to increase accuracy of the pressure determined from the time-resolved PIV measurements.

The high sampling rate required for time-resolved experiments in airflows compromises the achievable measurement volume of tomographic PIV. According to a recent survey (Scarano 2013), measurement rates achieved in tomo-PIV experiments range from 2.7 kHz (airfoil trailing edge by Ghaemi and Scarano 2011; bluff body wake by de Kat and van Oudheusden 2012) to 5 kHz (turbulent boundary layer by Schröder et al. 2008; rod-airfoil interaction by Violato et al. 2011). More recent experiments in turbulent boundary layers have been conducted at a rate up to 10 kHz (Ghaemi et al. 2012; Pröbsting et al. 2013), at the expense of a further reduction of the measurement volume. The above experiments were conducted with airflow velocities in the range from 7 to 14 m/s, which poses further restrictions on the value of the Reynolds number. To date, time-resolved tomographic PIV experiments at flow velocities on the order of 100 m/s are to be deemed unrealistic, considering that they would require acquisition rates on the order of 100 kHz.

The extension of dual-plane PIV (Kähler and Kompenhans 2000) or dual-time PIV (Perret et al. 2006) to dual-tomographic PIV systems overcomes the trade-off between measurement volume and recording rate affecting the time-resolved approach, in that it makes use of two low repetition rate lasers and CCD cameras. Such systems also allow investigating flows at higher velocity as one can arbitrarily reduce the time separation between the two velocity measurements, without the restriction set by the repetition rate of a single PIV system. A four-pulse tomographic PIV system has been described (Lynch and Scarano 2014) that can perform acceleration measurements in the compressible flow regime. The drawback is the complexity associated with 8–12 cameras that need to record images from a volume illuminated with two separate dual-pulse lasers.

Alternatives to the time-resolved or dual-PIV approaches are provided in the field of data assimilation. In periodic flows, phase-locked experiments using non-time-resolved PIV systems have been employed in order to obtain pressure from a phase-resolved description of the flow, as reviewed in van Oudheusden (2013). In addition, not relying on phase-locked experiments, Bai et al. (2015) have employed a reduced-order modelling approach using compressive sensing for reconstruction of velocity time-series from PIV measurements performed at limited temporal resolution. More advanced methods reconstruct both velocity and pressure by making use of simulation of the flow governing equations. Suzuki (2012) proposed a reduced-order Kalman filter technique combining PTV and DNS, and later a POD-based hybrid simulation (Suzuki, 2014). Recently, Gronskis et al. (2013), Lemke and Sesterhenn (2013) and Vlasenko et al. (2015) have proposed variational techniques for combination of numerical flow simulations with PIV measurement results. An advantage of these approaches is that they can naturally incorporate also local information from other measurement devices (e.g., surface pressure measurements) as alternative or in addition to PIV. Computational cost associated with the variational or Kalman-filter-based techniques has, however, limited practical application to real-world volumetric experiments.

Less computationally expensive data assimilation approaches solve directly the flow governing equations using the PIV data as initial or boundary conditions. For example, the use of CFD simulations to fill gaps in the measurement domain has been discussed by Sciacchitano et al. (2012). To alleviate measurement rate requirements which limit current pressure-from-PIV setups, Scarano and Moore (2011) proposed to leverage directly the spatial information available by the measurement to increase temporal resolution (“time-supersampling”) using a linearized model. The work is based on the assumption of frozen turbulence and advects spatial velocity fluctuations to produce intermediate velocity estimates in between the measured samples. The relatively low computational cost of the linearized model has allowed for demonstration of the method on real-world tomographic PIV data. A similar approach was later used by de Kat and Ganapathisubramani (2013), who discussed the importance of estimating the local convection velocity. To avoid this, the time-supersampling concept was generalized to broader flow regimes (separated flows, vortex-dominated regimes) by Schneiders et al. (2014), who introduced the use of the vortex-in-cell (VIC) technique for time-supersampling of tomographic PIV measurements in incompressible flows. The measured samples of the velocity field are used both as initial and final conditions for a numerical simulation of the vorticity transport equation, which is solved within the measurement domain. The study returned an accurate time-reconstruction, demonstrating that the sampling rate requirements could be significantly reduced with such a procedure.

The objective of the present work moves the attention to the use of VIC on a single velocity field snapshot to estimate the instantaneous pressure field in flows where the pressure fluctuations are dominated by vortical structures in the flow. In particular, the problem of the flat-plate boundary layer is considered, which has been studied in recent studies employing time-resolved tomographic PIV for pressure determination (Ghaemi and Scarano 2011, 2013; Schröder et al. 2011; Pröbsting et al. 2013, amongst others). These studies follow two decades of literature on turbulent boundary layer flows as reviewed in Marusic et al. (2010). Because of the inherent unsteady nature of the turbulent flow structures in the boundary layer, pressure evaluation from tomographic PIV in such flows has only been demonstrated using a time-resolved (repetition rate ~10 kHz) measurement setup.

The single-snapshot pressure evaluation using VIC follows a time-marching approach, whereby a single time step starting from the instantaneous tomographic PIV velocity measurements is needed to approximate the velocity material derivative and subsequently, the instantaneous pressure. As a result, a significant simplification of the measurement systems is potentially obtained, with respect to dual systems for the evaluation of pressure-from-PIV.

2 Pressure evaluation from a single PIV velocity field

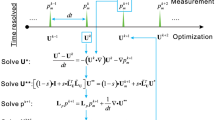
The discussion here is limited to incompressible and isothermal flows. It is furthermore assumed that the velocity field is measured by tomographic PIV, but the application to data from other 3D velocity measurement methods is also considered possible. Consider a velocity measurement u m ( x ,t 0 ) at time t = t 0 on a three-dimensional grid x with constant spacing h in the volume Ω, which is assumed a cuboid with boundary ∂Ω. The established time-resolved pressure-from-PIV procedure solves the Poisson equation for pressure (van Oudheusden 2013),

$$\nabla^{2} p = - \rho \nabla \cdot \frac{D\varvec{u}}{Dt}, \quad \left. p \right|_{{\partial \varOmega_{1} }} = f\quad {\text{and}} \quad \left. {\frac{\partial p}{\partial n}} \right|_{{\partial \varOmega_{2} }} = g,$$
(1)

by approximating Du/Dt from time-resolved tomographic PIV measurements and with mixed boundary conditions f and g as detailed in Sect. 2.3.1. The present study also employs (1) for pressure evaluation, but approximates Du/Dt from a single snapshot. It should be remarked that for detailed assessment of alternative, established pressure-from-time-resolved-PIV techniques, the reader is referred to Charonko et al. (2010) and van Oudheusden (2013). In the present study, second-order central differences are used in the interior domain and first-order single-sided differences on the domain boundaries. The discretized gradient operator is denoted by ∇ h and the discretized Laplacian by ∇ 2 h . The subscript h is used to denote the discretized fields and operators. The computational grid is Cartesian and chosen equal to the PIV measurement grid. The discretized Poisson equation for pressure becomes,

$$\nabla_{h}^{2} p_{h} = - \rho \nabla_{h} \cdot \left. {\frac{D\varvec{u}}{Dt}} \right|_{h} ,\quad \left. {p_{h} } \right|_{{\partial \varOmega_{1} }} = f_{p}\, {\text{and}}\quad \left. {\frac{\partial p}{\partial n}} \right|_{{h,\partial \varOmega_{2} }} = g_{p} .$$
(2)

The Poisson equation for pressure is discretized using second-order central differences. Ghost points at the external side of the domain boundary are eliminated through the Neumann boundary condition (see e.g. Ebbers and Farnebäck 2009).

For the unsteady flow regime, time-resolved measurements are typically performed to provide Du/Dt|h in the conventional pressure determination approach. Here, it is proposed to approximate the velocity material derivative from a single tomographic PIV snapshot by a vortex-in-cell (VIC) simulation (Sect. 2.1).

2.1 Approximation of Du/Dt from single velocity snapshot

From a tomographic PIV velocity measurement u m (x ,t 0 ), vorticity is approximated on the measurement grid,

$$\varvec{\omega}_{h} = \nabla_{h} \times \varvec{u}_{m} .$$
(3)

Following the VIC procedure outlined in Schneiders et al. (2014), the divergence-free approximation of the measured velocity field is calculated by solution of,

$${\mathbf{\nabla }}_{h}^{2} \varvec{u}_{h} = - {\mathbf{\nabla }}_{h} \times\varvec{\omega}_{h} ,\quad \left. {\varvec{u}_{h} } \right|_{\partial \varOmega } = \varvec{u}_{m} .$$
(4)

Although imposing the divergence-free condition has been demonstrated as an effective tool for noise reduction of 3D data (e.g. by de Silva et al. 2013; Schiavazzi et al. 2014), in the present study, the divergence-free approximation is an inherent step of the procedure and is not meant for preconditioning or noise reduction of the measured velocity field. In the interior domain, typically \(\varvec{u}_{h} \ne \varvec{u}_{m}\), which is mostly ascribed to measurement errors. Recent studies have proposed to estimate the measurement error with the difference between a divergence-free flow field and u m (Atkinson et al. 2011; Lynch and Scarano 2014; Sciacchitano and Lynch 2015, amongst others).

The temporal derivative of vorticity can subsequently be calculated by a finite-difference discretization of the inviscid vorticity transport equation,

$$\left. {\frac{\partial \omega }{\partial t}} \right|_{h,Eul} = \left( {\varvec{\omega}_{h} \cdot {\mathbf{\nabla }}_{h} } \right)\varvec{u}_{h} - \left( {\varvec{u}_{h} \cdot {\mathbf{\nabla }}_{h} } \right)\varvec{\omega}_{h} .$$
(5)

The subscript Eul stands here for Eulerian, as later an alternative discretization (using VIC) will be introduced. Approximation of \(\partial\varvec{\omega}/\partial t\) using (5) allows for approximation of the temporal velocity derivative, \(\left. {\frac{\partial u}{\partial t}} \right|_{h}\), by solution of

$$\nabla_{h}^{2} \left. {\frac{{\partial \varvec{u}}}{\partial t}} \right|_{h} = - {\mathbf{\nabla }}_{h} \times \left. {\frac{{\partial\varvec{\omega}}}{\partial t}} \right|_{h} ,\quad \left. {\frac{{\partial \varvec{u}}}{\partial t}} \right|_{h} = f_{du} \,{\text{on}}\,\partial \varOmega ,$$
(6)

with Dirichlet boundary conditions f du as discussed in Sect. 2.3.2. The velocity material derivative is subsequently approximated by,

$$\left. {\frac{{D\varvec{u}}}{Dt}} \right|_{h}^{{{\text{single}} - {\text{snapshot}}}} = \left. {\frac{{\partial \varvec{u}}}{\partial t}} \right|_{h} + \left( {\varvec{u}_{h} \cdot {\mathbf{\nabla }}_{h} } \right)\varvec{u}_{h} .$$
(7)

It should be remarked that solution of (5) requires approximation of the gradient of vorticity. VIC avoids this by employing a vortex particle discretization, as discussed in Schneiders et al. (2014). The VIC time-supersampling procedure detailed in the latter paper yields, when applied to an instantaneous measurement, ω h ( x ,t 0  + Δt) directly from a single forward-time integration in the interior domain. Using single-sided finite differences, the temporal vorticity derivative is subsequently approximated,

$$\left. {\frac{{\partial\varvec{\omega}}}{\partial t}} \right|_{h,VIC} = \frac{{\varvec{\omega}_{h} \left( {\varvec{x},t_{0} + \Delta t} \right) -\varvec{\omega}_{h} \left( {\varvec{x},t_{0} } \right)}}{\Delta t}.$$
(8)

The integration time step is chosen on the order of the PIV pulse time separation; sufficiently small to avoid truncation errors, but large enough to avoid rounding errors. On the two grid points adjacent to each volume boundary, the VIC procedure requires boundary values (as discussed in detail in Schneiders et al. 2014), which are here taken from (5),

$$\left. {\frac{{\partial\varvec{\omega}}}{\partial t}} \right|_{h} = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}l} {\left. {\frac{{\partial\varvec{\omega}}}{\partial t}} \right|_{h,VIC} } & {2 < i < L, 2 < j < M, {\text{and}}\; 2 < k < N} \\ \end{array} } \\ {\begin{array}{*{20}l} {\left. {\frac{{\partial\varvec{\omega}}}{\partial t}} \right|_{h,Eul} } & {{\text{otherwise }}\varvec{ }} \\ \end{array} } \\ \end{array} } \right.$$
(9)

where i ∈ {1,…,L}, j ∈ {1,…,M} and k ∈ {1,…,N} are the grid points indices in the computational volume. When (9) is employed instead of (5) in the full domain, this improves the pressure computation, as reflected by the slight increase in correlation coefficient as witnessed in the experimental assessment (Sect. 4).

2.2 Range of application and limitations

The first limitation regards reconstruction of pressure in flow cases where the pressure associated with the potential field dominates pressure associated with the vorticity field. Consider the Helmholtz decomposition of velocity into curl free and divergence-free parts,

$$\varvec{u}^{p} = - \nabla \varPhi$$
(10a)
$$\varvec{u}^{\varvec{v}} = \nabla \times \varvec{A}$$
(10b)
$$\varvec{u } = \varvec{u}^{p} + \varvec{u}^{v} .$$
(10c)

With this decomposition, Eq. (4) can be rewritten into

$$\begin{aligned} \nabla^2(u^p+u^v) &=-\nabla\times\omega, \quad (u^p+u^v)|_{\partial\Omega} = u_m \\ &=-\nabla\times\left(\nabla\times u^p\right)_{= 0} - \nabla\times\left(\nabla\times u^v\right) \end{aligned}$$
(11)

Thus, the source term of the Poisson equation to reconstruct velocity only contains u v and therefore the potential field u p is reconstructed using information from the boundary points only. As there is typically a much smaller number of points on the boundary than in the interior, measurement errors on the domain boundaries are expected to affect u p more significantly than u v. In flow cases where u p dominates, sensitivity of the reconstructed potential field to the domain boundary conditions should be cautioned. The present manuscript, however, focusses on a flow case dominated by u v.

The second limitation follows from the fact that the proposed technique can only use the information available from a single velocity measurement to approximate the velocity temporal derivative and subsequently pressure. The limitations of the technique become apparent upon splitting of Eq. (6) into a non-homogeneous Poisson equation with homogeneous boundary conditions and a homogeneous Poisson equation with non-homogeneous boundary conditions,

$$\nabla^{2} \left. {\frac{\partial \varvec{u}}{\partial t}} \right|_{A} = - {\mathbf{\nabla }}_{h} \times \frac{\partial \varvec{\omega} }{\partial t}, \quad \left. {\frac{\partial \varvec{u}}{\partial t}} \right|_{A} = 0\,{\text{on}}\,\partial\Omega ,$$
(12a)
$$\nabla^{2} \left. {\frac{\partial \varvec{u}}{\partial t}} \right|_{B} = 0,\quad \left. {\frac{\partial \varvec{u}}{\partial t}} \right|_{B} = f_{du}\,{\text{on}}\,\partial\Omega ,$$
(12b)
$$\frac{\partial \varvec{u}}{\partial t} = \left. {\frac{\partial \varvec{u}}{\partial t}} \right|_{A} + \left. {\frac{\partial \varvec{u}}{\partial t}} \right|_{B} .$$
(12c)

Equation (12a) can be solved directly from the temporal vorticity derivative approximated by (5) from a single tomographic PIV velocity snapshot. However, Eq. (12b) cannot be readily solved in the absence of knowledge about the boundary conditions on the temporal velocity derivative, which is not measured by the PIV system. When boundary conditions on (12b) cannot be approximated, the pressure field can only be determined up to the pressure induced by the irrotational acceleration field following from Eq. (12b). To illustrate this, consider the extreme case where pressure is determined solely by this component. Take for example the flow in a cylinder, which is uniformly accelerated by a piston: a uniform pressure gradient is associated with the acceleration caused by the piston motion. As a result, the absolute value of the pressure cannot be determined unless, for this example, the piston path is known, or in general, when the fluid flow acceleration at the domain boundary can be estimated. For many relevant applications in the turbulent flow regime, the instantaneous value of ∂ u /∂t is dominated by the contribution from Eq. (12a). Such cases include turbulent boundary layers, flow over stationary airfoils, wakes and jets. In addition to the above considerations, in Sect. 2.3.2, three types of boundary conditions are proposed to approximate boundary conditions for Eq. (12b) for a wider variety of cases.

2.3 Treatment of boundary conditions

For the present problem, the treatment of boundary conditions (BC) needs to be considered at two stages in the procedure: first for the Poisson equation for pressure (2) and second for the solution of the Poisson equation for the velocity temporal derivative (6).

2.3.1 Pressure boundary conditions

Mixed BCs on pressure are generally employed in PIV-based pressure determination methods, with a Dirichlet BC f p on ∂Ω1 and Neumann BC g p on ∂Ω2. The Dirichlet boundary condition f p may be obtained from additional experimental data, using pressure probes or surface pressure transducers. Alternatively, a more practiced approach is including in the measurement domain regions where the flow is known to be irrotational and possibly steady. In that case, pressure–velocity models as simple as the Bernoulli equation or isentropic relations may be employed (see e.g. Kurtulus et al. 2007; Ragni et al. 2009; de Kat and van Oudheusden 2012). The use of such a model for pressure yields a Dirichlet BC f p along an extended region ∂Ω1 of one or more volume boundaries.

Neumann boundary conditions g p are provided by the momentum equation, which in discretized form becomes,

$$g_{p} = - \rho \frac{{{\text{D}}\varvec{u}}}{{{\text{D}}t}} + \mu {\mathbf{\nabla }}_{h}^{2} \varvec{u} \approx {\mathbf{\nabla }}p.$$
(13)

For pressure evaluation, the viscous terms are typically neglected (van Oudheusden, 2013). Ghaemi et al. (2012) have directly evaluated the viscous terms from a PIV measurement in a turbulent boundary layer and showed that in a turbulent boundary layer these terms are typically two orders of magnitude smaller than the other terms in the momentum equation. It may be remarked that the viscous terms are only neglected for the computation of the instantaneous pressure. The measured velocity field inherently incorporates the physical effects of viscosity.

2.3.2 Velocity acceleration boundary conditions

Boundary conditions for (6) are not measured by the single-snapshot PIV experiment or readily provided by the system of equations, in contrast to the Neumann type BC for pressure. When the measurement volume boundary involves a free stream or steady flow, ∂ u /∂t = 0 can be imposed there. Similarly, at a wall the no-slip BC also implies ∂ u /∂t = 0. However, where the volume boundaries involve unsteady flow regions, a model for the unsteady boundary conditions is required depending on the flow case under consideration, as discussed in detail in Sect. 2.2. These models approximate the temporal velocity derivative on the domain boundary to account for boundary effects. In the interior domain, the VIC model approximates the temporal velocity derivative by simulation of the vorticity captured in the measurement volume. Three types of approximations for Dirichlet boundary conditions will be considered in the present study; in the experimental assessment, the sensitivity of the solution to the different approximations is assessed.

  1. 1.

    Convection boundary conditions of the form,

    $$\frac{{\partial \varvec{u}}}{\partial t} = - \left( {\varvec{u}_{c} \cdot \nabla } \right)\varvec{u},$$
    (14)

    which are expected to be accurate when the assumption of “frozen turbulence” holds on the boundary region and small velocity fluctuations are convected by a larger mean convection u c velocity (Taylor’s hypothesis). The problem of determining the correct value of the convective velocity has been addressed over the past decades (e.g. Wills 1964; Krogstad et al. 1998; de Kat and Ganapathisubramani 2013). For conciseness, however, in the experimental assessment (Sect. 4), the local instantaneous flow velocity is used as an estimate for the convection velocity. It should be remarked that similar models have also been used for boundary conditions for pure numerical simulations (e.g. Orlanski 1976) and the model has recently been employed by Gronskis et al. (2013) in an effort to combine direct numerical simulation with PIV measurements.

  2. 2.

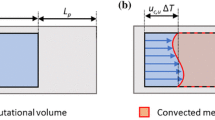
    Padding boundary conditions: when the vorticity outside of the measurement volume is small compared to the vorticity contained within the measurement volume, the measurement volume may be padded with an extension region of zero vorticity and a homogeneous boundary condition on the acceleration is prescribed on the enlarged domain, which allows the temporal velocity derivative on the measurement domain volume to become non-zero. This procedure is illustrated in more detail in Sect. 3 using a numerical example. It should be remarked that this boundary condition type is also used in pure numerical simulations using the vortex-in-cell technique (e.g. Cottet and Poncet 2003).

  3. 3.

    Homogeneous boundary conditions: when ∂ u /∂t ≈ 0 on the volume boundaries, the homogeneous boundary condition ∂ u /∂t = 0 is a trivial approximation. Additionally, this boundary condition is considered in the present investigation to assess sensitivity of the result when a homogeneous boundary condition is prescribed.

These three boundary condition types will all be considered in the experimental assessment (Sect. 4) using independent microphone measurement data to establish the sensitivity of the solution to a change in boundary conditions. In the next section, the use of the padding type of boundary condition will be illustrated for the numerical test case of an advecting Gaussian vortex.

3 Numerical illustration

Consider a two-dimensional Gaussian vortex being advected at a constant velocity u c and positioned in the centre of a simulated measurement domain at time t 0 (Fig. 1a). This case has been used previously for assessment of time-resolved PIV pressure evaluation procedures by amongst others de Kat and van Oudheusden (2012) and Lynch and Scarano (2014). The tangential velocity field induced by the Gaussian vortex blob is given by,

$$V_{\theta } = \frac{\Gamma }{2\pi r}\left( {1 - e^{{ - \frac{{r^{2} }}{{c_{\theta } }}}} } \right),$$
(15)

where Γ is the circulation and c θ  = r 2 c /γ. Choosing γ = 1.256, the tangential velocity peaks at the core radius r c . A positive uniform velocity u c is added to the velocity field. For this illustrative case, r c/L = 0.25 and u c L/Γ = 2, with L being the width of the square measurement domain. The analytical expression for the exact pressure field centred on the vortex core is given by

$$p = - \frac{1}{2}\rho V_{\theta }^{2} - \frac{{\rho\Gamma ^{2} }}{{4\pi^{2} c_{\theta } }}\left( {Ei\left( {\frac{{r^{2} }}{{c_{\theta } }}} \right) - Ei\left( {\frac{{2r^{2} }}{{c_{\theta } }}} \right)} \right),$$
(16)

with Ei(x) the exponential integral function. For reference, the exact ∂ u /∂t and pressure fields are plotted in, respectively, Fig. 2a, e. It should be remarked that the pressure fields given in this section are unique up to a constant and to allow for comparison to the exact pressure they are fixed to zero in the domain centre.

Fig. 1
figure 1

Vorticity field in the simulated measurement domain (a), exact temporal vorticity derivative (b) and the temporal derivative of vorticity calculated by VIC from the single velocity measurement (c)

Full size image
Fig. 2
figure 2

Temporal derivative of streamwise velocity (top) and pressure (bottom); a, e exact, b, f assuming ∂ u /∂t = 0, c, g single-snapshot VIC without boundary padding and d, h with boundary padding

Full size image

Consider now a simulated single-snapshot measurement of the exact instantaneous velocity field in a measurement domain equal to the region plotted in Fig. 1a (−2 < x/r c < 2, −2 < y/r c < 2). When pressure is calculated directly from this velocity field, neglecting the ∂ u /∂t term using the steady Poisson equation with Neumann boundary conditions, this leads to an unsatisfactory result as can be seen directly by comparison of Fig. 2e (exact pressure) and Fig. 2f (approximated pressure neglecting ∂ u /∂t).

The proposed single-snapshot method aims to improve upon this by approximating ∂ u /∂t. The temporal vorticity derivative estimated with the VIC method is given in Fig. 1c. The temporal derivative of vorticity is positive to the right of the vortex blob and negative to its left, according to the motion of the vortex blob to the right. The temporal velocity derivative is subsequently calculated by solution of Poisson Eq. (6). Figure 2a shows in this test case that ∂ u /∂t on the measurement domain boundary is non-zero. Prescribing ∂ u /∂t = 0 on the boundaries for solution of (6) forces, the temporal velocity derivative to zero near the domain boundaries (Fig. 2c). Nevertheless, an improved approximation of the exact pressure field is obtained in comparison with neglecting ∂ u /∂t entirely, as can be seen upon comparison of Fig. 2f, g.

To obtain a further improvement of the approximated pressure field, note that vorticity outside of the simulated measurement domain is practically zero (Fig. 1a). This can be exploited for solution of (6), by using padding type boundary conditions (Sect. 2.3.2). The approximated temporal derivative of vorticity calculated is padded with zeros around the domain, enlarging the computational domain (Fig. 3, left figure). The size of the padded region should account for the length scale of flow fluctuations and is in the present case chosen equal to the size of the vortex in the measurement domain (2r c). Hence, the domain is extended on all sides by 2r c. Prescribing the value of the temporal derivative to zero on the extended computational boundary for solution of (6) allows the temporal derivative to attain nonzero values in the actual measurement domain (Fig. 3, right figure). The results show that a more accurate approximation of the exact temporal derivative can be obtained with this approach (Fig. 2d). Also, the pressure field evaluated from a single velocity snapshot with VIC and boundary padding is reasonably accurate (Fig. 2h) and improves further upon the result without zero-padding (Fig. 2g).

Fig. 3
figure 3

Domain padding applied to the temporal vorticity derivative computed by VIC (left) and the corresponding ∂ u /∂t computed with homogeneous BC (right); the measurement domain is given by the dashed red line

Full size image

The padding boundary condition and the other two boundary conditions proposed in Sect. 2.3.2 are evaluated in a more realistic case in the next section, where the procedure is applied to a real tomographic PIV experiment in a turbulent boundary layer and validated against independent microphone pressure fluctuation measurements.

4 Experimental assessment

The experimental assessment employs the turbulent boundary layer tomographic PIV measurements of Pröbsting et al. (2013), where pressure-from-time-resolved PIV was compared to a surface-mounted pressure transducer. In the above study, the two independent measurements yielded a maximum cross-correlation coefficient of 0.6. This value repeats that obtained earlier by Ghaemi et al. (2012) under a more favourable measurement configuration. In the present validation of the single-snapshot method, the procedure follows the above studies, using the cross-correlation coefficient as a metric of measurement accuracy.

The experiment considers a turbulent boundary layer on a flat plate (Fig. 4) at a free stream velocity of 10 m/s, corresponding to a Reynolds number based on the local boundary layer thickness (δ = 9.4 mm) of Re δ  = 6240. The tomographic PIV measurements are performed at 10 kHz with four LaVision HighSpeedStar CMOS cameras equipped with Nikon Micro-Nikkor 105 mm prime lenses and a Quantronix Darwin Duo Nd:YLF laser. A multi-pass light amplification system is installed, following the indications of Ghaemi and Scarano (2010) to increase the illumination intensity. Knife edges are employed to obtain a top-hat intensity profile and avoid attenuation of laser intensity near volume boundaries. To obtain the vector field, the sequence of objects is analysed with a volume deformation iterative multigrid technique and boundary vectors are cropped to avoid loss-of-correlation effects. The surface pressure fluctuations are measured simultaneously with the PIV measurements at a single location within the measurement volume using a Sonion 8010T condenser microphone. Salient details of the experiment are given in Tables 1 and 2 and sketches of the setup are given in Fig. 5. For a more complete discussion, the reader is referred to Pröbsting et al. (2013). In the next section, first the benchmark time-resolved pressure evaluation procedure is outlined. Subsequently, in Sect. 4.2, results of the experimental assessment are discussed.

Fig. 4
figure 4

Photograph of the tomographic PIV experiment (figure reproduced from Pröbsting et al. 2013)

Full size image
Table 1 Measurement conditions
Full size table
Table 2 Tomographic PIV configuration
Full size table
Fig. 5
figure 5

Schematic of the tomographic PIV experiment (schematics not to scale); top view (left) and back view (right); the measurement volume is indicated by the black dashed line in details A and B

Full size image

4.1 Benchmark time-resolved pressure evaluation

The time-resolved pressure evaluation procedure is chosen equal to the procedure used originally by Pröbsting et al. (2013), allowing for direct comparison of the results. The latter paper employed the following stencil for approximation of the velocity material derivative,

$$\left. {\frac{{D\varvec{u}}}{Dt}} \right|_{{{\text{TR}} - {\text{PIV}}}} = \left( {{\varvec{\Delta}}\varvec{t}^{T} {\varvec{\Delta}}\varvec{t}} \right)^{ - 1} {\varvec{\Delta}}\varvec{t}^{T} {\varvec{\Delta}}\varvec{u},$$
(17)

where Δ t = [Δt −j ,…,Δt j ]T, with Δt j  = t j  − t 0 and similarly for Δ u, with Δu i  = u ( x p (t i ),t i ) − u ( x p (t 0 ),t 0 ), where,

$$\varvec{x}_{\varvec{p}} \left( {t_{ \pm j} } \right) = \pm \varvec{u}\left( {\varvec{x}_{\varvec{p}} \left( {t_{{ \pm \left( {j - 1} \right)}} } \right),t_{{ \pm \left( {j - 1} \right)}} } \right)\Delta t + \varvec{x}_{\varvec{p}} \left( {t_{{ \pm \left( {j - 1} \right)}} } \right),$$
(18)

and j = 1, …, M.

Pröbsting et al. (2013) found the M = 4 nine-snapshot stencil to be optimal for the present experimental dataset. The present manuscript does not aim to improve the time-resolved pressure evaluation procedure, but proposes a pressure evaluation procedure for non-time-resolved PIV measurements and therefore the case of M = 4 is taken as reference and benchmark result. In addition, a smaller three-snapshot stencil (M = 1) will be considered for comparison, which is illustrative for dual-PIV cases where only three to four consecutive measurements are available instead of nine. For a more extensive discussion on time-resolved PIV pressure evaluation methods, the reader is referred to van Oudheusden (2013) and references therein.

It should be remarked that due to the Lagrangian nature of the material derivative evaluation, the procedure does not yield values near the inflow and outflow boundaries as information from outside the measurement domain would be required in these regions. The extent of this region can be approximated by

$$L_{cr} \approx \frac{{u_{\infty } M}}{{\Delta x}},$$
(19)

and the measurement volume is cropped by this region, 12Δx, on both in- and outflow. In addition, a crop of 5Δx is applied on both sides in spanwise direction of 2Δy and 5Δy on, respectively, the bottom and top surfaces of the volume. The extent of the domain crop is sketched also in Fig. 6.

Fig. 6
figure 6

Overview of the measurement, cropped and padded volumes (schematic not to scale)

Full size image

For pressure evaluation in the cropped volume, mixed boundary conditions are employed for the Poisson equation for pressure. Neumann boundary conditions given by (13) are prescribed on all boundaries, except the top boundary (y/δ = 0.4), where Dirichlet conditions are prescribed based on an extended version of the Bernoulli equation, corrected for an unsteady convective perturbation as proposed by de Kat and van Oudheusden (2012),

$$p_{top}^{\prime} = - \frac{1}{2}\rho \left( {\varvec{u^{\prime}} \cdot \varvec{u^{\prime}}} \right) = f_{p} .$$
(20)

4.2 Results

First, the pressure-from-time-resolved PIV results are discussed to provide a benchmark for the proposed single-snapshot method (Sect. 4.2.1), after which the single-snapshot results (Sect. 4.2.2) are discussed.

4.2.1 Benchmark time-resolved results

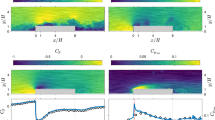
A single instantaneous pressure field in the plane parallel to the wall at y/δ = 0.2 evaluated using the time-resolved procedure with the three (M = 1) and nine (M = 4) snapshot stencil is plotted in, respectively, Fig. 7a, b. It is expected that the result with M = 1 is strongly affected by random errors in the velocity measurements, which can also be observed in Fig. 4a, b by comparison of the two results. In these figures, the free stream pressure level pref has been subtracted from the fields. For validation, the approximated pressure fluctuations at the microphone location are compared to the simultaneous instantaneous microphone surface pressure measurements (Fig. 8), where both the PIV and microphone results are band-pass-filtered for 300 Hz < f < 3 kHz (analogous to Pröbsting et al. 2013). For computation of the cross-correlation coefficients, the microphone signal is sub-sampled after application of the band-pass filter to match the sampling frequency of the time-resolved tomographic PIV measurement.

Fig. 7
figure 7

Comparison of the instantaneous pressure field at t = 2.5 ms and y/δ = 0.2, calculated from, a TR-PIV, M = 1, b TR-PIV, M = 4, c PIV, d PIV + VIC and ∂ u /∂t = 0, e–g PIV + VIC (∂ u /∂t ≠ 0) with BC type 1–3

Full size image
Fig. 8
figure 8

Pressure fluctuation time-series obtained from TR-PIV, single-snapshot PIV and single-snapshot PIV + VIC using type 3 boundary conditions, in comparison with the reference microphone measurements at x/δ = z/δ = 0 (grey line, increased thickness for clarity); all results have been band-pass-filtered between 0.3 and 3 kHz

Full size image

Comparison to the microphone surface pressure measurement in the centre of the measurement domain (Fig. 8, grey line) confirms low correlation to the reference microphone signal of the time-resolved pressure-from-PIV result using a small three-snapshot stencil (M = 1, blue line) and the peak value of the correlation coefficient is only R pp′ = 0.45 (Table 3). This result is significantly improved when the larger stencil of M = 4 is considered. Similarly to the results reported in Pröbsting et al. (2013), in the present study a correlation peak of R pp′,M4 = 0.65 is found with this stencil.

Table 3 Correlation coefficient peak values and RMS pressure fluctuation levels
Full size table

4.2.2 Single-snapshot pressure results

First, the single-snapshot pressure is calculated without the proposed procedure for approximation of ∂ u /∂t. The flow regime is incompressible (Ma = 0.03), and the velocity field and ∂ u /∂t are expected to be divergence free. Consequently, ∂ u /∂t drops out of the incompressible Poisson equation for pressure, and hence, it may be argued that it is not required for pressure evaluation. However, considering that (1) due to measurement errors velocity divergence is never exactly zero and (2) ∂ u /∂t is needed for Neumann boundary conditions for the Poisson equation for pressure, this is not expected to give acceptable results. To assess this, the approach of entirely neglecting ∂ u /∂t,

$$\left. {\frac{{{\rm D}\varvec{u}}}{{\rm D}t}} \right|_{\text{PIV}} = \left( {\varvec{u}_{m} \cdot \nabla_{h} } \right)\varvec{u}_{m} ,$$
(21)

is also included in the present study. This was attempted before by Imaichi and Ohmi (1983), who reported an increase in error levels and attributed these to neglecting the unsteady term. The present study also finds a low correlation coefficient peak of 0.46, a significant overestimation of the peak pressure levels (Fig. 7c) in case ∂ u /∂t is neglected, and pressure is calculated directly using the material derivative approximated using (21).

The proposed PIV + VIC single-snapshot procedure is expected to improve upon this. The first part of the procedure regularizes the velocity field u m through Eq. (4) to yield u h . The RMS difference between u m and the u h is 0.2 m/s at y/δ = 0.4, which is considered acceptable for a tomographic PIV experiment at a rather extreme measurement rate of 10 kHz. Still neglecting the unsteady term (i.e. setting ∂ u /∂t = 0), this regularized field can be employed to approximate the velocity material derivative,

$$\left. {\frac{{{\rm D}\varvec{u}}}{{\rm D}t}} \right|_{{{\text{VIC }}\partial {\text{u}}/{\text{d}}t = 0}} = \left( {\varvec{u}_{h} \cdot \nabla_{h} } \right)\varvec{u}_{h} .$$
(22)

Solving pressure with this approximation of the material derivative on the full measurement volume results in a significantly improved correlation coefficient of 0.6. This approaches the correlation coefficient obtained by the benchmark time-resolved PIV result (Table 3). The instantaneous pressure field depicted in Fig. 7d also shows significant improvement over Fig. 7c. However, the RMS level of the pressure fluctuations, p′RMS, is 31 % larger than the benchmark result.

In the second step of the proposed procedure, ∂ u /∂t is approximated using VIC to allow for approximation of the full velocity material derivative from (7). The velocity material derivative is evaluated on the full domain using the VIC procedure outlined in Sect. 2. Subsequently, as it is expected that the approximation of ∂ u /∂t is less accurate close to the volume boundaries, for pressure evaluation, the volume is cropped by the same amount as for the time-resolved procedure (Sect. 4.1). Three single-snapshot PIV + VIC cases are discussed, where for cases 1–3, respectively, boundary conditions 1–3 (Sect. 2.3.2) are employed for the Poisson equation for ∂ u /∂t (Eq. 6) on all volume boundaries except at the wall, where the no-slip condition (∂ u /∂t = 0) is prescribed.

The instantaneous pressure fields approximated using the single-snapshot PIV + VIC procedure with boundary condition types 1–3 are plotted in Fig. 7e–g, respectively. All three approaches yield similar results, indicating a low sensitivity of the VIC procedure to variations in the ∂u/∂t boundary condition approximation for the present flow case. In addition, minor improvement over the case where the unsteady term was neglected and u h was used to solve the steady Poisson equation is visible (e.g. at x/δ ≈ z/δ ≈ 0.5 in Fig. 7). The correlation coefficient is, however, not improved further and remains around 0.6, in comparison with 0.65 for the time-resolved benchmark result (Table 3). On the other hand, the inclusion of the approximation of ∂ u /∂t allows for prediction of the RMS pressure fluctuations, with 10 % difference with respect to the time-resolved result, whereas neglecting this term leads to 31 % higher RMS pressure fluctuations (Table 3, last column). For completeness, it should be recalled that in Sect. 2 it was anticipated that when \(\left. {\partial\varvec{\omega}/\partial t} \right|_{h,Eul}\) is employed instead of \(\left. {\partial\varvec{\omega}/\partial t} \right|_{h,VIC}\), a small reduction in quality of the pressure approximation is expected. This has been assessed for the present test case, and only a minor reduction in correlation coefficient was found, i.e. for case 3 boundary conditions, R pp’ becomes 0.60 instead of 0.61.

To assess the correlation of the results in the frequency domain, the magnitude of the coherence of the time-resolved and single-snapshot results is calculated with respect to the microphone signal using Welch’s overlapped segment averaging. The result is plotted in Fig. 9 (left figure) and shows that all results have the highest coherence at approximately 0.8–1 kHz and no coherence with the microphone signal for frequencies above 3 kHz, where it should be recalled that the results have been band-pass-filtered between 300 Hz and 3 kHz. The time-resolved result with M = 4 shows the expected significant improvement in coherence with respect to M = 1, with a peak of 0.77 around 900 Hz. Also, the single-snapshot result using VIC improves upon the M = 1 time-resolved result, showing similar coherence as the time-resolved result using the larger nine-snapshot stencil. The peak coherence around 800 Hz is approximately 10 % smaller than the benchmark M = 4 time-resolved result; however, at higher frequency the VIC result follows the trend of the benchmark result. For completeness, the phase lag is also compared in Fig. 9 (right figure), which shows similar results for all procedures.

Fig. 9
figure 9

Coherence (left) and phase of the cross spectrum (right) of the PIV results with the microphone measurements

Full size image

The higher correlation achieved by the single-snapshot procedure in comparison with the M = 1 time-resolved procedure is especially relevant for dual-PIV systems (Liu and Katz 2006; Lynch and Scarano 2014), where the limited number of exposures does not allow to regularize the results using a large time-stencil. However, considering that the present study focuses on single-snapshot pressure evaluation, no further speculation is made here that the time-resolved result with M = 1 may be improved when a larger time separation between the measurements is chosen to reduce the random error component, as discussed in studies by amongst others Jensen and Pedersen (2004) and Perret et al. (2006).

To assess the dependence of the method to measurement noise and spatial resolution, here an increase in measurement noise is simulated by adding normally distributed random errors to the velocity vectors and by sub-sampling the velocity fields. Subsequently, the pressure is evaluated as discussed above and the correlation coefficient of the pressure time-series with respect to the microphone measurements is calculated. It is expected that the established time-resolved pressure-from-PIV procedure is less sensitive to these error sources, as multiple PIV velocity snapshots are available for pressure evaluation. Recent literature has shown that the use of multiple snapshots from time-resolved analysis is an effective approach to reduce the effect of measurement errors (e.g. FTEE, Jeon et al. 2014; FTC, Lynch and Scarano 2013).

First, the effect of random noise is considered. Figure 10-left shows the resulting correlation coefficients with respect to the microphone measurements varying the standard deviations of the numerically simulated random errors. The time-resolved procedure is practically insensitive to the random errors, which results from the use of nine consecutive snapshots for pressure evaluation through the least-squares procedure that effectively cancels out the effect of random errors. For the single-snapshot procedure, a gradual reduction of correlation coefficient is observed by increasing the measurement noise. It should be remarked that type 3 boundary conditions have been used for the results plotted. For the other boundary condition types, the same behaviour is observed. A correlation coefficient of approximately 0.5 is retrieved when the error is increased towards 1 m/s, which corresponds to the order of the turbulent velocity fluctuations close to the microphone location.

Fig. 10
figure 10

Measurement sensitivity to measurement noise and spatial resolution. Cross-correlation coefficient with random errors (left) and grid point spacing (right)

Full size image

The effect of spatial resolution is considered by evaluating the velocity vectors from a coarser grid. Figure 4-right shows the cross-correlation coefficient when the grid point spacing is increased from hx0 in the original data to hx. Both the time-resolved and the single-snapshot methods are sensitive to the spatial resolution. The time-resolved approach still exhibits a plateau up to a fourfold decrease in resolution and a roll-off after that point. Instead, the single-snapshot technique appears to be more sensitive to the decrease in resolution: a small plateau is observed up to a twofold decrease in resolution and then a more rapid decrease is observed.

5 Conclusions

A method is proposed to approximate the instantaneous flow pressure field from a single instantaneous tomographic PIV velocity snapshot using the vortex-in-cell (VIC) technique and is applied to a flat-plate turbulent boundary layer. By solving the incompressible vorticity transport equation on the measurement volume, the spatial information available from the measurement is leveraged to approximate the temporal velocity derivative. Pressure is subsequently approximated by solution of the Poisson equation for pressure.

The experimental validation compared the correlation coefficient of instantaneous pressure obtained by both the single-snapshot procedure and a benchmark pressure-from-PIV procedure based on time-resolved data, with respect to simultaneous measurement with a surface pressure transducer. The results show that the instantaneous pressure field in a turbulent boundary layer can be evaluated from single-snapshot PIV, yielding very comparable results to those obtained with time-resolved measurement data acquired at 10 kHz and a stencil of nine consecutive measurements. When a smaller stencil of three consecutive measurements is employed for the time-resolved pressure evaluation, the single-snapshot VIC procedure even outperforms the time-resolved approach, giving a higher cross-correlation with the microphone signal.

The single-snapshot procedure requires a model for the flow acceleration to be used as boundary conditions on the flow governing equations and in the experimental assessment, three such models were assessed: convective, padding and homogeneous boundary conditions, which under the present conditions all yielded similar instantaneous pressure fields. The experimental assessment considered a solid profile along one domain boundary. If the tomographic PIV experiment experiences solid interfaces within the measurement volume, the Poisson solver needs to be adapted accordingly to handle such non-rectangular computational domains.

In the experimental validation, the method yields results corresponding well to those obtained by time-resolved PIV with a nine-snapshot stencil. The advantage of the proposed single-snapshot PIV + VIC procedure is that it does not rely on the acquisition of time-resolved velocity data. Use of the method should be cautioned when the contributions to fluctuating pressure from outside the measurement volume are significant. In the turbulent boundary layer considered here, the proposed method demonstrates that PIV camera and laser hardware requirements can be alleviated, which is relevant for the investigation of high-speed flows where pressure-from-time-resolved-PIV becomes prohibitive.