A study of droplet impact on static films using the BB-LIF technique

Abstract

This paper presents results of single droplet impacts on films of different heights taken using the brightness-based laser-induced fluorescence technique (BB-LIF). The dynamics of drop impingement such as the shape of the cavity and residual film thickness are investigated and analysed with a time resolution of 0.1 ms and spatial resolution of 70 μm. Additionally, a variation of the BB-LIF technique is used to investigate the change in profile of the droplet liquid during the inertial self-similar regime. The results of the analysis show that present models predicting initial development of the cavity show good agreement. Suggested amendments for some of the constants for cavity width and residual film thickness are proposed based on the film thickness that fit better with published data. The development of the profile of the droplet liquid demonstrates that for thin liquid films, the droplet liquid behaviour with strong similarity to droplet impacts on dry solid surfaces. It is noted that for some of the measured parameters, the use of the film height as the length scale gives a better fit.

Introduction

Droplet impingement on thin liquid films is a common phenomenon in nature as well as in industrial settings that has drawn the attention of researchers for more than a century. (Worthington 1877) was one of the first researchers to investigate impacts and studied the behaviour of impinging milk drops using an ingenious method of momentary electric sparks. Since that initial attempt, an extensive understanding has been achieved through experimentation and numerical modelling. This has accelerated through the development or cheaper high-speed camera (Thoroddsen et al. 2008).

Even though the works of Worthington were purely driven on intellectual interest, droplet impingement on films is of considerable importance to several industrial applications such as spray coating, 3D printing of mechanical parts, spray cooling, oil and gas transport in pipes and lubrication and heat management of jet engines. The influence of the impingement and subsequent dynamics on heat and mass transfer leads to technical and economic challenges demanding more insight into the matter as well as models that could be used in design and development of technologies with confidence. This work is motivated by the influence of droplet impact on heat and mass transfer in sheared two-phase flows in process industries and also in jet engines.

The experimental studies on droplet impingement on solid surfaces and liquid films extend to many areas; the main focus areas are (1) crater evolution, (2) formation of Worthington jet, (3) crown formation and splashing, (4) generation of secondary droplets. An extensive review of the work done on the above areas was provided by (Yarin 2006). The evolution of the above phenomena depends on the impact velocity, angle, droplet diameter and the film depth (Okawa et al. 2006; van Hinsberg et al. 2010). Extensive studies have shown that the droplet impact evolution is associated with a parameter K which is a function of Ohnesorge number and the Weber number relating the physical properties of the fluids and the droplet impact velocity (Cossali et al. 1997; Tropea and Marengo 1999; Okawa et al. 2006). This parameter is used in this work in analysing the impact evolutions and is defined in Table 1.

Table 1 Experimental properties

Based on the experimental data, several of the semi-empirical models have been developed to describe the post-impingement evolution of the film and the droplet in sprays. (Stanton and Rutland 1998) and (Mundo et al. 1997) have suggested empirical models to identify the evolution events such as coalescence, formation of Worthington jet, crown formation and splashing. More recently, a model has been suggested by (Bisighini et al. 2010) considering the impact of single and multiple droplets on deep and thick liquid layers.

Most of the studies to this date employ high-speed imaging techniques to achieve a series of time-resolved images showing the interaction between the droplet and the film (Thoroddsen et al. 2008). This method, even though very effective in capturing the crater and crown evolutions, has difficulty identifying droplet spreading on liquid films due to optical limitations. Techniques such as Fourier transform profilometry (Lagubeau et al. 2012) can measure the droplet spread during impacts ion dry surfaces, but have significantly lower resolution. The CHR sensor used by (van Hinsberg et al. 2010) has a lower spatial resolution and significantly higher uncertainty level. In this work, an attempt has been made to address this issue by tracking the droplet and the film dynamics visually using brightness-based laser-induced fluorescence technique. The technique has been successfully used for measuring the evolution and characteristics of disturbance waves in sheared flow (Cherdantsev et al. 2014) and has been used to measure height information in liquid films over large areas with spatial resolutions of up to 0.04 mm at temporal resolutions up to rates up to 10 kHz. The high spatial and temporal quality of the technique makes it ideal to make measurements in this application as will be explained in the next section.

Experimental procedure and methods

The experimental apparatus consists of a syringe with a flat-tipped hypodermic needle mounted on a sliding arm of a vertical stand placed above a transparent acrylic Petri dish. The syringe was filled with distilled water and operated with a pneumatic driver at a constant rate to produce repeatable droplets of 3.5 mm diameter. Analyses of the images show that the variation in the droplet size was negligible. The height of the syringe was varied between 100 and 500 mm above the impact plane to generate a range of velocities (1.4–3.1 m/s) at the point of impact. Properties of the liquid used and the range of Weber and Reynolds numbers used in the experiments reported in this work are shown in Table 1. All the experiments were carried out at room temperature around 20 °C. The depth of the film was varied (h* = h/D = 0.43, 0.86 and 1.29, where h/D is the film height to drop diameter ratio) to match similar measurements being taken for moving films for comparison.

The BB-LIF technique was used to measure the depth of the liquid over the area of the Petri dish and a second high-speed camera with lower resolution was synchronized to image the droplet impact from the side. This allowed us to confirm the stability of the droplet size and velocity and identify the time of contact of the droplet to the surface with an accuracy of ±50 μs. Five syringe heights were used to set to achieve different impact velocities. For each syringe height, five droplets were tested to generate statistics on the reliability of the measurements.

BB-LIF technique

The BB-LIF technique uses the absorption of the laser light (de Beers law) by a selected dye and measures the intensity of the light re-emitted. The intensity of light re-emitted is a function of the local dye concentration and the height of the film Eq. (1). Once the absorption rate of the dye at that concentration (α), the dark level of the camera D(x, y), the intensity distribution of the light over the image C(x, y), and the reflection coefficient of the water–air interface (k _refl ) are known, the height of the film at each pixel can be specifically determined (Alekseenko et al. 2008; Cherdantsev et al. 2014). The calibration of the measurement is done by comparing the images against a known depth of the dye. This calibration removes spatial variations of the light level which is included in the derivation of the C(x, y) matrix.

$$\frac{{J\left( {x,y} \right) - D\left( {x,y} \right)}}{{C\left( {x,y} \right)}} = \left[ {1 - e^{{ - \alpha .h\left( {x,y} \right)}} } \right].\left[ {1 + k_{refl} .e^{{ - \alpha .h\left( {x,y} \right)}} } \right]$$

(1)

The method to carry out BB-LIF involves doping the distilled water with a known quantity of Rhodamine 6G (about 8–15 mg/l depending on depth range desired) and illuminating the Petri dish through the base using a pulsed Nd-Yag laser (527 nm). The light is absorbed by the dye in the liquid and re-emitted at longer wavelength which passes through a filter to remove the original wavelength and is recorded on the camera also located below the Petri dish as shown in Fig. 1. According to (Koichiro et al. 2001), the introduction of Rhodamine dye has a negligible effect on the fluid properties and should have no significant effect on the results shown. At the noted concentration, the vertical resolution of the technique is related to the levels of thermal noise, which corresponds to about ±30 μm.

Fig. 1

Schematic diagram showing configuration of experiment and BB-LIF

The major disadvantage with this technique is that it assumes a reflection coefficient (k _refl ) of 0.02. In cases where the slope of the surface is large, such as could happen in the crown, this coefficient can increase to total internal reflection, which gives an over-prediction of the depth at that location. These values are easy to identify because they are an order of magnitude greater and can be filtered out. In certain cases, there can also be local focussing of the laser light which will also produce an over-prediction of the film thickness.

In this case, a 1280 × 496 pixel area was measured with a resolution of 70 microns/pixel at 10 kHz frequency to measure the height of the film and the droplet during the impact and the film interaction with the droplet.

It is possible with this technique to investigate separately the motion of the liquid in the film, or the motion of the liquid in the droplet separately for short periods immediately after the impact. This can be done by doping only the film liquid or the droplet liquid. For each of the droplet impact parameters studied, three cases were taken;

• Case 1: Both droplet and film were doped with the fluorescent dye.

• Case 2: Only the film was doped.

• Case 3: Only the droplet was doped.

Captured images for these cases can be analysed to obtain a number of features (Fig. 2) such as the cavity width W, cavity depth of the system z _C1, cavity depth of the film liquid only z _C2, minimum film thickness beneath the cavity h _res and droplet height as it deforms during the impact z _C3.

Fig. 2

Definition of the measurement variables

Results

In the literature, droplet impact has been split into a number of broad areas. For impact onto liquid films, it has been suggested that the initial crater evolution is dependent on the droplet momentum in the initial stages (Berberović et al. 2009) and that the correct normalisation of the film depth, crater depth, crater width and time with respect to the droplet diameter D is:

$$h^{*} = \frac{H}{D};\quad \Delta_{x} = \frac{{z_{x} }}{D};\quad \varOmega = \frac{W}{D};\quad \tau = \frac{tU}{D}$$

(2)

where z _x is the appropriate depth scale for each of the three cases and the other variables are defined in Fig. 2. The dynamics of the drop impact are also dependent on the properties of the droplet impact. Cossali et al. (1997) and Okawa et al. (2006) have used an impact parameter K = We OH ^−0.4 that can be used to predict the impact outcome. It was noted by (Alghoul et al. 2011) that there was a change in behaviour of the droplet impact around h* = 1. Below this value there was crown formation and crown break-up. Above this value there was jet formation.

Droplet impact onto a solid surface has many similarities with droplet impact onto a thin film. Lagubeau et al. (2012) and Roisman et al. (2008) have shown that the impact can be broken into several regimes. Initially there is a pressure dominated regime, when the droplet compresses under the influence of the impact, and this pressure leads to inertial motion in the radial direction (Lagubeau et al. 2012). Once this motion is present, the inertia dominates the flow over viscosity and so it is possible to derive a remote asymptotic solution for the thickness using the inviscid approximation (Yarin and Weiss 1995).

$$\Delta = \frac{\eta }{{\left( {\tau + \tau_{g} } \right)^{2} }}$$

(3)

(Lagubeau et al. 2012) and (Roisman et al. 2009) have shown that for droplet impact on dry surfaces, the profile of the droplet at time τ is given by:

$$\Delta = \frac{{{\text{Z}}_{\text{c3}} }}{D} = \frac{\eta }{{(\tau + \tau_{g} )^{2} }}\exp \left[ { - \left( {\frac{{6\eta r^{*2} }}{{(\tau + \tau_{g} )^{2} }}} \right)} \right]$$

(4)

where η is dependent on the film height and τ _g is the inverse of the initial gradient of the radial velocity. In their case, they determined constants of τ _g  = 0.25 and η = 0.39 for impact onto solid surfaces.

The results will be analysed using this methodology and nomenclature.

Evolution of the cavity

It is important to understand how the droplet liquid and film liquid interact, so the three cases were set up as explained earlier so that crown and droplet content could be determined.

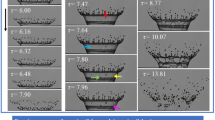
This can be seen in Figs. 3 and 4 for two cases with the same Weber and Reynolds number of impact, but different film heights. In Fig. 3, 5 time instances are highlighted for the three cases under study. It should be noted that each case was a separate experiment, so there is a slight variation in the droplet outcome, shape and location of secondary droplets; however, the general behaviour is consistent between the cases, so comparison can be made.

Fig. 3

A comparison of the three cases under study at 5 time periods of the impact. h* = 0.43, We = 378, Re = 9800. Colours represent depth normalized by droplet diameter

Fig. 4

A comparison of the three cases under study at 5 time periods of the impact. h* = 1.29, We = 378, Re = 9800. Colours represent depth normalized by droplet diameter

The main points highlighted by the selected stages of droplet impact and interaction of the liquid core are:

• Prompt splash: small droplets can be seen in Fig. 3a, f, k showing that the splash contains liquid from both the film and the droplet. Droplet fluid is spread over the surface of the crater and runs up the sides.

• Crown formation: Fig. 3b, g, l shows that the crown also contains liquid from the droplet and the initiation of secondary droplet formation can be seen.

• Crown ligaments formed: as shown in Fig. 3c, h, m, both film and droplet liquid are entrained into the secondary droplets generated from the crown break-up.

• Secondary droplet impact: as shown in Fig. 3d, i, n, secondary droplets produce craters on surface of film after impact and liquid from film and droplet are draining back towards the centre of the crater.

• Jet formation: as shown in Fig. 3e, j, o, jet is formed of film and droplet liquid.

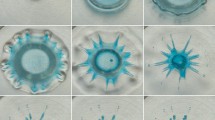
For the deeper film h* = 1.29, Fig. 4 shows that many of the same features are also visible. In this case, there is no droplet creation at the crown.

Itemizations of the stages of impact are as follows:

• Prompt splash: as shown in Fig. 4a, f, k, streaks (possibly ligaments) are seen around the point of impact containing film and droplet liquid.

• Crown formation: as shown in Fig. 4b, g, l, crown is formed, but in this case, the crown is sloped inwards. Droplet liquid spreads over surface of crater and up walls, but not as far as the surface and so is not collected in crown. Droplet liquid from prompt splash collects outside the crown.

• Crown receding: as shown in Fig. 4c, h, m, crown begins to recede. No secondary droplets are produced in this case.

• Fluid draining: as shown in Fig. 4d, i, n, droplet liquid and film liquid drain towards the centre of the crater to initiate the formation of the Worthington jet.

• Jet formation: as shown in Fig. 4e, j, o, surrounded by ripple wave that propagates out from the impact, most of the droplet fluid has collected in the jet.

When all the cases and droplet impacts were considered, it was noted that in all the cases with crown breaking, the droplet liquid was present in the secondary droplets. It also appeared as if the droplet remained largely coherent as it expanded up the side of the cavity, before receding to become present in the jet. This is truer in the deeper film experiments, where the droplet liquid often ends up as at the top of the jet or even as the topmost droplet during jet break-up. This has been observed elsewhere, but little comment has been made of this.

This has implications to heat transfer and regime limits that will be discussed later in this paper.

Development of the width of the cavity

The droplet impacts and the resulting structures are almost axially symmetrical, so another method of understanding the temporal behaviour of the droplet impact is to take profiles through the centre point of impact and present them as x–t diagrams such as those shown in Fig. 5 which shows the development of the cavity width and depth for h* = 0.43 as the droplet Weber number on the impact is increased. The three cases can be used to see clearly the locations of the droplet and film liquid. Features such as the width of the crater, time to crater collapse, capillary waves and location of droplet fluid can all be identified from these x–t diagrams, and some of these quantities will be studied in later sections.

Fig. 5

x–t diagrams showing the development of the centreline profile of the three cases and each of the five Weber numbers of impact. The predicted width of the cavity is shown as a dashed white line. This shows the results for h* = 0.86. Colours represent depth in dimensionless units normalized by droplet diameter

In the initial stages of impact, the width of the impact crater is shown to be a function of the time (Roisman et al. 2008)

$$\varOmega = \sqrt {\beta \left( {\tau - \tau_{0} } \right) - f\left( {\tau - \tau_{o} } \right)}$$

(5)

where

$$f(\tau - \tau_{0} ) = \left( {\frac{{2h^{*} }}{{Re_{crmax} We}} + \frac{4}{We} + \frac{{h^{*2} }}{Fr}} \right)(\tau - \tau_{0} )^{2} /h^{*}$$

(6)

and

$$R_{crmax} = \frac{\beta }{2}\sqrt {\frac{{h^{*} }}{G}} - \frac{{h^{*} }}{GWe},G = \frac{4}{We} + \frac{{h^{*2} }}{Fr}$$

(7)

It was theorized from their results that both β and τ ₀ are dependent on the film height, and β is independent on the Weber number.

$$\tau_{0} = 0.8h^{*(1.7)} ,\quad \beta = 0.62h^{*0.33}$$

Comparison was made between the values of βh*^0.33 published in (van Hinsberg 2010) for a range of liquids and the results of the cavity width fit for the distilled water in these results, and it was noted that both showed a dependence on the Weber number (Fig. 6) to provide a new relationship for β

Fig. 6

Weber number dependence of the fitting parameter from all three heights in this study compared to results published in (van Hinsberg 2010)

$$\beta = \left( {\frac{23.3}{We} + 0.5} \right)h^{* - 0.33}$$

This suggests that the value of β is in fact dependent on the Weber number. Looking again at Eqs. 5–7, it can be observed that there are numerous terms where the Weber number and Froude number are combined with the h ^* term. For example in Eq. 7, there is a term

$$\frac{G}{{h^{*} }} = \frac{4}{{We h^{*} }} + \frac{{h^{*} }}{Fr} = \frac{4}{{We_{H} }} + \frac{1}{{Fr_{H} }}$$

(8)

The same substitutions can be made for other terms in Eqs. 5 and 6. This suggests that β could be related to the Weber number and Froude number based on the height of the film rather than on droplet diameter.

To test this, β was plotted against We_H = ρU ² H/σ, where U is the velocity of the droplet at the impact and H is the height of the film. When this is shown (Fig. 7) for both our data and the data from (van Hinsberg 2010), it clearly shows that the data have a similar behaviour. In this case, a relationship with $\beta = 3.1 \;We_{H}^{ - 0.37} + 0.19$ is fitted to the data using linear regression. This still shows a h ^* relationship close to that of Fig. 6. The behaviour of this relationship is consistent with a simplistic understanding of the problem. β is related to the rate of expansion of the cavity. As the cavity depth increases, the height of fluid that needs to be pushed out of the way increases, so the β decreases with increasing height. When the depth of the film becomes significantly larger than the depth of the cavity, then the mass of fluid that needs to be displaced tends to a constant. Thus, the rate of the expansion of the cavity tends to a constant value.

Fig. 7

Comparison of this and Van Hinsberg data using the Weber number based on height

The implications of this are that the droplet diameter might not be the correct length scale to use for generation of dimensionless parameters in all cases.

The new relationship derived in Fig. 7 is demonstrated by generating theoretical curves of cavity, and comparison is made with the x–t diagrams in Fig. 5. These are shown to fit well with these data and with all other data in the set.

Evolution of the cavity depth for Case 1

It has been established that it is usual to normalize the depth by the droplet diameter and the time by the velocity and the diameter of the droplet for crater depth, and this is demonstrated in Fig. 8. This shows the height of the centre of the impact in Case 1 for all five droplet Reynolds and Weber numbers at all three film depths. The graphs show clearly the self-similar behaviour in the initial stages of the droplet impact. The height at the point of impact decreases linearly with τ until τ ≈ 1.5 as the top of the droplet liquid continues at its initial velocity. The base of the droplet material, however, is moving more slowly, and this results in an increase in pressure inside the droplet that forces the droplet material sideways. As the pressure in the liquid below the impact increases, the rate of cavity depth growth decreases. For a thinner film, the presence of the base wall acts to amplify the pressure below the cavity, which decelerates the increase in cavity depth. It was attempted to plot these parameters against film height, and they did not fit as well, so this suggests that the droplet diameter is the correct length scale in this case. For the length of time shown, only at the lowest Weber number impact has the base of the cavity started to rise as expected. It can also be noted that there is a local focusing effect due to internal reflection inside the droplet. This contributes to the variation of the depth value in the initial stages, but does not obscure the overall trend.

Fig. 8

Evolution of the depth of the centrepoint of the cavity for Case 1. The technique tracks the top surface of the droplet/film liquid. Colours correspond to different impact conditions. The different depths of impact are shown as different symbols. h* = 0.43, ‘+’, h* = 0.86, ‘o’, h* = 1.29, ‘Δ’

Evolution of the film only (Case 2)

One of the advantages of the BB-LIF technique is that the motion of the film and droplet liquid can be separated and the dynamics of the film liquid only can be analysed. Figure 9 shows the evolution of the film height only at the centre of the impact. This shows the response of the film to the impact without the influence of the droplet. While the top of the droplet is initially continuing at the speed of impact, the base of the droplet and the top of the film are moving at roughly 44 % of the droplet impact velocity as theorized by the work of (Berberović et al. 2009; Bisighini et al. 2010). This means that since the top of the droplet is moving at the initial droplet velocity until τ = 1.5 (Fig. 8), there is a pressure build-up in the droplet fluid that forces the droplet to expand sideways.

Fig. 9

Evolution of the depth of the centre point of the cavity for Case 2. The technique tracks the top surface of the film liquid only. Colours correspond to different impact conditions. The different depths of impact are shown as different symbols. h* = 0.43, ‘+’, h* = 0.86, ‘o’, h* = 1.29, ‘Δ’

Again, it was attempted to normalize this by film height, but again in this case, it was determined that the droplet diameter is the correct length scale for this problem.

In this case, there is again a local focusing effect in the initial stages. As the droplet collapses, it reflects additional laser light back to the region giving an over-prediction in the early times. This effect is negligible in the self-similar region for τ > 1.5.

Minimum depth of the film beneath the crater

It has been theorized that the minimum thickness of a film formed by a droplet impact is a function of the Reynolds number. (van Hinsberg et al. 2010) compared experimental and computational results to show that the minimum height is proportional to

$$h^{*} \sim ARe^{{ - \frac{2}{5}}}$$

It is shown in Fig. 10 that for the two thinnest films, this relationship holds well, with the constant of proportionality A being related to the height of the film. In the case of the deepest film however (two blue points in Fig. 10 that do not correlate to expected behaviour), the influence of viscous dissipation is negligible, so this defined relationship is not valid for low Reynolds numbers. Instead, the depth of penetration of the cavity and hence the residual film thickness is a complex function of the Weber, Reynolds and Froude number (Bisighini et al. 2010) except at the highest impact velocity when the cavity appears to be again affected by the wall. (van Hinsberg et al. 2010) looked in more detail at the dependence of the constant A for different liquids and suggested that it was dependent on the film height according to

Fig. 10

Investigation of the minimum film height h _res for the three different depths studied. Dashed lines show estimation of Re ^−0.4 dependance. Dotted line is best fit for deepest film thickness

$$A = 0.098h^{* - 0.404} + 0.79$$

However, it can be again suggested that if h* and Re have the same power, they might be combined in some way to produce a Reynolds number based on the height of the film. If the data from this study and the data from (van Hinsberg 2010) are plotted using h ^H = h _res /H and Re _H  = UH/ν, as shown in Fig. 11, we can see that for both cases, the data collapses onto single relationships except for points where the cavity has not penetrated far enough to interact with the wall.

Fig. 11

This shows that there is disagreement in the results showing the dependence of A, the constant of proportionality used to determine the minimum film thickness h _res , from (van Hinsberg 2010) and the results presented here. Error bars for our data are not clearly visible

However, the two curves do not coincide. The Van Hinsberg data use different liquids, so it cannot be because of liquid properties. The two main differences in the experiments were that they used droplet sized of the order of 2.1 mm compared to the droplet sizes of 3.5 in this work, and that they used a hydrophobic glass wall while this work used an acrylic wall. Acrylic has a surface roughness of twice that of glass, but it is unlikely that this is the issue, since the flow is laminar, so it is most likely either that the constant of proportionality is a function of the droplet diameter as well as the film height, or that the hydrophobic coating in the Van Hinsberg case has affected the friction loss at the wall. Further work will have to be completed to verify which of these was the correct reason for the discrepancy.

Evolution of the droplet liquid

The third case under study involved the doping of the droplet fluid only so that the thickness of the droplet liquid as it interacts with the film and the mixing generated can be quantified. Figure 12 shows that in the initial stages of the impact, the droplet liquid spread out and formed a rim around the edge of the crater. As discussed earlier in Eq. 4, spreading of the droplet liquid has many similarities to that of droplet spreading on dry surfaces.

Fig. 12

A sequence of profiles through the droplet liquid only (Case 3) showing the spreading of the droplet liquid. Dashed lines are a modified theory of the droplet profile based on predictions of droplet impact on dry surfaces. This also shows that the side peaks that relate to the droplet liquid that is spread up the cavity wall, rises to a height comparable with the cavity depth

Considering Fig. 12, it appears that the centre portion of the profile of the droplet in the inertial self-similar region is also a Gaussian profile similar to that of droplet impact onto a dry surface. The major difference is that the lamella away from the central portion is forced up the side of the cavity, and this can be seen by the apparent increase in thickness at the edge (the peaks on either side of the central peak). The side peaks therefore show the location of the sides of the cavity. To test the similarity of the centre portion further, a curve fitting was done using Eq. (4), using η and τ _g as fitting variables. It was evident that curves could be fitted with a single value of τ _g  = − 0.1905, and that the different thicknesses $h^{*} = 0.43, 0.86\;{\text{and}}\;1.29$ had to have values of $\eta = 0.39, 0.78\;{\text{and}}\;1.13$, respectively, which corresponds to $\eta = 0.9 h^{*}$.

The fit in the self-similar inertial region of the impact is quite good. The high thicknesses at the edge of spreading correspond to the location of the crater sidewall, and it is expected that the liquid from the droplet has spread up the walls, and this correlates with the earlier observation that for h* < 1, Fig. 3 demonstrates that some of the droplet liquid has reached the height of the crown and has been entrained in the crown. When the film is deeper, the droplet liquid does not contribute to the crown. This correlates with observations by (Alghoul et al. 2011) that crown formation happens at lower film thicknesses and that at higher film thicknesses the major outcome is jetting behaviour until the impact parameters are large enough, then a crown can form.

The physical interpretation of the variation in the value of η is that the droplet compression upon impact is less at higher film thicknesses. At deeper films, the effect of the base is less important, and so the droplet remains spherical for longer upon impact and penetrates deeper into the film before the pressure builds up enough inside the droplet for the fluid to be forced sideways.

From the series of measurements, it is possible to determine the minimum thickness of the droplet liquid during the entire impact. Using the same arguments as in the previous section, the measured droplet thickness should be a function of the Reynolds number of the flow. Figure 13 shows this using droplet diameter and film height as variables. It is clear in Fig. 13a that there is a film height dependence to the fit. Figure 13b shows that presenting these data with respect to film height generates a single curve. It can be noted that the minimum drop thickness decreases with increasing film height. In fact, if the curve is extrapolated, the minimum droplet thickness reaches zero at Re _H  ∼ 20,000. In (Watanabe et al. 2008; Hsiao et al. 1988), it is shown that at thicker films, the droplet and cavity react to produce vortex rings. There is no liquid at the centre of the ring, which means that the minimum thickness is zero as predicted by this extrapolation. This could be a consequence of the droplet liquid spreading over a steeper cavity therefore overturning to produce the vortex ring.

Fig. 13

This figure shows the minimum droplet thickness measured over each run. In a it is compared using droplet size as length scale. In b it is compared using film height as length scale

Discussion of results

The coherence of the droplet within the cavity has important ramifications for heat transfer. The drop spreads over the surface and then contracts with minimal mixing at low impact velocity and deep film. This suggests that conduction is the dominant mixing mechanism since the level of mixing between the droplet liquid and film liquid is small (even though they are the same liquid), and so convection will be small. At higher impact velocity, the droplet liquid is mixed due to being broken off the crown to form secondary droplets. For thicker films, the cavity deepens and the droplet liquid needs to have more energy to be able to reach the crown of the impact. This correlates with the result that thicker films need a higher velocity of impact to generate crown breaking. This could help explain the height of film dependence noted by (Cossali et al. 1997; Tropea and Marengo 1999). It is interesting that it is only the cases where the droplet liquid expands to the cavity width that show crown breaking in our results. The cavity width contains a $We_{D} \sqrt {We_{H}^{ - 0.4} }$ term, and the droplet expansion retains a Re ^−0.4 _H term. The transition to crown breaking is predicted to be related to $= We_{D} \left( {\frac{{\sqrt {We_{D} } }}{{Re_{D} }}} \right)^{ - 0.4}$. Combining the relationships above gives a possibility that the transition is actually related to $K = We_{D} \left( {\frac{{\sqrt {We_{H} } }}{{Re_{H} }}} \right)^{ - 0.4}$, although the cavity width is complicated and contains a Froude number term in addition. Further work at different droplet diameters and using different liquids should be completed to confirm or deny this suspicion.

Conclusions

The present study has used the new BB-LIF technique to investigate the physical mechanisms that occur during the impact of droplets onto films of varying height. It is shown that technique can separate out the motions of the liquid in the film and the droplet, and this can aid in the understanding of the relevant processes.

The comparison of the presence of the droplet liquid with the presence of the film liquid in the secondary droplets has determined that for h* < 1, the droplet liquid will rise to the level of the crown, and at values of K > 2100, the droplet liquid will be present in the secondary droplets generated by the crown break-up. At higher h*, the droplet liquid will remain contained in the crater formed by the impact and will drain back to form the tip of the Worthington jet.

An example of the x–t diagrams of the droplet profile has confirmed the theoretical width relationship proposed by (Roisman et al. 2008) holds, but a modified relationship for the dependence of the fitting parameter to the Weber number based on the film height is proposed and shown to be a better fit for our data as well as the data presented by (van Hinsberg 2010).

The minimum thickness of the film below the cavity is shown to be related by $h_{res}^{*} = ARe^{{ - \frac{2}{5}}}$ as suggested in (Bakshi et al. 2007). However, it is shown that using the film height as a length scale might also fit better. It is suggested that there might still be a droplet size component to the data fit, and this will need to be investigated further. The profile of the droplet liquid in the inertial self-similar regime is shown to have strong similarities to profiles measured for droplet impact onto solid surfaces with two fitting parameters η and τ _g . It is shown that the shape parameter η is almost linearly dependent on the film height in this range, but must change to become a constant as the film thickness increases. The value of the initial gradient of radial velocity τ _g has reversed in sign, possibly because the contact angle between the water drop and water film is reversed compared to the contact angle between water drop and solid surface.