Fourier transform profilometry for water waves: how to achieve clean water attenuation with diffusive reflection at the water surface?

Abstract

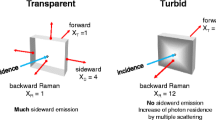
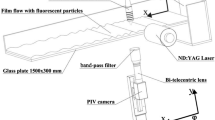
We present a study of the damping of capillary-gravity waves in water containing pigments. The practical interest comes from a recent profilometry technique (FTP for Fourier Transform Profilometry) using fringe projection onto the liquid-free surface. This experimental technique requires diffusive reflection of light on the liquid surface, which is usually achieved by adding white pigments. It is shown that the use of most paint pigments causes a large enhancement of the damping of the waves. Indeed, these paints contain surfactants which are easily adsorbed at the air–water interface. The resulting surface film changes the attenuation properties because of the resonance-type damping between capillary-gravity waves and Marangoni waves. We study the physicochemical properties of coloring pigments, showing that particles of the anatase (TiO₂) pigment make the water surface light diffusive while avoiding any surface film effects. The use of the chosen particles allows to perform space-time resolved FTP measurements on capillary-gravity waves, in a liquid with the damping properties of pure water.

Appendix

Let us consider the propagation of a plane wave in x positive direction (coordinate z being normal to the surface at rest) in an incompressible fluid with density ρ and dynamical viscosity μ. Neglecting the nonlinear terms, the Navier–Stokes equations for the velocity field $\mathbf{u}=[u_{x},u_{z}]$ read:

$$ \begin{aligned} \rho\frac{\partial u_{x}}{\partial t}&=-\frac{\partial p}{\partial x}+\mu\Updelta u_{x} \\ \rho\frac{\partial u_{z}}{\partial t}&=-\frac{\partial p}{\partial z}+\rho g+\mu\Updelta u_{z} \end{aligned} $$

(8)

where g denotes the gravity acceleration, and p is the pressure.

Considering the existence of the surface tension gradients, the kinematic boundary conditions on the surface (tangential and normal components, respectively) can be expressed as:

$$ \begin{aligned} &\frac{\partial\gamma}{\partial x}-{\mathbf{T}}_{xz}=0\\ &\gamma\frac{\partial^{2}\zeta}{\partial x^{2}}+p-p_{a}-\rho g\zeta-{\mathbf{T}}_{zz}=0 \end{aligned} $$

(9)

where $\zeta$ denotes the surface elevation, p _a is the atmospheric pressure, and $\mathbf{T}$ the stress tensor. It has to be noted that the only difference in the whole mathematical formulation compared to the clean surface case is the nonzero tangential component of the stress tensor (due to the Marangoni effect of surface tension gradients). This gradient can be expressed as:

$$ \frac{\partial\gamma}{\partial x}=\varepsilon\frac{\partial^{2}\xi}{\partial x^{2}} $$

Here, ξ is the horizontal displacement of the surface, and $\varepsilon$ denotes the surface-dilational modulus, which characterizes the viscoelastic fluid properties and is a complex number in general. The whole quantity is given by:

$$ \varepsilon=\left|\varepsilon\right|\exp(-{\hbox{i}}\theta) $$

A phase difference between the imposed area change and the surface tension variations, caused by a relaxation processes such as diffusion exchange, is expressed by the θ number.

Introducing the velocity field $\mathbf{u}$ as a sum of the velocity potential $\Upphi$ (providing an irrotational field) and the vorticity function $\Uppsi$ (providing a divergence-free field) and assuming zero velocity at infinite depth, we can obtain the harmonic wave solutions to the linearized Navier–Stokes equations (8).

Substituting these solutions into boundary conditions (9), it can be shown that the system has two solutions at each frequency. One solution corresponds to the classical capillary-gravity water wave and the other to the Marangoni wave. Lucassen (1968) showed experimentally that the wavelength of the capillary-gravity wave does not depend on the surface viscoelastic properties (is almost independent of $\varepsilon$), while the imaginary part of their wavenumber (damping coefficient) is strongly dependent on $\varepsilon$.

A simple way to obtain the dispersion relation of the Marangoni wave is to take the tangential component of the force balance at the surface assuming a horizontal Stokes boundary layer in the fluid:

$$ \varepsilon\frac{\partial^{2}\xi}{\partial x^{2}} \simeq \mu \frac{\partial u_x}{\partial z} $$

Then, the derivative ∂ _z u _x is equal to m u _x (with the exponential decrement of the Stokes boundary layer $m=\sqrt{{\hbox{i}} \omega \rho/\mu}$). Eventually, the continuity of horizontal velocity between the film surface and the fluid, u _x  = iωξ, is used to obtain

$$ \varepsilon\frac{\partial^{2}\xi}{\partial x^{2}} = i \mu \omega m \xi $$

that yields the dispersion relation for the Marangoni wave, given by Eq. 6.

This Marangoni wave is strongly damped. Assuming purely elastic film ($\varepsilon$ is a real quantity) and denoting $\mathbf{k}_{M}=\kappa_{M} + {\hbox{i}}\beta_{M}$:

$$ \begin{aligned} \kappa_{M}&= \cos(\pi/8) \left(\frac{\rho\mu}{\varepsilon^2}\right)^{1/4}\omega_{M}^{3/4}\\ \beta_{M}&=\tan(\pi/8) \kappa_{M} \approx0.414\kappa_{M} \end{aligned} $$

(10)

The real and imaginary part are of the same order of magnitude—the longitudinal waves are damped out very rapidly!

The capillary-gravity waves and surface waves are in general not oscillating with the same frequency and wavelength. However, the character of the dispersion relations allows to intersect the frequency-wavelength branches (Fig. 10). When the frequencies and wavelengths of the capillary-gravity wave and Marangoni wave are equal, the particle motion coincides for both waves, giving rise to a high velocity gradients in a Stokes boundary layer just beneath the surface film. This explains why the strongest enhancement of damping of capillary-gravity wave is found to be around the transverse-longitudinal resonance values.