1 Introduction

Liquid films are found in many technical applications, like falling film evaporators and packing columns (Helbig 2007). The film thickness δ and thus the characteristic velocity distribution within the film significantly determine the heat and mass transfer in many process engineering tasks. As a result of the hydrodynamic instability of the film flow and depending on the surface tension of the fluid, waves form on the fluid surface. Small high-frequency waves occur in the inlet region, which converge and collide downstream (Adomeit and Renz 2000; Ausner 2006; Brauner and Maron 1982; Kohrt 2012). As a result, the characteristic parameters, such as the wave frequency \({f}_{\mathrm{w}}\) and the average film thickness \({\delta }_{\mathrm{avg}}\), decrease on the way downstream until a state of equilibrium is reached (Takahama and Kato 1980). Thus, the wave formation and the resulting dynamics of the liquid film exhibit a pronounced dependence on the run length. In addition, the formation of waves and the attainment of the equilibrium state are significantly influenced by the inclination angle of the wetted surface, the flow rate and the material properties.

In the inlet area, the flow velocity, as well as the film thickness, agree very well with the theoretical solution according to Nusselt (Nusselt 1916; Takamasa and Kobayashi 2000). Unfortunately, the effect of run-length and inclination on the formation of the characteristic velocity distribution within the film is still unclear. It is known that with increasing distance to the inlet, the deviation from the theoretical solutions increases. Additionally, it is known that at high inclination angles and low flow rates, the steady-state wave characteristics are reached after a shorter run length (Brauner and Maron 1982; Brauner and Maron 1983).

Measurements of the surface velocity of thin vertically falling liquid films have been performed by Ishigai et al. (1972). Thin aluminum plates (0.04 mm2) floated on top of the film flow. The surface velocity was investigated via the distance traveled between the photos. It was shown that the surface velocities of wavy films are about twice as large as those according to Nusselt.

Alekseenko (1985) used the integral relations method to derive a nonlinear two-wave equation for long waves on the surface of vertically falling excited liquid films on tube walls. The method was confirmed with experimental measurements of instantaneous velocity profiles at Reynolds numbers of 5–50. For this purpose, a combination of the shadow method to measure film thickness and the stroboscopic particle method to measure velocities was used.

Mudawar and Houpt (1993) investigated the role of large waves in the transport of mass and momentum in vertically falling fluid films on a pipe outer wall. They simultaneously investigated the time-varying film thickness with a film thickness probe and the flow velocity with laser doppler velocimetry (LDV) at a measuring position of 1842.5 mm for Reynolds numbers from 209 to 414. It has been shown that about 40–70% of the flow is transported by large waves and that they behave like clumps of fluid sliding over a continuous substrate, while the substrate remains relatively unaffected.

Miyara (1999) numerically investigated the fluid dynamics and heat transfer of falling fluid films on a vertical plate. The velocity profiles of the different positions in the wave were compared with those of a laminar flow. The velocities at the wave crest and in the wave trough are very different from a laminar film flow, while the profiles at the wave rear and in the substrate region are very similar to a laminar flow. It was also determined that the time-averaged velocity profile in the region of the minimum film thickness, corresponds to that of the Nusselt theory.

Adomeit und Renz (2000) investigated laminar wavy film flows in the Reynolds number range from 27 to 200. Measurements of the velocity distribution are made by particle image velocimetry and film thickness measurements by fluorescence methods. The measurement plane is perpendicular to the tube wall and parallel to the tube axis. ZrSiO4 particles with an average diameter of 1.8 µm are used as tracer particles. The data of the velocity measurements differ greatly from those according to Nusselt. In the apex of the large waves, the flow velocities, with the same Nusselt film thickness \({\delta }_{\mathrm{Nu}}\), show values about 25–40% lower than the Nusselt solution. However, as in Ishigai et al. (1972) the surface velocity is more than twice that of the Nusselt solution. Waves already occur at small Reynolds numbers. As a result, the film flow can be divided into a layer close to the wall, the so-called base film, and the wave layer close to the surface. Investigations by Adomeit und Renz (2000) and Miyara (1999) could show that the Nusselt profile of the velocity distribution is only valid for the base film and deviates strongly from it in the wave layer. Therefore, this type of flow is called pseudolaminar.

Al-Sibai (2004) investigated characteristic parameters such as wave velocity and fluid flow velocities on an inclined flat Plexiglas plate. The wave velocity was determined using a cross-correlation of two film thickness measurements. From the determined time of the cross-correlation and the constant distance between the gauges (\(\mathrm{\Delta x}=2.9\mathrm{mm}\)), the wave velocities can be calculated. It was found that due to the different wave heights, the wave speed has a range dependent on the Reynolds number. In addition, particle image velocimetry measurements were made perpendicular to the film, through the sidewall, at Reynolds numbers from 1.4 to 60. A highly viscous fluid was chosen to avoid waves, since the flow velocity within the waves cannot be measured sufficiently well by the measurement technique. The flow velocities in the film, which is as free of waves as possible, agree very well with the theoretical Nusselt profile.

In his work, Lel et al. (2005) presented two different methods for measuring the thickness of wavy films. The first is a new non-intrusive technique called chromatic confocal imaging method. The accuracy of this technique depends on the optical components, the local gradient of the film thickness, and the accuracy of the refractive index used. Lel et al. (2004) showed that showed that the average film thickness data thus obtained agreed well with earlier experimental measurements. The second technique for simultaneous measurement of film thickness and wave speed is based on a fluorescence intensity technique. Here, film thickness and wave speed measurements of silicone films with different viscosities were studied for Reynolds numbers from 2 to 700 and different tilt angles. The experimental data are in good agreement with results from published experimental and theoretical studies. The minimum measurable film thickness with the confocal chromatic sensor in this work was in the range of 200 microns. It was shown that for most film flows the amplitude of the waves is small compared to the wavelength and the measurement error due to film curvature is only about 3 µm.

Ausner (2006) investigated the surface velocity of liquid films on a 60° inclined flat plate to identify influences of the feed type. An overflow weir and a feed pipe with multiple holes have been investigated as feed types. The water and water toloul flow are inoculated with ceramic isospheres SG-300B, which float on the surface of the film flow. In order to identify the surface velocities, the images of the particle images (50 particles or waves) are manually evaluated and compared. It could be shown that the velocities, when fed with the feeder tube, are greater than the Nusselt solution, while those of the overflow weir are lower. For example, the surface velocity according to Nusselt for Re = 190 is exactly between those of the two feed types.

Dietze et al. (2009) were able to show numerically and experimentally that for excited waves at Reynolds numbers of 8.6–15, flow separation occurs in the capillary wave region of falling liquid films within a tube. For this purpose, the methods of LDV and particle image velocimetry (PIV) were used to detect velocities in the capillary wave range. A confocal chromatic sensor was used to make simultaneous layer thickness measurements to correlate the velocity data with the wave dynamics. Using PIV, the existence of a separation vortex in the capillary wave region was shown. Due to the time-varying refraction effects of waves, a PIV measurement through the fluctuating phase interface is associated with measurement inaccuracies. Paschke (2011) developed an adapted µPIV measurement technique with a correction unit to reduce these inaccuracies in order to measure directly through the gas-liquid phase interface. As part of the work, Paschke validates this with the conventional µPIV technique through a transparent wall. For this purpose, measurements are performed with water-glycerol mixtures, on an inclined (45° and 60°) flat plate, at Reynolds numbers of 2–256. For the µPIV images, fluorescent particles were used, which are excited with the laser. In combination with a cut-off filter, only the fluorescence wavelength (\({\lambda }_{\mathrm{Particle}}>{\lambda }_{\mathrm{Laser}})\) passes the filter. This has the advantage that the particles are clearly displayed without background illumination. The measurements show good agreement between the new and the conventional measurement methodology as well as the theoretical solution according to Nusselt. After successful validation, measurements were performed on structured plates, as well as tetrahedral structures.

In their work, Charogiannis et al. (2015) investigate the hydrodynamic parameters of harmonically excited film flows on a flat soda-lime glass plate, which was tilted by 20°. A simultaneous measurement technique based on planar laser-induced fluorescence imaging (PLIF) and particle image/tracking velocimetry (PIV/PTV) is used for the investigation. A total of four water-glycerol mixtures with different Kapitza numbers Ka, as well as a Reynolds number range from 2.3 to 320 are investigated. Frequencies from 1 to 10 Hz are imposed on the film flow. Based on these data, velocity profiles of 20 sites along the wave topology are extracted and compared with analytically derived ones based on local film thickness measurements and the Nusselt solution. It is found that increasing the ripple by modulating the drive frequency leads to lower absolute deviations between experiments and theoretical predictions upstream of the crests and higher deviations downstream of the crests. At the crests, experimentally determined interfacial velocities are overestimated by almost 100%.

For high-resolution velocity measurement of thin liquid film flows on an inclined smooth glass plate, a combination of confocal chromatic distance measurement and µPIV is presented in this work. This combination makes it possible to obtain velocity data directly for defined positions in the flow, instead of having to match them using temporal film thickness data. The focus is on the determination of velocities in the wave crest, of naturally evolving film flows. The flow is not captured laterally, as is usually the case, but is scanned stepwise from below through the transparent plate across the film thickness and extended by wave triggering. This means that the flow profiles are not acquired instantaneously but averaged over several selected waves.

2 Experimental setup

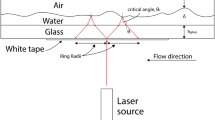
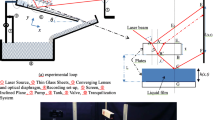
The film flow passes through a 1500 mm long and 300 mm wide glass channel. Hence, boundary effects can be minimized. The channel can be oriented at any angle \(\varphi\). The fluid is pumped by a centrifugal pump to the overflow weir. Depending on the impeller sensor, the volume flow can be adjusted via a mass flow controller in the ranges 0–100 l/h and 60–1800 l/h. Excess volume flow is returned to the collector-tank via a bypass valve. To compensate the pump-heat, a water-cooling system is integrated downstream of the mass flow controller. This consists of several Peltier elements and two temperature sensors in the overflow weir, which keep the fluid at a constant temperature of \(22\pm 0.2\) °C via an aluminum heat sink. The fluid slowly rises in the overflow weir until it flows purely gravitationally, initially as a smooth film along the channel, and is collected again in the collection tank, creating a closed circuit. To record the particles, the PIV camera (ILA.PIV.Nano) is located below the glass channel to avoid time-varying refraction effects at the gas-liquid phase interface. The camera has a 2/3" sensor with a resolution of 1392 × 1040 pixels with a pixel size of 6.45 × 6.45 µm. A bi-telecentric lens (SILL TZM 2533/3.0) with a magnification of 3 is used. This results in a maximum object size of 2.9 mm x2.2 mm. The scaling factor required for PIV evaluation is 467px/mm and was determined using a microscope-object-micrometer, with a scale of 1/100 mm. The camera and thus the position of the focal plane is moved by the motorized linear unit LTM 60–150-HSM from OWIS, which travels plane by plane. A 10 Hz ND:YAG double-pulse laser (Evergreen from Quantel) with a wavelength of \({\lambda }_{\mathrm{Laser}}=532\mathrm{nm}\) is used. The laser light is formed into a thin slice of light with a cylindrical lens but still illuminates the complete film. The film flow is seeded with fluorescent polystyrene particles with an average diameter of 4.99 µm at a density of 1050 kg/m3. Excitation of the laser light causes the particles to emit fluorescent radiation (\({\uplambda }_{\mathrm{Particle}}=607\mathrm{nm}\)), which, unlike laser light, can pass the bandpass filter (575 nm × 50 nm, optical density 4.0 50 nm from Edmund optics) because of the Stokes shift. The confocal chromatic sensor IFS2405-3, from micro-epsilon, is positioned above the channel, directly above the camera, and records the film thickness over time \(\delta (t)\). In combination with the controller IFC2421, measuring rates of up to 6.5 kHz are possible with the sensor. Due to the reduced measuring range at 6.5 kHz, a measuring rate of 1.5–4 kHz is used depending on the film thickness. The measuring range is three millimeters with a resolution of 15 nm (Fig. 1).

Fig. 1
figure 1

Schematic representation of the experimental setup for the investigation of thin film flows on inclined smooth planes. The fluid flows from the overflow weir into the glass channel purely gravitationally driven and forms waves which develop on the way downstream

Full size image

The following parameters have been varied: the inclination angle \(\mathrm{\varphi }\) (horizontal, 5°,10°, 15°), the measuring position (150, 300 and 500 mm), as well as the Reynolds number Re (30–200) at variation of the volume flow rate \(\dot{(\mathrm{V})}\). The fluid used is demineralized water with the following properties. The fluid used is demineralized water (Table 1).

Table 1 Material properties of demineralized water at 22 °C. The density and dynamic viscosity are taken from the VDI-Wärmeatlas (2013)
Full size table

3 µParticle image velocimetry

µParticle Image Velocimetry is used to measure the flow profiles of naturally wavy film flows. The focal plane is not defined by the laser light section, but by the position of the depth of field. To achieve the smallest possible depth of field, the aperture is set to F1.6 at maximum. This results in a depth of field of approx. 18.87 µm. The depth of correlation DOC was estimated using the equation of Olsen and Adrian (2000) and is 57 µm. Note, due to image pre-processing that eliminates blurry low-gray-value patterns, the depth of correlation is in fact slightly smaller. The refractive index of the fluid is accounted for when shifting the planes. A camera step size of 30-50 µm is chosen to scan the complete film resulting in up to 20 measurement planes (in case of a wave, i.e., Fig. 4). Smaller step sizes up to 1 µm are possible, but not necessary because of the depth of correlation. 450 double-exposed images respectively waves are captured per measuring plane. The camera is then shifted so that the next film plane is recorded.

Due to the shallow depth of field, very few particles are present in the images. As in the work by Paschke (2011), an image addition of the double images is performed to increase the particle density in the images. Figure 2 shows the ratio of white to black pixels as well as the number of particles per pixel as a function of the film plane of an approximately 1 mm high film flow.

Fig. 2
figure 2

Example of particles per pixel and the ratio of white to black pixels as a function of film thickness. Illustration of the influence of image addition to increase the particle density. The symbols show the corresponding curves with no addition ●, a fixed addition number of 5 ♦ and 15 ▲ images, and variable addition ■ for each layer

Full size image

Here, the particles are normally distributed within the film flow. Most of the particles are located in the middle part of the film flow, while the number of particles decreases significantly in the lower and upper part. By adding the particle images, the particles in the images increase significantly, but they are still normally distributed. In order to obtain the same number of particles in each layer as possible, a variable addition is performed. Depending on the layer, different numbers of images (for A and B each) are added, since there are enough particles in middle film layers and an overlapping of these should be avoided. To determine the addition number, the ratio of white to black pixels of the added images of each layer is determined. If this value is still too low, additional images are added until the specified ratio or a maximum number of added images is reached. The threshold was chosen to ensure that a sufficient number of particles occur in each interrogation window. The small number of particles can be significantly increased in Fig. 3 by adding 5–40 images allowing smaller interrogation windows to be selected.

Fig. 3
figure 3

Single particle image (left) with low particle image density and a particle image (right) with increased particle image density after image addition. Addition ensures a more even distribution of particles and ensures that there are always particles in the interrogation windows

Full size image

After the addition of the images for each plane, the evaluation of them is performed. For data analysis and image processing the software PIVview2C and PIVscheduler from ILA_5150 GmbH is used. The size of the interrogation area is 128 × 128, 256 × 256 or 512 × 512 pixels with an overlap of 50% depending on the final particle density. In addition, blurred particles that do not originate from the focal plane are eliminated in the PIV software by using a median filter. Due to the flow, without, e.g., the occurrence of vortices and in combination of the large interrogation windows, no spurious vectors occur.

Figure 4 represents the vector fields for each plane in the left figure. An averaged velocity for each plane is calculated from the individual vectors in the left figure and this is plotted over the film thickness as shown in the right figure. Here, the error bars of the axis of the flow velocity represent the standard deviation σ of all velocities of a plane and the axis of the plate distance represents the deviation of the focal plane due to the depth of field. According to the wall adhesion, the velocity should be 0 mm/s for y = 0. When compared with the approximated velocity profile, it is noticeable that for y = 0 the velocity is greater than 0 mm/s. This is due to the fact that fewer particles are present in lower film levels. As can be seen in Fig. 2, fewer particles are located at lower and higher levels of the film flow. Due to the depth of field, more particles are detected in higher film planes, which have higher velocities and thus the average velocity is slightly increased. In addition, reflections of particles may occur when measuring near the glass surface. These reflections also have higher velocities than particles near the wall would have.

Fig. 4
figure 4

Vector fields for each plane of the film flow with 128 × 128 query windows (left) and calculated flow profile from the mean values of the individual vector fields (right) for Re = 140 at x = 500 mm and a tilt angle of 10°

Full size image

Wave triggering is intended to allow the detection of the flow profile at any points in the wave. Here the focus is on the wave crest. The maximum and minimum limit values can be defined in the software of the confocal chromatic sensor, which also makes it possible to examine the wave front or the back of the wave. Simultaneously to the µPIV images, the local film thickness \(\delta (t)\) is recorded (1.5–4 kHz) using a confocal chromatic sensor. The choice of the measuring rate results from the Reynolds number and the wave amplitude. The factor F is used because not every wave reaches the maximum film thickness and varies between 0.1–0.125 depending on the parameter combination. When an upper limit value UL (wave crest) is reached:

$$\mathrm{UL}={\delta }_{\mathrm{max}}-F\cdot a$$
(1)

a 5 V TTL signal is generated by the control unit of the confocal chromatic sensor and sent to the synchronizer of the PIV system. UL is calculated using the maximum film thickness \({\delta }_{\mathrm{max}}\) as well as the wave amplitude a \({(\delta }_{\mathrm{max}}-{\delta }_{\mathrm{min}})\). The values are determined directly before the PIV measurements, by three measurements per 60 s with the confocal chromatic sensor. In addition, the average film thickness \({\delta }_{\mathrm{avg}}\) and the wave frequency \({f}_{\mathrm{w}}\) are also calculated from the measured film thickness over time. The difficulty of triggering is to have the wave specifically in the image section, otherwise no particles can be detected at higher film thicknesses. This can be counteracted by setting the focus level to the height of the wave crest at the beginning of the PIV measurements and checking whether particles are in the camera window or not.

4 Results

The decisive influencing factors in the investigations were the angle of inclination of the channel, as well as the Reynolds number, which can be determined according to equation:

$$\mathrm{Re}=\frac{\dot{V}}{{\nu }_{f}\cdot B}$$
(2)

This was set at constant kinematic viscosity \({\nu }_{f}\) and channel width B by varying the volume flow. Figure 5 exemplarily shows the phase-averaged velocity profile just within the wave for case φ = 10° and Re = 50. I.e. this velocity distribution was measured in the wave region. The velocity profile still exhibits a similar shape as the theoretical Nusselt profile. In this case, the Nusselt profile is also plotted to illustrate the theoretical velocity distribution in the temporal average.

Fig. 5
figure 5

Example of a velocity profile with wave triggering compared to the Nusselt velocity profile for Re = 50 at an angle of inclination of 10° and x = 300 mm

Full size image

Note, the Nusselt equations only apply exactly to waveless liquid films. However, it is widely used for the wavy part as well. As can be seen in Fig. 5 the waves lead to a fast transport of fluid in the upper part of the film (about 1.25 times faster than the maximum velocity in the mean case). However, in the lower part the velocity profiles are almost identical. This is a hint that the film can be divided into a base film part (< \({\delta }_{\mathrm{min}}\)) and a wave-part. In the base film, the flow can be assumed to be almost laminar. Furthermore, the theoretical and measured velocities in the base film are almost identical and differ strongly from each other in the wave range, which again confirms the results of Adomeit and Renz (2000) as well as Miyara (1999). Shortly before reaching the minimum film thickness (start of the wave part), the velocity profiles start to deviate from each other. This may be the influence of the wave layer sliding on the base film. To illustrate the size of the waves, the film thicknesses and wave amplitude for different Reynolds numbers, for a measurement position at 500 mm and an angle of 15° are shown in Fig. 6. On the right, three selected film thickness curves are shown for a better estimation of the existing local wave characteristics.

Fig. 6
figure 6

Minimum, average and maximum film thicknesses and wave amplitudes as a function of Reynolds number (left) at a measuring position of 500 mm and an inclination angle of 15°. Additionally, a selection of temporal film thickness profiles (right) for Reynolds numbers 30, 100 and 200 in descending order

Full size image

Here it is noticeable that the minimum film thickness \({\updelta }_{\mathrm{min}}\) is almost constant at about 0.2 mm. Accurate positioning of the confocal chromatic sensor is essential, otherwise a trigger signal may be released even though there is no wave directly above the camera. This leads to incorrect measurements. The minimum wave amplitude over all tests, occurs at a low inclination angle of 5° and a short distance to the inlet (x = 150 mm) and is 0.01 mm. No wave triggering is necessary here, since the film is smooth. On the other hand, at 15° and a Reynolds number of 160, the largest wave amplitude of about 0.88 mm occurs at the measuring position of 500 mm. Depending on the angle, measuring position and Reynolds number, wave triggering may or may not be necessary. Contrary to expectations, larger Reynolds numbers have a longer waveless range, which means that wave triggering is not always necessary for small measuring positions (x = 150–300 mm) and large Re. The distance \({\mathrm{x}}^{*}\) to the beginning of the wave formation can be estimated as follows:

$$x^{*} \approx 500 \cdot \delta_{{{\text{avg}}}} , {\text{for}}\;{\text{Re}} < 500$$
(3)

according to Brauner and Maron (1982). Due to the fact that the wave formation starts later with larger Reynolds numbers, smaller Re can have a larger maximum film thickness at the same measuring position, since this is significantly influenced by the waves. This results in a decrease of the wave amplitude in Fig. 6 from Re = 160. Figure 7 shows the dimensionless flow profiles at a distance of 150 mm from the inlet and an inclination angle of 5° for all investigated Reynolds numbers. In addition, the theoretical Nusselt velocity profile is also shown normalized as a red dashed line. This is calculated as follows:

Fig. 7
figure 7

Dimensionless representation of the µPIV flow profiles at 150 mm and φ = 5° compared to the dimensionless solution according to Nusselt

Full size image
$$w\left(z\right)= \frac{g\cdot \mathrm{sin}\varphi \cdot \rho \cdot {\delta }_{\mathrm{Nu}}^{2}}{2\cdot \eta }\cdot \left[\frac{2\cdot z}{{\delta }_{\mathrm{Nu}}} - {\left(\frac{z}{{\delta }_{\mathrm{Nu}}}\right)}^{2}\right]$$
(4)

This is largely determined by the inclination angle φ, the density \(\rho\) of the fluid, the theoretical Nusselt film thickness \({\delta }_{\mathrm{Nu}}\), and the dynamic viscosity \(\eta\). The average flow velocity \({\mathrm{w}}_{\mathrm{Nu}}\) can be calculated as follows:

$${w}_{\mathrm{Nu}}=\sqrt[3]{\frac{g\cdot \mathrm{sin}\varphi \cdot {\nu }_{f}}{3}}\cdot {\mathrm{Re}}^\frac{2}{3}$$
(5)

The Nusselt film thickness \({\delta }_{\mathrm{Nu}}\) also depends on the angle φ, the kinematic viscosity \({\nu }_{f}\) and the Reynolds number Re:

$${\delta }_{\mathrm{Nu}}=\sqrt[3]{\frac{3\cdot {\nu }_{f}^{2}}{g\cdot \mathrm{sin}\varphi } \cdot \mathrm{Re}}$$
(6)

Due to the inclination angle of φ = 5°, at this measuring position x < x* is for all cases. This leads to a larger scatter around the dimensionless Nusselt profile. In addition, it is possible that inlet effects at the overflow weir, at measuring positions close to the inlet, be also an issue for the strong scattering of the data. Interestingly, for smaller Reynolds numbers the velocity profiles exhibits a bulgier shape, whereas higher Reynolds numbers show a straighter curve above the theoretical solution. For larger angles (10°, 15°), at the measurement position of 300 mm x > x* for most cases. Compared to Fig. 7, the measured data are closer to the theoretical solution according to Nusselt.

At a measuring position of x = 500 mm, the film flow has already developed more strongly. Due to the effect of gravitation and wave formation, higher flow velocities occur compared to the measuring position of x = 150 mm. The scatter of the data is also significantly lower as can be seen in Fig. 8. Compared to the tilt angles 10° and 15°, the scatter of the data is also smaller. This could be due to larger wave amplitudes and a wider wave spectrum at angles 10–15°.

Fig. 8
figure 8

Dimensionless representation of the µPIV flow profiles at 500 mm and φ = 5° compared to the dimensionless solution according to Nusselt. Additionally, a selection of temporal film thickness profiles (right) for Reynolds numbers 30, 100 and 200 in descending order

Full size image

4.1 Influence of the angle of inclination

Figure 9 shows three velocity profiles at different angles. The Reynolds number and measuring position are identical. According to equations Eqs. (4) and (6), the velocity of the film flow increases with increasing inclination angle, but the film thickness decreases according to Nusselt. However, these equations do not consider the occurrence of waves.

Fig. 9
figure 9

Comparison of the velocity profiles (left) at different tilt angles for Re = 50 at the measuring position x = 500 mm. In addition, the corresponding time profiles (right) of the film thickness for 5°, 10° and 15°

Full size image

Despite the different angles, the maximum film thicknesses of the individual profiles are almost the same. Although the average film thicknesses are smaller with increasing angles, the maximum film thickness is defined by the appearance of waves on the film. The flow velocity increases with increasing angles as expected. Measuring position 300 mm: When the tilt angle increases from 5° to 10°, the average velocity increases by about 45% and the maximum velocity by about 43%, averaged over Re = 30–200. Here, the differences are larger for the small Reynolds numbers (≈60%) than for the larger Re (≈33%). This is due to less developed waves at larger Reynold numbers and low measurement positions. When the tilt angle increases from 5° to 15°, the average speed increases by about 87% and the maximum speed by about 77%. Here, the differences in the mean velocity at Re = 30–80 (≈110%), are about twice as large as at Re = 160–200. The same applies to the maximum velocity. At a distance of 500 mm from the inlet, the velocity differences for the larger Reynolds numbers approach (< 15%) those of the smaller ones. This increase is due to the fact that the waves have a greater distance to travel before reaching the measuring position and can develop more.

4.2 Influence of the measuring position

Due to the wave development, the measurement position has a strong influence on, for example, the wave frequency and flow velocity. As an example, Fig. 10 shows the film thickness curves over time at three measuring positions.

Fig. 10
figure 10

Extract of the local film thickness measurements with the confocal sensor at the measuring positions 115 mm, 300 mm and 600 mm to show the wave development as a function of the distance to the inlet for Re = 40 and φ = 15°

Full size image

At first, small sinusoidal surface waves are formed at the inlet, which collide and increase with increasing distance. The waves increase in size, i.e., the wave amplitude increases. In addition, the wave frequency decreases over the run length. It can be seen that more distinct wave crests form, which are followed by many smaller waves (x = 300 mm). At greater distances from the inlet (x = 600 mm), the wave crests are even more distinct and a short plateau forms between the waves, the so-called residual film. This occurs more or less developed, depending on the inclination, Reynolds number and measuring position.

Figure 11 shows the flow velocities of the individual Reynolds numbers at an inclination angle of 15°. It is noticeable that the flow velocities as well as the maximum film thickness increase with a further distance to the inlet. When comparing the measurement positions (x = 300–500 mm), the average flow velocity increases between 5 and 13%, depending on the angle. For the maximum flow velocity, the differences are between 6 and 16%, due to the gravitational influence of the inclined plate and the more developed waves that move faster on the base layer. The difference is particularly large at the higher Reynolds numbers. This is due to the fact that these have a significantly longer wave-free range, so that no or very small waves occur at x = 300 mm. The maximum film thickness at Re = 140–200 increases by ≈50% on average due to the waves. The wave amplitude even ≈250%.

Fig. 11
figure 11

Comparison of velocity profiles of film flows in for Reynolds numbers Re = 30–200 and measurement positions

Full size image

4.3 Comparison with the theoretical solution according to Nusselt

In Fig. 12 (left), the mean velocities are compared with those according to Nusselt, for the same Reynolds number. Almost all data show significantly higher velocities. The deviation from Nusselt also increases with increasing angle. This is due to the occurrence of large waves, which are not considered according to the theoretical solution. Only smaller angles (5°) agree well with the solution according to Nusselt, since fewer or very small waves occur. The deviations of the maximum velocity to Nusselt, are comparable to those of the mean velocity.

Fig. 12
figure 12

Ratio of the obtained average velocities of the flow profiles to the theoretical solutions according to Nusselt as a function of the measuring position as well as the Reynolds number (left). Ratio of the mean and maximum measured velocities of the flow

Full size image

The right figure shows the influence of the waviness on the deviation from the theoretical values according to Nusselt in more detail. On the x-axis, a ratio of wave amplitude to measured average film thickness is formed in order to obtain an influence of the waviness. The y-axis shows the ratios of the mean and maximum flow velocities with the corresponding theoretical velocities. Here, wavg/wNu = 1 means that the data are identical to the theory and wavg/wNu > 1 means that the measured flow velocities are greater. The data show that with a larger fraction of wave amplitude, i.e., larger waviness, the deviation increases, and at a low waviness, the data agrees well with the theory. It can also be seen that the deviations of the average and maximum flow velocities are almost identical.

4.4 Comparison with and without wave triggering

The potential of the wave triggering is shown in Fig. 13. Common PIV measurements without triggering have the disadvantage that images without particles are taken when waves occur. This has a negative effect on the quality of the results. An alternative is to take a plurality of images and do not use the empty images. This procedure represents the gray curve.

Fig. 13
figure 13

Representation of the flow profiles, for Re = 60 at a tilt angle of 15° and x = 300 mm, with and without using the wave triggering. Image addition was used for both cases

Full size image

In the wave-free region, the flow velocities are almost identical. Shortly before reaching the minimum film thickness, start of the wave layer, the two curves begin to diverge. Here, apparently, a first influence of the wave layer becomes noticeable. Without wave triggering, all kind of waves, that do not reach the maximum film thickness are also considered, which can lead to velocity gradients within the added particle images and to lower determined flow velocities. As can be seen here, different velocity profiles in the wavy area are calculated from the particle images. Furthermore, a few less layers could be detected than with triggering, since most of the images were without particles. This could possibly be compensated with a larger number of images.

5 Conclusion

In the paper, a combination for detecting the velocities of naturally evolving film flows at small tilt angles on a flat plate with wave triggering was presented. The film flow and its wave formation were decisively determined by the angle of inclination of the channel and the Reynolds number. The data were recorded at several measurement positions in order to obtain a dependency on the run length. By triggering with the confocal chromatic sensor, it is possible to selectively capture the velocity profile depending on the film thickness. The instantaneous velocity profiles were not recorded, but the data for each plane were averaged from several selected waves. Here, the focus was on the wave crest, since this can be selected very well, so that they differ only minimally. Of course, the method can also be applied to other positions in the film flow. In naturally evolving flows, unequal non-periodic waves occur, which can lead to larger scattering of velocities for positions between the wave crest and wave trough. This can be minimized by exciting the flow to produce nearly periodic identical waves. The resolution of the measurement method depends on the depth of field of the camera lens combination and the smallest possible travel distance of the camera on the linear unit. With a suitable design of the components, higher resolutions are possible through scanning than lateral viewing, but this also results in a high time expenditure, depending on how many waves are to be observed. With the measurement methodology, the averaged velocity profiles were examined as a function of the angle of inclination, the Reynolds number and the measurement position. The results of the confocal chromatic sensor show a distinctive dependency of the wave formation on the tilt angle of the channel, the Reynolds number and the run length, even for small angles. The data of the individual measuring positions (300–500 mm) at the different angles show a clear velocity shift or development. Thus, despite small angles, the average velocity increases by 5–13%, while the wave amplitude increases in part by up to 250%.

In comparison to the theoretical values according to Nusselt, it was shown that with increasing waviness, the deviation from the theoretical data also increases significantly. The higher the angle of inclination, the earlier and more developed the waves are at the various measurement positions. As a result, the deviation from Nusselt increases with increasing inclination angle and distance to the inlet. Comparative measurements could show that measurements within wavy film flows are possible without triggering, but show lower velocities than with wave triggering on the wave crest. It was also shown that the flow profiles start to diverge from each other near the wave layer. This is an indication that the wave layer influences the base layer. In future, further measurements will investigate the influence of the wave layer on the base film in more detail. In addition, the parameter range should be extended in order to obtain an empirical correlation of the parameters of naturally noisy film flows depending on the material properties, Reynolds number, inclination angle and the measurement position. With a newly developed measurement methodology (Bilsing et al. 2022), velocity profiles are to be carried out and validated as 3D measurements through the temporally varying phase interface for the first time.