1 Introduction

At first sight, obtaining average flow information in periodic flows, or instationary flows in general, using particle image velocimetry (PIV) seems straightforward: image pairs are recorded, vector fields are obtained using cross-correlation, and these vector fields are averaged to obtain the desired result. However, in some cases, the signal-to-noise ratio of data is insufficient to obtain reliable instantaneous results. For instance, due to difficult imaging conditions or limitations on the amount of seeding material a high percentage of spurious data can occur. In these cases, events with relatively small displacement and gradients will be over-represented, so that the resulting average will not be representative of the time-averaged flow. The presence of ‘gaps’ in vector fields at locations of large displacements (and gradients) will bias the statistics. A further complication arises from the difficulty of validating vector fields with more than 5–10% outliers in a reliable way (Westerweel 1994).

A common processing method for such noisy data is to perform the averaging step in the correlation domain (Delnoij et al. 1999; Meinhart et al. 2000). In this case, the local cross-correlation is computed for each image pair and then summed over all image pairs. Only after the processing of all data, the vector field is obtained from the location of the displacement peaks in these correlation sums. For stationary flows (or phase-locked experiments in the case of a periodic flow), this leads to a significant increase in the signal-to-noise ratio: for instance, Vennemann et al. (2006) showed that for one particular application the number of outliers (which could be seen as a measure of the quality of the result) decreased from nearly 50% to below 5% by averaging over 10 image pairs instead of a single image pair. Recently, a hybrid method has been introduced that combines averaging in the vector and correlation space to further reduce noise (Samarage et al. 2010).

Here, we demonstrate that the application of standard correlation averaging can lead to unreliable results for instationary flows, due to the method of displacement estimation that is currently used. We also present a relatively simple modification that significantly improves the outcome for the estimation of the average flow field. This study exemplifies how more information can be extracted from the correlation result than merely the location of the highest peak.

2 Illustration of the problem

To demonstrate the problem, a simulated data set based on a simple oscillating flow is generated. We describe this flow in terms of a displacement (\(\Updelta x\)) in pixel units, rather than velocities in physical units; similarly, the locations are expressed in pixels. This greatly clarifies the discussion in the remainder of this section. The displacement field, which has non-zero components only in the x-direction, has the form

$$ \Updelta x(y,t) = Cy {\rm cos} (2\pi t/T) $$
(1)

In this expression, C is a constant, and T the cycle duration. The flow field described by 1 describes a linear gradient in the y-direction (Cy), with a magnitude that oscillates with time (t). Averaged over time, the mean displacement field is zero. A series of 512 image pairs of 128 × 128 pixels is generated with an average of 512 particles with a particle image diameter (σ) of 2 pixels (defined by the range for which the Gaussian intensity distribution is higher than 1/e 2 of the central value). The value of C is chosen so that the maximum displacement is 5 pixels. Out-of-plane loss and intensity variation effects are not simulated, since they do not influence the arguments put forward in this study.

The data series is processed using a correlation averaging PIV algorithm implemented in MatLab (Poelma et al. 2008). A straightforward single pass with 32 × 32 pixel interrogation areas with 50% overlap is used here (more complex processing using multiple iterations and window deformation leads to comparable results). The PIV analysis yields an 8 × 8 vector field containing the mean displacement. Results for the linear oscillation case using simulated data are shown in Fig. 1. Here, the displacement \(\Updelta x\) in the x-direction is shown as a function of y-position (data from all eight x-positions are shown at each y-location).

Fig. 1
figure 1

Mean displacement as a function of position for the linear oscillation (simulated data set). The red lines indicate the true mean and maximum positive displacement profiles. Symbols indicate correlation-averaged data set (multiple x-positions per y-location shown). The dashed line indicates a displacement of twice the particle image diameter (2σ)

Full size image

The expected mean is zero for each y-position. However, this result is obtained only in regions with relatively small displacements. For larger values (in the figure for y > 50 px), the observed mean appears to be non-zero. This behavior can be explained by looking at the cross-correlation result at two y-locations (Fig. 2). For small displacements (y = 32 px, circle), the cross-correlation consists of a single peak, originating in the convolution of the particle image and the harmonically oscillating displacement distribution. For large displacements (e.g. data at y = 112 px, triangle), the peak actually splits into a bimodal distribution, as the displacement distribution increases in size. This probability density function of the displacement has the shape of \(P(x)\sim(1-x^2)^{-1/2}\) and is indicated by the black dashed lines in the figure. A standard PIV algorithm will pick either one of the peaks and use that to determine the displacement. Due to the finite number of image pairs that were generated, there is a very small imbalance between positive and negative displacement events that occur. This means that, in this particular case, our initial conditions dictate that the positive peak is slightly higher and thus all estimates lock onto the ‘positive’ motion. For smaller number of image pairs, noise may cause the result to alternate between positive and negative maxima of the bimodal distribution. Note that the displacement appears to follow the maximum displacement, but there is no trivial way of predicting what value of the flow it represents. The splitting of a single displacement peak into distinct peaks is similar to what is observed when spatial gradients are present within an interrogation area (Westerweel 2008).

Fig. 2
figure 2

Two profiles from the correlation results of the linear oscillation data set, taken in a region with relatively low (circle) and relatively high (triangle) displacements. The dashed lines indicates the probability density functions of the displacement, see Sect. 2 for details

Full size image

The transition between the correct (zero) and incorrect (non-zero) estimation of the mean displacement occurs around a maximum displacement of twice the particle image diameter (2σ, indicated by the dashed line in Fig. 1). This was also obtained in repeated experiments with other particle sizes (data not shown). So, for larger particles, more temporal variation is acceptable in an averaging process.

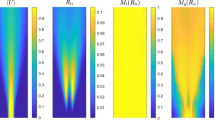
A second example is shown in Fig. 3. Here, data are simulated of a pulsating Poiseuille-like flow: a parabolic flow profile with a centerline velocity determined by the following equations:

$$ \Upphi = t/T\ {\rm mod} 1 $$
(2)
$$ \Updelta x(r,t) =V_0(1-r^2/R^2) {\rm exp}(-10\Upphi^2) \Upphi / 0.136 $$
(3)

in which \(\Upphi\) represents the phase. The parameters in equation 3 are chosen so that again the maximum displacement during the cycle is 5 pixels. Figure 3 (left) schematically shows the cycle of the flow field and centerline velocity. The results from a correlation-averaged PIV algorithm are shown in the (middle) figure. Especially in the core region, the correlation averaging method followed by a peak fit (cross, labelled ‘peak fit’ in the graph) significantly under-predicts the mean flow (dashed line). Again, the reason can be understood by looking at the cross-correlation function from the region at the centerline (Fig. 3 right): the summation of correlation results leads to a broad, asymmetric peak. This peak represents the histogram of the local displacement. The location of the maximum of the peak (indicated by the vertical dashed line labelled ‘peak fit’) does not coincide with the true time-average.

Fig. 3
figure 3

(Left) A pulsating Poiseuille-like flow, top figure shows the flow at 7 subsequent time steps, bottom graph shows centerline velocity during cycle. (Middle) Mean velocity profile (dashed: theoretical reference, cross: conventional correlation averaging PIV, circle: centroid method; the latter is introduced in Sect. 3). (Right) Average correlation function at centerline

Full size image

3 Displacement estimation using the centroid

To improve the accuracy of correlation averaging PIV, the displacement estimation method needs to be generalized. In conventional PIV, the estimation of the displacement is done by locating a single distinct Gaussian-shaped peak (within sub-pixel accuracy)—this follows from the assumption that the displacement within an interrogation area is uniform. Such a uniform displacement will appear as a δ function in the cross-correlation result, slightly broadened by the finite size of the particle images. The latter assumption no longer hold when the displacement is non-uniform, either in space or in time (see also Westerweel (2008) for a theoretical analysis). To better describe the shape of the resulting correlation function in these cases, we suggest to use the centroid (or first order moment) as the displacement estimator:

$$ \Updelta x_c = \sum_{\delta x} \sum_{\delta y} F(\delta x, \delta y) \delta x / \sum_{\delta x} \sum_{\delta y} F( \delta x, \delta y) $$
(4)

In this definition, \(\Updelta x_c\) is the centroid (and thus displacement estimation) in the x-direction. F(δx, δy) is the correlation function, expressed as function of the shifts δx and δy (cf. the horizontal axis in Fig. 2). The summation over these shifts range from −N/2 to N/2 − 1 for an interrogation area of size N (for the simple case without zero-padding). The expression for the estimation of the displacement in the y-direction is equivalent.

Fig. 4
figure 4

Schematic representation of the requirements for the minimum interrogation area size: the correlation peak should fall within the correlation plane, see text for details

Full size image

To understand why the centroid of the correlation of the correlation result is a good estimator for the temporal mean, one has to again realize that the correlation is the convolution of the (autocorrelated) particle image with the displacement histogram (Adrian and Westerweel 2010). The centroid can thus be interpreted as a number-averaged mean of all possible displacement events. Note that a similar reasoning was also used by e.g. Fouras et al. (2007) and Westerweel (2008) to explain the smearing of the correlation peak by spatial variations. Since the autocorrelated particle image is radially symmetric, the correlation is a ‘dilated’ version of true displacement distribution, but no bias is introduced. Further broadening of the peak can also occur due to Brownian motion of the tracer particles, particularly relevant in micro-PIV applications (Meinhart et al. 1999). The increase in peak radius will be proportional to the square root of the laser pulse delay time. However, as long as the Brownian motion is not strongly hindered by the presence of a wall, no bias is introduced (Sadr et al. 2005).

In Fig. 5, the convolution process is demonstrated for the simulated data of the pulsating flow: in the left image, the displacement at the centerline is shown. In the middle, the histogram of this centerline velocity is shown, together with the autocorrelated particle image. In the right hand figure, the convolution is shown of the latter two, which results in a correlation function that is the same as shown in Fig. 3. Also shown are the temporal mean (here determined from the centroid), the minimum and the maximum displacement for reference.

Note that in early PIV applications, the centroid was already used for estimating the displacement, see e.g. Keane and Adrian (1990). However, it is hardly used any more due to the severe pixel locking that it introduces (bias toward integer pixel displacements), especially for compact Gaussian peaks (Prasad et al. 1992). For the present cases, it is nevertheless very suited as an estimator. Pixel locking is not expected due to the broad shape of the averaged correlation peaks.

While the definition of the centroid is straightforward, implementation has to be done with some care. For instance, in a single-pass algorithm, an increasing displacement will shift the displacement peak toward the edge of the correlation plane (consider e.g. Fig. 3 with a displacement that is twice as high: a part will fall outside of the graph). This might result in a ‘missing’ side of the distribution, so that the displacement will be significantly underestimated due to the finite window sizes. We can derive an estimate of the minimal interrogation area size using the following reasoning: (1) The correlation peak radius (cpr) can be estimated from the particle image width (σ) and the width of the distribution of the displacements (\(\Updelta x^{\prime}\)) as \(cpr \approx(\sigma^2 + \Updelta x^{\prime 2})^{1/2}.\) For all these estimates (including the cpr), we use the 1/e 2 width of a Gaussian distribution. (2) We require this broadened correlation peak to fall within our correlation plane. For simplicity, we here assume that the correlation plane has the same dimensions as the interrogation areas (i.e. ‘no zero-padding’). Due to the presence of a mean displacement, the broadened peak can shift to the edges of the correlation plane. To ensure that the majority of the peak falls within the correlation plane (‘majority’ here means approximately 95%, as we are using the 1/e 2 width), we require a lower limit of the interrogation area size (IA):

$$ IA > ( \sqrt{\sigma^2 + \Updelta x^{\prime 2}} + \Updelta x_{{\rm mean}} ) $$
(5)

This criterium is illustrated schematically in Fig. 4. In all cases considered in this manuscript, both σ and \(\Updelta{x^{\prime}}\) are of the order of a few pixels, while the mean displacement \(\Updelta x_{{\rm mean}}\) is usually less than 10 pixels. So, a conservative estimate would suggest that 16 by 16 pixels is the bottom limit to avoid bias in the first iteration in these cases. Note that for subsequent passes in an iterative PIV analysis, the final peak will be located more and more toward the center of the correlation plane due to the use of window shifting. This sets the last term of Eq. 5 to zero. To avoid problems due to an asymmetrical peak location and effects due to noise, one can consider using only values for the correlation result above a certain threshold (e.g. a fraction of the maximum peak height).

Apart from the minimum interrogation area size, one also has to consider the effects of areas that are too large. This is the case if the interrogation areas are of the same scale as the spatial variations in the flow field. As a result, the velocity is then no longer uniform within each interrogation area, which leads to an additional broadening of the peaks (Westerweel 2008). Due to the nature of the convolution process, the origin of a broadened peak cannot be separated in temporal and spatial variations.

Applying the centroid estimator to the data sets improves the mean displacement estimation dramatically. For the case shown in Fig. 1, the centroid is located near the origin, due to the symmetry of the correlation function (data not shown). For the case of the pulsating flow, the results for the mean flow agree with the expected values (Fig. 3 (middle), open circles).

4 Application to blood flow measurements

To test the proposed method on experimental data, we use a data set taken from the study by Poelma et al. (2008). This data set was taken in the extra-embryonic blood vessels of a chicken embryo (the so-called vitelline circulation) using micro-PIV. Based on an elaborate phase-sorting method using hundreds of images, the flow fields during the cardiac cycle have been reconstructed in that study. For full details of how the data were processed, we refer to the original publication. The time-average of the resulting vector fields will serve as the reference case for the present study.

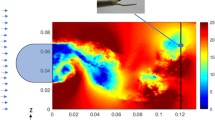
The image pairs (not phase-locked in the present study) are processed using a correlation averaging PIV algorithm (24 × 24 pixel window size, 50% overlap). The displacement is obtained both by conventional three-point Gaussian peak fitting, as well as using the centroid method. In Fig. 6, the result for the flow field using the centroid method is shown (the colors represent velocity magnitude). The result from Gaussian peak fitting was less noisy than the centroid-based result. However, when the average flow field is compared to the reference values, the advantage of the centroid method becomes clear: a cross section of the flow profile (indicated by the green line in the flow field) shows that the conventional method underestimates the mean flow by nearly a third (see Fig. 7).

Fig. 5
figure 5

(Left) The pulsating displacement at the centerline; (Middle) The histogram of the centerline velocity (symbols) and the autocorrelated particle image (line); (Right) Convolution of the histogram and the particle image

Full size image
Fig. 6
figure 6

The average flow field (magnitude) measured in blood vessels of the vitelline circulation of an embryonic chicken (see Poelma et al. 2008) for details. The velocity magnitude was determined using the centroid method

Full size image
Fig. 7
figure 7

A velocity profile along the cross section indicated by the green line in Fig. 6, comparing the conventional three-point Gaussian fit (‘peak fit’, cross) and new centroid method (diamond) to the reference velocity field (Asterisk)

Full size image

A more systematic comparison between the conventional method and the centroid method is shown in Fig. 8. This figure shows a scatter plot of the velocities at all locations as a function of the reference velocity (from the phase-locked results). The line y = x indicates a perfect agreement with the reference case. Clearly, the conventional method starts to systematically underestimate the velocity for displacements larger than 1.5 pixels. The size of the tracer particle images was estimated at approximately 1 pixel, which makes these results consistent with our earlier finding that the upper limit for the displacement was twice the particle diameter. Without any a priori knowledge about the temporal behavior of the flow, the systematic underestimation at larger displacements cannot be modelled (and thus not corrected).

Fig. 8
figure 8

Scatter plot of the measured velocity using the conventional three-point Gaussian fit (‘peak fit’, cross) and centroid method (diamond) versus the reference velocity (dashed line) in the vitelline data set. See text for details

Full size image

The results for the centroid method appear to remain unbiased for larger displacements. However, as will be clear from the graph, the noise level is somewhat larger than the conventional method. Note that a part of the scatter can be attributed to noise in the reference signal, which leads to uncertainty in the ‘horizontal’ location of the markers. In a previous, similar study (Poelma et al. 2010), we conservatively estimated the random error in the displacement at 5% of the maximum systolic flow, corresponding to approximately 0.4 pixels in Fig. 8. For accurate estimates of e.g. the blood flow rate from a fit to a velocity profile as shown in Fig. 7, this increased noise level is still preferable over a biased result. Note that, unlike the simulated case shown in Fig. 3, it is nearly impossible to tell that the bias effect is present in the conventional analysis: the radial flow profiles appear to have smooth Poiseuille-like shapes. However, the interpretation of e.g. the maximum velocity of these profiles is difficult, as this value has hardly any physical (or physiological) meaning.

The centroid is outperformed by the conventional method for small displacements (less than 1.5 pixels): it has a lower noise level and no significant bias. Naturally, we can combine the conventional and centroid method: first, an analysis is performed using the centroid method. For locations with a low displacement, the displacement estimation is switched to the conventional Gaussian peak fit. This does not require significant additional computational effort, as both use the same cross-correlation results.

5 Discussion and conclusions

We have shown that the conventional peak fit method is not suitable for correlation averaging PIV of transient flows. Variations in time lead to a broadened peak, whose maximum location will generally not coincide with the mean displacement. By generalizing the displacement estimation—for instance by using the centroid as estimator—more reliable results can be obtained. The noise level increases with this method, but is shown that it less biased than the conventional method for larger displacements. For the optimal result, a hybrid method is the best solution: only for large displacement regions of the image, the centroid method is used; for other regions, the conventional peak fit can be used.

The present study demonstrates that there is more information contained in the correlation peak than what is currently being used (i.e. the location of the highest or ‘displacement’ peak). Over the years, researchers have studied the possibilities of extracting this information. Already in 1986, it was realized that turbulent fluctuations will lead to a broadening of the correlation peak in speckle velocimetry, so that the turbulence level can be determined from its width (Arnold et al. 1986). As mentioned before, fluctuations due to Brownian motion will also broaden the peak, making it possible to deduce the local temperature from a cross-correlation analysis (Hohreiter et al. 2002). Recently, it has been proposed to determine the Reynolds stresses from ensemble-averaged single-pixel PIV by considering the shape of the resultant correlation function shape (Scharnowski et al. 2010). In all of these applications, one would ideally deconvolve the cross-correlation peak into its constituents: the particle image and the displacement distribution. Unfortunately, this deconvolution process is far from trivial in a realistic signal. While the simulated data (see e.g. Fig. 5) can readily be deconvolved to retrieve a histogram of the displacement, noise severely limits this approach when dealing with experimental data. A better approach will likely be to first fit a surface to the correlation result. Earlier work on methods of fitting broadened peaks can be found in e.g. a study by Ronneberger et al. (1998).

5.1 Application to spatially non-homogeneous data

In this study, the averaging process was performed over data that was non-stationary. The analysis can directly be translated to the spatial equivalent of non-homogeneous data: particles moving at different ‘depths’ in the field under consideration will cause multiple (merged) peaks in the correlation average if their local velocity is different. For a detailed analysis of this effect, see e.g. the study by Fouras et al. (2007).

Provided that the particle image at each depth is similar and parallax effects can be ignored, the centroid of the correlation result will be the spatial average. This requires uniform illumination and a large depth-of-focus to avoid biasing effects from out-of-focus particles. Obviously, the flow needs to be stationary or phase-locked too, as contributions from spatial and temporal inhomogeneities cannot be distinguished. Possible applications would be low-magnification micro-PIV (Kloosterman et al. 2010) and data obtained using synchrotron-based imaging (Lee and Kim 2005; Fouras et al. 2007). The use of conventional peak fitting leads to a result that is complicated to interpret, as it is somewhere between the maximum and spatial mean.