1 Introduction

For several decades, laser-induced incandescence (LII) has been an established in situ diagnostic technique to measure the concentration and size of nanoparticles such as soot produced under fuel-rich combustion conditions of hydrocarbons. It is based on the irradiation of the particles with a short laser pulse and the detection of the enhanced thermal radiation signal [1,2,3] . The concentration of the particles can be determined from the intensity of the prompt signal after the laser pulse, which scales almost proportionally with the volume fraction of the particles. To infer the primary particle size \(d_\text {p}\), the signal decay following the cooling rate of the particles is captured and typically compared to a heat transfer model for its quantification. One drawback of the technique is its sensitivity towards the wavelength-dependent optical properties of the particles, which are known to change throughout the particle evolution process (divided into formation and oxidation). Therefore, the detection at one or a few spectral ‘windows’ - often realized by photomultiplier tubes or cameras [3] equipped with bandpass filters - requires knowledge about the optical properties at these wavelengths, which is often widely scattered regarding the reported values. A higher information density can in general be obtained by spectrally resolved measurements [4,5,6,7]. These studies, however, obey the challenge of maintaining the high temporal resolution using, e.g., streak camera devices [8] or are limited to sequential recordings in steady processes [9].

In recent years, multiple studies have focused on the optical properties of soot particles including the complex refractive index \({\tilde{m}}=n-ik\), the absorption function \(\text {E}({\tilde{m}})\), the dispersion exponent \(\xi\) or the optical band gap \(E_\text {g}\). Various methods to infer these quantities have been established [10,11,12,13]. For example, heating a particle ensemble with two subsequent laser pulses of different wavelengths allows the determination of the \(\text {E}({\tilde{m}})\) ratio or even its absolute value [10]. Similarly, two laser excitation wavelengths can be used to obtain peak LII intensity curves in dependence on the laser fluence of various soot particles, in which the shift of the fluence curves relates to the dispersion exponent [12]. Another approach is the use of extinction measurements at multiple wavelengths [11, 14] .

The determination of the optical properties of soot is crucial to improve our understanding of its formation pathways and further yields information about soot maturity - following transformations from young to mature soot in flames. Besides soot particles, other engineered nanomaterials, such as iron, silver or molybdenum, have recently garnered significant interest due to their unique physical properties [15]. In these cases, knowledge about the optical properties is often even more imprecise than for soot particles and additional effects may superimpose the incandescence signal. Therefore, a roadmap to reliably estimate the optical properties from LII signals is required to improve our understanding of these materials.

This study reports the determination of the absorption function \(\text {E}({\tilde{m}})\) of soot particles in a well-characterized flame by the use of an LII model and spectrally as well as temporally resolved measurements. The absorption function impacts the absorption and the emission characteristics of the soot particles, where the latter are closely correlated to the particle temperature. Therefore, by applying multiple irradiation wavelengths and predicting the particle cooling using a heat transfer model at a well-defined measurement point allows inferring wavelength-dependent values for \(\text {E}({\tilde{m}})\). First, the experimental details of the measurements are presented, which is followed by a description of the LII model and the regression approach. Results for ethylene and propane flames are compared and discussed.

2 Experimental set-up

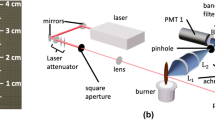
The experimental set-up is depicted in Fig. 1. For the measurements with 450 nm, 532 nm, 600 nm and 650 nm excitation wavelength, a Q-switched Quantel Q-smart 450 laser with 120 mJ at a wavelength of 355 nm, a pulse duration (full width at half maximum (FWHM)) of approximately 4.5 ns and a repetition rate of 10 Hz was used to pump an Optical Parametric Oscillator (OPO, Opotek MagicPrism), which enables tuning of the OPO-output wavelength quasi-continuously between 410 nm and 680 nm. The energy of the resulting OPO-beam was adjusted by neutral density (ND) filters. After passing the ND filters, the beam was focused onto a pinhole with an \(f=250\) mm lens and imaged in the detection volume via two subsequent \(f=200\) mm lenses in a 4f-set-up. The achieved beam profiles can be seen in the lower part of Fig. 1.

Fig. 1
figure 1

The used experimental set-up and the beam profiles of the four lasers used (normalized intensity)

Full size image

The detection system consisted of an \(f=60\) mm lens, which was positioned perpendicularly to the beam propagation direction at a distance of 120 mm from the measurement volume. The signal was collected by the subsequent \(f=35\) mm lens, which was positioned 155 mm behind the first lens. The collimated light then passed a filter array, whereby the used filters were dependent on the excitation wavelength to block the respective scattered laser light. For the experiments with 450 nm excitation wavelength, a 500 nm long pass filter was used. For 532 nm excitation wavelength, a 532 nm notch-filter (FWHM of 17 nm) was used, while for the measurements with an excitation wavelength of 600 nm a filter which blocks light between 530 nm and 650 nm was used. For the measurements with an excitation wavelength of 650 nm, a 658 nm notch-filter (FWHM of 26 nm) was used. To prevent spectral overlap with the second order diffraction of the spectrograph’s grating, a 400 nm longpass filter was additionally placed into the collimated detection path for all measurements. The light was then focused on the round end of a round-to-linear fiber bundle consisting of five 200 \({\upmu }\)m multimode fibers with another \(f=35\) mm lens. This arrangement also defined the measurement volume by blocking laser-induced signals from regions in the flame other than within a circle with a radius of approx. 0.6 mm perpendicular to the optical axis of the detection system due to the 1:1 imaging. The linear end of the fiber bundle was imaged onto the 200 \({\upmu }\)m slit of a spectrograph (Andor Kymera-193i-A) via a \(f=30\) mm lens positioned at 2f between the fiber end and the slit. A 150 lines/mm grating (blazed at 500 nm) was used together with an intensified CCD camera (Andor iStar 334T Series, Gen 2 (WE-AGT,-E3)) to record the raw spectra (range of approx. 410 to 820 nm). To account for the spectral efficiency of the detection system, a broadband calibration lamp with a known spectral irradiance was used (Ocean Optics HL-3P-CAL). Eventually, for the evaluation, the wavelength range from 450 to 750 nm was used, minimizing spectral edge effects (of the spectrograph and due to low output intensity of the calibration lamp at low wavelengths) and second-order diffraction artifacts in the data (specific ranges in Table 1). The exposure time of the camera was set to a minimum of 10 \({\upmu }\)s, and the gate width/time of the intensifier was set to 5 ns. The gain of the camera’s microchannel plate (MCP) was set to a value of 3200 with a theoretical maximum value of 4095. To reduce noise and ensure faster readout times, only 100 consecutive horizontal pixel rows with each 1024 pixels were considered and vertically binned. For each excitation wavelength at every temporal measurement position, 100 images were acquired. Both laser and the camera were triggered by a pulse generator. Measurements were carried out at different times before and after the occurrence of the maximum intensity of the laser pulse , whereby the respective measurement times correspond to the opening of the intensifier gate.

The temporal position of the laser pulse with respect to the measurements was derived by scanning the laser pulse in time with the 5 ns gate of the intensifier in 1 ns steps. Based on the resulting spectra and a convolution of a simulated Gaussian beam and a 5 ns gate window, the temporal position of the laser pulse could be calculated.

A laminar co-flow diffusion flame from a Gülder burner was investigated fueled either with ethylene (\(\text {C}_2\text {H}_4\)) or propane (\(\text {C}_3\text {H}_8\)) gas. For the measurements with \(\text {C}_2\text {H}_4\), the flow rates were 0.194 slm for the fuel gas and 284 slm for the airflow, both adjusted via two mass-flow controllers. These settings were chosen because they are standard ones for which extensive reference data are available, cf. [2]. For the \(\text {C}_3\text {H}_8\) measurements, however, a flow rate of 0.12 slm was used for the fuel gas, resulting in approximately the same flame length as for the \(\text {C}_2\text {H}_4\). Measurements of the background flame luminosity were acquired for each fuel.

Measurements were performed for a height above burner (HAB) of 40 mm on the central axis as this is a position with only minor changes of flame properties as a function of the exact axial and radial position. For ethylene, a similar measurement position has been extensively investigated previously [2].

Some exemplary results for the \(\text {C}_2\text {H}_4\) case are shown in Fig. 2 for the different excitation wavelengths: \(\lambda _{\text {exc}}=532\) nm in the upper part of the figure and \(\lambda _{\text {exc}}=650\) nm in the lower part (all spectra shown are background- and spectral efficiency-corrected). These spectra are normalized with respect to the corresponding maximum of the entire measurement series for each excitation wavelength. The temporal information in the legend relates relatively to the occurrence of the peak intensity of the laser pulse. It can be seen that the signal intensity first increases rapidly for timings shortly before and after the maximum intensity of the laser pulse and in the following decreases with increasing delay times. It can also be seen that the wavelength-dependent maximum of the spectra shifts from long to short wavelengths during and shortly after the laser peak. During the cooling of the particles, the maximum shifts again back to longer wavelengths.

Fig. 2
figure 2

Recorded spectra during heating (left side) and cooling (right side). An excitation wavelength of \(\lambda _{\text {exc}}=532\) nm was used in the upper diagrams of the figure and \(\lambda _{\text {exc}}=650\) nm in the lower diagrams

Full size image

3 LII model and spectral fitting procedure

Laser-induced incandescence is based on the heating of nanometer-sized particles by a short laser pulse, which leads to elevated temperatures and thus an increase in emitted thermal radiation [1]. In this work, flame-generated soot particles, which are present as fractal-like aggregates were investigated in situ by LII. To this end, the laser-induced spectral signals of the particles at different times with respect to the laser pulse (and therefore different particle temperatures) were acquired. To obtain the quantities of interest such as the soot particle size or their optical properties, the measured data are reconstructed with a spectroscopic model, whose parameters are optimized via regression. Therefore, the temperature-dependent spectral intensity \(S_\lambda\) of the particles has to be modeled, i.e.,

$$\begin{aligned} {S_\lambda }={I}_{\text {b},\lambda } {\cdot }C_{\text {abs},\lambda } . \end{aligned}$$
(1)

Here, \(I_{\text {b},\lambda }\) is the spectral intensity of a black body, which follows

$$\begin{aligned} \ {I}_{\text {b},\lambda } = \frac{2\pi h c^2}{\lambda ^5} \frac{1}{e^{(hc)/(\lambda T_\text {p} k_\text {B})}-1}, \end{aligned}$$
(2)

where h is Planck’s constant, c the speed of light, \(k_\text {B}\) Boltzmann’s constant and \(T_\text {p}\) the particle’s temperature. The absorption cross section \(C_{\text {abs},\lambda }\) in the Rayleigh regime (\(d_\text {p}<<\lambda _{\text {exc}}\)) can be calculated as

$$\begin{aligned} C{_{\text {abs},\lambda _{\text {exc}}}}={\frac{\pi ^2\cdot d_\text {p}^3 \cdot \text {E}({\tilde{m}})}{\lambda _{\text {exc}}} }. \end{aligned}$$
(3)

Here, \(d_\text {p}\) is the primary particle diameter, \(\lambda _{\text {exc}}\) is the respective excitation wavelength, and \(\text {E}({\tilde{m}})\) is the material-dependent absorption function, i.e., the quantity which is of major interest in this work. It can be expressed as

$$\begin{aligned} { \text {E}({\tilde{m}})=C_{\xi } \cdot \lambda ^{(1-\xi )}\,, }\end{aligned}$$
(4)

where \(C_{\xi }\) is a constant and \(\xi\) is the dispersion exponent [12, 16].

To calculate the temperature of the particles needed for calculating the emitted spectral intensities during and after the laser heating, a model solving the energy and mass balance equations was used. The model employed in this work is based on the publication by Bauer et al. [17], wherein detailed information can be found. Here, only a brief summary of the most important equations for the present work is provided.

The general form of the energy balance equation used in the LII model can be written as

$$\begin{aligned} \frac{\text {d}U_{\text {int}}}{\text {d}t}={\dot{Q}}_{\text {abs}}+{\dot{Q}}_{\text {cond}}+{\dot{Q}}_{\text {sub}}, \end{aligned}$$
(5)

where \(U_{\text {int}}\) is the internal energy of the particle, \({\dot{Q}}_{\text {abs}}\) is the absorptive heating rate, \({\dot{Q}}_{\text {cond}}\) the conductive cooling rate and \({\dot{Q}}_{\text {sub}}\) the evaporative cooling rate. This work especially aims at the term of the absorptive heating rate incorporating the optical property \(\text {E}({\tilde{m}})\) as well. It is given by

$$\begin{aligned} {\dot{Q}}_{\text {abs}}=H\cdot g(t) \cdot C{_{\text {abs},\lambda _{\text {exc}}}}=H\cdot g(t) \cdot {\frac{\pi ^2\cdot d_\text {p}^3 \cdot \text {E}({\tilde{m}})}{\lambda _\text {exc}} }, \end{aligned}$$
(6)

where H is the laser fluence and g(t) is the temporal profile of the laser pulse, where the latter yields a value of one if integrated over time.

The conductive cooling rate \({\dot{Q}}_{\text {cond}}\) is the major heat loss process for moderate fluences after the laser pulse [1]. However, based on the fractal dimension of the soot aggregates the heat transfer to the environment of the aggregates’ central primary particles can be reduced by those surrounding them due to the shielding effect. Therefore, \({\dot{Q}}_{\text {cond}}\) is dependent on the morphology of the aggregates. Moreover, the distribution of the primary particle sizes is relevant for the conductive heat transfer since larger particles cool slower than smaller ones, leading to a superposition of the radiated signals of all particle sizes [1]. In conjunction with the particle size, the accommodation coefficient \(\alpha\) determines the cooling rate of the particles by conduction, since it is a measure of the average energy transferred to a gas molecule when it collides with the heated particles [18]. Furthermore, \({\dot{Q}}_{\text {cond}}\) is influenced by the gas temperature \(T_\text {g}\), as this value is needed to determine the temperature difference between the particle at \(T_\text {p}\) and the surrounding.

To regress the thus modeled spectra against the measured data, the measurement conditions had to be mimicked. To this end, the modeled spectra were corrected for the measured spectral efficiency of the system. Furthermore, the calculated spectra within 5 ns were integrated within the model at the respective measurement positions in time due to the camera’s 5 ns gate time. The spectra calculated in this way were then the starting point of a weighted least-square fitting approach. It seeks to match the computed spectra with the corresponding measured spectra by optimization of the respective model parameters of the LII model contained in the vector x. As far as available, prior knowledge about the model parameters is taken into account. Assuming independent and normally distributed measurement noise and prior knowledge, the maximum a posteriori (MAP) estimate for the input parameters can then be calculated by [19]

$${\mathbf{x}}_{{{\text{MAP}}}} \;\widehat{ = }\;\arg \min \left[ {\sum\limits_{{j = 1}}^{{N \cdot n}} {\frac{{\left( {b_{j} - b_{{j,\mathrm{mod} }} ({\mathbf{x}})} \right)^{2} }}{{\sigma _{j}^{2} }}} + \sum\limits_{{k = 1}}^{{n_{{pr}} }} {\frac{{\left( {\mu _{{\mathrm{pr},k}} - x_{{\mathrm{mod},k}} } \right)^{2} }}{{\sigma _{{\mathrm{pr},k}}^{2} }}} } \right],$$
(7)

where N is the number of spectra used for the optimization, n the number of data points per spectrum, i.e., the number of discrete wavelengths measured by the spectrograph. \(b_j\) is the measured mean intensity value at the respective discrete wavelengths and \(b_{j,\text {mod}}\) is the calculated intensity value at the respective wavelengths based on the model. \(\sigma _j\) is the standard deviation of \(b_j\). \(n_{\text {pr}}\) is the number of prior information used in the optimization, \(\mu _{\text {pr},k}\) is the respective value of the prior, i.e., the mean value of the normally distributed prior knowledge and \(\sigma _{\text {pr},k}\) is the uncertainty of the respective prior information. As optimization parameters for the model, x contains the absorption function \(\text {E}({\tilde{m}})\) and additional stochastic parameters (so-called nuisance parameters). The latter are a scaling factor \(C_1\), the accommodation coefficient \(\alpha\) , the primary particle diameter \(d_\text {p}\) (assumed as monodisperse) and the gas temperature of the flame \(T_\text {g}\). The linear scaling factor \(C_1\) was used to match the absolute values of the modeled signal with the values of the measured spectra. Since all computed spectra at the respective times are multiplied with \(C_1\), the relative intensity of the computed spectra is maintained. This is necessary for a correct fitting procedure since the relative intensities of the measured spectra must be reproduced. The \(\text {E}({\tilde{m}})\) function was assumed to follow Eq. 4 and therefore \(\xi\) and \(C_\xi\) were the optimization parameters in the model for \(\text {E}({\tilde{m}})\).

Considering the gas temperature, the primary particle diameter and the accommodation coefficient, prior knowledge was used for the regression, i.e., for these stochastic parameters a value was assigned to \(\mu _{\text {pr},k}\) and \(\sigma _{\text {pr},k}\). For \(T_\text {g}\), measurements were carried out using a set-up based on [20], assuming that \(T_\text {g}\) equals \(T_\text {p}\) in the flame. This lead to a mean temperature of \(\mu _{T_\text {g}}=1620\) K for \(\text {C}_2\text {H}_4\) and \(\mu _{T_\text {g}}=1670\) K for \(\text {C}_3\text {H}_8\). The evaluated temperature for \(\text {C}_2\text {H}_4\) lies well within the specified temperature range in [2], that being \((1640\pm 60)\) K. Furthermore, for \(\sigma _{T_\text {g}}\) a value of 10 K was assigned for \(\text {C}_2\text {H}_4\) as well as for \(\text {C}_3\text {H}_8\).

Regarding the primary particle diameter, TEM samples were extracted and analyzed to obtain the primary particle size distribution. Exemplary images are shown in Fig. 3. From those results, the mean diameter for both fuels was used as prior knowledge, i.e., \(\mu _{d_\text {p},\text {C}_2\text {H}_4}=27.6\) nm for \(\text {C}_2\text {H}_4\) and \(\mu _{d_\text {p},\text {C}_3\text {H}_8}=35.5\) nm for \(\text {C}_3\text {H}_8\). As standard deviation for the respective mean diameters (not the width of the size distributions), \(\sigma _{d_\text {p},\text {C}_2\text {H}_4}=0.5\) nm and \(\sigma _{d_\text {p},\text {C}_3\text {H}_8}=0.7\) nm were obtained based on the TEM data.

Fig. 3
figure 3

Exemplary TEM images of soot particles sampled in 40 mm HAB from the flame with \(\text {C}_2\text {H}_4\) on the left side and for \(\text {C}_3\text {H}_8\) on the right side

Full size image

For \(\alpha\), \(\mu _{\alpha }=0.23\) was assumed to follow the reported value of Ref. [2]. Thus, the reduction of the conductive cooling rate due to aggregation, sintering or primary particle overlapping was taken into account in the model, since these ultimately leads to an effective and reduced accommodation coefficient [21]. As the width of the distribution, \(\sigma _\alpha =0.04\) was chosen following [17].

For the calculation of the temperature-dependent spectra of the soot particles, the laser fluences were set to a fixed value within the model. To this end, a mean fluence was used for the simulations, which was determined by calculating the fluence per pixel of the image recorded with the beam profiling camera (WinCam D) and the measured energy (Thorlabs ES111C) and subsequent averaging of these values.

For the simulations, the temporal shape of the temporally resolved laser beam intensity of the laser pulse was assumed to be Gaussian.

To fit the measured spectral data by the model, wavelength regions with contamination due to interfering signals such as fluorescence should be avoided. These contributing signals can lead to erroneous results since the shape of the spectrum differs from its undisturbed shape, which is due to the superposition of the incandescence and the fluorescence signals. Such signals can be observed in Fig. 2 in the upper left diagram: here, at 5 ns and 10 ns after the laser pulse, fluorescence signals can be seen at, e.g., 500 nm and 550 nm. These may arise from \(\text {C}_2\)-swan band emissions superimposed on the LII signal [22]. Broadband fluorescence signals from polycyclic aromatic hydrocarbons (soot precursors) may superimpose the incandescence signal additionally [23]. In the literature, interference-free wavelength regions are described, e.g., 680-820 nm for an excitation wavelength of 532 nm [9]. However, this would only allow to evaluate \(\text {E}({\tilde{m}})\) in a very narrow spectral range, in which a rather constant behavior is further assumed [24]. Moreover, for other excitation wavelengths than 532 nm and 1064 nm, no information about interference-free wavelength regions is available.

Yet, as our measurements show (c.f. Fig. 2), after 85 ns, exclusively the incandescence signal remains due to the short fluorescence life-time of the molecules [9]. Moreover, as described in the literature [5, 25] and as shown in our data (Fig. 2, upper left diagram), the fluorescence signal directly after the laser pulse is rather weak compared to the LII-signal (here, approx. 5 %). As these data very early after the laser pulse provide additional information about the peak particle temperature (and thus the absolute magnitude of \(\text {E}({\tilde{m}})\)), using spectra recorded shortly after the laser pulse turns out to be beneficial for the fitting procedure.

To summarize, in this work, measurement data recorded directly after the laser pulse (approx. 5 ns) and at timings relatively late after the laser pulse peak intensity (after 85 ns, 105 ns, 125 ns, 175 ns, 225 ns, 325 ns, 425 ns, 625 ns, and 775 ns) are employed for evaluation, allowing to reconstruct the measured spectra nearly over the entire examined wavelength range without expecting strong interference of superimposed signals, especially at the longer excitation wavelengths. The fluence was kept at below approximately 90 mJ/cm\(^2\) for all tested excitation wavelengths in this study (see Table 1) to further avoid altering the optical properties of the soot too much during the measurements [26, 27].

Table 1 Summary of the measurement conditions in HAB 40 mm
Full size table

4 Results and discussion

In the upcoming subsections, the results of the spectral reconstruction procedure described in section 3 for ethylene at HAB 40 mm as well as for propane at HAB 40 mm for excitation wavelengths of 450 nm, 532 nm, 600 nm and 650 nm are presented.

4.1 Results for ethylene

In the first step, the measured spectra for \(\text {C}_2\text {H}_4\) at HAB 40 mm were examined since a similar measurement position was already investigated in previous studies [2]. The spectra of the soot particles were calculated by the model while optimizing the scaling factor \(C_1\), the thermal accommodation coefficient \(\alpha\), the primary particle diameter \(d_\text {p}\), the gas temperature \(T_\text {g}\) and the absorption function \(\text {E}({\tilde{m}})\) by means of \(C_{\xi }\) and \(\xi\) simultaneously (section 3). Prior information according to the values provided in Sect. 3 were utilized. For the fluence, a fixed value was used, as previously determined experimentally (see Table 1).

Fig. 4 shows the measured and computed spectra exemplarily for an excitation wavelength of 650 nm. The depicted spectra correspond to the spectra recorded directly after and those recorded 85 ns, 105 ns, 125 ns, 175 ns, 225 ns, 325 ns, 425 ns, 625 ns, and 775 ns after the peak of the laser pulse, respectively. The inferred values in this case are \(\alpha\)=0.19, \(T_\text {g}\)=1525 K, \(d_\text {p}\)=29.2 nm, \(\xi\)=1.68 and \(C_\xi\)=25.9. These inferred values and those given the other excitation wavelengths are summarized in Table 2. Looking at these values, one can thus state that the values for \(\xi\) don’t differ much among each other. The inferred primary particle diameters are close to the prior value, i.e., 27.6 nm obtained from TEM.

Fig. 4
figure 4

Measured (blue) and computed (red) spectra for \(\text {C}_2\text {H}_4\)-flame at HAB 40 mm for an excitation wavelength of 650 nm

Full size image

4.2 Results for propane

To investigate the possible impact of the utilized fuel on the optical properties of the soot particles, additional measurements were performed for \(\text {C}_3\text {H}_8\) at HAB 40 mm. The resulting fitted spectra for propane can be seen in Fig. 5, again exemplarily for \(\lambda _\text {exc}=650\) nm.

Fig. 5
figure 5

Measured (blue) and computed (red) spectra for \(\text {C}_3\text {H}_8\)-flame at HAB 40 mm for an excitation wavelength of 650 nm

Full size image

The inferred value of the accommodation coefficient is \(\alpha\)=0.35, the dispersion exponent is \(\xi\) = 1.64 with \(C_\xi\) = 20.1, the temperature is \(T_\text {g}\) = 1596 K and the primary particle diameter is 36.2 nm. These values and the estimated parameters for the other excitation wavelengths are again summarized in Table 2. When comparing the results of \(\text {C}_2\text {H}_4\) and \(\text {C}_3\text {H}_8\), the values for the accommodation coefficient are higher in the latter case, however, the values for the dispersion exponent show strong similarities to the ones derived for \(\text {C}_2\text {H}_4\).

Table 2 Inferred values of all cases
Full size table

4.3 Discussion

To visualize the behavior of the resulting absorption function, mean \(\text {E}({\tilde{m}})\) curves based on the results for the respective \(\text {E}({\tilde{m}})\) from the simulations in this work were computed for C\(_2\)H\(_4\) and C\(_3\)H\(_8\). Those correspond to \(\xi\) = 1.68 and \(C_\xi\) = 22.8 for C\(_2\)H\(_4\) and to \(\xi\) = 1.75 and \(C_\xi\) = 35.5 for C\(_3\)H\(_8\). These are depicted as solid lines in conjunction with the respective standard deviation of the mean (as the red (C\(_2\)H\(_4\)) and blue (C\(_3\)H\(_8\)) areas) in Fig. 6. The latter was calculated by dividing the standard deviation from all \(n=4\) measurements with the square root of n, assuming independent measurement errors [28]. In the left part of the figure, the absolute values are shown and in the right part the same curves are used but normalized with respect to their respective maximum. The standard deviation, in this case, was calculated as described above but based on the respective normalized \(\text {E}({\tilde{m}})\) curves.

Fig. 6
figure 6

The left part of the figure shows the absolute value of \(\text {E}({\tilde{m}})\) for C\(_2\)H\(_4\) as well as for C\(_3\)H\(_8\). The right part shows the normalized \(\text {E}({\tilde{m}})\) functions for both fuels. The standard deviation of the mean is shown as red and blue area

Full size image

As it can be seen, the difference between the the curves for \(\text {C}_2\text {H}_4\) and \(\text {C}_3\text {H}_8\) is relatively small, which implies that there is only a minor difference in \(\text {E}({\tilde{m}})\) between the two fuel gases - a conclusion that was also drawn in [29] for the same fuel gases but only at one specific wavelength.

Regarding the standard deviation of the mean \(\text {E}({\tilde{m}})\) curves, it is important to mention that the derived (mean) values do not include shot-to-shot fluctuations of the fluence which could additionally influence the magnitude of \(\text {E}({\tilde{m}})\), as both, magnitude of \(\text {E}({\tilde{m}})\) and fluence H show a high correlation. To accelerate convergence and to prevent the solver from converging into local minima, the fluence was set to a deterministic value in the simulations based on results from measurements before the actual experiment (extinction corrected to account for attenuation within the flame). The value for H is thus considered accurate, implying only minor uncertainties in \(\text {E}({\tilde{m}})\). However, the shot-to-shot fluctuations of the laser fluence are in the range of 5–10 % of the mean value, increasing with increasing wavelength (possibly due to nonlinear thermal effects within the crystal of the OPO). To give an estimate of the influence of this uncertainty on the derived \(\text {E}({\tilde{m}})\) uncertainties, simulations for C\(_2\)H\(_4\) were performed with 10 % higher and 10 % lower fluence, exemplarily for the case of \(\lambda _\text {exc}=650\) nm. The inferred values together with the ones with the mean fluence (\(H_{\text {mean}}\)) used for the simulation are given in Table 3.

Table 3 Inferred values in the case of C\(_2\)H\(_4\) with an excitation wavelength of \(\lambda _\text {exc}=650\) nm for varying fluence
Full size table

As it can be seen, the inferred values in Table 3 are constant and therefore independent of the fluence except for \(C_\xi\). Here, large differences are obtained, leading to large variations in the magnitude of the \(\text {E}({\tilde{m}})\) curve of about 10 %. In detail, \(\text {E}({\tilde{m}})\) is increased by 11 % in the case of 90 % \(H_{\text {mean}}\) and lowered by 9 % in the case of 110 % \(H_{\text {mean}}\). This shows that uncertainties in the fluence propagate almost 1:1 into the uncertainty of the derived absolute value of \(\text {E}({\tilde{m}})\), but not in the derived value of the dispersion exponent (in the investigated fluence regime).

To further clarify the correlations between the dispersion exponent and the other inferred values, a Marcov Chain Monte Carlo (MCMC) approach was used to produce a series of x, which become ergodic to the posterior probability density function [17]. Again, \(\lambda _\text {exc}=650\) nm was chosen as an example case. The results of the MCMC with 30 random starting positions with a length of 40,000 steps each can be seen in Fig. 7.

Fig. 7
figure 7

Results of a MCMC with 30 random starting points with each 40,000 steps. The first 10,000 steps of each starting point were omitted to exclude the burn-in phase. The diagonal axes represent the marginalized histograms

Full size image

On the diagonals of this image, the marginalized histograms of the respective parameters are shown, which represent the probability density functions for each variable. Considering the histogram of \(\xi\), it can be seen that the absolute value has a relatively prominent peak at \(\xi =1.68\) (the value also derived by the least square method), while having a narrow width. This indicates that the uncertainty considering this value is relatively small. However, considering the scaling factor \(C_\xi\), a much broader distribution can be seen, ranging from approx. 23 up to 32, with a peak at 29. Looking at the \(\xi\)-\(C_\xi\) correlation plot, a strong positive correlation between the two is observed. A negative correlation can be seen for \(\xi\) and \(d_\text {p}\) as well as for \(C_\xi\) and \(d_\text {p}\). These correlations complicate the inference of the absolute value of \(\text {E}({\tilde{m}})\).

In this work, the simulations were performed using a monodisperse particle diameter. In flames, however, particle sizes usually follow a log-normal size distribution. Even though the particles are all heated to the same temperature by the laser pulse (assuming that the Rayleigh approximation is valid), the larger particles cool slower, leading to different spectra, as the latter ones are temperature-dependent. To test the influence of polydispersity on the inferred values, the simulations were also performed assuming a log-normal particle distribution with a median of 26.8 nm and a geometric standard deviation of 1.3 (based on the results from TEM) for \(\lambda _\text {exc}\) = 650 nm and C\(_2\)H\(_4\). This leads to an accommodation coefficient of \(\alpha\) = 0.2, a gas temperature of \(T_\text {g}\) = 1552 K and a dispersion exponent of \(\xi\) = 1.69 together with \(C_\xi\) = 28.2. Comparing these values with the ones derived in the case of the monodisperse simulation (cf. Table 2), only minor differences are present. Therefore, the influence of polydispersity on the derived values is considered negligible.

Additional information about the fitting procedure can be obtained from the residuals, which are shown for the case of C\(_2\)H\(_4\) in Fig. 8.

Fig. 8
figure 8

Residuum for \(\lambda _{exc}=450\) nm in the first line, for \(\lambda _{exc}=532\) nm in the second,\(\lambda _{exc}=600\) nm in the third and for \(\lambda _{exc}=650\) nm in the fourth line in the case of C\(_2\)H\(_4\). The images from left to right correspond to 5 ns, 85 ns, 105 ns, 125 ns, 175 ns, 225 ns, 325 ns, 425 ns, 625 ns, and 775 ns after the peak of the laser pulse

Full size image

As it can be seen, most deviations between the model and the measurement data are within two standard deviations, the general model thus seems suitable. Looking at early times after the laser pulse, systematic trends in the deviations are visible, especially for 450 nm and 532 nm. It is unlikely that fluorescence is the reason for this since the second images represent measurements 85 ns after the peak of the laser pulse, where no more fluorescence is present [9, 22]. Therefore, we assume the above-mentioned laser-induced changes in the optical properties (Sect. 3) as a reason for these deviations, especially, as they are more pronounced for the lower excitation wavelengths for which the highest absorptive heating rates were achieved (c.f. Table 1 and Eq. 6). Our assumption is further supported by the temporal behavior of the deviations: It is visible that the patterns become weaker for later time steps (for all excitation wavelengths), which might be due to the fast and strong altering of the optical properties shortly after the laser pulse, followed by only slow and weaker altering for later time steps [27]. However, despite these deviations at early measurement times, our results show that the model for \(\text {E}({\tilde{m}})\) and the derived values are very suitable for practical LII-measurements and evaluation.

Regarding our value obtained for \(\xi\), it appears relatively high in in comparison to other values from the literature [12, 13, 24, 26, 30,31,, 31]. For a better comparison, we evaluated \(\text {E}({\tilde{m}})\) with the values given in the references and normalized all obtained curves to their respective maxima, the results are shown in Fig. 9.

Fig. 9
figure 9

Comparison of the normalized derived mean \(\text {E}({\tilde{m}})\) functions with literature values. Data of Migliorini and Bauer are corrected by factors due to laser irradiation based on Migliorini et al. [27], see text

Full size image

The curves derived by Köylü et al. [31] deviate from other data sets in terms of their slope, rising from \(0<\xi <1\). A possible reason for this might be that the functional form was derived over a wide wavelength span ranging from 514 nm up to 5.2 \({\upmu }\)m. This might induce errors for the visible wavelength region due to the increase of \(\text {E}({\tilde{m}})\) for higher wavelength regions.

Török et al. [12], which used soot from a soot generator, measured \(\xi \approx 1.2\) for mature soot (OP1). However, they derived this value by heating the particles with two lasers at \(\lambda =532\) nm and at \(\lambda =1064\) nm and adjusted the fluences to generate the same LII signal at both wavelengths. This approach and the thus derived \(\xi\) might therefore not be directly comparable to the result derived in this work, as the wavelength-dependent absorption function is not monotonously decreasing but increases at wavelengths higher than approximately 900 nm, cf. [24]. This increase with wavelength leads to a decrease in the value of \(\xi\) to match both values. In [32], it is shown that the value of \(\xi\) strongly depends on the wavelengths used to evaluate it, ranging from \(\xi\)=1.1 when evaluated from 685 nm to 1064 nm up to \(\xi\)=1.45 when evaluated using 405 nm, 655 nm, 850 nm and 1064 nm simultaneously. One should keep in mind that the equation used to model the \(\text {E}({\tilde{m}})\) behavior (Eq. 4) is a monotonous function, leading to deviations in the exponent \(\xi\) when evaluated over a wide spectral range with non-monotonous behavior. For this reason, the \(\xi\)-value of this work might not be directly comparable to previously derived values which were evaluated using wavelength regions with increasing absorption function.

Chang et al. [30] derived values for the real (n) and imaginary (k) part of the complex index of refraction \({\tilde{m}}\) for a premixed propane–oxygen flame with a equivalence ratio of \(\Phi =1.8\) via extinction measurements and Kramers-Krönig relations. From n and k, \(\text {E}({\tilde{m}})\) can be calculated by evaluating \(\text {E}({\tilde{m}})=-\text {Im}\{({\tilde{m}}^2-1)/({\tilde{m}}^2+1)\}\) where \({\tilde{m}}=n-ik\) [1]. These values are in relatively good agreement with the values derived by Yon et al. [24], where diesel soot at room temperature was investigated via extinction measurements and Lorentz–Drude model for deriving the real and imaginary part of \({\tilde{m}}\). Both the function of Chang et al. and Yon et al. show a smaller slope compared to the functions derived in this work, implicating a lower value of \(\xi\).

Migliorini et al. [27] carried out measurements to obtain temporally and wavelength resolved extinction coefficients for laser irradiated mature soot with different fluences. Starting with a low value of \(\xi _0=1.0\) for non-irradiated mature soot particles [26], they observed an increase in the dispersion exponent with increasing fluence by factor of up to 2.25 for the highest fluence of 400 mJ/cm\(^2\) at 1064 nm used in this study [27]. To compare the results of Migliorini et al. [26, 27] obtained at 1064 nm laser wavelength with our results and taking Eq. 3 into account, we evaluated the factors of [27] at laser fluences of 130 mJ/cm\(^2\) and 220 mJ/cm\(^2\) as they roughly correspond to the minimal and maximal corresponding values in our study (comparable to our value at 650 nm and 450 nm, respectively). The value of \(\xi _0\) = 1.0 for pristine particles is then multiplied by those factors, the resulting normalized \(\text {E}({\tilde{m}})\) curve is plotted in Fig. 9. In general the curve obtained for 220 mJ/cm\(^2\) is in very good agreement with the derived curve in this work. At the lower corresponding fluence of 130 mJ/cm\(^2\) the slope is smaller, implicating a lower value of \(\xi\). However, one should keep in mind that the initial value of \(\xi _0\) corresponds to very mature soot in [26] and is thus comparably low, leading to low \(\xi\)-values even when including the correction factors caused by irradiation. As most recent extinction data published by Bauer et al. show, mature soot in the same flame and at the same measurement position as in this work exhibits a value of \(\xi _0\) = 1.25 [13]. A similar value is obtained when extracting \(\xi _0\) from the extinction data of Migliorini et al. [33]. Correcting this dispersion exponent with a correction factor of 1.5 corresponding to a fluence of 160 mJ/cm\(^2\) (the average corresponding value of our measurements) \(\xi \approx 1.9\) is obtained, the resulting curve for normalized \(\text {E}({\tilde{m}})\) is depicted in Fig. 9.

These comparisons demonstrate the applicability of our novel technique for the determination of \(\xi\) based on and thus suitable for practical LII-measurements.

5 Conclusion

In this work, a new approach to determine \(\text {E}({\tilde{m}})\) for laser-heated soot particles was presented. To this end, emission spectra of the heated particles were measured with a spectrograph coupled to an intensified camera, which was used for sequential recordings with various delay times to the laser pulse. Heating of the particles was achieved employing an OPO at four different excitation wavelengths. These measurements were performed at HAB 40 mm for ethylene and propane. By the use of an advanced LII model the temperature of the laser-heated particles could be calculated and thus the spectral emission was modeled. Accounting for the wavelength-dependent absorption function \(\text {E}({\tilde{m}})\), the modeled spectra were fitted to the corresponding measurements by optimizing input parameters via a least-squares approach. Similar results were obtained for \(\text {E}({\tilde{m}})\) independent of the utilized fuel gas.

With the presented approach it is possible to gain deeper insight into the optical properties of soot particles in practical LII-applications which ultimately helps to improve the knowledge about the formation process. Additionally, it might be used to follow changes in soot structure in situ, which shows strong correlation to the inferred quantities. Further, the technique can be applied to other nanomaterial systems that often suffer from incomplete knowledge about optical properties. These materials can be used in a wide range of applications such as catalysts, photovoltaics or batteries [15]. Concluding, as many optical diagnostics rely on precise knowledge about the optical absorption function in the measurement situation, the presented approach is a very promising alternative to extinction-based techniques to determine the optical properties of soot and possibly of other materials.