1 Introduction

Myriads of middle-infrared (midIR, 1400–3000 nm) applications require either broadband ultra-short pulses or wide tunability. In recent years, lots of research have been conducted on solid-state laser materials emitting in the midIR spectral range (such as Tm\(^{3+}\), Ho\(^{3+}\), Cr\(^{2+}\) or/and Er\(^{3+}\)-doped materials) [1, 2]. However, these active materials cannot directly generate few-cycles pulses (FCP) without a nonlinear (post-compression) stage [3, 4].

Optical parametric (chirped pulses) amplifiers (OP(CP)A) using second-order nonlinear processes are often used as an alternative approach. Bulk or structured nonlinear crystals, such as BBO, KTA, or APPLN (APeriodically Poled Lithium Niobate), have successfully been used to produce broadly tunable coherent midIR radiations [5] or wide spectra compatible with FCP with a passive stabilization of the carrier-to-envelope phase (CEP) [6]. While they exhibit a very good efficiency and exceptionally high damage threshold and/or low thermal loads at high repetition rate, crystal-based OP(CP)A generally suffers from rather poor beam quality. Thus, more recently, fibered OPCPA (f-OPCPA) based on third-order four-wave mixing (FWM) process have been proposed, to exploit the advantages of fiber confinement [7]. This confinement can be in the form of a hollow-core fiber with a FWM in gas [8], or in dispersion-engineered fibers, where its use near the zero-dispersion wavelength generated a broadband spectrum [9].

In this paper, we explore the generation of a broadband spectrum in the midIR through degenerated Four-Wave Mixing (d-FWM) far from the zero-dispersion wavelength (ZDW). This process, occurring in centrosymmetric media such as silica, is characterized by the generation of a pair of photons (resp. signal \(\lambda _s\) and idler \(\lambda _i\) with \(\lambda _s<\lambda _i\)), from two pump photons at \(\lambda _p\).

In order to characterize the taper properties, the gain bandwidth and phase matching curves are usually retrieved by measuring (as a function of the pump wavelength and power) the signal and the idler spectra resulting from the parametric generation (i.e unseeded or spontaneous). This technique has been widely applied for characterizing uniform fibers or fibers with exotic shapes and materials [10], or else directly for FWM-based Optical Parametric Oscillators (OPO) and Amplifiers (OPA) [11,12,13,14].

Through the phase matching curve of d-FWM process, large tuning ranges are accessible by tuning the central pump wavelength [15]. However at a fixed pump wavelength, the gain bandwidths obtained are relatively narrow. Highly nonlinear photonic crystal fibers (HNL-PCF) exhibit numerous advantages for spectrum broadening, with their large flexibility in design and the related chromatic dispersion management.

Our aim is to investigate home-made tapered HNL-PCF (later referred as "taper") which ZDW and higher-order dispersion shift along the taper in order to extend the range of d-FWM parametric gain over a spectral width of typically 200 nm at 1.8 \(\mu\)m. As shown later, this is 4 times larger than the spectrum obtained with the same untapered HNL-PCF.

2 Fabrication of taper

The fabrication of long tapers suited for parametric amplification raises several challenges. First the taper profile must vary smoothly enough (adiabatic variation) in order to preserve the transmission properties, to prevent random perturbation in the profile, to provide the required phasematching properties. Secondly one must avoid any hole coalescence. As a consequence, we have developed the following fabrication procedure.

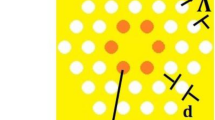
A constant diameter PCF is initially fabricated using the conventional "stack and draw" method. In such fibers the transverse profile geometry is characterized by the core diameter \(d_{\text {core}}\), the air-holes diameter \(d_{\text {hole}}\) and the pitch \(\Lambda\) (distance between two adjacent air-holes). This fiber can serve as a reference to compare the effect of spectral broadening investigated later.

The tapers are then obtained by reducing the PCF size. In practice, during the fabrication of the tapered fiber, the key parameter is the outer (cladding) diameter \(\phi _{\text {clad}}\), however, the other geometrical parameters (core and air holes sizes) of the structure vary in a homothetic way (e.g. \(\phi _{\text {clad}}=125\, \mu m\) and \(d_{\text {core}}=6.49\, \mu m\) for \(\Lambda _0=4.5\, \mu m\) while \(\phi _{\text {clad}}=139\, \mu m\) and \(d_{\text {core}}=7.20\, \mu m\) for \(\Lambda _0=5.0\, \mu m\)). Note that the homothety assumption is valid for the relative size variations <5% targeted here (see Table 1).

Table 1 Tapers characteristics: \(\phi _{\text {clad},<}\) and \(\phi _{\text {clad},>}\) are the smallest and the largest external diameters, L is the taper length. Fiber A external diameter is constant
Full size table

The size reduction is controlled by varying the coiling speed using a home-made automated software. Indeed at a fixed temperature and gas pressure, and assuming a homothety between the outer fiber diameter and all the other quantities, we can see from the mass flow conservation law between the preform (diameter \(\phi _p\), speed \(v_p\)) and the fiber (diameter \(\phi _{\text {clad}}\), speed \(v_f\)):

$$\begin{aligned} \phi _p^2\times v_p=\phi _{\text {clad}}^2 \times v_f \end{aligned}$$
(1)

that the fiber diameter \(\phi _{\text {clad}}\) can be controlled by adjusting the drawing speed \(v_f\). An in-line measurement monitors the outer diameter during the taper drawing (Fig. 1).

In order to explore the influence of the taper slope, length, and smallest/largest diameter, four different tapers respectively denoted B, C, D\(_1\) and D\(_2\) along with a reference fiber A were drawn and further characterized.

Fig. 1
figure 1

Variation of the measured external diameter for the taper B, C, D\(_1\), and D\(_2\)

Full size image

3 Numerical simulations

The proposed tapered HNL-PCF is based on a small and continuous variation applied on the external diameter of the fiber. The idea is to longitudinally change the dispersion properties of the fiber experienced by the pump radiation (close to 1.03 \(\mu\)m) and particularly its "local" zero-dispersion wavelength (ZDW) which progressively shift along the propagation. The concept is similar to an APPLN crystal, where the linear aperiodicity shifts the generated signal along the crystal [16]. As a consequence both the generated signal and idler output spectra are broadened. Compared to a uniform diameter fiber of the same length, a given d-FWM bandwidth within this composite spectrum is generated over a shorter fiber segment, thus reducing its parametric gain. In order to maintain a high parametric gain, the taper needs to be lengthened. Moreover, as the core diameter decreases, the effective nonlinear coefficient \(\gamma\) varies inversely:

$$\begin{aligned} \gamma =n_2\omega /A_{\text {eff}}c \end{aligned}$$
(2)

with \(n_2\) the nonlinear refractive index change due to Kerr effect, and \(A_{\text {eff}}\) the effective mode area. The interplay between these effects results in a complex behaviour than can be rendered by numerical simulations based on the general nonlinear Schrödinger equation (GNLSE) [17]. Nonetheless, accurately modelling the GNLSE including the minute details of the taper variation, although feasible, brings no further insight into the overall spectrum features, and we thus modelled the taper by dividing it into four different segments each being uniform as represented in Fig. 2.

Fig. 2
figure 2

Schematic representation of the tapered HNL-PCF used in simulations: the taper is divided into \(N=4\) fiber segments (F\(_0\), F\(_1\), F\(_2\), F\(_3\)), whose characteristic size varies linear from F\(_0\) to F\(_3\)

Full size image

The four fiber segments (noted F\(_0\), F\(_1\), F\(_2\) and F\(_3\) all 30 cm long) possess different external diameters, as shown in Fig. 2. The geometrical properties of the i-th segment are incremented according to \(\Lambda _i = \Lambda _0 \times (1+i\times 1.5\%)\), with \(\Lambda _0=4.5\, \mu m\) and the ratio \(d_{\text {hole},i}/\Lambda _i=0.59\) is kept constant. As an example, for each i-th section of the taper considered in our simulation, the outer diameter and ZDW are reported in Table2.

Table 2 Outer diameter \(\phi _{\text {clad}}\) and ZDW (in \(\, \mu m\)) of the F\(_0\), F\(_1\), F\(_2\) and F\(_3\) sections used in the simulation of the taper in Fig. 2
Full size table

The change in geometric parameters (core diameter, pitch, air-hole diameter) due to outer diameter variations causes the dispersion properties to vary. The most important parameter being the ZDW that is gradually shifting (see Table 2). The higher-order dispersion terms \(\beta _{n,\text {ZD}}\) are also varying along the taper (see Table 3). They too play an important role along the ZDW since the Stokes shift \(\Omega\) (\(\omega _{s,i}=\omega _p\pm \Omega\)) with respect to the pump angular frequency \(\omega _p\) is given by:

$$\begin{aligned} \Omega (\omega _p)=\bigg (-\Big (Q+\sqrt{Q^2-4P\beta _{\text {NL}}}\Big )/2P\bigg )^{1/2} \end{aligned}$$
(3)

where \(P=\left( \beta _{4,\text {ZD}}+\beta _{5,\text {ZD}}\cdot (\omega _p-\omega _\text {ZD})\right) /12\) and \(Q=\beta _{3,\text {ZD}}\cdot (\omega _p-\omega _\text {ZD})+\beta _{4,\text {ZD}} \cdot (\omega _p-\omega _\text {ZD})^2/2+\beta _{5,\text {ZD}}\cdot (\omega _p-\omega _\text {ZD})^3/6\) with \(\omega _\text {ZD}\) the zero-dispersion angular frequency, \(\beta _\text {NL}\) the nonlinear dispersion due to the cross-Kerr effect induced by the pump, and the \(\beta _{n,\text {ZD}}\) are the n-th-order dispersion evaluated at \(\omega _\text {ZD}\). As a consequence, the d-FWM phasematching curve is gradually changing along the taper as \(\omega _\text {ZD}\), the \(\beta _{n,\text {ZD}}\), and \(\beta _\text {NL}\) vary with the taper cross-section thus leading to a broadened gain spectrum.

Table 3 High-order propagation constant \(\beta _{n,\text {ZD}}\) for \(n=3, 4\), and 5 evaluated at the ZDW for 125, 128, 132, and 139 \(\, \mu m\) outer diameters
Full size table
Fig. 3
figure 3

(a, top) Wavelength dependence of the group index \(n_g\) for the PCF with 128 \(\mu\)m outer diameter. (b, bottom) Group index difference \(\Delta n_g\) between PCF with outer diameters of 125, 132 and 139 \(\mu\)m and the PCF with 128 \(\mu\)m outer diameter taken as reference

Full size image

Moreover, as illustrated in Fig. 3a, the group index \(n_g\) varies by \(\sim 0.01\) between the signal and idler wavelengths. This group velocity mismatch (GVM) may reduce the temporal overlap between the pump, the signal to be amplified and the resulting idler. However, this is not the case for the ASE source used here since its 50 ps are long enough to overcome this effect. However, as far as f-OPCPA is concerned, the quasi-monochromatic frequency of the chirped signal have a typical duration of \(\sqrt{\varphi ''}\) of few picoseconds (\(\varphi ''\) is the group delay dispersion introduced on the signal before its amplification). The pulse coherent length \(L_p\) is typically of 5 to 10 cm (\(L_p\) is due to temporal walk-off resulting from GVM and shall not to be confused with the wave coherent length \(L_w\) due to phase mismatch). This further highlights the necessity of using a taper for broadband chirped pulse amplification. Indeed each signal component will only be amplified in a given portion of length \(L_p\) within the taper of length L. Consequently, adjusting the pump and signal chirp and delay along with a suitable taper variation rate allows more frequency component to be amplified in a suitable taper portion than in an untapered fiber. The full discussion of f-OPCPA design (taper parameters, chirps rates, pump pulse shaping,...) is still subject to investigation and is not further detailed here as it lies beyond the scope of the present paper.

Figure 4 shows the numerical results from solving the GNLSE for each piece of fiber considered separately (Fig. 4a–d) and for the whole concatenated structure (Fig. 4e). The input pulse considered in the model is characterized by a central wavelength of 1.03 \(\mu\)m, a peak power of 44 kW and a 50 ps full width at half maximum (FWHM) with a repetition rate of 10 MHz. The effective indices and effective areas of each fiber segments are calculated through the Saitoh and Koshiba empirical method [18]. We can see from Fig. 4a–d that the central wavelengths of the generated idler are slightly red-shifted with the increase of the external fiber diameter. This shift is directly linked to the increase of the local ZDW of the taper as the core diameter increases. The composite idler spectrum of the ensemble (F\(_0\)-to-F\(_3\)) is represented on Fig. 4 e. The generated idler spans across the whole bandwidth resulting from the addition of the individual spectra. The use of the taper thus widens the idler spectrum in a considerable manner.

Fig. 4
figure 4

Numerical simulations of the generated idler spectra along the taper depicted in Fig. 2. The build-up of each spectra for the individual sections (a) F\(_0\), (b) F\(_1\), (c) F\(_2\) and (d) F\(_3\). The build-up of the full taper spectrum (e). The insets correspond to the output generated idler spectra

Full size image

4 Experimental setup

Fig. 5
figure 5

Experimental setup of the tunable stochastic pump source which allows a characterisation of the tapered fiber

Full size image

In order to experimentally validate the numerical results, HNL-PCFs have been fabricated, with their characteristics reference in Table 1. In this paper we only report the experimental study of the B taper (and its reverse B’), with a linearly varying external diameter from 125 to 132 \(\mu\)m over a 2 m long piece of fiber. In order to compare it with an untapered fiber, a same HNL-PCF with a constant external diameter of 128 \(\mu\)m close to the average B taper diameter has also been fabricated (fiber A).

The pump source developed to characterize the fibers is schematized in Fig. 5. The tunability is obtained by pumping an Ytterbium-doped fiber, which generates an Amplified Spontaneous Emission (ASE) over the 1020 to 1070 nm Ytterbium emission bandwidth. A tunable band-pass spectral filter (Waveshaper 1000A, Finisar) reduces the spectrum to a 0.2 nm bandwidth. After an amplification stage which compensates losses induced by the filter, the light seeded a commercial amplification stage (Manny, Irisiome), which not only amplifies the seed wave but also cuts the temporal profile in pulses with a periodicity controlled by an external RF synthesizer. It results in 50 ps pulses train with a repetition rate of 10 MHz, and for a maximum energy of 1 \(\mu\)J, which corresponds to a peak power of 20 kW, and an average power of 10 W. A telescope is used to adapt the beam size to the numerical aperture of the tapers and a half-wave plate combined with a polarizing cube control the pump power.

Compared with a coherent pumping, an ASE source exhibits numerous advantages for measuring the phasematching curves and/or the gain bandwidth of a nonlinear medium. First, for the same average power, incoherent sources are known to provide an enhanced yield for nonlinear effect [19], making the measurement easier and less likely to damage the material under test. Secondly, parametric gain response are broader with incoherent rather than coherent pumping [20].

The HNL-PCF under test is put on a three-axis support (Nanomax, Thorlabs) and the launched pump beam is done using a 8 mm focal lens. At the fiber output, to separate the pump from the generated idler and signal waves, different dichroic mirrors are used before the analyse of their average spectra with a spectrometer (NIRQuest, Ocean Optics) or an Optical Spectrum Analyser (OSA, AQ6370, Yokogawa). In order to effectively compare the spectrum obtained using either a tapered or an untapered fiber, the experimental study has been done using a pump power which generate 100 mW of signal power, and the same fiber lengths (two meters).

5 Discussion and conclusion

The resulting spectra are reported on Fig. 6 for different pump wavelengths. The idler spectra are a simple conversion of the signal spectra through energy conservation. This conversion has been validated with a mid-IR spectrometer. For sake of comparison, we first recorded the results for an untapered fiber. The reference fiber A idler spectra exhibit a blue detuning with the increase of the pump wavelength, while keeping approximately the same bandwidth: this is the expected behavior for a d-FWM with a pump wave far from the zero-dispersion wavelength [15].

As the reference, all tapers exhibit the same blue detuning as the pump is tuned toward long wavelengths. However, taper generally exhibit a more complex spectrum that peak at a slightly lower frequency than the untapered case. This shift has also been observed in simulation (Fig. 4e).

In order to explain the observed shift towards lower frequencies as compared to fiber A, we discuss below the case of the taper B, and consider the d-FWM parametric generation depending on the taper orientation denoted B as the pump propagates from the small to the large end, and B’ as pump propagates from large to small.

One should first recall that for a given pump wavelength, a larger core (i.e. outer diameter here) results in dispersion parameters (ZDW, \(\beta _{n,ZD}\)) that will generate longer idler wavelength (see Eq. 3). For taper B, shorter idler wavelength are generated first at the small diameter end, and experience the full taper length propagation and gain, while the longer wavelength are only generated at the exit of the large diameter end. Fiber A having a core diameter which is the average of the taper B two end diameters, one might expect the taper B idler spectrum distortion to be at shorter wavelengths compared to fiber A spectra. Conversely, one expect an idler spectrum distortion toward longer wavelength for taper B’ (long wavelength are first generated in the large end and further amplified.

However, we can see that (i) the amount of shift with respect to reference fibre spectra is more or less prominent, and (ii) the spectra are consistently shifted at a longer wavelength than the reference fiber.

While the former effect remains unclear, the latter counter-intuitive effect results from a complex interplay between the variation of the effective nonlinear coefficient \(\gamma\) that depends on the effective mode area \(A_{\text {eff}}\) (Eq. 2), the varying position at which phasematching (where a substantial parametric gain) occurs for a given idler frequency component, and the accessible build-up length for each component. Among these factors, the most important one is due the nonlinear dephasing \(\beta _\text {NL}\) whose increasing values tend to "redshift" the idler branch of the phasematching curve (Eq. 3). Since the taper B contains a whole section (half of the taper length) where the diameter is smaller, the reduced effective mode area results in higher \(\beta _\text {NL}\) than in fiber A thus resulting in the observed redshift regardless the taper orientation (B or B’).

In all cases, the obtained spectra are always broadened compared to a untapered fiber, with for example the 1050 nm pump wavelength, a broadening by a factor of four.

Fig. 6
figure 6

Experimental idler spectra as a function of the pump wavelength for a d-FWM in the B taper (red), the B’ taper (green) and the reference A fiber (black)

Full size image

In conclusion, we have presented a new HNL-PCF, with a linearly varying diameter along its length in order to widen its spectral bandwidth. We demonstrated through experiences and simulations a nearly four-times broadening of the spectrum (196 nm corresponds to 24.5 fs coherence time). This indicates that tapers are potentially favorable for the amplification of broadband pulses such as few cycles (4.1 cycles at 1.8 \(\upmu \hbox {m}\)) mid-IR pulse in a coherently seeded f-OPCPA configuration and with a suitable recompression. This new technique represents an interesting concept in order to design fibered and broadband mid-IR laser sources since the concept can be extended to any pumping wavelength and fiber structures or materials. Further numerical simulations are needed to understand the potential of this technology and its optimal design parameters.