1 Introduction

Soot formation and destruction in hydrocarbon flames have been under investigation for a considerable time [1]. Understanding soot evolution in flames requires knowledge of many interdependent and spatially correlated parameters that impact on both the chemical and physical processes and those contribute to the formation, fragmentation and oxidation of soot particulates. Measuring and corelating the controlling parameters with local soot evolution under simpler laminar conditions, e.g., laminar premixed flat flames, have been the focus of many studies in the past [2, 3].

The complexity of the soot formation process stems from the fact that many of the steps happen at broad temporal rate and are affected by a number of factors including, temperature, pressure, strain rate and fuel type. For example, the ratio of carbon to other elements within a hydrocarbon fuel has major impact on soot propensity, so does pressure which has a strong effect on the fuel pyrolysis and nucleation process, which in turn affects the rate of soot formation and oxidation in a flame [4]. Soot formation under atmospheric pressures has many practical applications such as in heating furnaces, boilers and kilns. Research into these flames with conditions emulating those in industrial systems have been ongoing for decades [5]. Nonetheless, understanding soot formation mechanisms at high pressure is also of great interest especially in engines and gas turbines. The introduction of optical diagnostic techniques provides significant advantages over physical sampling methods under such conditions. Optical diagnostic techniques provide high spatial and temporal resolutions, which are important for confined flames under high pressure and turbulent conditions [5,6,7]. The in situ soots diagnostic methods, and the need of new tools to probe soot chemistry, has been covered by Michelsen 2017. [8]

The major processes of soot formation, including formation of gas phase soot precursors, soot inception and surface reactions, and particle–particle interactions have been outlined in the review by Wang et al. 2019 and the references within [9]. The soot morphology in high-pressure co-flow laminar diffusion methane flames has been recently investigated by Li et al. 2022. It was concluded that the maturity and oxidation resistance of soot particles increased with elevated pressure [10].

Nonetheless, many studies have focused on the effect of pressure on the structure and formation of soot in laminar premixed [11,12,13,14,15] and non-premixed [1, 16,17,18,19,20,21,22,23] flame conditions using a variety of fuels. Such flames are easier to stabilize and measure, especially that the effect and complexity of turbulence is eliminated and solely focus on the effect of pressure. The investigation of soot particles in turbulent flames have attracted wide attention due to their practical applicability. For example, Mulla et al. demonstrated simultaneous imaging of soot volume fraction and qualitative LIF of PAH and OH radicals in turbulent n-heptane spray flames. It was found there is no strong instantaneous correlations between soots-PAH, due to different chemical timescales of soot and the imaged smaller-PAH [24].

Despite the valuable contributions these studies have provided, the underlying understandings of soot inception and growth with respect to pressure is still limited [25, 26]. The findings from these studies all agree that soot concentration increases with increase in pressure. They reported the main effect of pressure on soot formation is taken as the increase in soot formation with a proportionality degree of Pn, where 1 ≥ n ≥ 3, (fv = kPn) in pressure range from 1 to 70 bar.

Low-pressure conditions provide good opportunity to investigate the soot formation process, as flame thickness and soot zone expand. This provides improvement in the spatial resolution and can benefit investigating of the soot inception conditions and enables the measurements of soots’ growth rates. Most of the published studies have been conducted using laminar flames and utilized laser-induced fluorescence (LIF) and laser-induced Incandescence (LII) in several premixed (CH4/O2/N2) flames at low-pressure environment [11, 27,28,29]. A significantly high value of n, namely 11, for low-pressure CH4/O2/N2 flames has been reported [11]. These studies concluded that pressure exponent n increases significantly with the increase in the level of aromatics in the fuel. For example, the n value is found to be 1.6, 2.9 and 5.3 or benzene, naphthalene, pyrene, respectively.

There has been enormous research volume directed into the soot particles formation; however, the goal of complete understanding is yet to be reached. It is not trivial comparing the data from the literature due to the use of different fuels, different flow conditions in the presentence of phase changing process. To introduce a common focal points and standard flames, two dedicated international workshops have been established, namely, the international sooting flames workshop and the international workshop on laser-induced incandescence. The work in this paper utilized the targeted C2H4/ Air premixed flame, at a desirable phi = 2.1 stochiometric ratio. Low-pressure conditions were chosen to access the regions needed to measure the surface growth, which, to the best of the authors’ knowledge, has not been reported previously in this targeted flame.

The specific aims of this work are to investigate the effect of pressure on soot volume fraction and evaluate the dependence of the pressure exponent n on pressure. The distance between the flame front and the location of the first detected soot particles is determined by recording the location of the CH* and C2* radicals. The qualitative PAH LIF and the gas temperature are used for further understanding the soot’s inception conditions. Finally, the transition between soot inception and surface growth have been investigated to revel the soot’s surface growth.

2 Experimental apparatus

Flat ethylene/air premixed flames were stabilized on a water-cooled McKenna burner, which consists of a porous plate with a diameter of 60 mm. A steel plate of 80 mm in diameter was employed at a height of 25 mm above the burner surface to stabilize the flames. Mixture of ethylene and air was supplied through the central porous plate with a total flow rate of 5 Liters per minute (L/min) and an equivalence ratio (Φ) of 2.1. Nitrogen was used as co-flow to shield the flames from surrounding air. All gas flows were controlled using mass flow controllers (Bronkhorst).

The McKenna burner was fixed onto an electrically controlled traverse and housed in a stainless-steel low-pressure apparatus with a total volume of 39.8 L and four optically accessible windows, as shown in Fig. 1. The traverse has a resolution better than 0.1 mm. To achieve measurements at different heights along the flame centreline, the burner was traversed vertically with a spatial resolution of 0.5 mm. The chamber was pumped down using a vacuum pump (Edwards, EDM12). The Pressure was measured using a Baratron (MKS, 122AA-0100AB) with an accuracy of ± 0. 2 kPa. To achieve this accuracy, an electronic pressure regulator and controlling system (Equilibar, QPV 1) was installed in the exhaust gas pipeline. This provides excellent pressure stability and kept the chamber pressure constant with a variation of 0.66 kPa. A Nikon camera model (D7100), with micro lens, was used to record the flames’ appearance.

Fig. 1
figure 1

Low-pressure combustion apparatus

Full size image

The gas temperature, Tg, was measured using a 75-μm-diameter uncoated Pt/Pt-R thermocouple (Omega). The measured values were corrected based on the heat radiation loss method, Shaddix [30]. The fine wire thermocouple was selected to minimize conductivity and radiation effects and other catalytic effects at the junction.

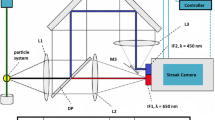
In the spatially resolved emission spectroscopy, the flame emission was imaged on the end of an optical fiber (Thorlabs, BFL200HS02) using two spherical lens, L1 and L2, as shown in Fig. 2 with focusing lengths of f1 = 300 mm and f2 = 250 mm. The fiber end was traversed vertically along the image of the flame centreline, thus collecting signals at different heights of the flame. The core diameter of the fiber is 0.2 mm and the position of the fiber end were controlled with an accuracy of ± 0.5 mm. The other end of the fiber was coupled into the slit of a spectrometer (Andor, Shamrock 500i) installed with a 150 lines/mm grating and an ICCD camera for signals record. The relative spectral response of this detection system was calibrated with a stabilize broad-band tungsten light source (Thorlabs, SLS201L). Then, the recorded spectra had been corrected for the relative spectral response of the detection system.

Fig. 2
figure 2

Experimental setup, where L1 and L2 represent lenses (f = 300 mm and f = 250 mm, respectively); OF is an optical fiber

Full size image

In the Laser-Induced Incandesces (LII) setup, the fundamental output (1064 nm and ~ 8 ns in duration) from a Nd:YAG laser (Surelite II) was used as an excitation source to heat up soot particles. The laser beam transmitted a half-wave plate and a Glen-laser polarizer, through which the laser power was varied. Then, the round laser beam was reformed into a horizontal laser sheet using a cylindrical lens (f = 750 mm). Within the detection volume on the centerline of the flames, the horizontally oriented laser sheet has a thickness of 1 mm and a width of 5 mm in the signal-viewing direction, which is perpendicular to the laser propagation direction. A laser fluence of 1.3 J/cm2 was used in all measurements, unless otherwise stated. LII signal, in the spectral region < 900 nm was collected using an intensified CCD camera (ICCD) and a short pass filter. The ICCD was set to operate at gate delay and gate width of 120 ns and 50 ns, respectively.

In the PAH Laser-induced fluorescence (LIF) measurements, the fourth harmonic (266 nm) of a 10 Hz pulsed Nd:YAG laser (Quantel, Q Smart) was used as laser source. The incident laser energy was kept at 23.3 mJ cm–2 per pulse to minimize possible interference from any LII signal from laser-heated soot particles. The laser beam was transmitted via a half-wave plate and a Glen-laser polarizer, through which the laser power was varied. The round laser beam was then reformed into a horizontal laser sheet using three cylindrical lenses. The LIF signal was collected at right angles to the laser propagation by a 100 mm focal lens. The lens was positioned so that the fluorescence is coupled to an optical fiber. The other end of the fiber was connected to a spectrometer (Andor, Shamrock 500i) equip with a 150 lines mm–1 grating. The fiber was fixed at the same position, while the burner was traversed vertically to obtain PAH LIF along different HABs. In this way, the incident laser energy is kept almost constant as the HAB changes. An ICCD (Andor, iStar) camera was connected to the spectrometer to record the LIF signals. The delay time and the gate width of the ICCD was set to zero and 30 ns, respectively. It was necessary to use a short gate width to avoid any contribution from possible LII signal of soot. To deal with minor flame fluctuation, the measurement was repeated 200 times to reach a reasonable average.

3 Results and discussion

To achieve stable low-pressure flames at Ф = 2.1, the flow rates for the C2H4, air and N2 co-flow were kept at 0.64 Lmin−1, 4.35 Lmin−1, and 1 Lmin−1, respectively. The total flow rate was 5 Lmin−1. It was found, by experiment, that the flame becomes unsustainable when the pressure was reduced below 27 kPa. The photos of stable C2H4/air flames, at different pressures, down to 27 kPa, are shown in Fig. 3.

Fig. 3
figure 3

Photographs of flat, rich premixed laminar flames at different pressures with Ф = 2.1

Full size image

To record the temperature profile, the thermocouple was fixed at one location and the burner was traversed vertically. The error from the thermocouple measurements was ± 75 K.

Typical recorded data for a pressure of 46 kPa, along with the correction parameters including velocity, viscosity, and thermal conductivity of the gas mixture, are listed in (Appendix 1_ Table 1), The velocity of the flow was simulated through a CFD model using the Ansys-Fluent software package, version 18.0. The viscosity and thermal conductivity of the gas mixture were calculated using the Chapman–Enskog theory and the relation of Wassiljwa [31], respectively. The viscosity was computed using Sutherland's formula [32] based on the Model of thermophysical parameters [33].

Figure 4 displays the corrected temperature profiles. All profiles show an almost linear increase of temperature in then preheat zone extending from 1 to 6 mm before a broad flame front from 6 to 10 mm and a steady decline up to 20 mm.

Fig. 4
figure 4

Corrected temperature axial profiles for flames with different pressures and HAB with Φ = 2.1

Full size image

Typical spatially resolved emission spectra are shown in Fig. 5. At heights from 0 to 23 mm above the burner surface with an increasing step of 1 mm, at each height 200 spectra were collected and averaged. Considering the configuration of the optical collection system, it is found that only the measurements below 3.2 mm were minorly influenced by the blocking edge of the burner by about 12%. Furthermore, flames images (Fig. 3) collected using a digital camera show no clear blue emission below 3 mm. In the hydrocarbon flame emission, the strong CH* (0,0) in from \({(A}^{2} \Delta - {X}^{3}\prod )\) system is noticeable at 431.5 nm partly overlapped by C2 emission at 436 nm, where the \({\mathrm{C}}_{2}^{*}\) emission reported by swan bands \({(d}^{3} {\prod }_{\mathrm{g}}- {a}^{3}{\prod }_{\mathrm{u}})\) are clearly detected at 436 nm, 472 nm and 517 nm [34]. The intensity of CH* and \({\mathrm{C}}_{2}^{*}\) was determined by integrating the peak in the range (418–431) nm and (500–525) nm, respectively.

Fig. 5
figure 5

Spatially resolved emission spectra for ϕ = 2.1 and pressure of 32 kPa at HAB = 4 mm (a) and HAB = 8 mm and (b)

Full size image

For the case with pressure of 48 kPa, the CH* radicals started to form at a height of 2 mm HAB, while the C2*radicals appeared at 3 mm HAB. The peaks of CH* and C2* increased from 3 to 5 mm HAB. The position of vanishing \({\mathrm{C}}_{2}^{*}\) was determined when the value of the peak of \({\mathrm{C}}_{2}^{*}\) was drop to 71% of the maximum value, However, The C2* emission profile disappeared at 6 mm HAB, while the CH* emission can be still seen at this location. The CH* emission decreased until it disappeared at 9 mm HAB. At 4 mm HAB, the emission of soot increased in intensity until 10 mm HAB from where it starts to decrease until the signal disappeared at 19 mm. At 32 kPa, the CH* radical appears at a height of 2 mm HAB, while the C2* started to form at 3 mm HAB. The signal intensifies by 4 mm, and the peak increases until a height of 6 mm HAB. At a height of 6 mm HAB, a soot emission was also observed, in addition to emission from CH* and C2* radicals. The emission from C2* vanishes at 8 mm HAB, and only emission from CH* and soot were recorded at this height. The peak of CH* diminishes once a height of 11 mm is reached, where at this height we can see only the emission of the soot profile. The soot emission starts to decrease from 12 mm and disappears at 17 mm.

The emission from CH* and C2* nearly overlaps with each other at atmospheric pressure, while the separation between them can be seen in the reduced pressure flames, particularly for pressure less than 40 kPa. It is also interesting to observe a clear separation between the C2* and CH* layers at reduced pressures.

At the lowest pressure case, 27 kPa, the peak of the emission of C2* appears later than that of CH*, at distance of ~ 0.6 mm. Moreover, the vertical distance between the two peaks decreasing linearly with increasing pressure with a slope of 25 × 10–9 ± 0.062 × 10–9 (mPa–1) indicating that the distance will approach zero at 53 kPa.

To extract the temperature of soot particles, the spatially resolved emission spectra recorded were used. It was necessary to remove the intensity data near the CH* and the C2* emission peaks, namely 431 nm, 436 nm, 472 nm and 517 nm. The recorded emission spectra were calibrated based of the detector response to a broad-band tungsten light source (Thorlabs, SLS201L). To obtain the soot temperature, it was assumed the soot’s emission can be approximated by blackbody radiation. A MATLAB function, Fit Blackbody Equation to Spectrum version 1.0.0.0 was used [34]. The function iterates to fit to the experimentally recoded spectra to yield the temperature, based on the best fit to the recoded data.

Figure 6 shows the measured Tg and Ts profiles. They show a slight difference between gas temperature and particles temperature at the height where the maximum temperature is found axially, particularly for the 48 kPa flame. This difference may be due to soot condensation on the thermocouple junction or the uncertainty of spectral properties of soot particles used to derive the temperature from the line-of-sight signals of soot luminosity. Nevertheless, the measured Tg agrees well and are fairly consistent with previous results [35, 36].

Fig. 6
figure 6

Axial profiles of gas and soot temperatures measured in three flames with a P = 48 kPa, b P = 35 kPa and c P = 27 kPa

Full size image

The LII signal was recoded at different HAB for flames with a pressure range of 48 to 27 kPa. A calibration process was performed to convert the recorded LII signals to soot volume fraction fv, between which a linear relationship exists [37]. A laser extinction measurement was carried out in a steady ethylene/air premixed sooting flame with equivalence ratio of 2.1. The flame was stabilized on the same McKenna burner at atmospheric pressure. A continuous laser beam at 1064 nm was used for the extension measurements. The mean soot volume fraction fv can then be calculated using the equation:

$$f_{{\text{v}}} = - \frac{\lambda }{6\pi E\left( m \right)L}ln\left( {\frac{I}{{I_{0} }}} \right),$$
(1)

where I/Io is the ratio of transmitted laser radiation to the incident, l is the laser wavelength and L is the optical path. The quantity \(6\pi E(m)\) represents the dimensionless extinction coefficient, Ke. The value of E(m) depends on the kind of soot, T and the laser wavelength [38]. The value of E(m) was set 0.265, as a reasonable choice for C2H4/Air premixed laminar flames, which results of Ke to be 5.01.

Figure 7 presents fv at different HAB for the different low-pressure flames investigated It is observed that the Soot volume fraction increases with HAB and that increasing the pressure has a significant enhancing effect on soot formation. A rapid increase in soot volume fraction starts at HAB of approximately 8–10 mm, where C2* and CH* emissions fade away.

Fig. 7
figure 7

Axial profiles of soot volume fractions under different reduced pressures

Full size image

Figure 8a present the soot volume fractions measured at HAB = 7 mm for the seven different pressure cases. A power fitting of the form fv = k Prn, where n is scaling factor, revels that n = 2.15. The exponential factor, n, slightly increases with HAB, as shown in Fig. 8b, revealing a weak dependence on the height above the burner surface. This slight increase in the exponential factor may also be attributed to the influence of the stabilizer plate at HAB = 25 mm, which can influence the flow fields when the flames’ propagate to the stagnation plate.

Fig. 8
figure 8

(a) Measured soot volume fraction (circles) measured at HAB = 7 mm for the different flames, and an exponential fit curve (dashed line) with a factor of n = 2.15, (b) the exponential factors fitted at different heights of the flames

Full size image

Figure 9 presents a summary of the values of the exponential factor n, including the value measured in the present work and those reported previously. The dependence of soot formation on pressure had been widely studied in pressure elevated flames, while the work performed in low-pressure flames is relatively rare. Interestingly, from Fig. 9 one can observe that the values of n are similar for different range of pressures and for different fuels investigated and found to in the range of 2–3.4. For N2-diluted C2H4 with co-flow laminar diffusion flames under high-pressure ranges, the exponent n was estimated as 1.8, when using CH4, CH4–air, C2H4 or C2H4–air. For C6H6–air, the pressure exponent value n was estimated as 2.0 for high-pressure ranges [13, 14, 18, 20, 39]. Karataş and Gülder [16] employed a circular co-flow burner type using an Abel-type inversion approach on a co-flow laminar diffusion flame type in their study on C2H4 flames diluted with N2 at pressures ranging between 0 and 20 bar; they estimated the exponent n to be 2.8. In [17, 19], pressure scaling was reported at the maximum volume fraction of the integrated soot with an exponent of n = 3.4 estimated for laminar diffusion n-heptane and co-flow laminar diffusion propane–air flames from 1 to 3 bar. Similarly, and also in accordance with the experimental results reported here, variation in the pressure exponential function of the soot volume fraction is very high when the experiment is conducted at low pressure. This was previously reported by Desgroux et al. who subjected CH4/N2/O2 at low pressure (20–28 kPa) at 30 mm HAB, as Our measured value is consistent with the previously reported vales at higher pressure and ~ 5 times lower than the value measure reported by Desgroux et al. for CH4/N2/O2 low-pressure flames [11], as illustrated in Fig. 9.

Fig. 9
figure 9

Comparison of the value of n obtained from this work with previous results. CH4/O/N [11], N2-diluted C2H4 [23] C7H16/air [17, 40], CH4/air [18, 20, 41], C3H8/ air [19], C6H6/ air and C2H4 /air [1, 13,14,15,16, 21, 22, 39]. the * indicates the measured value in this study

Full size image

Figure 10 presents a typical of PAH LIF spectra for a pressure of 40 kPa and at different HAB. The emission wavelength of PAHs increases along with an increase in aromatic ring size; hence, in several previous studies, the detection wavelength was varied to distinguish the relative size groups of PAHs. Three detection wavelength bands were used to distinguish three kinds of PAHs [42, 43].

Fig. 10
figure 10

PAH LIF spectra for Φ = 2.1 and pressure of 40 kPa at HAB = 1 mm (red), 4 mm (blue) and 14 mm (black)

Full size image

PAH LIF signal in the range 320–360 nm is due to 2–3-membered PAHs. Signals in the wavelength range 370–410 nm indicate the presence of 4-aromatic-ring-membered species. PAH LIF signals above 500 nm indicate the presence of PAHs with 5-membered ring structures, where the individual rings consist of five carbon atoms. Hence, PAH LIF signals of 500–550 are indicative of the presence of 5-membered PAHs. The signal strengths roughly indicate the concentration of the corresponding PAHs. The currently used LIF technique can only measure PAH concentrations in a qualitative manner, and it is still a big challenge to calibrate the PAH mole fractions from LIF signals measured in flames [44]. It is worth noting that LIF from liquid-like condense species and form PAH attached to soot surfaces may also contribute to the recorded LIF [45, 46].

Figure 11 a, b shows the PAH LIF over HAB (1–16 mm) at pressures of 40 kPa and 27 kPa, respectively, through three wavelengths range, 320–360 nm, 370–410 nm and 500–550 nm. From Fig. 11a with pressure 40 kPa, the wavelength range of 500–550 nm resulted in lower PAH LIF at low HAB than other wavelengths range, but PAH LIF increased after HAB = 12 mm and was higher than other wavelengths range. However, in the results shown in Fig. 11b, where pressure was 27 kPa, the wavelength range of 500–550 nm produced lower PAH LIF than did other wavelengths range over all values of HAB, and the wavelength range of 370–410 nm produced higher values of PAH LIF than did other wavelengths range for all values of HAB, but it decreased along HAB.

Fig. 11
figure 11

Axial profiles of three PAH LIF ranges corresponding to 2–3R, 3–4R and 35R at different pressures; (a) 40 kPa and (b) 27 kPa

Full size image

From Fig. 11a, b, the peak spatial distributions of (2–3R) PAH LIF were followed by the peak spatial distributions of (3–4R) PAH LIF with a difference of 1 mm HAB at both pressure settings. The peak intensity of (3–4R) PAH LIF was greater than (2-3R) PAH LIF at pressure of 27 kPa, where the peaks were close to each other at pressure 40 kPa. The spatial distribution of > 5R PAH LIF signals started to form when the (2-3R) PAH LIF signals reached their peak. These peaks are coincided with the location of maximum of intensity of C2*. However, it is hard to determine the peak spatial distribution of > 5R PAHs LIF signal, as the signal kept increasing inside the soot growth region which indicated soot and PAHs formation. However, The PAH LIF signal in the range 500–550 nm is strongly influenced by LII signal generated form the 266 nm laser radiation. Therefore, the PAH LIF for (R > 5) was not used further in the analysis. In both pressure setting, the soot signal started to rise after 1 mm the (2–3R) PAH LIF reached the peak intensity. The figure shows a negative relation in which the consumption of (3–4R) PAH LIF might be correlated with the soot onset. Such relationship is consistent with the findings reported at low pressure by Betrancourt et al. [47]. They reported, using butane/oxygen/nitrogen flames, that soot signal started at 1 mm after pyrene reached its peak intensity. In another study at atmosphere pressure, the onset of small PAHs when using an ethylene air flame was near the surface of the burner. The signal from the small aromatic species reaches a local maximum then the signal started to raise. After this, the signal of the large PAH starts to rise and continue to increase over the distance of measurement. The trend of soot volume fraction follows the large PAH. However, the onset of soot was located after the onset of both small aromatic species and large PAH around 2 mm [48].

Figure 12 summarizes the values of flame temperature for soot emergence, revealing a critical inception temperature, Tinception, of 1465 ± 66 K and that the value of critical inception temperature from soot formation slightly decreases with the pressure.

Fig. 12
figure 12

Temperature of first soot inception, as measured by the thermocouple, at Φ = 2.1, the datum at pressure 101 kPa was obtained from Saito et al.[49]

Full size image

To obtain reaction time scale, the velocity field of the flame was modeled by Computational Fluid Dynamics CFD, using the Ansys-Fluent software package, version 18.0. The CFD simulation model was the approach chosen to predict the velocity profile. However, the CFD model should be tested to ensure accurate and precise simulated results. To validate the model, the velocity profile was measured by a hot wire in a cold flow. The simulated profile was compared to the measured values, where the error margin is found to be better than 15%.

The total reaction time at each height above burner level, t(HAB), was calculated using Eq. 2, below:

$${\text{t}}({\text{HAB}} = i) = (\sum\limits_{{\text{HAB = 0}}}^{{\text{HAB = i}}} {{\text{dt}}_{{\text{HAB = i}}} } ),$$
(2)

where t(HAB = i) is the total reaction time at location HAB = i and dtHAB=i is the local reaction time at location HAB = i.

The local reaction time (dtHAB=i) was calculated based on Eq. 3, below:

$${\text{ dt}}_{{\text{HAB = i }}} = \frac{{x_{{\text{HAB = i + 1}}} - x_{{\text{HAB = i}}} }}{{v_{{\text{HAB = i}}} }},$$
(3)

where xHAB=i+1—xHAB=i is the distance between location xHAB=i+1 and xHAB=i, which equals to 1 mm, and vHAB=i is the velocity at location HAB = i. The time origin was set at the location where the first soot particles were detected.

Soot formation involves various physical and chemical mechanisms and reactions; however, soot particles nucleation and inception is the most important process in soot formation. This particularly because ~ 85% of the total carbon produced as a result of surface growth rather than soot inception. Models were developed and experiments were performed to define the rate of particle surface growth. Early models were based on the assumption that particle surface growth rate is dependent on either the surface area of the soot particle or the soot volume fraction.

Figure 13 presents reveal the spatial relationships among the parameters measured at the lowest pressure, 27 kPa. The spatial distributions include, T, CH* and C2*, chemiluminescence, (2–3R) and (3–4) PAH LIF, fv, and dfv/dt.

Fig. 13
figure 13

Spatial profiles for the premixed C2H4/ air flame stabilized at 27 kPa, temperature, a, chemiluminescence of CH* (dark blue triangle) and C2 * (light blue triangle), PAH LIF of (2–3R) (light brown circle) and (3–4R) (red square), b, soot volume fraction, c, Lagrangian time-derivative of soot volume fraction, d

Full size image

It is observed that the first detectable soot particles coincide with the location of maximum C2* emission. Soot particles are evidently formed within the descent region of the radical emissions, forming an overlap region of the radicals with soot. Above this region, a significant increase in soot volume fraction can be found in Fig. 11, indicating a faster soot formation rate than in the overlap region with the radicals. Another interesting observation is that Tg peaks in this soot–radical overlap region, indicating that this layer may be a critical region for understanding soot formation in this kind of premixed flames. Figure 11 also reveals the Tg where soot emerges, i.e., the temperature at the lowest location with detectable soot in the different flames.

Plotting \({df}_{\mathrm{v}}/dt\) versus HAB is expected to revel three important regions, region i with positive slope, region ii with a plateau and region iii with a negative slope, Bockhorn et al. [50]. When this has been tested for the flames investigated at phi = 2.1, the three regions were only observed at pressure of 27 kPa, as shown in Fig. 13 d. Region i, below 14 mm HAB, where the \({df}_{\mathrm{v}}/dt\) increases with increasing HAB can be connected to the soot particles inception process. region ii with a plateau observed from HAB ~ 14–17 mm, At HAB above 17 mm, a negative slope has been observed, as illustrated in Fig. 13 d.

One aim of this study was to measure the growth of a soot volume fraction at low pressure in premixed ethylene/air flames. Variables used were differential functions of soot volume fraction with respect to time (dfv /dt).

An early expression of this relationship was proposed by Wanger to express the relationship between the rate of particle surface growth and the soot volume fraction, as shown in Eq. 4. Harries and Weiner developed a model that helped in presenting a formulation to identify the rate of particle surface growth [51]. The state of the \({f}_{\mathrm{v}}\) profile has been found to follow the following first-order rate law, proposed by Bockhorn et al. [50]:

$$df_{{\text{v}}} /dt = k_{{{\text{SG}}}} \left( {f_{{\text{v}}}^{\infty } - f_{{\text{v}}} } \right).$$
(4)

In Eq. 4, \({f}_{\mathrm{v}}^{\infty }\) is the soot volume fraction at a vast distance away from the burner surface (i.e., plateau value) and kSG is a rate constant describing the time of active soot growth. The variable t is the ‘reaction time’, which describes the progress of measurable soot formation process.

To determine whether the pressure has some influence on kSG, a graphical representation was prepared by plotting \({df}_{\mathrm{v}}/dt\) as function of fv, as shown in Fig. 14.

Fig. 14
figure 14

dfv/dt as a function of soot volume fraction and linear fit for pressure 27 kPa (red line)

Full size image

Figure 14 shows the axial profiles of \({df}_{v}/dt\) as a function of \({f}_{v}\) for C2H4 flames stabilized at 27 kPa–48 kPa. The soot appearance rates are due to different processes including inception, surface growth, PAH addition, and oxidation Plotting \({df}_{\mathrm{v}}/dt\) versus \({f}_{\mathrm{v}}\) shows three regions, region I with positive slope, region ii with a plateau and region iii with a negative slope, Bockhorn et al. [50].

From HAB 14 to 17 mm, fv increases with time at a constant rate. Figure 15 shows the values \({df}_{\mathrm{v}}/dt\) as function of pressure.

Fig. 15
figure 15

dfv/dt at the plateau regains as a function pressure

Full size image

The values of \({df}_{v}/dt\) increased with increasing pressure to reach a maximum value of 3.4 × 10–7 s−1 at pressure 48 kPa. It was observed that \({df}_{v}/dt\) remains constant above 40 kPa. The smallest constant \({df}_{v}/dt\) recoded was 4.2 × 10–8 s−1 at pressure 27 kPa. This rate is still 40% more than the rate reported by [11] for CH4/N2/O2 low-pressure flame stabilized at 26.6 kPa. Equation 4 can be applied in region iii, where the slope is negative, to obtain the soot’s surface growth and PAH addition.

It was found that the evaluation of soot surface growth, \({k}_{SG}\), was only possible at lowest pressure of 27 kPa, where the slope declined sharpy after the plateau region. This decline was shown to be independent of temperature effect [52] and was interpreted as a decrease in the reactivity of the soot [52, 53]; however, the reason for the loss of reactivity remains unknown. The decline was also observed in flames of aromatic fuels [53].

The soot surface growth rate constant kSG was calculated to be 20 s−1, using linear fitting. It is worth noting that the temperature in the almost constant with HAB above 14 mm, with a \(dT/d(\mathrm{HAB})\) less than 50 K. In comparison with the previously published literature at elevated pressure [15, 54], atmospheric pressure [55, 56] and low pressure [11, 50], our recorded kSG is the lowest value, as shown in Fig. 16. The influence of low pressure on the soot volume fraction increases with almost the same magnitude as the increase in the peak value of \({df}_{v}/dt\). This corresponds to a slope change in \({df}_{\mathrm{v}}/dt\) as a function of \({f}_{\mathrm{v}}\). This further indicates the slowing or completion of the soot inception process [11].

Fig. 16
figure 16

Summary of previous studies’ soot growth rate, kSG, the * indicates the measured value in this study

Full size image

Figure 16 presents a summary of previously measured soot growth rate constant kSG along with values from this study. The figure indicates that the measured growth rate of soot in the current study is 80% lower, when compared to previous studies. The results presented above are also contrasted with a study by Tsurikov et al. [54], who examined the precise, spatially distributed soot concentration in flames employing various fuels, equivalency ratios, and pressures. In addition, to the aforementioned findings, Baumgärtner et al.[56] investigated the soot particles growth in terms of mass and number density was affected by the fuel type, temperature and the content of hydrogen atoms. The results showed that in the acetylene flames, the soot volume fraction grows dramatically, and the signals of light scattering can be seen effectively at just over 1 mm above the burner. The soot mass increase is likewise quite quick, and over 90% of the soot is created in less than 5 ms as particle coagulation occurs. Therefore, in conclusion, the current results and previous studies have deviating soot growth rate. This may be due to use different stabilizers at different places, for example, above the flame, which affects soot growth rate. The value of kSG is independent of pressure or fuel type and mixture composition, but it does depend on temperature.

4 Conclusion

The soot volume fraction, chemiluminescence of CH* and C2*, gas and particle temperatures have been measured in a series of flat premixed ethylene/air flames with a constant equivalence ratio of 2.1 and at sub-atmospheric pressures, from 27 to 48 kPa. The spatially resolved measurements reveal that the CH* layer thickness can be used as an indicator of the flame front, was larger than for C2*. It was observed that the distance between the maximum recorded intensity of CH* and C2* decreased linearly with increasing pressure—with a slope of 25 × 10–9 ± 0.062 × 10–9 (mPa–1). The lowest value of soot volume fractions was 0.19 ppb, recorded at 5 ± 0.5 mm above the burner surface in flames. This location coincides with the location of maximum C2*. It was found that the Soot volume fraction follows a power function with respect to pressure, i.e., fv ∝ pn and a value of n = 2.15 ± 0.7. It was also found that the value of n is weakly dependent on the measurement location above the burner. The measured gas temperature and particles temperature agree very well within ± 70 degree. Furthermore, a common temperature of 1465 ± 66 K was found at the early stage of soot inception. From the PAH LIF study, it was found that the maximum value for (2–3R) PAH LIF occurred at ~ 1 mm before the maximum value of (3–4R) PAH LIF. The soot surface growth rate kSG was calculated to be 20 s−1. This is 80% lower than previously published values recorded at elevated pressure.