1 Introduction

Fourier domain mode-locked (FDML) lasers are used for generating broadband frequency-swept pulses at a certain sweep-rate for imaging and detection applications. A common application of FDML lasers is in OCT imaging, which is widely used for diagnosing eye and cardiovascular diseases [1,2,3,4]. An FDML laser cavity features three essential elements, which are the semiconductor optical amplifier (SOA), the long optical fiber that is used for matching the sweep-period with the cavity roundtrip time, and the Fabry–Perot filter whose transmission band (passband) is periodically swept for cyclic tunable filtering [1, 2]. Ideally, FDML lasers should offer a distortion free output signal pattern. However, due to the internal dynamics of the semiconductor optical amplifier (SOA), irregular dips and fluctuations occur in the output signal pattern of FDML lasers [5,6,7]. The complete physical mechanism behind the formation of these power fluctuations is rather complicated due to the complexity of the overall system dynamics as imposed by the nonlinear electrical response of the SOA, the chromatic dispersion and self-phase modulation within the long optical fiber, and the time-varying frequency response of the tunable Fabry–Perot filter for the cyclic filtering of each spectral component within the gain-bandwidth of the SOA. The complicacy arises as the FDML laser operation continues for many roundtrips, and the nonlinear/dispersive/time-varying nature of the overall system renders the dynamics of each component, and each roundtrip, to be strongly dependent on the dynamics of other components and previous roundtrips, making it difficult to attribute these fluctuations to a certain instantaneous occurrence or a single component of the FDML laser.

Some of the most recent research on FDML lasers has focused on achieving ultra-stable, noise-free operation by eliminating the power fluctuations using different strategies [7,8,9]. In this paper, we will focus on the SOA linewidth enhancement factor (LWEF) and its effect on the FDML laser output signal via computing the number and depth of the power-dips (a.k.a. holes) for various values of the LWEF within the practical range. The LWEF stems from the refractive index fluctuations within the SOA active region owing to the variation in carrier density [10,11,12,13]. The value of the LWEF usually ranges from 1 to 10 for bulk SOAs, though it is shown to be much smaller for multiple quantum well (MQW)-based SOAs [14,15,16,17]. For SOAs with quantum-dot based active regions, the LWEF is shown to be extremely small (almost zero) [15] due to three-dimensional electron confinement. The LWEF itself is a measure of noise [18, 19] as it quantifies the fluctuations in the refractive index, which naturally introduce additional noise in the signal pattern of FDML lasers. Therefore, a high LWEF is expected to yield more dips in the signal pattern of FDML lasers, but the exact contribution of the LWEF on dip formation and the associated fluctuations in the signal pattern of FDML lasers has not been computed to our knowledge.

The frequent recurrence of power-dips is especially problematic for FDML lasers due to their highly nonlinear dynamics [20]. As the number of roundtrips in an FDML laser cavity increases, the frequency of power-dips may gradually increase and eventually push the system out of stability. Consequently, the signal to noise ratio is likely to keep on decreasing as the number of roundtrips increases, unless certain stability measures are taken [5, 7, 8]. The FDML laser dynamics are mainly determined by the dynamics of the SOA; therefore, the power-dips should originate due to the nonlinear SOA active region dynamics [6]. This is easy to predict since a high SOA LWEF signifies large fluctuations in the refractive index of the active region, which naturally cause sharp changes in the signal pattern [12,13,14,15,16,17,18,19]. Hence, we believe that using an SOA with a high LWEF is very likely to exacerbate the power fluctuations in an FDML laser output signal by amplifying the occurrence of power-dips.

The fluctuations in active region carrier density, which give rise to a higher LWEF, are both due to inter-band processes such as the Shockley–Read–Hall recombination and the Auger recombination, and due to the intra-band collisions of carriers [11]. The LWEF is mainly associated with the intra-band collision time [18]. It is suggested that a high intra-band collision time is associated with more intense carrier collisions as the carriers have more time to accelerate between each collision, which results in sharper changes in the refractive index considering the ensemble of carriers within the active region [18, 19]. For a given SOA pump current, minimizing the cross-sectional area of the active medium maximizes the carrier density, which decreases the time between each carrier-collision and reduces the LWEF. It is for this reason that the LWEF of an SOA can be minimized mostly at the design stage.

The span of several sorts of power fluctuations in FDML lasers are in fact due to a combination of different effects [6]. Our goal is to determine the percentage of the power-dips that can be eliminated by tuning down the LWEF. We intend to compute the effect of the LWEF on the quantity, strength, and duration of the dips. Measuring the duration of the dips may not always be very straightforward as some of the dips are not isolated from each other but rather occur intricately and interferingly [5, 7], thereby forming a complex pattern of fluctuations that may last for a much longer duration within a single roundtrip. Therefore, rather than focusing only on the duration of the dips, a concurrent investigation of the correlation of the LWEF with the number and strength of th

e dips is more useful. Most of the dips in the signal pattern have a duration between 10 and 100 ps. Notably, as the number of roundtrips in the FDML laser cavity increases, dips of longer duration with complex patterns (Fig. 1) may arise [5, 7].

Fig. 1
figure 1

Some of the dips and their patterns based on simulated data. The dips do not always have the same pattern

Full size image

Figures 1 and 2 illustrate the occurrence of power-dips based on the simulation parameters given in Table 1 [5, 7]. The identification of the dips and their counting along the signal envelope is based on the computation of the standard deviation \(\chi \) in optical power within a sliding frame of M grid-points (Eq. 1), which represent the discretization in time based on the sampling frequency. As indicated in the pseudocode below Eq. 1, dips are identified when a sudden change in power standard deviation occurs, and the durations of the dips are computed based on how much time the standard deviation in optical power remains above a certain threshold value. The statistics and observations on dip formation are as presented in Sects. 3.1 and 3.2 (Figs. 8, 10, 11). A basic illustration of the simulation model for generating the signal envelope is provided in Fig. 6. In this model, the laser operation self-starts via the amplified spontaneous emission (ASE) noise in the SOA. Once the signal is amplified in the SOA, it is passed through the optical fiber, and then filtered by the Fabry–Perot filter. The output of the Fabry–Perot filter is fed back to the SOA at the end of each roundtrip, and the operation continues in this sequence for many roundtrips. The resulting output signal envelope is given in the appendix section and the mathematical description of the whole process is outlined in Sect. 2 through Eqs. 2–8.

Fig. 2
figure 2

Simulated FDML laser signal envelope and the associated dips that arise mainly due to the SOA dynamics

Full size image
Table 1 Simulation parameters
Full size table
$$\mu \left(i\right)=\frac{1}{M}\sum_{k=i}^{i+M}u\left(k\right), \chi \left(i\right)=\sqrt{\frac{1}{M}\sum_{k=i}^{i+M}{\left\{u\left(k\right)-\mu \left(i\right)\right\}}^{2},} i=\mathrm{1,2},\dots ,N-M, N:{\text{Number of total grid points }} $$
(1)
$${\text{Computation of the dips }}\left(\mathrm{pseudocode}\right):$$
$$\mathrm{while}\, i< N-M+1$$
$$\mathrm{if} {U}_{\mathrm{step}}\left\{\chi \left(i-1\right)-\chi \left(i\right)-\rho \right\}=1$$
$$\Omega \to \Omega +1, \Delta T\left(\Omega \right)=0$$
$$\mathrm{while} \chi \left(i\right)>\rho $$
$$\Delta T\left(\Omega \right)\to \Delta T\left(\Omega \right)+\frac{1}{{F}_{s}}$$
$$i \to i+1$$
$$\mathrm{end} \, \left(\mathrm{while}\right) \mathrm{end} \left(\mathrm{if}\right)$$
$$i \to i+1$$
$$\mathrm{end}(\mathrm{while})$$
$$\Omega : \, {\text{Number of dips}}, { U}_{\mathrm{step}}:{\text{Unit step function}}, {F}_{s}:{\text{Sampling frequency}}, \Delta T:{\text{Dip duration}}$$
$$\rho : \,{\text{Threshold value of the standard deviation in power for dip detection}}$$

Based on our observations, the number and duration of these recurrent dips are correlated with their depth. Therefore, we believe that suppressing the depth and prevalence of the dips via tuning down the LWEF is expected to make their duration less of an issue. Hence, the relation of the LWEF and the average depth of the dips is worthy of additional investigation for the confirmation of such a relation.

As illustrated in Fig. 2, the signal quality is greatly distorted by the frequent recurrence of power-dips, which are superimposed on the signal envelope and can have a wide range of depths over a sweep. It is clear that the power-dips are not only frequent, but often have a large depth that is comparable to the signal power. To measure the dip strength throughout the FDML laser operation time, we have synchronously computed the standard deviation of the signal power using a sliding window of 16 grid-points corresponding to 24 ps. Here, the standard deviation of the signal power indicates the signal quality. A predominantly low standard deviation signifies that the power-dips are weak in depth and, therefore, would not affect the signal quality significantly. Figure 3 is a zoomed in image of Fig. 2, which illustrates the precise detection of these power-dips via the computation of standard deviation in power. For a sliding window of 16 grid-points, the dips are aligned with the peaks of standard deviation in power.

Fig. 3
figure 3

Detection of the dips via computing the standard deviation (orange) of the signal power (blue)

Full size image

According to our investigations on the signal pattern, a power-dip or a hole can be clearly observed when the power standard deviation is greater than 1 mW for a self-starting FDML laser under an SOA input noise power of 9.05 mW [7]. The standard deviation of the signal power turned out to be a very good measure to detect the dips as it is mostly constant due to the convergence of the FDML laser operation, but only occasionally peaks when a dip is present. As the dip strength varies greatly over a single FDML laser roundtrip, we computed the number of dips based on standard deviation for the indication of the dip strength and investigated the prevalence of its various ranges. Using the given experimental parameters in [7], the histogram of the power standard deviation with respect to the number of grid-points is shown in Fig. 4 for 200 roundtrips and for an LWEF of 1.5. The effect of a higher SOA LWEF on the histogram shape will be discussed in more detail in Results.

Fig. 4
figure 4

Bar plot of the power standard deviation of an FDML laser signal for an LWEF of 1.5 (200 roundtrips)

Full size image

2 Methods

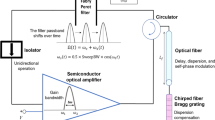
The configuration of an FDML laser is illustrated in Fig. 5. The FDML laser cavity involves three fundamental components, which are the semiconductor optical amplifier (SOA), optical fiber, and the wavelength-swept Fabry–Perot filter. The SOA provides amplification per roundtrip and determines the maximum possible range of the frequency sweep through its gain dynamics [20,21,22,23,24,25,26]. The long optical fiber introduces the necessary delay for each spectral component within the SOA gain-bandwidth, so that each spectral component is synchronously filtered by the tunable Fabry–Perot filter at each roundtrip [23,24,25,26,27]. The passband of the Fabry–Perot filter shifts in time for filtering each spectral component separately, such that only one spectral component is transmitted at a given instant. This way, the full content of the entire spectral sweep can be stored in the cavity for each and every roundtrip, unlike the case of conventional mode-locked lasers, which only allow for quasi-monochromatic storage at a given roundtrip [29, 30].

Fig. 5
figure 5

Configuration of an FDML laser. Basic components of an FDML laser include the SOA for light amplification, the long optical fiber for delay imposition, and the Fabry–Perot filter for tunable filtering

Full size image

At each roundtrip, the SOA-amplified laser light passes through the optical fiber, which typically has a length that ranges from several hundred meters to a few kilometers. The long optical fiber introduces different time delays for each spectral component due to the variation in its refractive index with respect to frequency. This naturally makes the group velocity of the laser beam a function of frequency and introduces chromatic dispersion [28,29,30,31,32,33]. Depending on the dispersion characteristics of the fiber, the chromatic dispersion usually distorts the signal pattern of the FDML laser. To compensate for this dispersion, a chirped fiber Bragg grating (CFBG) is often used to cancel out the dispersion that originates from the optical fiber. This way, a dispersion free operation can be attained and the power fluctuations in the signal pattern can be decreased to a great extent [7]. Hence, the dispersion compensation is carried out in accordance with the desired output signal quality via proper adjustment of the CFBG structure based on the dispersion characteristics of the optical fiber. For each roundtrip, the circulator couples some of the optical power within the cavity to the output, through the optical fiber and the CFBG. A portion of this output power is reflected back into the cavity due to the reflectivity of the CFBG. The tunable Fabry–Perot filter transmits each spectral component one by one at definite instants such that the roundtrip time of each spectral component is matched with the sweep-period of the filter. Hence, the driving frequency of the filter is set as the inverse of the cavity roundtrip time [7]. The input–output relationship for each element is shown in Fig. 5. At every roundtrip, the SOA output signal is the input signal of the optical fiber (and the CFBG) whose output is the input signal for the tunable Fabry–Perot filter via the circulator, after forward/backward propagation. Finally, the filter output is fed back to the SOA input through an isolator that is used to prevent reflections and the formation of a standing wave pattern by ensuring unidirectional laser beam propagation. The polarization dynamics are ignored in this study as the SOA is a single-polarization device, which minimizes the effect of the degenerate orthogonal fiber mode on the overall dynamics [7, 25].

Based on the defined parameters given as follows, the operation dynamics of an FDML laser and each of its associated components are described as follows [7]:

2.1 Semiconductor optical amplifier (SOA)

The input–output relationship for the SOA is described via the integrated power gain coefficient \(h(t)\) [7, 10]:

$$\frac{\mathrm{d}h(t)}{\mathrm{d}t}=\frac{{h}_{0}\{{f}_{c}+{f}_{s}\left(t\right)\}-h(t)}{{\tau }_{c}}-\frac{{\left|{u}_{in, SOA}\left(t\right)+{u}_{ASE}\left(t\right)\right|}^{2}}{{{P}_{sat}\left\{{f}_{c}+{f}_{s}\left(t\right)\right\}\tau }_{c}}\left(\mathrm{exp}\left\{h\left(t\right)\right\}-1\right) $$
(2)
$$h\left(t\right):{\text{Integrated power gain coefficient}}, { h}_{0}\left(f\right):{\text{Unsaturated static gain}}, { \tau }_{c}:{\text{Carrier lifetime}}$$
$${P}_{\mathrm{sat}}\left(f\right):{\text{Saturation power}}, {u}_{\mathrm{ASE}}\left(t\right):{\text{Amplified spontaneous emission noise}}, {f}_{c}:{\text{Center frequency of the sweep}}$$
$${f}_{s}:{\text{Relative sweep frequency}}, { u}_{\mathrm{in},\mathrm{ SOA}}: SOA {\text{input signal}}$$

Usually, the FDML laser self-starts via the SOA-amplified spontaneous emission (ASE) noise:

$${u}_{\mathrm{ASE}}\left(t\right)={\text{Additive white Gaussian noise with zero mean and standard deviation}} \sigma $$
$$\sigma ={(0.5{P}_{n}{\Delta }_{\mathrm{sim}}/{G}_{\mathrm{eff}})}^{1/2}, {G}_{eff}={\int }_{0}^{\infty }\mathrm{exp}[{h}_{0}(f)]df $$
(3)
$${P}_{n}:{\text{Amplified spontaneous emission}} \left(\mathrm{ASE}\right) {\text{noise power within the gain}}-\mathrm{bandwidth}$$
$${\Delta }_{\mathrm{sim}}:{\text{Simulation bandwidth}}, { G}_{\mathrm{eff}}:{\text{Effective gain}}$$

The output signal is related to the input signal via the gain coefficient \(h\) and the LWEF \(\alpha \):

$${u}_{\mathrm{out},\mathrm{SOA}} {u}_{\mathrm{in},\mathrm{SOA}} = \mathrm{exp}\left[0.5h\left(1-i\alpha \right)\right]$$
(4)

2.2 Optical fiber and the chirped Bragg grating (CFBG)

The output of the SOA is coupled to the optical fiber via the circulator. The optical fiber modifies the phase of the SOA output based on the following relation [7]:

$${u}_{\mathrm{out}, \mathrm{ fiber}}\left(t\right)={\sqrt{{\kappa }_{f}}u}_{\mathrm{in},\mathrm{fiber}}\left(t\right)exp\left\{i{L}_{f}\left[2{\pi }^{2}{\beta }_{2}{{f}_{s}}^{2}\left(t\right)+\frac{4}{3}{\pi }^{3}{\beta }_{3}{{f}_{s}}^{3}\left(t\right)+\frac{2}{3}{\pi }^{4}{\beta }_{4}{{f}_{s}}^{4}\left(t\right)\right]+i{\varphi }_{\mathrm{CFBG}}\left(t\right)+i\gamma {\kappa }_{f}{\left|{u}_{\mathrm{in},\mathrm{fiber}}\left(t\right)\right|}^{2}\frac{1}{2}{L}_{f}\left(1+R\right)\right\}$$
(5)
$${\kappa }_{f}:{\text{Fiber loss coefficient}}, \gamma :{\text{Nonlinearity of the fiber}}, R: {\text{CFBG reflectivity}}, {L}_{f}: {\text{Length of the fiber}}$$
$${\varphi }_{\mathrm{CFBG}}:{\text{CFBG introduced phase difference}}, { \beta }_{\mathrm{2,3},4}:{\text{Fiber dispersion coefficients}}$$

The fiber spool that is used in the experiment consists of a mix of SMF-28, HI1060 and LEAF fibers. The simulation parameters for modeling the fiber dispersion are chosen based on the product specifications of these fibers to model the entire fiber [5, 7]. The fourth-order dispersion is just used as a mathematical term here, and its practical significance is ignorable as can be deduced from the parameter values in Table 1. Here, the fiber length \({L}_{f}\) regards both forward and backward propagation through the fiber. The fiber loss coefficient \({\kappa }_{f}\) accounts for all losses, including reflection, circulator, and internal fiber losses. The last term in Eq. 4 describes the self-phase modulation due to the nonlinearity coefficient \((\gamma )\) of the fiber. To compensate for the fiber dispersion, a CFBG that introduces the following phase difference is employed [7]:

$${\varphi }_{\mathrm{CFBG}}\left(t\right)=-{L}_{f}\left[2{\pi }^{2}\widehat{{\beta }_{2}}{{f}_{s}}^{2}\left(t\right)+\frac{4}{3}{\pi }^{3}\widehat{{\beta }_{3}}{{f}_{s}}^{3}\left(t\right)+\frac{2}{3}{\pi }^{4}\widehat{{\beta }_{4}}{{f}_{s}}^{4}\left(t\right)\right], \widehat{ { \beta }_{\mathrm{2,3},4} }:{\text{CFBG dispersion coefficients }}$$
(6)

2.3 Fabry–Perot filter

The optical Fabry–Perot (FP) filter, which has a Lorentzian passband and a transmission bandwidth of \(\Delta f\), transforms the signal amplitude at every roundtrip based on the frequency domain relation given as follows:

$${u}_{out, FP}\left(f\right)={u}_{in,FP}\left(f\right){H}_{FP}\left(f\right) $$
(7)
$${H}_{FP}\left(f\right)=\frac{\sqrt{{T}_{max}}}{1-i2\pi f/\Delta f} ({\text{Frequency response of the FP filter}}) $$
(8)
$$\Delta f:{\text{Bandwidth of the FP filter}}, { T}_{\mathrm{max}}:{\text{Transmission coefficient of the FP filter}},$$

the passband of the tunable filter is centered at \({f}_{c}+{f}_{s}\left(t\right)\), which is taken as the swept-filter reference point.

The operation of the simulated FDML laser is as illustrated in Fig. 6, and the corresponding simulation parameters are as given in Table 1, which are identical with the experimental parameters in [5, 7] for a more precise comparison of the results. The laser operation self-starts via the SOA ASE noise. The internal ASE noise is processed by the SOA based on Eqs. 2–4. After that, the output signal of the SOA is considered as the input signal of the optical fiber in Eqs. 5–6. A portion of the fiber output is coupled as output power and the rest is considered as the input signal of the Fabry–Perot (FP) filter (Eqs. 7–8) which has a time-varying frequency response. Finally, the output signal of the FP filter is fed back as the input signal (\({u}_{\mathrm{in},\mathrm{ SOA}}\left(t\right)\) in Eq. 2) of the SOA, and the same process follows in this sequence for many roundtrips. The underlying dynamics of the FDML laser is modeled the same as in [5, 7]. However, to examine the pure effect of the LWEF on the power-dips, the optical fiber dispersion is assumed to be fully compensated by the CFBG. Hence, the LWEF of the SOA is tuned over the range 0.5–8 for the examination of the dips. The following section discusses the relation between tuning down the LWEF and the resulting characteristics of the dips [34].

Fig. 6
figure 6

Simulation framework for computing the number of power-dips on the FDML laser signal pattern

Full size image

3 Results

3.1 Convergence of error versus LWEF

An FDML laser can be considered as stable when the mean-squared error (MSE) between the signal patterns of two subsequent roundtrips converges to zero, which occurs when the number of dips in the signal pattern is negligible (ideally zero) [5, 7]. Figure 6 illustrates the convergence of error between two consecutive roundtrips. Evidently, for larger LWEF values (α \(\ge \) 2) the error does not converge to zero but stays rather constant, which means an ultra-stable operation cannot be attained for high LWEFs even under full dispersion compensation by the CFBG. However, it is observed that when the LWEF decreases from 6 to 2, the error converges to a lower value, suggesting that the LWEF plays a role in the stability and convergence of the FDML laser operation. Here, the MSE is computed as

$$\mathrm{MSE}=\frac{1}{{N}_{s}}\sum_{i=1}^{{N}_{s}}{{\{u}_{\zeta +1}\left(i\right)-{u}_{\zeta }\left(i\right)\}}^{2} $$
(8)
$$\zeta :{\text{Roundtrip number}}, { N}_{s}:{\text{Number of gridpoints for each roundtrip}}, u:{\text{FDML laser output signal}}$$

For an LWEF value below 2, the MSE between the signal patterns of consecutive roundtrips converges to zero. Notice that for LWEF = 1 and LWEF = 0.5, the error converges much quicker as compared to the case of LWEF = 1.5. This suggests that for an LWEF below 2, under full dispersion compensation by the CFBG, an ultra-stable operation can be achieved within a few hundred roundtrips. It is important to note that, here, the sole effect on error convergence is due to the LWEF as the computations were carried out under total dispersion compensation.

The convergence of the MSE for α < 2, but not for α > 2, is an interesting and a mysterious observation. It is possible that beyond a certain LWEF value (between 1.5 and 2), the gain dynamics of the SOA may exhibit a more chaotic behavior rather than a precisely steady one. In fact, FDML lasers have recently been shown to display a chaotic behavior under a great range of operating conditions [5, 6]. However, this has not been linked to the LWEF, and the LWEF has been treated as a totally independent constant in both studies, although its possible effect on stability has been noted. Most importantly, the frequency dependence of the LWEF throughout a single FDML laser roundtrip is also not examined in this study as we have only swept the value of the LWEF to examine the corresponding relation to the power-dips. Therefore, it may be the case that an SOA can mostly operate with a LWEF below 2, but occasionally has a LWEF greater than 2 for certain frequencies within its gain-bandwidth. In such a case, even an SOA with a predominantly low LWEF may prevent the convergence of the FDML laser operation if its LWEF becomes greater than 2 for some frequencies within a single full-sweep. The percentage of duration within which the LWEF is greater than 2 in a single roundtrip, may also be a critical determinant of whether the FDML laser operation will converge or not. Hence, we believe the MSE-convergence results shown in Fig. 6 is of importance concerning the possible variation of the SOA LWEF in a given FDML laser roundtrip.

In correspondence to the error convergence, the number of dips that are formed throughout an FDML laser operation of 800 roundtrips has been computed for different threshold power standard deviation values. Figure 7 shows the variation of the number of dips with respect to the LWEF against various standard deviations in power. Here, a dip is defined to have a standard deviation of power that is greater than 1 mW. The dips that have a power standard deviation above 3 mW are designated to be the major dips that tend to have longer durations, thereby causing greater distortion on the signal pattern based on our observations and the experimental results in [5]. Clearly, the number of dips decreases radically below an LWEF of 3 for all threshold standard deviations in power, and below an LWEF of 1.5 most of the dips are already eliminated.

Fig. 7
figure 7

Convergence of the MSE between the signal patterns of two subsequent roundtrips for an FDML laser based on different LWEFs. An LWEF value that is greater than 1.5 hinders error convergence

Full size image

It can be noticed that although the number of dips greatly increase above an LWEF of 1.5, there is a slight decrease in the number of dips above an LWEF of 3.5. The reason behind this small decrease can be understood by examining Fig. 8, which shows the relation between the peak intracavity signal power and the LWEF, for different values of the SOA input noise power (\({P}_{n}\)). It is clear that as the LWEF increases, the peak signal power decreases due to increased phase-mismatch between the intracavity signal and the time-varying impulse response of the Fabry–Perot filter. This decrease in signal power leads to a corresponding decrease in the dip strength in terms of power standard deviation (as dictated by the SOA dynamics), such that some of the dips that used to have a power standard deviation above 1 mW, end up having a power standard deviation that is less than 1 mW, hence unable to satisfy our initial criteria for dip classification. Therefore, the slight decrease in the number of dips above an LWEF of 3.5 does not indicate a real positive effect of the LWEF on dip elimination. More importantly, Fig. 8 shows another undesired effect of a high LWEF on the intracavity signal, which is significant decrease in power. Fortunately, most quantum well-based SOAs have LWEFs that are in the range of 1–5 [16]. Hence, the issue of LWEF related power-loss is relatively less significant in an FDML laser cavity as compared to dip formation.

Fig. 8
figure 8

Number of dips versus LWEF. Above an LWEF value of 1.5, there is a drastic increase in the number of dips

Full size image

3.2 Comparison with experimental results

Figure 9 illustrates the bar plot for the number of dips against dip duration for various LWEFs. Consistent with the experimental results [5], the number of dips steadily increases within the dip duration range 10–45 ps. The highest number of dips is observed in the 30–60 ps range, with the peak corresponding to approximately 50 ps, as also observed in the experiment. The number of dips decreases exponentially beyond a dip duration of 50 ps, with the highest dip duration being 200 ps, which is also in agreement with experimental observations [5]. For α = {5,3,2} and a total operation time of 800 roundtrips, the number of dips per each duration range is on the order of \({10}^{5}\), and for α = 1, it is on the order of \({10}^{3}\). Under the same optical delay of 29.5 ps (detuning by 5 Hz), the number of dips that was observed in the experiment is of the same order with our computationally attained values for α = {5,3,2}. Expectedly, for α = 1, the number of dips turned out to be much lower than experimental observations. A very precise agreement naturally cannot observed for all LWEFs, as the number of dips that we have computed via numerical simulations cannot be exactly compared with those measured in the experiment without the exact knowledge of the LWEF of the SOA that is used in the experiment. As illustrated in Fig. 7, the LWEF drastically affects the total number of dips and must be precisely known for accurate comparison of the dip densities (in [5], the dips are referred as holes). We have made use of the observation in Fig. 7, and estimated the LWEF of the SOA that was used to obtain the results in [5] to be mostly between 2 and 3 over a single roundtrip, based on the fact that the highest number of dips that are observed in the 15 ps interval, which is centered at 50 ps, is around \(2.3\times {10}^{5}\) in the experimental results. Since our computational results indicate that the highest number of dips is \(3.5\times {10}^{5}\) for α = 3 and it decreases to \(1.2\times {10}^{5}\) for α = 2 such assumption is reasonable. This can also be confirmed by checking the number of total dips, which is attained as \(9.52\times {10}^{5}\) in the experimentation. In our computational results, the total number of dips is \(1.43\times {10}^{6}\) for α = 3 and \(5.5\times {10}^{5}\) for α = 2, which also suggests that the employed SOA in [5] has an LWEF that varies between 2 and 3. It should be reiterated that the time dependency of the LWEF is not considered in this study, as was the case with prior studies [2, 5,6,7,8,9,10, 15,16,17,18,19]. Hence, our estimation for the LWEF of the employed SOA involves a range of values (2 < α < 3) over a single roundtrip rather than a constant value.

Fig. 9
figure 9

Peak signal power versus LWEF. The peak signal power decreases with increasing LWEF in an FDML laser

Full size image

As illustrated in Fig. 7, for an LWEF below 1.5, the number of power-dips is greatly reduced. However, concerning the stability of the FDML laser operation, the depth of the power-dips is also critical, as an FDML laser signal pattern with fewer dips would not indicate a noteworthy improvement on the MSE between consecutive roundtrips unless the depth of the dips also decreases. It is found that the reduction of the LWEF not only eliminates more than 95% of the power-dips but it also greatly reduces the depth of the power-dips that form during the FDML laser operation. To illustrate this effect, we have computed the histograms of the standard deviation of power for α = {8, 3, 2, 1} in terms of the number of grid-points, which are plotted in Fig. 10. It is clear that the distribution is more widespread for an LWEF that is greater than 2, which means that there are power-dips that are much larger in depth. Such strong dips are especially unwanted since they can have further negative effects on the FDML laser stability through their impact on the SOA gain dynamics, particularly when they are of longer duration (which they tend to be). For α = {1,2}, most of the grid-points indicate a standard deviation of power that is less than 2 mW, hence, the negative impact on laser stability is less significant (Fig. 11).

Fig. 10
figure 10

Plot of the number of dips (standard deviation > 3 mW) versus dip duration for α = {5,3,2,1}

Full size image
Fig. 11
figure 11

Plot of the number of grid-points versus standard deviation in power for α = {8,3,2,1}

Full size image

4 Discussion

To our knowledge, the LWEF is not listed or specified among the SOA product specifications in practice; however, it is a very important parameter that influences the gain dynamics of any integrated photonic device that employs an SOA [5,6,7, 10,11,12,13,14,15,16,17,18,19]. As the aim is to quantify the variation in the strength and density of the power-dips against the variation of the LWEF in this study, it is not necessary to know the precise value of the LWEF of the employed SOA in the experiment. Hence, we have provided an estimated range of values for the LWEF of the used SOA rather than an exact value. Since it is possible to minimize the LWEF of an SOA at its design stage [10,11,12,13,14,15,16,17,18,19], the main goal of this study is to propose the design of SOAs with lower LWEFs in order to achieve a more stable and a noise-free operation in FDML lasers.

To quantify the practical variation in the dip number and strength, solely due to a variation in the LWEF, all simulation parameters are set to be equal to the experimental parameters in [5] and [7], which are based on the same experimental setup. Fiber nonlinearity, dispersion compensation, and the detuning of the filter are adjusted to be identical with the experimentation and are set as fixed values (not swept) in the simulation.

The fiber nonlinearity is not so high in the experiment (\({2.67\times 10}^{-3}{\mathrm{W}}^{-1}{\mathrm{m}}^{-1}\)). In fact, we have varied the fiber nonlinearity within the range \({10}^{-3}{\mathrm{W}}^{-1}{\mathrm{m}}^{-1}\mathrm{ and }{10}^{-2}{\mathrm{W}}^{-1}{\mathrm{m}}^{-1}\), and did not observe a very significant rise in the number and strength of the dips for an SOA carrier lifetime of 70 ps. For larger intracavity power levels, higher SOA carrier lifetimes, and fiber nonlinearities above \({10}^{-2}{\mathrm{W}}^{-1}{\mathrm{m}}^{-1}\), there is a significant increase in the number and strength of the dips. However, this was not the scenario in this study. Therefore, partial contribution to the number and strength of the dips via aforementioned parameters is not practically significant.

The fiber dispersion is mostly compensated in the experiment [5, 7] and hence in the simulation. Therefore, its contribution on dip formation is very low. Most importantly, both the fiber dispersion compensation and the fiber nonlinearity are kept constant while the LWEF is varied. Therefore, it is not possible for the increase in the number and strength of the dips to be attributed to fiber dispersion or fiber nonlinearity.

Finally, the detuning of the filter is also adjusted to be identical with the experiment while the LWEF is swept. Hence, the only effect on the dips is due to the sole variation in the LWEF, and the corresponding change in the dip density and dip strength, via a sole change in the LWEF, is observed to be drastically high. Therefore, the design of SOAs with lower LWEFs seems promising for an improved FDML laser performance concerning noise and stability.

5 Conclusion

Although a high SOA LWEF is probably not the original cause of the power-dips in an FDML laser output signal, we have observed that it strongly amplifies the number of power-dips and makes a huge contribution to the output signal noise. The amplification of dips occurs both in terms of depth and quantity. Given that other parameters are unchanged, using an SOA with a smaller LWEF leads to a reduction of more than 95% of the dips in the signal pattern of FDML lasers. Moreover, the most critical dips, which have larger depths and have the potential to push the FDML laser towards instability, are eliminated in great numbers. The observations in this study suggest that using SOAs with very small LWEFs, such as SOAs with quantum-dot based active regions, can greatly improve stability and enhance the signal quality of FDML lasers in imaging and detection applications.