Impact of self-phase modulation on the operation of Fourier domain mode locked lasers

Abstract

Fourier domain mode locked (FDML) lasers are a class of frequency-swept lasers that are used to generate optical pulses with a wide sweep range, high repetition rate, and a low instantaneous bandwidth. They are commonly used in sensing and imaging applications, especially in optical coherence tomography. Ideally, the aspired features in the design of FDML lasers include a high coherence length, large sweep bandwidth, adjustable output power, and a high signal to noise ratio (SNR). However, the SNR of the output signal of FDML lasers is often lower than desired due to the presence of several irregularities in the output signal pattern, most notably because of the frequent occurrence of sharp power dips, also known as holes. These power dips originate due to the nonlinear gain dynamics of the semiconductor optical amplifier (SOA) that is employed in FDML lasers, while the occurrence frequency and strength of these dips are determined by the interaction of the FDML laser components, which involve the SOA, the tunable Fabry–Perot filter, and the optical delay fiber. Suppressing these power dips not only increases the output signal quality in terms of SNR, but also precludes the accumulation of phase offsets between subsequent roundtrips and facilitates convergence. As both current and future applications of FDML lasers are likely to require a higher signal power, in this paper, we are going to investigate the effect of self-phase modulation (SPM) in the optical fiber on dip formation and convergence. Since fiber nonlinearity, intracavity signal power, and fiber length all contribute to SPM, investigation of the effect of SPM on the formation of power-dips and operational convergence is critical. More importantly, the phase-mismatch that is caused by fiber-based SPM cannot be compensated easily in an FDML laser as in the case of chromatic dispersion, which necessitates a strategy for minimizing fiber-based SPM to ensure operational convergence and to secure a lower limit for the SNR of the output signal of FDML lasers.

1 Introduction

Fourier domain mode-locked (FDML) lasers are near-infrared (near-IR) frequency-swept lasers that are very frequently used in biomedical imaging applications such as optical coherence tomography (OCT) and deep-tissue imaging (Huber et al. 2006a; Jirauschek et al. 2009). They are also commonly used in sensing, metrology, nonlinear microscopy, and microwave generation, owing to their capability of storing a relatively wide range of frequency components in the near-IR region. Their high sweep-bandwidth, high sweep-rate, low instantaneous bandwidth, and large coherence length are especially useful for high-resolution biological tissue imaging (Aşırım et al. 2022; Eigenwillig et al. 2013; Grill et al. 2022). Given the exponential increase in global health expenditure due to an aging population in developed countries, their use is expected to increase proportionally. Moreover, because of their high coherence-length, FDML lasers are also a great alternative in telecommunications engineering and holography. As opposed to conventional mode-locked lasers which modulate the intracavity beam intensity via modulating the cavity loss, FDML lasers modulate the spectrum of the intracavity beam and generate wideband frequency-swept pulses. In its most simple structure, an FDML laser cavity contains three fundamental elements (see Fig. 1). These are the semiconductor optical amplifier (SOA), the Fabry–Perot (FP) filter, and the long optical delay fiber. The SOA is often considered to be the most essential element of an FDML laser, as it not only determines both the gain-bandwidth and the output power of an FDML laser, but also largely governs the operation of FDML lasers through its internal gain dynamics. Depending on the operating power-level and the intensity-fluctuations on its input signal, the nonlinear dynamics of the SOA causes and facilitates the occurrence of sharp amplitude changes, also known as power-dips. These power-dips degrade the performance of FDML lasers both in terms of stability and signal-to-noise ratio (SNR). Regarding FDML lasers, the most critical parameters of an SOA involve its carrier lifetime, saturation power, gain bandwidth, and linewidth enhancement factor (LWEF). The carrier lifetime and the saturation power of an SOA are especially important as they are among the major determinants of the output power of an FDML laser. On the other hand, the LWEF is important for the investigation of noise in the output signal of an FDML laser as it was shown to influence the occurrence of power-dips greatly and was found to be a key parameter in the stability and convergence of the FDML laser operation (Aşırım et al. 2022; Aşırım and Jirauschek 2022). The LWEF will be briefly discussed in this study in relation to fiber-based self-phase-modulation (SPM) in Sect. 3.

Fig. 1

Fundamental components of an FDML laser and their arrangement in the experimental setup (Aşırım et al. 2022; Grill et al. 2022; Schmidt et al. 2020, 2021)

The long delay fiber in FDML lasers is required to store the entire spectral content of the SOA gain-curve in each pulse at a given roundtrip, and to introduce the intended time-delay between subsequent pulses. The pulse repetition rate for FDML lasers is often in the MHz range as imposed by the dynamics of the SOA. This requires a time-delay on the order of microseconds, which necessitates the use of a delay fiber with hundreds of meters in length. When the fiber is this long, any phenomenon that occurs within the unit length of the fiber carries importance concerning the output signal. A major issue that occurs within the delay fiber is the chromatic dispersion within the spectral band of each pulse, which causes a phase-mismatch with the time-varying impulse response of the Fabry–Perot filter and leads to the attenuation of the intracavity signal power. Most importantly, in FDML lasers, the power-dips that are initiated based on the gain recovery dynamics of the SOA, are amplified both in terms of density and strength due to the occurrence of chromatic dispersion in the delay fiber, causing further distortion in the output signal. Fortunately, the chromatic dispersion in the long fiber can be almost fully compensated by using a chirped fiber Bragg grating (CFBG), whose structure is designed to imitate the phase-shift that occurs in the fiber for producing a reverse phase-shift in accordance, to cancel out the phase-mismatch with the FP filter. There are other effects that occur within the delay fiber such as bending losses, scattering losses, etc. These are not the focus of this study, but we will account for these effects in our computational analyses under the use of a general loss term.

The FP filter that is used in an FDML laser, is a tunable bandpass filter whose passband sinusoidally shifts in time within the range of the SOA gain-bandwidth in the near-IR region. This is achieved by a sinusoidal shifting of the cavity walls that are connected to an electronic driver operating at a certain frequency, which also determines the shifting cycle of the passband. Correspondingly, the FP filter has a time varying impulse response that is tailored to filter each spectral component within the intracavity beam at certain instants, such that only one frequency component is transmitted at a given instant. This feature of the FP filter is what allows the synchronized propagation and storage of all the harmonics within the cavity. The output of the FP filter is then fed back to the SOA input for further progress of the FDML laser operation.

A very important phenomenon that occurs in the delay fiber is the SPM that stems from the fiber nonlinearity, which is the main focus of this study in the context of FDML lasers. Unlike chromatic dispersion, there is no straightforward mechanism to compensate for SPM. Therefore, the effect of SPM on the output signal is worthy of detailed investigation. The degree of SPM is determined by the nonlinearity of the fiber, length of the fiber, and the signal power. Although in practice, the employed fiber nonlinearity is not so high in FDML lasers, for applications where a high output power is required, SPM can become a serious problem. Another case in which the SPM can become a great issue is when the intended time-delay between subsequent pulses is large, which requires the use of a longer fiber, thereby enhancing the degree of SPM. Based on the fiber characteristics and the signal power, the results of this study aim to illustrate and discuss what happens to the output signal under various degrees of SPM.

Previous theoretical works on FDML lasers have focused on the mathematical formulation of the cavity dynamics under various configurations, ultra-stabilization (noise elimination) via dispersion compensation and phase-matching, and the development of efficient computational techniques for simulating FDML lasers. Although some of the existing literature on FDML lasers have investiged the effect of self-phase modulation (SPM) in the optical fiber (Slepneva et al. 2013; Jirauschek and Huber 2017; Todor et al. 2012; Huang et al. 2022), this had been mostly on pulse-shape preservation and dispersion compensation via fiber-based SPM, whereas the isolated effect of fiber-based SPM on dip/hole (noise) formation and dip/hole characteristics such as quantity, strength, and duration, has not been examined for analyzing the operational convergence of FDML lasers. Fiber-based SPM is often thought as a mechanism to counter chromatic dispersion and aid in maintaining stable operation in FDML lasers. The goal of this study is to show that this is not exactly true by stating that beyond a certain level, SPM can kill the FDML laser operation. Here we have examined and evaluated the effect of fiber-based SPM regarding the number, strength, and duration of the power-dips. Additionally, we investigated the variation of dips with super-strength, which are known to induce long-term power instabilities (Aşırım et al. 2022; Grill et al. 2022; Schmidt et al. 2020, 2021; Li et al. 2021), with respect to the level of SPM. Most importantly, the impact of the degree of SPM on dip formation is investigated in association with the SOA parameters that are known to heavily influence noise formation, such as LWEF and carrier lifetime (Aşırım et al. 2022; Schmidt et al. 2021). Another noteworthy contribution of this study is the introduction of a compact but a highly accurate algorithm for dip detection, counting, analysis, and classification, which made it available to perform the computations in this study and can be applied for future studies.

As mentioned earlier, the power-dips that originate due to the SOA dynamics often heavily distort the output signal and are the main source of noise in FDML lasers. More importantly, the sudden change in the optical power through these dips can cause an avalanche effect that can lead to the drift of the FDML laser towards instability within a few thousand roundtrips. This is because the optical response of the SOA is nonlinear (Henry 1982; Haug and Haken 1967; Wang et al. 2007; Cassioli et al. 2000) and depends on its input optical power (through feedback, the SOA output eventually becomes its input again after traversing through the fiber and the FP filter). Correspondingly, when the SOA input contains many dips with sharp amplitude changes, the SOA tends to amplify the number and strength of these dips which leads to a greater distortion in the signal. Hence, the suppression of these power-dips at each and every round-trip is of great importance in terms of stability and SNR. For this reason, the long delay fiber should be ensured to cause minimum distortion on the signal. It is known that chromatic dispersion in the fiber greatly increases the number of dips in the FDML laser output signal (Aşırım et al. 2022; Eigenwillig et al. 2013; Grill et al. 2022; Schmidt et al. 2020, 2021). However, the effect of SPM on the output signal has not been investigated in an FDML laser cavity in relation to the formation of power-dips and their characteristics. In this study, we will investigate the influence of SPM on the dip-density, dip-strength, and dip-duration, using our elaborate computational model which perfectly emulates the experimental setup in Grill et al. (2022); Schmidt et al. 2020, 2021). Followingly, we will determine an upper bound for the fiber nonlinearity to keep the number of dips to a minimum under the experimental parameters given in Grill et al. (2022); Schmidt et al. 2020, 2021).

Based on the given formulations in Eqs. 2–14 and the corresponding experimental parameters given in Table 1, the formation of dips on the FDML laser signal envelope is shown in Fig. 2 for a single sweep. As it is clearly seen from Fig. 2, the degree of distortion on the signal envelope due to the formation of dips is profound. The distortion level is quantified by computing the number, strength, and duration of the dips, the increase of which indicates a greater signal distortion. Evaluation of the number, strength, and duration of the dips is carried out by computing the standard deviation in the optical power as discussed in Sect. 2.1. Here, we have computed the number and strength of the dips for a large range of fiber nonlinearities and analyzed the change in the dip density and strength according to the change in the degree of SPM as induced by the associated fiber nonlinearity. The results are given in Sect. 3.

Table 1 Main parameters of the performed simulations based on the experimental setup (Grill et al. 2022; Schmidt et al. 2020, 2021)

Fig. 2

Simulation result for a single frequency-sweep that depicts the formation of power-dips on the FDML laser signal envelope. Each consecutive grid-point corresponds to a sampling period of 1.5 ps

2 Methods

2.1 Computation of the number and duration of the dips from the FDML laser power pattern

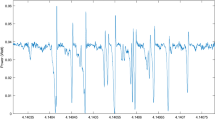
The precise identification of the power-dips is a challenging problem as some of the dips have longer durations and much more complex patterns that resemble the unification of multiple dips (see Fig. 3). Although many dips have the same basic pattern that is illustrated in Fig. 4, when a dip with a more complicated pattern arises, it becomes difficult to distinguish whether an irregular dip is indeed a single dip or a unified pattern of closely spaced multiple dips. Such distinguishing of the dips is important to determine the total number of dips for evaluating the stability of the FDML laser, and also to study the dip characteristics for evaluating the SOA performance and dispersion analysis. To distinguish and count each dip, we have developed a basic algorithm for the identification and classification of the dips, in which the power-dips are detected and counted based on the computation of the standard deviation of the optical power at the output. The standard deviation is computed via a shifting window of 16 grid-points, where the time difference between each adjacent grid-point corresponds to 1.5 ps. We identify a dip when the standard deviation in optical power is greater than 1mW and compute the duration of the dip based on for how long the standard deviation remains above the threshold value of 1mW. However, this is a bit problematic because often within a single dip, the standard deviation may fall below the threshold value for a very short instant and then quickly rise above the threshold level again. This indicates that the same dip still progresses, which requires caution to distinguish between the termination or continuation of a given dip. As a matter of fact, within a given irregular dip, the standard deviation in power may fluctuate rapidly and frequently rise/fall above/below the threshold. If each rise of the standard deviation (above the threshold) would be regarded as a separate dip, then one would compute many more dips than the actual number by mistakenly assuming that each dip has the same character and is a regular dip. In fact, there can be dips of many different characteristics, each representing different features of the FDML laser dynamics and containing information about the dynamics of the whole system. For this reason, it is important to distinguish between the regular and irregular dips to compute their duration accurately.

Fig. 3

Simulation result illustrating the formation of irregular dips with various patterns. Some of the dips have complex patterns with much longer durations as identified by the standard deviation in optical power. The horizontal axis is represented in terms of grid-points through temporal discretization as the pseudocode introduced below operates on grid-points. The time difference between each adjacent grid-point corresponds to a sampling period of 1.5 ps

Fig. 4

Basic (regular) dips with relatively short duration. A dip is clearly observable when the power standard deviation is greater than 1mW. The time difference between each adjacent grid-point is 1.5 ps

For differentiating each consecutive dip, and to distinguish between the termination or continuation of a given dip when the power standard deviation falls below the threshold for a certain time-interval, we set a lower limit for the duration for which the power standard deviation remains below the threshold value right after it falls below the threshold. If the standard deviation in power remains below the threshold for a duration that is longer than the lower limit, a subsequent increase of the power standard deviation above the threshold value is regarded as the formation of a new dip, if not, we assume that the same dip has just instantaneously fallen below the threshold power level and in fact continues to progress. Ideally, this minimum duration should not be chosen arbitrarily. Since the average dip-duration depends on the carrier lifetime of the SOA (Aşırım et al. 2022; Grill et al. 2022; Schmidt et al. 2020, 2021), to assume that a sudden fall below the threshold power standard deviation does not indicate the termination of the current dip, the duration of this event should be well below the carrier lifetime, which is usually close to the average dip duration ($\sim 50 \,mathrm{ps}$). For this reason, since the lower limit should be much lower than the carrier lifetime, and because the narrowest power dips have a duration of around 15 ps (Aşırım et al. 2022; Schmidt et al. 2021), we set the minimum duration for which the power standard deviation can remain below the threshold value within the same dip to 20% of the carrier lifetime based on the experimental parameters given in Grill et al. (2022); Schmidt et al. 2020, 2021). The following pseudocode describes how we identify and compute the duration of each single dip.

$$\begin{aligned} &Mean\,\left(i\right)=\frac{1}{M}\sum_{k=i}^{i+M}S\left(k\right),\,Stdev\left(i\right)=\sqrt{\frac{1}{M}\sum_{k=i}^{i+M}{\left\{S\left(k\right)-Mean\left(i\right)\right\}}^{2},}\\ &S:Signal\,power,\,i=\mathrm{1,2},\dots ,N-M, N:Number\,of\,total\,gridpoints, M:Window\,length\,\end{aligned}$$

(1)

$$Computation\,of\,the\,dips\,(pseudocode){:}$$

$$p=0\,(Initialize\,the\,number\,of\,dips\,to\,zero)$$

$$while\,i< N-M+1\, (loop\,through\,grid-points)$$

$$if\,Stdev\left(i\right)>Thr\,(Stdev\,in\,power\,is\,larger\,than\,a\,given\,threshold)$$

$$p\to p+1, \Delta T\left(p\right)=0\, (Define\,a\,new\,dip\,and\,initialize\,its\,duration\,to\,0)$$

$$while\,Stdev\left(i\right)>Thr\left(i\right)\,(As\,long\,as\,the\,stdev\,in\,power\,remains\,above\,the\,threshold)$$

$$\Delta\,T\left(p\right)\to\,\Delta\,T\left(p\right)+\frac{1}{{F}_{s}}\,\left(increase\,dip\,duration\right), i\,\to\,i+1$$

$$if\,Stdev\left(i\right)<Thr\left(i\right)\,(Stdev\,in\,power\,drops\,below\,the\,threshold\,value)$$

$$v=0$$

$$while\,Stdev\left(i\right)<Thr\left(i\right)\,(check\,for\,how\,long\,the\,stdev\,remains\,below\,the\,threshold)$$

$$v \to v+1, \dots i \to i+1$$

$$if\,Stdev\left(i\right)>Thr\left(i\right)\,(Stdev\,rises\,above\,the\,threshold)$$

$$c=0$$

$$if\,v<10\,(If\,Stdev\,remains\,below\,the\,threshold\,for\,less\,than\,10\,gridpoints,\,the\,dip\,continues)$$

$$\Delta\,T\left(p\right)\to\,\Delta\,T\left(p\right)+\left(\frac{v}{{F}_{s}}\right)\,(increase\,dip\,duration\,by\,v\,gridpoints)$$

$$break;\,else\,\left(The\,dip\,has\,ended\right)\,c=1 end\,\left(if\right)\,end\,\left(if\right)\,end\,\left(while\right)$$

$$if\,c=1,\,break;\,end\,\left(if\right)\,end\,\left(if\right)\,end\,\left(while\right)\,end\,\left(if\right)\,i \to i+1 end(while)$$

$$p:Number\,of\,dips,\,{F}_{s}:Sampling\,frequency,\,\Delta\,T:Dip\,duration$$

2.2 Implementation of the computational model based on the experimental setup

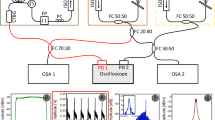
Figure 1 shows the fundamental components and their organization in an FDML laser cavity. As discussed earlier, an FDML laser contains three essential components, which are the SOA, the long optical fiber, and the tunable Fabry–Perot filter (Huber et al. 2006a). The SOA is the core element as it determines both the output power and the sweep bandwidth of an FDML laser, along with the pattern of the output signal envelope (Todor et al. 2011, 2012; Slepneva et al. 2013; Jirauschek and Huber 2017). The long optical fiber is necessary for the cavity to allow for a sufficient roundtrip time such that all frequency components within the gain spectrum of the SOA that are sampled by the Fabry–Perot filter, are stored in the cavity at a given roundtrip (Todor et al. 2012; Huber et al. 2006b; Kevin et al. 2011; Jeon et al. 2008). Moreover, the optical fiber should be long enough to introduce an adequate time delay between each consecutive sweep for the adjustment of the intended sweep rate. The Fabry–Perot filter, which has a time-varying impulse response, is required for the distinctive instantaneous filtering or sampling of each frequency component within the SOA gain-bandwidth. Apart from these three essential components, as depicted in Fig. 1, an optical isolator is included in an FDML laser cavity for attaining a unidirectional laser operation and to avoid the formation of standing waves in the cavity. Additionally, a CFBG is added to the output of the long optical fiber to suppress the chromatic dispersion that occurs in the fiber via phase-compensation, so that the phase-mismatch with the impulse response of the Fabry–Perot filter is minimized.

The FDML laser operation can start on its own via the SOA input noise which stems from the amplified spontaneous emission (ASE) in the active region of the SOA (Jeon et al. 2008; Oh et al. 2005). The ASE noise, which contains all the frequency content within the SOA gain-bandwidth (Aşırım et al. 2022; Schmidt et al. 2021; Huang et al. 2022), goes through the long optical fiber via a circulator (after being processed by the SOA). Consecutively, a CFBG is used to compensate for the chromatic dispersion in the fiber (Todor et al. 2011, 2012). Some of the signal is transmitted by the CFBG as the output signal and the remaining portion is reflected back into the FDML laser cavity. The Fabry–Perot filter, whose passband adaptively shifts over time for a precise sampling of the spectrum of the intracavity signal, filters each frequency component within the signal at distinct predetermined instants, such that only a single frequency component is transmitted at a given instant. Therefore, at a given roundtrip, the whole frequency content of the SOA gain-spectrum is stored in the cavity as opposed to conventional mode-locked lasers which can only store quasi-monochromatic frequency content (Huang et al. 2022; Tang et al. 2020; Lippok et al. 2019; Chen et al. 2013; Jirauschek and Huber 2015).

Our simulation model is as depicted in Fig. 5. The aforementioned three essential components of an FDML laser are arranged accordingly to simulate the associated feedback mechanism. At a given roundtrip, the SOA output becomes the input of the optical fiber (and the CFBG), whose output is split in two portions. Based on the reflectivity of the CFBG, a given percentage becomes the input of the Fabry–Perot filter, while the remaining portion is coupled as the output signal. The Fabry–Perot filter is modeled as an operator (on the signal amplitude) with a time varying impulse response to simulate a bandpass filter with a passband that sinusoidally shifts in time. The output of the Fabry–Perot filter is then fed back to the SOA input and the identical process repeats itself until the mean-squared-error (MSE) between the signal patterns of two consecutive roundtrips converges to a near-zero value. The signal envelope changes at each roundtrip owing to the nonlinear dynamics of the SOA which depends on the power of the intracavity signal. However, as the average signal power converges to a certain value, so does the SOA dynamics and the FDML laser operation, although this can take from thousands, up to hundreds of thousands of roundtrips, depending on the gain dynamics and the associated parameters of the SOA, such as carrier lifetime and the linewidth enhancement factor (Yang et al. 2021; Li et al. 2021; Huang et al. 2021; Aşırım and Jirauschek 2022). Sometimes, the FDML laser operation may not converge, the occurrence of which not only depends on the SOA dynamics, but also on the dynamics of the long optical fiber. It is naturally difficult to simulate the situations where the FDML laser converges after hundreds of thousands of roundtrips, in which case the components need to be efficiently modeled to minimize the computational cost. In our simulations, each component (which will be separately described below) is modeled as an operator for the signal amplitude as given in Eqs. 2,6,11. The parameters of the simulation and their values are taken from the experimental setup (Grill et al. 2022; Schmidt et al. 2020, 2021) and as provided in Table 1.

Fig. 5

Simulation model for the FDML laser operation

2.2.1 Semiconductor optical amplifier (SOA)

The operation of the SOA self-starts based on the ASE noise. The electrical response of the SOA is governed by the input-signal operator ${L}_{SOA}\{.\}$, which is expressed via Eqs. 3–4 and yields the output signal of the SOA

$${u}_{out,SOA}={L}_{SOA}\left\{{u}_{in,SOA}\right\}$$

(2)

$${L}_{SOA}=\{.\}exp\left[0.5h\{.\}\left(1-i\alpha \right)\right]$$

(3)

$$\frac{dh\{.\}}{dt}=\frac{{h}_{0}\{{f}_{c}+{f}_{s}\left(t\right)\}-h\{.\}}{{\tau }_{c}}-\frac{{\left|\{.\}+{u}_{ASE}\left(t\right)\right|}^{2}}{{{P}_{sat}\left\{{f}_{c}+{f}_{s}\left(t\right)\right\}\tau }_{c}}\left(exp\left\{h\{.\}\right\}-1\right)$$

(4)

$$h:Integrated\,power\,gain\,coefficient,\,{\,h}_{0}\left(f\right):Unsaturated\,static\,gain,\,{\,\tau\,}_{c}:Carrier\,lifetime$$

$${P}_{sat}\left(f\right):Saturation\,power, { u}_{ASE}\left(t\right):Amplified\,spontaneous\,emission\,noise,\,{ f}_{c}:Center\,frequency\,of\,the\,sweep$$

$${f}_{s}:Relative\,sweep\,frequency,\,{ u}_{in, SOA}:\,SOA\,input\,signal,\,{ u}_{out,SOA}:SOA\,output\,signal$$

$$\alpha: Linewidth\,enhancement\,factor$$

$${u}_{ASE}\left(t\right):\,Additive\,white\,Gaussian\,noise\,with\,zero\,mean\,and\,standard\,deviation\, \sigma$$

The standard deviation of the ASE noise is determined based on the following parameters;

$$\sigma ={(0.5{P}_{n}{\Delta }_{sim}/{G}_{eff})}^{1/2},\quad {G}_{eff}={\int }_{0}^{\infty }\mathrm{exp}[{h}_{0}(f)]df$$

(5)

$${P}_{n}:Amplified\,spontaneous\,emission\,\left(ASE\right)\,noise\,power\,within\,the\,gain\,bandwidth$$

$${\Delta }_{sim}:Simulation\,bandwidth,\,{ G}_{eff}:Effective\,gain$$

2.3 Optical fiber and the chirped Bragg grating (CFBG):

The dynamics of the fiber is mathematically represented by the input-signal operator ${L}_{Fiber}${.}, which is expressed via Eqs. 7–10 as follows

$${{u}_{out,fiber}={L}_{Fiber}\{u}_{in,fiber}\}$$

(6)

$${L}_{Fiber}=\sqrt{{\kappa }_{f}}\left\{.\right\}exp\left\{i{\varphi }_{CD}(t)+i{\varphi }_{CFBG}\left(t\right)+i{\varphi }_{SPM}\left\{.\right\}\right\}$$

(7)

$${\varphi }_{CFBG}:CFBG\,introduced\,phase\,difference,\,{ \varphi }_{CD}:Chromatic\,dispersion\,based\,phase\,difference$$

$${\varphi }_{SPM}:Self\,phase\,modulation\,induced\,phase\,difference,\,{\kappa }_{f}:Fiber\,loss\,coefficient$$

The\,SPM depends on the fiber nonlinearity $\gamma$, input signal amplitude ${u}_{in,fiber}$, and the fiber length ${L}_{f}$ (Huang et al. 2021; Lee et al. 2009; Li et al. 2013; Zheltikov 2018; Howe et al. 2006; Agrawal and Olsson 1989; Stolen and Lin 1978; Aşırım and Jirauschek 2022; Crosignani and Porto 1982)

$${\varphi }_{SPM}\left\{.\right\}=\gamma {\kappa }_{f}{\left|\left\{.\right\}\right|}^{2}\frac{1}{2}{L}_{f}\left(1+R\right)$$

(8)

$$\gamma: Nonlinearity\,of\,the\,fiber,\,R:\,CFBG\,reflectivity,\,{L}_{f}:\,Length\,of\,the\,fiber$$

The chromatic dispersion in the delay fiber is modeled using the relation

$${\varphi }_{CD}(t)={L}_{f}\left[2{\pi }^{2}{\beta }_{2}{{f}_{s}}^{2}\left(t\right)+\frac{4}{3}{\pi }^{3}{\beta }_{3}{{f}_{s}}^{3}\left(t\right)+\frac{2}{3}{\pi }^{4}{\beta }_{4}{{f}_{s}}^{4}\left(t\right)\right]$$

(9)

which can be compensated to an intended degree using the CFBG, whose dispersion coefficients are set accordingly

$${\varphi }_{CFBG}\left(t\right)=-{L}_{f}\left[2{\pi }^{2}\widehat{{\beta }_{2}}{{f}_{s}}^{2}\left(t\right)+\frac{4}{3}{\pi }^{3}\widehat{{\beta }_{3}}{{f}_{s}}^{3}\left(t\right)+\frac{2}{3}{\pi }^{4}\widehat{{\beta }_{4}}{{f}_{s}}^{4}\left(t\right)\right], \widehat{{\beta }_{\mathrm{2,3},4} }={\beta }_{\mathrm{2,3},4}-{\beta }_{\mathrm{2,3},4}/\Pi$$

(10)

$$\widehat{{\beta }_{\mathrm{2,3},4} }:CFBG dispersion coefficients, {\beta }_{\mathrm{2,3},4}:Fiber dispersion coefficients, \Pi :Scale \left(compensation\right) factor$$

Fabry–Perot filter: The Fabry–Perot filter (Lorentzian) is used for the instantaneous filtering of each spectral component based on the following time-varying response that is described via the input-signal operator ${L}_{FP}\{.\}$

$${u}_{out, FP}\left(t\right)={L}_{FP}\left\{{u}_{in, FP}\right\}={\int }_{0}^{\infty }{h}_{FP}\left(t;\tau \right){u}_{in, FP}(\tau )d\tau$$

(11)

$${h}_{FP}\left(t;\tau \right)={{\mathit{ }(T}_{\mathit{max}}}^{1/2})\times \mathrm{exp}\left(-\frac{(\Delta f/2)}{2\pi }\tau \right)\times \mathrm{cos}\left(2\pi \left({f}_{c}+{f}_{s}\left(t\right)\right)\tau \right)\,(Response\,of\,the\,FP\,filter)$$

(12)

$${f}_{s}\left(t\right)=0.5\times\,{\Delta \Omega }_{sweep}\times \mathrm{cos}\left(2\pi {f}_{0}t\right)$$

(13)

$$\Delta f:Bandwidth\,of\,the\,FP\,filter,\,{ T}_{max}:Transmission\,coefficient\,of\,the\,FP\,filter, { \Delta \Omega }_{sweep}:Sweep\,bandwidth$$

Finally, the signal at the SOA input can be computed for each consecutive roundtrip based on the relation (Fig. 5)

$${u}_{SOA, \zeta +1}\left(t\right)={L}_{FP}\left\{{(1-c)\times L}_{Fiber}\left\{{L}_{SOA}\left\{{u}_{SOA, \zeta }\left(t\right)\right\}\right\}\right\}, \zeta =\mathrm{1,2},\dots ,N$$

(14)

2.4 Convergence of the simulated FDML laser operation and comparison with experiment

Most of the dips that are computed in the experiment (greater than 90%) include the regular dips (shown in Fig. 6b), which only rise above and fall below the threshold once within a temporal range of 150 ps. These dips are usually shorter in duration compared to irregular dips, and they are almost identical in pattern. The probability distribution of the regular dips in a given intensity pattern, is computed based on the output signal of the experimental setup (Grill et al. 2022; Schmidt et al. 2020, 2021), and the simulated output signal using Eqs. 2–14, via the described algorithm in 2.1, under the given parameters in Table 1 for 800 consecutive roundtrips. The distribution of the investigated dips are observed to be in agreement with experiment under identical parameter values (Fig. 6a).

Fig. 6

a Probability distribution of the dips versus dip duration. b Comparison of the regular dip (hole) patterns regarding experiment and simulation

As illustrated in Fig. 7, the simulated FDML laser operation converges within a few hundred roundtrips in line with experimental observations (Huber et al. 2006a; Jirauschek et al. 2009; Aşırım et al. 2022; Eigenwillig et al. 2013; Grill et al. 2022; Schmidt et al. 2020, 2021). The convergence analysis is based on the MSE between the power patterns of each subsequent roundtrip. The presence of convergence indicates the gradual elimination of the power-dips by the FDML laser, demonstrating the self-correcting behavior of FDML lasers. However, this self-correcting behavior of FDML lasers is distorted by the presence of strong SPM as described in the next section.

Fig. 7

a Convergence of the simulated FDML laser operation in time. b Convergence of the MSE within the final 800 roundtrips (from 20 to 820th roundtrip) based on simulated FDML laser operation

3 Results

As already mentioned, the SPM of an optical pulse that propagates along an optical fiber is mainly dependent on the intracavity power level and the nonlinearity of the fiber. Most optical fibers that are practically used in FDML lasers, do not exhibit strong nonlinear optical response (Todor et al. 2011, 2012). However, even for small fiber nonlinearities, the SPM effect can become very influential when the intracavity power is large, which would cause a phase-mismatch among the intracavity signal and the impulse response of the Fabry–Perot filter and lead to power attenuation. Given that the synchronization of the cavity roundtrip time and the sweep period of the Fabry–Perot filter is very sensitive to any phase-change that can occur in the signal, concerning output signal power, the phase-change in the signal due to SPM cannot be ignored. Therefore, we have carried out an analysis on the FDML laser MSE convergence, by sweeping the fiber nonlinearity from 10⁻⁵ to ${{10}^{-1}\,\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$. This range encompasses the practical values of the most commonly used fibers in FDML lasers (Huang et al. 2022). Given that the optical power in the fiber is initially zero (when the FDML operation self-starts via the SOA ASE-noise), based on the solution of Eqs. 2–14, Fig. 8 shows the variation of the MSE against the number of roundtrips for different fiber nonlinearities. As it can be clearly noticed from Fig. 8, the MSE converges to a near-zero value for fiber nonlinearities below ${{10}^{-2}\,\mathrm{W}}^{-1}{\mathrm{m}}^{-1}.$ For higher fiber nonlinearities, the MSE does not converge to a near-zero value, indicating that the distortion in the optical pulses that arises due to the occurrence of power-dips, does not improve with increasing number of roundtrips because of the increased level of SPM in the long delay fiber. This means that the FDML laser operation self-corrects the distortion in the optical pulses up to a certain degree of SPM. Since the SPM effect is stronger when the intracavity power is larger, especially for applications that require high optical power (Aşırım 2022), using an optical fiber with a low nonlinearity seems crucial to prevent pulse distortion and an unstable FDML laser operation.

Fig. 8

MSE versus number of roundtrips for various fiber nonlinearities $\{\upgamma { (\mathrm{W}}^{-1}{\mathrm{m}}^{-1})\}$

Preventing the formation of power-dips due to SPM should be important because of the difficulty of compensating the effect of SPM in an FDML laser cavity. Excess dip-formation due to other effects such as the detuning of the filter and chromatic fiber dispersion, can be prevented by ensuring better filter synchronization and/or via using a CFBG to compensate for the fiber dispersion. However, the dips that are formed due to SPM in the optical fiber cannot be eliminated as easily since the SPM process is difficult to counteract. Although the intracavity power level in an FDML laser is often not high enough to cause such a strong SPM in the fiber that would drastically contribute to the density of power-dips, our investigation is especially useful for future/potential applications of FDML lasers that may require the generation of optical pulses with relatively high powers, which are prone to distortion due to fiber nonlinearity.

As mentioned earlier, the formation of power-dips strongly affects the convergence of the FDML laser operation. Since the fiber nonlinearity was observed to influence the convergence of the MSE between the signal patterns of two subsequent sweeps, we infer that the fiber nonlinearity should affect the total number of power-dips on the signal envelope, as the power-dips are reported to be the main hinderance to convergence (Aşırım et al. 2022; Eigenwillig et al. 2013; Grill et al. 2022; Schmidt et al. 2020, 2021). Figure 9 illustrates the variation of the number of dips against fiber nonlinearity for various dip-strengths, which are quantified by the standard deviation in the intracavity optical power. The classification of the dips into various strength categories via computing their associated standard deviation in power is helpful for assessing the impact of fiber-based SPM on FDML laser stability, since stronger dips can trigger long-term instability via the nonlinear optical response of the SOA. Here, one can observe that for low fiber nonlinearities, the total number of dips remains relatively constant with increasing fiber nonlinearity. However, once the fiber nonlinearity exceeds ${{10}^{-3}\,\mathrm{W}}^{-1 }{\mathrm{m}}^{-1}$, there is a drastic (~ eightfold) increase in the total number of dips for all dip-strengths. The percentage of increase in the number of dips appears to be similar for all dip-strengths. We observed dips up to 10mW in strength, where the standard deviation in power needs to be greater than 1mW for the sudden change in the optical power to be regarded as a dip. A concurrent analysis of Figs. 8 and 9 indicates that what prevents the convergence of the FDML laser operation is indeed the total number of dips, which radically increases with increasing fiber nonlinearity. Practically, the long optical delay fibers that are used in FDML laser cavities, usually have a nonlinearity that is smaller than ${0.01\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$. However, for large intracavity powers, the same rate of increase in the total number of dips would occur for lower fiber nonlinearities based on the definition of SPM. Hence it is especially important to employ a fiber with a low nonlinearity when dealing with high intracavity powers (Zheltikov 2018; Howe et al. 2006; Veith 1988; Agrawal and Olsson 1989; Stolen and Lin 1978), to avoid a drastic increase in the number of dips for ensuring both the stability of the operation and for noise elimination. Considering the SPM term in Eq. 8, the fiber nonlinearity should be decreased proportionally with a corresponding increase in the signal power to retain the same degree of SPM. Equation 8 also indicates that an increase in the fiber length also necessitates the use of a fiber with decreased nonlinearity. A longer fiber length is desirable for frequency sweeps over larger bandwidths (Karpf and Jalali 2019; Butler et al. 2020; Murari et al. 2011; Hao et al. 2019; Zhu et al. 2020). Hence, the fiber nonlinearity should be selected carefully in conjunction with the intracavity signal power and the bandwidth of the sweep. It is noteworthy that there is a decrease in the number of dips above a fiber nonlinearity of ${0.05\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$. This decrease does not indicate that an unusually high fiber nonlinearity leads to an elimination of the dips, but it rather indicates that the phase mismatch between the signal and the filter response is so high that the intracavity signal power has started to attenuate, thereby causing power fluctuations of lower strengths, which leads to some dips that used to have a power standard deviation above 1 mW, to become smaller in strength (less than 1 mW), so that they are not regarded as dips anymore based on our classification. This is better understood via Fig. 10, where peak signal power is plotted against the fiber nonlinearity.

Fig. 9

Number of dips vs fiber nonlinearity for various dip-strengths defined by the standard deviation in power. The classification of the dips into different strength categories is useful for evaluating the effect of fiber-based SPM on FDML laser stability

Fig. 10

Peak power versus fiber nonlinearity for different values of the carrier lifetime. The stability of the peak signal power with respect to the fiber nonlinearity decreases with an increase in carrier lifetime as a result of the corresponding increase in the number of dips (also see Fig. 11)

Expectedly, if the carrier lifetime of the employed SOA is increased, the intracavity signal power also increases as shown in Fig. 10. Since the SOA dynamics is nonlinear, and depends on the input signal power, a larger input power may lead to the formation of stronger dips based on Eqs. 3 and 4. Regarding this assumption, from Fig. 11, it may at first be inferred that the occurrence of stronger dips simultaneously stimulates the formation of additional dips due to the nonlinear SOA response, since a greater dip-density is present for higher carrier lifetimes. However, a more obvious and direct explanation is that a larger intracavity power increases the degree of SPM (Crosignani and Porto 1982; Suda and Takeda 2012; Liu et al. 2016; Wang et al. 1989), which can cause the formation of additional dips. The total increase in the number of dips for higher carrier lifetimes is naturally due to the combination of both effects as the two effects are interrelated through the feedback mechanism in FDML lasers.

Fig. 11

Number of dips versus fiber nonlinearity for different values of the carrier lifetime

As previously discussed, beyond a certain fiber nonlinearity the signal power in the cavity is expected to attenuate regardless of the power level and the carrier lifetime. A co-examination of Figs. 10 and 11 indicates that the decrease in the rate of increase of the dips for large fiber nonlinearities (above ${{10}^{-2}\,\mathrm{W}}^{-1 }{\mathrm{m}}^{-1}$) occurs via power attenuation due to the SPM in the fiber leading to a larger phase shift on the signal, which kills the synchronization of the filter response with the cavity roundtrip time, causing a simultaneous reduction in the average dip-strength. This explains why there is no actual positive effect of increased fiber nonlinearity on dip elimination. It can be clearly deduced that under a relatively stable intracavity power (${{10}^{-3}\,\mathrm{W}}^{-1}{\mathrm{m}}^{-1}<\gamma <{{5\times 10}^{-2}\,\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$), an increasing SPM in the fiber leads to a greater rate of increase of the dips. Figure 10 shows the reduction in the peak signal power in the cavity under large fiber nonlinearities, for the experimental carrier lifetime value of 70 ps (indicated in blue color) (Jirauschek et al. 2009; Aşırım et al. 2022; Eigenwillig et al. 2013; Grill et al. 2022; Schmidt et al. 2020, 2021) and also for the practical values of 120 and 150 ps (Huang et al. 2022).

Aside from the carrier lifetime, the LWEF of the SOA is another critical parameter that should be concurrently investigated with the fiber nonlinearity in the context of SPM. Figure 12 shows the plot of the number of dips against the fiber nonlinearity for different values of the LWEF. As mentioned earlier, the LWEF is the cause of SPM in the SOA (whereas the fiber nonlinearity is the cause of SPM in the fiber). It has been suggested that the LWEF of the employed SOA should be as small as possible for minimizing the density and strength of the power-dips (assuming all other parameters including fiber nonlinearity are chosen ideally) (Aşırım and Jirauschek 2022).

Fig. 12

Number of dips versus fiber nonlinearity for different values of the LWEF

Interestingly, we observed that the increase in the number of dips with higher fiber nonlinearity is sharper for lower values of the LWEF. As can be clearly noticed, for LWEF = 3, the increase in the number of dips is not so significant (less than 17%); however, for LWEF = 0.5 (such as for quantum dot based SOAs), the increase in the number of dips is tenfold. The rate of increase in the number of dips reduces gradually with increasing LWEF. This observation is particularly important for cases where SOAs with lower LWEF are preferred to minimize the dip-density, as this strategy appears to be less meaningful if the SPM in the fiber is strong either due to the fiber nonlinearity, intracavity power, or fiber length. Additionally, if the fiber nonlinearity and the LWEF are simultaneously high, this causes an increase in the peak power as shown in Fig. 13, which is presumably due to an increase in the average dip strength as both parameters have a strong effect on the dips.

Fig. 13

Peak signal power versus fiber nonlinearity for different values of the LWEF

3.1 Effect of increased fiber nonlinearity on the duration and strength of the dips

We have already observed that an increase in the fiber nonlinearity leads to a sharp increase in the number of dips. Here, we examine whether the same is true for the duration and strength of the dips. Figure 14 shows the histogram plot of the number of dips versus dip duration for fiber nonlinearities ${\gamma }_{1}=2.67\times {10}^{-3 }{\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$ and ${\gamma }_{2}=4\times {10}^{-2 }{\mathrm{W}}^{-1}{\mathrm{m}}^{-1},$ for 800 consecutive roundtrips under ultra-stable operation (as assumed throughout the manuscript unless a certain detuning is specified). It is observed that the frequency of the dips gradually increases with increasing dip-duration from 0 to 50 ps. Above a dip-duration of 50 ps, the frequency of the dips decreases sharply. In both cases, the minimum dip-duration is around 15 ps, the mean dip-duration is around 50 ps, and the maximum dip-duration is greater than 200 ps. The total number of dips is 25,849 for $\gamma ={\gamma }_{1}$ and 206,251 for $\gamma ={\gamma }_{2}$. It can be deduced that an increased fiber nonlinearity has a slight impact on the duration of the dips. The maximum dip-duration is around 220 ps for $\gamma ={\gamma }_{1}$ and 260 ps for $\gamma ={\gamma }_{2}$, which indicates that dips of longer durations arise under increased fiber nonlinearity. Similar distribution patterns are also observed for other fiber nonlinearities within the range ${\gamma }_{1}<\gamma <{\gamma }_{2}$. More importantly, increased fiber nonlinearity appears to have a profound effect on dip-strength. Table 2 shows the percentage of the total simulation duration that indicates the amount of time for which the standard deviation in power remains within a specified range, versus power standard deviation, for the fiber nonlinearities ${\gamma }_{1}$ and ${\gamma }_{2}$ under ultra-stable operation. The highest dip strength is around 15mW for both cases under the given experimental parameters in Schmidt et al. (2021). Evidently, dips with sharper amplitudes are more frequent for higher fiber nonlinearities, whereas a low fiber nonlinearity prevents the formation of major dips with a dip-strength above 3 mW.

Fig. 14

Number of dips versus dip-duration for 800 consecutive roundtrips under ultra-stable operation for ${\gamma }_{1}=$ 0.00267 ${\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$ and ${\gamma }_{2}=$ 0.04 ${\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$

Table 2 Percentage of total duration, which indicates for how long the standard deviation in power remains within a specified range, vs power standard deviation, for a fiber nonlinearity of ${\gamma }_{1}=$ 0.00267 ${\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$ and ${\gamma }_{2}=$ 0.04 ${\mathrm{W}}^{-1}{\mathrm{m}}^{-1}$ under ultra-stable operation for 800 consecutive roundtrips

4 Discussion

Through intensive trial and error, we have found out that the most accurate way to compute the number, duration, and strength of the power-dips is to compute the standard deviation in the optical power through a sliding window, with a window size of 16 grid-points (sampling period is 1.5 ps). This number of grid-points is chosen such that the dips with the smallest duration (~ 15 ps) can be effectively identified since a given time-window must not be so large to contain two dips at the same window, but should be long enough to identify a single dip. Two consecutive dips can only be considered as separate dips if the power falls below the threshold value for more than 10 grid-points (pseudocode in 2.1), which corresponds to the minimum dip-duration of 15 ps. Otherwise, one has a single irregular dip with multiple crossings over the threshold power value.

We have used the standard-deviation-window not only for identifying the dips, but also to compute their strength/magnitude and duration, as it not only seemed to be very useful to classify the dips but also prevented the definition of additional parameters for dip characterization, which would complicate the analysis. The stated standard deviation values for dip-classification are determined based on the experimental setup in Schmidt et al. (2020 , 2021), and they are in accordance with practical intracavity operation powers. The standard deviation in signal power is used as a measure here because it directly computes the dip-strength, and dips with higher strengths have greater potential to destabilize and/or prevent the operational convergence of FDML lasers due to the corresponding nonlinear optical response of the SOA causing further aberrations at each round-trip. Hence, we are not just interested in quantifying all dips, but also the "dangerous" dips with super-strength, which are easily detected and quantified via sliding the standard-deviation-window sample by sample.

Based on the obtained results, it can be stated that the FDML laser cavity tolerates the fiber-based SPM up to a certain level, beyond which the number of dips rises drastically, eventually causing a complete attenuation of the intracavity signal, killing the FDML laser operation. Although it is known that a certain degree of SPM in the fiber can be applied for chromatic dispersion compensation in the fiber, in this study we have shown that this is a dangerous strategy, one that is also not very effective in an FDML laser. Notably, SPM becomes even more dangerous for the long-term FDML laser operation under SOAs with higher carrier lifetimes, which facilitate SPM and enables it to occur under lower fiber nonlinearities as we have shown in Fig. 11. Most importantly, we observed that for SOAs with low LWEFs, the impact of fiber-based SPM on noise generation is stronger. This observation is important for FDML cavities employing quantum-dot based SOAs (which are known to exhibit a low LWEF) and suggests the use of a fiber with a low nonlinearity to make use of the noise-reducing effect of quantum-dot based SOAs via LWEF lowering. The SPM induced dips are of slightly greater duration (see Fig. 14), but of much greater strength as indicated in Table 2. This finding suggests that the power-dips that are generated via fiber-based SPM are more dangerous than those generated via chromatic dispersion, as the dips that are formed via chromatic dispersion was not found to be of greater magnitude and duration (Schmidt et al. 2020, 2021). Therefore, especially for FDML lasers that are used for applications demanding high intracavity power, SPM can become a very serious issue and must be carefully considered at the design stage.

5 Conclusion

The effect of optical delay-fiber based self-phase modulation (SPM) on the operational convergence and stability of FDML lasers has been analyzed. It is observed that an increased level of SPM, either due to an increased intracavity power or increased fiber nonlinearity, drastically increases the formation of power-dips (up to an eightfold increase). Consequently, the convergence of the FDML laser operation is greatly affected, and depending on the intracavity power level, the FDML laser operation does not converge for relatively high fiber nonlinearities. We have seen that a fiber nonlinearity below 0.01 ${\mathrm{W}}^{-1 }{\mathrm{m}}^{-1}$ mostly ensures stable operation and prevents the formation of an excess number of power-dips under practical optical powers. In addition, an increased level of SPM considerably increases the strength of the dips and also has a noticeable increasing effect on the duration of the dips, especially for highly irregular dips with longer durations. Our observations indicate that an optical delay-fiber with minimum nonlinearity should be employed in FDML lasers, especially for applications requiring high intracavity optical power. Most interestingly, the increase in the number of dips via an increase in the degree of SPM is much sharper for SOAs with low linewidth enhancement factors, which are preferred for keeping the number of dips to a minimum. This indicates that the use of a delay-fiber with a low nonlinearity is even more important for SOAs with minimized LWEFs in order to limit the occurrence of power-dips in FDML lasers.