Thermal lensing: outside of the lasing medium

Abstract

The thermal lens formed in a thermo-optical material as a result of its inhomogeneous heating, is a well-known phenomenon that has found widespread interest in the last decades, especially in the field of laser engineering and photo-thermal spectroscopy. In recent years, growing interest in the application of thermal lensing in different fields of optics and material studies has been observed. This review summarizes the latest efforts made by the scientific community to develop ways of using the phenomenon of thermal lensing. Its applications in spectroscopy, in laser beam formation and in imaging are described. The advantages and disadvantages of the thermal lensing in regard to these areas along with the potential future applications of the phenomenon are discussed.

1 Introduction

The relation between the temperature distribution and deformation of what we see must have been recognized by our predecessors at the very early stage of the human race evolution. While seeing a mirage in vast landscapes is something that not all of us will experience, the deformation of the images through the air above the flames of a bonfire or the “water” illusion effect on hot roads are the phenomena that probably everyone has seen or will see. So, the relation between temperature and optics is obvious for most of us. For a long time, we have known that these effects are related to the dependence of the air refractive index on temperature, n(T), but also on pressure, CO₂ abundance and water vapor partial pressure [1]. Similar distortions of the optical image seen through the walls of glass containers filled with water heated from the bottom led to the natural conclusion that the water refractive index n depends on temperature as well, and led to the first thorough thermo-optical (TO) studies of n(T) of water and other liquids [2, 3]. Simultaneously, the studies of n(T) of solids have begun [4, 5]. With the development of photography, it has been found that variable temperature may significantly affect the imaging process; thus, the interest was aroused in the thermo-optic coefficient, dn/dT, of optical glass [6, 7]. The discovery of lasers has been a pivotal event for the studies of thermo-optical processes [8]. The application of lasers has permitted effective (quick and significant in scale) generation of thermal distributions, ∆T, and simplified the measurements of the effects of such distributions on light. As the laser beam in the TEM₀₀ mode has the intensity that gradually decreases from the beam axis to its edges, absorption of such a beam, followed by non-radiative deactivation of the absorbing excited material, has to lead to the formation of a distribution ∆T, of which a simulated example is illustrated in Fig. 1. Such a distribution, formed in a thermo-optical material, characterized by dn/dT ≠ 0, corresponds to a refractive index distribution, ∆n, and is called the “thermal lens” (TL). The effect that ∆n takes on light is called the “thermal lensing”. Thus, defined thermal lensing is the main subject of this review, and it should be clearly distinguished from the way this term is used by specialist working on thermal light (infrared, IR) optics.

Fig. 1

Simulated temperature distributions, ∆T, obtained using the theoretical model described by Whinnery [9] for ethanol with assumed absorption coefficient α = 2 m⁻¹, formed by a laser beam of radius ω_HL = 0.5 mm and of power P_HL = 40 mW. The time t_c is the characteristic thermal time constant (see definition in Sect. 2). Subsequent curves correspond to indicated times after turning-on the laser beam. Dashed line—parabolic curve of a perfect thermal distribution that corresponds to a thin lens in term of induced optical phase delay

The first observations of thermal lensing were made in the resonators of the just discovered lasers [10,11,12]. Simultaneously, self-focusing was observed outside of the resonator [13, 14]. As the operation of lasers has been found strongly affected by thermal lensing, these initial studies were quickly followed [15] by many years of investigation, summarized already in many books and reviews (e.g. [16, 17]). It is not the purpose of this review to reiterate the already made very careful descriptions of the thermal lensing in lasing media. Therefore, the reader interested in this first initial area of thermal lensing studies is encouraged to take a look at the cited works. The same initial studies revealed that thermal lensing may be used in detection of very small absorbances in liquids [18]. These works and subsequent ones [19] indicated that the thermal lens focal length in liquids and in solids [20] depends not only on the absorbance of the thermal lensing medium but also on the intensity of the laser, the medium dn/dT and its thermal conductivity k. Therefore, it was clear that measurements of thermal lensing, by analysis of the focusing or defocusing of a probe beam, may be used for determination of these parameters of the medium. The photo-thermal spectroscopy was born [21, 22]. Next, many new applications of thermal lensing have been proposed. Simultaneously, efforts were made to form thermal lenses using electrical heating of a thermo-optical medium. The purpose of this publication is to review these new ideas with the focus on the newest advances in photo-thermal spectroscopy and in application of thermal lensing in imaging and laser beam formation, described both in scientific and patent literature. Note, that while much of the work made in the field of thermal blooming [23] is related to the subject of this review, this process of thermal lensing in the atmosphere will not be discussed here.

The structure of this review is as follows. Section 2 shortly describes the thermal lensing effect and the basic photo-thermal spectroscopic experimental setups that have been used over the decades of photo-thermal studies. Section 3 reviews the newest achievements in the field of photo-thermal spectroscopy. Section 4 describes the effect of thermal lensing in solid TO materials illuminated by high-power lasers and the methods proposed for corrections of the beam wave-front deformed by such thermal lenses. Section 5 is devoted to the application of thermal lens as a tunable lens, mostly in the image formation. Section 6 describes shortly some other applications of thermal lensing. Section 7 analyses the perspectives of thermal lensing in future potential applications.

2 Thermal lensing

2.1 Basics

To understand thermal lensing, it is worth reminding shortly the origins of the temperature-dependence of the refractive index. Let’s begin with the Clausius–Mossotti relationship [24, 25]

$$\frac{\varepsilon - 1}{{\varepsilon + 2}} = \frac{4\pi }{3}\frac{\alpha }{V}$$

(1)

in which ε is the dielectric constant of the material and α is the polarizability of the macroscopic small spherical volume V of the material. The temperature derivative of Eq. (1) at a constant pressure gives [26]

$$\frac{1}{{\left( {\varepsilon + 1} \right)\left( {\varepsilon + 2} \right)}}\left( {\frac{\partial \varepsilon }{{\partial T}}} \right)_{p} \, = \, - \frac{1}{3V}\left( {\frac{\partial V}{{\partial T}}} \right)_{p} \, + \,\frac{V}{\alpha }\left( {\frac{\partial \alpha }{{\partial V}}} \right)_{T} \frac{1}{3V}\left( {\frac{\partial V}{{\partial T}}} \right)_{p} \, + \,\frac{1}{3\alpha }\left( {\frac{\partial \alpha }{{\partial T}}} \right)_{V} \, = \,A\, + \,B\, + \,C$$

(2)

By substituting ε = n², one finds the relation for dn/dT

$$\left( {\frac{{{\text{d}}n}}{{{\text{d}}T}}} \right)_{p} \, = \,\frac{{\left( {n^{2} + 1} \right)\left( {n^{2} + 2} \right)}}{2n}\left( {A + B + C} \right)$$

(3)

While this simple model is not exact for many materials [25], it gives the idea of the most important processes that determine the dn/dT value. The A factor is related to the temperature changes in the density of the thermo-optical material, B is related to the change in polarizability of the material accompanying the temperature changes in its density, C is related to the pure temperature-dependence of polarizability without changes in the material density. An expansion in volume with temperature leads to a decrease in n, while an increase in polarizability leads to an increase in the refractive index. These two mechanisms exert the counteracting impact on n and depending on the one that actually dominates, dn/dT may be positive as is in most cases in glasses [7] or negative as in liquids [27] and polymers [28]. In most cases, in a relatively narrow T range of a few kelvins, n(T) is linear. In terms of absolute values, dn/dT is the highest in liquids (≤ 8 × 10^–4 K⁻¹ [27]), moderate in polymers and epoxy (< 5 × 10^–4 K⁻¹ [28]) and the smallest in glasses (< 3 × 10^–5 K⁻¹ [7]). This highest absolute dn/dT in liquids was the reason why thermal lensing was initially observed and studied in them. Today, the lowest values in solids are still high enough to apply these thermo-optical materials in optical-fiber communication TO devices e.g. thermo-optical switching, temperature sensors, optical modulators and other non-linear optical devices [25].

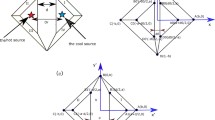
Take a look now at Fig. 2 showing schemes of three typical laser-induced thermal lensing measurement setups. In each configuration, a thermo-optical sample (TO) is placed in the focus of the laser beam that forms the thermal lens (TL).

Fig. 2

Typical thermal lensing experimental setups. HL—heating laser beam that forms the thermal lens, TO—thermo-optical material, TL—thermal lens formed by HL in TO, DM—dichroic mirror, D—point light detector, SH—Shack-Hartmann wave-front sensor built of lenslet array (Ls) and camera (C). a Single beam setup. b Dual beam setup with HL narrower than the probe beam—TL acts on the on-axis part of the probe beam only. c Dual beam setup with HL wider than the probe beam—TL acts on the whole probe beam. Rose probe beam—the beam shape without TL present. Red probe beam—the beam shape after propagation through the TL

Let us assume that all laser beams used in these setups work in the TEM₀₀ mode. The first configuration (Fig. 2a) is a single-beam setup as used in the earliest studies of TL. The same beam induces the TL and self-focuses. The thermal lenses formed in the TO material shown in Fig. 2 are assumed to be diverging. That is why the probe beam after having passed the TL in Fig. 2a becomes wider (red beam) compared to the original shape (rose beam) not affected by TL. Then, a pinhole is placed that let pass the near axis part of the probe beam that due to the divergent character of TL is supposed to be of smaller intensity than with TL absent, to the detector D. In this way, it is simple to monitor the time evolution of the TL formation process, by synchronizing the measurement with, e.g. a shutter in the heating beam path before the TO sample. The second and third configurations are dual-beam types, with the separate heating laser beam (HL) directed to be coaxial to the probe using a dichroic mirror. HL is in principle always focused at the TO sample. In the second configuration (Fig. 2b), HL beam is significantly narrower than the probe one. As a result, the TL formed refracts only the near-axial parts of the probe beam, leaving the edge rays unaffected. In consequence, the center of the probe beam is spread away from the axis, which induces changes in the signal behind the pinhole, detected by D, even more pronounced than in the single-beam configuration. Additionally, as shown by Hu and Whinnery [29], the configuration in which the probe beam is focused in front of the TO sample, called the “mode-mismatched” one [30, 31], magnifies the TL signal, that corresponds to the drop in intensity of the probe beam at D with TL present. Sometimes, additionally, a diverging lens is placed behind TL to additionally improve the signal-to-noise ratio (S/N). The third configuration (Fig. 2c) is characterized by the HL beam wider in diameter than the probe beam. In this configuration, the probe beam passes through a TO material in which the TL is certainly of a diameter wider than that of the probe beam. This allows easy monitoring of the TL operation by, e.g. measuring the probe beam wave-front using a Shack–Hartmann sensor, for instance [32, 33]. These three most common configurations differ mostly from each other by the relation of the probe and HL beams radii at the sample, ω_p and ω_HL, respectively. Especially, ω_HL is important and let us now see why.

The first model of the focal length, f, of the thermal lens formed as in Fig. 2 has been formulated by Gordon et al. [10,11,12], based on the theory that was used in ∆T simulation shown in Fig. 1:

$$\frac{1}{f}\, = \,\frac{{P_{{{\text{abs}}}} }}{{\pi k\omega_{{{\text{HL}}}}^{2} }}\frac{{{\text{d}}n}}{{{\text{d}}T}}\frac{1}{{1 + t_{{\text{c}}} /2t}}$$

(4)

where P_abs = P·α·L (approximated to the 1st term of the series expansion) is the power of the laser light (P) absorbed by the TO material, while α, L and k are the TO material absorption coefficient, length and thermal conductivity, and

$$t_{{\text{c}}} \, = \,\frac{{\omega_{{{\text{HL}}}}^{2} \rho c_{{\text{p}}} }}{4k}$$

(5)

with ρ and c_p being the TO material density and specific heat, respectively. The quantity t_c is the characteristic thermal time constant that as can be deduced from Eq. (4) determines the time evolution of the TL focal length. As can be seen, the thermal lens optical power increases with time at a rate depending on the TO material properties and HL beam diameter. The final focal length depends on several parameters, the HL power and ω_HL characterizing the HL beam, and a few other parameters that characterize the TO material. This model assumes that the steady-state ∆T(r) distribution formed by laser heating is parabolic in r, which is the radial distance from the HL beam axis. Thus, ∆T(r) corresponds to a parabolic ∆n(r) dependence, which is the property of the thin lens. In reality, the thermal lens is strongly aberrant, which was soon observed and theoretically treated [19, 20, 34, 35]. The same authors have reported that convection may significantly modify the thermal lensing effect in liquids. Thus, what followed was a multitude of publications that provided more complex models. Among them, the model proposed by Wesfreid et al. [36] is particularly worth noting. In their model of intra-cavity thermal lensing, they have taken into account the wave propagating in both directions in the liquid cell inside the laser cavity. Sheldon et al. have presented a model [37] based on the diffraction theory of aberrations, that showed improved correlation with experimental results. Then, Carter and Harris [38] have published a comparison of the first parabolic model of thermal lensing [11], the Sheldon’s et al. aberrant lens model [37] and a modified parabolic model. They have found their new modified parabolic model more accurate than the original one, leading to results similar to those predicted by the aberrant lens model. Next, Power [39] has provided a model of a dual-beam pulsed near-field detection of the thermal lensing signal based on the Fresnel diffraction to reduce the size of the measurement setup and to describe in detail the full probe beam wave-front in close distance to the thermal lens. Shen et al. [30] have formulated a diffraction model of the dual-beam mode-mismatched thermal lensing for cw illumination. This particular model deserves to be pointed out as it has been used in many publications, as can be deduced from the reviews [21, 22]. It is also worth noting that Gupta et al. [40,41,42] have formulated a model of formation of the thermal lens in a flowing medium for different configurations of the two-laser beams, at arbitrary angles between the probe, the heating beam and the fluid stream.

This short survey, certainly does not cover all literature pertaining to the models of thermal lensing. Nevertheless, it gives the idea what was the concern of the scientist when studying the thermal lensing, almost exclusively in liquids. These studies have been concentrated on the correctness of the models that describe thermal lensing, not on the modification of the thermal lens properties. Such an approach followed from the fact that thermal lensing has quickly become a widely used photometric/spectroscopic tool, that can be used to determine very small variations in different properties of different (mostly liquid) media. To quickly describe how to measure these quantities, let us refer to the already cited work of Shen et al. [30].

2.2 Photothermal spectroscopy

Let us analyze the experimental setup (Fig. 3) which is a variation of the scheme shown in Fig. 2b.

Fig. 3

Typical mode-mismatched dual-beam photothermal setup. HL—heating laser, S—computer controlled shutter, L—lens, TO—thermo-optical sample, ω_0p—probe beam radius at its waist, ω_1p—probe beam radius at TO sample center, ω_HL—heating laser beam radius at its waist at TO sample center, z₁—distance between probe beam waist and TO sample center, z₂—distance between TO sample center and detector D₁, D_1,2—fast detectors (photodiode, photomultiplier)

The HL beam is turned on by the shutter S. Then the signal from the D₁ detector is collected using a data acquisition device (scope, computer card, PXI module etc.). The trigger signal is taken from the shutter controller or D₂ detector. As shown in the inset in Fig. 3, the heating laser (excitation) beam is focused in the sample of the radius ω_HL. The probe beam is focused in front of the TO sample, at a distance of z₁ and radius ω_0p ≫ ω_HL. The probe beam radius at the TO sample center is ω_1p. The proper focusing of both beams is achieved by adequate selection of the two lenses L. The distance z₂ between TO sample and the D₁ detector is large when compared to the probe beam confocal distance, z_c. The intensity of the light measured by D₁ behind the iris is given as [30]:

$$\begin{gathered} I(t)\, = \,I(0)\left\{ {\left[ {1 - \frac{\theta }{2}\tan^{ - 1} \left( {\frac{2mV}{{\left( {{{\left[ {\left( {1 + 2m} \right)^{2} + V^{2} } \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {1 + 2m} \right)^{2} + V^{2} } \right]} {\left( {2t/t_{c} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2t/t_{c} } \right)}}} \right) + 1 + 2m + V^{2} }}} \right)} \right]^{2} } \right. \hfill \\ \;\;\,\quad \;\quad \quad \;\left. { + \left[ {\frac{\theta }{4}\ln \left( {\frac{{\left[ {1 + 2m/\left( {1 + 2t/t_{c} } \right)} \right]^{2} + V^{2} }}{{\left( {1 + 2m} \right)^{2} + V^{2} }}} \right)} \right]^{2} } \right\} \hfill \\ \end{gathered}$$

(6)

where m = (ω_1p/ω_HL)² indicates the degree of the mode-mismatching, V = z₁/z_c, I(0) is the initial probe beam intensity measured at t = 0 (the one without the HL beam present),

$$\theta \, = \, - \frac{{P_{{{\text{abs}}}} }}{{k\lambda_{{\text{p}}} }}\frac{{{\text{d}}n}}{{{\text{d}}T}}\left( {1 - \phi_{{\text{F}}} \frac{{\lambda_{{{\text{HL}}}} }}{{\left\langle {\lambda_{{\text{F}}} } \right\rangle }}} \right)$$

(7)

t_c is defined as in Eq. (4), λ_p is the probe beam wavelength, ϕ_F is the TO sample fluorescence quantum yield, λ_HL is the HL beam wavelength and $\left\langle {\lambda_{F} } \right\rangle$ is the average wavelength of the fluorescence spectrum of the TO material excited at λ_HL. The right-hand-side term in brackets in Eq. (7) takes into account the loss of the heat energy converted from the absorbed light due to the process of fluorescence, but simultaneously the heat deposited in the TO material through the material transition from its directly excited state to the light emitting one. Note, that this model assumes the absence of any photochemical reactions in the TO material. At the steady state, a relative signal is calculated as (I(∞) − I(0))/I(0) which is a single value. The time-dependent signal I(t) is commonly formed from a list of consecutive values to which Eq. (6) relation is fitted, as shown in Fig. 4. In this way, one can measure, dn/dT, k, ρ, c_p, ϕ_F, the lower the number of the parameters of the fit, the better the result. This method is a good representative of the photo-thermal spectrometry, whose achievements have been thoroughly described in several reviews [21, 22, 43, 44] and was found important enough to be intellectual property protected in several patent applications [45,46,47,48,49,50]. That is why, only basic examples of application of the thermal lensing in spectrometry from the period reviewed already in the cited works, are given below, focusing on the technique development. Then, the achievements of the last few years are reviewed more in details.

Fig. 4

Example of a fit of Eq. (6) to time-dependent experimental values. Reprinted from [30], page 393, Fig. 6, Copyright (1992), with permission from Elsevier

Grabiner et al. [51] have used a thermal lensing spectrometer (TLS) to study the rate of translational cooling of gas samples, namely C₂H₂, CH₃F and CH₃Cl. Later, Long and Bialkowski [52] have shown that using TLS, it is possible to detect a mass of 0.3∙10^–12 g of CCl₂F₂ in argon gas at 1 atm pressure in the volume irradiated by HL. In liquids, the limit of small concentrations detection is often posed by the absorption of the solvent in which a studied sample is dissolved and by the fluctuations of the lasers intensities. To avoid these problems, several different solutions have been proposed, among them: polarization-encoded beams by Pang and Morris [53], differential dual-beam by Harris et al. [54, 55], and Erskine and Bobbitt [56], roto-reflected double thermal lens by Yang [57] or differential polarization-encoded TLS by Yang and Hall [58]. Further important solution was the proposal of a dual-wavelength pump setup by Tran and Xu [59] that allowed simultaneous monitoring of absorption at two wavelengths in a configuration of perpendicular pump-beam (“crossed”) propagation directions. Such a configuration had been already earlier found suitable for small volume studies by Dovichi et al. [60, 61]. At the same time, a circular dichroism (CD) photo-thermal spectrometer was devised by Tran and Xu [62], which was found to be ~ 3 orders of magnitude more sensitive than the ordinary CD spectrophotometers used at that time. In such a device, the polarization of the heating beam has to be switched from right-handed circular into left-handed, and the TLS signal needs to be determined for both polarizations many times, to average the signal. Additionally, it has been shown that using the crossed beam configuration, it is possible to measure CD for small volumes. A somewhat similar small volume measurement philosophy has been adapted in the thermal lens microscope (TLM) [63]. Here, the probe and heating beams are focused by the same microscope objective. However, as they are not coaxial, these beams are focused at the same point but cross only in a tiny volume of the sample. As mentioned by Burgi and Dovichi [63], the TLM has the advantage of: (a) generating the signal only in the intersection region of the two focused laser beams, (b) high sensitivity compared to those of standard microscopes, (c) very high absorbance measurement dynamic range of over 9 orders, (d) formation of images based on differences in thermal diffusivity of the sample. These unique features of the TLM resulted in the intense development of this technique, that led also to patent applications by Kitamori et al. [64, 65], including one for a CD TLM [66]. The same group has shown that sub-attomolar concentrations can be detected using TLM in biological samples [67]. In next years, TLS and TLM were used in many fields in works mentioned in previous reviews in the field [22, 43, 44]. The next chapter describes the most recent studies in which these techniques have been used.

3 Recent photo-thermal spectroscopy achievements

3.1 Advances in TLM and TLS

Analysis of the scientific literature on thermal lensing from the last decade leads to the conclusion that TLM has become the most important TL tool in photothermal studies. One of the continuously growing scientific areas is the detection of particle at ultra-small concentrations in microfluidic chips using TLM. For instance, Liu and Franko [68] reformulated the TL theory by taking into account the divergence of the HL beam at the sample, which is inevitably nontrivial in strong focusing cases, as in microfluidic TLM setups. Next, the same setup, as used by them [68] to check their theory, was used by Gorkova et al. [69] to present the possibility of determination of trace concentrations of chromium(VI) using a micro-flow-injection analysis–TLM measurement procedure. In such setup, the sample volume is limited and it is injected into a carrier stream that flows through the micro-channel of the measurement chip. This way, the time the sample is exposed to the HL radiation is limited, which allows for the use of a highly concentrated sample of small volume. Thus, it makes the measurement shorter in time, increases the sensitivity and decreases the sample consumption. This study was next followed by one of its coauthor’s, Franko et al. in [70], where the authors investigated the dependence of the TLM signal on: the HL power, the micro-flow rate, the sample injection volume and the detection position in the micro-chip. They found the optimal measurement conditions and proved being able to measure the full TLM signal from 20 consecutive sample flowing volumes (of 0.6 μL) in a minute (thus 20 times/minute). In a similar work, Yamaoka et al. [71] have presented a flow-focusing microchip, which together with a TLM allowed the detection of ~ 85% of the polystyrene 500-nm particles injected individually into the chip. The microchip designed by them is shown in Fig. 5. Injecting a sheath fluid trough ports 1, 2 and 4 of the device and the sample fluid through port 3 allowed for limiting in space the sample flow. It was sandwiched horizontally and vertically between the sheath flows. As measured by the authors, the resulting sample flow profile was square and of approx. 10 μm side length. As a result, the sample nano-particles were always located in the TLM HL beam focus. Therefore, the device allowed for an increase in the TLM detection efficiency.

Fig. 5

Scheme of the flow-focusing microchip designed by Yamaoka et al. [71] for TLM detection of nanoparticles. Red—profile of the sample volume at the TLM measurement position. Widths of the chip channels: 100–300 μm. Reprinted from [71], page 583, Fig. 3, Copyright (2016), with permission from Elsevier

A TLM with enhanced sensitivity has been designed also by Cabrera et al. in [72]. The authors used a passive Fabry–Perot optical cavity in which the sample studied was placed. They found that due to multiple reflections of the probe beam inside the cavity, the TL signal increased ~ 13 times. They also reported an ultra-small concentration detection limit of 6 ng/L of Fe(II) ions in water. Recently, Cabrera et al. [73] have presented another application of TLM in the online detection of nanoparticles of two sizes and in monitoring of their separation in the channel of a miniaturized gel electrophoresis chip. The authors achieved a lowest detectable concentration of 23 pM of 10 nm size Au nanoparticles. As stated by them, such combo-setup can significantly lower the costs of monitoring of the separation of various components of biological samples. Another configuration of a TLM has been proposed by Liu [74]. His TLM allowed changing ω_HL—from small sub-μm values to 21 μm. Increasing ω_HL leads to an increase in the confocal range of the HL beam. Liu has shown that proper selection of ω_HL and sample length, L, may lead to a significant rise in TL signal. He has also shown that for flowing sample in microfluidic chips the selection of ω_HL and L is also crucial when seeking for maximal signals. And it is not for the smallest ω_HL that this signal is the highest. TLM was also implemented in the detection of captopril in human serum and pharmaceutical samples [75, 76]. Captopril is an angiotensin-converting enzyme inhibitor that helps to lower blood pressure in veins and arteries. Thus, its detection in any physiological samples is important. As noted by the authors, they succeeded in such a detection at a limit of 38.4 nM, which was at the time surpassed only by chemiluminescence. Later, the same group [77] has presented the possibility of DNA hybridization assay with use of gold nano-particles. Using a TLM and a fluid micro-chip sample holder, they were able to detect DNA at the lowest concentration of 27 nM. Gold nano-particles detection limits have been also studied in water by Lima et al. [78], who found possible to detect the presence of a single particle of 50 nm diameter. Another micro-fluidic TLM detection of traces of 2,4,6-trinitrotoluene (TNT) was presented by Yoosefian and Alizadeh [79]. They succeed in detecting of 1.6 nM of the material. By scanning the sample using a TLM, one can produce a 2D map of thermal diffusivity of a material showing anisotropy of thermal conductivity, which has been achieved by Heber et al. [80] in studies of a single gold nano-particles dispersed in a nematic liquid crystal. Traces of Cr(VI) have been monitored by Hernández-Carabalí et al. [81] using TLM to check whether photocatalytic reduction of chromium (VI) in water leads to purification of this water to a level acceptable for drinking. The reader interested in TLM application in single molecule imaging is encouraged to take a look at the review of the TLM techniques by Adhikari et al. [82]. One of the most recent advances that has attracted much attention is a TLM that takes into account the scattering from nano-objects [83, 84]. Figure 6 presents the setup built by Li et al. [84], which they used in the studies of Ag nanowires (Ag NW) dissolved in glycerol. It consisted of typical components of a TLM (and TLS as well): the function generator that provides the signal to the acousto-optic modulator that modulates the HL beam; the microscope objective that focuses the HL beam at the sample; the same objective collects the probe beam light reflected/scattered from the sample; the avalanche photodiode that detects the small reflected/scattered signal; the lock-in-amplifier that denoises the collected signal using as the reference the modulation signal from the function generator. As shown in Fig. 6b, the sample was illuminated by the probe beam from the side of the glass plate, which reflected a part of the probe light at its interface with the glycerol. This reflected light interfered with the light back-scattered from the Ag NW and together they were giving the detected signal (iSCAT). The intensity of the reflected light depended on the refractive index of glycerol, which was changed by heating in the TL formation process. From there was coming the TL signal. On the other hand, the scattered signal depended also on the polarization of the probe light. As a result, the authors observed an increase of the scattered light intensity after TL formation when the probe beam was polarized along the Ag NW and a decrease when for the probe beam polarized perpendicular to the NW axis.

Fig. 6

TLM setup used in Ag nanowires (Ag NW) light scattering studies. Depending on the polarization of the probe beam light vs the NW axis the observed scattered light was of high intensity (parallel polarization) or of low (perpendicular polarization). Reprinted with permission from [84], page 8398, Fig. 1, Copyright (2020), American Chemical Society

Larger nano-objects cause much stronger scattering of the probe light, depending also on ∆T of the nano-object surrounding. Thus, interpretation of the level of the scattered probe signal, in parallel with the light diverged by the TL, brings additional information on the sample. For instance, Gruwich and Spector [85] have developed a theoretical model that explains the nonlinear dependence of the intensity of scattered laser light by metal nano-sphere particles immersed in oil, on the intensity of the illuminating the laser light. As they have shown, it is the formation of thermal distributions in TLS that is responsible for such a dependence. Similar observations have been made by Huang et al. [86] who succeeded in detection of single nano-particles of 5 nm diameter.

While TLM seems to be on the top in terms of method development and new applications, thermal lensing spectrometry (spectroscopy) is still used and developed as well. For instance, ultra-small particle concentration has been detected by Mazza et al. [87, 88], who evidenced the possibility of detecting with TLS the presence of 0.05 ng of protein bands in polyacrylamide gels soaked in methanol/water and of 0.1 ng in gels soaked in water. As claimed by the authors, it has been by an order of magnitude smaller mass than detectable by other methods. Domené et al. [89] have provided the evidence of detecting 5.6 ppm using samples of 130 nm thick Ta₂O₅ layer. They analyzed the TL-induced distortion of the probe beam, called by them the focus error [90], by measuring the difference in intensities of the probe beam between two diagonals of a 4-quadrant detector. This difference depends on the TL formed in the sample and two cylindrical lenses, that introduce an initial astigmatism in the former Gaussian beam. Ventura et al. [91] used TLS to detect sulfentrazone pesticide in methanol at a concentration of 5 × 10^–6 mol/L. The same group [92] has shown that using near–near infrared (nnIR, wavelength close to 950 nm) TLS, it is possible to identify biodiesel content in fuel blends. Even small concentrations of some substances may be the sign of adulteration of food (intentional contamination). Raj et al. [93] used TLS to detect liquid paraffin oil in coconut oil. Almeida et al. [94] have proposed TLS to be used in the dosimetry field. They studied the influence of the irradiation of commercial glasses with beta radiation and found that the TLS signal level depends linearly on the irradiation dose to which the studied material was exposed. Thus, they proposed TLS as a method of dose determination. A similar work has been presented by Imran et al. [95] for soda-lime glass and gamma radiation. TLS was also used by Hannachi [96] to detect traces of permanganate in water, the former being frequently used in disinfection of water. The lowest detectable concentrations he has reported were of 0.22 and 0.08 μM of the compound for distilled and tap water, respectively. Pedrosa et al. [97] have shown that using TLS, it is possible to measure temperature variations of 0.01 °C, at least in case of the gold-nanoparticle they studied dissolved in water. Recently, Sebastian et al. [98] have shown that using TLS, it is possible to estimate the porosity of a nanomaterial composed of nano-particles. These authors have found that the porosity is linearly dependent on the thermal diffusivity, which is determined directly from TLS (Eq. 7). An interesting TLS setup has been proposed by Zhao et al. [99]. They coated a one-dimensional photonic crystal surface with the HL absorbing material. Next, they inclined the probe beam to the sample surface at such an angle as to obtain coupling between the probe beam and the resonant mode of the photonic crystal. In this way, the reflectance of the sample increased significantly. After turning on the HL, the heat resulting from absorption at the sample surface formed an air thermal lens. It decreased the coupling between the probe beam and the photonic crystal mode and thus, the intensity of the reflected probe beam. Thermal lensing was also employed as a probing tool in laser conditioning of thin-film surfaces in [100] by Liu et al. Laser conditioning is a technique of increasing material laser illumination damage threshold by pre-illuminating the material with a laser light of sub-damaging intensity. As the damage threshold is initially unknown, the authors developed a system of TLS measuring the absorption of the conditioned surface. In response to the measurement, the setup changes the laser conditioning intensity, to a level that is slightly below the damaging one. A similar work has been reported by Wan et al. [101] who studied damage threshold of fused silica using TLS. A thermal lensing few-fold enhancement of a cavity ring down spectrometer signal was presented by Yarai [102]. Zhang et al. [103] performed numerical simulations of thermal lensing/blooming in sea water. Their motivation was to study the influence of the water salinity, depth, and laser wavelength on the laser beam propagation in sea (e.g. for communication purposes). As water absorption is relatively small, at least in the visible range, they simulated propagation at distances from tens of meters to 1 km, which is an atmospheric thermal blooming range rather than that of TLS. They found that increasing salinity leads to stronger thermal lensing. Not surprisingly, the wavelength dependence followed the absorption spectrum of sea water. However, the depth dependence was found non-trivial, related to current velocities, depth dependencies of dn/dT and c_p.

One of the drawbacks of using laser heating beam is the limited spectral range of the heating light that can be used in TLS. Cabrera et al. [104] have shown a TLS setup with heating light provided by a halogen lamp, with light wavelength selected using an interference filter. In this way, they were able to scan the TL spectrum in the range of 430–710 nm. The probe laser beam generated by a He–Ne laser was counter-propagating to the heating beam. The interference filter was used as a mirror for the probe beam, which reflected back the beam in the direction of the sample, from which the beam was reflected again in the direction of the filter. Thus, amplified TLS signal allowed the measurement of absorbance spectra at the level of 10^–4 for Fe(II)-1,10-phenanthroline. The above-cited multi-pass setup was next developed by the same group [105] into a probe beam ten-pass setup. The authors modeled theoretically the system and obtained an up to ninefold enhancement of the TLS signal, which allowed a similar scale decrease in the lower detectable concentration of the same compound as in [104]. To speed up the process of absorbance spectra measurements using TLS, the wavelength multiplexing can be applied. It is based on simultaneous heating of the TO material with an HL beam formed of components of different wavelengths, each modulated in time and amplitude in a different way. An interesting survey of these methods may be found in [106] where Seto et al. presented a new pseudo-random multiplexing method of TLM spectral measurement that circumvents the problem related to different gain of the TL signals obtained at different HL wavelengths. The use of incoherent heating light, like the white light source mentioned above, results in difficulties in its focusing in TLM setups. A careful analysis of this process has been made by Liu and Li [107]. What they found is that the TLM signal increases almost quadratically with the size of the LED heating beam source, when the light is focused using a spherical lens. Meanwhile, using a hyperbolic lens, that introduces spherical aberrations of much smaller scale than the spherical one, the TLM signal increases linearly with the light source size. Thus, depending on the purpose of TLM using, a different incoherent source should be applied, if any. Instead of while light source, one can use a dye laser tunable in a wide range. Diaz et al. [108] have used a two-laser heating setup, in which two-laser beams overlapping each other in the sample were used. One of the HLs was a tunable dye laser, the second was a fixed wavelength one. The authors’ intention was to study the UV absorption spectrum of benzene and naphthalene dissolved in n-hexane, with focus at the ∆v = 6 overtone. The tunable HL was used to obtain the spectrum. The second fixed wavelength laser was used to induce additional electronic excitation of the sample, to increase the amount of heat dissipated in the sample through non-radiative deactivation from an excited electronic state. In this way, they significantly increased the TL signal making their TLS setup more sensitive.

3.2 Fluorescence quantum yield measurement

As follows from Eq. (7), knowing θ, it is possible to determine the fluorescence quantum yield, ϕ_F, of the studied compound with no need to measure reference spectra, as it is commonly made [109]. This approach is well known and has been used many times in the studies reviewed in [21]. Recently, this possibility has been exploited by dos Santos et al. [110] for the determination of ϕ_F of xerogels doped with Rhodamine B in a range of its concentrations. They found that increasing the rhodamine concentration decreases ϕ_F as a result of formation of aggregates of the dye molecules, which more efficiently undergo non-radiative deactivation. Correct measurement of ϕ_F using TLS for slightly absorbing samples may be hard, due to the problems with precise determination of P_Abs. Silva et al. [111, 112] have proposed a hybrid TLS and photoluminescence method which assumes that P_abs from Eq. (7) is extracted from the emission spectrum of the sample. In this way, they circumvented the problem of the correct measurement of small absorbances at the edges of the absorption spectrum of the sample. For strongly emitting samples, it is much easier to determine correctly their emission spectrum, and for the samples used by the authors, it is easier to determine ϕ_F from this spectrum. It is also important to note, that Silva et al. used the TL model in which the absorption of the whole sample was separated, as a parameter of the whole setup, from the absorption of the emitting component of the sample.

3.3 The effects determining thermal lensing and the correctness of its theoretical description

The model [30] described by Eq. (6) is widely used, even if it is based on assumptions that may be not fulfilled in many experiments. In response to the progress in methods of numerical simulations, Vyrko et al. have published an interesting work [113] in which they numerically simulated the results of a TLS experiment, using the Comsol Multiphysics and Matlab, two standard tools for such calculations. Their intention was to compare the results of numerical simulations with those obtained using the analytical model (Eq. 6). Most of all, they wanted to determine what the limits of correctness of the assumptions made are when formulating the model of Shen et al. [30]. There is no space here to cite all their conclusions; they are listed in a very clear way in the original paper. The reader interested in numerical simulations is strongly encouraged to study this paper, as it will certainly help correct formulation of his/her simulation problem. Another paper in which the correctness of the most common model, i.e. Eq. (7), was discussed is that of Liu [114]. He was concerned with the reciprocal relation θ~1/k, which as the author showed, does not hold for low thermal conductivity, k. Additionally, he found that for pulsed HL, increasing pulsing frequency makes this relation improper for higher k values. Recently, Isidro-Ojeda and Marín [115] have studied the upper limit of TL signal that can be correctly described by the Shen et al. model [30] and by the newer one proposed by Marcano et al. [116]. The latter model uses a collimated probe beam, instead of a diverging one. Isidro-Ojeda and Marín concluded that in the Shen et al. [30] model, the limit for detection of correct liquid thermal properties is θ < 0.30, while for the Marcano et al. [116] model, it is θ < 0.15. The time-resolved TL signal always begins with building up of the signal, followed in the case of pulse excitation, by a decay. Mohebbifar [117] has compared the thermal diffusion values obtained from analysis of both signal time ranges, separately for a set of common solvents and he found that the signal building up gives more precise values than the decay.

Ivanov et al. have developed a model of thermal lensing in a thin sample, whose thickness was significantly smaller than the size of the heating beam [118, 119]. Their model takes into account the Soret effect [120], called also the thermo-diffusion, that is, the drift of the molecules along the temperature distribution. In the distribution induced by HL, such a drift of the absorbing molecules, that are larger than the solvent molecules, may be present and may lead to inhomogeneous absorption of the sample. Next [121,122,123], the same authors have added to the model the effect of electrostrictive forces, following from the interactions between one of the sample components and the electric field of the HL beam. These models, of course, are based on some simplifying assumptions, but give an important insight into thermal lensing in more complicated systems than homogeneous liquids. Besides the Soret effect, a distribution of the concentration of the absorbing species, can also result from the photoreactions in which the components of a mixture take part. Such a process has been recently taken into account by Savi et al. [124] in a TLS study of biodiesel fuels. They observed that upon HL illumination, the fatty acid methyl esters (FAME) present in the fuels undergo the light-induced oxidation. This leads to a photobleaching, which is a significant drop in the sample absorptivity. This, in turn, leads to concentration distribution, that modifies the TL formed by HL, with time. Thermophoresis of the solvent molecules of a binary liquid mixture may lead to changes in TL signal as well. Soret effect leads to inhomogeneity in the solvents distribution, thus to distribution of the refractive index as well. Such effect was studied by Cabrera et al. [125,126,127]. They formulated a TL model that takes into account the solvents concentration gradients ∆c, which follows from the Soret effect, and they used it in the determination of the mass diffusion coefficients for mixture of several solvents. They compared their results with the ones modeled theoretically by other groups and obtained a relatively good agreement. Later, Malacarne et al. [128] added to the model the photochemical path of deactivation of the absorbing species, which they confronted with an experiment recently in [129]. They modeled with success the time-resolved TL signal of a lyotropic liquid crystal. In principle, all thermophoresis/Soret effect models do not take into account the intermolecular specific interactions that can take place between the molecules of the two or more compound of the solvent mixture, which is not surprising, as modeling such interactions requires Monte Carlo simulations. Meanwhile, such interactions (e.g. formation of hydrogen bonds) may significantly affect the heat conduction/convection and fraction separation in the HL-induced thermal distributions. The studies of this problem were undertaken by Rawat et al. [130], who studied the time-dependence of the TL signal collected from mixtures of methanol (MeOH) and water/dimethylsulfoxide (DMSO)/tetrachloromethane (CCl₄). As can be deduced from their polarity, the Kamlet-Taft coefficients, [27] MeOH is both a hydrogen donor and acceptor in the process of hydrogen bond formation, similarly as water. DMSO is only a hydrogen acceptor and CCl₄ has very low affinity to form hydrogen bonds. In the TL setup of these authors, the HL wavelength was set to the absorption line of MeOH. What they observed was an abrupt rise in TL signal upon addition of MeOH to CCl₄ and DMSO, while a continuous rise in water. They interpreted these observations qualitatively as the manifestation of the presence or lack of hydrogen bonding, which leads or not to the clustering of molecules of selected solvents. However, it is still not clear whether the hydrogen bonding affects only heat conduction/convection process, or dn/dT, excitation probability (coefficient of absorption), or fluorescence quantum yield as well.

Rodriguez et al. [131] have shown that at least for Tartrazine dye dissolved in water, the thermal diffusivity increases by 30% with the dye concentration increasing from 2 to 9 mM, so in a relatively small range of concentrations, typical of spectroscopic studies of dyes. As the authors claim, their results show that when analyzing thermally dependent results for such solutions one should take into account the possibility of such a dependence of thermal diffusivity. Vijesh et al. [132] used TLS to determine the dependence of the thermal diffusivity of carbon dots in water on their concentration. They found this dependence as reciprocal, which they speculated to be connected to the phonon–phonon coupling in the solution. Another TLS study of thermal diffusivity of nano-particles was made by Lopes et al. [133]. These authors studied the concentration dependence of the thermal diffusivity of Ag (silver) nanoparticles in water. They also found an inverse-dependence.

In principle, the HL beam profile does not need to be of Gaussian character. For instance, Li and Welsch [134] used numerical computation to compare the TL signal obtained with beams with Gaussian and top-hat profile and additionally for an Airy HL intensity distribution at the TL sample. They evaluated the TL signal for different configurations of the mode-mismatched TLS setup, varying the HL and probe beam radii, the distance z₁ between the probe beam waist and the sample and the distance z₂ between the detector and the sample. Their results have shown that the optimal geometry of the HL and probe beams, in terms of waist position and radius, that maximizes the TL signal, is different for the three types of HL illumination they studied. Additionally, they found that the top-hat HL beam allows obtaining a TL signal twice as strong as that found using the Gaussian HL profile, for a TLS setup correctly optimized. As for the Airy HL distribution, it was found more or less as effective as the Gaussian one. Next, the application of the top-hat HL beam profile in thermal lensing spectrometry was studied experimentally by Astrath et al. [135]. They have successfully investigated the possibility of using a diode-pumped multimode laser emission truncated by a pinhole to a nearly top-hat profile at the sample, instead of a TEM00 beam in TLS. Next, Sabaeian and Rezaei [136] have formulated an analytical model that took into account the HL top-hat profile and obtained results fully consistent with those given in [135]. The influence of the TL generated by a Gaussian beam on the propagation of a top-hat probe beam was studied numerically by Nossir et al. [137]. They formulated analytical expressions for the squared radius, waist position and squared far-field divergence angle of the probe beam that passed through the thermal lens. The most important finding of this work is probably the theoretical prediction of the decrease in TL signal, expressed by the probe beam divergence angle, which follows changing the probe beam profile from the Gaussian into the top-hat one. It indicates, that contrary to the HL beam case, application of the probe beam with top-hat profile is unfavorable from the TLS point of view.

The formation of the TL using an HL beam of Laguerre-Gaussian (LG) profile was recently studied theoretically by Ashraf et al. [138]. The authors formulated analytical expressions for the temperature distribution formed by LG beams of different modes, using typical assumptions of the TO sample being thin, wide in diameter and low light absorbing. They have shown that using LG HL beams of some particular modes leads to the formation of axial refractive index gradients of higher magnitudes than the one obtained with the Gaussian profile. The authors concluded that the application of these LG HL beams may lead to stronger TLS signals. However, no simulations of propagation of the probe beam through such thermal lenses were given by the authors; thus, their conclusion still needs to be verified. It is worth to mention that the propagation of LG beams in media with inhomogeneous refractive index distributions was studied already years ago [139] in the field of thermal blooming. The reader interested in this field is encouraged to follow the literature cited in this work. However, it seems that from the TLS point of view, the potential profit (or disadvantage) of using LG beam as the probe one needs further investigations.

In most of the photo-thermal experiments, the effect of convection is assumed to be negligible. While in many cases, such an assumption is justified, the problem of convection, especially the buoyancy, has interested researchers from the beginning of the thermal lensing studies [20, 34, 140, 141]. The problem was elaborated by Bogutarov et al. [142] for vertical convection induced by laser heating. The authors formulated a theoretical description of the auto-TL (HL self-induced TL) process in the presence of “moderate” and “developed” convection. The first one is present when the buoyancy is balanced by viscosity, while the other one when the buoyancy is balanced by the inertial forces. The model included vertical illumination of the TO liquid from the bottom and from the top, for a long cylindrical sample or for a wide cylindrical sample. Always the HL beam was assumed to be of a radius significantly smaller than the sample dimensions and the absorption was assumed to be small. Bogutarov et al. have shown that for illumination from the top, moderate convection induces changes in the HL beam propagation only in a limited range along the beam axis, below which no nonlinear effects are observed on the HL beam propagation. For the upward illumination, the moderate convection modifies the ∆T and HL beam itself in such a way that the vertical thermal gradient decreases while reaching the upper surface of the sample and the absolute highest temperature drops as well, when compared the value expected without the presence of convection. In the case of the “developed” convection, the scale of the effect does not depend on the direction of illumination. Later, Kucherov [143] has established the conditions for five convection regimes in the case of vertical illumination: moderate (high viscosity—$\eta$, low thermal conductivity—k), moderate (high $\eta$, high k), moderate (high $\eta$, very high k), developed (low $\eta$, low k), developed (low $\eta$, high k). Escalona [144] measured the time-dependent interferograms of TL formed horizontally, with clear buoyancy effects. From the interference patterns, he derived the phase patterns for each time-resolved measurement made with a time step of 250 ms. He observed equivalence between the measured-phase delays, converted into the refractive index changes and changes in temperature measured separately using a thermocouple. Escalona also discussed the conditions under which the buoyancy is significant enough to disturb the TL and finally came to the conclusions similar to the ones given above by Kucherov. Later Karimzadeh [145], with Arshadi [146] have measured the TL in the presence of significant convection in the horizontal and horizontal/vertical configurations of the HL propagation direction in the TO sample. They formulated some simplified theoretical models that they used to reproduce the experimentally observed TL signals. It is important to note that they used strongly absorbing samples. However, the authors in [146] used the vertical illumination setup as the one that allows omitting the convective effects, which as shown earlier by Bogutarov et al. [142] and by Hucharov [143], is not a justified assumption. Next, Goswami et al. have formulated a simplified model of TL that takes into account the convective effects in TLS [147, 148]. They studied the time-resolved TL signal in a series of n-alcohols starting with methanol of the shortest molecule and it is in this solvent they observed the highest convective effects. Their studies revealed that convective heat transfer coefficient, which determines the effectiveness of convective effect in the TL signal, decreases with the n-alcohol length, which can obviously be related to the solvent molecule size, thus the solvent viscosity and thermal conductivity. The viscosity of n-alcohols increases with the length of their molecules, while their thermal conductivity decreases. Thus, according to the criteria specified by Bogutarov et al. [142] and Hucharov [143], methanol revealed “developed” convection, while for long alkyl chain n-alcohols, the convection was moderate. Recently, Dobek [149] studied the effect of the vertical HL illumination from the top/from the bottom of a TO sample on the optical aberrations of the TL formed. He used a sample of very high absorption and a size similar to the HL beam diameter, as expected from a TL applied in imaging, where high TL optical power is needed, the TO sample should be relatively small and most importantly, the HL beam size must be larger than that of the probe/signal/imaged light to circumvent the spherical aberrations always present in a TL formed by a Gaussian HL. He found that the TL formed by the upward HL illumination was of significantly higher optical power than that formed by the same HL beam, but propagating downward through the TO sample. Numerical simulations have shown that convection significantly changes the TL thermal distribution, by elongating it and narrowing at the same time in the case of upward HL illumination and exactly opposite spreading TL in the horizontal plane and narrowing vertically in the case of downward HL propagation direction. Additionally, Dobek measured the time-dependent probe beam wave-front aberrations and approximated them by Zernike polynomials, from which he determined the time evolution of the modulation transfer function (MTF) of the TL formed in the two HL configurations. It turned out that the upward HL illumination leads to a transient optimal MTF.

3.4 Thermal lens studies related to high-power lasers and solid TO materials

It is interesting to note that studies of the thermal lensing in lasing materials and in, for instance, solid mirrors illuminated with high-power laser beams, were conducted mostly in parallel to the TLS studies, without some deep information exchange. It was probably related to the fact that studies of, e.g. thermal focusing induced by high-power lasers illuminating mirror surfaces were mostly conducted for solids of limited dimensions, for which the geometrical deformation resulting from heating needs to be taken into account, which is usually not taken into account in TLS. Obviously, the aim of the studies was different, TLS interprets the TL signal, while the laser crystal or mirror TL studies were aimed at finding solutions to overcome the TL phenomenon. As already mentioned, the thermal lensing in laser crystals was recognized soon after disclosing the phenomenon [15,16,17]. Then, high-power lasers were used, among other applications, in interferometric gravitational antennas, i.e. VIRGO and LIGO projects. An important problem was evaluation of the laser deformation of the interferometer mirror surface, which was addressed by Hello and Vinet [150, 151]. In their first work [150], they formulated analytical models for the TL formed in a mirror as a silica cylinder with a reflecting coating, suspended by wires in vacuum, which dissipated heat only through thermal radiation. They formulated time-resolved and steady-state models for the case of heating only the coating or the silica. Their models assumed low absorption, but the mirror was of limited dimensions. The authors calculated the coefficients of Zernike polynomials that best fitted to the heated mirror distorted wave-front. These coefficients were found to increase linearly with time up to some moment, after which they stopped changing. In [151], Hello and Vinet presented models of thermoelastic deformation of the mirror surface, upon high-power laser illumination. They used the same models for thermal distribution formation as in their previous work. For the sake of illustration, it is worth stressing that they modelled an HL of 2 cm waist at the surface of a silica mirror of 60 cm diameter and 20 cm length. The mirror was coated with a reflective layer from the side on which the HL beam was falling. For a 1 W HL, they predicted a 0.1 or 0.02 μm convex deformation of the mirror surface at the center, depending on whether the HL was assumed to be absorbed at the coating, or in the bulk silica. For this setup, they also calculated the coefficients of Zernike polynomials and obtained their time dependencies to be similar as previously. Such aberrations require correction. Potentially, the corrections can be introduced by use of spatial light modulators (SLM) [152] or deformable mirrors [153]. Another possibility is to compensate the thermally induced aberrations by secondary thermal wave-front modifications that can be treated as a second TL. Such a method was proposed by Wyss et al. [154] who predicted the formation, by the high-power laser beam, of an additional TL in a liquid or curing gel, which when diverging, will passively compensate the aberration introduced by the converging TL formed in a solid cylinder (rode, glass element, etc.). Another method has been designed by Lawrence et al. [155] who studied transmissive optics; nevertheless, the authors claimed that their method was applicable in reflective optics as well. In this method, the correction was introduced by radiative heating of the peripheral region of one of the two faces of the cylindrical optical element in which the laser beam formed a TL. Thus, in the same TO material (here fused silica), a thermal lens was formed with focal length of sign inverted relative to that of the one formed by the laser. The cylinder was shielded at the sides from the radiative heating by aluminum shielding. To evaluate their correction scheme possibilities, the authors have built a setup in which the wave-front of a low-power probe beam, aberrated by the TL induced by the high-power HL, was determined using a Shack–Hartmann wave-front sensor. Then, the departure of this wave-front from the original one, non-aberrated and obtained without the HL, was determined. This difference was measured continuously and used in a feedback loop in which the radiative heater was driven in such a way as to minimize the difference. Lawrence et al. were able to correct the aberrations by decreasing their maximal level 3.5 times. One drawback of this method is that the TO material is continuously heated, and as all the setup is maintained in a vacuum chamber, only radiative cooling carries away the excessive heat, which can take much time. Similar schemes of thermal corrections of TL in gravity interferometers have been devised also by Degallaix et al. [156]. Another method of aberration compensation has been proposed by Lück et al. [157], in which a similar control loop involving wave-front sensing and a control HL beam was used to compensate TL induced in the mirror. However, the HL was used to form an additional thermal distribution in the mirror by point-by-point heating of the mirror material using the control HL beam, a galvo-scanner and an HL intensity controller. Thus, the TL was not formed by a single illumination of the TO material, but by a 2D scan with variable intensity and/or exposure. In this way for the first time, a 2D control of the TL thermal distribution has been demonstrated. Lück et al. achieved an almost ×38 decrease in the level of wave-front distortion. A somewhat similar approach was followed by Saathof et al. [158, 159], in which the correction was introduced by a deformable mirror, but thermally actuated by illumination with a predefined distributed light. This heating light was provided and formed using a video projector and the mirror placed between the reflective layer and the substrate, was covered with an absorptive layer that was heated by the light provided by the projector. Note however, that the authors did relate the operation of their thermal mirror to thermo-elastic deformations only; thus, this type of device cannot be called a thermal lens, similarly as the device described by Michel et al. [160] working on the principle very similar to that of Saathof et al.

Thermal lensing in solid materials was certainly the primary subject of the studies by Reitze et al. Besides the studies of TL in laser resonators (amplifiers) [161], they also considered different schemes of TL compensation. In [162], Reitze et al. proposed formation of an additional correcting TL in a glass plate, which would absorb only the light of an auxiliary HL, and would be transparent to the main laser beam. By changing the HL power, the optical power of the additional TL was modified. A similar solution has been published by Scaggs in [163]. In [164], Reitze et al. have shown that a Gaussian HL, as in liquids, leads to spherical aberrations when it illuminates a mirror, but they also have shown that an HL with a top-hat intensity profile leads to much smaller aberrations. Next, the same group initiated studies of adaptive compensation of thermally induced aberrations using electrical heating of a transmissive element [165,166,167], which resembles somewhat the solution proposed by Lawrence et al. [155]. However, Reitze et al. proposed to heat a solid cylindrical optical element using quadrant ring heaters. These heaters were four independent heating elements, positioned symmetrically around the cylinder axis in thermal contact with the cylinder. By controlling the electric current flowing through each heater separately, it was possible to form symmetrical or asymmetrical thermal distributions in the cylinder. Thus, in response to a given need, a thermal axisymmetric lens could be formed (at least in the center of the cylinder), or a strongly astigmatic one, that could be used for instance for corrections of asymmetric absorption of the probe light in another optical element, or its astigmatism or birefringence. Obviously, the disadvantage of such a setup is its slow dynamics. The element was heated only at its sides; thus, it took time for the heat to reach the cylinder center and to establish a stationary state. In the case of a solid cylinder made of SF57 glass, 1 cm in length and 2.5 cm in diameter, upon 2.4 W heating from each of the four sides, the time needed for establishing a steady ∆T was ~ 500 s, which was significantly longer than expected from a quick adaptive correction of a laser beam profile. On the other hand, the ∆T was almost perfectly parabolic, at least in the slice of the cylinder passing through the cylinder axis and centers of the two opposite heaters. Next, in [168] Lee and Reitze formulated an analytical model of a TL formed by the impulse HL in solids. Their model does assume that the HL beam is of significantly smaller diameter than the cylindrical solid TO material, but the TO may have arbitrary absorption coefficient. However, the model does not take into account any effects related to thermoelastic deformations of the TO material. It is not surprising as the Hello and Vinet model of thermal deformation [151] takes as the starting point the steady-state ∆T distribution obtained from their model of temperature distribution formation. In the Lee and Reitze solution, ∆T changes with time, due to the pulse HL operation. Their work was continued by Kwon and Lee [169] who calculated what kind of material with negative dn/dT and of what geometry, needs to be put in front/back of a tested optical element with dn/dT > 0 in which a converging thermal lens is formed, to eliminate focusing of this lens. So, in principle, they have shown that it is possible to put an additional piece of glass with dn/dT < 0 to correct the laser beam aberrations produced by the thermal lens formed by the beam in a typical optical element (e.g. lens). Later Kim et al. [170] have developed a steady-state model of the thermal lens formed in a cylindrical solid optical element with a cylindrical heat sink around the optical element. They assumed known radiative and active cooling heat transfer rates of the cylinder (through the sink) and provided an analytical formula for the thermal lens focal length, for arbitrary absorption coefficient, including highly absorbing materials.

In parallel to the study related to gravitational interferometers, Malacarne et al. worked on the same subject, looking at it from a more spectroscopic point of view. In [171], these authors presented a new model of TL formed by HL in a glass sample surrounded by a fluid (air, water). The model included the thermoelastic deformation of the glass and the heat flow from the absorbing glass heated by HL to the external fluid. The model assumed small absorption and HL beam diameter much smaller than the TO sample dimensions; nevertheless, it can be helpful in predicting the TL that will be formed in a solid TO material. As shown by the authors, in the limits of its assumptions, the predictions of their analytical model corresponded very well to the results obtained by means of numerical simulations with the Comsol Multiphysics. As the model predicted that air heating in the vicinity of the absorbing sample does not influence the overall TL, in another model [172], the authors assumed no axial heat flow in the sample, as well as low absorption and again small HL beam diameter compared to that of the TO sample. However, this time, they took into account additionally the effect of thermal stress of the glass on its refractive index (namely two refractive indices: for radial and azimuthal polarization of HL). The authors developed the radial and time-dependent model of the HL-induced ∆T, surface displacement, and stresses, applicable for TL in glass windows, laser rods, etc. Recently, the same group presented experimental results that supported the applicability of their model [173] and most recently [174], they studied in-air TL and thermal deformation of laser-heated metal mirrors of limited dimensions, so including the so-called edge effects. They found out that for an HL beam of 646 μm in radius, limiting the mirror diameter from 50.8 to 12.7 mm (of 15 or 30 mm thickness) already results in the inaccuracy of the theoretical model of TL and surface deformation, which does not take into account edge effects.

4 Thermal lens applications as tunable lens

While, as described above, the application of thermally induced ∆n for correcting unwanted thermal aberrations in laser cavities or high-power laser interferometers was quickly realized; TL applications in other areas, for instance, as a tunable lens, have been suggested more frequently only in recent ten years. Earlier, for instance, Bialkowski [175] proposed the use of TL as an optical switching device that on demand refracts the signal beam in the desired direction/port of another device. A similar switch was proposed by Tanaka et al. [176, 177], who additionally presented another type of switch in [178]. It was built of a TO slab in which a TL could be formed by activating the HL beam. The TO slab was followed by a flat mirror with a hole in its center. The HL and signal beams fell perpendicularly to the TO slab face and at an angle of 45° to the mirror surface. When the switch was in the Off position, the HL was inactive and the signal beam passed through the hole in the mirror. When HL was turned On, a diverging TL was formed, the signal beam was spread and fell at the outer parts of the mirror. Thus, the signal light was reflected perpendicularly to the original propagation direction. Using such a switch, the same authors presented a more elaborated thermo-optical dual-switch device in [179]. It was a TL flip-flop switch, which controlled whether a continuous signal laser beam was or was not present at its output, by subsequent light pulses of the same intensity and duration, inputted to the switch on demand. In [176], the same group presented the implementation of the optical switch proposed in the same work in the transfer of data between a PC unit acting as the client and an external HDD acting as the server linked via an optical network. The authors transferred images of different sizes and even compared the data transfer rate obtained using their optical system with a 100Base LAN purely electronic system. And they found their setup to be quicker than the commercial one. In [180], the same authors presented an optically controlled optical communication data distribution device employing the optical switch described in [179]. Finally, in [181], Tanaka et al. presented a TO switch realization that made use of liquid TO materials, resisted high-temperature changes in the environment and cancelled convective effects that may deteriorate the TL symmetrical operation.

The application of the TL as an optical switch was also presented by Joseph et al. [182] who claimed being able to obtain a switching time of 600 ns in a water solution of gold nanoparticles using a thermal lens induced by a pulsed Nd:YAG laser. In [183], Bingi et al. proposed to use TL to switch the signal beam between different LG and Hermite–Gaussian (HG) modes. They used a TL formed in a sample of MoS₂ nanoflakes dispersed in a polymer solution. The convection in such material needs to be important enough to deform asymmetrically the TL, formed initially by an HL propagating horizontally. It is by propagating the signal beam through the upper part of the TL that this beam’s mode conversion takes place. The type of mode conversion depends on the position at which the signal beams travels through the TL; thus, a tunable mode conversion is achievable.

The thermal lens has also been envisaged as a tool that can be used in the generation of Bessel beams. Doan et al. [184] have shown that by proper configuring the signal and HL Gaussian beams, a zero-order Bessel beam may be formed that has elongated confocal range, proportional to HL power. The same subject was next investigated more deeply by Chen et al. [185], who measured the spatial distribution of a Gaussian probe beam that passed through a thermal lens and was next collimated by a converging lens. They found that the spatial distribution of intensity behind the lens corresponds to that of a Bessel beam with elongated confocal distance. And most important—the authors put an obstacle in the path of the Bessel beam—a drop of black ink of diameter large enough to block the central part of the beam. After some distance, the beam recovered its spatial profile, this way manifesting its “self-healing” ability — a Bessel beam feature, one can observe in Fig. 7.

Fig. 7

The intensity profiles of a Bessel beam formed using a TL, as measured along its propagation path. Note the long confocal distance of the beam. At ~ 529 mm, an obstacle of ~ 2.4 mm diameter obscures the beam. However, after few centimeters, the beam recovers itself. Reprinted from [185], with permission of AIP publishing

Doan et al. [186] proposed the use of thermal lensing for obtaining laser beams with a top-hat profile. While, the experiment they showed was not especially innovative, the idea alone was. The same authors [187] used their top-hat HL beam to produce a TL almost free of spherical aberrations, with the focal length tuned using the HL power. This result was in accordance with the Reitze et al. [164] observation of the supremacy of HL top-hat profile over Gaussian one in terms of spherical aberrations introduced by a TL formed by such an HL.

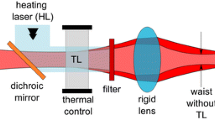
According to the author’s knowledge, the first presentation of the application of a tunable TL in imaging was done by Vartak and Lawandy [188]. The authors used the TL formed in a glass filter plate, in a setup similar to the one shown in Fig. 8.

Fig. 8

A typical imaging setup that uses the thermal lens (TL) as a tunable optical element. TL is formed by HL in a TO material, here additionally thermally controlled in its bulk volume. The TL moves the waist of the probe beam to the right due to its diverging character. Reprinted from [189], Fig. 1, licensed under Creative Common License, http://creativecommons.org/licenses/by/4.0/

They were able to observe the displacement of the image formed by their setup of a phase mask of 8 × 8 dots. The displacement resulted from changes in HL power. These HL changes implied changes in TL focal length, thus in the overall optical power of the imaging setup. Also, the authors estimated the focal length of the TL they formed as of ~ 2 mm in case of an HL beam of 1 W power and 50 μm diameter. Later, Donner et al. [190, 191] presented a micro-TL built of two layers. The first was a glass coverslip covered with a plasmonic nanostructure. The second layer adjacent to the first one, in direct contact, was a thin layer of a TO material, e.g. water. The first layer absorbed HL radiation and transferred heat to the second layer, in which the TL was formed. The authors have shown the application of the lens in microscopy, with its tunability achieved through the HL power changes. A similar concept, but used in the design of a spatial light modulator (SLM) was applied by Robert et al. [192]. In this design, a pattern of gold nanorods was placed on a BK7 glass and covered with glycerol as the TO material. The TO liquid was enclosed from the top by a sapphire glass. Because the thickness of the glycerol layer was small, and sapphire has a much higher k than glycerol, the ∆T obtained after HL absorption by the nanorod was much flatter than for a typical TL formed in a TLS sample. As a result, the ∆n was flat as well and a single nanorod cell (with the TO liquid and glasses) could act as a single cell of a typical liquid-crystal SLM. The response time of such a cell was found as sub-μs, but due to heat diffusion, the temperature of the whole pattern of gold nanorods stabilized thermally after ~ 1 ms. So, the build-up of a phase pattern may be very fast in such device, when compared to that in the liquid-crystal SLMs. However, as always with thermal devices, the heat diffusion, which is slow, deteriorates the rate of potential change in the phase pattern. Chen et al. [193] designed and simulated a micro-fluidic thermal lens of a new type. It comprised a chamber of mm length and width but tens of μm height, through which a thermo-optical fluid could flow at a controllable flowing rate. A fiber exit was aligned so that its axis was parallel to the direction the fluid flow, which was perpendicular to two smallest faces of the chamber. At the bottom of the chamber, two chromium strips were coated. According to the simulations, an illumination of the strips by a heating laser beam, coupled with a proper flow of the fluid, led to the formation of a thermal lens that refracted the emission of the fiber ends without any aberrations in the 2D plane parallel to the fiber axis. Such a device can in principle work as a perfect fiber 2D micro-collimator with tunable focal length. Another approach to formation of a tunable thermal lens in a fluidic micro-chip was presented by Liu et al. [194]. These authors built a flat microchip of a sub-mm dimension, with tens of μm height, which allowed the formation of a TO fluid stream by three basic adjacent streams: hot, cold, hot. By proper tuning of the streams flow rates, the authors succeeded in the formation of controllable ∆T distribution of a parabolic character that acted as a lens. As the central stream had lower temperature than the side ones and the fluid was characterized by dn/dT < 0, the lens was converging and could be used in living-cell entrapment as optical tweezers. The laser beam that was intended to be focused was introduced along the central stream axis.

The most common and obvious way of tuning the TL focal length is through changes in the HL power. However, as can be deduced from Eqs. 4 and 7, there are other ways of obtaining the same effect. One can change P_Abs by modifying the TO material coefficient of absorption at the HL wavelength. Potentially, one can also change ϕ_F or $\left\langle {\lambda_{F} } \right\rangle$ by some photo-physical or photochemical process. In [189], Dobek et al. have shown that it is possible to modify TL focal length, by changing the bulk temperature of the TO material. Some dyes (in fact many of them) exhibit spectral shifts of their emission and absorption spectra upon changing T. Such a process is called thermochromism [195], and is used in different applications, e.g. in battery power gauges [196, 197]. It was the thermochromism of a well-known dye dissolved in a TO solvent, that was the process responsible for the f(T) dependence of the TL formed with an HL of a constant power. As the bulk temperature changes, the absorption spectrum of the dye dissolved in the TO material undergoes a spectral shift as well. As a consequence, the coefficient of absorption of the TO material changes at the HL wavelength; thus, the TL focal length changes as well. Additionally, by means of numerical simulations, the authors confirmed the superiority of the top-hat profile of HL heating over the Gaussian one, in terms of aberrations of the TL formed, reported earlier by others. Later, Dobek and Brazevic [198] have shown that the absorption of the TO material can also be modified in another way. This time, they used a photochromic polymer as the TO material. Photochromism [199] is the process in which the absorption or emission spectrum of the photochromic material can be switched between two (or more) accessible spectra, clearly different in terms of spectral position and shape in most cases. The change occurs by excitation of the material with a light of a wavelength corresponding to one of the two (or more) spectra. As a result of such an excitation, the photochromic dye molecular structure changes and its absorption spectrum changes as well into the other one. In their setup [198], the TO material was continuously illuminated from one side of the sample by a cw HL laser of a wavelength from the range of one of the two absorption spectra of the TO material. From the other side, the sample was illuminated with a flat homogeneous light from a LED whose intensity was changed. The wavelength of this light was in the range of the second absorption spectrum of the TO material. The change in LED light intensity resulted in the change in the absorption coefficient of the TO sample at the HL wavelength, because LED light excitation was converting the photochromic material molecules into the state, at which they absorbed the HL light. As a result, the focal length of the TL formed by the HL beam could be changed. The TL was also presented by Dobek [200] as a tunable element of a microscope. The author evaluated the optical resolution achievable in a bright light microscope, using a TL of 360–550 μm in radius. The most important achievement of this work was the first presentation of the so-called multi-planar imaging. As shown by the author, using the TL and a microscope objective, it is possible to obtain a sharp image of two objects in the object planes separated by a distance that exceeds the depth-of-field of the microscope objective (Fig. 9).

Fig. 9

Multi-planar microscopic image of a 50 μm grid pattern lying over a biological sample, separated by 390 μm. Images obtained with the microscope focused at the grid (a), biological sample (b) and at the intermediate plane between the two samples (c). After TL activation and its appropriate positioning and tuning, the simultaneous sharp image of a part of the grid pattern and of a part of the biological sample (indicated by black circle) was obtained. Reprinted with permission from [200]. Copyright: The Optical Society

This new imaging method was later developed by Dobek and Baranowski [201] to be applicable in macro-imaging of an object of the human scale. This time, the authors used two thermal lenses, formed in dye solutions, which allowed them for multi-planar imaging of objects belonging to three distinct object planes, highly separated each from the each other. Additionally, the authors presented the geometrical limitations of the imaging setup must be met to obtain images of reasonable quality. The same imaging method was presented by Berto et al. [202]. These authors also used thermal lenses, but electrically heated [203], which were a more elaborated version of the tunable TL proposed by Zayhowski [204]. Berto et al. built a flat transparent module with resistive spirals made of gold, placed on the surface of a flat plate made of a polymer. Each spiral was individually electrically driven. Activation of a spiral heated the polymer material in the vicinity of the spiral, forming a TL in it. Proper design of the spirals geometry allowed minimization of optical aberrations introduced by TLs formed by them. As one can put many such spirals in an array pattern, they can be used in multi-planar imaging of as many separate objects placed at different object planes, as there are spirals in the module. However, in contrast to the TLs formed in the liquids used by Dobek and Baranowski, the spirals do not allow a smooth change in the TL position, which for the HL-induced TL can easily be achieved by moving the HL beam. Another type of an array of tunable lenses of thermo-optical character, was designed by Glebov et al. [205]. In this case, the authors proposed to heat the TO material that filled the space between two surfaces: the convex one and the concave one, of a non-TO material. An array of such convex/concave pairs formed a lens-let array. The heating was proposed to be homogeneous, through the whole array of lenses or through each lens individually. As a result, each of them could be tuned simultaneously or separately. The heating was proposed to be generated electrically. The application of electrically heated transparent cylindrical material in imaging has been also investigated by Sheil [206]. His work was based on simulations in which the physical characteristics of small smartphone cameras were taken into account. Sheil’s idea was to use a TL as a tool to extend the depth-of-field of the camera lens. He showed that by external heating of the cylindrical TO plate (from its side borders), it is possible to extend the depth-of-field toward the imaging setup that includes the TL, and toward infinity when heating the plate from its axis. He also showed that the ∆n of the polymer TO material used in the simulations attains a maximum after turning-on the heating and then decreases (in absolute scale). Moreover, the setup including his TL was proved to provide much better results in terms of imaging quality at lower heating temperatures (of the electrical heaters), but in shorter times, than for higher temperatures but in steady state. This finding indicates there is room for optimization of the process of heating in such setups, which can lead to imaging of significantly better quality.

It is worth noting the tunable lens devised by Angelini et al. [207]. These authors used a liquid sample composed of poly[1-[4-(3-carboxy-4-hydroxyphenyl-azo) benzene sulfonamido]-1,2-ethanediyl, sodium salt] (PAZO) dissolved in dimethylformamide and glycerin. They built a setup in which a 532 nm laser was used as the lens forming one, introduced into a microscopic system. In this way, the authors presented the possibility of tuning the microscope focus plane, without the need for mechanical displacement of the sample or the microscope objective lens. Angelini et al. attributed the lensing effect to the changes in the sample density following from changes in PAZO isomer structure induced by laser illumination. However, according to the author’s knowledge, it is unlikely that upon light-induced isomerization, PAZO does not undergo non-radiative deactivation with some yield, which inevitably has to increase the molecule environment temperature. Thus, in opinion of the author of this review, the tunable lens shown by Angelini et al. [207] had to be of thermal character to some extent. Later, the same authors [208] have shown a similar lens, however with another azopolymer dissolved in a cross-linked elastomeric blend. While the thermal character of the tunable lenses of both types is not considered by the authors, the size, focal length and time evolution of their lenses is exactly the same as that of thermal lenses of the same properties.

A thermally induced tunable lens has been also designed by Malyuk and Ivanova [209]. While it cannot be classified to the thermal lenses on the basis of the dn/dT ≠ 0 property only, its thermal character justifies its description in this review. The lens constructed by Malyuk and Ivanova was built of a liquid illuminated by a heating laser. But the liquid was a binary mixture, with one component having a surface tension higher and vapor pressure lower than the other one. The mixture contained also a dye that absorbed the HL light and transformed it non-radiatively and efficiently into heat. The solution was open from the top. Its heating formed the ∆T at its surface. Due to heating, one of the components was evaporating more effectively than the second one, which led to a distribution of concentrations of the two mixture components at the surface. As a result of the temperature- and concentration-dependent surface tension of the mixture, its top surface became convex; thus, a plano-convex lens was formed. The authors proved that by modifying the intensity of the heating laser beam, it was possible to tune the lens focal length (reaching min. f = 13 mm) and the lens diameter as well. In a demonstrative instrument, they used a mixture of ethylene glycol and ethanol, presenting its operation in the imaging of a micro-grid. Another type of thermally tunable lens was described by the same authors in [210]. This time they used the thermocapillary effect (thermal Marangoni forces) as the process responsible for the deformation of a liquid lens. An HL beam illuminating from the top the droplet of solution of crystal violet in ethylene glycol or benzyl alcohol led to the heating of the center of the droplet. As a result of the formed radially symmetric temperature distribution, a surface tension gradient was formed which led to a flow of the solvent molecules in the direction of higher surface tension. The surface of the droplet was changing in shape; thus, the focal length of the lens it formed was changing as well. Malyuk and Ivanova were able to produce in this way a lens of 3 mm in diameter with the focal length tunable in the range of −300 to + 100 mm. A similar solution has been proposed by Bezuglyj et al. [211].

Recently, Zablotsky and Maiorov [212] have explained an interesting phenomenon that can be observed in ferrofluids illuminated by a laser beam. In the absence of an external magnetic field, the illumination of a thin fluid layer of ferro-nano-particles by a laser beam, absorbed by the fluid, leads to the formation of a typical TL. As a result, the profile of the laser beam remains axisymmetric. In this particular system, besides the thermo-optical effect, the Soret effect induces also an axially symmetric concentration gradient of the magnetic nano-particles. However, due to this gradient, upon interaction with an external magnetic field, the nano-particles undergo magnetically induced convection (magnetophoresis), which—when of large scale—may lead to surprising asymmetric deformations of the laser beam that induces the TL.

5 Z-scan, thermal mirror and other applications

Analysis of the thermal lensing phenomenon can be pursued using the Z-scan method [213] in which the sample is shifted forward and backward along the HL axis and the signal dependent on z₁ (Fig. 3) is analyzed. For instance, Maurya et al. [214] used this method in the studies of the photothermal response of binary liquids. They found a correlation between the Z-scan signal and the strength of the hydrogen bonds and other type of interactions that occur between the binary components. Also, Sehnem et al. [215] used this technique to evaluate the optimized experimental setup configuration in which no Soret effect is observable in the TL Z-scan signal for a ferrofluid sample. As mentioned in several cited papers [151, 162, 172, 173], the heating of a thermo-elastic sample, may lead to the deformation of its surface and thus to changes in its refractive character. It may be used as a lens or as a mirror with a deformable surface. Such a thermal mirror was the subject of studies by Dong and Lu [216]. The readers interested in the thermal mirror spectroscopy are encouraged to follow the works cited by these authors. They presented a theoretical model of the method that incorporates thermal lensing effects that may appear above the mirror surface, due to the heat exchange between the sample and the fluid (air) surrounding it. They also provided an experimental verification of their model.

Finally, thermal lensing is not related to optical lensing only. Dzyapko et al. have shown [217] that by formation of a thermal gradient in a planar yttrium iron garnet (YIG) film, through which spin waves propagated, they were able to focus the spin waves or change the direction of their propagation.

6 Future applications

Based on the analysis of current literature related to thermal lensing, it seems that TLM will be further used in the studies of nano-particles, while TLS will be used in the studies of more and more complex fluidic samples. Simultaneously one can expect the development of miniaturized TLS/TLM setups (also commercial) designed for “pocket” measurements of small concentrations of different substances in gas and liquid state, in microfluidic devices as well.

On the other hand, the studies of the optical application of thermally induced ∆n will be probably still pursued, with the focus on the non-axial refractive index gradients. Thermal lensing, understood as the modification of optical ray trajectories by formation of ∆n, is the simplest and most effective method of formation of continuous refractive index distribution. Unfortunately, it is charged with many weaknesses. Its definite advantage is that the thermal diffusion allows the lens to disappear, thus of turning it off. However, simultaneously the same diffusion makes the formation and disappearance of the TL very slow. Convection and turbulences are the definite disadvantages of the method, which have to be omitted whenever possible. However, thermally induced ∆n allows the studies of active formation of optical refractive elements of complexity level unachievable by other methods of ∆n formation. Therefore, one can expect novel ideas of applications of such ∆n gradients, that may in the future result in development of new devices that take advantage of a more suitable mechanism of ∆n formation.