1 Introduction

Research concerning the behavior of partially coherent light has been an active area of study for the past few decades. In the time since Mandel and Wolf introduced the mutual coherence and cross-spectral density functions [1], the study of random light has matured and become its own discipline—statistical optics [2, 3]. Since roughly the year 2000, researchers, applying the foundational principles developed by Wolf, have created all manner of random light sources, e.g., sources that rotate [4, 5], self-split [6], self-steer [7], self-focus [8,9,10], produce far-fields patterns of any desired shape [11,12,13], and possess controllable angular momentum [14,15,16,17] (see Refs. [3, 18,19,20] for more details). The level of beam control afforded by coherence manipulation, as well as its innate resistance to scintillation and speckle [21,22,23], makes partially coherent light very well suited for free-space/underwater optical communications, optical trapping, biological, and manufacturing applications [24]. Indeed, this has served as the impetus for much of this work.

Most beam control research, whether utilizing partially coherent or fully coherent light, assumes that space and time are separable. Recently this has begun to change, as scientists have generated sources with spatiotemporal coupling resulting in beams with transverse (to the direction of propagation) angular momentum [25,26,27,28] and anomalous propagation and refractive behaviors [29,30,31,32,33,34]. A majority of this work has been performed using pulsed laser (coherent) sources, and only a few papers have discussed space-time-coupled partially coherent light [35,36,37,38,39]. Therefore, coupling space and time in the correlation function of a random light source is a new, relatively unexplored dimension of beam control research.

In this paper, we present a new space-time-coupled partially coherent beam. The beam couples space and time in an inhomogeneous correlation function resulting in controllable self-focusing after near-field propagation in space-time. The form of the correlation function derives from Lajunen and Saastamoinen’s non-uniformly correlated (NUC) purely spatial and temporal correlation functions discussed in Refs. [8] and [40], respectively.

We begin the analysis by deriving the mutual coherence function (MCF) of the spatiotemporal (ST) NUC beam using Gori and Santarsiero’s superposition rule for genuine partially coherent sources [41]. We then explore the free-space propagation behavior of these beams and demonstrate self-focusing in space-time. Following the theory discussion, we generate (in simulation) an ST NUC beam and compare Monte Carlo statistical moments (planar cuts through the MCF and mean intensities) to the corresponding theory. Lastly, we conclude with a summary of our work.

2 Methodology

2.1 ST NUC beam source-plane MCF

We begin with the necessary and sufficient criterion for partially coherent fields, also known as the superposition rule:

$$\begin{aligned} \Gamma \left( x_1,t_1,x_2,t_2\right) &= \iint _{-\infty }^{\infty } p\left( v_x,v_t\right) H\left( x_1,t_1;v_x,v_t\right) \nonumber \\ &H^*\left( x_2,t_2;v_x,v_t\right) \text {d}v_x \text {d}v_t, \end{aligned}$$
(1)

where \(\Gamma\) is the MCF, p is a positive function, and H is an arbitrary kernel [41]. As is customary for space-time-coupled light, we ignore the beam’s distribution in the y direction.

Borrowing from Lajunen and Saastamoinen [8, 40], the p and H to produce an ST NUC beam are

$$\begin{aligned} \begin{aligned} p\left( v_x,v_t\right)&= \frac{\delta ^4}{4{\pi }} \exp \left[ -\frac{\delta ^4}{4}\left( v_x^2+v_t^2\right) \right] \\ H\left( x,t;v_x\right)&= \tau \left( x,t\right) \exp \left[ -{j}\left( x - \beta t - \gamma \right) ^2v_x\right] , \end{aligned} \end{aligned}$$
(2)

where \(\delta\) controls the coherence of the source in space-time (has units of meters), \(\beta\) is a constant that scales the time coordinate (has units of meters per second), \(\gamma\) is a shift parameter that affects the x, t location of self-focusing, and lastly, \(\tau\) is the complex envelope, amplitude, or shape of the space-time pulse. For our purposes, we assume \(\tau\) is Gaussian-shaped in both time and space, such that,

$$\begin{aligned} \tau \left( x,t\right) = \exp \left( -\frac{t^2}{4W_t^2}\right) \exp \left( -\frac{x^2}{4W_x^2}\right) \exp \left( -{j}\omega _c t\right) , \end{aligned}$$
(3)

where \(W_t\) and \(W_x\) are the pulse widths in time and space, respectively, and \(\omega _c\) is the light’s carrier frequency. Substituting Eqs. (2) and (3) into Eq. (1) and evaluating the integrals produces the source-plane (\(z = 0\)) MCF:

$$\begin{aligned} \Gamma \left( x_1,t_1,x_2,t_2\right) & = \exp \left( -\frac{t_1^2+t_2^2}{4W_t^2}\right) \exp \left( -\frac{x_1^2+x_2^2}{4W_x^2} \right) \exp \left[ - {j}\omega _c\left( t_1-t_2\right) \right] \nonumber \\ & \exp \left\{ -\frac{\left[ \left( x_1 - \beta t_1 -\gamma \right) ^2 - \left( x_2 - \beta t_2 -\gamma \right) ^2\right] ^2}{\delta ^4} \right\} .\end{aligned}$$
(4)

2.2 ST NUC beam mean intensity at any plane \(z \ge 0\)

The MCF at any plane \(z \ge 0\) in free space can be found by evaluating

$$\begin{aligned} \begin{aligned} \Gamma \left( x_1,t_1,x_2,t_2,z\right) & \approx \frac{1}{\lambda _c z} \iint _{-\infty }^{\infty } \Gamma \left[ x_1',t_1-\frac{z}{c}-\frac{\left( x_1-x_1'\right) ^2}{2cz}, \right. \\& \left. x_2,t_2-\frac{z}{c}-\frac{\left( x_2-x_2'\right) ^2}{2cz}\right] \text {d}x_1' \text {d}x_2', \end{aligned} \end{aligned}$$
(5)

where c is the speed of light in vacuum and \(\lambda _c\) is the beam’s carrier wavelength. This form of the MCF propagation integral is accurate for a narrowband source (i.e., \(\omega _c \gg \varDelta \omega\)) and paraxial observation. The mean intensity, which we are ultimately interested in, can be found by evaluating \(\Gamma\) at a single space-time point, i.e., \(\langle I\left( x,t,z\right) \rangle = \Gamma \left( x,t,x,t,z\right)\).

Direct substitution of Eq. (4) into (5) requires the numerical evaluation of two integrals. We can derive a simplified version of Eq. (5) by substituting in Eq. (1), with the p and H given in Eq. (2), and interchanging the integration order, such that,

$$\begin{aligned} \begin{aligned} \Gamma \left( x_1,t_1,x_2,t_2,z\right) & = \frac{\delta ^2}{2\sqrt{\pi }} \int _{-\infty }^{\infty } \exp \left( -\frac{\delta ^4}{4}v_x^2\right) \\& H\left( x_1,t_1,z;v_x\right) H^*\left( x_2,t_2,z;v_x\right) \text {d}v_x, \end{aligned} \end{aligned}$$
(6)

where \(H\left( x,t,z;v_x\right)\) is

$$\begin{aligned}H &\left( x,t,z;v_x\right) \nonumber \\ &\approx \frac{1}{\sqrt{\lambda _c z}} \int _{-\infty }^{\infty } H\left[ x',t-\frac{z}{c}-\frac{\left( x-x'\right) ^2}{2cz};v_x\right] \text {d}x'.\end{aligned}$$
(7)

The integral in Eq. (7) can be evaluated in closed form. Substituting this result into Eq. (6) and evaluating the resulting MCF at a single space-time point yields the following expression for the mean intensity:

$$\begin{aligned} \langle I\left( x,t,z\right) \rangle & = \frac{k_c}{2z} \frac{\delta ^2}{2\sqrt{\pi }} \exp \left( -\frac{{\bar{t}}^2}{2W_t^2}\right) \nonumber \\& \int _{-\infty }^{\infty } \exp \left( -\frac{\delta ^4}{4}v_x^2\right) \frac{1}{\sqrt{\varOmega \left( v_x\right) }} \nonumber \\& \exp \left\{ -\frac{\left[ k_c x/z - 2\left( \beta {\bar{t}} + \gamma \right) v_x \right] ^2}{8W_x^2 \varOmega \left( v_x\right) }\right\} \text {d}v_x, \end{aligned}$$
(8)

where \(k_c = 2\pi /\lambda _c\), \({\bar{t}} = t - z/c - x^2/\left( 2cz\right)\), and \(\varOmega \left( v_x\right) = \left[ 1/\left( 4W_x^2\right) \right] ^2 + \left[ v_x - k_c/\left( 2z\right) \right] ^2\). The integral over \(v_x\) must be evaluated numerically.

2.3 Propagation behavior

Fig. 1
figure 1

Mean intensity \(\langle I\left( x,t,z\right) \rangle\): a \(z = 0\) m, b \(z = 1.25\) m, c \(z = 2.5\) m, d \(z = 5\) m, e \(z = 7.5\) m, and f \(z = 10\) m

Full size image
Fig. 2
figure 2

Temporal (a) and spatial (b) mean pulse shapes at the z locations in Fig. 1

Full size image

To investigate how ST NUC beams evolve as they propagate, we evaluated Eq. (8) at \(z = 0\)–10 m in 10 cm steps. The ST NUC beam parameters were \(\lambda _c = 1 \text { } \mu\)m, \(W_x = 1.5\) mm, \(W_t = 50\) ps, \(\delta = 1.25\) mm, \(\beta = W_x/W_t\) m/s, and \(\gamma = 0.6\) mm. Figure 1 shows the mean intensities at six z locations; the associated movie (included as supplementary materials) shows the entire sequence. Figure 2 shows the temporal (a) and spatial (b) mean pulse shapes for the six z locations in Fig. 1 at \(x = 0\) m and \(t - z/c = 0\) s, respectively.

Note that the peak \(\langle I\left( x,t,z\right) \rangle\) occurs at \(z \approx 2.5\) m and at an “off-axis” space-time location. For all z thereafter, the spatial width of \(\langle I\left( x,t,z\right) \rangle\) grows due to diffraction, resulting in a drop in peak intensity; however, the general shape of \(\langle I\left( x,t,z\right) \rangle\) remains roughly the same.

3 Validation

In this section, we generate (in simulation) source-plane realizations of ST NUC beams, and then propagate them to the self-focusing plane at \(z = 2.5\) m. We compute two-dimensional slices through the source-plane MCF, and the mean intensities in both the source plane and at \(z = 2.5\) m to validate the theory in Eqs. (4) and (8), respectively. Before presenting the results, we discuss the particulars of the simulation.

3.1 Simulation setup

For the Monte Carlo simulations, we generated 5000 source-plane ST NUC beam realizations with the parameters listed in Sect. 2.3: \(\lambda _c = 1 \text { } \mu\)m, \(W_x = 1.5\) mm, \(W_t = 50\) ps, \(\delta = 1.25\) mm, \(\beta = W_x/W_t\) m/s, and \(\gamma = 0.6\) mm. We discretized the optical fields using grids that were \(N = 512\) points per side with sample spacings equal to \(10W_x/N \approx 29.30\) \(\mu\)m and \(10W_t/N \approx 0.9766\) ps in the x and t dimensions, respectively.

After generating an ST NUC beam realization \(U\left( x,t\right)\) (see Sect. 3.2), we propagated the stochastic field instance \(z = 2.5\) m. We performed the simulated propagation using the following procedure:

  1. 1.

    We transformed U from the time to the frequency \(\omega\) domain using a fast Fourier transform (FFT) computed along the t axis of U.

  2. 2.

    We evaluated Fresnel’s integral [42] using an FFT computed along the x dimension of \(U\left( x,\omega \right)\) [43, 44].

  3. 3.

    We inverse transformed U back to the time domain using an FFT computed along the \(\omega\) axis of \(U\left( x,\omega ,z\right)\).

Lastly, we computed \(\Gamma \left( x_1,0,t_2,0\right)\), \(\langle I\left( x,t\right) \rangle\), and \(\langle I\left( x,t,z\right) \rangle\) from 5000 U to compare to Eqs. (4) and (8).

3.2 Generating ST NUC beam realizations

We note that while the superposition rule [see Eq. (1)] is purely mathematical in nature, it can be physically interpreted or applied to generate partially coherent sources in two main ways. If an incoherent primary source of shape p is passed through a linear optical system with impulse response H, Eq. (1) is the result. This “incoherent interpretation” of Eq. (1) has been used to generate many spatial and pulsed partially coherent beams, all of which (to the author’s knowledge) have been uniformly correlated or Schell-model sources, where H is simply the Fourier kernel [19, 41, 45, 46]. Generating a NUC beam by filtering a spatially incoherent source is theoretically possible; however, the requisite optical system is inhomogeneous (shift- or space-varying) and, therefore, difficult to physically realize.

The second interpretation of Eq. (1) views H as a coherent optical field parameterized by \(v_x,v_t\). The function p weights the H with specific values of \(v_x,v_t\), such that, the incoherent sum of all possible H produces the desired MCF. This approach is referred to as the pseudo-modes technique [47]. For example, the pseudo-mode H to produce any Schell-model source is a tilted plane wave with a tilt angle given by \(v_x,v_t\). The form of p ultimately determines the correlation function of the source. Using pseudo-modes, both Schell-model and NUC beams have been produced [48,49,50,51,52,53]. In all cases, the pseudo-mode is generated using a laser and some form of the spatial light modulator. The partially coherent source is produced by incoherently summing many such pseudo-modes, properly weighted by p.

Here, we use a hybrid technique which combines the two described above [54]. In this approach, H is composed of a function modeling the pulse shape and a kernel [the H in Eq. (2) is in this form]. The “input” into the linear system is a delta-correlated, circular-complex-Gaussian (CCG) random function, which is scaled by p. Specialized to an ST NUC beam, this is

$$\begin{aligned} U\left( x,t\right) & = \exp \left( -\frac{t^2}{4W_t^2}\right) \exp \left( -\frac{x^2}{4W_x^2}\right) \exp \left( - {j}\omega _c t\right) \nonumber \\ & \int _{-\infty }^{\infty } r\left( v_x\right) \left[ \frac{1}{2}\frac{\delta ^2}{2\sqrt{\pi }} \exp \left( -\frac{\delta ^4}{4}v_x^2\right) \right] ^{1/2} \nonumber \\ & \exp \left[ - {j}\left( x - \beta t - \gamma \right) ^2v_x\right] \text {d}v_x, \end{aligned}$$
(9)

where r is the delta-correlated, CCG random function and U is a stochastic ST NUC pseudo-mode, more aptly called an ST NUC field realization or instance. We note that since Eq. (9) is a linear transform of a Gaussian random process, the field U is also a Gaussian random process. Therefore, U has the same first-order statistics as fully developed speckle fields, namely, uniform phase and Rayleigh amplitude [55].

Being a superposition integral, Eq. (9) is equivalent to a matrix-vector product and is numerically evaluated as such. Digitally, Eq. (9) can be cast as

$$\begin{aligned} U\left[ ij\right] = \tau \left[ ij\right] \odot \left\{ h\left[ ij,m\right] \left( r\left[ m\right] \odot \sqrt{p\left[ m\right] }\right) \right\} \sqrt{\frac{\varDelta v_x}{2}}, \end{aligned}$$
(10)

where ij is a double index representing every combination of discrete x, t, m is an index representing discrete \(v_x\), \(\odot\) is the Hadamard product, and \(\varDelta v_x\) is the spacing in the \(v_x\) dimension. In the ST NUC beam simulations, \(\varDelta v_x = 5.49 \times 10^4\) 1/m\(^2\). This spacing results in 100 grid points across the width of p. The other symbols in Eq. (10) are \(\tau\), which is an \(N^2 \times 1\) vector representing Eq. (3); h, which is an \(N^2 \times M\) matrix representing the complex exponential kernel in Eq. (9); r, which is an \(M \times 1\) vector of zero-mean, unit-variance CCG random numbers; and p, which is an \(M \times 1\) vector representing continuous p in Eq. (2). For the simulations, \(N = M = 512\).

Fig. 3
figure 3

ST NUC beam realizations: a, c, and e \(\left| U\right|\) and b, d, and f \(\arg \left( U\right)\)

Full size image

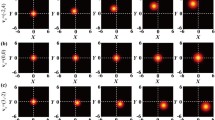
The ST NUC beam realizations produced by Eq. (10) are \(N^2 \times 1\) vectors. They must be reshaped into \(N \times N\) matrices to physically represent optical fields. Figure 3 shows example ST NUC field instances with the source parameters listed above. We note that ST NUC beam realizations, like those in Fig. 3, can be physically generated using a device called a Fourier transform pulse shaper. This device has been described in the literature many times, e.g., Refs. [27, 29, 35, 42, 45, 56, 57].

3.3 Results

Fig. 4
figure 4

Source-plane MCF \(\Gamma \left( x_1,0,t_2,0\right)\) and mean intensity \(\langle I\left( x,t\right) \rangle\) results: a theory \({\text {Re}}\left( \Gamma \right)\), b simulation \({\text {Re}}\left( \Gamma \right)\), c theory \({\text {Im}}\left( \Gamma \right)\), d simulation \({\text {Im}}\left( \Gamma \right)\), e \(\Gamma \left( x_1,0,t_2,0\right)\) root-mean-square-error (RMSE) \(\epsilon\) versus trial number q, f theory \(\langle I \rangle\), g simulation \(\langle I \rangle\), and h \(\langle I\left( x,t\right) \rangle\) root-mean-square-error (RMSE) \(\epsilon\) versus trial number q

Full size image
Fig. 5
figure 5

Mean intensity \(\langle I\left( x,t,z\right) \rangle\) at \(z = 2.5\) m: a theory, b simulation, c \(\langle I\left( x,t,z\right) \rangle\) root-mean-square-error (RMSE) \(\epsilon\) versus trial number q, d temporal pulse shape at \(x = 0\) m (theory versus simulation), e subplot (d) with simulated result shifted by \(-50\) ps, f spatial pulse shape at \(t - z/c = 0\) s (theory versus simulation), and g subplot (f) with simulated result shifted by \(-1\) mm

Full size image

Figures 4 and 5 show the simulation results. In Fig. 4, (a) and (b) report the theoretical and simulated real part of the source-plane MCF \({\text {Re}}\left[ \Gamma \left( x_1,0,t_2,0\right) \right]\), respectively; (c) and (d) show the imaginary part \({\text {Im}}\left[ \Gamma \left( x_1,0,t_2,0\right) \right]\). Subfigures (f) and (g) display the theoretical and simulated source-plane mean intensities. Subfigures (a) and (b), (c) and (d), and (f) and (g) use the same false color scales defined by the color bars on the right sides of (b), (d), and (g), respectively.

Lastly, subfigures (e) and (h) plot the root-mean-square errors (RMSEs) \(\epsilon\) for \(\Gamma \left( x_1,0,t_2,0\right)\) and \(\langle I\left( x,t\right) \rangle\) versus trial number q on log-log scales. The RMSEs were computed using the following expression:

$$\begin{aligned} \epsilon \left( q\right) = \left[ \frac{1}{N^2}\sum _{i=1}^N \sum _{j=1}^N \left| f^{\text {Thy}}\left( i,j\right) -f^{\text {Sim}}\left( i,j,q\right) \right| ^2\right] ^{1/2}, \end{aligned}$$
(11)

where f is the moment of interest. Also included on (e) and (h) are the best-fit lines to show the asymptotic behavior of the error.

Figure 5 shows the mean intensity results in the self-focusing plane at \(z = 2.5\) m. The top row of figures shows the theoretical and simulated mean intensities in (a) and (b), respectively, while (c) plots the RMSE for \(\langle I\left( x,t,z\right) \rangle\), with best-fit line, on a log-log scale. Figure 5a and b are encoded using the same color scale defined by the color bar immediately to the right of (b). The middle row of figures reports the theoretical and simulated temporal pulse shapes at \(x = 0\) m: (d) is a direct comparison of theory versus simulation and (e) is the same result with the simulated \(\langle I\rangle\) shifted by \(-50\) ps. Lastly, the bottom row of figures displays the theoretical and simulated spatial pulse shapes at \(t - z/c = 0\) s. Like the row above, (f) is a direct comparison of theory versus simulation and (g) is the same result with the simulated \(\langle I\rangle\) shifted by \(-1\) mm.

The agreement between theory and simulation in Figs. 4 and 5 is excellent. These results validate the analysis presented in Sect. 2. The slopes of the best-fit lines in the RMSE plots in Fig. 4e, h, and Fig. 5c are \(-0.5070\), \(-0.5471\), and \(-0.5045\), respectively. Therefore, the error asymptotically goes like \(\epsilon \left( q\right) \sim q^{-1/2}\). Recall that ST NUC beam realizations, generated using Eq. (10) and pictured in Fig. 3, are CCG distributed. Thus, they have the same first-order statistics as fully developed speckle fields [2, 55]. From Goodman’s seminal work on speckle [55], we know that the speckle contrast, after incoherently summing M statistically independent speckle patterns, is \({\mathcal {C}} = 1/\sqrt{M}\). This, of course, is the same as the asymptotic behavior of the error and physically explains why the RMSE behaves as it does.

4 Conclusion

In this paper, we developed and analyzed a new space-time-coupled a partially coherent source called a spatiotemporal (ST) non-uniformly correlated (NUC) beam. The ST NUC beam combined space and time in an inhomogeneous (shift-variant or space-variant) correlation function and exhibited self-focusing at a near-field location in space-time.

Using the superposition rule for genuine partially coherent sources, we first developed the source-plane ST NUC mutual coherence function (MCF). We then derived the mean intensity for any plane \(z \ge 0\) in free space by propagating the source-plane MCF. We used the mean intensity expression to predict the space-time pulse shapes at numerous z locations, for the purpose of understanding the beam’s propagation behavior.

To validate our analysis, we performed Monte Carlo simulations in which we generated and propagated 5,000 ST NUC beam realizations and computed sample statistics (the MCF and mean intensity) to compare to theory. After discussing the simulation details, we presented the results and observed excellent agreement amongst the simulated and theoretical moments. The quality of these results validated our analysis.

Engineered space-time coupling with stochastic light sources is a new, relatively unexplored aspect of beam control research. Potential applications of this work include optical trapping, particle manipulation, optical tweezing, medicine, and atomic optics.