1 Introduction

Time-resolved diagnostics of combustion processes are a prerequisite for the development and validation of chemical reaction mechanisms that are required for the development and optimization of combustion systems. Shock tubes are routinely used for ultra-fast investigations of compressible flow phenomena, gas-phase (combustion) reactions, and explosions. To unravel the complex dynamics of the involved physico-chemical processes, time-resolved monitoring of temperature, total pressure, and concentrations of key species is required. The low repetition rate of experiments and the high costs involved in operating shock tubes require the simultaneous determination of multiple quantities as a function of time in a single experiment.

Most of the established spectroscopic techniques for measuring these quantities, such as, e.g., tunable diode laser absorption spectroscopy (TDLAS) [1], are based on narrowband laser sources. High detection sensitivity is typically achieved by either reducing the noise, i.e., by exploiting wavelength modulation techniques (WMS) [2] or by increasing the optical path, typically employing passive cavities, as in the case of cavity-enhanced absorption spectroscopy (CEAS) [3]. Although enabling measurements with high time resolution, all these techniques are typically limited to monitoring one single species or parameter per laser system, e.g., concentration of CO, H2O, CO2, or CH4 [4,5,6,7], while multi-species detection requires multiplication of laser and detection systems [1].

Alternatively, absorption measurements with broadband light sources have been used for multi-species detection, but typical single-path absorption schemes provided limited sensitivity and selectivity [8,9,10]. In contrast, ultra-sensitive broadband absorption techniques, such as intracavity absorption spectroscopy (ICAS), are limited in time resolution [11]. Additionally, these methods require high-resolution spectrometers for species selectivity. On the other hand, fast and multi-species non-laser spectroscopic techniques, such as, e.g., the sampling-based time-of-flight mass spectrometry (TOF–MS) [12], lack on sensitivity in highly diluted mixtures. Consequently, to satisfy the above outlined requirements for shock-tube studies, novel diagnostics concepts are needed. A particularly promising technique is the recently emerged quantum-cascade-laser (QCL)-based dual-comb spectroscopy (DCS), the potential of which is investigated in the current work.

Dual-comb spectroscopy [13,14,15] has already been applied as a direct absorption technique in the UV to THz spectral regions, enabling simultaneous monitoring of multiple spectral features within broad spectral regions with high time resolution. DCS utilizes frequency-comb lasers with hundreds of individual narrow-band emission lines (modes) within a broad spectral range and exploits their spectral equidistance for simultaneous spectral detection [16]. There are several methods to generate frequency combs in the infrared spectral region, including doped fibers [17], pumped silicon microresonators [18] and interband cascade lasers [19]. In addition, frequency combs can be generated at shorter wavelengths and converted to the mid-infrared through difference frequency generation [20]. For a thorough review of recent advances in frequency combs, we recommend reference [15]. In our paper, QCL-based combs are used to perform DCS in the mid-infrared spectral region. The necessary condition for frequency-comb generation is phase locking for all oscillating modes (frequencies). Phase locking in QCLs is a result of four-wave mixing leading to a relative phase correlation, similar to a frequency-modulated (FM) laser. Saturable absorption mode-locking techniques leading to short pulses that are often used in, e.g., fiber-based comb systems are not applicable in QCLs due to the short lifetime of the upper laser state [21]. The QCL combs are free-running (not phase-locked to each other) in the present study. The mode spacing in a laser (frep) is determined by the resonator length and refractive index, which is controlled by choosing combs of similar physical length and fine-tuned by temperature adjustments.

The QCL DCS detection scheme works as follows: The mode spacings of two frequency combs (frep,1 and frep,2) are set close to each other, with Δfrep = frep,1 − frep,2 usually lying in the 1–10 MHz range. When both lasers overlap on a fast photodetector, each comb–tooth pair of both frequency combs produces a beat signal. The resulting beating signal in the frequency domain is also a frequency comb with a line spacing of Δfrep that can be recovered from the time-domain signal of the detector by Fourier transformation. This interferogram observed in the time domain is similar to the one resulting from a Michelson interferometer, however, without the need for moving parts and associated speed limitations. Currently, the absorption pathlength through the sample limits the sensitivity of DCS (as any single-pass absorption spectroscopy method). Although stabilized passive cavities have been successfully employed in recent frequency-comb studies [22], this concept requires complex experimental arrangements. Furthermore, it is not applicable for many practical measurement situations with optical windows, such as shock tubes or combustion chambers. However, multi-pass cells serving as integral parts of the apparatus might improve on this parameter in future.

As recently shown, near-IR dual-comb spectroscopy is well-suited for many major species in combustion diagnostics in single-pass arrangements [23]. With the development of compact and electrically pumped mid-IR QCL combs, the spectroscopically attractive MIR spectral range becomes increasingly accessible [24,25,26]. As a consequence, the field of QCL-based frequency-comb spectroscopy grows rapidly, resulting in a variety of promising applications [26,27,28], including recent shock-tube studies using a QCL DCS in the spectral range of 1200 cm−1 [26, 28]. In the current work, we use recently developed QCL-based frequency combs [29], specifically tailored for accessing the spectral range of 1740–1790 cm–1 with QCL DCS for the first time. From a spectroscopic point of view, this spectral range is particularly interesting since it contains strong vibrational absorption lines of such species as H2O, NH3, HCOOH, and HCHO [30, 31].

Being the target species of the current work, formaldehyde (HCHO) is the key species during hydrocarbon combustion, with its concentration being a benchmark for tracing the reaction progress. As a consequence, HCHO is one of the most important species for the development of chemical reaction mechanisms. A well-known precursor for the formation of HCHO is 1,3,5-trioxane, which is also utilized in the current work. The reaction proceeds in a single step:

$${\text{C}}_{{3}} {\text{H}}_{{6}} {\text{O}}_{{3}} \to {\text{3 HCHO}}.$$
(R1)

Previous high-temperature studies of the pyrolysis and oxidation of formaldehyde exploited different on- and off-line detection techniques. The most recent work of Wang et al. [32] investigated the oxidation of HCHO in a shock tube by simultaneously monitoring time histories of OH and CO using conventional laser absorption measurements. The exact timing of the CO and OH build-up was found to be sensitive to the residual of H impurities in the shock tube. From the measured CO and OH profiles the rates of the reactions H + O2 = OH + O and CO + OH = CO2 + H have been improved. Alquaity et al. [33] investigated the unimolecular dissociation of 1,3,5-trioxane between 775 and 1082 K and at a pressure of ~ 1.2 bar using high-repetition-rate time-of-flight mass spectrometry (TOF–MS) in a shock tube. At these conditions, formaldehyde was identified as the sole product. The experimental findings have been supported by quantum chemical and RRKM calculations. It was found that the dissociation proceeds via a concerted reaction with an energy barrier of 200.92 kJ mol−1. Irdam and Kiefer [34] also studied the thermal decomposition of 1,3,5-trioxane (by laser schlieren technique) at 900–1350 K and confirmed that HCHO is the sole decomposition product. They suggested a rate constant of (k∞/s−1) = 7.2 × 1015 exp(– 209.3 kJ mol−1/RT).

Wang et al. [35] developed a laser absorption diagnostics method for quantitative measurements of HCHO near 3.6 µm. A two-color scheme was adopted by tuning the laser on and off the HCHO peak to separate possible broadband absorption from other hydrocarbons (e.g., CH4). Additional measurements at 32,601.10 cm−1 were performed to discriminate against the absorption of acetaldehyde, while OH was monitored at 32,606.52 cm−1. The decomposition of 1,3,5-trioxane was investigated by Aldridge et al. [36] using FTIR at lower temperatures (523–603 K) in a heated quartz vessel. In that study HCHO was also found to be the main product. Matsugi et al. [37] used broadband cavity-enhanced absorption spectroscopy at 280–420 nm (and a time resolution of 5 µs) for measurements of HCHO, produced from 1,3,5-trioxane in a shock tube. However, the studies have been carried out only at the temperature of T = 955 K.

The goal of our current work is twofold: (1) investigating the potential of the QCL DCS as a promising diagnostics tool for shock-tube studies while (2) monitoring the kinetics of HCHO formation and oxidation at T = 800–1500 K and p = 2–3 bar to validate (and improve) the results achieved in the cited studies.

2 Experiment

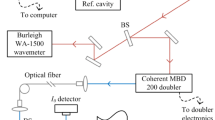
The details of our shock-tube setup are reported in [38] and, therefore, sketched here and in Fig. 1 (bottom) only briefly. The lengths of the driver and driven sections are 3.0 and 5.5 m, respectively. The inner tube diameter is 80 mm. Between experiments, the driven section is pumped down to a pressure of 1.0 × 10–7 mbar. As a driver gas, helium (Air Liquide, 99.999%) is used. The gas mixtures are prepared using a flow of high-purity argon (Air Liquide, 99.9999%) through a bubbler containing solid 1,3,5-trioxane, the initial concentration of which has been measured by gas chromatography. The shock-wave velocities are determined using four pressure transducers (Kistler, 603B) that are placed at equidistant intervals (150 mm) close to the end wall of the driven section. An additional pressure transducer is installed in the test section for time-resolved monitoring of the absolute pressure during the experiment. Calculations of temperatures and pressures are performed using one-dimensional gas-dynamic equations with the CHEMKIN software [39], with uncertainties in the calculated temperatures of ± 1%.

Fig. 1
figure 1

Experimental setup, with BS: beam splitter and BPF: bandpass filter

Full size image

The upper part of Fig. 1 shows the dual-comb-spectroscopy system (IRsweep AG, IRis-F1) consisting of two free-running QCL frequency combs, both emitting in the same spectral range of 1740.8–1788.0 cm−1. Each QCL comb simultaneously emits 188 frequencies, with a spacing of about 0.252 cm−1. Using a 50/50 beam splitter (BS), the comb beams are split and overlapped into a reference and a sample beam, each resulting in a beat signal of the two QCL combs. As explained in the introduction, such a beat signal is a frequency comb itself, though in the radio-frequency range, constituting the basis of DCS. The reference beam is attenuated and focused onto a high-bandwidth thermoelectrically cooled MCT detector (reference detector). The sample beam is also attenuated, transmitted through the shock tube (CaF2 windows), spectrally filtered by a bandpass filter tailored to the emission of the dual-comb system (to suppress thermal radiation), and focused on the sample MCT detector. The attenuation is applied to keep the detection system in the linear regime. The signal of the sample detector is normalized by the reference signal to account for relative intensity noise of the frequency comb lasers. The line separation of the resulting RF frequency comb is set to Δfrep = 4.7 MHz, allowing to observe all multi-heterodyne lines within the system’s analog detection bandwidth of 1 GHz (equivalent to the separation between the first and the last tooth of the RF comb: 187 × 4.7 MHz = 879 MHz). The maximum time resolution is determined by tres,max = 1/Δfrep ≈ 0.2 µs; however, to increase the signal-to-noise ratio (SNR), data are acquired for 4 µs before transforming a recorded interferogram to the frequency domain. As a consequence, the effective maximum time resolution in the following experiments is 4 µs (referred to as single slices).

The spectral point spacing of the combs is 0.252 cm−1, as indicated above. However, each heterodyne beat note carries spectral information of the two laser spectral elements that contribute to that beat note. Those two laser spectral elements are each narrow (< 10 MHz, 3.3 × 10–4 cm–1 at millisecond observation times), but since they are by construction spectrally separated by the frequency of the respective beat note (fheterodyne = fcomb1 – fcomb2), each heterodyne beat note carries an uncertainty about which of the two laser spectral elements has been absorbed by the sample. This uncertainty ranges from ~ 10 MHz (0.0003 cm–1) to ~ 900 MHz (0.03 cm–1) for the highest frequency heterodyne lines and determines the measurement accuracy in frequency. This uncertainty can be avoided when only a single comb is transmitted through the sample and subsequently overlaid with the second comb after the shock tube. However, such a configuration is less sensitive (as only one comb is absorbed) and is more prone to beam steering.

The left panel of Fig. 2 shows the multi-heterodyne signal (interferogram) after conversion to the frequency space. The uneven power distribution among the heterodyne lines is a result of the uneven power distribution among the QCL laser lines originating from the FM-like emission of the QCL frequency comb and from background absorptions (e.g., ambient air humidity). This results in varying signal qualities for the different spectral elements, as shown in the lower panel as standard deviation for each spectral element. This information can be used to select individual spectral elements of high quality for analysis, or as the basis of a weighted fitting procedure, exploiting the information content of all comb teeth (cf. Sect. 3). The right panel of Fig. 2 shows an Allan–Werle plot of the standard deviation of a single line as a function of the integration time. When using the cumulative information on multiple (all) spectral elements for fitting an absorption spectrum, the species can be well sampled (cf. Fig. 5) for the purpose of extracting time-dependent concentration profiles [40], even if the linewidth of individual absorption lines of the species may be smaller than the spectral point spacing of the comb teeth (undersampling), as is the case in the current work. Newbury et al. [41] define a figure of merit for dual-comb spectroscopy systems as the product of the SNR (the root-mean-square absorption noise level) normalized by the square root of the acquisition time, and the number of resolved spectral elements. Due to the nonuniform power distribution in the present dual-comb system—which is in part caused by the QCL comb emission itself and in part due to background absorption lines (mostly atmospheric water vapor)—we apply a threshold to eliminate low intensity/high noise spectral elements before calculating the SNR of the remaining 140 spectral elements to be 14.3 at a measurement time of 4 µs. From this, we derive a figure of merit of 1.0 × 107 Hz1/2.

Fig. 2
figure 2

Left panel, top: multi-heterodyne spectrum in the RF domain (upper x-axis labels) and after mapping back to the optical domain (lower x-axis labels). Left panel, bottom: standard deviation of each spectral element for an integration time of 100 µs. The dashed vertical lines are a guide to the eye for a random selection of lines. Right panel: Allan–Werle plot showing the standard deviation of a single line as a function of integration time over the typical timescales considered in this work

Full size image

When an experiment is initiated, data from the reference and sample detectors are continuously stored in a loop-acquisition buffer. After the trigger, derived from the signal of the first pressure transducer, data are retrieved for 14.7 ms and additional 2 ms of averaged pre-trigger data are used for background subtraction.

3 Multi-line data analysis

The possibility of a multi-line analysis is a significant advantage of a broadband technique, such as the DCS. Several data-evaluation techniques and algorithms are applied in this work to fully extract the contained information from the recorded data. The entire information from all experimentally available laser lines can be utilized for two different purposes: (1) monitoring of kinetics, based on absorbance traces, and (2) determination of HCHO concentrations by fitting experimental spectra using the HITRAN database. The latter procedure is well known and will be discussed briefly in the next section, whereas the multi-line analysis of kinetics traces is rarely used due to the fact that shock-tube diagnostics is mostly based on narrow-band sources usually monitoring a single absorption line only. Therefore, the relevant details on multi-line treatment of kinetics data are discussed in this section.

3.1 Evaluation of kinetics traces

To fully utilize the potential of the multi-line datasets for kinetics studies, the information from all lines must be considered. Additionally, the individual noise characteristics of each laser line, i.e., a weighting of each line’s contribution, must be included. This can be accomplished using the weighted expectation maximization principal component analysis (weighted EMPCA) particularly applicable for noisy spectra [42]. According to this theory, a set of experimental data can be represented by:

$${\mathbf{X}} = {\mathbf{RC}} + {\mathbf{N}},$$
(1)

where X is a matrix composed of consecutively recorded experimental spectra with variables (i.e., absorbance values at specific laser wavelengths) in rows and observations (i.e., different time-slices) in columns, R is a matrix composed of principal components, i.e., eigenvectors or eigenspectra of X, C is a matrix of coefficients to fit the experimental data, and N is a residual matrix containing, e.g., experimental noise. The dimensions of these matrices are: X and N [nvar, nobs], R [nvar, nvec], and C [nvec, nobs], where nobs, nvar, and nvec are the numbers of observations, variables, and eigenvectors, respectively.

In general, this approach allows for extraction of the information on different species by identifying their eigenspectra (dominant components of R), as well as on the individual kinetics of each species (corresponding components of C). Since in the current work we have HCHO as the only species to analyze, the problem can be simplified and the matrix R in Eq. (1) can be replaced by a dominant vector, which is the reference spectrum R of HCHO for the given experimental conditions (T5, p5). Note that the matrix C also becomes a vector C in the case of nvec = 1. To find R, we use the above-mentioned EMPCA algorithm [42]. In the second step, the expression

$${\mathbf{X}} = RC + {\mathbf{N}},$$
(2)

is solved for C by minimizing N. For this purpose, we use the Nelder–Mead algorithm included in python’s SciPy optimize package [43]. Importantly, this algorithm allows the individual noise characteristics of each laser line to be taken into account. This is implemented by the corresponding weights.

$${w}_{\uplambda }={R}_{\uplambda } /{\upsigma }_{\uplambda }^{2},$$
(3)

where for each spectral line λ, \({w}_{\uplambda }\) is the weight, \({R}_{\lambda }\) is the amplitude, and \({\upsigma }_{\uplambda }^{2}\) is the variance, which is determined from the data recorded by the reference detector (cf. Fig. 2). This particular weighted analysis is applicable if only a single species is considered, as is our case. For the case of multiple species, more elaborated algorithms can be used [42].

The resulting vector C describes the kinetics of HCHO as the temporal evolution of the entire reference spectrum R. However, the magnitude of individual coefficients ct in vector C can be related to absorbance values aλ of individual lines as follows: The absorbance values of all absorption lines in R are proportional to each other, such that each absorbance value can be expressed as a multiple of the absorbance aref of a reference line. With this, the coefficients in C can be expressed as:

$$c_{t} = a_{\lambda } /a_{{{\text{ref}}}} .$$
(4)

By setting aref = 1, or practically normalizing R to aref, the resulting kinetic coefficients in C are scaled to the absorbance of a specific line. In the current work, we chose to scale our data to the spectral line at 1764.93 cm−1, as this is a strong HCHO line approximately in the center of the recorded spectra and the corresponding laser line has one of the highest signal-to-noise ratio (cf. Fig. 2). As a result, the final vector C represents the kinetic evolution of the reference spectrum as a whole, however, it is scaled to the absorbance of the line at 1764.93 cm−1. It should be noted that this scaling procedure is only applicable if either the temperature changes are small during the experiment, or the temperature dependence of all absorption lines is almost the same. As will be discussed below, the temperature changes during our experiments are about ∆T = 60 K, which cannot be neglected. However, the temperature dependence of all lines has been analyzed using the HITRAN database and found to be almost identical in the whole temperature range of our experiments, i.e., for T = 800–1500 K. On the one hand, this fact prevents the determination of temperature from absorbance ratios of different lines; however, on the other hand, this leads to the required fixed relation of absorbances of different lines and enables the described scaling of vector C.

As a demonstration of the validity of the described multi-line evaluation and its advantages, Fig. 3 shows kinetics traces resulting from the described weighted analysis of the whole spectrum (red), and the kinetics resulting from the evaluation of only the single line at 1764.93 cm−1 (green).

Fig. 3
figure 3

Kinetics traces of HCHO formation in the shock tube, recorded at T5 = 824 K and p5 = 2.88 bar. The time t = 0 marks the arrival of the reflected shock wave at the diagnostics location. The green trace results from the evaluation of the single absorption line at 1764.93 cm−1, while the red line is a result of the multi-line analysis described above

Full size image

The data form Fig. 3 are part of the series of experiments investigating the pyrolysis of 1,3,5-trioxane, which will be discussed in detail in the next section. Here, it should be noted that the scaling in the multi-line analysis works well, resulting in the same absorbance trend as the single-line evaluation. This particularly enables a direct comparison of the multi-line kinetics extracted from experiments with the kinetics predicted by different models, because a model typically uses the absorbance value of one specific line. The most important point, however, is the reduction of noise in the multi-line trace by typically a factor of four due to the inclusion of the weighted information on all recorded laser lines. It should be noted that the noise-reduction factor for lines with lower SNR than the chosen line at 1764.93 cm−1 can be significantly larger. Therefore, the described multi-line analysis of kinetics traces is used throughout the current work.

4 Results and discussion

4.1 Pyrolysis of 1,3,5-trioxane

The pyrolysis of 1,3,5-trioxane and the subsequent formation of formaldehyde has been studied in the shock tube for the temperature range of 800–1300 K and pressures between 2 and 3 bar. The following experiments have been performed with mixtures of 0.9% C3H6O3 diluted in argon.

The top diagram of Fig. 4 shows an exemplary absorbance trace (red) recorded with a time resolution of 4 µs (single slices) behind a reflected shock wave. The values of T5 = 953 K and p5 = 1.94 bar were calculated from the velocity of the incident shock wave using the Rankine–Hugoniot relations. It should be noted that T5 refers to the initial temperature after arrival of the reflected shock wave (t = 0); whereas, the actual temperature at t = 1.34 ms is lower by about 61 K due to the endothermicity of the reaction (see discussion below). The actual time-dependent temperature T has been calculated from the full reaction mechanism (Cai and Pitsch [44]) using Chemical Workbench [45] and is shown in the upper diagram of Fig. 4 in brown. To account for this effect, the following spectral calculations using the HITRAN database [31] are performed with the plateau temperature T = T5 – 61 K = 892 K.

Fig. 4
figure 4

Top: exemplary absorbance trace (red) recorded behind a reflected shock wave at T5 = 953 K and p5 = 1.94 bar. The calculated actual temperature is shown in brown. Bottom: single-slice (black open circles, t = 1.342 ms) and averaged (red dots, t = 1–3 ms) experimental spectra of HCHO recorded after the reflected shock wave, superimposed with a HITRAN spectrum of HCHO calculated with T = 892 K, p = 1.94 bar and pHCHO = 52 mbar

Full size image

As can be seen from the absorbance trace (Fig. 4, top, red), the formation of HCHO reaches a plateau within ~ 0.3 ms after the arrival of the shock wave. This fact can be used for a first spectral evaluation of the DCS performance, which is shown in the bottom diagram of Fig. 4. The 500-fold averaged experimental transmission spectrum (red dots), obtained from the plateau region between t = 1 and 3 ms (with a time resolution of 4 µs, we record 500 spectra within 2 ms) shows good agreement with the superimposed calculated spectrum of HCHO (blue, HITRAN) in the entire investigated spectral range. The only noticeable deviation occurs at ν ≈ 1752 cm−1. This systematic deviation may be attributed to deficiencies of the HITRAN database, especially at high temperatures. The spectral calculation has been performed using the experimental values of temperature T = 892 K, total pressure p = 1.94 bar, absorption path length L = 8 cm, and spectral resolution Δνres = 0.03 cm−1 as input parameters. The partial pressure of formaldehyde has been used as a variable for a spectral multi-line fitting procedure, resulting in a HCHO concentration of about 2.68% (pHCHO = 52 mbar). This is in good agreement with the initially measured concentration of 0.9% of 1,3,5-trioxane (in argon), that decomposes into 2.7% of HCHO, according to (R1). The experimental single-slice spectrum (black open circles), recorded at t = 1.342 ms, exhibits a notably higher noise compared to the averaged spectrum (as expected from Fig. 2). Nevertheless, this signal quality is sufficient for a multi-line spectral fitting procedure using the HITRAN database, thus enabling a sufficient precision for shock-tube diagnostics.

As the sample spectra are normalized by the spectrum recorded before the arrival of the reflected shock wave, the experimental spectra in Fig. 4 do not contain any measured atmospheric absorption lines of H2O. However, since the beam-path remained unpurged, almost complete absorption of several laser lines by atmospheric H2O occurred. To avoid the division of zero by zero during the normalization, the corresponding spectral points have been excluded from the evaluation. As a consequence, the experimental spectra consist of 140 instead of the 188 available frequencies of the DCS signal. However, a purging system that prevents interaction of the laser beam with the atmosphere outside the shock tube would improve on this issue in future experiments making all 188 frequencies provided by the QCL DCS system available for an evaluation.

Figure 5 (left) shows experimental kinetics traces (colored) obtained at different experimental shock-wave conditions (T5, p5). The time-dependent HCHO absorbance profiles (left axes) have a temporal point spacing of 4 µs. Note that the absorbance traces reveal the exact timing of the incident and reflected waves as schlieren peaks around t = 0 (originating from beam steering). The right axes are scaled such that the absorbance can be approximately translated into the actual HCHO concentration.

Fig. 5
figure 5

Left: time-dependent variation of the absorbance for selected experimental conditions. The superimposed black lines are the results of iterative simulations using Chemical Workbench. The right axes are scaled such that the absorbance can be directly translated into HCHO concentration. Right: examples of multi-line spectral fitting of the HCHO concentration for the experiment at T5 = 868 K, p5 = 2.82 bar. Colored spectra are experimental results at given time t, while black lines are best-fit results from HITRAN

Full size image

The relation of the absorbance (left axis) and concentration (right axis) has been performed by spectral multi-line fitting procedures using the HITRAN database. During this fitting process, the HCHO partial pressure is used as a variable, while the actual temperature T has been previously obtained from a simulation using Chemical Workbench. For species that provide absorption lines with significantly different temperature response within the spectral range of the DCS measurement, the temperature could be determined along with the concentration measurements from the line-intensity ratios. In our specific case, however, the difference in temperature sensitivities, as well as the temperature variations, is relatively small, thus preventing the use of HCHO as a target species for temperature measurements. Therefore, the actual temperatures are obtained from kinetics simulations.

The right diagram of Fig. 5 illustrates the fitting procedure by exemplary experimental spectra (colored) and corresponding best-fit HITRAN spectra (black) obtained at selected times t at the initial shock-wave conditions of T5 = 868 K and p5 = 2.82 bar. For the reduction of noise, 25 subsequently measured spectra are averaged before fitting, resulting in an effective time resolution of 100 µs. The uncertainty of this fitting procedure is estimated to be about 4%. Similar procedures have been executed for all experiments, resulting in concentration–time profiles, thus enabling approximately relating the absorbance and concentration axes in Fig. 5 (left). The detection limit for HCHO at exemplarily chosen experimental conditions of T = 900 K, p = 2 bar and a noise level of 1%, is estimated to be about 500 ppm.

Although concentration–time profiles are in general more suitable for an intuitive interpretation of experimental data, absorbance–time profiles are often more appropriate for comparison with simulations, because they clearly separate the measured quantities (absorption) from the calculated ones (calculating the concentration requires additional data from the simulation). For this reason, the following determination of the rate coefficient for 1,3,5-trioxane decomposition (i.e., formaldehyde formation) is performed using the absorbance data. In Fig. 5 (left), the experimental data are shown in comparison to simulations (black lines). The details of the simulations are discussed in the following paragraphs.

The rate coefficients of HCHO formation have been determined by simulations with Chemical Workbench [45] using the kinetics mechanism of Cai & Pitsch [44] to describe the depletion of HCHO at T > 1013 K. The temperature- and pressure-dependent absorption cross sections at ν = 1764.93 cm−1 required for this simulation have been retrieved from the HITRAN database. It should be noted that since the temperature decreases by about 50–70 K due to the endothermic decomposition of 1,3,5-trioxane, fitting of the rate constant of (R1) using a single exponential is not adequate. Instead, the profiles are simulated with a complete reaction set of the mechanism, hence considering the thermochemistry of the species. Figure 6 shows two examples of such simulations of HCHO formation behind reflected shock waves, explicitly for T5 = 868 (left) and for T5 = 953 K (right).

Fig. 6
figure 6

Experimental absorbance–time histories of HCHO (black) at initial temperatures of 868 K (left) and 953 K (right), superimposed with simulated profiles determined in this work (red) and with those from earlier works of Irdam and Kiefer [34] (blue), Wang et al. [35] (green) and Alquaity et al. [33] (cyan)

Full size image

The red solid line is the best-fit result of the experimental data; while the blue, green and cyan lines are results of simulations using different rate coefficients reported in literature [33,34,35]. An iterative procedure is used to determine the best-fit for each experiment shown in Fig. 5 (left). In a first step, the activation energy of reaction (R1) reported by Irdam and Kiefer is used as initial parameter and the A-factor is varied until an agreement between the measured and simulated profile is achieved. In a second step, the rate coefficients determined at the different experimental (average) temperatures are fitted with an Arrhenius expression and the fitting procedure is repeated with the activation energy of this Arrhenius expression. After that, the rate coefficients determined with the new activation energy are again plotted in an Arrhenius diagram. When the determined activation energy is almost identical with the second-step value, the iteration is stopped and the result is the best-fit of the experiment.

When comparing our results with the rate coefficients of (R1) from literature, it becomes obvious that the coefficient of Wang et al. [35] (green) is notably too slow at T5 = 953 K (right) and this becomes even more dramatic at higher temperatures. This is probably due to the fact that Wang et al. [35] fitted their experiments with a single-exponential growth and did not consider the temperature decrease due to the endothermicity of the 1,3,5-trioxane decomposition. The coefficient of Irdam and Kiefer [34] (blue) is only slightly too slow, while simulations with the rate coefficient of Alquaity et al. [33] show the best agreement with our measurements. Figure 7 makes these first conclusions even more evident through an Arrhenius representation of the rate coefficients from literature together with the values measured in the current work.

It can be seen that the activation energies obtained in different works agree well, with the only exception of the value of Wang et al. [35] (green). Additionally, Fig. 7 reveals that the absolute values of the rate coefficients determined in shock tubes at high temperatures of Irdam and Kiefer [34] (blue) and Alquaity et al. [33] (cyan), and the extrapolated flow-reactor value of Hochgreb and Dryer [33] at 700–800 K (magenta), agree well with our values. On the other hand, the extrapolation of the rate coefficients determined at lower temperatures by Aldridge et al. [36] (orange), Hogg et al. [47] (brown), and Burnett and Bell [48] (gray) shows a too slow 1,3,5-trioxane decomposition. Since the work of Matsugi et al. (mentioned in the introduction) was carried out for only one temperature (T5 = 955 K), it is not included in Fig. 7. However, it should be mentioned that the determined rate in their work is about 30% lower than the rate determined in our work of k = 6 × 1015exp(– 205.58 kJ mol−1/RT) s−1. The uncertainty of the determined reaction rate is estimated to be between 10 and 20% (depending on the temperature), based on uncertainties in the initial 1,3,5-trioxane concentration, the absorption coefficient, the fitting accuracy and the precision of the experimentally determined pressure and temperature.

Fig. 7
figure 7

Arrhenius representation of the rate coefficient obtained in this work k = 6 × 1015exp(– 205.58 kJ mol−1/RT) s−1 (red line) compared with literature values: blue line (Irdam and Kiefer [34]), Cyan (Alquaity et al. [33]), green (Wang et al. [35]), magenta (Hochgreb and Dryer [46]), orange (Aldridge et al. [36]), brown (Hogg et al. [47]), gray (Burnett and Bell [48])

Full size image

4.2 Oxidation of HCHO

HCHO measurements under oxidizing conditions have been carried out in a mixture of 0.36% C3H6O3 and 1.02% O2 in argon. Figure 8 shows HCHO absorbance–time histories recorded at different conditions after the reflected shock wave. The experimental absorbance profiles are shown together with simulations using the Aramco3.0 [49] (dashed black lines) and the Cai and Pitsch [44] (solid black lines) mechanisms.

Fig. 8
figure 8

Measured HCHO absorbance–time profiles at different initial temperatures (T5) and pressures (p5), superimposed with simulated data using the Aramco3.0 [49] (dashed black lines) and the Cai and Pitsch [44] mechanisms (solid black lines). The initial conditions are: [(HCHO)3]0 = 0.36% and 1.02% O2 in argon. The calculated actual temperatures are shown as brown dotted lines (right axes)

Full size image

The simulations show good agreement with the measurements. The stronger noise in Fig. 8 compared to Fig. 5 (left) can be attributed to a lower HCHO concentration and higher initial temperatures in these experiments. The reason for the seemingly unphysical signal drop below zero around t = 1 ms, which is observable at higher temperatures, is presumably stimulated emission of species excited during the oxidation (combustion) of HCHO. Thermal lensing may also contribute to the observed signal drop. These assumptions are supported by the corresponding calculated temperature profiles shown in brown (right axes). It can be seen that the signal drop (i.e., higher detected intensity than the one recorded prior to the experiment) coincides with the duration of the heat release that characterizes the combustion process. However, these hypotheses have to be verified in further experiments.

5 Conclusions

A quantum-cascade dual-frequency-comb spectrometer emitting in the spectral range of 1740–1790 cm−1 is successfully applied for spectroscopic and kinetic studies of HCHO in the temperature and pressure ranges of 800–1500 K and 2–3 bar. The time resolution of 4 µs enables monitoring of fast processes, which is very advantageous for shock-tube studies. In particular, we apply the DCS to (1) study the decomposition of 1,3,5-trioxane by monitoring HCHO concentrations and (2) to investigate the combustion system HCHO/O2. The rate of 1,3,5-trioxane decomposition is found to be k1 = 6.0 × 1015 exp(– 205.58 kJ mol−1/RT) s−1. This value is in good agreement with former shock-tube and flow-reactor studies. The measured HCHO profiles for oxidation conditions could be well predicted by two kinetics mechanisms from literature. This result is an important validation for the HCHO oxidation chemistry of both mechanisms, which is essential for every hydrocarbon oxidation mechanism. With this, it can be concluded that the DCS diagnostics approach has shown great potentials for kinetics studies.

The demonstrated possibility of using multiple lines for spectral fitting is a significant advantage of the DCS technique. This may be particularly important for multi-species kinetics studies. The broad spectral coverage of a DCS system can also be used for high-pressure (~ 20 bar) studies of HCHO, where the spectrum transforms into a structured broadband feature that can be simultaneously analyzed as a whole, in cases where the analysis with individual narrow-band light sources is challenging.

The high spectral resolution of 0.03 cm–1 of the individual comb lines of the instrument is promising for accurate determination of spectroscopic quantities at elevated temperatures and pressures that are barely studied up to now. For this purpose, longer laser cavities can be used to reduce the point spacing between comb teeth. Furthermore, consecutive measurements with shifted line spacings of the frequency combs can be used to record spectral data in-between the current comb teeth, thus avoiding undersampling. The estimated detection limit for HCHO of 500 ppm can be further enhanced by increasing the absorption path length inside the shock tube in future experiments by exploiting a multi-pass cell as an integral part of the shock tube.