Characterization of the angular-dependent emission of nitrogen-vacancy centers in nanodiamond

Abstract

We report on the characterization of the angular-dependent emission of single-photon emitters based on single nitrogen-vacancy (NV-) centers in nanodiamond at room temperature. A theoretical model for the calculation of the angular emission patterns of such an NV-center at a dielectric interface will be presented. For the first time, the orientation of the NV-centers in nanodiamond was determined from back focal plane images of NV-centers and by comparison of the theoretical and experimental angular emission pattern. Furthermore, the orientation of the NV-centers was also obtained from measurements of the fluorescence intensity in dependence on the polarization angle of the linearly polarized excitation laser. The results of these measurements are in good agreement. Moreover, the collection efficiency in this setup was calculated to be higher than 80% using the model of the angular emission of the NV-centers.

1 Introduction

Single-photon sources are promising candidates to be used in many quantum applications such as quantum key distribution and biomedical applications [1,2,3,4,5]. It is also discussed that single-photon sources may be able to become a new standard photon source in radiometry [6,7,8,9]. Here, the photon flux should be emitted, ideally, at one specific wavelength with a repetition rate higher than ${10^{6}}$ photons per second, so that they can be detected with a low-noise analogue reference standard detector. Such a source can then be used to close the gap between traditional radiometry ($\ge$ pW) and quantum radiometry ($\sim$ fW). One candidate for the above-mentioned applications is the nitrogen-vacancy (NV-) center in nanodiamond. The NV-center can be operated at room temperature, has a high photostability [2, 6, 10,11,12], exhibits a bright emission and the surrounding diamond crystal structure ensures robustness [13]. A single-photon source based on an NV-center in nanodiamond has already been absolutely calibrated, its absolute optical radiant flux and spectral power distribution are traced back to the national standards via an unbroken traceability chain [8, 9].

In this paper, we focus on the theoretical and experimental investigation of the angular-dependent emission of such an NV-center. This is considered to be the next step towards the realization of a deterministic absolute single-photon source with respect to the possibility of calculation and therefore optimization of the collection efficiency of a single-photon source.

2 Experimental setup

Fig. 1

Experimental setup for characterization and back focal plane imaging of NV-center emission. ND neutral density filter, LL 532 laserline filter, L1 and L2 lenses for beam preparation, DBS dichroic beam splitter, Notch 532 notch filter at 532 nm, FEL0550, FES0750 and FES0800 long/short-pass band filter (cut-off wavelength 550 nm, 750 nm and 800 nm)

For the experiments, a sample of NV-centers in nanodiamonds with an average diameter of 75  nm (GAF 0.15, microdiamond AG), spin-coated on cover glass was investigated in a confocal laser-scanning microscope setup (see Fig. 1). The sample was fabricated by Friedrich Alexander University (FAU) Erlangen–Nürnberg, Germany. A laser with a wavelength of 532 nm (Ventus 532, LaserQuantum) was used to excite the NV-centers using an oil immersion microscope objective (CFI Plan Apochromat $\lambda$ 100$\times$ NA 1.45, Nikon). A single-mode optical fiber with a core diameter of 9 $\upmu$m was used as a pinhole. For the Hanbury Brown and Twiss interferometer measurements, two avalan-che photodiodes (SPCM-AQRH-13-FC, Perkin Elmer) behind a nearly 50:50 beamsplitter (F-CPL-1X2-OPT, Newport) were used to determine the single-photon purity via a 2nd order correlation measurement. The setup is described in detail in reference [8]. For back focal plane imaging, a switchable mirror and a Bertrand-lens were brought into the fluorescence light path. The position of the Bertrand lens is indicated in Fig. 1. The distance to the back focal plane of the microscope objective, which is usually inside the objective itself [14], needs to match the focal length of the Bertrand lens (f = 500 mm). An sCMOS camera (Orca Flash 4.0, Hamamatsu) with a tube lens set to infinity was used to depict the back focal plane. This configuration for back focal plane imaging, where Bertrand lens and tube lens form a finite conjugate pair has major advantages over other configurations [14], e.g. an easier alignment.

3 Theoretical model

Fig. 2

Orientation of the NV-center axis defined by the angles $\theta$ and $\phi$ in the laboratory coordinate system, which also defines the orientation of the plane perpendicular to this axis (gray circle). The dipoles are rotated within this plane by $\beta$. Figure inspired by [15]

The NV-center consists of two perpendicular dipoles (${d}_{\mathrm {x}}$, ${d}_{\mathrm {y}}$) in a plane perpendicular to the symmetry axis (NV-axis) of the center [15,16,17]. Therefore, these three directions form a Cartesian coordinate system. The orientation of the symmetry axis in the laboratory coordinate system is indicated by the out-of-plane angle $\theta$ and the in-plane angle $\phi$. For $\theta =\phi =0^{\circ }$ the NV-axis is parallel to the optical axis in the setup. By rotating the symmetry axis, the orientations of the emitting dipoles are unambiguously described, which is shown in Fig. 2. Furthermore, the x- and y-axis are arbitrary but fixed in the laboratory frame of reference. Due to crystallographic symmetry the NV-centers interact in multiple orientations with an incident laser beam [17]. These orientations are rotations of the dipole plane, which is shown in gray in Fig. 2. The corresponding rotation angle around the NV-axis is the angle $\beta$. In spherical coordinates, the orientations $\theta _{\mathrm {x}}$, $\theta _{\mathrm {y}}$, $\phi _{\mathrm {x}}$ and $\phi _{\mathrm {y}}$ of the emitting dipoles are as follows:

$$\begin{aligned} \mathrm {cos}(\theta _\mathrm {x})&= -\mathrm{cos}(\beta )\,\mathrm {sin}(\theta ), \end{aligned}$$

(1)

$$\begin{aligned} \mathrm {cos}(\theta _\mathrm {y})&= \mathrm {sin}(\beta )\,\mathrm {sin}(\theta ), \end{aligned}$$

(2)

$$\begin{aligned} \mathrm {cos}(\phi _{x})&= \frac{\mathrm {cos}(\beta )\,\mathrm {cos}(\theta )\,\mathrm {cos}(\phi )-\mathrm {sin}(\beta )\,\mathrm {sin}(\phi )}{\sqrt{\mathrm {cos}^2(\beta )\,\mathrm {cos}^2(\theta )+\mathrm {sin}^2(\beta )}}, \end{aligned}$$

(3)

$$\begin{aligned} \mathrm {cos}(\phi _{\mathrm {y}})&= \frac{-\mathrm{sin}(\beta )\,\mathrm {cos}(\theta )\,\mathrm {cos}(\phi )-\mathrm {cos}(\beta )\,\mathrm {sin}(\phi )}{\sqrt{\mathrm {sin}^2(\beta )\,\mathrm {cos}^2(\theta )+\mathrm {cos}^2(\beta )}}. \end{aligned}$$

(4)

Because of the ambiguity of the inverse tangent function in the Euclidean plane, if any of the two conditions

$$\begin{aligned}&\mathrm {sin}(\beta )\ \mathrm {cos}(\phi )+\mathrm {cos}(\beta )\ \mathrm {cos}(\theta )\ \mathrm {sin}(\phi )<0, \end{aligned}$$

(5)

$$\begin{aligned}&\mathrm {cos}(\beta )\ \mathrm {cos}(\phi )-\mathrm {cos}(\theta )\ \mathrm {sin}(\beta )\ \mathrm {sin}(\phi )<0, \end{aligned}$$

(6)

is fulfilled, $\phi _\mathrm {{x}}$ (Eq. 5) respectively $\phi _\mathrm {{y}}$ (Eq. 6) must be corrected such that

$$\begin{aligned} \phi _\mathrm {{corr}} = 2\pi -\phi . \end{aligned}$$

(7)

This correction is derived from the quadrant correction of the inverse tangent function in the Euclidean plane.

A sample of NV-centers in nanodiamonds with a diameter far below the wavelength of the nitrogen-vacancy emission is investigated. The near-field of the emitting dipoles of the NV-center interacts with the dielectric interface, namely the cover glass. These evanescent waves are refracted as plane waves into angles above the critical angle of refraction [18,19,20]. Note that this is only true, when the refractive index of the cover glass ${n_2}$ is higher than the refractive index ${n_1}$ of the medium that contains the emitting dipoles [20], which is air in this case. The NV-centers in sub-wavelength nanodiamonds can be idealized as free dipoles in air [21].

Lukosz developed and described a model [18,19,20] to compute the angular-dependent emission patterns of an arbitrary oriented dipole in medium ${n_1}$ near a dielectric interface to a second medium ${n_2}$. The dipole in medium ${n_1}$ has an out-of-plane orientation angle $\theta$ with the optical axis and an in-plane orientation angle $\phi$. The angular dependency of the emission is described by the angle $\alpha$ against the optical axis and the in-plane angle $\phi$. The formulas, which are used to calculate the angular-dependent emission pattern are shown in Appendix 1 Eqs. (19)– (25). The required angle $\theta$ is inserted according to the results of the Eqs. (1) and (2). The in-plane orientation angles $\phi$ of the emission dipoles of the NV-center, which are calculated in Eqs. (3)–(7), are included as an in-plane offset. This is necessary because Lukosz calculated emission patterns for dipoles that have no in-plane rotation.

Far from saturation the dipoles can not absorb linearly polarized laser light evenly because of the different projections of the excitation dipole into the polarization dipole of the incident light [22]. Still, the emission of photons is distributed evenly between the dipoles [17]. Therefore, the angular-dependent emission pattern of an NV-center is just the sum of the angular-dependent emission patterns of each dipole. As the back focal plane image is the Fourier-transformed of the angular emission pattern, $k_x$ and $k_y$ are the positions in the back focal plane. Conversion between angular-dependent emission patterns P($\theta$) and back focal plane images P($k_x$, $k_y$) is done according to reference [23] using

$$\begin{aligned} {P}(\theta )\,\mathrm {d}\Omega = {P}(\mathrm {arcsin}(\mathrm {k}_{\perp }/|\mathbf {\mathrm {k}}|)\,\mathrm {cos}(\theta )\,\mathrm {d}\Omega , \end{aligned}$$

(8)

where k is the wave vector of the emitted light and $k_{\perp }$ is defined by

$$\begin{aligned} k_{\perp }=\sqrt{k_x^2 + k_y^2}. \end{aligned}$$

(9)

In practice, a back focal plane image is converted using the inverse sine function of the distance to the center of the image. This inverse sine is normalized to the back focal plane images edge, which corresponds to the opening angle of the microscope objective.

Fig. 3

A calculated back focal plane image with the orientation of the NV-center axis (NV-axis) shown in the laboratory coordinate system. The distance between the dipoles and the interface is $z_{0} = 60$ nm. Inset: The back focal plane image as it would be measured in a back focal plane imaging setup

In Fig. 3, such a calculated back focal plane image of an NV-center with orientation $\theta = 30^{\circ }$ and $\phi = 45^{\circ }$ is shown together with the NV-axis. The in-plane projection of the NV-axis is an axis of symmetry of the back focal plane image, which means that the in-plane orientation angle $\phi$ can be recognized in the back focal plane image. This is true for every angle $\theta$. However, $\theta = 0^{\circ }$ shows rotational symmetry, making an in-plane orientation angle obsolete.

Fig. 4

Calculated back focal plane images with in-plane-orientation $\phi = 0^{\circ }$, distance between the dipoles and the interface $\mathrm {z}_{0} = 60$ nm and variation of the out-of-plane angle: a $\theta = 0^{\circ }$, b $\theta = 30^{\circ }$, c $\theta = 60^{\circ }$ and d $\theta = 90^{\circ }$

$\theta$ itself can be derived from the location of the minimum intensity in the back focal plane image. For illustration the shifting of the minimum intensity location is shown in Fig. 4, where in b) the minimum is on the top side at the border to the red circle and in d) it is in the center of the back focal plane image.

4 Experimental results

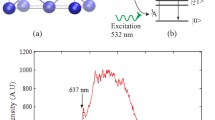
Using the laser-scanning confocal microscope setup, a sample of nanodiamonds spin-coated on cover glass was investigated. One bright emission spot has been chosen for further investigation. Spectroscopic measurements show that the emission of this object can clearly be attributed to an NV-center with negative charge state, which corresponds to a zero-phonon line at 637 nm [21, 24, 25].

Fig. 5

a A calculated back focal plane image with $\theta = 70^{\circ }$, $\phi \,=\,345^{\circ }$ and $\mathrm {z}_{0} = 60\,\mathrm {nm}$. b A measured back focal plane image of an NV-center

To verify the single-photon emission of that NV-center, a measurement of the second order correlation function $g^{(2)}(\tau )$ in a Hanbury-Brown and Twiss setup has been carried out. A three-level model [24] has been used to fit the data without any background subtraction but taking into account the timing jitter of the detection system, which results in a value of $g^{(2)}(\tau =0)=0.09$ and a lifetime of the NV-center emission of 12.2 ns, which is a rather low value compared to the literature values between 10 and 40 ns [12, 26].

The back focal plane image of the NV-center is shown in Fig. 5b. Instead of one circle of high intensity, two circles show up. It is assumed that such behavior is due to a reflection of the fluorescent light at an optical element, e.g. a lens. Although the image seems to be distorted and blurred, the orientation of the NV-center can be easily obtained. An ideal back focal plane image was calculated with the out-of-plane angle $\theta =70^{\circ }$, the in-plane angle $\phi =345^{\circ }$ and the distance between dipoles and the interface ${z}_{0}=60\,\mathrm {nm}$, which is shown in Fig. 5a.

Fig. 6

Comparison of measured and calculated angular-dependent emission patterns of the NV-center. Inset: The measured back focal plane image and the cross-section, indicated with a double arrow straight line, from which the data was extracted

Fig. 7

Smoothed measurement of the photoluminescence intensity versus laser polarization angle of an NV-center with orientation $\theta = 60^{\circ }$ and $\phi = 334^{\circ }$

A more direct comparison between calculation and measurement can be seen in Fig. 6, where the data of the back focal plane measurement on a straight line is extracted and translated into an angular-dependent emission pattern and shown together with a calculated curve. Both curves are normalized so that the area under each curve is equal. This area is proportional to the total emitted power [20]. The curves fit well except at the highest intensity, where the calculated emission pattern has a sharp, very high peak and the measurement peak is rather broad and noisy. As blurriness mostly affects parts of the image with a high intensity gradient, this may partly explain the differences between the curves.

In Fig. 7, a smoothed measurement of the photoluminescence intensity of the NV-center versus the laser polarization angle $\delta$ is shown. Far from saturation of the NV-center, the absorption depends on the projection of the incident polarization dipole into the absorption dipoles of the NV-center [17, 22]. From this measurement, the in-plane orientation of the NV-center excitation dipole $\phi$ can be obtained through the angle of minimum intensity $\delta _{\min }$ [15]. This means that $\phi$ is twofold degenerate, since the measured curve is symmetric. The out-of-plane angle $\theta$ is $\theta =\mathrm {cos}^{-1}\left( \sqrt{\frac{I_{{\min }}}{I_{{\max }}}}\right)$ [15], where $I_{{\min }}$ and $I_{{\max }}$ are the minimum and the maximum fluorescence intensity respectively. With this, the orientation of the nitrogen-vacancy axis is determined to be $\theta = 60^{\circ }$ and $\phi = 334^{\circ }$.

Comparison between the orientation angles determined by back focal plane imaging and photoluminescence intensity versus the laser polarization angle is possible, since parallelism of excitation and emission dipoles can be assumed [22]. It should also be noted that this method of measuring the absorption dipole does not take into account the change of the incident light polarization by the microscope objective [27, 28].

Fig. 8

Collection efficiency of the confocal microscope setup depending on the out-of-plane angle $\theta$ of the NV-center

By using the model of the angular-dependent emission, the collection efficiency can be calculated. This is done by first integrating the formulas of Lukosz [20] over the in-plane angle $\phi$, which gives

$$\begin{aligned} P _{\mathrm {I}}^{(\mathrm {p})}(\alpha _{1}, \alpha _{2})&= \frac{3}{2}\frac{\textit{n}^3\,\mathrm {cos}^2(\alpha _2)\left[ 2\,(\mathrm {cos}(\theta )\,\mathrm {sin}(\alpha _1))^2+(\mathrm {sin}(\theta )\,\mathrm {cos}(\alpha _1))^2\right] }{\left[ \textit{n}\,\mathrm {cos}(\alpha _1)+\mathrm {cos}(\alpha _2)\right] ^2}, \end{aligned}$$

(10)

$$\begin{aligned} P _{\mathrm {I}}^{(\mathrm {s})}(\alpha _{1}, \alpha _{2})&= \frac{3}{2}\frac{\textit{n}^3\,\mathrm {cos}^2(\alpha _2)\,\mathrm {sin}^2(\theta )}{[\mathrm {cos}(\alpha _1)+\textit{n}\,\mathrm {cos}(\alpha _2)]^2}, \end{aligned}$$

(11)

$$\begin{aligned} P _{\mathrm {II}}^{(\mathrm {p})}(\alpha _{1}, \alpha _{2})&= \frac{6\textit{n}^5\,cos^2(\theta )\,\mathrm {sin}^2(\alpha _2)+\mathrm {sin}^2(\theta )\,\left[ \textit{n}^2\,\mathrm {sin}^2(\alpha _2)-1\right] }{(2\textit{n}^{2}-2)\,(\textit{n}^{2}+1)\,\mathrm {sin}^2(\alpha _2)-1}\nonumber \\&\quad \mathrm {cos}^2(\alpha _2)\,\mathrm {exp}\left[ \frac{-2\textit{z}_{0}}{{\Delta }{} \textit{z}(\alpha _2)}\right] , \end{aligned}$$

(12)

$$\begin{aligned} P _{\mathrm {II}}^{(\mathrm {s})}(\alpha _{1}, \alpha _{2})&= \frac{3\textit{n}^3}{2\textit{n}^{2}-2}\,\mathrm {cos}^2(\alpha _2)\,\mathrm {sin}^2(\theta )\,\mathrm {exp}\left[ \frac{-2\textit{z}_{0}}{{\Delta }{} \textit{z}(\alpha _2)}\right] , \end{aligned}$$

(13)

$$\begin{aligned} P _{\mathrm {III}}^{(\mathrm {p})} (\alpha _{1}, \alpha _{2})&= \frac{3}{2}\frac{\cos ^{2}(\alpha _{1})\left[ 2\textit{n}\cos (\theta )\,\sin (\alpha _{1})\right] ^2 + \left[ \sin (\theta )\,\cos (\alpha _{2})\right] ^{2}}{\left[ \textit{n}\cos (\alpha _{1}) + \cos (\alpha _{2})\right] ^{2}}, \end{aligned}$$

(14)

$$\begin{aligned} P _{\mathrm {III}}^{(\mathrm {s})}(\alpha _{1}, \alpha _{2})&= \frac{3}{2}\frac{\cos ^{2}(\alpha _{1})\,\sin ^{2}(\theta )}{\left[ \cos (\alpha _{1}) + \textit{n}\cos (\alpha _{2})\right] ^{2}}, \end{aligned}$$

(15)

with

$$\begin{aligned} {\Delta }{} \textit{z}(\alpha _2) = \frac{\lambda }{2\pi }\left[ \textit{n}^2 \mathrm {sin}^2(\alpha _2)-1\right] ^{-\frac{1}{2}} \end{aligned}$$

(16)

and

$$\begin{aligned} \textit{n}=\frac{\textit{n}_2}{\textit{n}_1}, \end{aligned}$$

(17)

where ${n_1}$ and ${n_2}$ are the indices of refraction at both sides of the dielectric interface. The emission intensity ${ P _{x}^{\text {(s,p)}}}$ for s- and p-waves is separated into three sections x = I, II or III [19]. Section I is valid for $\alpha _{2}$ below the critical angle of total internal reflection $\alpha _{\mathrm {crit}} = \mathrm {sin}^{-1}\left[ \frac{{n}_1}{{n}_2}\right]$ in ${n}_{2}$. Consequently, Section II is valid above the critical angle of total internal reflection in ${n}_{2}$ and Section III is valid in the second half-space ${n}_{1}$.

With Snell’s law $\alpha _1 = \mathrm {sin}^{-1}\left[ {n}\,\mathrm {sin}(\alpha _2)\right]$ these formulas are then numerically integrated over $\alpha$, so that

$$\begin{aligned} {\text {CE}}\,=\,\frac{\displaystyle \int _{0}^{\alpha _{0}}{\left( P ^{(\mathrm {s})}+ P ^{(\mathrm {p})}\right) \mathrm {d}\alpha }}{\displaystyle \int _{0}^{\pi }{\left( P ^{(\mathrm {s})}+ P ^{(\mathrm {p})}\right) \mathrm {d}\alpha }} \end{aligned}$$

(18)

is the collection efficiency CE of the setup defined by the power that is collected by the microscope objective divided by the total emitted power. The opening angle of the microscope objective is $\alpha _{0}$. The collection efficiency as a function of the out-of-plane orientation $\theta$ is shown in Fig. 8. It increases from about 80% at $\theta =0^{\circ }$ to almost 83% at $\theta =90^{\circ }$.

5 Conclusion

The orientations of the NV-center determined by the two methods shown in this paper are presented in Table 1. The difference is satisfactory taking into account possible uncertainties of the methods. In future work quantification of the uncertainties is planned.

Table 1 Comparison of the orientation angles from back focal plane imaging (BFP imaging) and the photoluminescence versus laser polarization (absorption dipole)

A tool to predict measured back focal plane images by computing an ideal back focal plane image and angular emission patterns was developed. Using this, the collection efficiency from NV-centers was characterized to be between 80 and 83% depending on the orientation of the NV-center. This is a very similar value to the one that has been calculated for a specific single dipole orientation before [9]. The reason for the dependence of the collection efficiency from the orientation of the NV-center is that a horizontal and a vertical dipole’s near-field evanescent waves are coupling into the medium with refractive index $n_2$ with different efficiencies.

Here, an NV-center has been characterized by spectroscopy and by measurement of the second order correlation function, which has shown single-photon emission with a value of $g^{(2)}(\tau =0)\,=\,0.09$. The measured back focal plane image is in good agreement with a calculated back focal plane image and the estimated height of the NV-center emission of ${z_0}$ = 60 nm above the dielectric interface is consistent with the nanodiamond size of 75 nm. The orientation angles of the NV-center, which have been obtained by this comparison, are close to the orientation angles obtained from a measurement of the photoluminescence dependence on laser polarization. It can be assumed that an even better agreement may be reached through improvements in the setup, e.g. a higher image quality in back focal plane imaging by an improved arrangement method for the Bertrand lens. To our knowledge, this is the first time that the NV-center orientation in nanodiamond was determined by back focal plane imaging, although the principle has been shown for molecules [29] and NV-centers in bulk diamond [30].

For our target to realize a deterministic absolute single-photon source we will look into other emitters like silicon-vacancy centers [31], tin-vacancy centers [32] and hexagonal boron-nitride [33, 34], which offer some beneficial properties, e.g. a better Debye-Waller-factor than the NV-center. Moreover, the theoretical model of the angular emission and the experimental methods of orientation determination will be adapted in the future.

Appendices

Appendix 1: Equations for angular emission patterns

The function of the intensity $P(\theta , \phi )$ emitted into a given direction $\alpha = \alpha _2$ are [20]

$$\begin{aligned}&{P}^{(\mathrm {p})}(\alpha _{1}, \alpha _{2}) = \frac{3}{2\pi }\frac{{n}^3\,\cos ^2\alpha _2\left[ \mathrm {cos}\,\theta \,\mathrm {sin}\,\alpha _{1}+\mathrm {sin}\,\theta \,\mathrm {cos}\,\phi \,\mathrm {cos}\,\alpha _1\right] ^2}{[n\,\mathrm {cos}\,\alpha _{1+\mathrm {cos}}\,\alpha _2]^2} \end{aligned}$$

(19)

$$\begin{aligned}&{P}^{(\mathrm {s})}(\alpha _{1}, \alpha _{2}) = \frac{3}{2\pi }\frac{n^3\,\mathrm {cos}^2\alpha _2\,\mathrm {sin}^2\theta \,\mathrm {sin}^2\phi }{[\mathrm {cos}\,\alpha _{1+n}\,\mathrm {cos}\,\alpha _2]^2}. \end{aligned}$$

(20)

$$\begin{aligned}&{P}^{(\mathrm {p})}(\alpha _{2}) = {f}^{(\mathrm {p})}(\alpha _2)\left[ {n}^2\,\mathrm {cos}^2\theta \,\mathrm {sin}^{2}\alpha _{2}+\mathrm {sin}^2\theta \,\right. \nonumber \\&\quad \left. \mathrm {cos}^2\phi \,(\mathrm {n}^2\ \mathrm {sin}^2\alpha _2-1)\right] \end{aligned}$$

(21)

$$\begin{aligned}& {P}^{(\mathrm {s})}(\alpha _{2}) = \mathrm {f}^{(\mathrm {s})}(\alpha _2)\,\mathrm {sin}^2\theta \,\mathrm {sin}^2\phi . \end{aligned}$$

(22)

$$\begin{aligned}&{f}^{(\mathrm {s})}(\alpha _2) = \frac{3}{2\pi }\frac{n^2}{n^{2}-1}\mathrm {cos}^2\alpha _2\ \mathrm {exp}[-2 \mathrm z_{0}/\Delta \,\mathrm {z}(\alpha _2)] \end{aligned}$$

(23)

$$\begin{aligned}&{f}^{(\mathrm {p})}(\alpha _2) = {f}^{(\mathrm {s})}(\alpha _2)\left[ ({n}^{2}+1)\mathrm {sin}^2\alpha _2-1\right] ^{-1} \end{aligned}$$

(24)

$$\begin{aligned}&\Delta \,\mathrm{z}(\alpha _2) = \frac{\lambda }{2\pi }\left[ {n}^2\,\mathrm {sin}^2\alpha _2-1\right] ^{-\frac{1}{2}}. \end{aligned}$$

(25)

$\alpha _1$ can be converted into $\alpha _2$ using Snell’s law $\alpha _1 = \mathrm {sin}^{-1}\left[ {n}\,\mathrm {sin}(\alpha _2)\right]$ so that $\alpha _2$ can be written as $\alpha$ and n is the quotient of the indices of refraction $n_2$ and $n_1$. Formulas 19 and 20 are valid for $\alpha _2<\alpha _{\mathrm {2,crit}}$, while for $\alpha _{\mathrm {2,crit}}<\alpha _{2}<90^{\circ }$ the Formulas 21–25 are valid.

Appendix 2: Back focal plane dependence on dipole height $\mathbf {z_0}$

Fig. 9

Calculated back focal plane images with in-plane-orientation $\phi = 0^{\circ }$, out-of-plane angle $\theta = 90^{\circ }$ and variation of the between the dipoles and the interface: a $z_{0} = 0$ nm, b $z_{0} = 60$ nm, c $z_{0} = 120$ nm and d $z_{0} = 500$ nm

The dependence of the back focal plane image on the height of the emission dipoles ${z_0}$ can be seen in Fig. 9. While $\theta$ and $\phi$ are the same for each back focal plane image, ${z_0}$ varies. The exponential decay for $\alpha _2 > \alpha _{\mathrm {2,crit}}$ changes moderately for the heights in a) ${z_0}\,=\,0\,\mathrm {nm}$ to c) ${z_0}\,=\,120\,\mathrm {nm}$, which are realistic in the experiment. When ${z_0}$ approaches the diameter of the nanodiamonds as in d) ${z_0}\,=\,500\,\mathrm {nm}$, almost the whole emission $\alpha _2 > \alpha _{\mathrm {2,crit}}$ vanishes. Indeed, in this case the idealization of the emission dipoles in air is not valid anymore and therefore such a back focal plane image is very unlikely to be measured.

Appendix 3: Back focal plane imaging technique verification

Fig. 10

a A calculated back focal plane image with $\theta = 55^{\circ }$, $\phi \,=\,13^{\circ }$ and ${z_{0} = 15}$ nm. b A measured back focal plane image of an NV-center

As a verification for the back focal plane imaging method used to determine the orientation of the NV-centers, a second NV-center emission has been compared to the model. In Fig. 10 the measured and calculated back focal plane images for this NV-center are shown. The orientation of the NV-center was determined to be $\theta = 55^{\circ }$ and $\phi \,=\,13^{\circ }$, while the dipole emission height is ${z_{0} = 15\,nm}$. The direct comparison of the angular emission patterns is shown in Fig. 11. The angle of highest intensity and the exponential decay of the intensity for $\alpha \ge \alpha _{\mathrm {crit}}$ agree with the calculated emission patterns. Though, as for the first NV-center, at the critical angle the intensities of calculated emission pattern and the measurement differ. The orientation of this NV-center was also calculated from the measurement of the absorption dipole, which can be seen in Fig. 12. Here $\theta$ was calculated to be ${54^{\circ }}$ and $\phi \,=\,1^{\circ }$. The orientation angles are again shown to be similar between the two methods showing the validity of the back focal plane imaging method.

Fig. 11

Comparison of measured and calculated angular-dependent emission patterns of the NV-center. Inset shows the cross-section from which the data was extracted

Fig. 12

Smoothed measurement of the photoluminescence intensity versus laser polarization angle of an NV-center with orientation $\theta = 54^{{\circ }}$ and $\phi = 1^{{\circ }}$