1 Introduction

Polymer films with embedded azobenzene chromophores have attracted broad interest due to their ability to convert optical energy into mechanical deformations of large magnitude (up to few hundred nanometers) [1,2,3]. One of the peculiar examples here is the formation of a surface relief grating (SRG) in thin polymer films irradiated with a holographic interference pattern (IP) of visible light [4,5,6,7]. Although the polymer film is in a solid, glassy state, it deforms following the intensity and/or polarization pattern of the incident light [8]. The mechanism of the SRG inscription involves internal, opto-mechanical stresses, which are quite high (100 MPa up to  ~ 1 GPa) to deform a material of Young modulus up to several GPa [3, 9,10,11,12]. The appearance of internal stresses is initiated by photo-induced isomerization cycles between the trans and cis states of the azobenzene chromophore. This drives a local re-orientation of azobenzene side chains perpendicular to the optical polarization (formation of a bulk birefringence grating, BBG) [13], which, in turn, results in the re-orientation of the polymer backbones. The subsequent generation of local gradients in the internal stresses within the material causes a viscoplastic deformation of the film that manifests itself in the SRG (topographical grating) [14,15,16,17,18,19]. Following this mechanism, one can state that the response of the polymer film to irradiation with an IP depends strongly on the local distribution of the optical polarization within one period of the pattern [20]. The IPs are usually generated by two-beam lithography, where two coherent laser beams interfere to form a holographic pattern. Their nominal period (called “optical period” in the following) depends on the angle between the two interfering beams and the irradiation wavelength. One distinguishes between intensity interference pattern (IIP), where the polarization of the light stays constant across the irradiated spot, while the intensity varies between zero and maximal over one optical period. The examples here are the so-called SS (two interfering beams with S-polarization), PP, and DD (“D” means a diagonal polarization at + 45°). In the case of polarization interference patterns (PIP), the intensity of the incident light is constant over the period, but the local field polarization varies, e.g., Dd (“d” is the diagonal polarization at − 45°), SP, and RL (right- and left-handed circular polarizations). It has been reported that the SP configuration (one beam is S-polarized; the other one is P-polarized) is quite peculiar, because it inscribes a surface relief whose period is half the optical one (Fig. 1b) [21, 22, 26, 27], while all other configurations (SS, PP, DD, Dd, RL, etc.) result in a 1:1 match between optical and topographical periods. In this way, it is possible to structure a polymer film with topographical features smaller than the diffraction limit of the used light (usually in the visible range) [23], which is, otherwise, only possible by utilizing near fields (e.g., from surface plasmons) [24, 25]. In the SP configuration, the local distribution of the electric field vector represents linear and circular polarized components that alternate over a period, as shown in Fig. 1b. One optical period has two linearly polarized regions at ± 45° angle relative to the S-polarization, surrounded by alternating left- and right-circular polarizations.

Fig. 1
figure 1

a In situ recorded SRG and DE signal (solid curves) of a Pazo polymer film under irradiation with SP-IP (\( \lambda_{\text{pump}} = 491\;{\text{nm}} \), \( I = 200\;{\text{mW}}/{\text{cm}}^{2} \), optical grating pitch \( {{\varLambda }} = 2\;{\upmu}\text{m}, \) and film thickness \( d = 1\;{\upmu}\text{m}) \). The gray rectangle marks the irradiation period with the SP-IP. The first-order DE (red curve) increases first and saturates after a short time, while the second-order DE (blue curve) grows continuously. The SRG amplitude (black dots) increases also continuously. The increase and the relaxation of the first-order DE is fitted with an exponential function (dashed line) giving the time constant \( \tau_{\text{write}} = 43\;{\text{s}} \) and \( \tau_{\text{relax}} = 70\;{\text{s}} \). The inset shows the chemical structure of the Pazo polymer. b In situ recorded AFM micrograph of the polymer film topography during irradiation. Scanning is from top to bottom, showing the temporal evolution of the topography (red arrow at bottom right). The scanning starts without irradiation (flat film), and at the time marked by the dashed white line, the irradiation with the SP-IP is switched on. The local polarization of the electric field relative to the topography maxima and minima is shown by white arrows. The surface profile after irradiation displays a half-period relief (\( {{\varLambda }}/2 = 1\;{\upmu}\text{m} \)). c Polarization analysis of the first- (red) and second-order (blue) diffraction spot. The first order is purely cross-(S-) polarized (90° rotated), while the second order is polarized in the same direction as the probe beam (P-polarized, black arrow)

Full size image

In the few existing reports on structuring polymer films with the SP-IP, it was suggested that the half-period SRG arises from the interference between zeroth- and first-order irradiation beams scattered on the bulk birefringence grating [26, 27]. The half-period grating is then developing with time, but is not showing the same growth rate like the grating with the nominal period.

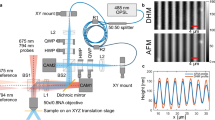
Here, we present a comprehensive experimental investigation of the dual grating formation (SRG and BBG) in a polymer film under SP irradiation, utilizing a home-made set-up that combines in situ probe beam diffraction and atomic force microscopy (AFM) measurements (Scheme 1). The AFM is continuously scanning the polymer surface during irradiation and detects directly the change in the SRG height. The integrated diffraction efficiency (DE) set-up probes in parallel bulk and surface gratings. By including the AFM data in a model of the recorded DE, one obtains information about the birefringence grating. The writing part of the set-up performs the two-beam interference lithography. Here, intensity, polarization, and relative phase of the interfering beams can be changed in a controlled way.

Scheme 1
scheme 1

Sketch of the experimental set-up consisting of three parts: (i) a two-beam interference part for generating the IP (blue laser line), (ii) AFM for in situ recording the surface morphology and (iii) DE set-up (red laser line) enabling information collection about surface and birefringence gratings in real time. The mirror M4 is combined with a piezo actuator to shift its position, introduce a phase shift between the two interfering beams and thereby shifting laterally the whole interference pattern along the polymer film in a controlled way. The Wollaston prism (WP) is analyzing the light in the first diffraction order of S- (D2) and P- (D3) polarized components. Photodiode D4 collects the second-order diffraction. Sh shutter, Sa sample, M mirror, D detector, P polarizer, H half-wave plate, BS beam splitter, Q quarter-wave plate, CL collimating lens, FL focusing lens, PH pin hole)

Full size image

We find that the SRG maximum forms at the positions of linearly polarized light (with ± 45° orientation), causing the formation of the half-period topography. A rotation by only ~ ±1° of the linear polarization in the interfering beams affects the amplitude of the half-period grating significantly: this may explain why the half-period SRG was often missed experimentally. We observe by turning the polarization that one may easily generate a blazed grating with a saw-tooth profile [28,29,30]. Changing the IP from SP to PP finally results in a grating whose period matches the optical one.

All in one, the structuring of the photo-sensitive polymer films with SP-IP makes it possible to initiate several unique processes not available with other types of IP, i.e., the formation of a sub-wavelength topographical grating, an easily tunable SRG period, and the generation of sawtooth profiles (blazed gratings) with adjustable shape.

2 Experimental part

2.1 Materials and methods

2.1.1 Photo-sensitive polymer

(Poly[1-[4-(3-carboxy-4-hydroxyphenylazo)benzenesulfonamido]-1,2-ethanediyl, sodium salt] (Pazo)) is purchased from Sigma-Aldrich. The polymer solution is prepared by dissolving 170 mg Pazo in 1 ml solvent containing a mixture of 95% methoxyethanol and 5% ethylene glycol.

2.1.2 Sample preparation

The polymer films of thickness 1 μm are prepared by spin casting at 3000 rpm for 1 min of 100 μl polymer solution on thin glass slides. The thickness of the film is measured using an atomic force microscope (AFM) by scanning across a scratch within the polymer film.

2.2 Methods

2.2.1 Home-made set-up for studying SRG formation in situ

The set-up consists of three parts: (1) two-beam interference irradiation, (2) atomic force microscopy (AFM), and (3) equipment for measuring the diffracting efficiency (DE) (Scheme 1). The two-beam irradiation with a continuous wave diode pumped solid-state laser (Cobolt Calypso, λ = 491 nm) permits the generation of well-defined spatial interference patterns (either intensity or polarization) by changing the polarization of two interfering beams in a controlled way. The beam diameter is set to 4 mm by a beam expander and spatial filter. The intensity is set to 200 mW/cm2 and a 50:50 beam splitter is added to separate the initially single beam into two beams of equal intensity. These two beams then pass through a set of wave plates and polarizers allowing independent control of intensity and polarization. Adding a half-wave plate to each of the beam paths of the interference set-up (H3, H4 in Scheme 1), one with an angle of \( 0^\circ \) and the second with \( + 45^\circ \) with respect to the optical axis, results in the SP interference pattern (IP). A rotation of the half-wave plates permits to rotate the linear polarization of the beams without introducing any additional phase shifts (provided that there are no birefringent elements downstream). This is a convenient feature to check experimentally the assignment of the local polarization pattern relative to the SRG. To introduce a phase shift between the two interfering beams, one mirror in the two-beam-interference set-up is mounted on a piezo stack actuator (PiezoSystemJena, PA8-14 SG) with a closed-loop feedback system and a travel maximum of 9.5 μm, controlled by a piezo-controller (PiezoSystemJena, 12V40SG).

The second part of the set-up is an AFM that measures the polymer topography changes in situ, i.e., under varying irradiation conditions. The in situ AFM measurements are performed using a PicoScan (Molecular Imaging) AFM working in intermittent contact mode. The scan speed of the AFM is set to 1 Hz with a scan area of 10 × 10 μm and a resolution of 512 × 512 pixel. Commercial tips (Nanoworld-Point probe) with a resonance frequency of 130 kHz and a spring constant of 15 N/m are used for measurements. The sample is oriented with the polymer surface pointing towards the AFM tip, such that irradiation takes place “from below”, i.e., through the glass substrate (Scheme 1). The SRG amplitude is determined from the AFM surface profile by measuring the difference in height between topography maximum and minimum. A plot of this value as a function of time gives the SRG growth kinetic. Scanning profiles are analyzed to determine the relative amplitudes of half-period and nominal period gratings.

To obtain in real-time information about the alignment of the azobenzene side chains in the polymer film, a red probe laser beam (uniphase, HeNe, 633 nm, I = 30 mW/cm2, beam diameter 3 mm) is integrated into the set-up. Its intensity is weak and its wavelength falls outside the absorption bands of the photo-sensitive polymer studied in this work. The probe beam is P-polarized for all experiments reported here, which is inclined to the molecular alignment in those areas within the sample that are irradiated with linearly polarized light (in the SP-IP, these are polarized at \( \pm 45^\circ \) relative to the P-polarization). To calibrate the DE, a beam splitter with a ratio T:R = 90:10 is used in the DE set-up, such that 90% of the light arrives on the sample (intensity \( I_{0} \)) and 10% on a photodiode. The signal of this photodiode is recorded during the whole measurement for controlling the stability of the probe beam during the experiment. The diffraction efficiency is defined as the ratio of the intensity of the nth diffraction order (\( I_{n} \)) and the intensity of the incoming light (\( I_{0} \)). The first-order diffracted beam passes through a Wollaston prism which splits the light into S- and P-polarized components. The detector D2 measures the S-polarized light, while detector D3 records the P-polarized light.

The three different set-ups, two-beam interference, AFM and DE equipments, are controlled and operated with a software (Profilab-Expert, Abacom) designed in the laboratory to record signals of the photodiodes, control the irradiation shutter, and mirror position. To synchronize DE set-up and the AFM, a computer-generated signal is regulating the irradiation with the help of an AD/DA converter (Kolter Electronic, PCI-AD12N-DAC2). These signals are sent to the diffraction efficiency set-up as well as to the AFM using the “aux” input of the AFM controller.

Silicon detectors (Thorlabs DET 100A/M) are used in the DE set-up to measure the intensity of the diffracted probe beam. A 600 nm long-pass filter is placed in front of each photodiode to be sensitive to the probe beam only. The intensity of the diffracted light is recorded every 200 ms, limited by the signal-to-noise ratio.

All experiments are carried out under yellow light to avoid undesirable photo-isomerization and under ambient conditions, i.e., at room temperature with a relative humidity of 55%. The whole set-up is covered with a non-transparent encapsulation to avoid any influence of the environment on the measurement (parasitic light, air circulation, and vibration).

3 Results and discussion

Figure 1a shows the in situ recorded SRG amplitude and diffraction efficiency during irradiation with the SP-IP. The first-order diffraction signal (red curve) increases rapidly and saturates to a fraction of a percent within the first 5 min of irradiation. The second-order (blue curve) and the SRG amplitude (black dots) continuously increase and saturate only after hours of irradiation [31]. It seems that the first-order DE is very little correlated with the SRG amplitude. After switching off the irradiation, the first-order DE partially relaxes, in contrast to the second-order DE and the SRG amplitude.

The polarization analysis of the P-polarized probe beam reveals that the first-order DE signal is purely cross-(S-)polarized, while the second-order is purely co-(P)-polarized (Fig. 1c).

This means that the polarization of the probe beam is rotated, in the first order, by 90° (like in a wave plate) and indicates the existence of a birefringence grating in the bulk of the film (BBG for short). Indeed, the topographic relief cannot diffract into the crossed polarization, because S and P are the principal polarizations in this geometry (they have distinct signatures with respect to the reflection symmetry in the plane of incidence). In Fig. S1 of the Supporting Information, the in situ recorded DE and SRG signals are shown for different polarizations of the probe beam, confirming the existence of the BBG. Figure 1b depicts the in situ recorded evolution of the polymer topography: the vertical scanning direction corresponds to the irradiation time (from top to bottom). The local distribution of the electrical field vector relative to the topography variation is assigned as described elsewhere: the topography maxima develop at the positions of linearly polarized light (\( \pm 45^\circ \)) [23].

3.1 Information stored in the first-order and second-order DE

A straightforward evaluation of the Bragg–Laue equation for the diffraction of the probe beam (\( \lambda_{\text{probe}} = 633\;{\text{nm}} \)) with a grating of \( {{\varLambda }} = 2\;{\upmu}\text{m} \) pitch (called “optical period”) shows that the first- and second-order diffraction spots appear at angles of 18° and 39°, respectively (Scheme 2). Since the polymer topography has half the optical period, \( {{\varLambda }}/2 = 1\;{\upmu}\text{m} \), the diffraction by this relief grating results in a first diffraction order at an angle of 39° (i.e., second order for the optical grating), while the second order is already evanescent (Scheme 2). This means that the first-order DE contains only the information about the birefringence grating, while the second diffraction order carries information about both the SRG and the BBG. This is in contrast to, e.g., the ± 45°-IP, where the topography responds at the optical period \( \left( {{\varLambda }} \right) \), although the pattern of the field polarization is just the same apart from a rotation by 45° (the linearly polarized regions are S- or P-polarized, see Fig. S2 of Supporting Information).

Scheme 2
scheme 2

Scheme highlighting different gratings: PIP, SRG, and BBG together with paths of writing (blue) and recording beams (red). The SP-IP is a polarization pattern whose optical period \( {{\varLambda }} \) is set by the angle θ between the two interfering beams. The local polarization of the SP-IP relative to the topography variation is depicted as blue arrows (marked PIP). The molecular orientation in the polymer film (yellow) responds at the optical period (white arrows marked BBG). The film surface responds at half the optical period \( {{\varLambda }}/2 \) (SRG). The first-order diffraction spot for a grating of period \( {{\varLambda }} = 2\;{\upmu}\text{m} \) is at an angle of 18°, while the second order appears at 39°. Performing the same calculation for the relief grating (\( {{\varLambda }}/2 = 1\;{\upmu}\text{m} \) period) results in a first-order scattering angle of 39°, while the second order is evanescent

Full size image

To check the dual grating structure in the polymer film, we study how the DE signal in the first and second order varies when the local polarization is switched, keeping the optical period constant. By adjusting the position of the mirror M4 (Scheme 1), one introduces a phase shift between the two interfering beams, resulting in a shift of the whole interference pattern along the sample surface. Figure 2a shows the in situ recorded AFM micrographs for several shifting events. The start of the irradiation with the SP-IP is marked by the dashed line no. 1. At line no 2, the IP is shifted by half the optical period, i.e., by \( {{\varLambda }}/2 \), giving a configuration denoted \( {{S\bar{P}}}. \) This corresponds to a polarization rotation by 90° in the linearly polarized regions and a transformation of the circularly polarized regions from left to right and vice versa (compare white arrows in Fig. 2a).

Fig. 2
figure 2

a AFM micrographs of the polymer film when shifting the SP-IP (same parameters as in Fig. 1). At each irradiation step, the local polarization pattern is indicated by white arrows. AFM scanning starts at the top in the dark (time direction indicated by the red arrow); at white line no. 1, the irradiation with the SP-IP is switched on. The topography responds with a half-period grating (\( {{\varLambda }}/2 = 1\;{\upmu}\text{m} \)). At line 2, the IP is shifted by half its period (1 μm), by displacing one mirror in the set-up. At line 3, the IP is shifted back by 1 μm. At line 4, the IP is again shifted by 500 nm (\( {{\varLambda }}/4 \)). At line 5, the irradiation is switched off. b SRG height (black line) and diffraction efficiency in first (red) and second order (blue) as a function of irradiation time (the gray rectangle marks the irradiation period with the SP-IP; the vertical dashed lines mark the switching). The first order shows significant changes, as the molecular orientation adapts to the new local polarization. c SRG profile recorded at four lines marked \( \alpha {-}\delta \) in panel (a). The \( {{\varLambda }}/2 \) shift of the IP does not affect the surface grating, while the \( {{\varLambda }}/4 \) shift makes the SRG drift by \( {{\varLambda }}/4 \) (see red reference line in panel a)

Full size image

The AFM micrographs demonstrate that the SRG is very little affected by this shift, nor is the second-order DE. The first-order DE, however, drops down to zero and recovers on a time scale of 1–2 min. At line no. 3 in Fig. 2a, the IP is shifted back to its initial position. It appears again that this shift of the IP is neither affecting the SRG nor the second-order DE, but transiently eliminates the first-order DE completely. At line no. 4 (Fig. 2a), the IP is shifted by a quarter of the optical period (\( {\text{SP'}} \) configuration) which corresponds to swapping regions of linear and circular polarizations. This shift results in a drop of all signals followed by recovering in the course of further irradiation, albeit more slowly compared to the previous shifts. The AFM scan shows that the SRG “drifts” by half a period (500 nm) while its amplitude goes through a minimum. Eventually, the topography maximum has moved again to the linearly polarized regions (Fig. 2a, c). At line no. 5, the irradiation is switched off, and the first-order DE decreases, indicating a certain relaxation of the molecular orientation (alignment), while no changes in SRG amplitude and second-order DE are observed. These results confirm the statement that the first-order DE appears due to diffraction from the birefringence grating.

3.2 Dependence of SRG and DE signal on optical period

In the following, we investigate how the optical period of the IP alters the AFM and DE signals in amplitude and temporal evolution. Figure 3a shows the in situ recorded AFM micrograph for the irradiation of the polymer film with SP-IP of 500 nm in period. This period of the interference pattern is far below the wavelength of the probe beam (633 nm), which is the reason why no DE can be recorded. Nevertheless, the AFM is still sensitive to the surface grating and shows a half-period SRG (250 nm) with a height amplitude of 3 nm. When the period of the IP is set to 650 nm, which is close to the diffraction limit of the probe beam, the first order DE can be recorded and shows a fast increase at the beginning of irradiation followed by saturation (Fig. 3b).

Fig. 3
figure 3

In situ performed AFM and DE data for different optical periods of the SP-IP: a \( {{\varLambda }} = \) 500 nm, b 650 nm, c 1 μm, d 2 μm, and e 3 μm. The gray color in the plots on the right marks the irradiation time. In all cases, the polymer film responds with an SRG of period \( {{\varLambda }}/2 \). a The period of the SRG is well below the diffraction limit of the probe beam (\( \lambda_{\text{probe}} = 633\;{\text{nm}} \)). b The optical period is large enough to see the first order of the probe beam (red curve) at the BBG. c For a 1 μm optical period, one observes only the first-order DE (red curve). In the AFM data, the SRG amplitude appears to saturate around 20 nm. d One can record both the first order (red curve) and the second order (blue curve) in diffraction. The second-order DE shows a growth kinetics similar to the SRG amplitude. After 30 min of irradiation, the SRG height has increased to 50 nm. e At the optical period of 3 μm, the SRG growth is most pronounced. The first diffraction order shows some decline at large times, while the second order steadily increases

Full size image

The final SRG height is again 3 nm and its period 325 nm. With 1 μm period of the IP, one gets a topography with a height of 15–20 nm after 30 min of irradiation. Changing the IP period to 2 μm allows to record also the second-order DE (Fig. 3d). Here, the SRG period is 1 μm and the height is 50 nm after 30 min irradiation. At the IP of 3 μm, one gets an efficient topographic deformation: after 30 min of irradiation, the SRG height is 85 nm with a period of 1.5 μm. The intensity of the second-order diffraction spot overcomes that of the first order after 15 min of irradiation. We conclude that the SRG development is more efficient for larger periods of the IP and that the optical probing method, i.e., the DE signal is unable to detect small periods of the SRG due to the diffraction limit. These gratings can only be probed with the AFM.

3.3 Topography response at slight polarization mismatch

Under irradiation with the SP-IP, the topographic response strongly depends on the exact alignment of the interfering beams. Figure 4 shows in situ recorded AFM micrographs and DE for different angles between the polarizations of the two beams (\( {{\varLambda }} = 2\;\upmu {\text{m}} \)). In Fig. 4a, the SP-IP is well aligned, so that the SRG shows a half-period grating of constant amplitude. Rotating the polarization of the S-polarized beam by only 1° results in asymmetric peaks of the SRG: its period doubles and now coincides with the optical one (Fig. 4b). The height of the surface grating after 30 min of irradiation is not affected by this change in the PIP. Like in the case of a perfect aligned SP-IP, the first-order DE is still cross-(S-) polarized (blue curve in Fig. 4, left column, the probe beam is P-polarized), but shows also a slowly increasing co-(P)-polarized component (red curve in Fig. 4, left column). This is to be expected, since now also the topographic relief (which diffracts in the polarization-preserving channel) shows a periodic structure at the optical period \( {{\varLambda }} \). Further rotation of the S-polarized beam by 6° causes a further decrease in the amplitude of the half-period relief, while the final SRG height of the grating with period \( {{\varLambda }} \) increases to 75 nm (Fig. 4c). The recorded DE now shows a strong increase of the co-(P)-polarized component which matches with the increase of the second-order DE, while there is no change in the cross-(S-) polarized component. For an + 20°:P-IP, the DE is mainly determined by the co-(P)-polarized component (Fig. 4d). The cross-(S-) polarized component shows the same behavior as for the other IP, but the absolute value is now decreased similar to the second-order DE (green curve in Fig. 4). This can be explained by inspection of the surface profile, which now looks similar to a blazed grating (sawtooth profile in Fig. 5d). The SRG height now is 130 nm after 30 min of irradiation. Further rotation in the polarization angle forms the + 45°:P-IP. Here, the blazed structure vanishes and a smooth sinusoidal surface profile is recorded with period equal to the optical one (Fig. 4e). The co-(P)-polarized component of the 1st order DE increases very fast until it starts to drop at the SRG height of 100 nm, as expected from the Raman–Nath theory that predicts a first-order Bessel function [32]. The final SRG height is 190 nm after 30 min of irradiation. The second-order DE continuously increases and reaches a final value of one percent.

Fig. 4
figure 4

AFM micrographs (left column) and changes in topography and DE (right) for the transition from SP to PP-IP. The insets in AFM micrographs show a computed map of the IP intensity and polarization. The shading in the inserts indicate the intensity modulation: blue—low; yellow/red—high intensity. a SP configuration: the PIP is well aligned; the SRG is sinusoidal with \( {{\varLambda }}/2 \) period. On the right, the in situ recorded first [in blue the cross-(S-) and red the co-(P-) polarized component] and second-order DE (green) are shown. The gray rectangle marks the irradiation time. b Rotating the S-polarization by only 1° results in an asymmetric relief grating with period of \( {{\varLambda }} \). The growth kinetics is unaffected. c The polarization is further rotated by 6° showing a stronger growth in SRG amplitude. The co-polarized first-order DE grows to the same level as the cross-polarized one. d In the 20°:P-IP configuration, the half-period grating is nearly completely degraded. The co-polarized first order is now dominant. In Fig. 5d, the corresponding “sawtooth” cross-section is shown. e The 45°:P-IP generates a nearly sinusoidal surface grating with the nominal period \( {{\varLambda }} \). f For the PP-IP, a sinusoidal surface profile of period \( {{\varLambda }} = 2\;{\upmu}\text{m} \) emerges

Full size image
Fig. 5
figure 5

SRG profile (black dots and line), the intensity (light blue line), the helicity (light brown line, see text for its definition), and the polarization (blue lines and ellipses) as a function of position for the same sequence of IPs as in Fig. 4: a SP, b 1:P, c 6:P, d 20:P, e 45:P, and f PP. The surface profiles (black dots) are taken from Fig. 4 after 150 s of illumination with optical period \( {{\varLambda }} = 2\;\upmu {\text{m}} \). The black solid lines are fits with two harmonics (periods \( {{\varLambda }} \) and \( {{\varLambda }}/2 \))

Full size image

In the case of the P:P-IP, there is a sinusoidal surface profile whose period matches the optical one (Fig. 4f). The first-order DE is now purely co-(P)-polarized, indicating that also the SRG component contributes to the signal. The SRG shows a fast kinetic, i.e., within the first 150 s of irradiation, it has reached an amplitude of 100 nm. At this height, there is again a drop in the DE when passing through the maximum of the Bessel function. [33] After 30 min of irradiation, the SRG amplitude has reached 210 nm. The second-order DE develops to the same absolute value as in the case of the + 45: P-IP, but shows a faster kinetic at the beginning.

The transition from the SP- to the PP-IP thus converts the first-order DE from pure cross-(S-) to purely co-(P)-polarization. In the case of the SP-IP, the first-order DE contains only the birefringence grating, as can be seen from its pure cross-polarization due to the ± 45° orientation of the azo-chromophores in the bulk. For the PP-IP, the half-period structure is degraded, so that the first-order DE now also carries the SRG signal.

Figure 5 shows the surface profile (black dots and line) for the same sequence of IPs [(a) SP, (b) + 1:P, (c) + 6:P, (d) + 20:P, (e) + 45:P, and (f) PP-IP] after 150 s of illumination, together with the local intensity distribution (blue line) and the helicity (brown line). The blue ellipses and lines in the center illustrate the local polarization. The helicity is computed according to \( \left| {\text{Im} \left( {E^{*} \times E} \right)} \right| \), it coincides with the intensity \( \left| E \right|^{2} \) for a purely circular polarization and vanishes for a linearly polarized field. The calculation takes into account the three-dimensional field which is tilted out of the film plane because of the finite angle of incidence ϑ in Scheme 1.

In the case of the SP-IP, there is no intensity modulation and the SRG minimum appears at a local maximum of the helicity. The intensity modulation increases when the polarization of the S-polarized beam is rotated towards the P-polarization (Fig. 5b, c), although the local polarization is only slightly changing. The impact on the surface profile indicates the interplay between two processes: on one hand, the photo-orientation due to the local polarization gradients and the intensity modulation. On the other, the additional intensity modulation first reduces the amplitude of the half-period component of the SRG and, finally, suppresses it. For the PP-IP, the polarization is keeping a fixed direction and only intensity gradients occur, which results in a grating with period \( {{\varLambda }} \).

Concluding this part, we can state that when the polarizations between the two interfering beams are well adjusted, one gets a symmetric, sinusoidal SRG with period \( {{\varLambda }}/2, \), i.e., half the optical one. Changing the angle slightly results in an asymmetric SRG with harmonics at both \( {{\varLambda }} \) and \( {{\varLambda }}/2. \)

The change in polarization described above can also be applied during the irradiation, and its consequences studied in real time. This provides a way to ascertain the position of the optical polarization pattern relative to the surface relief. We used the results obtained here for the polarization pattern sketched in the previous figures. Figure 6a shows the in situ recorded AFM micrographs for a direct switching from the SP-PIP to the PP-IIP and to a PP-IIP with a π phase shift (out-of-phase or \( {\bar{\text{P}}\text{P}} \), similar to Fig. 2, although with a different technique, see below). The irradiation with the SP-PIP is applied between the dashed lines 1 and 2. The topography shows a half-period grating and the SRG amplitude is continuously increasing. After a dark period of 2 min follows an exposure (between lines 3 and 4) with the PP-IIP (see arrows in Fig. 6a for the polarization pattern). This switch in IP results in the vanishing of the half-period grating. The irradiation with a PP out-of-phase pattern (\( {\bar{\text{P}}\text{P}} \)) is resumed between lines 5 and 6. Here, the polarization of one of the beams is rotated by 180° resulting in a shift of the IIP by half a period, i.e., the intensity minima and maxima swap their positions (see white arrows). Responding to the IP shift, the SRG maxima are drifting over 1 µm to adjust their positions to the low-intensity region.

Fig. 6
figure 6

AFM micrograph (a) and kinetics of the DE (b) when switching from SP-PIP to PP-IIP (all other parameters as in Fig. 1). AFM scanning is from top to bottom (red arrow). Between the dashed lines 1 and 2, the irradiation with SP-PIP is switched on (local distribution of polarization is indicated by white arrows). The topography responds with a half-period grating (\( {{\varLambda }}/2 = 1\;{\upmu}\text{m} \)). Between the lines 3 and 4, the sample is irradiated with PP-IIP, which makes one SRG maximum out of two. Between lines 5 and 6, an PP out-of-phase (\( {\bar{\text{P}}\text{P}} \)) pattern is applied (the polarization of one beam is rotated by 180°). This results in a drift of the SRG maxima by half a period. b Kinetics of the first-order DE: cross-(S)-polarized component in blue and co-(P)-polarized component in red; the gray rectangles mark the irradiation periods. c SRG profile recorded at lines marked by α–γ (see Fig. 6a) after irradiation with SP- or PP-IIP, respectively

Full size image

We thus demonstrate that the local erasure of one of the topographic maxima inscribed during exposure to SP-IP can be selectively controlled by the change to the PP- or \( {\bar{\text{P}}\text{P}} \)-IP. In addition, one can now assign the topography maxima under SP-IP to the regions of linear polarization as follows: it is well known from other experiments that in the PP-IIP, the minimum appears “in the bright” where the intensity is maximal (see dashed red line in Fig. 6a) [34, 35]. This corresponds to a constructive interference of the two beams. The polarization rotation is performed in such a way (rotating half-wave plates) that no additional phase shifts appear. Hence, at this position, also the S- and P-polarized beams interfere constructively, leading to a linear polarization. Indeed, at this position, an SRG maximum under the SP-PIP has developed (and is suppressed when we switch to the PP-IIP).

The kinetics of the probe beam diffraction (P-polarized) is shown in Fig. 6b when switching the irradiation pattern. Similar to Fig. 4, the polarization state of the first-order changes from purely cross-(S)-polarized (PIP) to mostly co-(P)-polarized (IIP). The switch from PP to \( {\bar{\text{P}}\text{P}} \) forces the azobenzene molecules to re-orient, as manifested in a first drastic drop in the co-(P)-polarized component of the first order, followed by its recovery as the irradiation continues. This drop corresponds with a decrease of the SRG height and a slow drift of the relief by half a period of the IP. When the re-orientation of the azobenzene molecules is completed, the SRG height and DE signal increases again. The first-order DE now contains contributions from both topography and birefringence gratings and, thus, shows continuous increase till the light is switched off (line no. 6).

The results of these changes in polarization are even more striking when we repeat the experiment with a switch from the SP- to the ± 45°-IP. Both are polarization interference patterns and only differ by a local polarization rotation by 45°. The data in Fig. 7 show again the disappearance of the half-period grating. This time, the SRG minimum develops at the position where the local electric field vector is P-polarized (destructive interference, i.e., taking the difference between + 45° and − 45° polarized fields). At this position in the SP-PIP, a linear polarization prevails and has formed an SRG maximum. The change to a ± 45° out-of-phase grating (± 45π, by rotating the polarization of one beam by 180°) is again shifting the SRG by \( {{\varLambda }}/2 \) and corresponds to a rotation of the linearly polarized components by 90° and the conversion from left- to right-handed circular polarization. As in Fig. 6b, the first-order DE rapidly changes from pure cross-(S)-polarization to co-(P)-polarization, as soon as the PIP is switched from SP to ± 45°. The change to the ± 45π-PIP (locally S- and P-polarized regions are swapped) results in a fast decrease of the DE which recovers somewhat faster (compare to Fig. 6b). Here, the SRG does not drift to its new position, but the “old” hills are flattened “in place”. If we switch from ± 45° to the ∓ 45°-PIP (by rotating the polarization of both beams by 90°), no effect is seen in the SRG and birefringence grating. This switch just flips the helicity of the circularly polarized regions (between left- to right-handed, see Fig. S3). From this observation, one may conclude that the irradiated polymer does not show any circular dichroism nor optical activity.

Fig. 7
figure 7

AFM micrograph (a) and DE kinetics (b) when switching the irradiation between two polarization interference patterns: SP-PIP to ± 45°-PIP (all other parameters as in Fig. 6, \( {{\varLambda }} = 2\;{\upmu}\text{m} \)). a In the AFM scan, the SP irradiation is applied between the dashed lines 1 and 2. The topography responds with a half-period grating (\( {{\varLambda }}/2 = 1\;{\upmu}\text{m} \), the local distribution of the polarization is indicated by white arrows). Between lines 3 and 4, the sample is irradiated with ± 45°-PIP. Between lines 5 and 6, irradiation with ± 45° out-of-phase configuration (± 45π) is applied. b Kinetics of the first-order DE: cross-polarized component (S, blue curve) and co-polarized component (P, red curve) as a function of time; gray rectangles mark the irradiation. c SRG profile recorded at lines marked by α–γ after irradiation with the SP- and ± 45°-PIPs

Full size image

4 Conclusions

We have studied the formation of two gratings, SRG and BBG, within photo-sensitive polymer films under exposure to light of spatially modulated intensity and polarization, i.e., interference patterns (IPs). For this, we combine two-beam interference equipment with diffraction efficiency measurements and AFM. Special attention is paid to the SP-IP, where the response of topography differs from all other types of IPs, i.e., the SRG has half the optical period, while the BBG has the same period as IP. By simultaneously recording the topographical and DE signals, we understood how the topography variations correlate with the local distribution of the electrical field vector. We find that the SRG maximum appears at the positions of linearly polarized light, oriented at ± 45° relative to the grating vector, which occurs twice per one period. This results in the formation of the half-period topography. Moreover, we demonstrate that a symmetric SRG can be inscribed by SP-IP, but only slight changes in the alignment of one of the interferes result in a blazed grating with a sawtooth profile and a period equal to the optical one.