Solving an old puzzle: fine structure of diffraction spots from an azo-polymer surface relief grating

Abstract

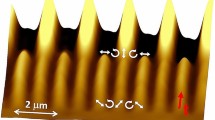
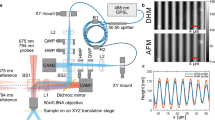
We report on the experimental and theoretical interpretation of the diffraction of a probe beam during inscription of a surface relief grating with an interference pattern into a photo-responsive polymer film. For this, we developed a set-up allowing for the simultaneous recording of the diffraction efficiency (DE), the fine structure of the diffraction spot and the topographical changes, in situ and in real time while the film is irradiated. The time dependence of the DE, as the surface relief deepens, follows a Bessel function exhibiting maxima and minima. The size of the probe beam relative to the inscribed grating (i.e., to the size of the writing beams) matters and has to be considered for the interpretation of the DE signal. It is also at the origin of a fine structure within the diffraction spot where ring-shaped features appear once an irradiation time corresponding to the first maximum of the DE has been exceeded.

Graphic abstract

Appendix

We get a tractable calculation of the diffraction efficiency and the spot profile, when the sample is modeled as a reflecting phase screen. This means that the light wave, after (partial) reflection from the sample, is given by a complex reflection function that contains a spatially modulated phase [39]

$$\psi_{\text{out}} \left( \varvec{r} \right) = R { \exp }\left[ {i\varphi \left( {x,y} \right)} \right] \psi_{\text{in}} \left( \varvec{r} \right)$$

(3)

where $R$ is the overall reflection amplitude and $x, y$ are coordinates parallel to the screen [we write $R \psi_{\text{in}} \left( \varvec{r} \right)$ although this wave has actually a reversed propagation direction due to reflection from the non-modulated screen (specular order)]. We first compute the diffraction pattern in the far field: it is given in the Fraunhofer–Kirchhoff approximation, by

$$I\left( \varvec{q} \right) = \left| {\tilde{\psi }_{\text{out}} \left( \varvec{q} \right)} \right|^{2}$$

(4)

where $\tilde{\psi }_{\text{out}} \left( \varvec{q} \right)$ is the the 2D Fourier transform of $\psi_{\text{out}} \left( \varvec{r} \right)$. We consider first the simple case of an infinitely extended phase grating where $\varphi \left( {x, y} \right) = u { \sin }\left( {\varvec{G} \cdot \varvec{r}} \right)$ and $\varvec{G}$ is the grating vector. Then, the outgoing wave is

$$\psi_{\text{out}} \left( \varvec{r} \right) = R { \exp }\left[ {iu\sin \left( {\varvec{G} \cdot \varvec{r}} \right)} \right] \psi_{\text{in}} \left( \varvec{r} \right)$$

(5)

The first factor (the phase modulation) is periodic in $\varvec{r}$ along the direction $\varvec{G}$ with period $\varLambda = 2\pi /G$. It can be expanded in a Fourier series

$${ \exp }\left[ {iu\sin \left( {\varvec{G} \cdot \varvec{r}} \right)} \right] = \mathop \sum \limits_{n} J_{n} \left( u \right){ \exp }\left( {in\varvec{G} \cdot \varvec{r}} \right)$$

(6)

with coefficients $J_{n} \left( u \right)$ given by Bessel functions (Jacobi-Anger expansion). If the incoming wave is a plane wave, $\psi_{\text{in}} \left( \varvec{r} \right) = \sqrt {I_{\text{in}} } { \exp }\left( {i\varvec{k}_{\text{in}} \cdot \varvec{r}} \right)$, the outgoing wave contains the wave vectors

$$\varvec{k}_{n} = \varvec{k}_{0} + n\varvec{G}$$

(7)

We may choose the $x$-axis along $\varvec{G}$ and introduce the diffraction angle $\theta_{n}$ via $k_{nx} = k\sin \theta_{n}$ with the wavenumber $k = 2\pi /\lambda$. The discrete diffraction orders appear under the angles (Bragg–Laue condition)

$$\sin \theta_{n} - \sin \theta_{0} = \frac{nG\lambda }{2\pi }$$

(8)

where $\lambda$ is the wavelength of the wave. For an infinite grating, the diffraction efficiencies are thus given by the squared coefficients in Eq. (6):

$$\eta_{n} = \frac{{I_{n} }}{{I_{\text{in}} }} = \left| R \right|^{2} \left| {J_{n } \left( u \right)} \right|^{2}$$

(9)

In the experiment, the grating does not have a constant modulation amplitude u, but rather a circular shape set by the profile of the writing beams. We assume here a Gaussian grating profile

$$\varphi \left( {x, y} \right) = u\left( \rho \right)\sin Gx\quad u\left( \rho \right) = u e^{{ - \rho^{2} /2w^{2} }}$$

(10)

with $\rho^{2} = x^{2} + y^{2}$. The width $w$ is much larger than the grating period $\varLambda$. This motivates an approximate evaluation of the Fourier transform $\tilde{\psi }_{\text{out}} \left( \varvec{q} \right)$ (the far field)

$$\tilde{\psi }_{\text{out}} \left( \varvec{q} \right) = R\sqrt {I_{\text{in}} } \int {\text{d}}x\;{\text{d}}y\;{\text{e}}^{{iu\left(\varvec{\rho}\right)\sin Gx}} {\text{exp}}\left[ {i\left( {\varvec{k}_{\text{in}} - \varvec{q}} \right) \cdot \varvec{r}} \right]$$

(11)

that we explain in the following. We split the integral along x into periods of size $\varLambda$ centered in $x_{l} = l\varLambda$ and replace $x \to x_{l} + x$ with $- \varLambda /2 \le x \le \varLambda /2$ and $l = 0, \pm 1, \pm 2, \cdots$. We also focus on a far-field direction close to the n’th order and set $q_{x} = k_{{{\text{in}} x}} + nG + \delta q$ with $\delta q \ll G$ (angular fine structure of the diffraction spot). Observe that $\left( {q_{x} - k_{{{\text{in}} x}} } \right)\left( {x_{l} + x} \right) \equiv \delta q x_{l} + \left( {nG + \delta q} \right)x$ mod 2π. We apply a multiple-scale approximation and assume that the grating modulation $u\left( \rho \right)$ varies slowly across the grating period $\varLambda$. This means that we can set

$$u\left( \rho \right) \approx u\left( {\rho_{l} } \right),\quad \rho_{l}^{2} = x_{l}^{2} + y^{2}$$

(12)

The integral along x over one grating period then gives

$$\mathop \int \limits_{ - \varLambda /2}^{\varLambda /2} {\text{d}}x e^{{iu\left( {\rho_{l} } \right)\sin Gx}} { \exp }\left[ { - i\left( {nG + \delta q} \right)x} \right] \approx \varLambda J_{n} \left( {u\left( {\rho_{l} } \right)} \right)$$

(13)

where a small phase $\left( {\left| {x \delta q} \right| \le \varLambda \delta q} \right)$ was neglected. (This will be justified from the end result Eq. (15) below.) The sum over the grating periods is replaced back by an integral

$$\begin{aligned} \tilde{\psi }_{\text{out}} \left( \varvec{q} \right) & \approx R\sqrt {I_{\text{in}} } \mathop \sum \limits_{l} \varLambda \int {\text{d}}y\;J_{n} \left( {u\left( {\rho_{l} } \right)} \right) e^{{ - i\delta \varvec{q} \cdot \varvec{r}_{l} }} \\ & \approx R\sqrt {I_{\text{in}} } \int d^{2} r\;J_{n} \left( {u\left( \rho \right)} \right) e^{{ - i\delta \varvec{q} \cdot \varvec{r}}} \\ \end{aligned}$$

(14)

This is the key result of the calculation: the shape of the diffracted beam (as measured by the angular deviation $\delta q$ from the n’th order) is the Fourier transform of the local diffraction amplitude (the Bessel function $J_{n} \left( {u\left( \rho \right)} \right)$).

We finally compute the near-field profile of the diffraction spot. It is easy to read off the back Fourier transform from Eq. (14). We get for the beam shape in the n’th order:

$$\psi_{n} \left( \varvec{r} \right) = R\sqrt {I_{\text{in}} } J_{n} \left( {u\left( \rho \right)} \right)$$

(15)

This proves Eq. (1) in the main text.

To evaluate Eq. (14), one simplification is possible by switching to polar coordinates: ${ \exp }\left( { - i\delta \varvec{q} \cdot \varvec{r}} \right) = { \exp }\left( { - i\rho \delta q\cos \phi } \right)$. The $\phi$ integral gives $2\pi J_{0} \left( {\rho \delta q} \right)$, and we finally get

$$\tilde{\psi }_{\text{out}} \left( \varvec{q} \right) \approx 2\pi R\sqrt {I_{\text{in}} } \mathop \int \limits_{0}^{\infty } \rho d\rho J_{n} \left( {u e^{{ - \rho^{2} /2w^{2} }} } \right) J_{0} \left( {\rho \delta q} \right)$$

(16)

For large $\rho \gg w$, the Bessel function $J_{n}$ becomes proportional to $e^{{ - n\rho^{2} /2w^{2} }}$ so that the integral converges for $n > 0$. Its numerical evaluation presents no difficulties. We can estimate its typical width as a function of the scattering wave vector as $\delta q\sim 1/w$. Since we assumed a scale $w$ for the grating profile much wider than the period $\varLambda$, the phase neglected in Eq. (13) is at most ${\mathcal{O}}\left( {\varLambda /w} \right) \ll 1$.

Finally, we consider the case that incident and specular beams have a Gaussian profile

$$\psi_{\text{in}} \left( \varvec{r} \right) = R\sqrt {I_{\text{in}} } e^{{i\varvec{k}_{\text{in}} \cdot \varvec{r}}} { \exp }\left( { - \rho^{2} /2\sigma^{2} } \right)$$

(17)

We assume that the waist of the probe beam $\sigma$ is also larger than the grating period. The preceding calculation can be carried through, and we get Eq. (16) with an additional factor ${ \exp }\left( { - \rho^{2} /2\sigma^{2} } \right)$ under the integral. The predictions of this theory are illustrated in Fig. 3. The angular profile of the diffraction spot is shown in Fig. 3a, assuming that the probe beam is matched in size to the grating covered area ($\sigma = w$). As the grating amplitude grows (from bottom to top), a “dark ring” enters the spot profile (top curves). This happens when the total diffracted intensity is beyond its maximum, as shown in Fig. 3b (dots on the red curve). There, we also show the influence of the probe beam size: a narrow beam ($\sigma = w/2$) diffracts similar to an infinite grating, with an efficiency related to the Bessel function $\left| {J_{1} \left( u \right)} \right|^{2}$ that oscillates beyond the maximum efficiency. For a much wider beam ($\sigma \gg w$), the diffraction efficiency increases monotonously. An analytical proof of this property is given in the Supporting Information.