Abstract
We report on the design, fabrication, and performance of dual-wavelength distributed-feedback (DFB) quantum cascade lasers (QCLs) emitting at several wavelengths in the mid-infrared (mid-IR) spectrum. In this work, two new designs are presented: for the first one, called “Neighbour” DFB, two single-mode DFB QCLs are fabricated next to each other, with minimal lateral distance, to allow efficient beam-coupling into multi-pass gas cells. In addition, the minimal distance allows either laser to be used as an integrated heater for the other, allowing to extend the tuning range of its neighbour without any electrical cross-talk. For the second design, the Vernier effect was used to realize a switchable DFB laser, with two target wavelengths which are distant by about 300 cm\(^{-1}\). These devices are promising laser sources for Tunable Diode Laser Absorption Spectroscopy applications targeting simultaneous detection of multiple gasses, with distant spectral features, in compact and mobile setups.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Quantum cascade lasers are unipolar semiconductor devices, based on intersubband transitions, emitting in the mid-IR and THz parts of the electromagnetic spectrum [1, 2]. They offer excellent tailoring of their spectral gain by band structure engineering of the active region, as well as by stacking cascades of different gain profiles [3, 4]. In addition, they offer the possibility of precise mode control via distributed-feedback (DFB) and distributed-Bragg reflector (DBR) gratings [5,6,7]. Their performance in the mid-IR range, in which one can access the fundamental ro-vibrational transitions of many pollutant and greenhouse gas molecules, makes them the preferred choice for laser-based trace gas sensing applications [8,9,10].
To realize broadband spectral coverage, QCL sources with an active region gain that covers a wide spectral range with equilibrated intensity [3, 4, 11] are required, as well as a mode control scheme that allows wavelength selection and tunability over this whole spectral gain. Several approaches that have been realized can be categorized in three main types: (1) external-cavity QCLs (EC-QCLs), where the emission mode is controlled by elaborated mechanical tuning optics [4, 12, 13], (2) multi-wavelength QCL arrays consisting of narrowband mode selectors that are electrically switched [5, 14, 15], and (3) broadband frequency-comb QCLs, used in more sophisticated schemes such as dual-comb spectroscopy [16, 17].
External-cavity QCLs offer an extended tuning range, and a broad selection of wavelengths, thus allowing for optical setups which can be less complex because of the limited number of beams needed to be combined through the interaction volume. However, the mechanically controlled frequency tuning rate of these laser sources, which is in the range of 0.1–25 cm\(^{-1}\)/ms for state-of-the-art commercial devices [13], and <1000 cm\(^{-1}\)/ms for the fastest one based on acousto-optic modulators [18], imposes limitations to measurement sensitivity.
Multi-wavelength QCL arrays are monolithic devices that offer a number of DFBs over a wide spectral range, with fast electrical switching capability. Despite the research efforts to realize those sources with either surface-emitting QCL arrays [15], master-oscillator power-amplifier QCL arrays [19], or monolithically beam-combined QCL arrays [20], these approaches still suffer from practical limitations such as beam combination difficulties, lack of precise frequency control, low efficiency or widely spread performance efficiency over the optical bandwidth of the array. Monolithic beam combination was tried with either second-order DFB gratings to a single waveguide [15, 21] or with combination of Y-couplers and funnel couplers [20]. However, the performance uniformity over the target optical bandwidth has remained limited.
An alternative, straightforward approach is to select specific regions of interest in the mid-IR spectrum and probe them with a few multi-wavelength lasers [22]. In this work, we propose and discuss the realization of three different designs of dual-wavelength DFB quantum cascade lasers, as sources for a multi-species trace gas sensor. Each device covers one of the following spectral regions: (1) 4.25 and 4.55 \({\mu }\)m (2353 and 2198 cm\(^{-1}\)) [23], (2) 5.26 and 6.25 \({\mu }\)m (1900 and 1600 cm\(^{-1}\)), and (3) 7.4 and 9.5 \({\mu }\)m (1352 and 1053 cm\(^{-1}\)). These spectral regions were chosen to measure 10 of the most important pollutant and greenhouse gases (NH\(_3\), O\(_3\), NO, NO\(_2\), CO, N\(_2\)O, H\(_2\)O, CH\(_4\) and CO\(_2\)[\(^{12}\)C and \(^{13}\)C]) at their strong absorption lines. By reducing the number of lasers needed for all desired wavelength regions by factor of two, we simplify significantly the complexity of combination optics needed to guide the beams through the same interaction volume and onto the detector. Several of these devices are already employed in a spectrometer for trace-gas sensing: the spectroscopic technique, as well as the results of the measurements obtained for eight gases with the newly designed system are presented in more detail in a separate publication by Hundt et al. in this issue [24].
One of the above designs of dual-wavelength QCLs was demonstrated in the work of Jágerská et al. [25] for NO and NO\(_2\) detection, reaching sub-ppb detection limits, and of Süess et al. [23], where successful measurements of the gases CO\(_2\), CO and NO\(_2\) were reported, using devices realized in a dual-section (front and back) configuration, lasing independently at 4.25 and 4.55 \({\mu }\)m. However, these devices suffered from inherent to the design problems, such as mode hopping and output power modulations, caused by interference of the DFB mode of the active laser section with the Fabry–Perot (FP) modes of the inactive section. These limitations could be strongly reduced with anti-reflection (AR) coatings applied on the facets of the devices [23]. Here, two new approaches are presented that can overcome these problems: one where the laser ridges are fabricated very close next to each other side-by-side (Neighbours) and one that makes use of the Vernier effect. Both designs allow for simplified beam combination schemes, and extensive tuning over resonances that are spectrally distant by a few hundred cm\(^{-1}\) through the design of the active region gain and mode-selection mechanism.
2 Neighbour (side-by-side) dual-wavelength DFB QCLs emitting at 7.4 and 9.5 \(\mu\)m (1352 and 1053 cm\(^{-1}\))
Starting from the dual-section DFB QCLs [23], a simple approach to overcome the inherent problems of these devices was to design the two-section device with sections next to each other, instead of front and back. This alternative design, thereafter referred to as “Neighbour” DFB (NDFB), is comprised of two laser ridges which are very close to each other, in the order of a few tens of micrometres, i.e 20 to 35 \({\mu }\)m, but each having different, single wavelength DFB gratings, aimed at different resonances, which in this case are about 300 cm\(^{-1}\) apart. The DFB QCLs are electrically separated to allow independent operation. A concept schematic can be found in Fig. 1a. The advantage of this design is the proximity of the two ridges, that allows to use each as an integrated heater to the other, as long as the bias current is below the lasing threshold. Thus, it is possible to extend the tuning range of each DFB laser of the device. Finally, it is possible to design optics in a setup, nearly as it would be the case for a single-wavelength DFB device, as one can efficiently couple the two beams into multi-pass gas cells, as shown by Hundt et al. [22, 24].
a Device concept schematic of a Neighbour DFB QCL. b The etched gratings of a NDFB on top of the InGaAs layer covering the active region. Notice the different periodicities of the corrugations, corresponding to different target emission wavelength. c SEM image of the front facet of a Neighbour DFB QCL pair, with centre-to-centre distance of the laser ridges of 30 \({\mu }\)m. Green colour indicates the insulating InP:Fe cladding layer. d LIV characteristics of the left and right laser of the same NDFB pair, at 1% duty cycle for 100-ns long pulses for substrate temperatures of −20, 0, and 20 \(^{\circ }\)C. Width of both ridges is 5 \({\mu }\)m and length is 2.5 mm. The left laser has the DFB aimed at 1352 cm\(^{-1}\) and the right laser at 1053 cm\(^{-1}\). The device is HR-coated. e and f Tuning of the emission mode frequency for the left and right DFB, respectively, over long pulses of 50 \({\mu }\)s applied with a period of 200 \({\mu }\)s, as a function of time delay over the pulse and for three different values of the CW bias current applied on the neighbouring laser. Substrate temperature is \(-20 ^{\circ }\)C
2.1 Device fabrication
The NDFB QCLs are fabricated following an inverted buried hetero-structure protocol [26, 27]. The active region is grown by means of Molecular Beam Epitaxy (MBE) on a low-doped (1.3\(\times 10^{17}\) cm\(^{-3}\)) InP:Si substrate, and consists of a heterogeneous quantum cascade stack of three bound-to-continuum active regions, covering two different wavelengths. The first stack consists of 16 In\(_{0.584}\)Ga\(_{0.416}\)As and In\(_{0.335}\)Al\(_{0.665}\)As period layers in the following sequence 54.0/ 10.8/ 41.4\(^{1.17}\)/ 11.0\(^{0.69}\)/ 39.8\(^{1.17}\)/ 12.0/ 35.9/ 16.3/ 38.9/ 31.0/ 32.0/ 10.2/ 67.6/ 5.0/ 56.3/ 7.7 optimized for emission at 9.5 \({\mu }\)m, followed by 20 periods of In\(_{0.595}\)Ga\(_{0.405}\)As and In\(_{0.36}\)Al\(_{0.64}\)As with a sequence of 44.9/ 12.7/ 37.9\(^{1.32}\)/ 12.9\(^{0.81}\) / 32.3\(^{1.32}\)/ 16.0/ 28.9/ 18.9/ 30.1/ 31.0/ 25.2/ 12.3/ 57.7/ 7.4/ 50.1/ 10.1, optimized for emission at 7.4 \({\mu }\)m, followed by additionally 16 periods of the same stack of 9.5 \({\mu }\)m. The layer thickness (in Å) of each InAlAs barrier in the period is given in bold script, and for each InGaAs quantum well in standard script, while any layers that are Si-doped are underlined, with their doping concentration (10\(^{17}\) cm\(^{-3}\)) given in the superscript. The gain was designed to be balanced for both wavelengths, to not favour lasing of one over the other.
The active region is covered by a 200-nm lattice-matched layer of InGaAs, which is used for defining the neighbouring DFB gratings. Two DFB gratings were etched on top of this layer by means of wet etching, with different grating periodicities, aimed at 1352 cm\(^{-1}\) and 1053 cm\(^{-1}\), with a lateral distance of 20 or 35 \({\mu }\)m between them. In Fig. 1b a microscope image of the DFB etching result is shown. The DFB length was chosen to have \(\kappa\)L<3 for the shorter wavelength of a laser pair for a 3-mm long device, where \(\kappa\) is the coupling constant, given as \(\kappa = \Delta n/(\Lambda \cdot n)\), with \(\Delta n\) the refractive index step at the grating, and \(\Lambda\) the grating periodicity [28].
Afterwards, neighbouring pairs of laser ridges of widths 5–6 \({\mu }\)m and ridge-to-ridge distance of 20 to 35 \({\mu }\)m were wet-etched. Between the laser ridges, and on the vertical side-walls around them, a cladding layer of insulating InP:Fe with roughly the same vertical thickness as the active region was laterally grown by means of Metal-Organic Vapour Phase Epitaxy (MOVPE). In Fig. 1c, see a Scanning Electron Micrograph (SEM) of a device pair front facet, where the insulating layer is highlighted with green). The structure was overgrown with a n-doped cladding by MOVPE consisting of several layers of n-doped InP:Si of (20/ 460/ 40/ 4000/ 500/ 300) nm thickness and doped as (1/ 0.5/ 1/ 0.2/ 1/ 30) \(\times\)10\(^{17}\) cm\(^{-3}\).
To electrically isolate the two lasers ridges of a device from each other, and thus be able to operate them independently, we applied a dry etching technique with inductively-coupled plasma etching (ICP). The result is a narrow trench with straight walls, all the way through the conducting InP:Si layers to the insulating InP:Fe layer. Afterwards, electrical contacts are deposited on each section of the device, effectively forming a pair of lasers, with left and right sections. The wafer is also thinned down to less than 200 \({\mu }\)m (important for efficient heat removal, as the lasers are mounted epilayer-up), with an additional metallization contact layer deposited on the bottom.
Finally, the processed wafer is cleaved into device pairs of 2–3 mm length. They are mounted epilayer-up on Alpes Lasers NS submounts with indium solder. In addition, a two-layer, high-reflectivity (HR) coating was applied on the back facet of these devices, consisting of Al\(_2\)O\(_3\) and Au of thickness (300/150) nm.
a, b Emission mode frequency tuning of the right and left DFB, by varying the device substrate temperature, from −20 to 40 and 60 \(^{\circ }\)C, respectively, recorded with 50-ns long pulses at 0.5% duty cycle. Laser bias current is 620 mA for the right and 850 mA for the left. c, d Emission mode frequency tuning of the right and left DFB varying the injected CW bias current into either neighbour DFB laser. The lasers are operated with 50-ns long pulses, at 0.5 % duty cycle, with the bias current being 680 mA for the right DFB and 630 mA for the left. The substrate temperature is \(-20 ^{\circ }\)C for both. e Spectra, in logarithmic scale, of the emission mode of the right DFB (1053 cm\(^{-1}\)) and left DFB (1352 cm\(^{-1}\)), with red and blue lines, respectively. The current driving conditions are the same as mentioned in parts a and b, with substrate temperature of 0 \(^{\circ }\)C. The selectivity of the emission modes, with a SMSR of >20 dB for both, is shown
2.2 Characterization methods
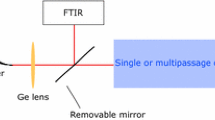
The measurements are performed using Laboratory Laser Housing (LLH) laser boxes (Alpes Lasers SA, Switzerland) (in the actual field-setup, High Heat Load, HHL, and housing boxes are used), that offer temperature control with Peltier elements and dry atmosphere with N\(_2\) purging. The lasers are driven using either a pulse generator (8114A, Agilent Technologies, Inc., USA) or a direct-current source (QCL 2000, Wavelength Electronics, USA). Light–current–voltage curves are recorded using a calibrated photodiode (AN/2 OPH-09, Ophir, Optronics, Israel). Spectral measurements are acquired by Fourier transform infrared spectroscopy (FTIR), with a maximum spectral resolution of 0.075 cm\(^{-1}\) (Vertex 80, Bruker Corp., USA), with the signal acquired by a pyroelectric deuterated triglycine sulphate (DTGS) detector.
The applied method of operation of these lasers in the actual spectroscopic setup is the intermittent continuous-wave (iCW) operation concept [29]. Here, the laser emission wavelength is shifting over a long pulse, during which it can be used to scan over a specific molecular absorption feature. The detector output then can be used to observe sequentially both the reference (baseline) and the absorption signal. To characterize the long pulse performance of the lasers, a boxcar integrator (SR250, Stanford Research Systems, Inc., USA) is used to gate and record the laser signal at specific trigger delay and gate width. The gate width is set at 100 ns and the steps are happening in intervals of 100 ns. The lasers are set to operate at few \({\mu }\)s long pulses with a period of 200 \({\mu }\)s. The signal from the laser is recorded on a mercury–cadmium–telluride (MCT) detector (PVM-2TE-10.6-1x1, Vigo System S.A., Poland), gated by the boxcar integrator, and then again fed back to the FTIR spectrometer through an analogue-to-digital coupler.
2.3 Device performance
The light–voltage–current (LIV) characteristics of a HR-coated device are shown in Fig. 1d, for substrate temperatures of −20, 0, and 20 \(^{\circ }\)C. Here, a pair of 5 \({\mu }\)m wide and 2.5-mm long ridges, laterally separated by 30 \({\mu }\)m, is operated at 1 % duty cycle with 100-ns long pulses. At T= −20 \(^{\circ }\)C, the lasing threshold current is for both quite similar: 320 mA (2.65 kA/cm\(^2\)) for the right DFB emitting at 1053 cm\(^{-1}\) and 350 mA (2.8 kA/cm\(^2\)) for the left DFB, emitting at 1352 cm\(^{-1}\). These similar values for the lasing threshold current indicate that the active region gain is well balanced. The peak power that the lasers of the pair can reach for these driving conditions is 437 mW for the right laser, and 374 for the left one.
The performance of the same device under iCW operation is also assessed. The lasers of the pair are operated with pulses as long as 50 \({\mu }\)s, with a period of 200 \({\mu }\)s, and a substrate temperature of −20\(^{\circ }\)C. The emission mode spectrum is recorded over the whole applied pulse. In addition, the same measurement is repeated for both lasers of the pair, after applying a CW bias of 100 and 200 mA on their Neighbour laser. These current values are well below the lasing threshold of these devices, and the idea is to use the neighbouring device as an integrated heater to extend the tuning range of the operating DFB. In Fig. 1e and f these time-resolved long pulse measurements are shown. The DFB modes of the pair tune continuously and almost mode-hop free over the entire pulse length. The only exception to that is for the right (1053 cm\(^{-1}\)) laser, which mode-hops when pulses longer than 40 \({\mu }\)s are applied to it, and when it’s neighbour DFB is biased with current more than 100 mA. This behaviour could potentially be suppressed to a good extension by applying suitable anti-reflective coatings on the front facets. It is also observed that the applied dissipated power from the neighbouring laser, corresponding to 0.75 and 1.8 W for 100 mA and 200 mA bias currents, respectively, can extend the tuning range of the NDFB QCLs by about 3–4 cm\(^{-1}\), similar to the approach previously reported in Ref. [30].
Figure 2a and b shows the emission mode frequency tuning of both DFBs of the pair, by varying the Peltier substrate temperatures from −20 to 40 and 60\(^{\circ }\)C, for the right and left DFB, respectively, for the same device with the same characteristics as reported before. The devices are driven with 50-ns long pulses, at 0.5% duty cycle, and bias current is 620 mA for the right and 850 mA for the left DFB. Temperature tuning is happening mode-hop free for both DFBs, and from the linear fit we can deduce a tuning coefficient \(\beta = \frac{1}{\lambda }\frac{d\lambda }{dT}\) of \(7.17\times 10^{-5}\) and \(7.01\times 10^{-5}\) \(K^{-1}\) for the DFB lasing at 1352 cm\(^{-1}\) and 1053 cm\(^{-1}\), respectively.
In part (e) of Fig. 2, the spectra in logarithmic scale for both DFBs, at a substrate temperature of 0\(^{\circ }\)C and under the same driving conditions as mentioned before, are shown, to assess the mode selectivity of the two DFBs. A side-mode suppression ratio (SMSR) of >20 dB is reported .
To estimate the thermal resistance \(R_\mathrm{th}\) associated with the heating of the laser active region by the dissipated power P in its neighbour counterpart, we performed the measurement on the power tuning coefficients as shown in Fig. 2c and d. The devices were driven with 50-ns long pulses, at 0.5 % duty cycle, and a substrate temperature of \(-20^{\circ }\)C. Laser bias current was 680 mA for the right DFB and 630 mA for the left. The emission mode spectrum was recorded as a function of the dissipated power of the neighbouring laser. By linear interpolation, we extracted the emission mode tuning rate as a function of the dissipated power, being −11.8 GHz/W for the 1053 cm\(^{-1}\) DFB and −16.6 GHz/W for the 1352 cm\(^{-1}\) DFB) which yield the values of the thermal resistance as \(R_\mathrm{th}\) \(\approx 5.33\) K / W and \(\approx\) 5.69 K / W, respectively. The latter values are smaller than those reported for extended tuning lasers with resistive integrated heaters [30, 31], but here there is the advantage of electrical isolation between the laser and heater sections.
a SEM image of the front facet of a NDFB QCL device, with gratings at 5.26 and 6.25 \({\mu }\)m and a laser ridge-to-ridge separation of 35 \({\mu }\)m. Ridge widths are 7.4 \({\mu }\)m, length 3 mm. b LIV characteristics of the device pair operating at short-pulse of 100 ns with a duty cycle of 1% at a substrate temperature of −20, 0, and 20 \(^{\circ }\)C. Device dimensions are reported in a. c Emission mode spectra of the device pair, being 1600 cm\(^{-1}\) (red) for the left DFB and 1900 cm\(^{-1}\) (blue) for the right. The lasers were driven with 20-ns pulses, at 0.2% duty cycle, with substrate temperature of \(-20 ^{\circ }\)C. The selectivity of emission modes, with SMSR of >22 and 26 dB, is observed
3 Dual-wavelength NDFB QCLs at 5.26 and 6.25 \({\mu }\)m (1900 and 1600 cm\(^{-1}\))
3.1 Device fabrication
A Neighbour DFB QCL design was also realized for the 5.26 and 6.25 \({\mu }\)m wavelengths. Following the same fabrication procedure, as presented in the previous section, we realized good performance devices in these wavelengths as well. The active region is grown on a low-doped (1.3\(\times 10^{17}\) cm\(^{-3}\)) InP:Si substrate, and consists of a heterogeneous quantum cascade stack of two bound-to-continuum active regions, covering two different wavelengths. The first stack consists of 18 In\(_{0.635}\)Ga\(_{0.365}\)As and In\(_{0.335}\)Al\(_{0.665}\)As period layers in the following sequence 38/ 12/ 33/ 13/ 29/ 14/ 26\(^{2.23}\)/ 15\(^{1.23}\)/ 24\(^{2.23}\)/ 16\(^{1.23}\)/ 26/ 23/ 23/ 35/ 15/ 10/ 45/ 10/ 41/ 11 optimized for emission at 5.26 \({\mu }\)m (1900 cm\(^{-1}\)), followed by 21 periods of In\(_{0.635}\)Ga\(_{0.365}\)As and In\(_{0.335}\)Al\(_{0.665}\)As with a sequence of 44/ 11/ 37/ 11/ 36/ 12/ 32\(^{1.95}\)/ 13\(^{1.12}\)/ 29\(^{1.95}\)/ 15\(^{1.12}\)/ 32/ 21/ 27/ 31/ 19/ 9/ 52/ 9/ 48/ 10, optimized for emission at 6.25\({\mu }\)m (1600 cm\(^{-1}\)). The etched gratings were aiming for emission at 1600 and 1900 cm\(^{-1}\), and the ridge-to-ridge separation achieved was from 20 to 35 \({\mu }\)m. Devices with widths 7–8 \({\mu }\)m and 3 mm lengths were mounted epi-up on Alpes Lasers NS submounts. Figure 3a shows the SEM image of the front facet of a NDFB pair, with separation distance of 35 \({\mu }\)m, and ridges width 7 \({\mu }\)m and length 3 mm.
3.2 Device performance
In Fig. 3b the LIV characteristics of the NDFB device of figure part (a) are shown. The device is operated with 100-ns long pulses, at a duty cycle of 1% and a substrate temperature of −20, 0, and 20 \(^{\circ }\)C. At T= \(-20 ^{\circ }\)C, lasing current threshold is 370 mA (1.55 kA/cm\(^2\)) for the right DFB (mode at 1900 cm\(^{-1}\)) and 480 mA (2.01 kA/cm\(^2\)) for the Left DFB (mode at 1600 cm\(^{-1}\)). Peak output power for these driving conditions is 317 mW and 181 mW, respectively. In part (c), in logarithmic scale, the emission mode spectra for the left and right sections are shown, driven by 20-ns pulses, at 0.2 % duty cycle and at a substrate temperature of \(-20 ^{\circ }\)C. These results demonstrate a high SMSR in these as-mounted devices, reaching >22 dB and 26 dB at 1600 cm\(^{-1}\) and 1900 cm\(^{-1}\), respectively.
The device pair was driven in iCW operation mode, with the result shown in Fig. 4a and b. The substrate temperature is \(-20 ^{\circ }\)C and the lasers of the pair are driven by 35-\({\mu }\)s long pulses, with a period of 200 \({\mu }\)s. These devices are tuning continuously and mode-hop free, for wavelengths in this spectral region as well.
To assess the applicability of these devices as sources for other, more simplified laser absorption schemes, where a constant optical output is required, the continuous-wave (CW) operation of the devices is demonstrated. The results are shown in Fig. 5a and b. The substrate temperature in this case is \(-27 ^{\circ }\)C. In Fig. 5a, the LIV characteristics are shown, with a lasing threshold of 293 mA (1.32 kA/cm\(^2\)) for the right DFB (mode at 1900 cm\(^{-1}\)) and 441 mA (1.99 kA/cm\(^{2}\)) for the left DFB (mode at 1600 cm\(^{-1}\)). The maximum output optical power under these conditions is 29.0 and 7.2 mW, respectively. The corresponding emission mode spectra of the pair are reported in Fig. 5b, driven at 570 and 561 mA for the right and left DFB, respectively. The CW operation of NDFBs devices can potentially be improved, and have higher operating temperatures, by reducing the size of the laser ridge or by junction-down mounting.
4 Vernier based dual-wavelength DFB QCLs at 5.26 and 6.25 \({\mu }\)m
Integrated sampled grating reflectors using the Vernier effect were demonstrated to extend the tuning range of the emission wavelength of semiconductor lasers [32, 33]. This approach was successfully applied to QCLs with multiple sections [34,35,36,37]. Although such designs allow the switching from one Vernier channel to the other, since the shift of the DBR stop band and gain are both controlled via bias current in one section of laser, a relatively sophisticated electronic driving scheme is required for continuous tuning that is desired for intermittent operation in TDLAS.
Recently, a different design of a DFB QCL with integrated heaters next to the laser ridge was demonstrated by Bidaux et al. [38]. In this reported design, the n-doped InP cladding layer was partially etched to realize integrated heaters next to the laser ridge, significantly simplifying the electrical driving scheme. By applying CW current to the heaters one can switch the lasing channel, and together with the driving current of the laser, the emission wavelength can be continuously tuned. The heater and laser are not electrically isolated in this structure, but the effect was shown to be marginal on the device performance. This can, however, limit the usage of heater for precise frequency tuning and stabilization of laser.
In this work, we demonstrate a proof-of-principle of an alternative design of a Vernier-based dual-wavelength DFB QCL. The Vernier effect is exploited on a new type of digitized grating, that allows switching between DFB modes that are 300 cm\(^{-1}\) apart. Tuning is thermally induced by two heater sections, (front and back), which are made from wide ridges of the active region, etched in close proximity to the laser ridges. The front and back heater sections are separated by a narrow dry-etched trench that allows efficient tuning as well as electrical separation between them. The active region gain is designed such that it is balanced around the wavelengths of laser emission.
a, b The periodic function with periodicity corresponding to the first-order Bragg reflection condition for each of the two target frequencies, i.e. 1900 and 1600 cm\(^{-1}\) (5.26 and 6.25 \({\mu }\)m), respectively. c Sum of the two analogue periodic functions (blue line) as well as the two-level digitalized profile (orange line). d Microscope image of the photo-lithography result of the grating using standard, contact deep-UV lithography, from a mask with minimum feature size of \(\ge\) 300 nm
4.1 Digital grating design
Here we propose a design of digitalized dual-frequency grating. According to coupled-mode theory, the first-order Bragg reflection condition for light occurs when the wavelength is twice as large as the inverse of the spatial frequency component of the grating (\(k_\mathrm{grating}\)). Similar to sampled grating Vernier QCLs, we design two DFB mirrors for each of the front and back sections of our laser. Each mirror section consists of two reflectivity modes. One of the modes is kept aligned in frequency in both DFB mirrors and the other mode of one mirror is offset in frequency, with respect to the same mode in the other mirror. The mode which will be favoured for lasing is, of course, the aligned one. By tuning the effective refractive index \(n_\mathrm{eff}\) using a heater close to the front section, we can then red shift the reflectivity of the front mirror to now align the offset modes and, therefore, switch the lasing mode. A schematic drawing that illustrates this method is shown in Fig. 7e.
To implement two reflectivity modes on the grating, we combine two periodic functions (see Fig. 6a, b) such that
where \(\Lambda _i= \frac{1}{2. n_\mathrm{eff}. f_i}\) is the grating periodicity to have Bragg reflection condition at frequency \(f_i= \frac{10000}{\lambda _i}\) (frequency \(f_i\) is in cm\(^{-1}\), wavelength \(\lambda\) in \({\mu }\)m). The same function with slight frequency shift of one of the target frequencies is applied to the DFB grating of the other mirror section, i.e.,
where \(\Lambda '_1\) is kept the same as \(\Lambda _1\), and \(\Lambda '_2\) is slightly offset by \(\delta f\) as \(\Lambda '_2=\frac{1}{2\cdot n_\mathrm{eff} \cdot (f_2+\delta f)}\).
The analogue profile resulting from functions f(x) or \(f'(x)\) is very difficult to be fabricated by standard lithography techniques. The grating could be realized by modulating the depth of the grooves, an approach which would be very difficult to implement, or alternatively by applying digitalization on these functions and design a grating with double periodicity of the pitch length instead [39]. Here, the functions f(x) and \(f'(x)\) were digitalized to 0 (for f(x) or \(f'(x)< 0\)) and 1 (for f(x) or \(f'(x)> 0\)) sequences, which correspond to etched and un-etched stripes of the laser ridge InGaAs cladding, with respective effective modal refractive indices \(n_e\) for InP and \(n_u\) for un-etched InGaAs layer (see Fig. 6c).
The features with size < 300 nm were suppressed from the lithography mask to be able to use standard deep-UV contact lithography at 220 nm in our fabrication process. The microscope image of the photo-lithography results of the digitalized grating is shown in Fig. 6d. While for a simple, single-mode DFB the widths \(d_i\) of the stripes with different refractive index are chosen to be \(d_i =\lambda /(4n_i)\), where \(\lambda\) is the vacuum wavelength of interest and, therefore, a fully periodic structure is realized, for the digitalized grating no particular periodicity can be distinguished.
a COMSOL simulation of the heat distribution inside a device, when the front heater is operated. The inset shows the simulation over the whole device. The device geometry is based on the schematic shown in Fig. 9a. b Temperature difference profile along the laser ridge, when front heater is driven at a current density value of: \(J_H=J_\mathrm{th}/2\). The simulation parameters are listed on this panel. c, d Variation of the effective refractive index \(n_\mathrm{eff}\) along the laser ridge for two different driving conditions of the front heater, i.e. \(J_H= 0\) and \(J_H=J_\mathrm{th}/2\), respectively. The red line shows the \(n_\mathrm{eff}\) modulated by \(\Delta n \approx 0.004\) in the front and back of the laser ridge in absence of any heating, while the blue shows the \(n_\mathrm{eff}\) along the laser, when the front heater is driven. e Schematic drawing of the switching in a Vernier DFB QCL. When the grating is aligned to one colour, lasing is favoured there, indicated by the orange square. Applying heat, the grating will shift, and the other colour will eventually be favoured for operation
The resulting grating has the front mirror shifted for one of the wavelengths (here for \(\lambda = 5.26\) \({\mu }\)m or 1900 cm\(^{-1}\)) by an offset \(\delta f= 3\) cm\(^{-1}\) with respect to the back mirror, while for the other wavelength (\(\lambda = 6.25\) \({\mu }\)m or 1600 cm\(^{-1}\)) both mirrors are initially aligned at the same frequency. Thus the losses are minimum for 1600 cm\(^{-1}\), favouring emission through this channel. By applying current through the heater, which in turn will dissipate that electrical power into heat, the reflectivity spectrum of the front mirror will start to red-shift, until the offset \(\delta f\) is compensated. At that point, the initial channel is no longer favoured for lasing, but the other channel instead starts to align and lase. The value of \(\delta f\) was chosen based on COMSOL finite elements simulations (see Fig. 7), such that it can be reached by biasing the front integrated heater of the device to a reasonable value of half the threshold current density \(J_\mathrm{th}/2\). In addition, this value of \(\delta f\) ensures enough contrast in the lasing threshold gain, according to TMM calculations (described below). In our laser design, since one of the modes is aligned in the front section, mode switching can be achieved by heating only the front mirror. Combination of the front and back heater, however, can be used for switching the channel as well as further expanding the tuning range, similarly to what was shown for the NDFB design.
Figure 7a shows the finite element simulation of the heat distribution in the device when the front heater is operated. Figure 7b illustrates the temperature profile along the device, for the parameters used in the fabrication (the centre-to-centre distance of the heater ridge to the laser ridge of 30 \({\mu }\)m, and the top n-contact separation trench width approximately 7 \({\mu }\)m). The heater can cause \(\sim\)20 \(^\circ\)C of temperature difference between the front and back sections of the laser at a heater driving current density of \(J_H=J_\mathrm{th}/2\). The temperature profile along the device \(\Delta T(x)\) is used to calculate the spatial position dependence of the effective refractive index \(n_\mathrm{eff}(\Delta T, x)\) along the device length (x-direction) as:
where T\(_0\)= 0 \(^\circ\)C is the base temperature, and \(\beta\)= 8\(\times 10^{-5}\) \(^{\circ }\)K\(^{-1}\) is the thermal tuning coefficient, in agreement with literature [28, 40]. In parts (c) and (d), the effective refractive indices for the front and back mirrors as function of position along the laser ridge are shown for J\(_H\)= 0 and J\(_H\)= J\(_\mathrm{th}/2\), respectively.
Transfer matrix method (TMM) calculations were performed using \(n_\mathrm{eff}(\Delta T, x)\) for different bias currents of the heater, to predict the transmission spectrum and the lasing threshold gain of the Vernier DFB devices (Fig. 8). The four left panels of Fig. 8 depict the calculation of transmission (blue solid line) and lasing threshold gain (blue stars) of the device when no bias current is applied to any of heaters . As expected in this case, for f= 1600 cm\(^{-1}\) the transmission of both the front and back mirrors is aligned and threshold gain is minimum at this frequency. However, at f= 1900 cm\(^{-1}\) the two reflectivity modes of the front and back mirrors have an offset \(\delta f\)= 3 cm\(^{-1}\) that leads to much higher threshold gain. Therefore, the device is expected to lase only at f= 1600 cm\(^{-1}\) when no heating is applied. When driving the front heater at J\(_H\)= 0.5 J\(_\mathrm{th}\), the stop band of the front mirror red-shifts and, therefore, the minimum of lasing threshold occurs at \(f=1900\) cm\(^{-1}\) for a large enough value of red shift that corresponds to \(\delta f\), as shown in the right panel of Fig. 8.
a Concept design of a Vernier-based dual-wavelength DFB QCL with integrated heaters. b SEM image of the cross-section of a device. On the right side the heater ridge, on the left the laser ridge. Ridge-to-ridge distance is 30 \({\mu }\)m. Separation trench depth is 5 \({\mu }\)m, as deep as the n-contact InP:Si top cladding, (see contrast difference). c LIV characteristics of an AR-coated Vernier DFB QCL with ridge width of 8 \({\mu }\)m and length 3.5 mm, for two different values of the heater bias current, corresponding to lasing at either of the target channels. Substrate temperature is \(-20^{\circ }\)C and the device is driven with 100 ns pulses at 1 % duty cycle. For the CW bias current of 348 mA, the front heater dissipates 3.7 W of power. The blue and pink areas under the L-I curve during front heater operation, correspond to the laser bias current values, where it is single-mode, for less than \(\approx\)1100 mA, or double-mode
In these simulations, perfect anti-reflective coating at the device facets was considered as the boundary condition. In practice, the higher reflectivity at the device facets can strongly diminish the contrast of the gain threshold and, therefore, reduce the mode selectivity of the device.
4.2 Device fabrication
The dual-wavelength Vernier DFB QCLs are fabricated following an inverted buried hetero-structure protocol [26, 27], using the same active region as described in Sect. 3 and the same with procedure and parameters as in Sect. 2. A concept design scheme is illustrated in Fig. 9a, with all the relevant details shown.
The active region is covered by a 200-nm lattice-matched layer of InGaAs, which is used for defining the grating corrugations. The digital Vernier gratings were etched on top of this layer by means of wet-etching, with different grating periodicities, aimed at 1600 and 1900 cm\(^{-1}\). The total DFB QCL length was chosen to be 3.5 or 5 mm.
Afterwards, laser and heater ridges of widths 6–8 \({\mu }\)m and 15 \({\mu }\)m, respectively, are wet-etched. The size of the heater ridges is chosen to be large enough to avoid lasing at the injected current density to the heater. We apply the same dry etching technique as in the case of NDFB QCLs. The resulting narrow trench goes all the way through the conducting InP:Si layers to the insulating InP:Fe layer, electrically separating the laser and heaters sections from each other. An SEM image of a device front facet is shown in Fig. 9b, where the difference in contrast of the InP layers, active regions and trench can be seen. The widths of the trench are chosen to be small enough to have the highest tuning thermal efficiency possible (see simulation in Fig. 7).
Finally, the processed wafer is cleaved into single devices of 3.5 or 5 mm length which are then mounted epilayer-up.
To increase the difference of threshold gain and hence the mode selectivity of Vernier lasers, both facets were coated with AR coatings, consisting of layers of Al\(_2\)O\(_3\)/Ge/Al\(_2\)O\(_3\) of thickness 170/130/1020 nm, which leads to a flat and very low reflectivity spectrum, below 1%, from 1600 to 1900 cm\(^{-1}\).
4.3 Device performance
The LIV characterization of a 3.5-mm long device with 8-\({\mu }\)m wide laser and 16-\({\mu }\)m wide heater ridges, under short-pulse operation is shown in Fig. 9c. The substrate temperature is \(-20 ^\circ\)C, the device is operated with 100-ns long pulses, at 1% duty cycle, and data are recorded for two different CW bias currents on the front heater, 0 and 348 mA, that correspond to lasing at either of target frequencies as shown later in the spectral maps in Fig. 10a and b. Lasing current threshold, when the front heater is not biased, is \(\approx\)620 mA (2.2 kA/cm\(^2\)), while it is around \(\approx\)790 mA (2.8 kA/cm\(^2\)) when the heater is biased with a current of 348 mA (1.2 kA/cm\(^2\)). Respectively, peak output optical power is 166 mW and 152 mW. The coloured areas under the light–current curve when the front heater is operated indicate the laser bias currents under which the device is emitting a single or a double DFB mode. For laser bias currents more than 1100 mA, the DFB mode at 1600 cm\(^{-1}\) can overcome the losses, and lase as well. Below that current value, however, the device remains purely single mode, as it can be seen also in Fig. 10f. Operating under the initially aligned channel, no such behaviour was observed for the device, which remains single mode up to roll-over.
Full DFB mode switching is demonstrated in short-pulse operation mode. The substrate temperature is \(-20 ^\circ\)C, and the device is driven by 30 ns pulses, at a period of 10 \({\mu }\)s and a laser bias current of 1000 mA. The grating is initially aligned to the 1600 cm\(^{-1}\) channel, and by biasing the front heater, the channel starts to detune, with the emission mode dropping in intensity, until at a heater CW bias current of \(\approx\)250 mA or 2.67 W of dissipated power, the grating aligns to 1900 cm\(^{-1}\), as shown in Fig. 10a and b. The second channel becomes fully aligned at a CW bias current of 347 mA or 3.7 W of dissipated power. Parts (c) and (d) of the same figure illustrate the integrated intensity over a window of \(\approx\) 10 cm\(^{-1}\) at each colour, as a function of heater current, extracted from the spectral maps of parts (a) and (b). Figure 10e shows the I–V characteristic of the front heater, which has a width of 16 \({\mu }\)m and a length of 1.75 mm, and is continuous-wave driven at \(-20 ^\circ\)C.
a, b Spectral map of the two channels as a function of the heat CW bias-current. The laser is driven by 30-ns long pulses, at a period of 10 \({\mu }\)s, and a bias current of 1000 mA. Switching starts at a heater bias current of 250 mA, corresponding to 2.67 W of dissipated power and full alignment occurs when heater current bias is 346 mA, or 3.7 W of power are dissipated. c, d Integrated intensity of the two channels, as a function of heat CW bias-current. e Current–voltage characteristics of the device front heater. Heater ridge width is 16 \({\mu }\)m and length is 1.75 mm. Substrate temperature is the same as reported in sections a,b of this figure, and current bias is CW. f Emission mode spectra of the device, in logarithmic scale around the spectral areas of interest, when the front heater is not operated and when it is biased with 347 mA. Driving characteristics, as well as temperature are the same as in parts a,b. The SMSR is 25 dB for the 1600 cm\(^{-1}\) mode and 27 dB for the 1900 cm\(^{-1}\) mode. When the laser is aligned to a specific channel no DFB mode is observed in the other one
In Fig. 10f, the laser emission modes, driven under the same short-pulse conditions as described before, are shown in logarithmic scale, over the two spectral areas of interest and for zero or 347 mA heater bias currents. In both cases, a great SMSR can be distinguished, with 25 dB for the mode when the 1600 cm\(^{-1}\) channel is aligned and 27 dB, when the 1900 cm\(^{-1}\) channel is aligned. At the same time, in both cases, no parasitic DFB mode is observed around the spectral area of the other channel.
In Fig. 11a and c, the iCW-operation results of the same device are shown. The substrate temperature is \(-20 ^\circ\)C, and the laser is driven with 15 \({\mu }\)s pulses, at a period of 200 \({\mu }\)s. When the front heater is not driven, and the device is aligned to the 1600 cm\(^{-1}\) channel, good iCW performance is demonstrated, with the device undergoing mode-hop free tuning over the whole 15 \({\mu }\)s pulse. Spectral purity is also demonstrated in the logarithmic plots of part (b), where the emission mode spectrum is shown for three instances, 4, 7 and 10.4 \({\mu }\)s, of the applied 15 \({\mu }\)s pulse. For the other channel, i.e. 1900 cm\(^{-1}\), however, iCW performance is limited, and the device can only operate under pulses shorter that 1\({\mu }\)s. This limited operation mainly comes from the thermal management of the device, which has to handle the heat load coming from the large ridge width of the laser section as well as the increased temperature of laser ridge by approximately 27 \(^{\circ }\)C caused by the power dissipation of the heater. One should also consider the self-heating effect that is expected to be \(\ge\) 30 \(^{\circ }\)C in the first 500 ns of the applied pulse, as deduced from the measurement on the other channel.
a iCW operation of the Vernier QCL device, when the front heater is not operating. The mode at 1600 cm\(^{-1}\) is favoured for lasing. Substrate temperature is \(-20 ^{\circ }\)C. The laser is driven with 15 \({\mu }\)s pulses, at a period of 200 \({\mu }\)s. b Emission mode spectra snapshots for various time instances, 4, 7 and 10.4 \({\mu }\)s, of the applied 15 \({\mu }\)s pulse. c iCW operation of the Vernier QCL device, when the front heater is biased with CW current, corresponding to 3.7 W of dissipated power. Substrate temperature is \(-20 ^{\circ }\)C. The laser can only operate up to 400-ns long pulses with a 200 \({\mu }\)s period
5 Conclusion: outlook
We fabricated and analysed the operation of two new designs of dual-wavelength DFBs, emitting at several wavelengths of the mid-IR spectrum. For the first design, called Neighbour DFB or NDFB, the laser ridges are placed close to each other, as close as 20–35 \(\mu\)m and showed reliable performances, at short-pulse, iCW operation with pulses as long as 50 \({\mu }\)s, and moreover continuous-wave operation. The tuning range of NDFB was shown to be extended considerably by about 3–4 cm\(^{-1}\) using the neighbour DFB as an integrated heater that features thermal resistance of \(>5\) K/W. We also simulated, fabricated, and characterized the performance of a digitalized grating DFB Vernier-based QCL, which was experimentally demonstrated to switch between emission lines 300 cm\(^{-1}\) apart in short pulse operation. Even though the limited thermal management of our device and the applied anti-reflective coatings do not allow the full demonstration of switching and tuning at long pulses, the continuous and mode-hop free tuning of the initially aligned channel of digital DFB grating was successfully shown. Improvement of the efficiency of the active region, as well as of the thermal management of the laser by fabricating narrower ridges, reducing the cavity optical losses by waveguide design or by junction-down mounting of the devices, can make the Vernier-based DFB QCLs even more attractive for spectroscopy. This design allows switching to single-mode emission at different frequency channels, which are spectrally distant, as well as continuous frequency tuning, without adding any complexity to a conventional optical setup for TDLAS, as there is only one laser ridge.
References
J. Faist, F. Capasso, D. Sivco, C. Sirtori, A. Hutchinson, A. Cho, Quantum cascade laser. Science 264(5158), 553–556 (1994)
R. Kohler, A. Tredicucci, F. Beltram, H. Beere, E. Linfield, A. Davies, D. Ritchie, R. Iotti, F. Rossi, Terahertz semiconductor-heterostructure laser. Nature 417(6885), 156–159 (2002)
C. Gmachl, D. Sivco, R. Colombelli, F. Capasso, A. Cho, Ultra-broadband semiconductor laser. Nature 415(6874), 883–887 (2002)
A. Hugi, R. Maulini, J. Faist, External cavity quantum cascade laser. Semicond. Sci. Technol. 25, 083001 (2010)
B.G. Lee, H.A. Zhang, C. Pfluegl, L. Diehl, M.A. Belkin, M. Fischer, A. Wittmann, J. Faist, F. Capasso, Broadband distributed-feedback quantum cascade laser array operating from 8.0 to 9.8 mu m. IEEE Photon. Technol. Lett. 21(13), 914–916 (2009)
P. Rauter, S. Menzel, A.K. Goyal, C.A. Wang, A. Sanchez, G. Turner, F. Capasso, High-power arrays of quantum cascade laser master-oscillator power-amplifiers. Optics Express 21(4), 4518–4530 (2013)
S. Song, S.S. Howard, Z. Liu, A.O. Dirisu, C.F. Gmachl, C.B. Arnold, Mode tuning of quantum cascade lasers through optical processing of chalcogenide glass claddings. Appl. Phys. Lett. 89(4), 041115 (2006)
D. Weidmann, F. Tittel, T. Aellen, M. Beck, D. Hofstetter, J. Faist, S. Blaser, Mid-infrared trace-gas sensing with a quasi-continuous-wave Peltier-cooled distributed feedback quantum cascade laser. Appl. Phys. B-Lasers Opt. 79(7), 907–913 (2004)
S. Cristescu, S. Persijn, S. te Lintel, Hekkert, F. Harren, Laser-based systems for trace gas detection in life sciences. Appl. Phys. B 92, 343 (2008)
B. Tuzson, K. Zeyer, M. Steinbacher, J.B. McManus, D.D. Nelson, M.S. Zahniser, L. Emmenegger, Selective measurements of NO, NO\(_{2}\) and NO\(_{y}\) in the free troposphere using quantum cascade laser spectroscopy. Atmos. Meas. Tech. 6(4), 927–936 (2013)
N. Bandyopadhyay, M. Chen, S. Sengupta, S. Slivken, M. Razeghi, Ultra-broadband quantum cascade laser, tunable over 760 cm-1, with balanced gain. Optics Express 23(16), 21159–21164 (2015)
S. Riedi, A. Hugi, A. Bismuto, M. Beck, J. Faist, Broadband external cavity tuning in the 3–4 \({\mu }\)m window. Appl. Phys. Lett. 103(3), 031108 (2013)
R. Ostendorf, L. Butschek, S. Hugger, F. Fuchs, Q. Yang, J. Jarvis, C. Schilling, M. Rattunde, A. Merten, J. Grahmann, D. Boskovic, T. Tybussek, K. Rieblinger, J. Wagner, Recent advances and applications of external cavity-QCLs towards hyperspectral imaging for standoff detection and real-time spectroscopic sensing of chemicals. Photonics 3(2), 28 (2016)
E. Mujagic, C. Schwarzer, Y. Yao, J. Chen, C. Gmachl, G. Strasser, Two-dimensional broadband distributed-feedback quantum cascade laser arrays. Appl. Phys. Lett. 98(14), 141101 (2011)
P. Jouy, C. Bonzon, J. Wolf, E. Gini, M. Beck, J. Faist, Surface emitting multi-wavelength array of single frequency quantum cascade lasers. Appl. Phys. Lett. 106, 071104 (2015)
A. Hugi, G. Villares, S. Blaser, H.C. Liu, J. Faist, Mid-infrared frequency comb based on a quantum cascade laser. Nature 492, 229–233 (2012)
G. Villares, A. Hugi, S. Blaser, J. Faist, Dual-comb spectroscopy based on quantum-cascade-laser frequency combs. Nature Commun. 5, 1–9 (2014)
A. Lyakh, R. Barron-Jimenez, I. Dunayevskiy, R. Go, C.K.N. Patel, External cavity quantum cascade lasers with ultra rapid acousto-optic tuning. Appl. Phys. Lett. 106(14), 141101 (2015)
P. Rauter, S. Menzel, A.K. Goyal, B. Gokden, C.A. Wang, A. Sanchez, G.W. Turner, F. Capasso, Master-oscillator power-amplifier quantum cascade laser array. Appl. Phys. Lett. 101(26), 261117 (2012)
W. Zhou, D. Wu, R. McClintock, S. Slivken, M. Razeghi, High performance monolithic, broadly tunable mid-infrared quantum cascade lasers. Optica 4, 1228–1231 (2017)
M.J. Süess, P. Jouy, C. Bonzon, J. Wolf, E. Gini, M. Beck, J. Faist, Single-mode quantum cascade laser array emitting from a single facet. IEEE Photon. Technol. Lett. 28, 1197–1200 (2016)
M. Hundt, M. Shahmohammadi, F. Kapsalidis, B. Tuzson, C. Liu, P. Scheidegger, M. Sess, H. Looser, J. Faist, L. Emmenegger, Multi-species trace gas analysis with dual-wavelength DFB-QCLs, in 2017 Conference on Lasers and Electro-Optics (CLEO) (2017), pp. 1–2
M.J. Süess, P.M. Hundt, B. Tuzson, S. Riedi, J.M. Wolf, R. Peretti, M. Beck, H. Looser, L. Emmenegger, J. Faist, Dual-section DFB-QCLs for multi-species trace gas analysis. Photonics 3(2), 24 (2016)
M. Hundt, B. Tuzson, O. Aseev, C. Liu, P. Scheidegger, H. Looser, F. Kapsalidis, M. Shahmohammadi, J. Faist, L. Emmenegger, “Multi-species laser spectroscopic mid-infrared trace gas sensor.” Appl. Phys. B: Lasers Opti. (2018) (submitted)
J. Jágerská, P. Jouy, A. Hugi, B. Tuzson, H. Looser, M. Mangold, M. Beck, L. Emmenegger, J. Faist, Dual-wavelength quantum cascade laser for trace gas spectroscopy. Appl. Phys. Lett. 105, 161109 (2014)
M. Beck, D. Hofstetter, T. Aellen, J. Faist, U. Oesterle, M. Ilegems, E. Gini, H. Melchior, Continuous wave operation of a mid-infrared semiconductor laser at room temperature. Science 295(5553), 301–305 (2002)
M.J. Süess, R. Peretti, Y. Liang, J.M. Wolf, C. Bonzon, B. Hinkov, S. Nida, P. Jouy, W. Metaferia, S. Lourdudoss, M. Beck, J. Faist, Advanced fabrication of single-mode and multi-wavelength MIR-QCLs. Photonics 3(2), 26 (2016)
J. Faist, Quantum cascade lasers, 1st edn. (Oxford University Press, New York, 2013)
M. Fischer, B. Tuzson, A. Hugi, R. Brönnimann, A. Kunz, S. Blaser, M. Rochat, O. Landry, A. Müller, L. Emmenegger, Intermittent operation of QC-lasers for mid-IR spectroscopy with low heat dissipation: tuning characteristics and driving electronics. Opt. Express 22, 7014–7027 (2014)
A. Bismuto, Y. Bidaux, C. Tardy, R. Terazzi, T. Gresch, J. Wolf, S. Blaser, A. Muller, J. Faist, Extended tuning of mid-ir quantum cascade lasers using integrated resistive heaters. Opt. Express 23, 29715–29722 (2015)
K. Grel, S. Schilt, A. Bismuto, Y. Bidaux, C. Tardy, S. Blaser, T. Gresch, T. Südmeyer, Frequency tuning and modulation of a quantum cascade laser with an integrated resistive heater. Photonics 3(3), 47 (2016)
V. Jayaraman, Z.M. Chuang, L.A. Coldren, Theory, design, and performance of extended tuning range semiconductor lasers with sampled gratings. IEEE J. Quantum Electron. 29, 1824–1834 (1993)
R. Todt, T. Jacke, R. Laroy, G. Morthier, M.C. Amann, Demonstration of vernier effect tuning in tunable twin-guide laser diodes. IEE Proc. Optoelectron. 152, 66–71 (2005)
S. Kalchmair, R. Blanchard, T.S. Mansuripur, G.-M. de Naurois, C. Pfluegl, M.F. Witinski, L. Diehl, F. Capasso, M. Loncar, High tuning stability of sampled grating quantum cascade lasers. Opt. Express 23, 15734–15747 (2015)
T.S. Mansuripur, S. Menzel, R. Blanchard, L. Diehl, C. Pfluegl, Y. Huang, J.-H. Ryou, R.D. Dupuis, M. Loncar, F. Capasso, Widely tunable mid-infrared quantum cascade lasers using sampled grating reflectors. Optics Express 20(21), 23339–23348 (2012)
S. Slivken, N. Bandyopadhyay, Y. Bai, Q.Y. Lu, M. Razeghi, Extended electrical tuning of quantum cascade lasers with digital concatenated gratings. Appl. Phys. Lett. 103(23), 231110 (2013)
Q.Y. Lu, S. Slivken, N. Bandyopadhyay, Y. Bai, M. Razeghi, Widely tunable room temperature semiconductor terahertz source. Appl. Phys. Lett. 105(20), 201102 (2014)
Y. Bidaux, A. Bismuto, C. Tardy, R. Terazzi, T. Gresch, S. Blaser, A. Muller, J. Faist, Extended and quasi-continuous tuning of quantum cascade lasers using superstructure gratings and integrated heaters. Appl. Phys. Lett. 107(22), 221108 (2015)
M. Yan Li, G. Xu, P. Voirin, O. Sixt, M. Parriaux, “Experimental study of digitalized dual-frequency coupling gratings,” in Proc.SPIE, vol. 2891, pp. 2891–2893 (1996)
C. Gmachl, A. Straub, R. Colombelli, F. Capasso, D. Sivco, A. Sergent, A. Cho, Single-mode, tunable distributed-feedback and multiple-wavelength quantum cascade lasers. IEEE J. Quantum Electron. 38, 569–581 (2001)
Acknowledgements
We thank Dr. Pierre Jouy and Dr. Yves Bidaux for fruitful discussions.This work was supported by the Nano-Tera.ch foundation under project “IrSens II”. The authors would like to thank the staff as well as the equipment responsibles of FIRST clean-room at ETH Zürich for the use of facilities and continued assistance.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article is part of the topical collection “Mid-infrared and THz Laser Sources and Applications” guest edited by Wei Ren, Paolo De Natale and Gerard Wysocki.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kapsalidis, F., Shahmohammadi, M., Süess, M.J. et al. Dual-wavelength DFB quantum cascade lasers: sources for multi-species trace gas spectroscopy. Appl. Phys. B 124, 107 (2018). https://doi.org/10.1007/s00340-018-6973-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00340-018-6973-2