Topological spin models in Rydberg lattices

Abstract

We show that resonant dipole–dipole interactions between Rydberg atoms in a triangular lattice can give rise to artificial magnetic fields for spin excitations. We consider the coherent dipole–dipole coupling between np and ns Rydberg states and derive an effective spin-1/2 Hamiltonian for the np excitations. By breaking time-reversal symmetry via external fields, we engineer complex hopping amplitudes for transitions between two rectangular sub-lattices. The phase of these hopping amplitudes depends on the direction of the hop. This gives rise to a staggered, artificial magnetic field which induces non-trivial topological effects. We calculate the single-particle band structure and investigate its Chern numbers as a function of the lattice parameters and the detuning between the two sub-lattices. We identify extended parameter regimes where the Chern number of the lowest band is $C=1$ or $C=2$.

1 Introduction

Regular arrays of ultracold neutral atoms [1, 2] are a versatile tool for the quantum simulation [3–5] of many-body physics [6]. Recent experimental progress allows one to control and observe atoms with single-site resolution [7–12] which makes dynamical phenomena experimentally accessible in these systems. One promising perspective is to use this set-up for investigating the rich physics of quantum magnetism [13–15] and strongly correlated spin systems that are extremely challenging to simulate on a classical computer. However, the simulation of magnetic phenomena with cold atoms faces two key challenges. First, neutral atoms do not experience a Lorentz force in an external magnetic field. In order to circumvent this problem, tremendous effort has been made to create artificial gauge fields for neutral atoms [16–32]. For example, artificial magnetic fields allow one to investigate the integer [33] and fractional quantum Hall effects [27–29] with cold atoms, and the experimental realization of the topological Haldane model was achieved in Ref. [30]. Second, cold atoms typically interact via weak contact interactions. Spin systems with strong and long-range interactions can be achieved by admixing van der Waals interactions between Rydberg states [34, 35] or by replacing atoms with dipole–dipole interacting polar molecules [36–38]. In particular, it has been shown that the dipole–dipole interaction can give rise to topological flat bands [39, 40] and fractional Chern insulators [41]. The creation of bands with Chern number $C=2$ via resonant exchange interactions between polar molecules has been explored in Ref. [40].

Recently, an alternative and very promising platform for the simulation of strongly correlated spin systems has emerged [42]. Here resonant dipole–dipole interactions between Rydberg atoms [43] enable quantum simulations of spin systems at completely different length scales compared with polar molecules. For example, the experiment in Ref. [42] demonstrated the realization of the XY Hamiltonian for a chain of atoms and with a lattice spacing of the order of $20\,\upmu \text {m}$. At these length scales, light modulators allow one to trap atoms in arbitrary, two-dimensional geometries and to apply custom-tailored light shifts at individual sites [44–46]. The resonant dipole–dipole interaction is also ideally suited for the investigation of transport phenomena [47–49] and can give rise to artificial magnetic fields acting on the relative motion of two Rydberg atoms [50–52].

Here we show how to engineer artificial magnetic fields for spin excitations in two-dimensional arrays of dipole–dipole interacting Rydberg atoms. More specifically, we consider a triangular lattice of Rydberg atoms as shown in Fig. 1 where the resonant dipole–dipole interaction enables the coherent exchange of excitations between atoms in np and ns states. We derive an effective spin-1/2 Hamiltonian for the np excitations with complex hopping amplitudes giving rise to artificial, staggered magnetic fields. This results in nonzero Chern numbers of the single-particle band structure, and the value of the Chern number in the lowest band can be adjusted to $C=1$ or $C=2$ by changing the lattice parameters.

Note that in our system all atoms comprising the lattice are excited to a Rydberg state. This is in contrast to the work in Refs. [34, 35], where the atoms mostly reside in their ground states and the population in the Rydberg manifold is small. Consequently, our approach is in general more vulnerable towards losses through spontaneous emission. On the other hand, the magnitude of the resonant dipole–dipole interaction is much stronger compared with a small admixing of van der Waals interactions, and hence, the coherent dynamics takes place on much shorter timescales. In addition, the distance between the atoms can be much larger in our approach which facilitates the preparation and observation of the excitations.

This paper is organized as follows. We give a detailed description of our system in Sect. 2 where we engineer an effective Hamiltonian for the np excitations. We then investigate the single-particle band structure and provide a systematic investigation of the topological features of these bands as a function of the system parameters in Sect. 3. A brief summary of our work is presented in Sect. 4.

2 Model

Fig. 1

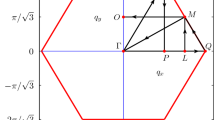
(Color online) Triangular lattice of Rydberg atoms in the $x-y$ plane. The lattice is comprised of two rectangular sub-lattices $\mathcal {R}$ and $\mathcal {B}$ that are shifted by $\mathbf {a}/2+\mathbf {b}/2$ with respect to each other, where $\mathbf {a} = a \mathbf {e}_x$ and $\mathbf {b} = b \mathbf {e}_y$ are the primitive basis vectors of each sub-lattice. The sites of the $\mathcal {B}$ ($\mathcal {R}$) lattice are indicated by blue squares (red dots). The unit cell of the whole lattice is shown by the shaded area and contains two lattice sites. $\varPhi _\mathrm{u}$ is the flux through the upward pointing triangle $1\rightarrow 2\rightarrow 3\rightarrow 1$, and $\varPhi _\mathrm{d}$ is the flux through the downward pointing triangle $2\rightarrow 4\rightarrow 3\rightarrow 2$

We consider a two-dimensional triangular lattice of Rydberg atoms in the $x-y$ plane as shown in Fig. 1. Each lattice site contains a single Rydberg atom which we assume to be pinned to the site. The triangular lattice is comprised of two rectangular sub-lattices $\mathcal {B}$ and $\mathcal {R}$ that are labelled by blue squares and red dots in Fig. 1, respectively. Each sub-lattice is described by two orthogonal primitive basis vectors $\mathbf {a} = a \mathbf {e}_x$ and $\mathbf {b} = b \mathbf {e}_y$, and the two sub-lattices are shifted by $\mathbf {a}/2+\mathbf {b}/2$ with respect to each other. In the following, we derive an effective spin-1/2 model for Rydberg excitations in the np manifold over a background of ns states with principal quantum number $n\gg 1$. After introducing the general Hamiltonian of the system, we first engineer an effective Hamiltonian for np excitations on the $\mathcal {B}$ sub-lattice. We then apply the same procedure to the $\mathcal {R}$ sub-lattice but choose a different np state compared to the $\mathcal {B}$ atoms. Finally, we show that the dipole–dipole interaction couples the two sub-lattices and the corresponding Hamiltonian contains complex hopping amplitudes giving rise to artificial magnetic fields.

The atomic level scheme of each atom is comprised of two angular momentum manifolds $ns_{1/2}$ and $np_{3/2}$ with principal quantum number $n\gg 1$ as shown in Fig. 2. The Zeeman sub-levels of each multiplet are denoted by $|l_jm\rangle$, where l labels the orbital angular momentum, j is the total angular momentum and the projection of the electron’s angular momentum onto the z-axis is denoted by m. The Hamiltonian of a single atom at site $\alpha$ is given by

$$\begin{aligned} H_{\alpha }^{(0)} &= \hbar \omega _\mathrm{p} \sum \limits _{m=-3/2}^{3/2} | p_{3/2} m \rangle _{\alpha } \langle p_{3/2}m |_{\alpha } \nonumber \\&+ \hat{L}_{\alpha }[p_{3/2}] + \hat{L}_{\alpha }[s_{1/2}] \, , \end{aligned}$$

(1)

where the first line is the Hamiltonian for the degenerate $np_{3/2}$ manifold in the absence of external fields, $\hbar \omega _\mathrm{p}$ is the energy of the $np_{3/2}$ multiplet and we set the frequency of the $ns_{1/2}$ multiplet $\omega _\mathrm{s}=0$. In the second line of Eq. (1), $\hat{L}_{\alpha }[l_j]$ are level shift operators removing the Zeeman degeneracy of the multiplet $l_j$ at site $\alpha$. An example for the operators $\hat{L}_{\alpha }[l_j]$ is given in Eq. (17) at the end of Sect. 2. In the following, we assume that all atoms in rows labelled by $\mathcal {B}$ and indicated by a blue square in Fig. 1 experience the same level shifts. Similarly, all atoms in rows labelled by $\mathcal {R}$ and indicated by a red dot in Fig. 1 have equivalent level schemes. However, atoms in sites $\alpha \in \mathcal {R}$ have a different internal level structure compared with atoms in sites $\alpha \in \mathcal {B}$. The full Hamiltonian for the system shown in Fig. 1 is then given by

$$\begin{aligned} H = \sum \limits _{\alpha } H_{\alpha }^{(0)} + \frac{1}{2}{\mathop {\mathop {\sum }\limits _{\alpha ,\beta }}\limits _{\alpha \not =\beta }} V_{\alpha \beta }\, , \end{aligned}$$

(2)

where $V_{\alpha \beta }$ is the dipole–dipole interaction [53] between atoms at sites $\alpha$ and $\beta$,

$$\begin{aligned} V_{\alpha \beta } = \frac{1}{4\pi \varepsilon _0 R^3}[{\hat{\mathbf {d}}}^{(\alpha )}\cdot {\hat{\mathbf {d}}}^{(\beta )} -3({\hat{\mathbf {d}}}^{(\alpha )}\cdot \tilde{\mathbf {R}})({\hat{\mathbf {d}}}^{(\beta )}\cdot \tilde{\mathbf {R}})] \,. \end{aligned}$$

(3)

Here $\varepsilon _0$ is the dielectric constant, ${\hat{\mathbf {d}}}^{(\alpha )}$ is the electric-dipole-moment operator of atom $\alpha$, $\mathbf {R} = \mathbf {R}_{\alpha }-\mathbf {R}_{\beta }$ is the relative position of the two atoms located at $\mathbf {R}_{\alpha }$ and $\mathbf {R}_{\beta }$, respectively, and $\tilde{\mathbf {R}}=\mathbf {R}/R$ is the corresponding unit vector. In the following, we consider only near-resonantly coupled states and neglect all matrix elements between two-atom states differing in energy by $\Delta E_{\text {FS}}=\hbar \omega _\mathrm{p}$ or more. This is justified if the dipole–dipole coupling strength $V_0$ is much smaller than the fine structure interval $\Delta E_{\text {FS}}$, which is the case for the typical parameters based on rubidium atoms (see Sect. 3).

Fig. 2

(Color online) The level scheme of each atom consists of the $ns_{1/2}$ and $np_{3/2}$ manifolds. Dashed lines denote allowed dipole transitions. a The effective spin-1/2 system at sites $\mathcal {B}$ is formed by states $|p_{3/2}-1/2\rangle$ and $|s_{1/2}1/2\rangle$. The corresponding dipole transition with transition frequency $\omega _{\Box }$ is indicated in blue. b The effective spin-1/2 system at sites $\mathcal {R}$ is formed by states $|p_{3/2}3/2\rangle$ and $|s_{1/2}1/2\rangle$. The associated dipole transition with transition frequency $\omega _{\circ }$ is indicated in red

Next we focus on the $\mathcal {B}$ lattice and reduce the level scheme at each site to a two-level system by a suitable choice of the shift operators in Eq. (1). To this end, we assume that the level shifts break the degeneracy of the Zeeman sub-levels as shown in Fig. 2a such that all dipole transitions can be addressed individually. In particular, we require that the strength of the dipole–dipole coupling between nearest neighbours is much smaller than the splitting between Zeeman sub-levels. For all $\mathcal {B}$ atoms, we choose the states $|p_{3/2}-1/2\rangle$ and $|s_{1/2}1/2\rangle$ as the effective spin-1/2 system. The dipole matrix element of the $|p_{3/2}-1/2\rangle \leftrightarrow |s_{1/2}1/2\rangle$ transition with transition frequency $\omega _{\Box }$ is (see “Appendix 1”)

$$\begin{aligned} \mathbf {d}_{\mathcal {B}}=\langle p_{3/2}-1/2 |{\hat{\mathbf {d}}}|s_{1/2}1/2\rangle = \mathcal {D}\frac{1}{\sqrt{6}}\left( \mathbf {e}_x + \mathrm {i}\mathbf {e}_y\right) \,, \end{aligned}$$

(4)

where $\mathcal {D}$ is the reduced dipole matrix element of the $s_{1/2}\leftrightarrow p_{3/2}$ transition. In an interaction picture with respect to the bare atomic energies, the Hamiltonian H in Eq. (2) restricted to all $\mathcal {B}$ atoms can thus be written as

$$\begin{aligned} H_{\mathcal {B}} = -\frac{1}{6} {\mathop {\mathop {\sum }\limits _{\alpha \in \mathcal {B}}}\limits _{\beta \in \mathcal {B}}} \mathcal {C}_{\alpha \beta } \left( S_{\alpha }^{+}S_{\beta }^{-}+S_{\beta }^{+}S_{\alpha }^{-}\right) \,, \end{aligned}$$

(5)

where

$$\begin{aligned} \mathcal {C}_{\alpha \beta }&= \frac{|\mathcal {D}|^2}{4\pi \varepsilon _0 |\mathbf {R}_{\alpha }-\mathbf {R}_{\beta }|^3} \end{aligned}$$

(6)

describes the coupling strength between two $\mathcal {B}$ atoms located at $\mathbf {R}_{\alpha }$ and $\mathbf {R}_{\beta }$, respectively. In the following, it will be useful to characterize the strength of the dipole–dipole interaction between two atoms separated by a, and hence, we introduce the parameter

$$\begin{aligned} V_0 = \frac{|\mathcal {D}|^2}{4\pi \varepsilon _0 a^3} \,. \end{aligned}$$

(7)

The raising operator for a spin excitation in Eq. (5) is defined as

$$\begin{aligned} S_{\alpha }^{+} = |p_{3/2}-1/2\rangle \langle s_{1/2}1/2 |\,, \quad \quad \alpha \in \mathcal {B}\,, \end{aligned}$$

(8)

and its adjoint is the corresponding lowering operator, $S_{\alpha }^{-}=[S_{\alpha }^{+}]^{\dagger }$.

Next we follow a similar procedure within the $\mathcal {R}$ lattice. In contrast to $\mathcal {B}$ atoms, we choose the states $|p_{3/2}3/2\rangle$ and $|s_{1/2}1/2\rangle$ as an effective spin-1/2 system as shown in Fig. 2b. We assume that all other transitions within $\mathcal {R}$ atoms are so far-detuned that the dipole–dipole interaction remains restricted to this sub-system. We find that the dipole matrix element of the corresponding transition $|p_{3/2}3/2\rangle \leftrightarrow |s_{1/2}1/2\rangle$ is (see “Appendix 1”)

$$\begin{aligned} \mathbf {d}_{\mathcal {R}}= \langle p_{3/2}3/2 |{\hat{\mathbf {d}}}|s_{1/2}1/2\rangle = -\mathcal {D}\frac{1}{\sqrt{2}}\left( \mathbf {e}_x-\mathrm {i}\mathbf {e}_y\right). \end{aligned}$$

(9)

The raising operator of this transition with resonance frequency $\omega _{\circ }$ is defined as

$$\begin{aligned} S_{\alpha }^{+} = |p_{3/2}3/2\rangle \langle s_{1/2}1/2 |\,, \quad \quad \alpha \in \mathcal {R}\,, \end{aligned}$$

(10)

and $S_{\alpha }^{-}=[S_{\alpha }^{+}]^{\dagger }$ is the lowering operator. In a rotating frame where $S_{\alpha }^{+}$ oscillates with the frequency $\omega _{\Box }$ of excitations in the $\mathcal {B}$ lattice, the Hamiltonian for excitations in the $\mathcal {R}$ lattice can be written as

$$\begin{aligned} H_{\mathcal {R}} = \hbar \Delta \sum \limits _{\alpha \in \mathcal {R}} S_{\alpha }^{+}S_{\alpha }^{-} -\frac{1}{2} {\mathop {\mathop {\sum }\limits _{\alpha \in \mathcal {R}}}\limits _{\beta \in \mathcal {R}}} \mathcal {C}_{\alpha \beta } \left( S_{\alpha }^{+}S_{\beta }^{-}+S_{\beta }^{+}S_{\alpha }^{-}\right) \,, \end{aligned}$$

(11)

where $\Delta = \omega _{\circ }-\omega _{\Box }$ is the detuning between excitations in the $\mathcal {R}$ and $\mathcal {B}$ lattices and $\mathcal {C}_{\alpha \beta }$ is defined in Eq. (6).

For our given geometry and chosen transitions, we find that the dipole–dipole coupling between the two sub-lattices is different from zero. If the detuning $\Delta$ between $\mathcal {B}$ and $\mathcal {R}$ excitations is smaller than the strength of the dipole–dipole coupling between the two sub-lattices, the np excitations can hop between the $\mathcal {B}$ and $\mathcal {R}$ sites. With the expressions for the dipole matrix elements in Eqs. (4) and (9), the Hamiltonian governing the coupling between the two sub-lattices is given by

$$\begin{aligned} H_{\mathcal {B}\mathcal {R}} = \frac{\sqrt{3}}{2} {\mathop {\mathop {\sum }\limits _{\alpha \in \mathcal {R}}} \limits _{\beta \in \mathcal {B}}} \mathcal {C}_{\alpha \beta } \left( e^{-2\mathrm {i}\phi _{\alpha \beta }} S_{\alpha }^{+}S_{\beta }^{-}+e^{2\mathrm {i}\phi _{\alpha \beta }} S_{\beta }^{+}S_{\alpha}^{-}\right) \, , \end{aligned}$$

(12)

where

$$\begin{aligned} e^{\mathrm {i}\phi _{\alpha \beta }}&= \left( \tilde{\mathbf {R}}_{\alpha }-\tilde{\mathbf {R}}_{\beta }\right) \cdot \left( \mathbf {e}_x + \mathrm {i}\mathbf {e}_y \right) \,. \end{aligned}$$

(13)

Note that the phase $\phi _{\alpha \beta }$ of excitation hopping between sites $\alpha \in \mathcal {R}$ and $\beta \in \mathcal {B}$ is determined by the azimuthal angle of the relative position vector $\tilde{\mathbf {R}}_{\alpha }-\tilde{\mathbf {R}}_{\beta }$ between the two sites.

In summary, by restricting the effective level scheme on each site to a two-level system we obtain

$$\begin{aligned} H_{\text {eff}}&= H_{\mathcal {B}} + H_{\mathcal {R}} +H_{\mathcal {B}\mathcal {R}} \nonumber \\&= \hbar \Delta \sum \limits _{\alpha \in \mathcal {R}} S_{\alpha }^{+}S_{\alpha }^{-} -\frac{1}{6} {\mathop {\mathop {\sum }\limits _{\alpha \in \mathcal {B}}}\limits _{\beta \in \mathcal {B}}} \mathcal {C}_{\alpha \beta } \left( S_{\alpha }^{+}S_{\beta }^{-}+S_{\beta }^{+}S_{\alpha }^{-}\right) \nonumber \\&\quad -\frac{1}{2} {\mathop {\mathop {\sum }\limits _{\alpha \in \mathcal {R}}}\limits _{\beta \in \mathcal {R}}} \mathcal {C}_{\alpha \beta } \left( S_{\alpha }^{+}S_{\beta }^{-}+S_{\beta }^{+}S_{\alpha }^{-}\right) \nonumber \\&\quad +\frac{\sqrt{3}}{2} {\mathop {\mathop {\sum }\limits _{\alpha \in \mathcal {R}}}\limits _{\beta \in \mathcal {B}}} \mathcal {C}_{\alpha \beta } \left( e^{-2\mathrm {i}\phi _{\alpha \beta }} S_{\alpha }^{+}S_{\beta }^{-}+e^{2\mathrm {i}\phi _{\alpha \beta }} S_{\beta }^{+}S_{\alpha }^{-}\right) \, , \end{aligned}$$

(14)

where the definition of the spin operators $S_{\alpha }^{\pm }$ depends on the lattice site as described by Eqs. (8) and (10). The operators $S_{\alpha }^{\pm }$ obey Fermi anticommutation relations on the same site,

$$\begin{aligned} S_{\alpha }^{+}S_{\alpha }^{-}+ S_{\alpha }^{-}S_{\alpha }^{+} = {1\!\!1}\,, \quad S_{\alpha }^{+}S_{\alpha }^{+}= S_{\alpha }^{-}S_{\alpha }^{-}=0\,, \end{aligned}$$

(15)

and Bose commutation relations between different sites,

$$\begin{aligned} \left[ S_{\alpha }^{-},S_{\beta }^{+}\right] = \left[ S_{\alpha }^{+},S_{\beta }^{+}\right] = \left[ S_{\alpha }^{-},S_{\beta }^{-}\right] = 0\,,\quad \alpha \not =\beta \,. \end{aligned}$$

(16)

It follows that the raising and lowering operators $S_{\alpha }^{+}$ and $S_{\alpha }^{-}$ are equivalent to hard-core bosonic creation and annihilation operators $a_{\alpha }^{\dagger }$ and $a_{\alpha }$, respectively. The Hamiltonian in Eq. (14) describes the hopping dynamics of these hard-core bosons on the two coupled sub-lattices $\mathcal {A}$ and $\mathcal {B}$.

An example for the dipole–dipole coupling strengths in rubidium atoms and the magnitude of the level shifts required for realizing the effective Hamiltonian in Eq. (14) is provided in “Appendix 2”. Here we outline two physical implementations of the level shifts $\hat{L}_{\alpha }[l_j]$ in Eq. (1). First, we consider linear Zeeman shifts induced by an external magnetic field $B_{\alpha }$ in z direction,

$$\begin{aligned} \hat{L}_{\alpha }[l_{j}] = \frac{g[l_j]}{\hbar } \mu _B B_{\alpha } \hat{J}_z[l_j]\, , \end{aligned}$$

(17)

where $\mu _B$ is the Bohr magneton, $\hat{J}_z[l_j]$ is the z component of the angular momentum operator restricted to the multiplet $l_j$, and $g[l_j]$ is the Landé g-factor,

$$\begin{aligned} g[l_j] = \frac{3}{2} + \frac{3/4-l(l+1)}{2j(j+1)} \, . \end{aligned}$$

(18)

Since $g[s_{1/2}]=2$ and $g[p_{3/2}]=4/3$, the magnitude of the Zeeman shifts is different for the $s_{1/2}$ and $p_{3/2}$ manifolds, respectively. We assume that atoms in lattices $\mathcal {B}$ and $\mathcal {R}$ experience different magnetic field strengths,

$$\begin{aligned} B_{\alpha } = \left\{ \begin{array}{ll} B_{\mathcal {B}},&{}\alpha \in \mathcal {B}\,, \\ B_{\mathcal {R}},&{}\alpha \in \mathcal {R} \, , \end{array} \right. \end{aligned}$$

(19)

where $B_{\mathcal {B}}\not =B_{\mathcal {R}}$. Exact resonance $\varDelta =0$ between the two sub-lattices can be achieved for $B_{\mathcal {B}}=-5 B_{\mathcal {R}}/3$, and periodic magnetic fields could be engineered by a regular array of micromagnets [54, 55].

Second, the effective Hamiltonian in Eq. (14) can be realized with a uniform magnetic field across all lattice sites and static or AC Stark shifts that are different for the $\mathcal {B}$ and $\mathcal {R}$ lattices. For example, one could employ AC Stark shifts using a standing wave with periodicity b such that all $\mathcal {B}$ and $\mathcal {R}$ atoms are located at the nodes and antinodes, respectively. Since the magnitude of the AC Stark shifts depends on $|m_j|$, a relative shift between the $|p_{3/2}3/2\rangle \leftrightarrow |s_{1/2}1/2\rangle$ and $|p_{3/2}-1/2\rangle \leftrightarrow |s_{1/2}1/2\rangle$ transitions can be induced such that the resonance condition $\Delta \approx 0$ holds.

3 Results

Fig. 3

(Color online) Magnetic flux $\varPhi$ enclosed in an elementary triangle of the lattice in Fig. 1 as a function of b / a, where b and a are the lattice constants of the rectangular sub-lattices. $\varPhi _\mathrm{u}$ ($\varPhi _\mathrm{d}$) is the flux through the upward (downward) pointing triangle $1\rightarrow 2\rightarrow 3\rightarrow 1$ ($2\rightarrow 4\rightarrow 3\rightarrow 2$) in Fig. 1 and for the effective Hamiltonian in Eq. (14) with only nearest-neighbour interactions taken into account

The effective Hamiltonian in Eq. (14) exhibits complex hopping amplitudes for exciton transitions between the $\mathcal {B}$ and $\mathcal {R}$ lattices which correspond to an artificial vector potential $\mathbf {A}$ according to the Peierls substitution [56]. This result can be understood as follows. Excitations in the $\mathcal {B}$ and $\mathcal {R}$ lattices couple to different dipole transitions with complex dipole moments $\mathbf {d}_{\mathcal {B}}$ and $\mathbf {d}_{\mathcal {R}}$, respectively. The two different transitions on sites $\mathcal {B}$ and $\mathcal {R}$ are tuned into resonance through external fields that break time-reversal symmetry. Since $\mathbf {d}_{\mathcal {B}}$ and $\mathbf {d}_{\mathcal {R}}$ have a well-defined relative phase, hopping between the two sub-lattices gives rise to a complex hopping amplitude that depends on the azimuthal angle of the relative position vector $\mathbf {R}_{\alpha }-\mathbf {R}_{\beta }$ between sites $\alpha$ and $\beta$ (see Eq. (13)). The total magnetic flux $\varPhi _\mathrm{u}$ through the upward pointing triangle $1\rightarrow 2\rightarrow 3\rightarrow 1$ is shown in Fig. 1. For nearest-neighbour interactions only, the total flux is determined by the sum of the phases along the edges of the triangle,

$$\begin{aligned} \varPhi _\mathrm{u}&= 2(\phi _{32}-\phi _{13})+\pi \,. \end{aligned}$$

(20)

We find that the total flux is in general different from zero and can be adjusted by varying the lattice parameters. This is shown by the red solid line in Fig. (3), where $\varPhi _\mathrm{u}$ is depicted as a function of ratio b / a. $\varPhi _\mathrm{u}$ is different from zero except for $b/a=1$ and attains all possible values between $-\pi$ and $\pi$, which is the maximal range for the flux defined mod $2\pi$. Similarly, the total magnetic flux $\varPhi _\mathrm{d}$ through the downward pointing triangle $2\rightarrow 4\rightarrow 3\rightarrow 2$ in Fig. 1 is given by

$$\begin{aligned} \varPhi _\mathrm{d}&= 2(\phi _{34}-\phi _{23})+\pi \,, \end{aligned}$$

(21)

and $\varPhi _\mathrm{d}$ is shown by the blue dot-dashed line in Fig. 3. Since $\varPhi _\mathrm{d}+\varPhi _\mathrm{u}=0$ for all values b / a, the flux in neighbouring triangles has the same magnitude but the opposite sign, and hence, the complex transition amplitudes in our system correspond to a staggered artificial magnetic field. This result is consistent with the assumed translational symmetry of the lattice, which requires that all magnetic fluxes within the unit cell must add up to zero.

Next we investigate the single-particle band structure of $H_{\text {eff}}$ using a rectangular unit cell containing two lattice sites as shown by the shaded area in Fig. 1. It follows that the k-space Hamiltonian $\mathcal {H}(\mathbf {k})$ is represented by a $2\times 2$ matrix, where $\mathbf {k}$ describes a point in the first Brillouin zone of the reciprocal lattice (see “Appendix 3”). We include all hopping terms between sites separated by $R\le r_\mathrm{D}$. Through a numerical study we find that $\mathcal {H}(\mathbf {k})$ describes the bulk properties of our system well for $r_\mathrm{D} \ge 6 a$ and $a\ge b/2$. The band structure for the special case of equilateral triangles as in Fig. 1 (i.e. $b/a=\sqrt{3}$) is shown in Fig. 4. There are two separate bands, and the band gap varies in size across the Brillouin zone. The gap is the smallest near the following points at the zone boundary,

$$\begin{aligned}&\mathbf {k}_1=(0, \pi /b)\,&\mathbf {k}_2=(0, -\pi /b) \, \end{aligned}$$

(22a)

$$\begin{aligned}&\mathbf {k}_3=(\pi /a,0)\,&\mathbf {k}_4=(-\pi /a,0) \,. \end{aligned}$$

(22b)

The magnitude of the band gap near these points is of the order of $V_0/2$, where $V_0$ is defined in Eq. (7). The broken time-reversal symmetry in our system endows the band structure with non-trivial topological properties. We numerically calculate the Chern number as described in Ref. [57] and find that the lower and upper bands have Chern numbers $C=1$ and $C=-1$, respectively.

Fig. 4

(Color online) Single-excitation band structure for $\varDelta =0$ and $b/a=\sqrt{3}$. All hopping terms between sites within a radius of $r_\mathrm{D}=6 a$ are taken into account. The two bands are separated by a gap and the lower (upper) band has Chern number $C=1$ ($C=-1$)

Various topological regimes can be realized in our system by adjusting the lattice parameters and the detuning between the excitations on the sub-lattices $\mathcal {B}$ and $\mathcal {A}$. This is illustrated in Fig. 5, where we show the Chern number of the lower band as a function of the ratio b / a and $\Delta$. First, we note that the phase diagram in Fig. 5 exhibits extended regions with nonzero Chern numbers that are robust with respect to small variations in $\Delta$ and b / a. The solid lines in Fig. 5 indicate topological phase transitions where the lower and upper bands touch in at least two of the $\mathbf {k}$ points in Eq. (22) which then represent a Dirac point.

Fig. 5

(Color online) Topological regimes for the lower band for $r_\mathrm{D}=8$. The black lines indicate topological phase transitions where the Chern number of the lower band changes. The red dot and magenta star correspond to the parameters of the band structures in Figs. 4 and 6, respectively

The qualitative features of the $C=1$ region marked in orange in Fig. 5 can be understood by noting that nonzero Chern numbers require an efficient coupling between the sub-lattices $\mathcal {B}$ and $\mathcal {R}$. In particular, the dipole–dipole coupling needs to be larger or comparable to the detuning $\Delta$. For fixed lattice constant a, reducing b / a corresponds to an increased dipole–dipole coupling between the sub-lattices and hence the region with $C=1$ broadens along the $\Delta$ axis for $b/a<1$. The narrowing of the $C=1$ region near $b/a=1$ can be understood from Fig. 3. For nearest-neighbour interactions only, the magnetic flux vanishes for $b/a=1$ and hence the corresponding bands would have Chern number $C=0$. Taking into account interactions beyond nearest neighbours gives rise to modifications as shown in Fig. 5. In particular, these interactions are responsible for the blue wedged area with Chern number $C=2$. The single-particle band structure for the parameters corresponding to the magenta star inside the blue wedged area in Fig. 5 is shown in Fig. 6a. The lower and upper bands have Chern numbers $C=2$ and $C=-2$, respectively. The two bands are gapped, but in contrast to the parameters in Fig. 4 the gap is the smallest near the Brillouin zone centre $\mathbf {k}=(0,0)$ where it is approximately given by $0.1 V_0$.

The asymmetry of the phase diagram in Fig. 5 with respect to the $\varDelta =0$ axis can be traced back to the fact that the dipole–dipole interaction differs in strength for the $\mathcal {B}$ and $\mathcal {R}$ lattices. In order to illustrate this, we focus on the blue wedge with $C=2$ in Fig. 5 and show the band structures of the uncoupled, individual sub-lattices in Fig. 6b for $\hbar \Delta =2.5 V_0$ and $b/a=1$. Both band structures are convex surfaces with their minimum at $\mathbf {k}=0$, but the depth of the potential well is significantly larger for the upper band. The reason is that the strength of the dipole–dipole interaction is three times stronger for the $\mathcal {R}$ lattice compared to the $\mathcal {B}$ lattice for $b/a=1$ (see Eqs. (5) and (11)). A necessary condition for non-trivial topological bands is that the two sub-lattices are efficiently coupled by the Hamiltonian $H_{\mathcal {B}\mathcal {R}}$ in Eq. (12), which depends on the magnitude of the dipole–dipole interaction connecting the $\mathcal {B}$ and $\mathcal {R}$ lattices and the energy spacing between $\mathcal {B}$ and $\mathcal {R}$ excitations at each $\mathbf {k}$ point. As shown in Fig. 6b, the two surfaces touch near $\mathbf {k}\approx \mathbf {0}$, and hence, the relatively weak next-nearest-neighbour coupling in $H_{\mathcal {B}\mathcal {R}}$ can give rise to nonzero Chern numbers for $\hbar \Delta =2.5 V_0$ and $b/a=1$. On the other hand, the distance between the two uncoupled bands increases quickly if $\Delta$ is decreased from zero to negative values. This explains why $H_{\mathcal {B}\mathcal {R}}$ cannot induce a $C=2$ band for $\hbar \Delta \lesssim -0.3V_0$.

Fig. 6

(Color online) Single-excitation band structure for $\hbar \varDelta =2.5 V_0$ and $b/a=1$. All hopping terms between sites within a radius of $r_\mathrm{D}=6 a$ are taken into account. a Band structure corresponding to the effective Hamiltonian in Eq. (14). b Band structure for the same parameters as in (a) but without the Hamiltonian $H_{\mathcal {B}\mathcal {R}}=0$ coupling the two sub-lattices. The upper (lower) surface is the band structure for excitations on the $\mathcal {R}$ ($\mathcal {B}$) lattice

Finally, we discuss the physical realization of our system and the observation of its topological features. The experimental realization of a one-dimensional chain of resonantly coupled Rydberg atoms has been reported in Ref. [42]. Here the excitation of all atoms to a Rydberg state is achieved within $\tau \approx 0.5\,\upmu \text {s}$ [42]. Note that this process is not hampered by the dipole blockade since the van der Waals shifts are small for the considered lattice constants a. For example, for Rubidium ns states with $n=70$ and $a=20\,\upmu \text {m}$, the van der Waals shift is $\varDelta _{\text {vdW}}\approx 13\,\text {kHz}$ [58], which is small compared with the Rabi frequency of the lasers exciting the Rydberg state [42]. The time interval $\Delta T$ where excitation hopping can take place is limited by the lifetime of the Rydberg states and the residual atomic motion. For atomic temperatures of the order of $10\,\upmu \text {K}$, motional effects are negligible for $\Delta T \approx 10\,\upmu \text {s}$ [42]. This is typically much smaller than the Rydberg state lifetime and large compared with the inverse hopping amplitude such that many coherent hops can take place (see “Appendix 2”). Note that these considerations also show that auto-ionization processes due to Rydberg atom collisions can be neglected [59, 60] since the initial positions of the atoms in the lattice change only very slightly during $\Delta T$. Recently, tremendous experimental progress towards the extension of the experiment in Ref. [42] to two dimensions and arbitrary lattice geometries has been made [44, 45]. In particular, it is now possible to create arbitrary lattice structures where each site is filled with exactly one atom [46]. It follows that our system can be realized with a combination of state-of-the-art experimental techniques.

Fig. 7

(Color online) Quantum dynamics of a single excitation on a lattice with 53 atoms, $b/a=2$, $\varDelta =0$ and $r_\mathrm{D}=6 a$. At time $t=0$, only the atom in the bottom row indicated by a magenta triangle is excited. The population of each lattice site at time $t = 4 \hbar /V_0$ is indicated by the colour of the halo around each site. The dashed line is used as a guide to the eye (see text). a Quantum dynamics according to the Hamiltonian $H_{\text {eff}}$ in Eq. (14). The magnetic flux through the indicated triangular plaquettes is negative and thus favours counterclockwise motion of the excitation. b Same as in (a), but with all phases $\phi _{\alpha \beta }$ in Eq. (14) set to zero

A direct signature of the artificial magnetic fields associated with the complex hopping amplitudes in Eq. (14) can be obtained by investigating the quantum dynamics of a single excitation as shown in Fig. 7. We consider a lattice with 53 sites where only the site in the middle of the lower edge is excited at time $t=0$. The excitation probability of the lattice sites at a later time is shown in Fig. 7a, b, where Fig. 7a the dynamics according to the effective Hamiltonian in Eq. (14). We find that the largest excitation probabilities can be found along the lower edge and to the right of the initially excited site. Figure 7b is generated by setting all phases $\phi _{\alpha \beta }$ in Eq. (14) to zero. In this case, the distribution of excitation probabilities is symmetric with respect to the dashed line. The latter result is expected since the magnitude of the hopping amplitudes does only depend on the distance between two sites. It follows that the marked asymmetry in Fig. 7a is a direct consequence of the complex hopping amplitudes and the associated artificial magnetic field. More specifically, the magnetic flux through the upward pointing triangles shown in Fig. 7 and for the considered parameters is negative (see Fig. 3). The force associated with the artificial magnetic field thus favours an anticlockwise motion around each triangular plaquette. This explains why the propagation moves along the edge in an anticlockwise direction. Note that this asymmetry develops within a few hopping events such that the residual motion of the atoms hosting these excitations can be neglected. Our results are also consistent with the fact that a semi-infinite version of our lattice exhibits chiral edge states for nonzero Chern numbers according to the bulk-edge correspondence [61, 62].

The Chern number of the individual bands can be determined by observing the motional drifts due to the nonzero Berry curvature in each band. To this end, the excitations need to be selectively prepared in either the upper or lower band. This can be achieved in different ways. First, one could prepare an excitation in one of the sub-lattices with a large detuning $\Delta$ such that the $\mathcal {R}$ and $\mathcal {B}$ lattices are uncoupled. This is followed by an adiabatic reduction of $|\Delta |$ in order to adjust the required parameter regime. Second, one could prepare all atoms in the $|ns_{1/2}1/2\rangle$ state and apply a weak microwave field such that only a single $\mathbf {k}$ mode is resonantly excited. Efficient methods to extract the local Berry curvature from motional drifts are described in Ref. [63] and require an external force acting on the particle. In our set-up, this could be realized by making the detuning $\Delta$ position-dependent through magnetic field gradients along a certain direction.

4 Summary

We have shown that the resonant dipole–dipole interaction between Rydberg atoms allows one to engineer effective spin-1/2 models where the spin excitations experience a staggered magnetic field in a triangular lattice. A necessary condition for engineering artificial magnetic fields is that time-reversal symmetry of the system is broken. In our system, this is achieved by external fields shifting the Zeeman sub-levels of the considered $ns_{1/2}$ and $np_{3/2}$ manifolds. In this way, we ensure that the spin excitation couples to different dipole transitions on the $\mathcal {B}$ and $\mathcal {R}$ lattices with dipole moments $\mathbf {d}_{\mathcal {B}}$ and $\mathbf {d}_{\mathcal {R}}$, respectively. These dipole moments have a well-defined relative phase which is different from zero. Since $\mathbf {d}_{\mathcal {B}}$ and $\mathbf {d}_{\mathcal {R}}$ are orthogonal, we find that the phase of the hopping amplitude is determined by the azimuthal angle associated with the relative position of the two sites connected by the hop.

We find that the magnitude of the magnetic flux through an elementary triangular plaquette can be controlled by changing the ratio b / a of the rectangular sub-lattices. In addition, the staggered magnetic field endows the single-particle band structure with non-trivial Chern numbers. The Chern number of the lower band can be adjusted between $C=0,\,1$ and 2 and its value depends on the lattice parameters and the detuning $\Delta$ between the $\mathcal {B}$ and $\mathcal {R}$ lattices.

The quantum simulation of the dynamics of a single excitation shows that an excitation placed at an edge of the lattice will propagate along the edge in a specific direction. This effect is a direct consequence of the artificial magnetic field. The topological features of the bands can be explored by monitoring the deflection of the exciton motion due to the nonzero Berry curvature in either the lower or upper band. An intriguing prospect for future studies is the investigation of quantum many-body states. Here the hard-core interaction between the particles is expected to modify the single-particle picture considerably, and the interplay of strong interactions and complex hopping amplitudes may give rise to exotic quantum phases like fractional Chern insulators.

Appendices

Appendix 1: Dipole matrix elements

We evaluate the matrix elements of the electric-dipole-moment operator $\varvec{\hat{d}}$ of an individual atom via the Wigner–Eckert theorem [64, 65] and find

$$\begin{aligned} \langle nl'_{j'}m' |\varvec{\hat{d}}|nl_{j}m\rangle&= \mathcal {D} \sum _{q=-1}^1 C_{jm1q}^{j' m'} {\varvec{\mathbf {\epsilon }}}_q \, , \end{aligned}$$

(23)

where $C_{jm1q}^{j'm'}$ are Clebsch–Gordan coefficients and the spherical unit vectors ${\varvec{\mathbf {\epsilon }}}_q$ in Eq. (23) are defined as

$$\begin{aligned} \mathbf {\epsilon }_{1}=-\frac{\mathbf {e}_x-i \mathbf {e}_y}{\sqrt{2}},\quad \mathbf {\epsilon }_{0}=\mathbf {e}_z,\quad \mathbf {\epsilon }_{-1}=\frac{\mathbf {e}_x+i \mathbf {e}_y}{\sqrt{2}} \,. \end{aligned}$$

(24)

The reduced dipole matrix element is [64, 65]

$$\begin{aligned} \mathcal {D} =&(-1)^{\mathrm {j+l'-1/2}}\sqrt{2j+1}\sqrt{2l+1} \nonumber \\&\left\{ \begin{array}{ccc} l' &{} l &{} 1 \\ j &{} j' &{} 1/2 \end{array} \right\} C_{10l0}^{l'0} e \langle n' l' |r|nl\rangle \, , \end{aligned}$$

(25)

where the $3\times 2$ matrix in curly braces is the Wigner $6-j$ symbol, e is the elementary charge, and $\langle n'l' |r|nl\rangle$ is a radial matrix element.

Appendix B: Rubidium parameters

Here we calculate the strength of the dipole–dipole interaction for rubidium atoms and estimate the magnitude of the level shifts required for realizing our model. For $ns_{1/2}\leftrightarrow np_{3/2}$ transitions in rubidium with principal quantum number $n=70$, the reduced dipole moment $\mathcal {D}$ in Eq. (25) is given by

$$\begin{aligned} \mathcal {D} \approx 2909 e a_0\,, \end{aligned}$$

(26)

where e is the elementary charge and $a_0$ is the Bohr radius. It follows that the strength of the dipole–dipole coupling $V_0$ in Eq. (7) for $a=20\,\upmu \text {m}$ is

$$\begin{aligned} V_0/\hbar \approx 2\pi \times 1.03 \,\text {MHz}\,. \end{aligned}$$

(27)

The lifetime of the $ns_{1/2}$ and $np_{3/2}$ states at temperature $T=300\text {K}$ and for $n=70$ is $T_\mathrm{s}\approx 151.6\,\upmu \text {s}$ and $T_\mathrm{p}\approx 191.3\,\upmu \text {s}$, respectively [66]. Note that these values take into account the lifetime reduction due to blackbody radiation. The hopping rates vary with the lattice parameters but are typically of the order of $V_0$. It follows that in principle many coherent hopping events can be observed before losses due to spontaneous emission set in. This finding is consistent with the experimental observations in Ref. [42]. Note that the magnitude of $V_0$ can be increased by reducing the size of the lattice constant a or by increasing n.

Next we discuss the requirements for reducing the general Hamiltonian in Eq. (2) to our model in Eq. (14). First, we note that the level shifts induced between Zeeman sub-states must be large compared to $V_0$ and hence of the order of $10\,\text {MHz}$. Shifts of this magnitude can be realized with weak magnetic fields [67] or AC stark shifts [42]. Furthermore, the fine structure splitting between the $ns_{1/2}$ and $np_{3/2}$ manifolds is $\Delta E_{\text {FS}}\approx 2\pi \times 10.8\,\text {GHz}$ [68], which is much larger than $V_0$, and hence, it is justified to neglect off-resonant terms in Eq. (3). Finally, we note that the energy difference between the $np_{3/2}$ manifold and the nearby $np_{1/2}$ manifold is approximately $285\,\text {MHz}$ [68], which is also much larger than $V_0$. It follows that the $np_{1/2}$ states can be safely neglected.

Appendix C: k-space Hamiltonian

The k-space Hamiltonian can be obtained by considering the single-excitation sub-space $\mathcal {E}_1$ spanned by the basis states

$$\begin{aligned} |\alpha \rangle = S_{\alpha }^+|0\rangle \,, \end{aligned}$$

(28)

where $|\alpha \rangle$ denotes one p excitation at site $\alpha$ and $|0\rangle$ is the “vacuum” state with zero excitations, i.e. the atoms at all lattice sites are in state $|s_{1/2}1/2\rangle$. In order to solve the eigenvalue equation

$$\begin{aligned} H_{\text {eff}}|\psi \rangle = E |\psi \rangle \end{aligned}$$

(29)

with $|\psi \rangle \in \mathcal {E}_1$, we describe the lattice in Fig. 1 by a rectangular Bravais lattice with a two-atomic basis. More specifically, the direct lattice points are given by the $\mathcal {R}$ atoms such that the basis is comprised of one $\mathcal {R}$ atom at $\mathbf {0}$ and one $\mathcal {B}$ atom at $(\mathbf {a}+\mathbf {b})/2$. According to Bloch’s theorem [69], we can solve Eq. (29) with the Ansatz

$$\begin{aligned} |\psi \rangle = \sum \limits _{\alpha } u_{\alpha } |\alpha \rangle \,, \end{aligned}$$

(30)

where the coefficients $u_{\alpha }$ can be written as

$$\begin{aligned} u_{\alpha } = \left\{ \begin{array}{ll} \psi _{\mathcal {R}}e^{\mathrm {i}\mathbf {k}\cdot \mathbf {U}(\alpha )} ,&{} \alpha \in \mathcal {R}\,, \\ \psi _{\mathcal {B}}e^{\mathrm {i}\mathbf {k}\cdot \mathbf {U}(\alpha )} ,&{} \alpha \in \mathcal {B} \, , \end{array} \right. \end{aligned}$$

(31)

and $\mathbf {k}$ is a point in the first Brillouin zone of the direct lattice. The vector $\mathbf {U}(\alpha )$ in Eq. (31) is the Bravais lattice point associated with site $\alpha$,

$$\begin{aligned} \mathbf {U}(\alpha ) = \left\{ \begin{array}{ll} \mathbf {R}_{\alpha } ,&{} \alpha \in \mathcal {R}\,, \\ \mathbf {R}_{\alpha }-(\mathbf {a}+\mathbf {b})/2 ,&{} \alpha \in \mathcal {B} \, . \end{array} \right. \end{aligned}$$

(32)

With Eqs. (30) and (31), Eq. (29) can be reduced to the following matrix equation for the amplitudes $\psi _{\mathcal {R}}$ and $\psi _{\mathcal {B}}$,

$$\begin{aligned} \mathcal {H}(\mathbf {k}) \left( \begin{array}{l} \psi _{\mathcal {R}} \\ \psi _{\mathcal {B}} \end{array} \right) = E \left( \begin{array}{l} \psi _{\mathcal {R}} \\ \psi _{\mathcal {B}} \end{array} \right) \,, \end{aligned}$$

(33)

where the $2\times 2$ matrix $\mathcal {H}(\mathbf {k})$ is the k-space Hamiltonian. We find $\mathcal {H}(\mathbf {k})$ using the software package MATHEMATICA [70] for each set of lattice parameters a and b. In general, the resulting expressions are too complicated to display here. In the special case of nearest-neighbour interactions only, we find

$$\begin{aligned} {[}\mathcal {H}(\mathbf {k})]_{11}&= -V_0 \cos (\mathbf {k}\cdot \mathbf {a})+ \hbar \Delta \,, \end{aligned}$$

(34a)

$$\begin{aligned} {[}\mathcal {H}(\mathbf {k})]_{12}&=\frac{V_0 \sqrt{48}}{[1+(b/a)^2]^{3/2}} \left( e^{- \mathrm {i}(\mathbf {k}\cdot \mathbf {a}+\mathbf {k}\cdot \mathbf {b})}e^{-2\mathrm {i}\alpha }+e^{-2\mathrm {i}\alpha } \right. \nonumber \\&\qquad \quad \left. +e^{-\mathrm {i}\mathbf {k}\cdot \mathbf {a}}e^{2\mathrm {i}\alpha } +e^{ -\mathrm {i}\mathbf {k}\cdot \mathbf {b}}e^{2\mathrm {i}\alpha }\right) \,, \end{aligned}$$

(34b)

$$\begin{aligned} {[}\mathcal {H}(\mathbf {k})]_{22}&= -\frac{1}{3} V_0 \cos (\mathbf {k}\cdot \mathbf {a})\,, \end{aligned}$$

(34c)

where $\cos (\alpha )=1/[1+(b/a)^2]^{1/2}$ and $[\mathcal {H}(\mathbf {k})]_{21}=[\mathcal {H}(\mathbf {k})]_{12}^*$.