High spatial resolution laser cavity extinction and laser-induced incandescence in low-soot-producing flames

Abstract

Accurate measurement techniques for in situ determination of soot are necessary to understand and monitor the process of soot particle production. One of these techniques is line-of-sight extinction, which is a fast, low-cost and quantitative method to investigate the soot volume fraction in flames. However, the extinction-based technique suffers from relatively high measurement uncertainty due to low signal-to-noise ratio, as the single-pass attenuation of the laser beam intensity is often insufficient. Multi-pass techniques can increase the sensitivity, but may suffer from low spatial resolution. To overcome this problem, we have developed a high spatial resolution laser cavity extinction technique to measure the soot volume fraction from low-soot-producing flames. A laser beam cavity is realised by placing two partially reflective concave mirrors on either side of the laminar diffusion flame under investigation. This configuration makes the beam convergent inside the cavity, allowing a spatial resolution within 200 μm, whilst increasing the absorption by an order of magnitude. Three different hydrocarbon fuels are tested: methane, propane and ethylene. The measurements of soot distribution across the flame show good agreement with results using laser-induced incandescence (LII) in the range from around 20 ppb to 15 ppm.

1 Introduction

Soot particles generated from combustion are both a significant atmospheric pollutant and a contributor to climate change [1–4]. Many techniques have therefore been developed to measure soot particles from a variety of sources, both via sampling and via non-intrusive techniques. Eckbreth [5] discovered laser-induced incandescence (LII) from soot, and Melton [6] proposed the possibility of a laser-heating method to investigate soot particles based on the linear response of LII signal to soot volume fraction. Over the last several decades, LII has become the main non-intrusive method for in situ soot volume fraction measurement in flames, given its ability to resolve soot concentrations quantitatively and with good spatial resolution. Nevertheless, LII requires independent calibration, typically via line-of-sight extinction (LOSE) measurements [7], and unsteady measurements are only possible with high power, high repetition rate lasers. As an alternative to calibration via extinction, Snelling et al. [8] developed a quantitative LII calibration system by collecting the radiation from a strip filament lamp of known brightness temperature to relate to the observations using LII, after certain assumptions are made about the soot particle temperature. Calibration via extinction remains the preferred (and simpler) method for quantitative LII measurement of soot particles in flames. Shaddix et al. [9, 10] exploited these combined measurements to produce a popular database of quantitative soot measurements in laminar hydrocarbon diffusion flames. The same technique was also applied by other researchers in the investigations of various flames, such as laminar diffusion flames [11–13], laminar premixed flames [14–16] and turbulent diffusion flames [17–20].

On the other hand, LOSE measurements have some intrinsic advantages: they (a) provide close to absolute measurements of soot mass fraction, (b) are easily adapted to unsteady measurements and (c) are relatively simple and inexpensive to set-up. Thus, they have been used to monitor unsteady soot formation in diesel engines during the cycle [21–23], as well as in heavily sooting flames [24], requiring only continuous wave (CW) lasers with modest powers (tens of milliwatts), and photodiodes. The key disadvantages of LOSE are: (a) as line-of-sight measurements, they provide an integrated measurement of the soot attenuation, which can only be deconvoluted for symmetric paths or by multi-path tomography, (b) limited signal-to-noise ratio (SNR) due to low extinction in single-pass configurations and (c) poor spatial resolution in the cross-path direction, particularly when multi-pass configurations are adopted.

The cross-path spatial resolution can be improved, for example by using CCDs rather than point detectors for measurements, such as those used by Thomson et al. [11, 25], but which require sources with high power stability and spectral selectivity. Solutions for the limitations of low SNR can be mitigated by adding a beam stabiliser [9, 26], but which cannot eliminate other instrumental noise. SNR issues can be improved by using multi-pass cells, often at the expense of spatial resolution [27–30]. As alternatives, cavity ring-down spectroscopy (CRDS) [14, 31–36] and multi-pass tunable diode laser absorption spectroscopy (TDLAS) absorption methods [37–46] have been developed to obtain high SNR when concentrations are very small.

In the present study, we combine the advantages of LOSE to a multi-pass cavity absorption system using spherical mirrors to compensate for the typical loss of spatial resolution. This improves the SNR by two orders of magnitude over a single-pass system, whilst maintaining a spatial resolution of the order of 200 μm in measurements of low-sooting laminar diffusion flames. The primary distinction between the present technique and previous efforts in soot detection via CRDS [14, 34] is that the present technique does not rely on pulsed, shot-to-shot measurements, but rather a low-power, low-cost CW laser. This allows for a much simpler, less expensive system, which does not require a fast response detector and signal receiver capable of nanosecond time resolution. Moreover, it becomes possible to employ the LOSE system in unsteady situations, as demonstrated in engines [21–23]. Since soot absorption takes place over a wide range of wavelengths, the method does not require a tuneable light source. As demonstrated further on, however, the present CW-cavity LOSE method sensitivity is limited to around tens of ppb, which is higher than what CRDS methods can possibly achieve. The results obtained by this CW-cavity LOSE system are used to calibrate the LII measurements taken on the same flames. The calibrated LII and deconvoluted LOSE measurements are then compared across the radial dimension. The next sections describe the background theory, experimental set-up and results, including a detailed uncertainty analysis.

2 Methodology

2.1 Theory of cavity extinction

The LOSE method is based on the fact that light passing through a flame is scattered and absorbed by particles according to the Beer–Lambert law [47, 48]:

$$\ln \frac{I_{\mathrm{{t}}}}{I_{\mathrm{{i}}}} = - \int _{-\infty } ^{+\infty } K_{\mathrm{{e}}}(x)\; {\mathrm{{d}}}x = - P_0$$

(1)

where $I_{\mathrm{{t}}}$ and $I_{\mathrm{{i}}}$ are the intensities of the transmitted and incident beams, respectively, $K_{\mathrm{{e}}}$ is the extinction coefficient of the medium—which is determined by local soot volume fraction and optical properties—and $P_0$ represents the logarithmic loss of intensity across one pass.

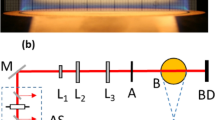
In many conditions, the extinction of light by soot is very small and cannot be detected accurately over a single pass. A multi-pass system can be organised as shown in Fig. 1.

Fig. 1

Schematic of the cavity (in the figure, $A=e^{-P_0}$; BS beam splitter; ND neutral density filter; PD photodiode; PRM partial reflective mirror)

In this diagram, the medium is confined between two mirrors of high reflectivity, $r_1$ and $r_2$, and low transmissivities $t_1$ and $t_2$, whose values are carefully measured. The total transmitted intensity $I_{\mathrm{{T}}}$ after adding up an infinite number of passes through the mirrors is:

$${{I}_{\mathrm{{T}}}}=\sum \limits _{n=1}^{\infty }{{{I}_{\mathrm{{t}}}(n)}}=\frac{{{I}_{0}}TA}{1-{{A}^{2}}R}$$

(2)

where $R=r_1r_2$, $T=t_1t_2$and A is the ratio of intensities across the flame, $A = \exp (-P_0)$. The ratio of transmitted to incident power across the cavity system is:

$$\frac{{{I}_{\mathrm{{T}}}}}{{{I}_{0}}}=\frac{TA}{1-{{A}^{2}}R}$$

(3)

and the logarithmic loss of intensity across the cavity, $P_{\mathrm{{t}}}$, is:

$${{P}_{\mathrm{{t}}}}=-\ln \frac{{{I}_{\mathrm{{T}}}}}{{{I}_{0}}}=-\ln \frac{{{I}_{\mathrm{{T}}}}}{{{I}_{0}}}=- \ln \frac{TA}{1-{{A}^{2}}R}$$

(4)

Assuming we can measure the total ratio $\frac{{I}_{\mathrm{{T}}}}{I_0} = B = \exp (-P_{\mathrm{{t}}})$, we can solve for A and thus $P_0$ by solving the quadratic equation (4):

$$A= \frac{T}{2R B}\left[ \sqrt{1+\frac{4 R B^2 }{T^2}} - 1\right]$$

(5)

$$-P_0 = \ln A = \ln \left( \frac{T}{2R}\right) - \ln B + \ln \left[ \sqrt{1+\frac{4 R B^2}{T^2}} - 1\right]$$

(6)

$$P_0= -P_{\mathrm{{t}}} - \ln \left( \frac{T}{2R}\right) - \ln \left[ \sqrt{1+\frac{4 R\exp ^2(-P_{\mathrm{{t}}})}{T^2}} - 1\right]$$

(7)

Once the value of $P_0$ is known for each chord location across the flame, it is possible to invert the function to obtain the extinction coefficient using the Abel transform, by assuming radial symmetry. The projection of the line-of-sight extinction coefficient along the chord coordinate y from the centreline is:

$$P_0(y) = 2 \int _0^{+\infty }K_{\mathrm{{e}}}(x) \; {\mathrm{{d}}}x$$

(8)

Taking $x^2+y^2=r^2$ and substituting for ${\mathrm{{d}}}x$ at fixed y, we have:

$$P_0(y)=2\int _{y}^{\infty }\frac{r K_{\mathrm{{e}}}(r)}{\sqrt{r^2-y^2}}\; {\mathrm{{d}}}r$$

(9)

which admits the inverse Abel transform:

$$K_{\mathrm{{e}}}(r)=-\frac{1}{\pi }\int _{y}^{\infty }\frac{P_0^\prime(y)}{\sqrt{y^2-r^2}}\; {\mathrm{{d}}}y$$

(10)

The integration is conducted by using the three-point scheme by Dasch [49]. The details of the calculation of $K_{\mathrm{{e}}}(r)$ are described in “Appendix 1”.

2.2 Extinction coefficient and soot volume fraction

The extinction coefficient $K_{\mathrm{{e}}}(r)$ represents the sum of the scattered and absorbed energy fraction per unit length. The scattered light contribution to the extinction increases with the relative size of aggregate particles. Primary soot particles have been shown to be sufficiently small relative to the wavelength of the light, so that their direct scatter contribution is negligible [50–52]. However, soot particles are formed of aggregated and transformed primary particles, an effect that becomes more significant under high soot loading. Krishnan et al. [53] found that the ratio of scattering to extinction cross section could be as large as 0.47 in the visible range for heavy sooting diffusion flames fuelled with n-heptane, benzene and toluene. Nevertheless, Liu et al. investigated the signal trapping effect in LII measurements using the Rayleigh–Debye–Gans model to show that the contribution of scattering of soot particles in laminar diffusion flames should be negligible [52].

In the approximation of negligible contribution of scattering, the extinction coefficient is equal to the absorption coefficient, which is expressed as [50]:

$${K}_{\mathrm{{a}}}=n\frac{{\pi }^{2}}{\lambda _{\mathrm{{e}}} }E(m)\int _{0}^{\infty }p(D){D}^{3}\; {\mathrm{{d}}}D$$

(11)

where n is the number density of soot particles, D is the particle diameter, p(D) is the particle diameter probability function and E(m) is the soot absorption function:

$$E(m)=-\text {Im}\left( \frac{{{m}^{2}}-1}{{{m}^{2}}+2} \right)$$

(12)

where m is the complex index of refraction of soot. Given that the soot volume fraction is equal to $f_{\mathrm{{v}}} = n\pi \bar{D}^3/6$, and taking $\bar{D}$ to be the mean diameter $\bar{D}^3 = \int _{0}^{\infty }P(D){D}^{3}\; {\mathrm{{d}}}D$, we have:

$${{K}_{\mathrm{{e}}}}=K_{\mathrm{{a}}} = \frac{6\pi E(m)}{\lambda _{\mathrm{{e}}} }{{f}_{\rm{v}}}$$

(13)

In reporting the experimental results, we therefore have two options: (a) neglect the contribution of scattering and choose a value for the refraction coefficient to extract the soot value fraction and (b) report the experimentally obtained values of $K_{\mathrm{{e}}}$, so that the results are useful even as the controversy regarding the contribution of scattering and the value of the refraction coefficient is resolved. In the present study, we use the same assumptions as in Shaddix et al. [9, 10], in comparison with the respective values, e.g. negligible scattering and the same assume value of E(m), in order to compare the published values of E(m). The LII results of the present study are thus calibrated and compared with extinction data. Meanwhile, the values of $K_{\mathrm{{e}}}$ are reported as well, which are independent of any assumptions about E(m), and can be useful in the validation of future models. The values are available in the form of numerical data as supplemental material.

3 Experiment

3.1 Burner and flames

The experiments were performed on a laminar diffusion burner and operating conditions almost identical to that used by Shaddix et al. [9, 10] (Fig. 2). The diameter of the inner fuel tube is 10.5 mm, and that for the outer air co-flow tube is 96.8 mm. The mass flow controllers (MFC, Alicat MC20 for fuel, MCR500 for air, accuracy $\pm 0.8\,\%$ FS) are used to control the mass flow of fuels and co-flow air. The burner is mounted on a traverse platform to scan the position with precision of 0.01 mm along the horizontal direction and 0.5 mm along the vertical. Methane, ethylene and propane flames are investigated, with operational conditions listed in Table 1, mirroring the prior work of Shaddix et al. Figure 3 shows natural light photographs of the five tested flames.

Fig. 2

Schematic cross section (left) and top view (right) of the burner used in present work

Table 1 Tested conditions for laminar diffusion flames

Fig. 3

Natural luminosity of laminar diffusion flames tested (camera model: Canon EOS 6D DLSR, exposure time $=$ 1/60 s, photographic sensitivity (ISO) $=$ 1250; lens model: Canon EF 24–105 mm f/4L IS, f $=$ 4.0, focal length $=$ 105 mm)

3.2 Cavity extinction measurement

Fig. 4

Diagram of the LOSE system (DL diode laser, M mirror, BS beam sampler, ND neutral density filter, PD photodiode, CVL convex lens, CCL concave lens, NB narrow band filter, PRM partially reflective mirror, AMP Amplifier, DAQ data acquisition board)

The schematic of the laser cavity measurement system is shown in Fig. 4. A diode laser (Omicron ${\mathrm {LuxX}}-638-150$, 638 nm wavelength, 150 mW maximum power) is used as laser source. Near-infrared light is preferred because visible wavelengths can be absorbed by polycyclic aromatic hydrocarbons (PAHs), creating uncertainties. A longer wavelength also means that the Rayleigh approximation is still valid for larger soot aggregates. The incident laser beam is split via a beam sampler (Thorlabs BSF05-A) into a reference laser beam ($\le$1 % of the power) and the probe laser beam. A neutral density filter ND1 (Thorlabs NE40A, optical density $=$ 4.0) is used to attenuate the beam density to a range relevant for the reference photodiode. The probe beam is focused by a planar-convex lens P-CVL1 (Thorlabs LA1301-A, 250 mm focal length) and a planar-concave lens P-CCL (Thorlabs LC4888, $-100$ mm focal length) down to a diameter of 200 $\upmu$m before entering the cavity. The two mirrors PRM1 (COMAR Optics customised, 25 mm diameter, 1000 mm focal length, reflectivity: $r_1=98.11 \pm 0.20\,\%$, transmissivity: $t_1=1.530 \pm 0.147\,\%$ at 638 nm wavelength) and PRM2 (COMAR Optics customised, 1000 mm focal length, reflectivity: $r_2=98.11\,\pm \,0.19\,\%$, transmissivity: $t_2=1.537 \pm 0.159\,\%$ at 638 nm wavelength) are aligned and separated by 17.5 cm, with the burner in the middle. The small separation distance and the large radius of curvature of the mirror surfaces ensure that the laser beam diameter is nearly constant between the mirrors. The spatial resolution of the measurements has been characterised by profiling of the laser beam using a sharp blade to block the radial intensity and differentiating. The results show that the beam profile is approximately Gaussian, with FWHM $\approx$ 210 μm. The distance selected between two points in the LOSE measurements is 0.25 mm, which is larger than the diameter of the beam. The spatial resolution of the measurements is therefore approximately 200 μm throughout the measurement region. Unlike species with low molecular weight, absorption of soot laser light takes place over a wide range of wavelengths, so that phase matching is not required for maximum light extinction. The detection system consists of two identical photodiodes, PD1 and PD2 (Thorlabs SM05PD1A Silicon Photodiode, 350–1100 nm, Cathode Grounded), which detect the light sampled from the transmitted and reference beam, respectively. Maximum signal-to-noise ratio is ensured by selecting mirror reflectivity close to unity. The photocurrents obtained from the two photodiodes PD1 and PD2 ($i_1$ and $i_2$) have been determined to be linearly proportional to the respective incident intensities. These are compared using a logarithmic amplifier (Texas Instrument LOG104), which improves the SNR relatively to a linear amplifier for this application. The output voltage of the amplifier, V, is obtained as:

$$V=C \log _{10} \frac{i_1}{i_2}$$

(14)

where the calibration constant $C = 0.496 \pm 0.0088$ V was obtained using an accurate reference current. A data acquisition board (NI USB-6009) was used to acquire the amplifier signal at 14-bit resolution and at 2000 Hz for 10 s using LabView software. The value of the current ratio is affected by laser intensity fluctuations, flame luminosity and dark noise of the photodetectors. The description of the uncertainty calculations is detailed in “Appendix 2”.

3.3 LII measurement

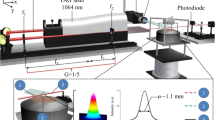
The 2D LII measurements were taken using the set-up described in Fig. 5. The laser source is a 532 nm Nd:YAG laser (Litron nanoPIV) firing at 10–25 Hz. The laser sheet was collimated into a parallel sheet by a series of beam shaping optics (Thorlabs cylindrical lens with focus lengths of 75, $-25$ and 100 mm, respectively), followed by an aperture to generate a top-hat profile. The laser beam energy profile was detected using a cuvette filled with fluorescent dye (Rhodamine 6G in ethanol solvent) using an unintensified CCD camera (LaVision Imager Pro X 4M, 1 $\upmu \hbox {s}$ gate width, $1024\times 1024$ pixels) equipped with a Nikon AF Micro Nikkor 60 mm lens (f/5.6) and a narrow band filter (Thorlabs FB600-10, central $\hbox {wavelength}=600\pm 2 \,\hbox { nm}, \hbox { FWHM}=10 \pm 2$ nm). The laser power was verified to be top hat from dye imaging measurements. The LII signal induced by the laser sheet was captured by an ICCD camera (LaVision Intensified Relay Optics and Imager Pro X 4M, $1024\times 1024$ pixels) through a Nikon AF Micro Nikkor 60 mm lens 175 (f/2.8) and band filter (Thorlabs FB400-40, central $\hbox {wavelength}=400\pm 8\, \hbox { nm}, \hbox { FWHM}=40\pm 8 \hbox { nm})$ to minimise luminosity from PAH fluorescence, $C_2$ radiation and flame. A gate width of 100 ns was used to maximise the signal-to-noise ratio. The relatively long gate width may bias the SVF measurements towards larger particles [7], but since focus of the paper is on comparisons between the multi-pass method and LII, this effect is relatively unimportant.

Fig. 5

Schematic of LII measurement setup (P prism, BS beam splitter, NB1 $400\pm 20$ nm band filter, NB2 $600\pm 5$ nm band filter, BD beam dump)

Figure 6 shows the dependence of the LII signal on the fluence of the laser sheet. The LII signal at each fluence is an average value of all pixels of the LII signal (100 ns gate width) from HAB $=$ 34 to 66 mm for ethylene flame case B. In the low laser fluence region $({\sim }0.2\,\hbox {J/cm}^2)$, the LII signal rises rapidly with increasing laser fluence, since the radiation intensity scales with $T^4$. As the fluence increases, the sublimation of soot particles becomes significant, so that the LII signal reaches a maximum around 0.2–0.3 $\hbox {J}/\hbox {cm}^2$), as indicated in the marked rectangle. In this region, the LII signal is less sensitive to local laser fluence. In this work, it is assumed that the fluence dependence of LII signal is similar in the $\hbox {CH}_4$ and $\hbox {C}_2\hbox {H}_4$ flames, even though the soot particle sizes in these two flames are likely to be significantly different, as discussed by Shaddix et al. [9]. Figure 7 shows the beam profile and variance over 500 shots, as characterised by the resulting fluorescence in a cuvette containing Rhodamine 6G dye. The local intensity fluctuation of laser sheet is as small as 2.5 % in 500 shots as shown in Fig. 7, and the error introduced by either laser shot fluctuations or spatial fluency is smaller than 1 %. A total of 250 LII images are acquired for each condition, at an acquisition rate of 25 Hz. All images are averaged, with the background noise subtracted. The nominal spatial resolution is $33\; \upmu \hbox {m}/\hbox {pixel}$ for an imaging area of $34.1\times 34.1\, \hbox { mm}^2$.

Fig. 6

Fluence dependence of the LII signal as a function of the fluence of laser sheet; the plateau region (in the marked rectangle) is selected to conduct LII measurements

Fig. 7

Normalised laser beam intensity profile used for LII excitation. Left Rhodamine 6G fluorescence excited by laser sheet in cuvette; right integrated fluorescent light intensity profile over the region shown in the highlighted rectangle

3.4 LII calibration

According to Planck’s law, the power per unit area and solid angle emitted by an object with emissivity of $\varepsilon _{\lambda _{\mathrm{{s}}}}$ at the respective wavelength equal:

$$E={\varepsilon }_{\lambda _{\mathrm{{s}}}}\frac{2 h c^{2}}{\lambda _{\mathrm{{s}}}^{\text {5}}\left[ \exp \left( \frac{h c}{\lambda _{\mathrm{{s}}} {k}_{\mathrm{{B}}} T} \right) \ -\; 1 \right] }$$

(15)

where h is Planck’s constant, c is the speed of light, $k_{\mathrm{{B}}}$ is Boltzmann’s constant, ${\lambda _{\mathrm{{s}}}}$ is the emission signal wavelength and T is the surface temperature, often taken to be the sublimation temperature of the soot. The total solid angle for a grey element of surface $\text {d}{{A}_{\mathrm{{P}}}}$ is the hemispherical $2\pi,$ and the total area of a spherical particle of diameter D is $A_{\mathrm{{P}}} = \pi D^2$, so that the total emitted power is:

$${{S}_{D}}={{\varepsilon }_{\lambda _{\mathrm{{s}}} }}\frac{\text {2}{{\pi }^{2}}{{D}^{2}}h{{c}^{2}}}{{{\lambda _{\mathrm{{s}}} }^{\text {5}}}\left[ \text {exp}\left( \frac{h{{c}}}{\lambda _{\mathrm{{s}}} {{k}_{\mathrm{{B}}}}T} \right) \ -\ \text {1} \right] }$$

(16)

According to Kirchhoff’s law [54–56], absorptivity is equal to emissivity; thus, the spectral emissivity is assumed to be:

$${{\varepsilon }_{{{\lambda _{\mathrm{{s}}}}}}=\frac{4\pi D E(m)}{{{\lambda _{\mathrm{{s}}} }}}}$$

(17)

Taking Eq. (17) into Eq. (16), we have:

$${{S}_{D}}=\frac{48{{\pi }^{2}}h{{c}^{2}}E(m)}{{{\lambda _{\mathrm{{s}}} }^{\text {6}}}\left[ \text {exp}\left( \frac{h{{c}}}{\lambda _{\mathrm{{s}}} {{k}_{\mathrm{{B}}}}T} \right) \ -\ \text {1} \right] }\ \frac{\pi {{D}^{3}}}{6} ={{C}_{\mathrm{{em}}}}\frac{\pi {{D}^{3}}}{6}$$

(18)

where $C_{\mathrm{{em}}}$ depends on $\lambda _{\mathrm{{s}}}$, T and the index of refraction of the particle at the emitting wavelength. The LII signal from a collection of particles in the sample region is obtained as the integrated signal from each particle over the probe volume $\Delta V$, and accounting for the mean collection angle ${\Omega _{\mathrm{{c}}}}$, optical efficiency $\eta _{\mathrm{{o}}}$, detector sensitivity $\phi _{\mathrm{{d}}}$, number of particles per unit volume n and particle size probability distribution function p(D), we have:

$$S_{\text {LII}} =C_{\mathrm{{em}}} \frac{{\Omega _{\mathrm{{c}}}}}{4\pi } \eta _{\mathrm{{o}}} \phi _{\mathrm{{d}}} \Delta V n\int _0^{\infty } p(D) \frac{\pi {D}^{3}}{6} \; {\mathrm{{d}}}D = C_{\mathrm{{det}}} C_{\mathrm{{em}}} f_{\mathrm{{v}}} = K_{\text {LII}} f_{\mathrm{{v}}}$$

(19)

where $C_{\mathrm{{det}}}=\frac{{\Omega _{\mathrm{{c}}}}}{4\pi } \eta _{\mathrm{{o}}} \phi _{\mathrm{{d}}} \Delta V$, and $K_{\text {LII}}=C_{\mathrm{{det}}} C_{\mathrm{{em}}}$ is the calibration constant connecting the LII signal to the soot volume fraction. $K_{\text {LII}}$ is obtained by connecting the measured extinction to the corresponding integrated soot volume fraction, as follows:

$${{P}_{0}(0)} = \int _{-\infty }^{+\infty }{{{K}_{\mathrm{{e}}}}(r)}\; {\mathrm{{d}}}r = \frac{6\pi E(m)}{\lambda _{\text {e}} }\int _{-\infty }^{+\infty }{{{f}_{v}}(r)} \; {\mathrm{{d}}}r$$

(20)

$$=\frac{6\pi E(m)}{\lambda _{\text {e}} } \frac{1}{K_{\text {LII}}} \int _{-\infty }^{+\infty } {S}_{\text {LII}} (r)\; {\mathrm{{d}}}r$$

(21)

The calibration constant ${{K}_{\text {LII}}}$ can therefore be obtained from measurements using:

$${K}_{\text {LII}}= \frac{1}{{P}_{0}(0)} { \frac{6\pi E(m)}{\lambda _{\text {e}} }\int _{-\infty }^{+\infty }{S_{\text {LII}}(r)}\; {\mathrm{{d}}r} }$$

(22)

$C_{\mathrm{{det}}}$ is only a function of the probe volume and light collection efficiency, and $C_{\mathrm{{em}}}$ is a function of soot emissivity characteristics. Their product, ${{K}_{\text {LII}}}$ is the ratio of the mean collected LII signal at $\lambda _{\mathrm{{s}}}$ per unit soot extinction.

The calibration hinges on the assumption that scattering is unimportant relative to absorption, as has been discussed above. In these particular calibrations, the measurement height is selected to be in the region where the highest soot concentration exists (as determined from extinction measurements). For the calibration of the methane flames, we consider case B at a height of 75 mm above the burner (HAB = 75 mm). For the ethylene and propane flames, we consider the ethylene flame (Case B) at HAB = 50 mm. The calibration constants, calculated via Eq. (22), give ${{K}_{\text {LII}}}=8.75\times {{10}^{8}}$ for methane flames and ${{K}_{\text {LII}}}=3.33\times {{10}^{7}}$ for ethylene and propane flames. The difference in the calibration constants arises due to the difference in the detector sensitivity via the intensifier gain used. Methane soot production is much lower than that of ethylene, requiring a gain of 75 % compared to 40 % for the other fuels. A linear change in gain setting on the camera changes the actual gain constant exponentially; thus, the ratio in calibration constant is not linear. The value of the soot absorption function, E(m), used for comparison with the work of Shaddix [9, 10], is assumed to be 0.26, based on an estimated value of the index of refraction $m=1.57-0.56i$ by D’Alessio et al. [57]. However, as discussed above, the particular value of the constant is not important for the comparisons, but only for the absolute value obtained of the soot volume fraction.

4 Results and discussion

4.1 Measured extinction coefficient K_e

Since measurements of soot volume fractions depend on the particular choice of E(m), it is useful to consider the direct, Abel unwrapped measurements of ${K_{\mathrm{{e}}}(r)}$ from the light attenuation. Figure 8 shows measured extinction coefficient $K_{\mathrm{{e}}}$ for all tested flames at different HABs. We note that in all cases, the peak extinction moves from the outer to the inner region as the HAB increases, and that values for the extinction coefficient in the case of ethylene and propane are up to two orders of magnitude higher than in the case of methane. The numerical measured values of $K_{\mathrm{{e}}} (r)$ appear as supplemental material to the paper. The measured values of $K_{\mathrm{{e}}}$ are used to obtain the SVF according to Eq. (13) and an E(m) value of 0.26, for calibration of LII and further comparison with other studies, as shown in the next subsection.

Fig. 8

Extinction coefficient $K_{\mathrm{{e}}}$ measured for various test flames at different HABs. a methane case A; b methane case B; c propane; d ethylene case A; e ethylene case B. Note that not all HABs’ data are shown in this figure. The dataset of $K_{\mathrm{{e}}}$ data is available in the supplemental material of this paper

4.2 Comparison of cavity extinction and LII

Figure 9 shows LII images for each case considered. In order to accommodate the length-to-width ratio of the flames, three different series of images were taken (250 images for each series), with images connecting at heights of 34–68 mm. Comparisons with the extinction measurements are provided for one half of the flame, which is symmetric. The methane flame produces significantly less soot (sub-ppm) than the other two fuels.

Fig. 9

LII images for various test flames (from left to right): methane case A, methane case B, propane, ethylene case A, ethylene case B. Note that there is an order of magnitude difference in scale between the methane cases and other fuels. Images are composites of three separate series, with overlaps at 34–68 mm

The present LII measurements are compared with previous measurements by Shaddix et al. [9, 10], extracted from NIST’s website [58], as shown in Fig. 10. The two studies differ slightly in the size of the diffusion jet diameter (10.5 mm for the current study and 11 mm in [9, 10]). Therefore, the results are compared based on the non-dimensional radius $r/r_0$, where $r_0$ is the inner radius of the fuel tube for each burner. The peak concentrations measured in this study are within 20 % of those previously measured, for the worst case scenario of low soot (methane). Other cases for propane and ethane differ by around 15 %. There are two differences between the current study and the previous one: (a) the tube diameter is different by 0.5 mm and (b) the tube material may be different. In the present study, the tube is made of copper, but the material in the previous work is not reported. If the original measurements were taken using a material with lower thermal conductivity, one would expect lower soot production, as shown in Fig. 10.

Fig. 10

LII measurements in the present work (blue) and from Shaddix et al.’s [9, 10, 58] (red) for methane flame Case B, plotted against the non-dimensional radial distance $r/r_0,$ for different heights above the burner (HAB)

The LII and cavity extinction measurements obtained are directly compared in Figs. 11, 12, 13, 14 and 15 at various flame heights, for methane, propane and ethylene flames. The error bars represent the combined uncertainty associated with estimated instrument error, variances due to flame fluctuations, and the tomographic inversion, as discussed in further on. Since the LII is calibrated from the extinction measurements from the integral of the volume fraction, the absolute uncertainties from the extinction measurements are propagated to the LII measurements, and the error bars on the latter only represent the variances in the images.

Starting with the measurements with higher concentrations, for propane and ethylene flames shown in Figs. 13, 14 and 15, it is clear that the cavity LOSE measurements are in good, if not perfect agreement with the LII measurements throughout the domain. Measurements in the outer zone are in better agreement than in the inner zone, owing to the compounded uncertainties in the inversion (Sect. 4.3). Nevertheless, the peaks are well resolved, and the agreement is good throughout the flame. In cases where the peak concentrations are of the order of tens of ppm, the resolution of the peak is very good (Case B, Fig. 15). As the peak SVF dips below 1 ppm, however (Figs. 11, 12), the uncertainties become larger, and disagreements appear. Nevertheless, the LOSE measurements are able to capture the gradients indicated by the LII images, at values below 1 ppm. To our knowledge, there have been no prior reported CW-extinction measurements of soot volume fraction extending below 0.1 ppm. Further data analysis shows that for a stable measurement target without flickering, the measurement error can be lower than 20 ppb, resulting in a measurement range of down to tens of ppb, but not lower.

Fig. 11

Soot volume fraction $f_{\mathrm{{v}}}$ measured using cavity extinction (blue circles) and LII (red line) for the methane flame (case A). Error bars for extinction (blue) are discussed in the text; upper and lower limits for LII (light red regions) represent image variances

Fig. 12

Soot volume fraction $f_{\mathrm{{v}}}$ measured using cavity extinction (blue circles) and LII (red line) for the methane flame (case B)

Fig. 13

Soot volume fraction $f_{\mathrm{{v}}}$ measured using cavity extinction (blue circles) and LII (red line) for propane. The blue error bars for the extinction measurements are too small to be displayed at this scale

Fig. 14

Soot volume fraction $f_{\mathrm{{v}}}$ using cavity extinction (blue circles) and LII (red line) for LII results for ethylene flame (case A)

Fig. 15

Soot volume fraction $f_{\mathrm{{v}}}$ using cavity extinction (blue circles) and LII (red line) for ethylene flame (case B)

4.3 Analysis of uncertainties

The uncertainties attributed to the LOSE measurements arise from three sources: (a) instrumentation error, (b) tomographic inversion via the Abel transform and (c) flame fluctuations. Systematic errors in $f_{\mathrm{{v}}}$ can also arise from errors in the assumed value for E(m). These uncertainties are discussed in the following paragraphs.

The instrumentation errors are due to the intrinsic uncertainty in light signal measurements, as outlined in “Appendix 2”. The relative importance of instrumentation uncertainty can be considered by selecting a region of the flame where flame fluctuations and Abel transform errors are negligible. This is done by selecting a point sufficiently far upstream on the flame, at an edge position. Figure 16 shows the relationship between the instrumentation uncertainty and local soot volume fraction at $r=3.75$ mm, height above burner (HAB) $=$ 10, 15 mm, which closely obeys a linear relationship with slope of 0.15 and intercept of 0.0171 ppm.

Fig. 16

Instrumentation uncertainty as a function of local soot volume fraction at flame edge positions ($r=3.75$ mm, HAB $=$ 10, 15 mm)

The Abel transform leads to cumulative errors between the edge and the centreline of the domain. These errors are a function of the intrinsic fluctuation, convoluted with the discretisation of the field. Dasch [49] investigated the error generated by the three-point Abel transform and compared it with three other one-dimensional tomographic methods (two-point transform, onion-peeling and filtered back-projection methods), concluding that the three-point Abel transform generated the smallest error. The uncertainty arising from the algorithm depends on the field, so it cannot be quantified in general, but only in reference to a particular field. Here, we use a numerical test to bracket the uncertainties, as shown in Figs. 17 and 18. The smooth Gaussian test distributions in Figs. 17 and 18 are similar to the distribution of the soot volume fraction in positions downstream and upstream of the flames, respectively. Different sampling intervals (0.125, 0.25 and 0.5 mm) are used to test the inversion uncertainties. The projection values are obtained based on the field given, and the three-point Abel transform is utilised to calculate the constructed field value. As expected, the smallest interval resolution offers the lowest error. In the present work, the spatial resolution of the cavity extinction measurements is around 200 μm, so a 0.25 mm interval is representative, yielding a relative error around the peak of 10 % for the lower flame height (where we have more soot in flame edge) and 18 % for the greater flame height (more soot in flame centre). For a sample interval of 0.125 mm, the error values are 5 and 12 %, respectively. The error due to tomography is therefore relatively large, and the spatial resolution is very important. However, a smaller sampling interval does not always result in a reduction in error. Because of the cumulative effect of the Abel transform, the error at the edge region can be accumulated to the centre. If we simply assume the instrumental error of each projection value P to be the same, the error of each deconvoluted value (after Abel transform) can be calculated as [49]:

$$u({{r}_{i}})=\frac{{{u}_{\mathrm{{p}}}}}{\Delta r}{{\left( \sum \limits _{j=0}^{\infty }{{{D}_{ij}}^{2}} \right) }^{\frac{1}{2}}}$$

(23)

where ${r}_{i}=i\Delta r$ is the distance from the centre of the field, $u_{\mathrm{{p}}}$ is the error in the projection value and $\Delta r$ is the sampling interval. ${{{D}_{ij}}}$ is a function of the linear Abel transform operators $I_{ij}(0)$ and $I_{ij}(1)$:

$$\begin{aligned} {{D}_{ij}}=\left\{ \begin{array}{lr} 0 &j<i-1 \\ {{I}_{i,j+1}}(0)-{{I}_{i,j+1}}(1) &j=i-1 \\ {{I}_{i,j+1}}(0)-{{I}_{i,j+1}}(1)+2{{I}_{ij}}(1) &j=i \\ {{I}_{i,j+1}}(0)-{{I}_{i,j+1}}(1)+2{{I}_{ij}}(1)-{{I}_{i,j-1}}(0)-{{I}_{i,j-1}}(1) &j\ge i+1 \\ {{I}_{i,j+1}}(0)-{{I}_{i,j+1}}(1)+2{{I}_{ij}}(1)-2{{I}_{i,j-1}}(1) &i=0,\quad j=1 \end{array} \right. \end{aligned}$$

(24)

One can define ${{\left( \sum \nolimits _{j=0}^{\infty }{{{D}_{ij}}^{2}} \right) }^{1/2}}\Delta {{r}^{-1}}$ as a noise coefficient, which indicates a transfer efficiency from the error of the projection value to the error of the deconvoluted value. Equation 23 suggests that the noise is inversely proportional to $\Delta r$, which means that smaller sampling step can yield a larger cumulative error. The noise coefficients for sampling steps of 0.125, 0.25 and 0.5 mm are plotted in Fig. 19. This suggests that even if the instrumental error in the projection value is constant at each measuring point, deconvolution leads to error accumulation towards the centre.

Fig. 17

Reconstruction of a given Gaussian field distribution similar to the soot volume fraction distribution at the base of the flame, for different sampling distances (top), absolute error (middle) and relative error (bottom)

Fig. 18

Reconstruction of a given Gaussian field distribution similar to the soot volume fraction distribution at the top of the flame, for different sampling distances (top), absolute error (middle) and relative error (bottom)

Fig. 19

Comparison of noise coefficients using different sampling distances

Figure 20 shows representative estimates of uncertainties across the radial distance. For the methane cases [(a) and (b) in Fig. 20], the uncertainty increases towards the centre of the flame, due to the cumulative effect of the three-point Abel transform. The flame oscillation causes an increase in uncertainty at the edge of the flame (${\approx } 4$ mm), which is more obvious in ethylene and propane flames [(c) to (e) in Fig. 20], because the soot concentrations at the edge of those flames are tens of times higher than in methane flames, so that a small oscillation of this region can generate large uncertainty. The error progressively accumulates towards the centre region of the flame.

Fig. 20

Absolute error in extinction measurement for soot volume fraction of a methane case A, b methane case B, c propane, d ethylene case A and e ethylene case B

Figure 21 shows the composition of experimental uncertainties at 40 mm flame height for two different flames, methane Case A (top) and ethylene Case A (bottom). For the methane flame, the Abel transform uncertainty and instrumental uncertainty play the main roles in the overall uncertainty, as the flame is shorter and experiences lower flame oscillations. For the ethylene flame Case A (lower), the flame oscillation contributes a significant portion of the total uncertainty, because of the high soot concentration at the flame edge.

Fig. 21

Composition of experimental uncertainties at 40 mm flame height for two different flames, methane Case A (top) and ethylene Case A (bottom)

4.4 Uncertainty from E(m)

The absorption function, E(m), is a function of the complex refractive index of soot m (Eq. 12), where m and E(m) are both wavelength and fuel dependent [59, 60]. Dalzell et al. suggested that within the wavelength range from 435.8 to 806.5 nm, the mean value of m is $1.57-0.46i$ for acetylene and $1.57-0.50i$ for propane diffusion flames [60]. In 1973, D’Alessio [57] suggested the value $1.57-0.56i$ as a mean value in visible range [61]. Whilst this value has been widely cited for its simplicity, a number of values of m have been reported by various of investigators as well, as shown in Table 2. For a wavelength of around 638 nm, calculations using the values suggested by D’Alessio’s rather than Yon’s data [$E(m)=0.30$ at 632 nm] yield a difference of 15 %; however, when compared with Williams’ data [$E(m)=0.37$ at 638 nm], the discrepancy can be as large as 40 %. Using the value of 0.26 is likely to underestimate the SVF deduced by extinction measurement. However, given the Rayleigh approximation may still overestimate SVF (by neglecting scatter) [61], further accurate measurements of E(m) would still directly improve the accuracy of the LOSE method.

Table 2 Previously measured complex refractive indices

5 Conclusions

A high spatial resolution laser cavity extinction technique has been developed and implemented to measure soot volume fractions from producing laminar diffusion flames down to sub-ppm levels. Data analysis shows that for stable measurement targets, the measurement error can be lower than 20 ppb. The high sensitivity is obtained through the multiple reflections of the high reflectivity mirrors, and the fine spatial resolution of the cavity system can be obtained with the use of concave mirrors.

The extinction measurements are used in the absolute calibration of LII measurements. The direct comparisons with LII measurements across the flame on the same flame show good agreement and good ability to resolve peaks, particularly in the cases with higher volume fractions. The spatial resolution of around 200 μm compares well with the LII resolution of 33 μm, given the simplicity of the technique. The uncertainty arising due to tomographic inversion and discretisation of the Abel transform is estimated to be around 10–20 % at the peak SVF position along flame radials, with a sampling resolution of 0.25 mm. The study shows that the laser cavity extinction technique can be successfully applied even for low soot concentrations, with uncertainties and spatial resolution similar to those in LII, but with the significant advantage of an absolute measurement and following unsteady fluctuations.

Appendices

Appendix 1: Abel transform

Since the measurements of $P_0(y)$ are taken at discrete points along the y axis, one uses discretization of the integral in y, which is replaced by the index j for each element spaced by delta point $y_j$ [49]:

$$\ f(r_i)=-\frac{1}{\pi }\sum _{j=i}^{\infty }\int _{0,j=i; -\frac{\Delta {y}}{2}, j>i}^{\infty }\frac{P_0^{\prime}(y_j+\delta )}{\sqrt{(y_j+\delta )^2-{r_i}^2}}{\mathrm {d}}\delta$$

(25)

$P_0^{\prime}(y)$ is approximated by the second-order derivative with respect to y, as follows:

$$P_0^{\prime}(y_j+\delta )=\frac{P_0(y_{j+1})-P_0(y_{j-1})}{2\Delta {y}}+\frac{[P_0(y_{j+1})+P_0(y_{j-1})-2P_0(y_j)]\delta }{{\Delta {y}}^2}$$

(26)

In Eqs. (25) and (26), the quantity f(r), which is the local extinction coefficient $K_{\mathrm{{e}}}(r)$ , can be obtained from:

$$K_{\mathrm{{e}}}(r_i)= f(r_i)=-\frac{1}{\Delta {y}}\sum _{j=i}^{\infty } \left\{ \left[ I_{ij}(1)-I_{ij}(0)\right] P_0(y_{j-1})-2I_{ij}(1)P_0(y_j)+ \left[ I_{ij}(1)+I_{ij}(0)\right] P_0(y_{j+1}) \right\}$$

(27)

in which:

$$\ I_{ij}(k)=\frac{1}{2\pi }\int _{0, j=i; -1, j>i}^{1}\frac{\delta ^n}{\sqrt{(2j+\delta )^2}-4i^2}{\mathrm {d}}\delta$$

(28)

$I_{ij}(k)$ is the linear deconvolution operator of Abel transform, and $k=0$ or 1.

Appendix 2: Uncertainty propagation in extinction coefficient

The extinction coefficient, and ultimately the volume fraction, is extracted from the total extinction measured, to yield $P_0$ via Eq. (7), which is susceptible to uncertainties in $P_{\mathrm{{t}}}$ and the smaller uncertainties in R and T. $P_{\mathrm{{t}}}$ is obtained from the measurement in the attenuation of light using the photodetectors. The uncertainties are obtained from estimates of the error induced by laser light fluctuations, flame intensity interference and background currents, estimated from their respective rms fluctuations. These are collected in expressions using the logarithmic amplifier (base 10) to allow the uncertainties to be calculated from the overall expression for $P_{\mathrm{{t}}}$:

$$\begin{aligned} {P}_{\mathrm{{t}}}&=f({\mathbf {V}},C)=-\ln \frac{i_T}{i_0}=-\frac{\ln 10}{C}({{V}_{\mathrm{{LF}}}}-{{V}_{\mathrm{{IN}}}})+\ln \left( 1-{{10}^{\frac{{{V}_{\mathrm{{ref1}}}}-{{V}_{\mathrm{{IN}}}}}{C}}} \right) \\ &\quad - \ln \left( 1+{{10}^{\frac{{{V}_{\mathrm{{ref3}}}}-{{V}_{\mathrm{{ref2}}}}}{C}}}-{{10}^{\frac{{{V}_{\mathrm{{ref1}}}}-{{V}_{\mathrm{{B}}}}}{C}}}-{{10}^{\frac{{{V}_{\mathrm{{F}}}}+{{V}_{\mathrm{{ref3}}}}-{{V}_{\mathrm{{ref2}}}}-{{V}_{\mathrm{{LF}}}}}{C}}} \right) \\ \end{aligned}$$

(29)

where ${\mathbf {V}}$ is the vector representing the various measured voltages detailed in Table 3 and C is a calibration constant for the amplifier.

Table 3 Definition of variables and case studies for decoupling interferences

The uncertainty in $P_0$ can be calculated via error propagation as:

$$u_{{{P}_{0}}}^{2}=\left( {{\left( \frac{\partial {{P}_{0}}}{\partial {{P}_{\mathrm{{t}}}}}\cdot \frac{\partial {{P}_{\mathrm{{t}}}}}{\partial {\mathbf {V}}} \right) }^{2}},{{\left( \frac{\partial {{P}_{0}}}{\partial {{P}_{\mathrm{{t}}}}}\cdot \frac{\partial {{P}_{\mathrm{{t}}}}}{\partial C} \right) }^{2}},{{\left( \frac{\partial {{P}_{0}}}{\partial R} \right) }^{2}},{{\left( \frac{\partial {{P}_{0}}}{\partial T} \right) }^{2}} \right) \left( {\begin{array}{*{20}c} {{{\mathbf {U}}}^{2}} \\ u_{C}^{2} \\ u_{R}^{2} \\ u_{T}^{2} \\ \end{array}} \right)$$

(30)

where ${\mathbf {U}}=[{{u}_{{{V}_{\mathrm{{IN}}}}}};{{u}_{{{V}_{\mathrm{{LF}}}}}};{{u}_{{{V}_{\mathrm{{F}}}}}};{{u}_{{{V}_{\mathrm{{B}}}}}};{{u}_{{{V}_{\mathrm{{ref1}}}}}};{{u}_{{{V}_{\mathrm{{ref2}}}}}};{{u}_{{{V}_{\mathrm{{ref3}}}}}}]$ contains the uncertainties in ${\mathbf {V}}$. The additional uncertainty in the local extinction ratio, $u_{K_{\mathrm{{e}}}}$, due to the Abel transform may be expressed as [49]:

$$u_{K_{\mathrm{{e}}}}^2= \frac{1}{\Delta {y}^2}\sum _{j=i}^{\infty } \left\{ \left[ I_{ij}(1)-I_{ij}(0)\right] ^2u^2_{P^\prime(y_{j-1})}-\left[ 2I_{ij}(1)\right] ^2u^2_{P^\prime(y_j)}+ \left[ I_{ij}(1)+I_{ij}(0)\right] ^2u^2_{P^\prime(y_{j+1})} \right\}$$

(31)

where $I_{ij}(0)$ and $I_{ij}(1)$ are the operators in the Abel transform and $\Delta {y}$ is the horizontal distance between the two measured positions.