Extension of the classical Fabry–Perot formula to 1D multilayered structures

Abstract

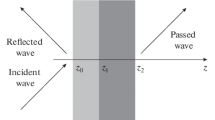
In any field theory the interaction of a wave packet with a multilayered potential is of high theoretical and practical relevance. In the present work we show an extension to any number of layers of the classical Fabry–Perot formula that works for any level of absorption, any thickness of the composing layers, any number of layers, any angle of incidence and for evanescent waves as well. More specifically, the ability of dealing with input evanescent waves and complex metal-based structures is of special interest for superlenses analysis and design. Some explicit examples in electromagnetism are also discussed.

Appendix 1: energy conservation

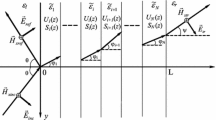
In this appendix we recall some expressions for the Poynting vectors of the incident, reflected and transmitted fields. They are used to check that the analytical expression for the transmitted and reflected fields, as derived in the paper, do not violate the energy conservation every time we are in the presence of a non-dissipative system.

When the incident wave has the x component of the wave vector different from zero (i.e., we are not at normal incidence) the expression of energy conservation can be obtained by deriving the expression of the z component of the Poynting vectors for the incident, reflected and transmitted wave, respectively. In addition, this has to be done separately for s- and p-polarization. Let us start with the s-polarization case.

1.1 S-polarization case

Let us assume that the incident wave has an electric field component of type

$$ E_y^{(1)}(x,z) = A_E^{(i)} \exp{(i {\bf k}^{(i)}\cdot{\bf r})} $$

(12)

with k ⁽ⁱ⁾ = (k ⁽ⁱ⁾ _x , 0, k ⁽ⁱ⁾ _z ) the wave vector of the incident field and r = (x, y, z). The energy flow along z for the incident field can be written, starting from the definition of the Poynting vector as

$$ \left\langle {\bf S}\right\rangle = \frac{1}{2} Re\{{{\bf E}\times{\bf H^{\star}}}\} $$

(13)

We need to look at the z component for the incident, reflected and transmitted field. After simple algebra we obtain,

$$ \left\langle {S_z^{(i)}}\right\rangle = \frac{1}{4} \frac{|A_{E}^{(i)}|^2}{\omega \mu_i} [k_{z}^{(i)}+(k_{z}^{(i)})^{\star}] $$

(14)

where ω is the angular frequency and μ _i is magnetic permeability of the input medium i. For the Poynting vectors of the reflected and transmitted field we get,

$$ \left\langle {S_z^{(rs)}}\right\rangle = \frac{1}{4} |r_s|^2 \frac{|A_{E}^{(i)}|^2}{\omega \mu_r} [k_{z}^{(r)}+(k_{z}^{(r)})^{\star}] $$

(15)

(k ^(r) _z  = k ⁽ⁱ⁾ _z and μ _i  = μ _r , since incident and reflected wave lie in the same medium),

$$ \left\langle {S_z^{(ts)}}\right\rangle = \frac{1}{4} |t_s|^2 \frac{|A_{E}^{(i)}|^2}{\omega \mu_t} [k_{z}^{(t)}+(k_{z}^{(t)})^{\star}] $$

(16)

with obvious meaning of the notation. To check energy conservation, we look at the following normalized quantity

$$ \frac{\left\langle {S_z^{(rs)}}\right\rangle +\left\langle {S_z^{(ts)}}\right\rangle }{\left\langle {S_z^{(i)}}\right\rangle } =|r_s|^2+ |t_s|^2 \frac{\mu_i}{\mu_t} \frac{[k_{z}^{(t)}+(k_{z}^{(t)})^{\star}]}{[k_{z}^{(r)}+(k_{z}^{(r)})^{\star}]} $$

(17)

that should always (i.e., for all k _x ) be equal to one for absorption-free systems. In case k ⁽ⁱ⁾ _x  = 0 (normal incidence), in absence of absorption and with same input and output medium, Eq. 17 reduces to the well-known form |r _s |² + |t _s |² = 1.

1.2 P-polarization case

In this case it is easier to consider the y component of the incident magnetic field

$$ H_y^{(1)}(x,z) = A_H^{(i)} \exp{(i {\bf k}^{(i)}\cdot{\bf r})} $$

(18)

For the z component of the Poynting vector of the incoming field we obtain

$$ \left\langle {S_z^{(i)}}\right\rangle = \frac{1}{4} \frac{|A_{H}^{(i)}|^2}{\omega \varepsilon_{i}} [k_{z}^{(i)}+(k_{z}^{(i)})^{\star}] $$

(19)

All formulas derived in the previous subsection can be extended to the current case by replacing r _s and t _s by r _p and t _p and μ by $\varepsilon$ in the medium. After doing that we get

$$ \frac{\left\langle {S_z^{(rp)}}\right\rangle +\left\langle {S_z^{(tp)}}\right\rangle }{\left\langle {S_z^{(i)}}\right\rangle } =|r_p|^2+ \frac{n_{\hbox{input}}^2}{n_{\hbox{output}}^2}|t_p|^2 \frac{[k_{z}^{(t)}+(k_{z}^{(t)})^{\star}]}{[k_{z}^{(r)}+(k_{z}^{(r)})^{\star}]} $$

(20)

which represents the energy conservation formula for the p-polarization case.