Temperature measurements of the gas-phase during surrogate diesel injection using two-color toluene LIF

Abstract

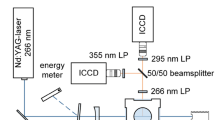
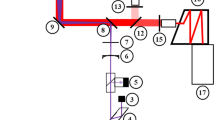
Planar laser-induced fluorescence (LIF) of toluene has been applied in an optical engine and a high-pressure cell, to determine temperatures of fuel sprays and in-cylinder vapors. The method relies on a redshift of the toluene LIF emission spectrum with increasing temperature. Toluene fluorescence is recorded simultaneously in two disjunct wavelength bands by a two-camera setup. After calibration, the pixel-by-pixel LIF signal ratio is a proxy for the local temperature. A detailed measurement procedure is presented to minimize measurement inaccuracies and to improve precision. n-Heptane is used as the base fuel and 10 % of toluene is added as a tracer. The toluene LIF method is capable of measuring temperatures up to 700 K; above that the signal becomes too weak. The precision of the spray temperature measurements is 4 % and the spatial resolution 1.3 mm. We pay particular attention to the construction of the calibration curve that is required to translate LIF signal ratios into temperature, and to possible limitations in the portability of this curve between different setups. The engine results are compared to those obtained in a constant-volume high-pressure cell, and the fuel spray results obtained in the high-pressure cell are also compared to LES simulations. We find that the hot ambient gas entrained by the head vortex gives rise to a hot zone on the spray axis.

Appendices

Appendix A: Comparison with LES

The LES code used in this study is the fully compressible AVBP solver co-developed by IFP Energies Nouvelles and CERFACS for structured and unstructured meshes [20]. The second order centred Lax–Wendroff convective scheme [21] is combined with an explicit time advancement. Unresolved subgrid-scale turbulence is modeled by a Smagorinsky model [22] with constant coefficient. The dispersed liquid phase is resolved using a mesoscopic Eulerian formalism [23]. The region close to the injector, dominated by high volumetric ratios of liquid fuel and breakup effects, is not included in the simulations. The DIturBC injector model [24] is used to bridge that region by imposing physical flow conditions at a distance approximately 10 nozzle diameters downstream of the injector outflow plane. Its principle is to impose boundary conditions for the two phase flow at a distance downstream of the injector nozzle, in regions where the flow has been dispersed by breakup phenomena and can be addressed by a diluted mesoscopic Eulerian formalism.

The LES has been run on a computational mesh which represents a closed combustion vessel with slightly larger dimensions than the HPC (112³ versus 108³ mm³). It consists of a tetrahedral mesh with local refinement. The mesh size near the nozzle exit is 80 μm and gradually increases to 800 μm toward the other end of the domain, yielding approximately 0.7 million nodes and 4.3 million cells. All boundaries, except for the injection plane, are taken as adiabatic walls which have negligible influence on the spray internal structure. This mesh has been chosen on the basis of spray formation results presented in [25].

The simulated spray penetration is compared to the measured one. The fuel vapor penetration in the LES is taken at the point in space where the mass fraction of the fuel is Y _fuel = 0.001, as defined in the first Engine Combustion Network workshop [26]. For the experiments, the vapor edge is clearly visible and determined visually. The spray penetration length of a single LES and one experiment are shown in Fig. 21. The first measured point in time (t ₀ = 0.58 ms) is fixed on the LES penetration. Subsequently, this is taken as a reference for all other measured points. The error bar of the point at 2.08 ms is defined from the minimum and maximum values from the 9 measurements. Figure 21 shows a good agreement between the experiments and the LES.

Fig. 21

Spray length as function of injection time

The results of the LES are also given in Fig. 19; velocity vectors are colored with the corresponding temperature at that point. Furthermore, the contour of the fuel spray (Y _fuel = 0.001) is indicated with the solid black line. The LES results reveal heavy mixing in a pulsating fashion due to spray-induced vortices at the edge, resulting in hot spots of ambient air enclosed in the spray core region. The LES predicts temperatures in the order of 500 K for the inner spray areas, whereas the experimental results are much closer to the ambient condition of 590 K. Possible reasons might be the averaging effect in the experiment due to the laser thickness.

Appendix B: Data processing

The complete data processing procedure includes removing background, spatial alignment, flat-field correction, ratio calculation and converting to temperature distribution. Suppose we obtain an image pair, of which I _r(x, y) is the pixel intensity of the “red” part of the spectrum (320 nm) at position x, y and I _b(x, y) is the pixel intensity of the “blue” part of the spectrum (280 nm). In the case of a one-side configuration, the data correction procedure for both images can be expressed as:

$$ I_{\rm r,corr}(x,y)= (I_{\rm r}(x,y)-B_{\rm r}(x,y))\,{\rm TR}(x,y)\, F_{\rm r}(x,y) $$

(1)

and

$$ I_{\rm b,corr}(x,y)= (I_{\rm b}(x,y)-B_{\rm b}(x,y))\, F_{\rm b}(x,y), $$

(2)

where B(x, y) is the background signal, TR(x, y) the spatial transformation matrix and F(x, y) is the flat-field matrix. In case of opposite configuration, the data processing procedure can be expressed as:

$$ I_{\rm r,corr}(x,y)= (I_{\rm r}(x,y)-B_{\rm r}(x,y))\,{\rm TR}(x,y)\, C_{\rm r}(x,y) $$

(3)

and

$$ I_{\rm b,corr}(x,y)= (I_{\rm b}(x,y)-B_{\rm b}(x,y)), $$

(4)

where the major difference is the relative flat-fielding matrix C _r(x, y). To only present temperature regions, which have reasonable accuracy, pixels with less than 300 counts are neglected because of the low signal-to-noise ratio. The temperature distribution can be obtained with the calibration relation.

$$ T(x,y)= T(R(x,y)) = T\left(\frac{I_{{\rm r},2}(x,y)}{I_{{\rm b},2}(x,y)}\right){\rm BS}\,(x,y), $$

(5)

where R(x, y) is the LIF ratio distribution and BS(x, y) is the correction for the beam splitter, which is only used in one-side configuration of the HPC experiments.