1 Introduction

Due to the rapid industrial and population growth, the two most important issues facing society today are energy scarcity and environmental contamination [1]. The efficient mutual conversion between heat and electricity is one of the most explorable task in thermoelectric compounds in this era. The quality of thermoelectric materials is evaluated by the dimensionless figure of merit, \(ZT=\frac{{S}^{2}T}{\kappa \rho }\), where S is the Seebeck coefficient, T is the absolute temperature, κ is the total thermal conductivity, and ρ is the electrical resistivity [2, 3]. However, the interdependence of the above parameters hinders the efficiency of thermoelectric materials for practical applications.

Bismuth chalcogenides are well-known materials for thermoelectric energy generation at low and near room temperatures due to their high power factor and significant electronic weighted mobility [4]. Doping other elements such as tin, indium, antimony, and so on can improve the power factor value of this class of materials. Increased high-frequency phonons diminishes the thermal conductivity by producing a mass differential and a shift in chemical bonding [5]. Although it is frequently interpreted in a phenomenological sense that specific type of defects directly target scattering phonons with specific frequency range, resulting in substantial strain and mass fluctuations [6], this is not the case. The key difficulty is that altering the electrical structure of bismuth selenide may disturb charge carrier mobility. As a result, maintaining a balance in electrical resistivity and thermal conductivity for bismuth chalcogenides is difficult [7].

At low and near room temperature, V–VI group binary compounds such as Bi2Te3, B2Se3, Sb2Te3, and ternary compounds such as Bi2Te1-xSex and BixSb1-xTe3 are efficient thermoelectric systems [8]. There are several reports available on various synthesis processes for Bi2Se3-based compounds, such as thermochemical, solvothermal, hydrothermal, melt growth, hot pressing, and so on [9,10,11,12,13]. Furthermore, doping and alloying are used to enhance the thermoelectric performance of these binary systems. Co-doping, in particular, is a novel approach for lowering thermal conductivity and electrical resistivity. Bi2Se3 defect physics is well-known and widely studied. Tellurium is a dopant that is responsible for the formation of vacancies and changes the Fermi level in the molecule. Furthermore, tin works as a resonant impurity, amplifying the production of resonant levels and so increasing the thermoelectric parameters in every way. As a result, we are motivated to co-dope tin and tellurium in bismuth and selenium sites [14].

In our earlier work, we examined the thermoelectric properties of Bi2Se3 single crystals that were melt-grown and co-doped with tellurium and tin at temperatures between 10 and 400 K [15]. Additionally, rather than Sn doped Bi2Se3, the researchers have concentrated on Sn doped Bi2Te3 [16,17,18]. Therefore, we used a solid-state reaction approach to synthesize tin and tellurium co-doped Bi2Se3 polycrystalline samples for this investigation, and examined their thermoelectric properties from 10 to 350 K. The Fermi level is moved from the conduction band to the valence band by Sn’s acceptor activity in this technique. As a result, the Fermi level appears inside the bulk band gap. Another approach of controlling the Fermi level is defect engineering in a Se-rich growth environment.

Co-doping in polycrystalline has been revealed to improve the power factor while decreasing electrical resistivity. A shift from p- to n- type semiconducting nature in (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples has also been notified to fabricate a thermoelectric generator (TEG) in near future.

2 Experimental methods and characterizations

The polycrystalline samples were prepared using a solid-state reaction process and characterized using X-ray diffraction (XRD), field emission scanning electron microscope (FESEM), energy dispersive X-ray analysis (EDS), electrical resistivity, seebeck coefficient, and thermal conductivity [provided in supplementary section].

3 Results and discussion

3.1 Powder X-ray diffraction

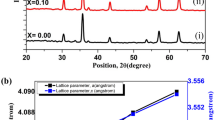
The XRD patterns of Bi2Se3 and (Bi1-xSnx)2Se2.7Te0.3 polycrystals are shown in Fig. 1. (Fig. 1a). The (105) plane is found to be the most dominating peak among the samples, with the exception of (Bi0.98Sn0.02)2Se2.7Te0.3 [(216) plane], which is attributed to crystallite recrystallization during sintering. The strong peaks in the XRD profiles indicate that the generated (Bi1-xSnx)2Se2.7Te0.3 materials have high crystallinity. From pristine Bi2Se3 to (Bi0.98Sn0.02)2Se2.7Te0.3, XRD peak patterns shift to the higher angle side, whereas there is an abrupt shift to the lower angle side in (Bi0.96Sn0.04)2Se2.7Te0.3 [as seen in Fig. 1b]. This observation can be explained by tellurium and tin ion occupancy at either interstitial locations or bismuth and selenium sites. As more Sn ions fill the interstitial regions in the van der Waals gaps, the lattice parameter of (Bi0.96Sn0.04)2Se2.7Te0.3 varies [15, 19]. In the doped samples, there is a peak shifting at around 28°. This is because the difference in the ionic radii between Se and Te from one side and between Sn and Bi from the other side, changes the diffraction patterns of a material and causes compressive micro-stress. These macro-stresses are quantified by a lattice parameter analysis. In the doped samples, there exist a peak shifting at around 28°. This is because the difference in the ionic radii between Se and Te from one side and between Sn and Bi from the other side, changes the diffraction patterns of a material and causes compressive micro-stress. These macro-stresses are quantified by a lattice parameter analysis. Consequently, the crystallite size of the sample (Bi0.96Sn0.04)2Se2.7Te0.3 has been modified [20, 21].

Fig. 1
figure 1

a Powder XRD peak patterns of (a) Bi2Se3 (b) Bi2Se2.7Te0.3 (c) (Bi0.98Sn0.02)2Se2.7Te0.3 (d) (Bi0.96Sn 0.04)2Se2.7Te0.3 polycrystalline samples. b The shifting of the (015) peak for (a) Bi2Se3 (b) Bi2Se2.7Te0.3 (c) (Bi0.98Sn0.02)2Se2.7Te0.3 (d) (Bi0.96Sn 0.04)2Se2.7Te0.3 polycrystalline samples. c Rietveld refinement plots of (a) Bi2Se3 (b) Bi2Se2.7Te0.3 (c) (Bi0.98Sn0.02)2Se2.7Te0.3, (d) (Bi0.96Sn 0.04)2Se2.7Te0.3 polycrystalline samples

Full size image

Table 1 shows the crystallite size obtained using the Williamson Hall formula. The Rietveld refinement of the XRD patterns (EXPO 2014 Software) indicate that the samples tested crystallize in a hexagonal crystal structure with the R\(\overline{3 }\)m space group [Fig. 1c]. The profile factor (Rp), weighted profile factor (Rwp), expected profile factor (Rep), and goodness of fit (2) are all within acceptable limits [Table 1]. Furthermore, the elemental phases of all compounds are investigated using “Profex 3.14”, and the results are shown in Table 2. All of the doped polycrystals have accompanying phases such as Bi-Te, Sn-Te, and Sn-Se.

Table 1 Characteristic reliability factors such as the profile factor (Rp), weighted profile factor (Rwp), expected profile factor (Rep), the goodness of fit (χ2), lattice parameter (a, b, and c), and lattice strain information obtained from the powder XRD analysis of (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples
Full size table
Table 2 The chemical compositions of different phases in (Bi1-xSnx)2Se2.7Te0.3 compounds
Full size table

3.2 Surface morphological features and elemental compositions

The surface microstructure of (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples is shown in Fig. 2. Bi2Se3 and Bi2Se2.7Te0.3 have a well-packed grain surface with minimal porosity in the majority of the microstructure. However, because to the dislocation generated during hand pestling, several pits can be seen in the middle of the compact construction (Fig. 2a and b) [22]. Because of grain boundary diffusion during sintering, the average grain size increases. The particles agglomerate at the site of imperfection in the interstitials caused by impurities such as tin and tellurium, as seen in Fig. 2c and d. Furthermore, all of the samples had some white spots that indicate selenium volatilization during the sintering process. Furthermore, all of the samples had some white spots that indicate selenium volatilization during the sintering process. The effect of Te buildup can be clearly seen during colour changes and grain enlargement [23].

Fig. 2
figure 2

FESEM images of a Bi2Se3 b Bi2Se2.7Te0.3 c (Bi0.98Sn0.02)2Se2.7Te0.3 d (Bi0.96Sn 0.04)2Se2.7Te0.3 polycrystalline samples

Full size image

The presence of selenium and bismuth is confirmed in the pristine Bi2Se3 sample (Fig. 3a), although tellurium is also present in Bi2Se2.7Te0.3 (Fig. 3b). The presence of tin in (Bi1-xSnx)2Se2.7Te0.3 has been detected, as shown in Fig. 3c and d. The anticipated atomic percentage of the examined crystals agrees well with the measured atomic percentage, as shown in Table 3. We noticed some changes in the level of tin composition due to the unrestricted vaporization and volatilization of selenium [15].

Fig. 3
figure 3

EDS images of a Bi2Se3 b Bi2Se2.7Te0.3 c (Bi0.98Sn0.02)2Se2.7Te0.3 d (Bi0.96Sn0.04)2Se2.7Te0.3 polycrystalline samples

Full size image
Table 3 Elemental composition of (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples
Full size table

3.3 Electrical resistivity

Figure 4 depicts temperature-dependent electrical resistivity in the 10–350 K temperature range. The electrical resistivity of Bi2Se3 compound exhibits a metal–semiconductor transition near 100 K due to the overlapping of half-filled 6p and fully filled 6 s bands, whereas the semiconducting behavior above 100 K is due to the presence of thermally excited carriers [23, 24]. Metallic conductivity in semiconductors is generally caused by degenerate doping. The conduction type retains metallic behavior at a specific temperature, and as the temperature rises, the conductivity falls. With a Te/Se ratio of 2.7:0.3, the conductivity exhibits a metallic behavior across the entire temperature range as it continuously drops with temperature. Se vacancies are the primary cause of defects in Bi2Se3. The antisite defects in doped compounds grow significantly when Se and Bi are partially replaced by Te and Sn. The chemistry of defects, which are controlled by Bi antisite defects and the positively charged vacancies in Se that function as electron donors. Both electronegativity and atom size differences between Bi and the cation (Se, Te) diminish with the partial substitution of Se on Te, which enhances antisite defects and increases electron density. In this circumstance, the inclusion of Te should result in an increase in conductivity [25, 26].

Fig. 4
figure 4

The temperature-dependent electrical resistivity of pristine and (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples

Full size image

As a result, rising tellurium and tin doping concentration causes a systematic decrease in electrical resistance. The (Bi0.96Sn0.04)2Se2.7Te0.3 polycrystals has a marginally lower electric resistivity than the (Bi0.98Sn0.02)2Se2.7Te0.3, polycrystals, which is apparently due to the small pores among grains that grow with Te concentration [26, 27], as seen in Fig. 2d [28,29,30]. Co-doping results in a fourfold decrease in electrical resistivity for (Bi0.96Sn0.04)2Te2.7Se0.3 compared to Bi2Se3.

The small polaron hopping (SPH) model (Fig. 5) has been employed to elucidate the electrical resistivity data of the studied samples in the high-temperature range 189–333 K by using the formula [31,32,33]

Fig. 5
figure 5

The fitting plot of the SPH model for the pristine and (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples

Full size image
$$\rho = {\rho }_{0}T\text{exp}\left(\frac{{E}_{A}}{{k}_{B}T}\right)$$
(1)

The SPH model’s slope (Eq. 4) is used to compute the activation energy of all compounds. Electrons and holes in a disordered chalcogenide system connect with their atomic surroundings via electron–phonon coupling with sufficient strength to form tiny polarons. The chalcogenide compounds’ SPH is based on localized electrons. The lattice is soft enough to allow the coupling of two tiny polarons (opposite spins) with electrons that capture the defect site. Doped bismuth selenide has a higher number of these flaws. As a result, the interaction of electrons with local vibrations such as polarons causes deformation in nearby sites. This causes the activation energy to decrease as doping concentration increases (Table 4). The comparison of activation energy of present compound with the other research work has been depicted in Table 5. Sn and Te atoms exist in an unknown impurity phase forming the defect, they also stay in some metastable positions in the Bi2Se3 lattice. Concerning the assumption, though various locations of Sn dopants have been experimentally verified by including the interstitial sites and the intercalation sites in van der Waals gap, it is not clear, yet which location is responsible for the superconductivity [34]. Due to the large separation between adjacent quintuple layers, metal atoms diffuse quite freely inside van der Waals gap [35, 36].

Table 4 Experimental (nExp), theoretical carrier concentration (nTh); experimental (μExp), theoretical (μTh) carrier mobility; experimental (γExp), theoretical (γTh) carrier scattering factor; effective mass (m*), weighted mobility (μw), activation energy (EA), pre-exponential factor (ρ0), characteristic temperature (T0) of the (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples at 300 K
Full size table
Table 5 The comparison of present activation energy with other research work
Full size table

3.4 Seebeck coefficient

Figures 6 and 7 depicts the temperature-dependent Seebeck coefficient and theoretical Hall effect carrier concentration of (Bi1-xSnx)2Se2.7Te0.3 polycrystals across the temperature range 10–350 K. Even at 10 K, the p-type Bi2Se3 degenerate semiconductor displays a high density of mobile holes and hole conduction at the acceptor band-valence band overlap. In the remaining crystals, the donor band exhibits n-type degenerate semiconducting behaviour, with the donor atoms’ fifth electron occupying quantum state above the donor band [37]. All other states of energy bands are empty, with the exception of a small number of lower energy states of the composite band are filled by electrons. Hence the Seebeck coefficient of Bi2Se3 has shown p-type semiconducting nature. The Seebeck coefficient of the pure Bi2Se3 sample increases with temperature up to 300 K before saturation, most likely due to the presence of flaws. Because surface state bands are not found in pristine Bi2Se3, the Seebeck coefficient is positive across the temperature range examined, indicating that the Fermi level is below the energy of the Dirac point [38]. The remaining samples exhibit negative Seebeck coefficient values. This sort of transition from p- to n-type is attributed to tellurium’s partial substitution of selenium, where Te acts as an electron donor at grain boundaries via its vacancy (VTe). If Bi-Se hosts had more Bi, the bonding would be disrupted, resulting in more electrons for the same amount of Se vacancies. The increased electrons provided by Bi could not be compensated for the holes created by Sn doping [38, 39]. The growing Seebeck coefficient values [40] indicate that diffusive thermoelectric transport exists in the (Bi1-xSnx)2Se2.7Te0.3 system. Furthermore, the replacement of tin atoms (x = 0.02 and 0.04) in the Bi site introduces dual holes, compensating for binary defects. The holes generated by the antisite defect counterbalance the electrons, resulting in a considerable decrease in S value (− 66 μV/K at 350 K) in (Bi0.98Sn0.02)2Se2.7Te0.3 and (Bi0.96Sn0.04)2Se2.7Te0.3. The Eq. 5 can be used to connect the carrier concentration to the Seebeck coefficient.

$$S\left( T \right) = \frac{{8k_{B}^{2} \pi^{2} m^{*} }}{{3eh^{2} }}\left( {\frac{\pi }{3n}} \right)^{2/3} T$$
(2)

where S(T) is the temperature-dependent Seebeck coefficient, kB is the Boltzmann constant, m* is the effective mass of electron, e is the charge of an electron, h is the Planck constant, and n is the carrier concentration. The theoretical value of mobility was calculated using

$${\mu }_{H}=\frac{1}{ne\rho }$$
(3)

where ρ is the electrical resistivity. The theoretical and experimental values of Hall measurement, such as carrier concentration and Hall mobility, are found to be of the same order; however, a deviation is observed in carrier concentration and carrier mobility due to some inevitable experimental restrictions of the experiment (Table 4). The collective anisotropic orientation causes the rapid drop of resistance in the direction of high mobility, which is challenging to measure the precise values of mobility and carrier concentration simultaneously [41]. The electrical properties are also impacted by bipolar conduction because the discrepancies in electron anisotropy. The anisotropy produces discrepancies in the energy of effective masses that affect the change in carrier concentration [42]. The conduction band electrons are localized and continue to contribute to the electrical conductivity instead of Hall voltage. As a result, no systematic variation with respect to the doping concentration in the values of scattering factors (γ), activation energy (EA), weighted mobility (μW), and effective mass (m*) (Table 4). Usually, Bi2Te3 doped with Sn and Se have the highest known weighted mobility near room temperature related to the larger band degeneracy like that found in chalcogenides [43]. The Fermi energy is calculated using the formula [15]

Fig. 6
figure 6

Temperature-dependent Seebeck coefficient of the pristine and (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples

Full size image
Fig. 7
figure 7

Temperature-dependent Carrier concentration (Hall effect) of the pristine and (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples

Full size image
$${E}_{F}=-\frac{{\pi }^{2}{{{k}_{B}}^{2}}_{ }^{ }T}{3eS}$$
(4)

Here, Sn acts as an acceptor and downshifts the Fermi level from the conduction band to the valence band. Hence the Fermi level is located inside the bulk band gap. Another way of tuning the Fermi level is the defect engineering as in a Se-rich growth condition. It showed a p- to n-type transition by the increase in Se vacancies during sintering [44]. It is also observed that there is a systematic decrease in N(EF) with doping. It is well-documented that selenium is pointedly vaporized from the sample during sintering, which creates lattice vacancies of VSe. Similarly, Bi cations produce the anionic lattice vacancies to generate antisite defect BiSe. The minor crystallites in the crystals are linked by grain boundaries of complex structure as a result of disorders formed in atomic layers. This will cause a significant transformation in electronic properties [45]. The carrier scattering factor γ is calculated using the formula.

$$\gamma =\text{ln}n+S$$
(5)

where n is the carrier concentration and S is the Seebeck coefficient [46]. The values of γ are depicted in Table 4. The calculated carrier scattering factor, γ, which is intimately linked to carrier concentration and the Seebeck coefficient, provides valuable insights into the scattering mechanisms governing charge transport. By analysing γ, we gain a deeper understanding of how carriers interact with lattice imperfections and boundaries, crucial for optimizing material performance in thermoelectric applications. The electronegativity of Sn (1.96) is closer to that of Bi (2.02) than of Se (2.55), and the ionic radius of Sn2+ (83 pm) is substantially closer to that of Bi2+ (90 pm) than to that of Se3− (64 pm). Activation energy, scattering factor, mobility, and density of states data imply that a Sn-dopant is more likely than a Se-atom to replace a Bi-atom in the lattice [47, 48]. Harnessing this knowledge opens avenues for designing thermoelectric materials with tailored transport properties, offering potential advancements in energy conversion and electronic device technologies [49].

3.5 Thermal conductivity

Figure 8a depicts the temperature-dependent thermal conductivity K(T) of the investigated polycrystals. Due to Umklapp scattering, all of the samples show a rapid rise of K(T) at low temperatures and a phononic peak at roughly 30 K. The largest peak (35 W/mK) is observed in Bi2Se3, and the lowest peak (18 W/mK) is found in Bi2Se2.7Te0.3. Because of increased phonon energy, thermal conductivity decreases with increasing temperature, resulting in greater electron–phonon and phonon–phonon scattering [50, 51]. The thermal conductivity of inorganic solid solutions is made up of a lattice component (L) owing to heat conduction via the atomic lattice and an electronic component (e) due to heat conduction by free charge carriers. The Wiedman Franz law (\({\kappa }_{e}=\frac{{L}_{0}T}{\rho }\)), where Lo is the temperature-dependent Lorenz number calculated by \({L}_{0}=1.5+\frac{\text{exp}\left(-\left|s\right|\right)}{116}\) (Fig. 8b) [15], can be used to calculate the electronic thermal conductivity. Because the Seebeck coefficient increases with resonant electron scattering, the Lorenz number falls. A charge density wave system in polycrystalline Bi2Te3 supports high electron–phonon coupling, reducing the impact of Peierls distortion on the lattice thermal conductivity mechanism. The lower lattice thermal conductivity seen in single crystals of Bi2Te3 [52] is caused by the quantum confinement effect and the charge density wave caused by Periels distortion.

Fig. 8
figure 8

a Total thermal conductivity of the pristine and (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples. b Temperature-dependent Lorenz number of the pristine and (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples. c Lattice thermal conductivity of the pristine and (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples. d Electronic conductivity of the pristine and (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples

Full size image

The point defect scattering has the least effect on low-frequency phonons, and even the Umklapp process is likely to be ineffectual for these phonons. As a result, in all compounds, the lattice thermal conductivity (Fig. 8c) is found to be dominant over the electronic thermal conductivity (Fig. 8d). Because polycrystalline bismuth selenide is a layered structured material with variable directional orientations in its grains, both lattice thermal conductivity and electronic thermal conductivity obey the anisotropy law. At high temperatures (100–350 K), no systematic variation in total and lattice thermal conductivity about doping concentration is found [53]. Sn doping has been seen to induce distortion faults in the samples, lowering the thermal conductivity of the lattice. At 350 K, the overall thermal conductivity of (Bi0.98Sn0.02)2Se2.7Te0.3 is 1.1 times lower than that of Bi2Se3.

3.6 Thermoelectric power factor (PF) and figure of merit (ZT)

Figure 9 illustrates the thermoelectric power factor (\(PF=\frac{{S}^{2}}{\rho }\)) and Fig. 10 depicts figure of merit \(ZT=\left(\frac{{S}^{2}T}{K\rho }\right)\) of the studied (Bi1-xSnx)2Se2.7Te0.3 samples. It is found that the sample (Bi0.96Sn0.04)2Se2.7Te0.3 has the highest PF (150 μW/mK2) and ZT (0.0026) values, whereas the pristine Bi2Se3 has the lowest PF (10 μW/mK2) and ZT (0.0003) value at 350 K. By co-doping, it is accomplished an enhancement of about 15 times and 9 times, respectively, in PF and ZT values of (Bi0.96Sn0.04)2Se2.7Te0.3 than that of the pristine sample.”

Fig. 9
figure 9

Temperature dependent power factor of (Bi1-xSnx)2Se2.7Te0.3 polycrystalline samples

Full size image
Fig. 10
figure 10

Thermoelectric figure of merit of (Bi1-xSnx)2Se2.7Te0.3 polycrystalline sample

Full size image

4 Conclusion

In this work, we describe the low and near room temperature (10–350 K) thermoelectric performance of (Bi1-xSnx)2Se2.7Te0.3 polycrystalline system. The XRD analysis shows that the crystal structure is hexagonal with the space group of \(R\overline{3 }\)m. The precipitation rate of surface morphology is affected by the co-doping of tin and tellurium. A four times reduction in electrical resistivity is observed for (Bi0.96Sn0.04)2Te2.7Se0.3 than the pristine Bi2Se3. There is a reduction of 1.1 times in total thermal conductivity for (Bi0.98Sn0.02)2Se2.7Te0.3 compared to the pristine at 350 K. We have observed an enhancement of power factor by 15 times in the (Bi0.96Sn0.04)2Se2.7Te0.3 system as compared to Bi2Se3. The Seebeck coefficient measurements indicate a transition from p- to n-type due to the partial substitution of selenium by tellurium, which would make (Bi0.96Sn0.04)2Te2.7Se0.3 compound suitable for sensor applications.

5 Summary statement

In the temperature range of 10–350 K, thermoelectric characteristics such electrical resistivity, thermal conductivity, and Seebeck coefficient have been studied. It is discovered that co-doping indium and tellurium in Bi2Se3 significantly lowers the system’s thermal conductivity. The output power rises as the temperature difference exceeds 50 °C, peaking at 40 nW at 70 °C due to improved thermal conductivity that produces electromotive force.