Judd–Ofelt and photoluminescence analysis of Nd₂O₃-doped within host fluoroborate glass from the system B₂O₃–NaF–La₂O₃

Abstract

Undoped glass of chemical composition 70B₂O₃–25NaF–5La₂O₃ together with Nd₂O₃-doped samples were prepared via conventional melt and annealing procedure. The prepared glasses were investigated through photoluminescence measurements to find out their extent for the lasing application. The undoped sample reveals two UV absorption peaks while Nd₂O₃-doped samples show 10 well-characterized peaks in the UV–Visible range that are correlated to different transition states of Nd³⁺ ions. Three different bands are detected in the emission spectra at 875 nm (⁴F_3/2 → ⁴I_9/2), 1056 nm (⁴F_3/2 → ⁴I_11/2), and 1326 nm (⁴F_3/2 → ⁴I_13/2). The Judd–Ofelt parameters (Ω2, Ω4, Ω6) and radiative properties were estimated using the Judd–Ofelt theory. The represented data indicated that the transition line ⁴F_3/2 → ⁴I_11/2 is the sharpest and lowest bandwidth value than other detected transitions. The structural analysis by FTIR vibrational modes suggested that the IR absorption bands within the range 800–1200 cm⁻¹ originate from both combined vibrations of tetrahedral (BO₄) and (BO₃F) groups together with (NaF₄) groups beside triangular BO₃ groups which are vibrating within the range 1200–1600 cm⁻¹. The addition of Nd₂O₃ is assumed to cause the possible transformation of some structural B–O bonds within the range of triangular borate units referring to the possible formation of pyroborate units or similar structural groups.

1 Introduction

Borate glasses belong to the three most interesting, highly distinguished and widely studied inorganic vitreous materials beside silicate and phosphate glasses [1,2,3]. However, borate glasses possess unique and exceptional structural configurations in which two variant building groups (BO₃ and BO₄) can be both identified in various borates with different ratios depending on the nature and percent of partner oxides [1,2,3]. The maximum limiting compositions of binary oxides with B₂O₃ are quite different and variable. The alkali oxides with B₂O₃ can form stable glasses by normal melting-annealing techniques approaching 30% while the alkaline earth oxides and other divalent with percent oxides such as ZnO and CdO can show higher percent for these oxides with B₂O₃ [4, 5]. Also, the binary alkali fluorides can form stable glasses with B₂O₃ with higher percentages than the related alkali oxides [6, 7]. Glasses containing rare earth (RE) ions have attracted great investigations due to their valuable lasing action in the visible and near-infrared regions [8,9,10,11,12,13,14,15,16,17,18]. Among all rare earth lanthanum oxide (La₂O₃) is a potential candidate for modifying various physical and optical properties of glasses and glass–ceramics and improving their chemical stability [9,10,11,12]. The incorporation of rare-earth neodymium oxide (Nd₂O₃) into glasses produces interesting colored samples which can show distinct dichroism in certain concentrated Nd₂O₃ -glasses [13,14,15,16]. The suitability of Nd³⁺ ions in emitting strong near-infrared emission at 1.06 μm makes it the best possible candidate for high-power laser applications [8, 16, 17]. Among different rare-earth ions, Nd³⁺ ion is one of the most studied and also one of the most efficient ions for photonic devices [12,13,14,15,16,17,18].

It has been recognized by many glass scientists [2, 5, 7, 17, 18] that the introduction of fluoride ions into phosphate or borate glasses produces mixed candidates of fluorophosphate or fluoroborate glasses with superior combining the better properties of mixed partners. Also, research on fluoroborate glasses by several authors [2, 5, 7, 17, 18] has reached the conclusion that primarily the limiting compositions for glass formation are much higher in binary borates like (LiF–B₂O₃), (NaF–B₂O₃) and (CaF₂–B₂O₃) and beside their properties are different and refer to their ability to share in optical component candidates. This work is a second step of studying rare earth (Nd³⁺ ions) in fluoroborate glass (LiF–CaF₂–B₂O₃) with the intention of justifying their difference from ordinary alkali or alkaline earth oxide borate glasses. In a previous publication by the sharing of the authors [19] we studied the behavior of Bi³⁺ ion in the two glassy systems (LiF–P₂O₅) and (LiF–B₂O₃) by the same spectral tools experienced in the current study.

Generally, fluoride glasses are characterized by their low dispersion and small non-linear refractive index which may be attractive for handling high laser power density [20]. In addition, they are stable in the ambient atmosphere as long as condensation of water is prevented. Obviously, the previous features lead to conducting studies for improving the optical behavior of fluoride glasses.

A current study by Espinosa-Cerón et al. [21] has reached the conclusion that the Nd³⁺ ions possess spectral properties to be recommended for near-infrared laser applications and further studies are needed to confirm this assumption.

The main objective of the study is to evaluate the building structure and optical properties Nd³⁺ -doped fluoroborate host glasses. In addition to the optical properties, theoretical model Judd–Ofelt (J–O) calculations are carried out to account for the radiative parameters and NIR-photoluminescence efficiency of the Nd³⁺ ion in the present glass matrix.

2 Experimental details

2.1 Materials and preparation of the glasses

About 20 gm of glasses of the chemical composition 70B₂O₃–25NaF–5La₂O₃–xNd₂O₃ in mol% (where x = 0, 0.05,0.1, and 0.2) were prepared by melting the weighed batches from laboratory chemicals (with purity 99.9%) in platinum crucibles at 1100 °C for 90 min in SiC heated furnace (Vecstar, UK). The chemicals used include orthoboric acid (H₃BO₃) and sodium fluoride (NaF), lanthanum oxide (La₂O₃), and a dopant of neodymium oxide (Nd₂O₃). After complete melting, the homogeneous melts were poured into preheated stainless steel molds with the required dimensions. The prepared glassy samples were immediately transferred to an annealing muffle furnace regulated at 300 °C to avoid the thermal stress of glass caused by quenching. The muffle was switched after 1 h and left to cool to room temperature at a rate of 30 °C/h with the glass samples inside.

The density of the glass samples was determined by the standard Archimedes principle using a sensitive balance and xylene as an inert immersion liquid. The density (listed in Table 1) of undoped and Nd₂O₃-doped glasses was obtained from the relation ρ = (a/a–b) ρ_x where a is the weight of the glass sample in air, b is the weight of the glass sample when immersed in xylene of density (ρ_x) 0.865 g/cm³.

Table 1 Chemical composition of the prepared glasses in mol%

2.2 Techniques for property measurements

2.2.1 Optical absorption measurements

The prepared glasses (Table 1) were characterized by measuring their optical (UV–visible) spectra by means of a recording spectrophotometer type (JASCO V-570, Japan) within the range 200–1100 nm.

2.2.2 Photoluminescence measurements

Photoluminescence measurements were recorded at room temperature under the excitation wavelength of 402 nm in the spectral region 500–760 nm using a fluorescence spectrofluorometer (type FS5 Edinburgh, England) equipped with a light source of Xenon arc lamp 150 W as an excitation light source.

On the basis of the Judd–Ofelt theory, the f–f intensity and transitions can be estimated using the following standard relations [22,23,24]

From the absorption spectra, the experimental oscillator strength (f_exp) for a transition definitely starting from a Ln³⁺ ion's ground state can be calculated according to the following formula:

$${f}_{\mathrm{exp}} = 4.318 \times {10}^{-9} \int \varepsilon (v)dv$$

(1)

where ε is the molar extinction coefficient at average energy v cm⁻¹.

$${f}_{\mathrm{cal}}=\left[8{\pi }^{2}mcv/3h(2J+1)\right]\left[({{n}^{2}+2)}^{2}/9n\right]\sum_{\lambda =\mathrm{2,4},6}\Omega {(\psi J\parallel {U}^{\lambda }\parallel {\psi }^{\mathrm{^{\prime}}}{J}^{\mathrm{^{\prime}}})}^{2}$$

(2)

A transition between two multiplets of an electric dipole's oscillator strength, f, is given by the f–f intensity model of the JO theory. Therefore, from the ground state to an excited state, the predicted oscillator strength is given by

$${S}_{\mathrm{ed}} = {e}^{2}\sum_{\lambda =\mathrm{2,4},6}\Omega {\left(\psi J\parallel {U}^{\lambda }\parallel {\psi }^{^{\prime}}{J}^{^{\prime}}\right)}^{2}$$

(3)

$${S}_{\mathrm{md}} = ({e}^{2}{h}^{2}/16{\pi }^{2}m{c}^{2}){(\psi J\parallel L+2S\parallel {\psi }^{^{\prime}}{J}^{^{\prime}})}^{2}$$

(4)

where m equals the electron mass, c the velocity of light in vacuum, h the Planck’s constant, n the refractive index of the medium, J the total angular momentum of the initial state, v the mean energy of the transition in cm⁻¹ and Ω_λ (λ = 2,4,6) the JO intensity parameters and ||U^λ||² the squared doubly reduced matrix elements of the unit tensor operator of the rank = 2, 4, and 6 which are calculated from the intermediate coupling approximation for a transition ψJ → ψ'J'. The oscillator strengths of the observed transitions can be estimated from Eq. 2 to calculate Ω_λ parameters by a standard least-square fitting method. Through the JO theory, the electric and magnetic dipole line strengths for a transition from a level ψJ to a level ψ'J' can be estimated from;

$$A(\psi J,{\psi }^{^{\prime}}{J}^{^{\prime}})={A}_{\mathrm{ed}}+{A}_{\mathrm{md}}$$

(5)

Using S_ed and S_md, the radiative transition probability (A) for a transition ψJ → ψ'J' can be calculated from the relation;

$${A}_{ed}=[64{\pi }^{4}{\upsilon }^{3}/3h(2J+1)][{({n}^{2}+2)}^{2}/9n]{S}_{\mathrm{ed}}$$

(6)

$${A}_{md}=[64{\pi }^{4}{\upsilon }^{3}/3h(2J+1)]{{n}^{3}S}_{\mathrm{md}}$$

(7)

where A_ed and A_md are the electric and magnetic dipole radiative transition probabilities, respectively, given by

$${A}_{T}(\psi J)= \sum_{{\psi }^{^{\prime}}{J}^{^{\prime}}}A(\psi J,{\psi }^{^{\prime}}{J}^{^{\prime}})$$

(8)

The total radiative transition probability (A_T) for an excited state is given as the sum of the A (ψJ, ψ'J') terms calculated over all the terminal states.

$${\tau }_{R }(\psi J)=[{A}_{T}(\psi J){ ]}^{-1}$$

(9)

$${\beta }_{R}(\psi J,{\psi }^{^{\prime}}{J}^{^{\prime}}) = A(\psi J,{\psi }^{^{\prime}}{J}^{^{\prime}})/{A}_{T}(\psi J)$$

(10)

A_T is related to the radiative lifetime (τ_R) and the branching ratio (β_R) of an excited state by.The peak stimulated emission cross-section, σ(λ_P), which is essential in predicting the laser performance, is related in terms of the radiative transition probability (A) of a transition as;

$$\sigma ({\lambda }_{P}) = ({\lambda }_{P}^{4}/8\pi c{n}^{2}\Delta {\lambda }_{\mathrm{eff}})A(\psi J,{\psi }^{^{\prime}}{J}^{^{\prime}})$$

(11)

where λ_P is the average emission transition peak wavelength and Δλ_eff is its effective line width found by dividing the area of the emission band by its average height.

2.2.3 Fourier transform infrared absorption measurements (FTIR)

The FT infrared absorption spectra of the prepared glasses were measured at room temperature using the KBr disc technique on a Fourier transform computerized infrared spectrometer type (FTIR 4600 JASCO Corp Japan). The glasses were tested in the form of a crushed powder that was combined with KBr at a 1:100 mg glass powder to KBr ratio. The weighed mixes were then exposed to a 5-ton/cm² pressure to yield clear homogenous discs.

3 Results and discussion

3.1 Optical absorption spectra

Figure 1 illustrates the UV–visible spectra of the base undoped glass and also that for samples doped with 0.05, 0.1, or 0.2% Nd₂O₃. The base glass without Nd₂O₃ reveals a spectrum consisting of two distinct UV absorption bands at 223 nm and at 280 nm with the first band with higher intensity than the second band and without any further absorption to the end of measurements.

Fig. 1

Optical absorption spectra of a undoped and b Nd₂O₃-doped sodium fluoroborate glass

The glasses containing dopants of Nd₂O₃ show beside the mentioned UV-bands as the undoped glass, distinct and extended absorption extending from 430 to 875 nm. The identified 10 absorption bands are observed at 431, 472, 511, 526, 582, 625, 683, 743, 804 and 875 nm. The three bands at 582, 743, and 804 are distinctly more intense than the others but decrease in intensity with the increase of wavelength. On the other hand, the intensities of all the absorption bands identified are generally observed to increase with the increase of Nd₂O₃ content. The identified spectra indicate that the Nd³⁺-containing glasses display characteristic bands which are repetitive and quite different than that for the parent undoped glass. The identified two UV absorption bands from the spectrum of the undoped glass are attributed to originate from unavoidable trace ferric ions present as impurities (even in ppm) in the laboratory chemicals used for the preparation of the glasses and agree with the assumption of many glass scientists who identified and characterize UV absorption in many undoped glasses [16,17,18, 25,26,27,28].

The various extended bands identified within the spectra of Nd₂O₃-doped glasses are related to the following transitions [8, 17, 18]:

(1) 431 nm(²P_1/2), (2) 472 nm(²G_9/2), (3) 511 nm(⁴G_9/2), (4) 526 nm(⁴G_7/2), (5) 582 nm(⁴g_5/2), (6) 625 nm(²H_11/2), (7) 683 nm(⁴F_9/2), (8) 743 nm(⁴S_3/2 + 4F _5/2), (9) 804 nm(4F_5/2), (10), and 875(⁴F_3/2). These described bands were previously identified by referring to their energies as shown by Carnal et al. [29] and to that reported by other authors [27, 28]. The increase in absorbance intensity with an increase in the doping can be related to the increase of Nd³⁺ ions as color centers.

3.2 Photoluminescence spectral data

Figure 2 displays the excitation spectra of the three doped Nd₂O₃ glasses (0.05, 0.1, 0.2% Nd₂O₃). The excitation spectra are identified to comprise 11 peaks owing to the quantum transition from a lower energy state to an excited state. The excitation peaks correspond to 430 nm, 455 nm, 474 nm, 512 nm, 525 nm, 586 nm, 625 nm, 681 nm, 745, 802 nm, 875 nm [30,31,32,33]. It is identified that the peak at 580 nm is the most prominent among all peaks and which is chosen as an excitation wavelength specific for measurements of emission spectra.

Fig. 2

Excitation spectra of Nd₂O₃-doped sodium fluoroborate glass at λ_em = 1056 nm

Figure 3 illustrates the emission spectra after excitation at (580 nm) of Nd₂O₃-doped glasses. The collected emission spectra show three distinct bands at 875 nm (⁴F_3/2 → ⁴I_9/2), 1056 nm (⁴F_3/2 → ⁴I_11/2) and 1326 nm (⁴F_3/2 → ⁴I_3/2) which are attributed to Nd³⁺ ions transitions. The emission spectrum demonstrates that the emission intensity decreases with the increase of Nd₂O₃ content from 0.05 to 0.1% Nd₂O₃ and then returns to its previous intensity with the increase of Nd₂O₃ to 0.2%. This phenomenon is known as luminescence quenching. This means that the intensity of emission spectra depends on the number of active centers.

Fig. 3

Emission spectra of Nd₂O₃-doped sodium fluoroborate glass at λ_ex = 580 nm

It is assumed that the density or concentration effect of Nd³⁺ ions rises with the increase of doping and with the rise of the concentration of Nd³⁺ ions, the intramolecular gap decreases and the Nd³⁺ ions are very closed resulting in a significant interaction between the dopant ions. Thus, there is an effective transfer of energy among Nd³⁺ ions which leads to luminescence quenching. These findings are consistent with previous studies [27, 28].

Ramteke et al. [32] studied optical and photoluminescence spectra of Nd³⁺ in lithium borate glasses and showed that optical spectra are due to Nd³⁺ ions and the luminescence intensity was maximum at 1% Nd₂O₃ and a further increase in Nd₂O₃ resulted in luminescence quenching. They attributed this quenching behavior to the Nd³⁺–Nd³⁺ interaction in the glass matrix. The results and attribution are in good agreement with previously reported results [33]. Kaewnum et al. [34] studied the luminescence properties of Nd³⁺ doped lithium lanthanum borate glass and made Judd–Ofelt analysis and concluded that this glass can be used as a laser medium in a glass emitting laser device.

Recently a study by Aljewaw et al. [35] on Li–Al–borate glass with varying Nd₂O₃ contents has reached the nomination of this glass system for diverse applications such as laser application and radiation dosimetry.

3.3 Judd–Ofelt analysis and radiative parameters

The analysis of the Judd–Ofelt parameters was performed using the oscillator strengths of the recorded transitions in the Nd³⁺4f quantum states. The experimental f_exp and calculated oscillator strength f_cal values of the prepared Nd₂O₃-doped glasses are listed in Table 2 adopting the root mean square error (RMS) deviation. According to Yaacob et al. [36], the oscillator strength values are an indication of the environmental symmetry around the rare earth in the glass network, and they refer to conclude that lower oscillator strength values indicate a highly symmetrical rare earth environment, whereas high oscillator strength values indicate that the glass is asymmetry and the ligands are covalently bonded. As observed from Fig. 2 the most intensive peak is located at 580 nm which is assigned to ²G_7/2 + ⁴G_5/2 electronic transitions and denoted by the hypersensitive transition (HST). The decrement in the RMS values indicated that the agreement between the calculated and experimental values and the considerable reduction in oscillator strength could be attributed to enhancing site symmetry around the Nd³⁺ ion and decreased covalent character of the bonds [36, 37].

Table 2 The experimental and calculated oscillator strengths (× 10^–6) for Nd-doped borate glasses

The estimated Judd–Ofelt parameters Ω₂, Ω₄, and Ω₆ of Nd₂O₃-doped glasses are given in Table 3. According to the recorded values in the table, the intensity trend of parameters is varied with Nd₂O₃ content and has been found to be Ω₆ > Ω₂ > Ω₄ for 2N sample, Ω₂ > Ω₆ > Ω₄ for 3N sample, and Ω₆ > Ω₂ > Ω₄ for 4N sample. The intensity parameter Ω₆ is assumed to be closely related to the local structure of the rare earth ions and the covalency degree Nd–O bonds while Ω₂ and Ω₄ parameters are strongly affected by the toughness and viscosity of the glass matrix and the greater Ω₆ in the current glass indicates its rigidity, while the lower Ω₂ suggests increased asymmetry and less covalency between the Nd–O group in 4N glass [36,37,38,39].

Table 3 Judd–Ofelt parameters Ω_{2, 4, 6} (× 10^–20 cm²) for the Nd-doped borate glasses

The literature indicates that JO characteristics are typically correlated with the covalency between RE ions and ligand anions as well as the local environment's asymmetries at the site of RE ions. Therefore, as the JO parameters increase, the ion site becomes less centrosymmetric and the chemical interactions between the ligands become more covalent [40, 41]. Additionally, the increase in 2, 6 values show a more distorted local structure at the Nd^3 +ions sites, which may be caused by increased polymerization of the glass dominant network and a higher covalency of the Nd–O bond in the current glassy system [41].

Numerous studies [41,42,43] have indicated that any observable shift of peak wavelength of the fluorescence spectrum of Nd³⁺ ion to a longer wavelength was caused by the increase of the covalency between the Nd³⁺ and the oxygen in oxide glasses. Hence, for glasses, the Judd–Ofelt parameters are related to the local structure in the vicinity of rare earth ions and/or the covalency of rare earth ions sites. For instance, the transition whose intensity is determined mainly by the Ω₂ < ║U⁽²⁾║ > ² term, called the hypersensitive transition, is sensitive to the local structures in the vicinity of the rare–earth ions relating to the anion structures of the host glasses while the other hand, the intensity parameters Ω₄ and Ω₆ are insensitive to the local structures but related to the covalency of the rare–earth ion sites in silicate, borate, and phosphate glasses [40,41,42,43]. As for alkali-containing glasses, when the rare earth ion is incorporated into the anion network oxide glasses as a modifier, the RE³⁺, modifying cations and NBO’s probably form depolymerized regions throughout the network resulting in the variations of the covalency of the rare earth – ion sites, which proceeds from an increase in the ionic packing ration, caused by changing the type of the alkali ion [40,41,42,43].

On the other hand, from the Judd–Ofelt theory, the line strength S_cal(J → J’) between the initial state J characterized by (S, L, J) and the final state J' given by (S', L', J') has been estimated. Hence, Table 4 introduces the values of radiative probabilities A (s⁻¹), branching ratio (β_R), and the radiative lifetime (τ_R) for the transitions ⁴F_3/2 → ⁴I_15/2, ⁴F_3/2 → ⁴I_13/2, ⁴F_3/2 → ⁴I_11/2, ⁴F_3/2 → ⁴I_9/2 and their correlation to the Nd₂O₃ content. The decrease in radiative transition probability can be attributed to rare-earth ion (Nd³⁺) accumulation and coupling with the phonon lattice vibration and through the phonon-electron interaction, the excited electron is most likely transferred to the phonon subsystem and releases some energy in the form of heat [37]. In the same context, the branching ratio (β_R) data indicated the ability to increase particularly stimulated emission transitions. The results show that the maximum value of the branching ratio is corresponding to ⁴F_3/2 → ⁴I_11/2 transition, hence the most prospective emission with high intensity occurs due to ⁴F_3/2 → ⁴I_11/2 transition. The obtained results are matched with that obtained and also suggested by previous study [36]. The trend of a lifetime is observed to be increased with increasing the Nd₂O₃ content.

Table 4 Radiative (A) and total radiative (A_T) transition probabilities, branching ratio (β_R) and lifetime (τ_R) for emission levels of Nd-doped borate glasses

The emission band positions, effective bandwidths and the stimulated emission cross-sections for Nd-doped borate glasses are listed in Tables 4 and 5. It can be assumed that under excitation at 580 nm, the electrons are absorbed and transferred from the highest energy levels to the most stable energy level ⁴F_3/2 as a result of the non-radiative relaxation. The emission of photons mainly depends on the allowed transitions from the relations process that induced ⁴F_3/2 → ⁴I_9/2, ⁴F_3/2 → ⁴I_11/2 and ⁴F_3/2 → ⁴I_13/2 transitions. According to data listed in Table 5 the largest stimulated emission cross-section is for the transition ⁴F_3/2 to ⁴I_11/2 and also is observed in glass with 0.05 mol% Nd₂O₃, which is higher than that with other listed glasses. It was reported by many previous studies [44,45,46], that materials used in the development of solid-state lasers should have a high effective emission cross-section to produce maximum photon emissions. The represented data indicated that the transition line ⁴F_3/2 → ⁴I_11/2 is the sharpest and lowest bandwidth value than other detected transitions, making it more appropriate for laser applications as suggested by previous assumption [44,45,46]. The bandwidth gain value is a predictive tool for the amplification of the laser glass, hence glasses with high gain bandwidth can be applied to operate the continuous wave laser directly that depends mainly on the host material, emission cross section and the duration of the excited level [44,45,46].

Table 5 Emission band positions (λ_p, nm), effective bandwidths (∆λ_eff, nm) and stimulated emission cross-sections (σ(λ_p) × 10^–20 cm²) for Nd-doped borate glasses

Fluoroborate glasses typically offer the best overall mix of properties for many different laser applications, but rarely exhibiting the extreme property values achievable when compared to other glasses. The number of commercially accessible laser glasses is extremely tiny in compared to the vast array and variety of glasses evaluated spectroscopically [8]. Large, regular variations in the Judd–Ofelt parameters with glass type and composition have been found for lanthanide ions based on knowledge of these fluctuations. Comparing the spectra in the current study, the ⁴F_3/2 → ⁴I_11/2 fluorescence of Nd-doped fluoroborate glass is more intensive than that for the other glasses [14, 16,17,18]. In contrast, to multicomponent silicate, phosphate, or other oxide or halide glasses, simple fluoroborate glasses show a higher degree of covalent bonding of Nd³⁺. The second attribute indicates a stronger local field strength and/or more site-to-site changes in the field. The examined glass has an acceptable optical quality that is within bounds and can satisfy the requirements of lasing applications.

3.4 FT infrared absorption spectra of the prepared glasses

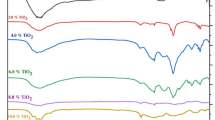
Figure 4a and b illustrate the deconvoluted IR spectra of both the undoped glass and 0.2% Nd₂O₃-doped glass. The curve fitting of IR absorption spectra is a useful technique that can be used to facilitate data interpretation. In curve fitting, the experimental spectrum is modeled as a sum of individual spectral contributions.

Fig. 4

FTIR absorption spectra of a undoped glass and b 0.2%Nd₂O₃-doped sodium fluoroborate glass

The measured IR spectrum of the undoped glass reveals distinct and extended far-IR peaks from 400 to about 600 cm⁻¹ and ended by an attached small band at about 650 cm⁻¹. The rest of the IR spectrum comprises a first very broad band extending from 800 to 1200 cm⁻¹ and revealing two bands, a medium band at about 900 cm⁻¹ and a high intense band with a peak at about 1020 cm⁻¹. A further second broad band is identified to be extending from 1200 to 1650 cm⁻¹ with a high intense band with a peak at about 1416 cm⁻¹ and followed by an attached medium band at 1600 cm⁻¹. The inside spectrum of the undoped glass (Fig. 4a) reveals extended absorption peaks at 413, 497, 557, 651, 897, 1020, 1104, 1416, 1487, and 1635 cm⁻¹.

The IR spectrum of the 0.2% Nd₂O₃-doped glass shows an intense far-IR broad band centered at about 469 cm⁻¹ and followed by a very broad band with higher intensity and extending from about 800–1200 cm⁻¹ and revealing a medium band at about 900 cm⁻¹ and a high intense band with a peak at about 1020 cm⁻¹. A further second broad and distinct band is identified extending from 1200 to 1650 cm⁻¹ with a band at about 1400 cm⁻¹ and followed by an attached medium band at 1600 cm⁻¹. The inside spectrum of the undoped glass (Fig. 4a) reveals extended absorption peaks at 413, 497, 557, 651, 897, 1020, 1104, 1416, 1487 and 1635 cm⁻¹.

The spectrum of the 0.2 Nd₂O₃-doped glass reveals extended deconvoluted peaks at 402, 461, 550, 635, 910, 1021, 1105, 1401, 1615 and 1660 cm⁻¹.

The details of the FTIR vibrational modes and their assignments are listed in Table 6.

Table 6 Infrared absorption spectra and their assignment

The understanding and interpretations of the identified IR spectral peaks from the undoped fluoroborate glass are based on the following basis [3, 47,48,49,50,51,52,53,54,55,56,57]:

• (a) It is agreed that the identified IR absorption bands are originating from vibrations of the structural building units or fingerprints of them within the studied glasses which depend on the detailed chemical composition of the glass constituents and the expected structural groups formed.

• (b) The chemical composition of the base host glass consists of main 70% B₂O₃, 25% NaF and 5% La₂O₃.

• (c) It is recognized that alkali and alkaline earth fluorides behave in a similar way as the corresponding oxides. Alkali fluorides are assumed to progressively convert some of the initial structural BO₃ groups in (B₂O₃) to be changed to (BO₃F) groups in a similar behavior to the formation of tetrahedral (BO₄) with alkali oxides. This conversion process proceeds to a certain limit which is characteristic to each alkali fluoride and the excess of the alkali fluoride is assumed to form additional tetrahedral alkali fluoride groups or units (e.g., NaF₄) and not to form nonbridging oxygens as with alkali oxide.

• (d) The confirmation of the previous assumption can be realized by referring to the intensities of the IR bands. It is accepted that the triangular BO₃ groups are vibrating within the range of 1200–1600 cm⁻¹ while the tetrahedral (BO₃F) groups are vibrating within the range 800–1200 cm⁻¹. The high intensities of the IR bands within the range 800–1200 cm⁻¹ refer to the assumption that it is assumed to originate from the combination mode of vibrations of tetrahedral (BO₃F) and (NaF₄) groups [7, 48].

• (e) The identified changes upon the increase of Nd₂O₃ content on the IR spectra (Fig. b) can be attributed to any or all of the following reasons [3, 7, 50]:

• (f) Suggested depolymerization effects causing the extension of the IR vibrational bands due to (BO₃) groups or derivatives group to extend from 1200 to 1650 cm⁻¹ with different distributions including the appearance of vibrational bands at 1401, 1615 and 1660 cm⁻¹, accompanied by the observed decrease of the band at 1416 cm⁻¹ in the undoped glass (Fig. 4a).

• (g) The assumption that Nd₂O₃ can cause the transformation of some structural B–O bonds within the range of triangular borate units such as the formation of pyroborate units or similar structural groups.

There is also a characteristic limit of the maximum concentration of [BO₄] structural groups. If it exceeds the maximum concentration, the reconversion of [BO₄]—units to [BO₃]—and [BO₃]—units (boron with one and two nonbridging oxygen atoms) would have been occurred. The creation of non-bridging oxygen atoms would leads to the disappearance or shift in the position of absorption bands [51]. Obviously, the addition of Nd₂O₃ causes some changes in the structural building units and due to loosely connected linkage or units of the bridging oxygen from network building units (BO₃/BO₄) cause a change in the shape and the position of the absorption bands to the higher wave number.

4 Conclusion

A novel host fluoroborate glass of chemical composition 70%B₂O₃–25% NaF–5 La₂O₃ together with Nd₂O₃-doped samples was prepared via melting and annealing technique. The undoped glasses reveal two UV absorption peaks at 223 nm and 280 nm that related to traces of ferric iron impurities. Nd₂O₃-doped glass show beside the UV-peaks as the undoped glass distinct extended absorption peaks from 430 to 875 nm with identified 10 absorption peaks at about 431(² P_1/2), 472 (² G_9/2), 511(⁴G_9/2), 526 (⁴G_7/2), 582 (⁴g_5/2), 625 (²H_11/2), 683(⁴F_9/2), 743 (⁴S_3/2 + 4F _5/2), 804 (4F_5/2) and 875 nm (⁴F_3/2). The emission after excitation at (580 nm) of Nd₂O₃-doped glasses spectrum shows three distinct bands at 875 nm (⁴F_3/2 → ⁴I_9/2), 1056 nm (⁴F_3/2 → ⁴I_11/2) and 1326 nm (⁴F_3/2 → ⁴I_3/2) which are attributed to Nd³⁺ ions transitions. The emission spectrum shows that the intensity of the emission reduces as Nd₂O₃ content rises from 0.05 to 0.1% and then returns to its initial intensity when Nd₂O₃ rises to 0.2%. The intensity trend of the parameters varies with Nd₂O₃ content and has been found to be Ω₆ > Ω₂ > Ω₄ for the 2N sample, Ω₂ > Ω₆ > Ω₄ for the 3N sample, and Ω₆ > Ω₂ > Ω₄ for 4N sample. The analysis of the Judd–Ofelt parameters indicates that the most intense peak is located at 580 nm and is assigned to ²G_7/2 + ⁴G_5/2 electronic transitions. The Ω₂ and Ω₄ intensity parameters are strongly influenced by the toughness and viscosity of the glass matrix, and the maximum value of the branching ratio is corresponding to the ⁴F_3/2 → ⁴I_11/2 transition, the most prospective emission with high intensity occurs as a result of the ⁴F_3/2 → ⁴I_11/2 transition. The intensity parameter Ω₆ is assumed to be closely related to the local structure of the rare earth ions and the covalency degree Nd–O bonds. According to FTIR studies, the IR absorption bands in the 800–1200 cm⁻¹ range are caused by the combined tetrahedral vibrations of the (BO₄), (BO₃F), and (NaF₄) groups, while the vibrations in the 1200–1600 cm⁻¹ range are caused by the triangular (BO₃) groups. The presence of Nd₂O₃ alters some structural B–O bonds in the range of triangular borate units, which may cause depolymerization and the emergence of pyroborate units or other structural groups. The examined Nd₂O₃-doped B₂O₃–NaF–La₂O₃ can be advised to be suited for laser applications, according to the overall measured spectrum features.