1 Introduction

Perovskite manganites have been studied with great enthusiasm since the discovery of its renowned phenomenon, which is known as the colossal magnetoresistance (CMR) effect in the 1990s [1, 2]. The hole-doped perovskite manganites with the general formula of R1-xAxMnO3, where R is a rare earth ion (R = La, Nd, Pr) and A is a divalent alkaline earth metal ion (A = Ba, Sr, Ca) have drawn much research interest in the scientific community. This is attributed to the correlation between charge, spin, orbital, and lattice degrees of freedom which makes it highly desirable to be applied in spintronic devices [3,4,5]. The CMR effects can be classified into two, which are intrinsic and extrinsic magnetoresistance (MR) [6]. The intrinsic MR is expressive at high magnetic fields while the extrinsic MR is significantly greater at low magnetic fields (LFMR). LFMR refers to the MR exhibited by a conductor under the influence of an external magnetic field, H ≤ 2 kOe. This intriguing phenomenon (LFMR) is one of the focus topics for manganite research in recent years as it is more appealing to modern world applications and it can also be enhanced in a wide temperature range [7].

The enhancement of LFMR can be achieved by the addition of a secondary oxide phase into the manganite composite. The composite samples are normally prepared by a 2-step sintering process and the oxide phase will be appended into the manganite phase after the first sintering process. This procedure has been demonstrated by LCMO: NiO [8, 9], LCMO: Sm2O3 [7], LSMO: NiO [10], and LBCO: WO3 [11]. The purpose of the 2-step sintering process is to facilitate the formation of the manganite phase through the first sintering process before the addition of the secondary phase. Thus, this could prevent the reaction between two compounds in the composite. However, the 2-step sintering process will cause the preparation time longer and might end up with a higher cost.

We have reported a study on the (1 − x) La0.67Ca0.33MnO3: x NiO nanocomposites prepared by the 2-step sintering process [9]. It was the first attempt to synthesising LCMO: NiO composite in bulk form. In that work, different concentrations of NiO nanoparticles (x = 0.00, 0.05, 0.10, 0.15, and 0.20) were added and the findings revealed that no interfacial diffusion reaction occurred between the two materials. Nonetheless, a slight reduction of LFMR was observed in the composites compared to the pure LCMO sample. This might be caused by the thick boundary layer (excessive addition of NiO) near grain boundaries and the impaired spin-polarised tunnelling process. Over the years, many attempts have been done to study the influence of NiO addition on the manganite composite [8,9,10, 12,13,14,15]. NiO nanoparticle is one of the excellent metal oxide nanoparticles attributed to its high magnetic permeability, high electronic conductivity, and phase stability [16].

Therefore, this study was carried out as an extension of the previous work on the (1 − x) LCMO: x NiO nanocomposites and aims to improve its shortcomings. Current work has simplified the preparation work of the sol–gel method by reducing the number of heat treatment processes. Besides that, the concentration of NiO nanoparticles in the composite has also been reduced. In this work, a systematic study of the structural, microstructural, magnetic, electrical, and magneto-transport of (1 − x) LCMO: x NiO, x = 0.00, 0.01, 0.03, 0.05, and 0.10 is presented.

2 Research methodology

(1 − x) LCMO: x NiO composite samples were synthesised using a similar procedure as reported in our previous work by the sol–gel method [9]. However, the heat treatment process was simplified in this study. The fine powder obtained from the dried gel was calcined at 500 °C for 5 h. Later, it was added with different contents of NiO (Sigma Aldrich, 99.8%) nanoparticles (< 50 nm) at x = 0.00, 0.01, 0.03, 0.05, and 0.10. These mixed powders were ground for 0.5 h and pressed into 13 mm pellets, then sintered at 800 °C for 6 h.

The phase identification and structural analysis were performed by an X-ray diffractometer (XRD, X’Pert Pro PW 3040) and HighScore Plus software, respectively. The surface morphologies were observed by a field emission scanning electron microscope (FESEM, FEI Nova NanoSEM 230). The compositions of samples were determined using an energy-dispersive X-ray spectrometer (EDX, Oxford Instrument Max 20). A vibrating sample magnetometer (VSM, Lakeshore 7407) was utilised in the temperature range of 100–300 K to characterise the magnetic behaviour and to determine the Curie temperature (TC). The temperature dependence of the resistivity and magneto-transport were assessed by a standard four-point probe method using a Hall effect measurement system (HMS, Lakeshore 7604) from 80 to 300 K.

3 Results and discussion

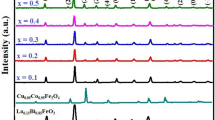
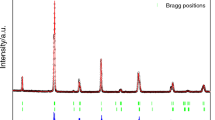
The structural characterisation of the composite samples was done by XRD within the 2θ range from 20° to 80°. Figure 1 shows the XRD patterns of (1 − x) LCMO: x NiO, x = 0.00, 0.01, 0.03, 0.05, and 0.10 samples in this work. All peaks were successfully matched and indexed by LCMO and NiO phases, indicating the composites were crystallised without other phase impurities. The relative peak intensities corresponding to the NiO phase were found to increase with its concentration. However, there is no sign of NiO peak observed for the x ≤ 0.03 samples. This can be attributed to the NiO content in those samples being below the XRD detection limit [17, 18]. The XRD data were further analysed by Rietveld refinement and the structural parameters are presented in Table 1. The low value of goodness of fit, χ2 (close to 1) signifies the good fit between the experimental and calculated patterns. The lattice parameters were found to have negligible changes with increasing content of NiO nanoparticles. The same observation was also applied to the bond angle and length between Mn and O ions, which are important indicators to determine the double exchange (DE) mechanism between Mn3+ and Mn4+ ions in the perovskite manganites, specifically on the interaction between the delocalised eg electrons and the localized t2g spins [19]. Besides that, the average crystallite size, D was computed by Scherrer’s equation [20] below and listed in Table 2:

$$D = \frac{0.9 \lambda }{{\beta \cos \theta }}$$
(1)

where β = βsample − βinstrumental, β is the full width at half maximum (FWHM) in radian, λ is the X-ray wavelength (1.5406 Å) and θ is the position of the most intense diffraction peak in degree, which is (121) peak in this work. The calculated crystallite sizes are found to be in the range of 29–34 nm, where the changes are considered insignificant with the increasing content of NiO in the composites. The analysed structural data reveal that there is no reaction between NiO and LCMO within the composite samples. Thus, it can be deduced that the NiO nanoparticles are segregated on the surface of LCMO grains or at the grain boundaries [7, 9, 21].

Fig. 1
figure 1

XRD patterns of LCMO: NiO composite samples

Full size image
Table 1 Rietveld refinement data of LCMO: NiO composite samples
Full size table
Table 2 The D, GS, TC, Tirr, TMI, ρpeak, and ΔT for the composite samples
Full size table

Figure 2f shows the typical FESEM micrograph of composite samples. All samples were observed to have grains with irregular shapes accompanied by distinguished grain boundaries. Figure 2a–e show the grain size distribution histograms with Gaussian fit (red colour solid line). The average grain size (GS) was determined by selecting 100 particles randomly from the FESEM micrograph. The grain sizes are found to gradually decrease with increasing NiO concentration as listed in Table 2. Interesting outcomes can be observed from the distribution plots, where the distribution becomes narrower and skewing to the left as the NiO content increases. These results are attributed to the segregation of NiO nanoparticles near grain surfaces or grain boundaries and agree with the XRD outcomes, as well as the observation made by the previous work [9]. Figure 3 shows the scanning region and EDX spectrum of the x = 0.03 sample. The presence of La, Ca, Mn, O, and Ni was confirmed by the EDX analysis despite the NiO phase was not detected by XRD in this sample due to the equipment limitation. Moreover, the atomic composition from EDX analysis was found to be very close to the nominal ratio of the composites and no additional impurities were noticeable, revealing that samples prepared in this work are chemically pure in the composition.

Fig. 2
figure 2

a–e Grain size distribution histograms and f typical FESEM micrograph of LCMO: NiO composite samples

Full size image
Fig. 3
figure 3

Scanning region and EDX spectrum of x = 0.03

Full size image

The field-dependent of magnetisation measurement (M-H) was carried out in the range of temperature from 100 to 300 K for x = 0.00 sample as displayed in Fig. 4a. The sample has undergone a ferromagnetic (FM) to paramagnetic (PM) transition, where the hysteresis loops were observed to become narrower and eventually changed to a positive gradient straight line as the temperature rose. The coercivity was observed to increase with the decrease in temperature as shown in the inset of Fig. 4a. This is attributed to the influence of thermal fluctuations of the blocked moment across the anisotropy barrier [22]. Figure 4b shows the temperature-dependent zero-field-cooled (ZFC) and field-cooled (FC) magnetisation under an applied field of 200 Oe in the temperature range of 100 to 300 K. For the ZFC measurement, the sample was first cooled from room temperature (300 K) down to 100 K without the application of the magnetic field. Then, the magnetisation was measured under the magnetic field of 200 Oe in the warming cycle. Whereas for the FC measurement, the sample was cooled down to 100 K from 300 K in the presence of a magnetic field (200 Oe) and the magnetisation measurement was followed later under the same applied field of 200 Oe. The magnetisation is irreversible as shown by the bifurcation between ZFC and FC curves below the irreversible temperature (Tirr), which is due to the movement of magnetic domain walls [23] and the presence of magnetic anisotropy [24]. It is known that the magnitude of ZFC depends on the anisotropy and the difference between FC and ZFC will be larger for the highly anisotropic compounds [25]. The difference between these two curves is almost similar for all samples (not shown) and the Tirr values (listed in Table 2) are also having insignificant changes as the concentration of NiO increases, indicating the addition of NiO does not disturb the magnetic behaviour of composites in this work. All samples exhibit a distinct magnetic transition from PM to FM as shown by the M-T plots in Fig. 5. The TC was determined by the inflexion point of dM/dT (inset of Fig. 5) and the values are grouped in Table 2. The TC values observed in this work do not experience any changes (260 K) with the increasing content of NiO. Hence, the magnetic findings here suggest that the LCMO perovskite lattice is free from the substitution or the formation of a new phase with NiO nanoparticles.

Fig. 4
figure 4

a Hysteresis loops at different temperatures and b M–T (FC & ZFC) measurement of x = 0.00 sample

Full size image
Fig. 5
figure 5

Temperature dependence of magnetisation for LCMO: NiO composites

Full size image

Figure 6 shows the temperature dependence of the electrical resistivity for the LCMO: NiO composites. The resistivity increases with the concentration of NiO in the composites as demonstrated by its peak resistivity, ρpeak (see Table 2). Besides that, all samples showed a distinct metal–insulator transition, TMI in the range of 120–246 K as tabulated in Table 2. The TMI decreases with the increasing content of NiO because the NiO nanoparticles near the grain interface have acted as a barrier to charge transport and caused an increment in the resistivity, as well as the dilution to the DE interaction [26]. The decrease in TMI value also indicates that the extrinsic transport (inter-grain connectivity) behaviour is highly influenced by the interface and grain boundary effects [27, 28]. Other than that, the transport behaviour of the composite can be elucidated by the two-channel conduction model [29,30,31]. The charge transport in the pure LCMO sample is contributed by the direct contact between LCMO grains. Whereas the presence of insulating NiO nanoparticles near the grain boundaries in composites has interrupted the charge transport. TC and TMI are important indicators of magnetic and electrical properties of perovskite manganites, respectively. These two values are not far from each other for bulk manganites [32]. The discrepancy between TC and TMI is presented as ΔT and summarised in Table 2. The ΔT value is getting greater with the NiO content because the electrical behaviour (TMI) is highly dependent on the microstructural properties while the magnetic behaviour (TC) is a cumulative effect of intrinsic properties in manganites [33, 34]. Thus, the changes of TC are insignificant as observed in magnetic analysis by considering the FM-PM transition is an intrinsic and intragrain behaviour [14].

Fig. 6
figure 6

Resistivity as a function of temperature for LCMO: NiO composites. The red solid line represents the theoretical fitting of experimental data

Full size image

The electrical resistivity data were fitted with theoretical models in the metallic and insulator regions. To gain insight into the conductive nature at low temperatures (T < TMI), the electrical resistivity data were fitted with the equation below [35,36,37]:

$$\rho \left( T \right) = \rho_{0} + \rho_{2} T^{2} + \rho_{4.5} T^{4.5}$$
(2)

where \(\rho_{0}\) is the grain/domain boundary effect, \(\rho_{2} T^{2}\) is due to electron–electron scattering and \(\rho_{4.5} T^{4.5}\) represents the electron-magnon scattering process. The experimental data were fitted with Eq. 2 in ρ–T plots as shown in Fig. 6. The fitting quality was determined by the squared linear correlation coefficient (R2), and it is noteworthy that the theoretical model is in good agreement with the experimental data. The fitting parameters are given in Table 3, and it is observed that \(\rho_{0}\) is greatest among all parameters, which shows that the residual resistivity due to the grain/domain boundary is mainly responsible for the conduction process in the metallic region. This fitting result complements the insulating nature of NiO nanoparticles that are scattered near the LCMO grain interface. The polaron conduction is likely to have the responsibility for the conduction in the insulator region (T > TMI) [38]. The experimental data were fitted by Holstein’s adiabatic small polaron hopping (ASPH) model (graph not shown) arising from the strong phonon coupling due to the Jahn–Teller distortion at T > θD/2 (θD is the Debye's temperature, θD/2 is defined as the temperature at which the deviation from the linearity of ln (ρ/T) against 1/T plot) [39], and Mott's variable range hopping model (VRH) [40] corresponding to the localized electrons in the absence of electron–electron interactions at TMI < T < θD/2. ASPH conduction mechanism is given by [41, 42]:

$$\rho \left( T \right) = \rho_{{\upalpha }} T {\text{exp}}\left( {\frac{{E_{{\text{a}}} }}{{k_{{\text{B}}} T}}} \right)$$
(3)

where \(\rho_{{\upalpha }}\) is the temperature independent coefficient, \(k_{{\text{B}}}\) is Boltzmann’s constant and \(E_{{\text{a}}}\) is the activation energy of the polaron. Figure 7 shows the graph of ln (ρ/T) against 1/T. All plots followed a linear relation at the high-temperature region and the obtained parameters are summarised in Table 3. The \(E_{{\text{a}}}\) is recognised as the height of the phase boundaries [13, 43], and it was found to increase from 1.520 to 1.630 meV as the NiO increases. It can be deduced that the magnetic disorder in the composites (addition of NiO) dominates the conduction process at the high-temperature region and leads to a higher resistive phase boundary. Thus, a higher \(E_{a}\) is required for the sample with higher NiO concentration [31, 44]. The hopping process at T > θD/2 can be explained by the ASPH model as it accords well with the theoretical conduction mechanism. The resistivity data at TMI < T < θD/2 were fitted with the VRH model and it is expressed by [33]:

$$\rho \left( T \right) = \rho_{{\text{o}}} \exp \left( {\frac{{T_{{\text{o}}} }}{T}} \right)^{\frac{1}{4}}$$
(4)

where \(\rho_{{\text{o}}}\) is residual resistivity and \(T_{{\text{o}}}\) is the Mott characteristic temperature which can be expressed as:

$$T_{{\text{o}}} = \frac{{16\alpha^{3} }}{{k_{{\text{B}}} N\left( {E_{{\text{F}}} } \right)}}$$
(5)

and it can be calculated from the slope of the graph of ln (ρ) against \(\left( T \right)^{{ - \frac{1}{4}}}\) (not shown), \(k_{{\text{B}}}\) is Boltzmann’s constant, \(\alpha\) is the inverse of localization length which is estimated to be 2.22 nm−1 for manganites [45] and N(EF) is the density of states at the Fermi level [46]. The parameters of VRH are listed in Table 3. The obtained N(EF) for the x = 0.00 sample is in good agreement with the reported value for La0.67Ca0.33MnO3 manganite [47].

Table 3 Parameters obtained corresponding to the best fit of the experimental data based on Eqs. (2), (3), and (4) for (1−x) LCMO: x NiO, (x = 0.00, 0.01, 0.03, 0.05, and 0.10)
Full size table
Fig. 7
figure 7

Fitting of resistivity curves of LCMO: NiO composites by Eq. (2)

Full size image

Figure 8a illustrates the resistivity as a function of temperature (ρ–−T) for x = 0.00 sample under a magnetic field of 0 kOe, 2 kOe, and 10 kOe. The magnetic field has caused the local ordering of magnetic spins and suppression of magnetic spin scattering, thus enhancing the electron hopping process and lowering the value of resistivity. This phenomenon is known as magnetoresistance (MR) and its magnitude is defined by Eq. (6) [32]:

$$MR \left( \% \right) = { }\frac{{\rho_{H} - \rho_{O} }}{{\rho_{O} }} \times 100$$
(6)

where \(\rho_{O}\) and \(\rho_{H}\) represent the resistivities without and with an applied magnetic field, respectively. The MR (%) as a function of externally applied magnetic field (0–10 kOe) curves from 80 to 300 K for pure LCMO sample was depicted in Fig. 8b. The MR (%) curves have displayed two regions as the magnetic field increases. The first region (H ≤ 2 kOe) or LFMR exhibits a steeper slope attributed to the spin-polarised tunnelling across the grain boundaries [28]. The disorder spins in manganite align when the magnetic field starts to apply and causes a drastic drop in resistivity at the low-field region due to the electron hopping enhancement. Then, the MR (%) increases linearly with the applied magnetic field with a reduced slope in the high field region (> 2 kOe) and it can be explained by the relatively slower rotation of the grain core [39, 48]. As observed from the plots in Fig. 8, LFMR is more pronounced at low-temperature regions and decreases as the temperature increases. To investigate the variation of magnetic fields on the MR (%) of LCMO: NiO composites, plots of MR (%) against T in the magnetic field range of 1–10 kOe are presented in Fig. 9a–d. Slight improvement of LFMR has been observed for composite samples above 280 K as shown in Fig. 9b. Moreover, the MR (%) of LCMO and its composites was found to increase monotonically with the decrease in temperature at low magnetic fields (1 kOe & 2 kOe). On the other hand, the MR (%) at 10 kOe has been enhanced over a wide range of temperatures as demonstrated in Fig. 9d. This enhancement is attributed to the suppression of spin fluctuation, where the spins are aligned parallel to the magnetic field and exhibit a higher MR (%) value near the TMI.

Fig. 8
figure 8

a ρ–T plot and b MR (%) as a function of magnetic field for x = 0.00 sample

Full size image
Fig. 9
figure 9

Temperature dependence of MR (%) for LCMO: NiO composite samples at a 1 kOe, b 2 kOe, c 5 kOe, and d 10 kOe

Full size image

Since this study is an extension of our previous work [9], several comparisons have been made to highlight the improvement. First, the structural parameters presented here are comparable with our previous work, indicating the crystal structure formation is not influenced by the shortened period of the heat treatment process. However, the microstructural behaviour (average grain size) of the composites in this work is highly suppressed due to the short heating period. The grain sizes in the current work are almost half of the value compared to the previous work, attributed to the less energy supplied during the grain growth. Sample resistivity here is one order down when comparing the x = 0.00 sample between both studies. This is an unusual trend because smaller grain size will contribute to higher resistivity as demonstrated by the previous work [32, 33, 49]. This might be attributed to the composites obtained in this work being denser and more compact with better grain connectivity, which favoured the electron hopping process although more grain boundaries have been formed in the samples. However, high-temperature resistivity data fitting by the SPH model showed that the Ea obtained here is almost similar to the previous work. Hence, we can deduce that the simplified heat treatment process of LCMO: NiO composites has favoured the conduction mechanism in the metallic region but has almost no effect on the Jahn–Teller mechanism. Lastly, the enhancement of MR has also been observed over a wide range of temperatures in the current work.

4 Conclusion

The LCMO: NiO nanocomposites have been successfully synthesised with a simplified heat treatment process by the sol–gel method in this work. XRD patterns confirmed the coexistence of LCMO and NiO phases in the composites with no phase impurities. Morphology analysis revealed the average grain size decreases as the NiO content increases, attributed to the segregation of NiO nanoparticles near the grain interfaces or grain boundaries. The chemical homogeneity of the samples and their elements were confirmed by the EDX. The TC values determined by M–T plots indicated samples do not experience any changes (260 K) with the increasing content of NiO. The presence of insulating NiO nanoparticles near the grain boundaries in composites has acted as a charge transport barrier to suppress the electron hopping process and caused the increment in the electrical resistivity. The MR (%) at 10 kOe has been enhanced over a wide range of temperatures, which is attributed to the suppression of spin fluctuation, where the spins are aligned parallel to the magnetic field and exhibit a higher MR (%) value near the TMI. In a conclusion, this work has demonstrated an important approach to obtaining MR enhancement in a wide temperature range. It also constituted an important step towards the development of an improved application of LCMO: NiO nanocomposite for future spintronic and memory devices.