Introduction

The development of technology has led to an increase in energy demand day by day. The primary source of this energy is non-renewable fossil fuels such as oil, natural gas, and coal [1]. These resources are finite and have negative effects on the environment. For this reason, the need for more efficient systems has emerged in cooling systems as well as in all areas. The development and testing of higher energy efficiency systems have become the center of recent studies. The basic working principle of the cooling systems used today is based on the compression and expansion of gases that harm the environment [2, 3]. It is known that these systems are at low levels in terms of energy efficiency and the regulations to be made to increase their efficiency require high costs [4]. Therefore, studies are being conducted to develop alternative systems that can replace today’s cooling systems. Among them, magnetic refrigeration systems (MRSs) are considered the cooling systems of the future due to their advantages [5, 6].

The main factor that makes MRSs advantageous compared to other systems is the magnetocaloric effect (MCE), which is the working principle. This effect involves a reversible change in temperature when exposed to varying magnetic fields, and it ensures high energy efficiency [5, 7]. Two critical magnitudes are primarily considered when selecting materials for MRSs: magnetic entropy \((-\Delta {S}_{{\text{M}}})\) and adiabatic temperature change (\(\Delta {T}_{{\text{ad}}}\)) [8]. In the selection of materials for the MRSs to be designed in the operating temperature range, after reaching the desired values for these two quantities, the type of magnetic phase transition and the relative cooling power (RCP) values are checked [9]. In the literature, many material groups exhibit high \(-\Delta {S}_{{\text{M}}}\) and \(\Delta {T}_{{\text{ad}}}\) values for different operating temperatures [10,11,12,13]. Although few of them have a high potential for use in magnetic cooling systems, it has been reported that most of them exhibit one or more undesirable properties such as high hysteresis, low chemical stability, and high raw material cost. [9, 14]. Considering factors such as acceptable MCE, adjustable transition temperature, low hysteresis, and low cost, manganites are one of the material groups with higher potential to be used for MRSs [15,16,17,18].

The magnetic and MC properties of manganites have been extensively studied for MRSs [19,20,21,22,23]. It has been stated that MRS should operate efficiently in the temperature range where coolant material has a relatively high constant \(-\Delta {S}_{{\text{M}}}\) value over a wide temperature range [24]. The \(-\Delta {S}_{{\text{M}}}(T\)) curve of such a material has a table-like shape [25, 26] and is required for the Ericsson cycle, which is the most suitable process for magnetic cooling at room temperature. This table-like shape of \(-\Delta {S}_{{\text{M}}}\) curve can be achieved for composites obtained by combining MC materials having consistent transition temperatures and acceptable \(-\Delta {S}_{{\text{M}}}\) values [24,25,26,27,28,29]. Additionally, it is stated that MC materials exhibiting multiple successive magnetic phase transitions may also have a table-like shape of the \(-\Delta {S}_{{\text{M}}}(T\)) curve [30]. The coexistence of magnetic multiple phases can widen the \(-\Delta {S}_{{\text{M}}}(T\)) curve, resulting in an increase in the RCP value [28, 29, 31,32,33].

In this paper, magnetic and MC properties of composite systems formed from manganites exhibiting second-order magnetic phase transition around room temperature and above have been studied in detail. One of the main phases chosen to form composite is La0.67Ca0.27Sr0.06MnO3 (LCSM) manganite, which exhibits a magnetic phase transition around room temperature and has a high \(-\Delta {S}_{{\text{M}}}\) value [28]. The magnetic and MC properties of the other main phase, La0.7Sr0.3Mn0.95Cu0.05O3 (LSMC) manganite, are given in detail in our previous study [34]. These manganites were chosen since they have a proper Curie temperature (TC) and favorable \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) values [35]. The two main phases prepared by using the sol–gel method have a rhombohedral crystal structure. Therefore, LCSM and LSMC main phases were mixed to form their composites according to the chemical equation yLa0.67Ca0.27Sr0.06MnO3/1−yLa0.7Sr0.3Mn0.95Cu0.05O3 (y = 0.25, 0.50, and 0.75). The structural, magnetic, and MC properties of the composites were characterized and checked for suitability for MRS applications.

Experimental

Composite materials obtained by combining yLa0.67Ca0.27Sr0.06MnO3/1−yLa0.7Sr0.3Mn0.95Cu0.05O3 (y = 0.25, 0.50 and 0.75) manganites in a specified ratio were produced using sol–gel method. The main phases La0.67Ca0.27Sr0.06MnO3 and La0.7Sr0.3Mn0.95Cu0.05O3 are named LCSM and LSMC, respectively. The details of the method used to obtain the main phases and the processes and technicality applied for each sample are given in our previous studies [28, 34]. La(NO3)3·6H2O (99.999%, Sigma), CuO (99.99%, Sigma), SrO (99.9%, Sigma), CaO (99.995%, Sigma), and Mn(NO3)2.6H2O (97%, Sigma) starting compounds were used to synthesize the LCSM and LSMC samples. yLa0.67Ca0.27Sr0.06MnO3/1−yLa0.7Sr0.3Mn0.95Cu0.05O3 (yLCSM/1−yLSMC) composites were prepared by mixing the LCSM and LSMC samples depending on the ratios of y = 0.25, 0.50 and 0.75. The codes 0.25LCSM/0.75LSMC, 0.50LCSM/0.50LSMC, and 0.75LCSM/0.25LSMC were used for naming the ratios of y = 0.25, 0.50, and 0.75, respectively. The composites were pelleted and sintered at 1200 °C for 24 h. PANalytical Empyrean brand X-ray diffractometer (XRD) and FEI Quanta 650 Field Emission scanning electron microscope (SEM) were used to investigate the structural and morphologic properties. The necessary measurements for the investigation of the magnetic and MC properties of the samples were carried out with the Quantum Design PPMS (DynaCool-9 T).

Results and discussions

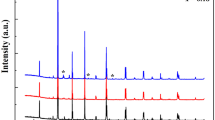
In this study, the structural, magnetic, and MC properties of the 0.25LCSM/0.75LSMC, 0.50LCSM/0.50LSMC, and 0.75LCSM/0.25LSMC composite systems consisting of perovskite manganites have been examined. The LCSM and LSMC main phases were synthesized by the sol–gel method. The main phases were determined using the High Score Plus program, and the structural properties of the main phases were given in detail in our previous studies [28, 34]. For the composites, XRD patterns have been obtained at room temperature and are shown in Fig. 1a–c. The diffraction peaks of both main phases have been detected in the XRD patterns of the composites. The patterns were analyzed by Rietveld refinement method using Fullproof software. Similar diffraction peaks were observed when the XRD patterns of the composite compounds were examined. The diffraction peaks of the composites were identical to the main phases overlapping the diffraction peaks of the perovskite structure. This prevents the determination of which main phase the diffraction peaks belong to. It was also observed that no third phase was formed in the diffraction patterns other than the main phases. The diffraction peaks of the main phases overlap, forming a sharp- and narrow-based diffraction pattern. Therefore, it can be said that the crystallization of the composites occurs well. Refined structural parameters for all composites are given in Table 1.

Fig. 1
figure 1

a–c XRD patterns of yLCSM/1−yLSMC composites a y = 0.25, b y = 0.50, c y = 0.75 at room temperature

Full size image
Table 1 Some structural parameters that attained from Rietveld refinement for the composites
Full size table

SEM images were taken at 20 kx magnification to examine the morphological properties of the composites. In our previous studies [28, 34], it has been reported that the average particle size of the LSMC (the grains are mostly oval-shaped) main phase is smaller than that of the LCSM (sharp-edged grains) phase. The SEM images of the composites are given in Fig. 2a–c. When the particle structures of the composites are investigated, the particle structures of different shapes and sizes are observed. This indicates that the main phases with different particle shapes and sizes coexist in the composites. Depending on the ratio of the main phases that form the composites, changes in particle sizes, shapes, and the volumes of intergranular spaces are noticed. Simultaneously, an improvement was also observed in the grain boundaries due to the change in the ratio of main phases. With the increase of the LCSM phase ratio, the volume of the intergranular spaces decreased and the sharpness of the grain boundaries increased. An increase in magnetic and MC properties can be observed as the decrease in intergranular spaces, the sharping of grain boundaries, and the increase in grain size may strengthen the connections between grains [36,37,38]. Consequently, an increment in the magnetic and MC properties may be observed.

Fig. 2
figure 2

a–c SEM images of the yLCSM/1−yLSMC composites at 20 kx magnification a y = 0.25, b y = 0.50, c y = 0.75

Full size image

Temperature-dependent magnetization (M(T)) measurements were carried out to examine the magnetic properties of the composites obtained by mixing the main phases, which exhibit magnetic phase transition around and above room temperature. The measurements were made in the range of 5–380 K under 100 Oe magnetic field at zero field cooling (ZFC) and field cooling (FC) modes. To collect magnetization data in ZFC mode, the composites were cooled from 380 to 5 K without applying an external magnetic field. Then, magnetization data were obtained until reaching 380 K by applying a magnetic field of 100 Oe. The M(T) has been measured by cooling the composites down to 5 K after applying a field of 100 Oe in FC mode. The M(T) curves were obtained for all composites using the data obtained from the measurements. Figure 3a–c represents the M(T) curves of the composites. From the M(T) curves of 0.50LCSM/0.50LSMC and 0.75LCSM/0.25LSMC composites, it is seen that the ZFC magnetization shows a slight increase with an increase in temperature up to a certain temperature value. At this temperature value, all ferromagnetic (FM) clusters in the antiferromagnetic (AFM) matrix are oriented along the applied external field. At a temperature above the temperature at which ZFC magnetization reaches its maximum value, its magnetization gradually decreases to zero and the composites exhibit a magnetic phase transition from FM to paramagnetic (PM) phase. It is seen that a step-like transition is observed from the M(T) curves of the composites, indicating the presence of two phases (see Fig. 3d). Although the M(T) curves show similar behavior in general, the sharpness of the transition region varies depending on the ratio of the main phases. It is thought that this situation may be due to the characteristic feature of the M(T) curves of the main phases. At low-temperature regions, it has been observed divergence between the ZFC and FC curves of the composites. It is known from the literature that this difference is due to some factors such as magnetic inhomogeneity [39,40,41,42], domain pinning effect [20, 43], and spin-canted states [44]. Although the ZFC and FC magnetization curves overlap in the high-temperature region, they appear to diverge below a temperature value known as the irreversibility temperature (Tirr). This irreversibility is known to be related to the blocking of large particles [45].

Fig. 3
figure 3

The M(T) curves of yLCSM/1−yLSMC composites under 10 mT magnetic fields at ZFC and FC processes (a–c), dM/dT − T graph of yLCSM/1−yLSMC composites (d)

Full size image

In Fig. 4a–c, M(H) curves for composites obtained from the isothermal magnetization data taken at 4 K temperature steps up to 5 T magnetic field in the temperature range of 264 and 360 K are given. The M(H) curves exhibit a change with increasing temperature, representing the transition from FM to PM. In the high-temperature region, the M(H) curves exhibit a linear variation confirming the PM behavior. However, with the application of magnetic field in the low-temperature region, they initially increase rapidly and reach saturation in a certain magnetic field. The saturation magnetic moment has been calculated from the M(H) curve at 5 K measured up to 5 T and is shown in Fig. 4d. The saturation magnetization (Ms) values of the composite materials were calculated as 87.6, 90.1, and 92.1 emu g−1 for 0.25LCSM/0.75LSMC, 0.50LCSM/0.50LSMC, and 0.75LCSM/0.25LSMC, respectively. The Ms values show parallelism with the magnitude of the \(-\Delta {S}_{{\text{M}}}\) values. In this context, it is thought that the \(-\Delta {S}_{{\text{M}}}\) value of the 0.75LCSM/0.25LSMC composite may be higher since it has the highest saturation magnetization value among the composites in the study.

Fig. 4
figure 4

The isothermal M(H) curves of yLCSM/1−yLSMC composites taken up to 5 T applied magnetic field around the magnetic phase transition temperatures a y = 0.25, b y = 0.50, c y = 0.75 and d The M(H) performed at 5 K for all samples

Full size image

The order of magnetic phase transition is a crucial factor in the evaluation of magnetocaloric materials (MCMs) and the magnetic phase transitions in the MCMs are divided into two groups first-order magnetic phase transition (FOMT) and second-order magnetic phase transition (SOMT) [46]. It is known that the total entropy of a material with SOMT is a continuous function of temperature regardless of the magnetic field. However, at a constant temperature and pressure, the entropy change is discontinuous for the FOMT, and the heat capacity gets infinite [47]. The \(-\Delta {S}_{{\text{M}}}\) values of the materials exhibiting FOMT are larger than SOMT ones. However, FOMT takes place in a narrower temperature range than SOMT and the thermal and magnetic hystereses affecting cooling capacity are generally too large for FOMT [48, 49]. The application of a magnetic field has an entirely discrete effect on a first-order magneto structural transition when compared with the SOMT one [9]. Therefore, the evaluation of a material as a candidate refrigerant in applications also depends on the type of magnetic phase transition. The order of magnetic phase transitions of the MCMs can be determined by using Banerjee criterion [50], Landau theory [28, 29, 51], the universal master curve proposed by Franco et al. [52, 53], and mean field theory criteria [48]. There are studies in the literature stating that these approaches are compatible with each other [29, 33, 54, 55]. In our study, we tried to determine the type of magnetic phase transition using Banerjee criterion. The criterion gives information about whether the transition is SOMT or FOMT, depending on the sign of the slope around the transition temperature region of Arrott plots obtained using M(H) data. The negative slope indicates FOMT, while the positive slope indicates SOMT. The Arrott curves obtained for our samples are given in Fig. 5a–c. The positive slope of all samples in the transition temperature region indicates that the order of the transition is second.

Fig. 5
figure 5

The Arrott plots of yLCSM/1−yLSMC composites a y = 0.25, b y = 0.50, c y = 0.75

Full size image

In order to calculate \(\mathrm{the }-\Delta {S}_{{\text{M}}} \mathrm{ values},\) Maxwell equations are applied to the magnetic field dependence of magnetization (M(H)) curves obtained from isothermal measurements for calculating the \(-\Delta {S}_{{\text{M}}}\) values and the numerical value is calculated with the equation given below [8].

$$ - \Delta S_{{\text{M}}} \left( {H,T} \right) = \sum \frac{{M_{{\text{i}}} - M_{{{\text{i}} + 1}} }}{{T_{{{\text{i}} + 1}} - T_{{\text{i}}} }}\Delta H_{{\text{i}}} $$
(1)

The terms Mi and Mi+1 in the equation represent the magnetization values at Ti and Ti+1 temperature values, respectively. To determine the \(-\Delta {S}_{{\text{M}}}\) values of the yLCSM/(1−y)LSMC (y = 0.25, 0.50, and 0.75) composite series, Maxwell’s equations were applied to the M(H) curves obtained around the temperatures in the range of 260–360 K, and the temperature dependence of \(-\Delta {S}_{{\text{M}}}\) (\(-\Delta {S}_{{\text{M}}} (T))\) was obtained for different magnetic field values. The \(-\Delta {S}_{{\text{M}}} \left(T\right)\) curves of the composites are shown in Fig. 6a–c. It can be seen from the \(-\Delta {S}_{{\text{M}}} \left(T\right)\) curves that there are two maximum peaks defined as the maximum magnetic entropy change (\(-\Delta {S}_{{\text{M}}}^{{\text{max}}})\) for all composites, especially for low magnetic field changes. This is a sign that the composites have magnetic phases with two different transition temperatures [56]. However, although the 0.25LCSM/0.75LSMC and 0.75LCSM/0.25LSMC composites contain two separate phases with two different transition temperatures, the \(-\Delta {S}_{{\text{M}}} \left(T\right)\) curves have exhibited almost a single behavior for 5 T. The different magnetic field dependence of the individual entropies at the transition temperatures of each major phase causes the curves to flatten [35]. The reason for this observed situation for these two composites may be due to the different magnetic field dependence of the individual phases. A similar result was observed in different studies [57]. For all composites, the increase in the maximum peak intensities with increasing magnetic field is because more magnetic moments are directed in the direction of the field as the magnetic field increases. A higher \(-\Delta {S}_{{\text{M}}}\) value is observed in the transition temperature region of the main phase, whichever main phase amount is larger in composites. In cases where composite materials are formed by combining two materials with close temperatures, the maximum points in the \(-\Delta {S}_{{\text{M}}}\) curves are very close to each other and these curves pass into each other. Thus, the temperature ranges in which the \(-\Delta {S}_{{\text{M}}}\) is observed are revealed. As can be seen from Fig. 6c, the \(-\Delta {S}_{{\text{M}}}\) peaks have intertwined and turned into a single curve for the 0.75LCSM/0.25LSMC composite. It is seen from the dM/dT − T curve of 0.75LCSM/0.25LSMC composite that the main phases are intertwined. The overlap of the \(-\Delta {S}_{\text{M}}\) peaks of the main phases may significantly expand the temperature width range, resulting in an increase in RCP [55]. However, this may also cause a decrease in \(-\Delta {S}_{M}\) value. Therefore, it may not be accurate to say that overlapping of the \(-\Delta {S}_{M}\) peaks unequivocally causes an increase in RCP. The \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) value has been calculated as 3.18, 3.24 and 4.05 J kg−1 K−1 at 5 T magnetic field for the composites 0.25LCSM/0.75LSMC, 0.50LCSM/0.50LSMC, and 0.75LCSM/0.25LSMC, respectively. For 0.25LCSM/0.75LSMC and 0.75LCSM/0.25LSMC composites, large \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) was calculated in the TC region of the dominant phase, while the 0.50LCSM/0.50LSMC composite has two \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) peaks with the same value at 292 and 332 K temperatures. The \(-\Delta {S}_{{\text{M}}}\left(T\right)\) curves for all samples are shown in Fig. 7 to compare the \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) values. It is observed that \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) values of the composites increase with the increase of the y ratio.

Fig. 6
figure 6

The \(-\Delta {S}_{{\text{M}}} \left(T\right)\) curves of yLCSM/1−yLSMC composites a y = 0.25, b y = 0.50, c y = 0.75

Full size image
Fig. 7
figure 7

The \(-\Delta {S}_{{\text{M}}}\left(T\right)\) curves for the main phases and their composites

Full size image

The criteria to be considered in the selection of coolant materials for magnetic cooling systems have been emphasized in various studies [9, 16, 58]. In addition to high \(-\Delta {S}_{{\text{M}}}\) and \(-\Delta {T}_{{\text{ad}} }\) values, relative cooling power (RCP) value should be at satisfactory values. The area under the \(-\Delta {S}_{{\text{M}}} \left(T\right)\) curve obtained for each magnetic field value gives RCP value, which defines the cooling efficiency of the magnetic cooler for that magnetic field value [59]. The RCP value has been calculated using relation.

$$ {\text{RCP}} = \left| { - \Delta S_{{\text{M}}}^{\max } } \right| \times \delta T_{{{\text{FWHM}}}} . $$
(2)

In Eq. (2), the \(\left|-\Delta {S}_{{\text{M}}}^{{\text{max}}}\right|\) describes the magnitude of \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) value, while \({\updelta T}_{{\text{FWHM}}}\) represents the full width at half maximum of the \(-\Delta {S}_{{\text{M}}}\left(T\right)\) curve. The RCP value of all composites has been calculated for a magnetic field value of 5 T and is given in Table 2. It is seen that the RCP values calculated for all composites are higher than the main phases. It has been stated in the literature that higher RCP values are obtained for composite samples compared to single phase samples [35, 56, 60]. A comparison of the RCP value of the main phases with some composites and other perovskite phases found in the literature is given in Table 2 [33, 60]. Several factors cause a change in RCP value. The fraction of phases, the difference between Curie temperatures and the maximum magnetic field, etc., can be given as an example of this change [61]. The overlapping of the \(-\Delta {S}_{{\text{M}}}\) peaks of the main phases forming the composite also affects the RCP value [55]. The highest RCP value was obtained for 0.5LCSM/0.5LSMC composite. It can be thought that this increase may be due to the expansion of the temperature range. According to the results, it can be said that the studied materials have the potential to be used for MRSs around room temperature.

Table 2 The comparison of the RCP values of main phases and their composites and some composites composed of two manganites in the literature
Full size table

Conclusions

Briefly, this study provides information about the magnetic and MC properties of composites obtained by mixing the manganites in certain proportions by mass, which exhibit FM-PM transition at different temperatures and have acceptable \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) values. XRD analyses were performed at room temperature to determine the structural characteristics of the composites. Diffraction peaks belonging to both main phases can be seen from the XRD patterns of the composites. The diffraction peaks of the main phases have overlapped to form a sharp- and narrow-based diffraction pattern, and no peaks have been observed implying the presence of a third phase. It has been determined that particles of different shapes and sizes coexist in SEM photographs. This confirms that the composites are composed of separate phases with different shapes and grain sizes. A step-like transition has been observed from low field magnetization measurements, indicating the existence of two separate phases. The Arrott curves of all composites have a positive slope confirming the second-order phase transition around TC. The \(-\Delta {S}_{{\text{M}}}^{{\text{max}}}\) and RCP values have been calculated as 3.18, 3.24, and 4.05 J kg−1 K−1 and 287.72, 301.61, and 291.60 J kg−1 at 5 T magnetic field for 0.25LCSM/0.75LSMC, 0.50LCSM/0.50LSMC, and 0.75LCSM/0.25LSMC composites, respectively. The highest RCP value was obtained for 0.5LCSM/0.5LSMC composite, and it may be a satisfactory candidate for room-temperature MR applications.