1 Introduction

The long history of the study of the peculiarities of the interaction of the ultrashort laser pulses with matter dates back to the advent of the availability of high-energy fs pulses [1]. In the case of transparent dielectrics incoming pulse interacts with the electric field of the atoms of the target material pulling electrons out from the valence band to the conduction band by photoionization. The free electrons gain more energy by absorption pulling more and more electrons out from the atoms by an avalanche process [2] leading to the Coulomb explosion [3]. When the density of the hot plasma reaches a critical value the remaining part of the incoming pulse is reflected from the plasma mirror formed [4,5,6,7] weakening the energy coupling efficiency, diminishing thereby the effectivity of the material removal, materialized in changes in the ablation characteristics [8, 9]. Therefore, optimization of the procedure requires a comprehensive description of ionization induced effects when processing targets at intensities in the strong field domain.

Comparative studies with multiple types of targets describing the material response to ultrashort pulses have been reported for decades [10,11,12,13,14]. Optical quality silica is the favorite material of the field due to improved and well-defined chemical and surface standards. Ablation characteristics of silica have been studied intensively [8, 11,12,13, 15,16,17,18,19,20,21,22,23,24]. Authors report effects of highly ionizing ultrashort pulses on the optical response of silica focusing on nonlinear absorption [12, 25], nonlinear refractive index [25, 26], plasma reflectivity [5, 6] in a broad range of pulse durations from 7 fs to 4 ps. Commercial multicomponent borosilicate and crown glasses may serve as cheaper and more accessible alternatives, however, investigations in the literature related to glasses using few-cycle pulses are scarce [11, 27, 28]: the majority of the studies were performed with longer and moderate-intensity pulses examining either material [14, 17, 19, 29,30,31,32,33,34], or optical [25, 26, 35,36,37,38,39,40] response. Therefore, available data for the description of the aftermath of strong-field ionization in the ablation process of glasses is inconveniently deficient.

In this contribution, an analysis of the evolution of the morphology and main geometrical properties of ablated craters of three different optical glasses, namely Borofloat, BK7, and B270 of Schott processed by ultrashort, high-intensity pulses is reported. The behavior of the morphology and the ablated depth of the craters is discussed in the frame of accompanying ionization of the targets and a model based on depth data.

2 Materials and methods

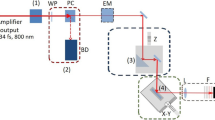
The experimental setup of the single-shot measurements is sketched in Fig. 1. The driving laser of the experiments was the TeWaTi laser system [41], which is based on a mode-locked Ti:Sapphire oscillator (Spectra-Physics Rainbow™) and a home-made Ti:Sapphire chirped-pulse amplifier. The system provided pulses with 34 ± 0.16 fs duration and 1 mJ energy at 800 nm central wavelength with stability at the output of the amplifier better than 1% RMS. The temporal contrast of the amplified pulses was 107 as measured by a third-order cross-correlator (SEQUOIA™ from Amplitude Technologies). Single pulses were selected by a mechanical shutter (Thorlabs Inc. SH05 + SC10). Pulse energies set by the combination of a half-wave plate (HWP) and a polarization beam splitting cube (PBSC), were measured with an energy meter (Gentec QE50SP-H-MT-V0). The reproducibility of the measurements was better than 5%. An off-axis parabolic mirror (Thorlabs Inc. MPD169-P01) with a reflected focal length (RFL) of 152.4 mm (F-number: f/19) focused the beam onto the target.

Fig. 1
figure 1

Scheme of the setup. HWP half-wave plate, PBSC polarization beam-splitter cube, BD beam dumper, OAPM off-axis parabolic mirror, L focusing bi-convex lens, F filters, PD photodiode

Full size image

Uncoated optical glass pieces: Schott’s BOROFLOAT® provided by Edmund Optics (ID #48-542), Schott’s N-BK7® provided by Eksma Optics (ID 215-0222), and Schott’s B270® Superwhite provided by Edmund Optics (ID #48-538) were applied as targets, placed at an angle of incidence of 45°. The ablation of the pristine surface was ensured by shot-to-shot repositioning of the target using translation stages. The beam reflected from the irradiated area was re-focused by a lens with a focal length of 35 mm and a diameter of 25.4 mm onto a photodiode (PD) (Thorlabs DET36/A). Long-pass filters with cut-on wavelength below 800 nm excluded the light of the plasma formed while reflective filters placed in front of the PD reduced the intensity to appropriate levels.

Sample matrices were produced by moving the stage stepwise with 1000 µm while increasing the pulse energy from row to row up to 450 µJ. Each row contained 11 craters 200 µm apart ablated with single pulses with the same energy. The craters were characterized by stylus profilometry (Veeco DEKTAK8 surface profiler with 0.1 nm vertical and 0.17 µm lateral resolution). Depth and diameter values were derived for each crater from line scans along the minor axes. The depths and diameters, defined as the maximal difference between the pristine surface level and the deepest point of the trace and the distance between the two points where the trace crosses the surface level within the rim of the crater, respectively, given below, are averages of the 11 values recorded within the same row.

To determine the actual diameter of the beam on the sample surface the standard expression connecting the ablated crater diameter and the fluence/pulse energy was applied:

$$D=\sqrt{2{w}^{2}\mathrm{ln}\left(\frac{F}{{F}_{\mathrm{th}}}\right),}$$
(1)

where w is 1/e2 beam radius, while F and Fth stand for the peak and ablation threshold fluences, respectively [42]. In-line with Eq. (1), D2 vs. log(F) curve proved to be linear, which indicates that even though the measurements were carried out in the air, beam distortion was not occurring (for details see Fig. 2 in [43]).

The actual peak fluence values were calculated from the measured pulse energy, Ep and the area of the laser spot on the sample surface, where w is the half of the minor and \(w\sqrt{2}\) is the half of the major axes, according to

$$ F = {{2E_{p} } \mathord{\left/ {\vphantom {{2E_{p} } {\left( {\pi w^{2} \sqrt 2 } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\pi w^{2} \sqrt 2 } \right)}}. $$
(2)

The ablation thresholds were derived both by the diameter-regression technique (DR), according to Eqs. (1), (2), and by the multiphoton absorption-based fitting of the depth vs. fluence functions (MA), applying

$${d}_{\mathrm{max}}=\frac{{\tau }^{m-1}}{\left[\left(m-1\right){\alpha }_{m}{\left(1-R\right)}^{m-1}\right]}*\left(\frac{1}{{F}_{\mathrm{th},\mathrm{dep}}^{m-1}}-\frac{1}{{F}^{m-1}}\right),$$
(3)

with dmax as the depth, m as the order, αm as the non-linear absorption coefficient, τ as the pulse duration (actually 34 fs), and R as the measured linear reflection coefficient [12, 14].

3 Results

The profilometer traces recorded along the minor axes shown in Fig. 2 reveal that the shape of the craters reliably follows the Gaussian-like energy distribution of the processing beam for all three glasses with small differences in morphology. While the craters ablated into Borofloat and B270 possess a smooth finish, the fs pulses leave rough cracked surfaces behind in BK7 with hills and valleys of dimensions increasing with increasing fluence up to several tens of nanometers. The formation of the cavity is always accompanied by the rise of a rim around, which is the highest in the case of B270 ablation. Both the shape and the roughness of the craters remain essentially unchanged with increasing fluence for Borofloat and BK7. In B270 the evolution as a function of fluence is different: while the contours remain smooth, the shape changes. As the fluence increases a bump evolves resulting in slightly smaller depth at the center as compared to the maximum depth measured towards the edges.

Fig. 2
figure 2

Evolution of the cross-sections along the minor axes of the craters ablated into a Borofloat, b BK7 and c B270 glasses. Beam radii on the surface: 25.1, 26.1, and 24.83 µm, respectively. Continuous lines: recorded profiles, dash-dotted lines: quartic fits

Full size image

In Fig. 3 changes in the diameter and the depth of the ablated craters are plotted together with the evolution of the part of the processing beam reflected from the irradiated area measured as the photodiode signal as a function of fluence for the three glasses. In each case, the results represent averages of minimum of three independent experimental series. In the majority of the data points, the error bars proved to be smaller than the size of the symbols.

Fig. 3
figure 3

Ablation and reflection characteristics of the glasses. Dashed curves in (a–c) are logarithmic fits, while continuous curves denote in (d–f) the fits according to Eq. (3). Dashed and continuous vertical lines denote the ablation thresholds derived from diameter regression, DR, and multiphoton absorption fits, MA, respectively. Rnorm denotes normalized reflectivity. Dash-dotted vertical lines indicate the breakpoints between the two straight sections of the reflectivity. Dash-dotted and dotted fits with slopes ap and at stress the difference between the evolution of permanent and transient reflectivities in (g–i)

Full size image

The ablation threshold values indicated in Fig. 3 were derived applying both DR and MA techniques. The DR resulted in 5.85 ± 0.20, 6.43 ± 0.54, and 5.95 ± 0.31 J/cm2, while MA produced 5.80 ± 0.21, 6.65 ± 0.71 and 5.65 ± 0.24 J/cm2 for Borofloat, BK7, and B270, respectively. Being within the 6.1 ± 0.55 J/cm2 domain with overlapping confidence intervals the threshold values derived from both approaches are equal, i.e. the single-shot ablation thresholds of all three glasses are considered to be the same within experimental error.

Above threshold the diameter values follow the well-documented logarithmic dependence [13, 21, 29, 42, 44] in the whole range investigated, reaching values around 45 µm at 30 J/cm2 for all three glasses. The depths increase with increasing fluence and—contrary to the diameters—show saturation which starts at slightly different fluences: above 20, 17, and 18 J/cm2 for Borofloat, BK7 and B270, respectively. The maximal depth values decrease moderately in the Borofloat-BK7-B270 order reaching 250, 240, and 220 nm, respectively. The comparison of the ablation behavior of the three glasses led to the conclusion that there were no significant differences in the material response characteristics.

Monitoring the changes in the energy of the beam reflected from the processed area with the fluence offered an independent diagnostic tool for following the irradiation-induced surface processes. The Rnorm functions can be fitted by two straight sections with different slopes (ap and at) joining just above the ablation thresholds for all glasses (Fig. 3g–i). The breakpoints mark the fluence where the optical response of the irradiated area changes. Below the breakpoint, the slopes differ only slightly. The ratio of the three ap slopes (2.51:3.67:3.94) coincides with the ratio of the absolute values of the front side permanent reflectivities of the p-polarized beam at 45° (0.0068:0.0089:0.0093) of the respective glasses, evidencing that what we measure in this domain is the evolution of the permanent reflectivities. This means that the pulses see pristine surfaces. The steep increase in the Rnorm above the breakpoint is due to the emergence of a plasma mirror [43]. The difference in the at slopes indicates that at higher fluences the evolution of the reflectivity from the irradiated surface area of the glasses is different. This results in differences in the absorbed energy and thereby in the actual effective fluences.

Note that the actual values of the breakpoints differ only slightly for the three glasses (9.5, 10, and 8.0 J/cm2 for Borofloat, BK7, and B270, respectively) and correlates with the ablation thresholds [33], further supporting the feasibility of the approaches (DR, MA and Rnorm) and justifying the statement that the ablation characteristics of the glasses investigated are rather similar.

4 Discussion

We could not find crater profiles of glasses ablated with pulses in the vicinity of 30 fs duration for direct comparison. 200 fs pulses produce craters of smooth and regular shapes in Borofloat [29], similar to those shown in Fig. 2. Within similar fluence domains, longer pulses give rise to more elevated rims: the height of the rims surrounding the craters is 2–4 times larger as compared to those recorded for 34 fs (Fig. 2). The height grows further from 50 to 100 nm with increasing fluence from 25.5 to 55 J/cm2 [29]. The mechanism of rim formation is well-documented: it is the consequence of a thin molten surface layer moving toward and resolidified at the edge of the crater driven by hydrodynamic forces caused by the recoil pressure.

For 150 fs pulses, the results of Campbell [30] claimed that the contour could be fitted with squared, or Gaussian functions for BK7. Lebugle and Sanner described that the contour of the profiles changed gradually from Gaussian to top-hat with increasing fluence for fused silica processed with 7 fs [9] and 30 fs [46] pulses, respectively. As Fig. 2 demonstrates in our case quartic functions fit best to all profiles shown except the two profiles recorded for the two highest fluences for B270. Mirza [33] shows for Willow glass ablated with 130 fs pulses that the overall shape of the ablated craters bears resemblance to ours until 59 J/cm2. A comparison of the relevant results reported in the literature [8, 9, 12, 46, 47] with those shown in Fig. 2 leads to the conclusion that at low fluences glasses and fused silica give very similar responses in terms of crater geometry. The general shape of the craters ablated into the glasses investigated with pulses in the 34–600 fs temporal domain does not depend significantly on pulse duration. The craters ablated into Borofloat and B270 exhibit high smoothness (Fig. 2a, b), while a surprisingly rough finish characterizes the BK7. The reason for this difference is that the BK7 is less resistant to thermal shock than the B270 glass, and the Borofloat possesses the highest thermal shock resistivity [48].

Minor differences in the shape of the craters in Borofloat/BK7 and B270 glasses appear only above a certain fluence. When processing B270 glass with pulses of fluences exceeding 24 J/cm2 an intriguing phenomenon has been observed: a bump emerged in the middle of the bottom of the crater: cf. Fig. 2c. While not mentioned for fs ablation of glasses, Uteza [8, 45] describes such a bump formation at the bottom of the craters ablated into fused silica target with 7 fs and 30 fs pulses developing with increasing fluence above 10 J/cm2. Explanation of the bump formation is a challenge, indeed. One possible source of the bump formation could be the Marangoni flow, an effect driven by surface tension temperature gradients [49]. However, because the relevant thermal properties of all three investigated glasses are very much the same, pure thermal effects do not provide an adequate explanation for the different behavior.

Two aspects of overcritical plasma formation could be considered while seeking an explanation for the bump formation [8, 9, 46]: (i) transient reflectivity enhancement in the central part of the irradiated area [8] and (ii) saturation of nonlinear absorption at high fluence/intensity [9, 46]. The tendency observed in the reflectivity curves shown in Fig. 3g–i does not support the former one. The effect of the changing absorption with the fluence on the profiles seems to be more rational due to the earlier saturation of the depth values in B270 glass as compared to the behavior of the other two glasses shown in Fig. 3d–f.

The diameter vs. fluence functions follows logarithmic dependence, while the depths saturate for 34 fs pulse duration as shown in Fig. 3. This behavior can be favorable compared with those recorded for both glasses [14, 29, 33] and fused silica [8, 9, 12, 13, 21, 24]. Note that the saturating characteristic of the depth vs. fluence functions prompted us to use the MA fit proposed by Grehn [14] instead of a logarithmic one.

At first glance, a comparison of our data with those listed in Table 1 does not help too much in the evaluation of our ablation threshold data. Data on ablation characteristics of glasses in the intensity range of the vicinity of our intensities applied are scarce: very few data are available around 30 fs pulse duration. Kautek determined thresholds of 0.4 and 0.9 J/cm2 [27] for Corning 7059 glass with 20 fs and 50 fs pulses, respectively, while Machado gives 4.6 J/cm2 threshold values for BK7 glass processed with 55 fs pulses [31].

Table 1 Ablation thresholds of glasses processed in the 20–800 fs temporal domain for comparison
Full size table

Taking into account that Ben-Yakar [29] defined Φth as Ep/πw2 and worked at 200 fs, their 2.55 J/cm2 threshold fits fairy well our 5.85 J/cm2 value. Grehn [14] derives 4.4 J/cm2 as 2Ep/πw2 ablation threshold of the Borofloat glass claiming agreement with the value reported in [29]. The 5.6 J/cm2 threshold given by Campbell using 150 fs, 800 nm pulses to follow the changes in crater diameter and depth as a function of focal position for BK7 perfectly agrees with ours. On the other hand, Lee [34] reports significant differences in the ablation thresholds: 2.53, 5.34, and 7.23 J/cm2 for aluminosilicate, soda-lime, and borosilicate glasses, respectively. Due to the differences in process parameters, the absolute values reported [14, 17, 19, 27, 30, 31, 34] are hardly comparable, nevertheless, the 5.34 J/cm2 threshold given for the soda-lime glass [34] fairly well matches our 5.65–6.65 J/cm2 domain. While scattering within a broad fluence domain, the thresholds reported do not show any tendency to differentiate between the glass types, further strengthening our conclusion.

When discussing the interaction of ultrashort pulses with glasses [25, 35,36,37,38,39,40] there are approaches considering both two-, three- and four-photon absorption depending on the actual bandgap. Since the bandgaps of the glasses investigated are around 4 eV, when fitting Eq. (3) to the measured depth values (Fig. 3d–f) three-photon absorption was considered [14].

Besides the ablation thresholds which are in good agreement with those derived from the DR analysis the fit resulted in three-photon absorption coefficients, α3: 6.45, 6.35, and 8.28 × 10–25 cm3/W2 for Borofloat, BK7, and B270, respectively. Data available in the relevant literature are compiled in Table 2. Our figures match fairly well with those reported for commercial glasses [35, 36, 38, 39]. The α3 value of the ULE glass [37] is four orders of magnitude smaller as compared to the more commercial glasses as measured by the same authors [35, 36, 38, 39] therefore it is not considered in the forthcoming analysis. At the other extreme Grehn [14] derived α3 values of two orders of magnitude higher than ours for multiple component silicate glasses both from transmission [25] and ablation [14] measurements by working in the intensity ranges of 2 × 1011–4 × 1011 W/cm2 and 1.7 × 1013–1.8 × 1014 W/cm2, respectively.

Table 2 Three-photon absorption coefficient data in the ultrashort regime found in the literature for glasses
Full size table

Since the algorithm applied by us for evaluating the dependence of depth on fluence was the same as that used by Grehn (Eq. 3) a comparison is feasible. Their depth data were recorded in intensity domains where plasma formation just starts [14, 25], while our results cover a domain with increasing transient reflectivity induced by plasma formation. The absorption-shielding effect of the plasma might be reflected in the lower α3 values obtained.

Moreover, we ablated with much shorter pulses as compared to those used by Jamshidi and Grehn (35 vs. 200 and 120 fs, respectively). The fact that pulse shortening results in less effective ablation [22, 50] further supports the smaller α3 values obtained. The less effective ablation is clearly demonstrated by the smaller depth values measured on Borofloat in this study (250 nm at 26 J/cm2) as compared to the ~ 300 nm at 22 J/cm2 reported by Grehn [14].

In the applied intensity domain the three-photon picture is a simplified approach. According to the Keldysh picture [51] ionization takes place via multiphoton absorption for lower and via tunneling for higher intensities. The parameter characterizing the contribution of the two mechanisms is the so-called Keldysh-parameter [51] which is > 1 for the multiphoton regime and < 1 for the tunneling regime. As shown in Fig. 4 our results refer to an intensity domain with increasing contribution from tunneling while in the case described by Grehn the three-photon absorption is more dominant, which further supports our smaller α3 values as compared to those reported in [14, 25].

Fig. 4
figure 4

The fluence dependence of the Keldysh-parameter for the three glasses investigated and for the Borofloat glass ablated by Grehn [14]

Full size image

The consistent explanation of the lower absorption coefficient validates the three photon absorption fit which thereby validates the reality the thresholds derived by this approach. All three approaches emphasize the decisive role of pulse duration in the analysis of the results. Nevertheless, further studies, dedicated to the clarification of the apparent inconsistency in applying multiphoton absorption-based approach in a fluence domain where, according to the Keldysh picture, tunneling seems to be dominant, are certainly necessary.

5 Conclusions

The evolution of the contour of the craters with fluence is very much the same for all three glass types up to approximately 20 J/cm2. Above 20 J/cm2 the Borofloat and BK7 continue behaving similarly, while a bump emerges in the middle of the bottom of the crater of the B270 glass. The surface of the craters ablated into Borofloat and B270 is smooth melt-like, contrary to the rough fragmented appearance of the BK7 craters. The appearance of the craters is explained in terms of both the thermal characteristics of the glasses and overcritical plasma formation.

Being within the 6.1 ± 0.55 J/cm2 domain with overlapping confidence intervals the ablation threshold values derived from both the diameter- and multiphoton absorption-based fits proved to be equal within experimental error, leading to the conclusion that the single-shot ablation thresholds of all three glasses are similar. The literature data, scattering within a broad fluence domain, do not show any tendency to differentiate between the glass types, further strengthening the similarity.

The logarithmic dependence of the diameter values and the saturation in depths obtained for 34 fs pulse duration favorable compare with the behavior reported for both glasses and fused silica in the fs temporal domain.

Following the changes in the energy reflected from the processed surface optical fluence thresholds marking the onset of plasma formation are defined. The actual values: 9.5, 10, and 8.0 J/cm2 for Borofloat, BK7, and B270, respectively, are well correlated with the ablation thresholds. Lying in the same magnitude the three-photon absorption coefficients derived from the multiphoton absorption-based fit are also similar for the glasses investigated. The corollary: the fluence dependence of the ablation characteristics is the same with minor differences in the optical response of the glasses.