1 Introduction

Since high-energy pulses are available in the fs temporal domain [1] there is a continuous race to increase the peak intensity of the pulses. Keeping the pulse duration fixed, out of the two possibilities i.e. increasing the pulse energy at a fixed irradiated area, or reducing the size of the irradiated area at constant pulse energy, the latter approach is not only more effective but also a lot easier to perform. Nevertheless, as evident from the relevant studies in materials processing applications, the outcome of the two approaches is different: the response of the material to be processed is not the same when tuning the intensity/fluence by changing the pulse energy while keeping the dimensions of the processing beam on the target surface fixed, or performing the experiment with altering the spot size at constant pulse energy. This effect materializes e.g. in the apparent discrepancy between the ablation threshold fluences reported for fused silica, one of the best characterized standard dielectric [2,3,4,5,6,7].

Energy control is far better preferred within the materials processing community, with much less attention paid to the elucidation of the effects of changing spot size on the ablation characteristics of dielectrics in general and glasses in particular [7,8,9,10,11]. While the rise of the threshold fluence with decreasing radius of the processing laser beam on the target surface was documented for both metals and semiconductors [12], dielectrics [7, 9,10,11], polymers [13, 14] and even for hard tissue [15], satisfactory interpretation of the effect in different spot size domains remained a challenge. For relatively large radii, between tens and hundreds of µm, the point defect model [16] worked well [9, 10, 12], while explaining the significant increase in the single shot damage threshold of sapphire and fused silica when decreasing the spot size below ≈ 10 µm the researchers at the Aix-Marseille University considered possible effects of both surface defects and formation of a high electron density plasma reflecting a part of the pulse energy [7, 11].

In this paper, the spot size dependence of the ablation threshold of BK7 optical glass is reported as a result of a comparative study of the evolution of the diameter and depth of the ablated craters and changes in the reflected part of the processing laser pulse recorded in real time while varying systematically both pulse energy and spot size. The outcome of the analysis in our case is that the dominant process behind the spot size dependence of the ablation thresholds is the plasma mirror formation.

2 Experimental

The laser source was a multipass CPA amplification system with a Spectra-Physics Rainbow oscillator [17] providing near transformation-limited amplified pulses with M2 < 1.1 in both directions, 34 ± 0.16 fs duration, 200 Hz repetition rate, and 1 mJ energy at 800 nm, characterized with energy stability at the output of the amplifier better than 1% (RMS). The temporal contrast of 107 at the nanosecond temporal range measured by a third-order cross-correlator after the amplifier resulted in an ns component of less than 3 × 10–3 mJ energy at 0.1 mJ pulse energy, corresponding to a fluence of ≈ 0.67 J/cm2 even for the smallest spot radius of 10.1 µm. Since this value was more than two orders of magnitude below the ns ablation threshold of optical glasses [18], it was safe to say that the ns component did not produce preplasma. The effects described in the following were assigned to the fs component of the processing pulse.

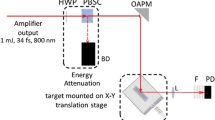
The optical setup used in the experiments is shown in Fig. 1. Single pulse processing was realized by selecting pulses from the amplified pulse train by a mechanical shutter, (1). Pulse energies on the target surface tuned with a polarization-rotation-based beam attenuator, (2) were calibrated by an energy meter (Gentec-EO). An off-axis parabolic mirror, (3) directed the converging beam onto the target surface, (4) at a 45° angle of incidence. The size of the irradiated area on the surface was changed by translating the parabolic mirror along the propagation direction of the beam, z while keeping the position of the target fixed. Pristine areas to be processed on the target surface were defined by moving the x–y translation stages along x and y axes at a 45° angle and perpendicularly to the z axis, respectively. The reflected part of the incoming nearly perfect beam was focused onto the sensor area of a photodiode (5), the signal of which scaled proportionally to the time-integrated energy of the reflected pulse. Longpass filters with a cut-on wavelength of 650 nm and reflective filters placed before the photodiode ensured the detection of the reflected beam exclusively.

Fig. 1
figure 1

Scheme of the experimental setup where WP is a half-wave plate, PC is polarizing beamsplitter cube, BD is beam dump, EM is energy meter, Z and X–Y are translation stages along z and x–y directions, L is focusing lens, and F are filters

Full size image

Moving the stage in the x direction with 10 µm precision, 11 craters 200 µm apart were ablated. Lifting the sample stepwise with 1 mm in the y direction while increasing the pulse energy from row to row up to 450 µJ crater matrices were produced. Optical microscopy revealed that these steps ensured debris-free areas for consecutive pulses. From line scans recorded with a Veeco DEKTAK8 surface profiler, depth and diameter values were derived for each crater along the minor axis with 0.1 nm vertical and 0.17 µm lateral resolution [19]. The depth and diameter data, defined as the maximal difference between the pristine surface level and the deepest point of the trace and the distance between the two points where the trace crosses the surface level within the rim of the crater, respectively, are averages of 11 values recorded within the same row.

The diameter of the ablated holes satisfies the following expression:

$${D}^{2}=2{w}^{2}\mathrm{ln}\left(\frac{F}{{F}_{\mathrm{th}}}\right),$$
(1)

where w is the 1/e2 beam radius, F = 2Ep/(πw2√2) and Fth are peak and threshold fluences, respectively [20]. The peak intensity is described as:

$$I={2E}_{\mathrm{p}}/(\pi {w}^{2}\tau \sqrt{2)},$$
(2)

where \(\tau\) is the full width of half maximum (FWHM) pulse duration and πw2√2 term gives the size of the elliptic irradiated area with the minor, w and major, w√2 axes.

The spot radii, w and the ablation thresholds, Fth were derived from Eq. (1) [20], referred to the following as the diameter-regression (DR) method. Threshold fluences were derived also from the fluence dependence of the crater depths by a multiphoton-absorption (MA) based fit [21].

3 Results

In Fig. 2 the squared diameters of the ablated craters are displayed as a function of the natural logarithm of fluence for five sample positions along the beam path with the respective spot radii added.

Fig. 2
figure 2

Squared diameter vs. fluence plots for the five spot radii resulting in ablation threshold fluences, \(F_{{{\text{th}}}}^{{{\text{diam}}}}\) of 10.8, 7.1, 5.2, 5.0 and 6.4 J/cm2 at spot radii, w of 10.1, 11.7, 13.5, 20.0 and 26.1 µm, respectively

Full size image

The most salient feature of Fig. 2 is that for all but the largest beam radius, 26.1 µm the plots are composed of two sections: exceeding a fluence threshold the squared diameters grow faster resulting in a steeper slope. The breakpoints suggest different mechanisms at low vs. high fluences. The ablation thresholds determined by applying the DR method for the low fluence sections of the plots, \(F_{{{\text{th}}}}^{{{\text{diam}}}}\) fall from 10.8 ± 0.5 J/cm2 down to 5.2 ± 0.4 J/cm2 with spot radii increasing from 10.1 to 13.5 µm, followed by an increase up to the highest radius of 26.1 µm.

Figure 3 shows the evolution of the ablated depth with increasing fluence for the same five target positions. The gathering of the data points within shrinking fluence domains with rising spot size is even more apparent here as compared to Fig. 2. For the sake of better visibility, different fluence scales have been introduced ranging from zero to 100 and 50 J/cm2 in Fig. 3a–e, respectively. Accordingly, Fig. 3a, b do not contain all data points measured, nevertheless all depth values have been used in each case when fitting.

Fig. 3
figure 3

Fluence dependence of the depths of the ablated craters

Full size image

The crater depths evolve similarly, except for the largest spot radius of 26.1 µm again, with rates increasing with expanding spot area. All depth vs. fluence functions level at around 200 nm with minor differences in the shape of the curves, while the depth approaches ≈ 240 nm at the largest spot size, 26.1 µm.

The MA fits calculated to appear as solid curves of different colors in Fig. 3. The good matching indicates that the MA model is appropriate for describing the process. The ablation threshold \(F_{{{\text{th}}}}^{{{\text{depth}}}}\) is defined as the intercept of the fit function with the fluence axis. In the low fluence range, which is critical in determining \(F_{{{\text{th}}}}^{{{\text{depth}}}}\), all fits were reliable. Nevertheless, since in the steeply increasing part of the fit function the number of data points was necessarily low due to the ≈ 10 µJ limit in energy sampling, to determine the threshold with high confidence, an error analysis had been performed. Following the calculation of the fit function a virtual data point was defined to the data set on the low fluence part of the fit curve just below the first measured data point. The fits were repeated while varying systematically the position of this point along the fluence axis. From each fit reduced chi-square value (the ratio of the residual sum of squares and the degrees of freedom) and threshold fluence pairs were derived. Plotting the reduced chi-square figures as a function of the threshold fluence a parabolic curve was obtained for all spot sizes. The uncertainty of the threshold, defined as the minimal deviation influence that increased the reduced chi-square values by 20%, resulted in an uncertainty in the ablation threshold fluences lower than ± 0.75 J/cm2 in worst case, demonstrating that the first few measured points were enough to determine reliably the thresholds.

The threshold values derived by applying both the DR and MA techniques are compared in Table 1. It is reassuring to see that with overlapping confidence intervals the threshold values derived from both approaches are equal for all spot radii, and—more importantly—show the same dependence with increasing spot radii: a fall from almost 11 J/cm2 down to ≈ 5 J/cm2 at 13.5 µm followed by a slight increase up to ≈ 6.5 J/cm2.

Table 1 Compilation of the ablation threshold fluences
Full size table

The time integrated energy of the part of the incoming pulse reflected from the processed area was monitored in real time during each single pulse, functioning as an independent diagnostic tool for following the irradiation-induced changes in the optical characteristics of the surface within the duration of the processing pulse. When discussing the results it is supposed that the changes in the energy of the reflected beam monitored the temporal behaviour of the surface. In this frame volume effects are excluded.

The photodiode signals recorded for pulse energies increasing up to ≈ 400 µJ are plotted in Fig. 4. At first glance the picture seems to be rather hard to interpret. Recalling that in this representation the changes in the slopes of the straight lines fitted to the sections of the photodiode signal vs. energy plots represent actually changes in reflectivities, it becomes clear that the three reflectivity values indicate three types of the optical response of the material to the processing beam, depending on the actual energy of the pulse hitting the surface.

Fig. 4
figure 4

Evolution of that part of the pulse energy which is reflected from the irradiated area as a function of the incident energy and fluence

Full size image

There appear clear trends with changing spot size. At the largest spot size, the curve can be fitted with two straight lines joining at around 150 µJ. The slope of the first, low energy section, s1 which is the same for spot sizes of both 26.1 and 20.0 µm is assigned to the permanent reflectivity of the BK7 glass [22]. The higher slope, s2, appearing at ≈ 150 µJ (> 2 × 1014 W/cm2) for w = 26.1 µm, indicates an increase in reflectivity. The energy domain where permanent reflectivity shows up shrinks with decreasing spot size and cannot be seen anymore on the plots with radii at and below 13.5 µm. The s1 → s2 threshold shifts to lower energies accordingly. The slopes characterizing the second section are 0.90 and 0.95 mV/µJ for spot sizes of 13.5, 20.0 and 26.1 µm radii with a rise accelerating up to 1.28 ± 0.10 mV/µJ at 10.1 µm radius, revealing a significant increase in reflectivity with decreasing spot size. In this scenario, the only reasonable explanation for the increase in reflectivity is plasma mirror formation on the target surface above 2 × 1014 W/cm2 as a result of the ionization of the target by the leading edge of the fs pulse [23].

At spot sizes but 26.1 µm, from a second breakpoint on, a third section with lower slope, s3 < s2 appears indicating the onset of a new optical effect becoming active at the highest pulse energies. This second threshold also shifts to lower pulse energies: from ≈ 220 µJ at 20.0 µm radii down to ≈ 62 µJ at 10.1 µm radius. The scales of the drop in reflectivity as compared to the respective plasma mirror values are not the same either: s3/s2 ratios of 0.28, 0.42, 0.38 and 0.39 were derived for 20.0, 13.5, 11.7 and 10.1 µm radii, respectively, suggesting a diminishing effect when reducing the spot size.

4 Discussion

In the quest for the evaluation of the results obtained, the role of the surface defects [9, 10, 12, 16] and plasma mirror formation [7, 11] were considered.

In the case of semiconductor-grade silicon and SAE 304 stainless steel with intentionally increased density of low-density (near-)surface defects the point defect model worked well in a broad domain of spot sizes [12]. The decrease of the ablation threshold of Corning 7059 glass between 20 and 400 µm spot radii [10] and that of Schott BG18 filter glass between 50 and 400 µm spot radii [9] could also be well described by supposing a surface defect-dominated mechanism. The significant increase in the single shot damage threshold of sapphire and fused silica when decreasing the spot size below ≈ 10 µm reported by the Marseille group is directly comparable to our findings [7, 11]. When interpreting this behaviour the authors of the SPIE paper considered possible effects of both surface defects and the plasma mirror [7], while Uteza and coworkers speculated on the possible effect of the latter only [11].

By accounting for the accumulation and incubation effects, the generic model introduced by the Kautek group [13] explains successfully the spot size and pulse number dependence of the fs laser-induced ablation thresholds in the case of high-impact polystyrene. Apparently, this approach does not work in the single pulse case. As discussed in [10], while offering a feasible approach to the interpretation of the beam size and repetition rate dependencies of the effective ablation threshold in high repetition rate ablation of dental tissue with 130 fs@800 nm pulses [15], the heat accumulation model is not appropriate in the case of single pulse ablation of dielectrics of much smaller absorption either.

Though in our case the changes in the optical response of the surface to the incident pulse suggested an optical origin behind the tendency in threshold fluence, possible effects of the surface defects were also evaluated. For a Gaussian beam of spot radius w0 the point-defect model describes the probability of hitting at least one defect with the P(w0) distribution function [16] in which the mean distance between two defects, d0 determines the actual value of P(w0). The ablation threshold scales with 1 − P(w0), the probability of hitting a defect-free surface area. To determine the surface defect density of the samples processed, different areas of the pristine surface of three BK7 substrates were mapped by differential interference contrast, DIC microscopy. Image processing of the records revealed an average mean distance of 18.6 µm with a standard deviation of 3.8 µm between point defects. Additional characterization of the defects by atomic force microscopy with a model PSIA XE-100 AFM in tapping mode using tips with ≈ 10 nm radius of curvature and a Veeco Dektak 8 surface profiler showed that they were nodules with 1 µm maximum diameter and several tens of nm average height coming out of a background of RMS roughness, Rq ≈ 1.2 nm, validating the reliability of the DIC results. The 1 − P(w0) function calculated with d0 = 18.6 µm mean distance for the 0–100 µm spot size domain is shown in Fig. 5. The dependence obtained predicts a spot radius around 60 µm as the onset of the rise in fluence threshold with decreasing spot size. This figure is several times larger than 13.5 µm obtained experimentally, convincingly suggesting that our results can hardly be accounted for by the point defect model.

Fig. 5
figure 5

The probability of hitting a defect-free surface area with d0 = 18.6 µm mean defect distance as a function of spot radius

Full size image

The performance of the reflectivity, on the other hand, strongly suggests that the apparent increase in the ablation threshold is connected to the formation of a plasma mirror. The identical permanent reflectivities derived for the spot sizes, where it was appropriate, guarantee the rationality of the reflectivity assignments.

The evolution of the s2/s1 ratios with decreasing spot radius is shown in Fig. 6. The transient reflectivity as compared to the permanent one rises within the whole spot size domain covered. The matching of the onsets of the first reflectivity change (cf. Fig. 4) at around 2.7 × 1014 W/cm2 [23] supports that the increase in reflectivity is due to plasma formation. From a comparison of the reflectivity enhancement, s2/s1 and the ablation threshold values derived it becomes apparent that the dependences are very similar: the figures remain equal for spot radii at and above 13.5 µm, followed by a rise with decreasing spot size, revealing that the plasma mirror formation could be affirmed as the governing process behind the spot size dependence of the ablation thresholds in our case.

Fig. 6
figure 6

The spot size dependence of the ablation threshold fluences derived by diameter regression (filled blue triangle) and multiphoton-absorption-based fit (filled blue circle) together with the reflectivity enhancements, s2/s1 (filled red square)

Full size image

In a quest for the understanding of the physics behind the lowering in the reflectivity at pulse energies exceeding the second threshold (cf. Fig. 4.), possible effects of air ionization by the incoming laser pulse before the target were also considered. Air breakdown caused by impact ionization initiated by free electrons ejected from the target [24] could give an explanation for the lowering in the reflectivity at the highest energies when exceeding the second threshold. The onsets of air breakdown in fs processing scatter between 2.2 × 1014 and 9.2 × 1014 W/cm2, depending on the focusing conditions, actual pulse durations and repetition rates [25,26,27]. Acting as a screening cloud in our beam propagation geometry air ionization materializes in the loss in the reflected energy. Simulation results [25] show that the energy loss due to air breakdown is negligible if the laser peak power density is lower than 5 × 1014 W/cm2. This energy loss becomes discernible if the applied power density exceeds 5 × 1014 W/cm2, which explains the rationality of the 6.5–8.1 × 1014 W/cm2 values of the second thresholds derived from the reflectivity measurements (cf. Fig. 4.).

Mirza et al. [28] related the air ionization to a significant change in the shape of the ablated crater, to the development of crater-in-crater structures due to back etching. When ablating with pulses focused onto spots of 26.1 µm diameter the craters carved out of the BK7 glass surface possessed a single-rim structure throughout the fluence domain executed [22]. Tighter focusing resulted in the evolution of a double-crater structure, actually two craters of different diameters defined by the outer vs. inner rims, indeed, the effect becoming clearly visible at and below 13.5 µm in the high fluence domain.

As exemplified in the inset of Fig. 7 for 13.5 µm, at and above 29 J/cm2 a secondary, shallower crater of larger diameter appeared surrounding the main one defining the depth. The appearance of the second breakpoint in the respective reflectivity curve at 6.5 ± 0.3 × 1014 W/cm2, equivalent to 22.1 ± 1.0 J/cm2, well agrees with the threshold fluence of ≈ 20 J/cm2 derived from the regression of the diameters of the secondary craters as the x-intercept of the second section of the squared diameter vs. fluence plot in Fig. 7. The good agreement supports the assumption that though the processes determining the two quantities (reflectivity and ablated spot diameter) have rather different characteristic times, both are mainly influenced by the onset of air ionization. The saturation of the crater depth sets on also in this fluence domain, since both the development of the plasma mirror acting as an optical shutter [29], and the saturating absorption efficiency [30] due to air ionization reduce the energy reaching the surface.

Fig. 7
figure 7

The squared diameter vs. fluence plot for the 13.5 µm spot radius revisited including both the inner (filled red circle) and outer (filled blue circle) diameters visualizing that the inner diameters of the double-crater structures (cf. inset) belong to the low fluence section of the plots, while the outer diameters of the high fluence section are the result of another ablation mechanism

Full size image

The revision of the crater profiles recorded led to an approach to explain the origin of the two sections in the squared diameter vs. fluence plots shown in Fig. 2. The results obtained at 13.5 µm spot size as an example shown in Fig. 7 was taken again. Replotting both the squared outer and inner diameters defined as the distance between the two points where the recorded profile crosses the surface level on the side of the outer rim facing the crater center and where the extrapolated rising section of the inner crater crosses the surface level, marked by blue and red symbols in Fig. 7, respectively, the formers and latters lie on the straight lines of higher and lower slopes. This representation well illustrates the contribution of two different mechanisms active in the low vs. high fluence domains. Distortion(s) in the energy distribution within the beam due to air ionization and/or air ionization-assisted ablation might account for the appearance of craters with double-diameter structure marking the steeper slopes of the squared diameter vs. fluence plots.

Note that the crater-in-crater structures, exemplified on the inset of Fig. 7, resembled very much those described in [31] therefore we readily adopt the Matrjoska-term coined by Kudrjasov due to its illustrative description of the effect. While using the same terminology for the end product we do not adopt the description of the mechanism put forward by the authors since the mechanisms behind the two cases are thought to be different. Kudrjasov and coworkers differentiate three sections in the squared diameter vs. log(energy) function by their slopes decreasing with increasing energy and relate the multiple crater formation to changes in the order of non-linearity [31], while in our case the change in the slopes is just the reverse and the dominant mechanism is three-photon absorption.

5 Conclusions

Ablation thresholds were determined by analyzing the fluence dependence of both crater diameter and depth. With overlapping confidence intervals the thresholds derived applying both approaches proved to be equal, showing a clear dependence on the spot size: a slight decrease from ≈ 6.5 J/cm2 down to ≈ 5.1 J/cm2 at 13.5 µm followed by a steep rise exceeding 10 J/cm2 at 10.1 µm spot radius.

The photodiode signal vs. pulse energy curves could be fitted by three straight lines representing three reflectivity values. The slope of the low energy section, being independent of spot size, was identified as the permanent reflectivity of the BK7 glass, while that of the middle section, increasing with decreasing spot size, was assigned to the transient reflectivity of the plasma mirror formed. The similarity of the spot size dependence of the reflectivity enhancement, s2/s1 and the ablation threshold highlighted that the rise in the threshold was connected with the increase in the transient reflectivity via the decrease in the energy of the pulse reaching the surface to be ablated. This result suggests that the dominant process behind the spot size dependence of the ablation thresholds in our case is the plasma mirror formation. The smaller slope of the third, high-energy linear section indicates a lowering in the reflectivity is assigned to air ionization. The concomitant decrease in the pulse energy reaching the surface is manifested in the saturation of the ablated depth values. The occurrence of the Matrjoska structures is another consequence of this effect. The formation of the double-crater structure also explains the appearance of the two linear segments in the squared diameter vs. fluence plots.

The principal parameter of the studies of this type is the fluence. Threshold fluences are regularly related to pulse duration and wavelength. An outcome of the study reported is that to ensure reproducibility and chance of comparison in describing the ablation effects, the spot size should also be considered as a significant control parameter.