1 Introduction

Ultra-precise surface machining (UPM) attracts increasing attention as enabling technologies for future developments in optics, microelectronics, and precision mechanics. The ideal properties of such surfaces are low roughness, high lateral and vertical dimensional precision, and low damage of the material near the surface. Traditionally, UPM is related to optical production where both etching processes and sophisticated polishing technologies are utilized for fabrication [1]. However, modern system design calls for new approaches and technologies which enable local material processing that can be used for etching, deposition or modification of materials. In consequence, new beam-based tools are required that enable innovative fabrication processes. Current examples are ion beam figuring and electron beam writing. These processes are limited in their flexibility as they require complex vacuum systems.

A prominent beam-based technology is laser processing. With laser processing, a laser beam is focused onto a surface. The absorbed laser photons induce numerous processes near the surface which causes material removal that is accomplished by melting, evaporation, and plasma plume formation. For laser microprocessing, the size of the laser spot is commonly in the range of ~ 10 µm. The size and shape of the laser spot, as well as the energy of the laser beam, can be easily adjusted during processing with standard optical-mechanical components. In special applications, it is possible to achieve with laser processing a high surface quality in terms of surface roughness and surface/subsurface damage. Examples include laser processing of polymers with UV lasers. However, laser processing of standard materials which are widely used for application in microelectronics and optics like Si, SiO2, SiC, Ge, SiC result in height surface roughness and subsurface damage. Additionally, the ablation rate (material removal/pulse) is commonly found in the range of 10–100 nm per pulse [2]. The high ablation rate makes usage of laser processing technology difficult for applications which require ultra-high precision processing, such as the correction of optical elements.

To increase the surface quality of the laser-machined surface, different laser-hybrid methods have been developed. Laser-induced chemical etching (LICE) is one of these laser-hybrid methods [2, 3]. LICE removes material due to the laser activation of the gaseous or liquid etchant. The etching process is enhanced or induced by the interaction of the laser photons with the etchant and/or the sample surface. LICE can be divided into wet and dry. In wet–LICE, the etching process is performed in an aqueous medium such as KOH, HCl, or NaOH. In dry-LICE, the etching process is performed in a gaseous atmosphere. Common etchants include halides and halogenated compounds. The etching in dry-LICE is mainly photochemical or thermal driven. In photochemical driven processes, the radical generation is induced by photodissociation e.g. Cl2 which is used for dry etching of Si [2, 4, 5]. However, for activation of photochemical processes, the gases must have sufficient absorption of the laser photon Therefore, the laser sources for dry—LICE are mainly limited to UV laser wavelengths.

Plasma-based etching techniques are another example of beam-based material processing methods. Plasmas at low pressure are widely used for various applications, particularly in the semiconductor industry [6]. Low-pressure plasma can produce a large concentration of reactive species without extensive heating of the sample. Furthermore, the ion produced in the plasma can accelerate towards the sample which enables directional, anisotropic etching. However, low-pressure plasma requires a vacuum system which increases the complexity of the equipment and the operation cost of the material processing.

Atmospheric-pressure plasma jets (APPJ) enable plasma etching of surfaces at atmospheric pressure. During the last decade, APPJ was investigated extensively. It was shown that the excitation caused by APPJ can be induced by RF or microwave power. The interaction of APPJ with substrates have been experimentally [7,8,9] and theoretically [10] investigated. It has been demonstrated that APPJ processing can be used to etch a variety of different materials such as Si [11], technical glass [12], and SiC [13]. As with other plasma etching methods, the material removal process results from APPJ causing chemical etching of the substrate. A typical etch rate in the range of ~ 10 µm/min (e.g. Si [11]) can be achieved. The footprint of APPJ is typically in the mm or sub-mm range [11]. Plasma etching methods have in common that the plasma is not only in contact with the substrate but also with the electrode which is required for the plasma generation by RF powering and/or with the chamber if the plasma is generated by microwave power. Additionally, in the case of APPJ processing, the nozzle can be corroded by the plasma, requiring regular maintenance. Besides plasma ignition by electrical energy like RF or microwave power, plasma can also be generated in gas by laser radiation due to optical break down [14,15,16]. An optical breakdown can be achieved by focusing a laser beam in a gas when a critical power density is exceeded. The threshold for this critical power density depends on several factors such as wavelength and pulse duration [17,18,19]. For example for plasma generation in air using nanosecond laser pulses (tp = 10 ns, λ = 1064 nm), pulse energies of ~ E = 75 mJ are used [20]. The generated plasma has a temperature of ~ 12,000 K and a strong shock wave is induced [20]. With ultrashort laser pulses, however, the high electrical field strengths cause non-linear interaction of the laser pulse with the gas and, in consequence, the plasma at lower pulse energies. Currently, laser-plasma in gases is mainly used for analytic applications such as laser-induced breakdown spectroscopy (LIBS) [21]. Elhadj et al. [22] used a nanosecond laser (ND:YAG, λ = 355 nm, t = 7.5 ns, f = 10 Hz) to generate plasma in ambient air or an N2 stream. The laser-plasma was brought into close proximity of a SiO2 surface to etch the SiO2 with the laser-induced plasma. However, the authors found that the surface was damaged due to interactions with the laser beam. Applying the laser beam at a glancing angle in relation to the sample surface achieved material removal by melting and evaporation of the material only.

In this study, dry etching of SiO2 with laser-induced CF4 plasma was investigated. The free-standing reactive microplasma was generated by focusing femtosecond laser pulses in a CF4 atmosphere. Due to this generation process, the plasma is free from contamination generated by electrodes or chamber material. By positioning the plasma in a suitable distance to the substrate surface, the activated plasma species caused material removal of the substrate surface. The dependency of the etching depths and etching rate were investigated against several parameters including plasma-surface distance, laser pulse energy, and etching time. The experimental results were analysed in detail to reveal the mechanisms involved in this process. Due to the special characteristics of this hybrid laser-plasma process, a wide range of applications are possible. This includes optical applications such as the generation of free form optics or correction of optical waviness, selective modification and trimming of microelectronic elements, and local surface modification for biomedical applications.

2 Experimental details

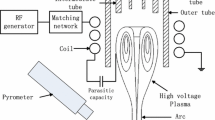
A schematic sketch of the laser-plasma etching setup is shown in Fig. 1. The main components of the system comprise of: an ultrashort pulse laser system (wavelength λ = 775 nm, pulse duration tp = 150 fs, pulse repetition rate f = 1 kHz) and a chamber for performing the etching. The laser is focused by a lens with a focal length of 60 mm into the chamber where the plasma is ignited. The spot size is calculated to be rg = 6.5 µm and the focal length lRy = 685 µm. The plasma is generated in the focal point range due to optical break down with laser pulse energies (Ep) exceeding 200 µJ. The laser-plasma is generated at a fixed location given by the focal point in relation to the base system.

Fig. 1
figure 1

Sketch of the experimental setup

Full size image

The chamber is mounted on a computer-controlled x–y–z stage system which enables the movement of the whole chamber with the sample inside relative to the plasma generated in the laser focus. The chamber consists of an entrance window for the laser beam, two inspection windows, and a sample holder. The sample holder can be heated by a silicon nitride ceramic heater up to a temperature of 500 °C. For the experiments, the heater temperature was set at 210 °C, based on pre-experiments which show that no etching at room temperature was possible. The samples were fixed in the holder with clamps and were moved into the proximity of the plasma by moving the chamber. The direction of the laser beam was parallel to the sample in order to avoid direct irradiation of the sample. The distance and position of the sample relative to the plasma were monitored and adjusted under observation by a camera.

For etching the sample, the chamber was first evacuated and subsequently filed with the etching gas. The gas flow and the gas pressure in the chamber were controlled and adjusted by a gas feeding system which was attached to the chamber. Tetrafluoromethane (CF4) with a flow rate of 500 sccm was continuously fed into the chamber during the experiments. A vacuum pump was attached in order to allow the evacuation of the chamber before the experiments and the adjustment of the gas pressure in the chamber. During the experiments, the pressure in the chamber was set to an absolute pressure ranging from 800 to 900 mbar.

In Fig. 2, the plasma above the sample surface is shown exemplarily. The distance between the plasma and surface is measured from the sample surface to the centre of the plasma.

Fig. 2
figure 2

Optical photograph of a laser-induced plasma close to the samples surface in a distance of 200 µm. The arrow indicates the propagation direction of the laser beam

Full size image

The samples were inspected after processing by optical microscopy, scanning electron microscopy SEM (Gemini Ultra 55; Carl Zeiss), atomic force microscopy AFM (Dimension ICON; Bruker) and white light interference microscopy (WLIM, Bruker NPFLEX). A polished SiO2 wafer (fused silica, surface roughness Rq ~ 1 nm rms) with a thickness of 450 µm was used as sample material. The wafer was divided into pieces with a size of ~ 5 mm × 10 mm. The SiO2 samples were rinsed with distilled water and subsequently dried in a nitrogen stream to remove attached particles from the surface.

3 Results

Figure 3a shows a contour plot of the surface topography of a sample etched for 3 min at a distance between plasma and surface of 120 µm. The SiO2 surface was etched by the laser-plasma and an etching pit was generated. The etching pit was symmetric to the beam propagation direction but does not match the dimension of the laser focal spot. In particular, the width of the etching pit (~ 275 µm) is much larger than the Gaussian spot radius. The length is ~ 750 µm, which is in a similar range to the focal length. The maximum etching depth achieved is 1.74 µm. In Fig. 3b and c, the depth profiles along the main and minor axes are shown. In Fig. 4c an optical microscope image of an etching pit is shown. The image of the etching pit was taken directly after the etching process without additional cleaning. An SEM image of the etching pit (see Fig. 4a) and a magnified section is shown in Fig. 4b), respectively. The inspection of the etching pit shows that the surface is smooth without cracks or LIPSS (laser-induced periodic surface structures). The AFM analysis of the etching pit section marked in Fig. 4a) is shown in Fig. 4d). Also, this surface analyse shows a smooth surface. Within the analysed area of 10 × 10 µm a roughness value of 1.4 nm rms (root-mean-squared) was found.

Fig. 3
figure 3

a Contour plot of an etching pit measured by WLI. b Shows a cross-section of the etching pit along the Y-axes, marked in (a) with the dotted line. c Shows a cross-section of the etching pit along the X-axes, marked in (a) with the dotted line. The etch parameter values for etch time, laser pulse energy, the plasma-surface distance was 3 min, ~ 700 µJ and 120 µm, respectively

Full size image
Fig. 4
figure 4

a SEM and c optical microscope image of an exemplary etching pit in the SiO2 surface. b A magnified section of the marked area in image a. d AFM measurement of the area which is marked in image (a)

Full size image

In Fig. 5 a), the dependence of the maximum etching depth of the etching pits on the etching time is shown. The depth increases with etching time up to a depth of ~ 12 µm after 10 min etching. The slope of the depth can be divided into two time ranges with linear slopes, respectively. For a short etching time up to ~ 3 min the depth increases with a slope of ~ 1.7 µm/min for longer etching times the slope decreases to a value of ~ 1 µm/min. An average etching rate can be calculated by dividing the maximum measured depth by the etching time. Using the laser pulse repetition rate, the average etching rate per laser pulse was also calculated. Both the etching rate over time and per laser pulse is depicted in Fig. 5 b). These values were calculated from the data shown in Fig. 5a). It has to be noted that the average etching rate per laser pulse is approximately 0.1 Å and therefore approximately 2% of the lattice constant of silicon with 5.4 Å. For a short etching time, the average etching rate rises sharply with increasing etching time. In a time ranging between 1 and 3 min the etching rate reaches a maximum value of ~ 0.26 nm/pulse which then decreases slightly for higher etching times.

Fig. 5
figure 5

a Etch depth in dependency on the etch time. The lines indicate the linear fit of the measured data in the two time ranges. b The calculated etch rate from data shown in a. The etch rate given in [nm/pulse] was calculated by taking in account the laser pulse repetition rate of f = 1 kHz. The shown lines are for guiding the eyes. The laser pulse energy for the experiment was fixed at a value of ~ 700 µJ

Full size image

In Fig. 6, the etching depth in relation to the plasma-sample surface distance is shown. The investigated distance ranged from 60 to 180 µm. By moving the laser beam and the plasma closer than ~ 50 µm to the sample surface the laser beam is partially blocked by the face of the sample. Therefore, the total laser pulse energy that contributes to the optical break down is reduced. The etching rate decreases almost linearly with increasing the distance. The linear fit of the data is shown in Fig. 6 by a red line. Using linear extrapolation, a threshold distance for etching of ~ 190 µm can be calculated for a pulse energy of 700 µJ.

Fig. 6
figure 6

Etch depth in relation to the plasma surface distance. The red line is a linear fit of the experimental data (Depth [µm] = 7.4 [µm]—0.041*x [µm]; with x [µm] plasma surface distance). The laser pulse energy was fixed at a value of ~ 700 µJ and the etch time 3 min

Full size image

The etching depth—pulse energy relationship is shown in Fig. 7. The etching depth has a linear relationship between the etching depth and the pulse energy, whereas the depth increases with increasing of the pulse energy. By linear extrapolation of the data shown in Fig. 7, a pulse energy threshold for etching of ~ 280 µJ can be found for the plasma–surface of 100 µm. By changing the pulse energy, the luminous spot produced by the plasma which can be observed with the camera also changes. In Fig. 8, images of the plasma are shown which are taken by three different pulse energy values. It can be seen in Fig. 8 that by decreasing the pulse energy, the brightness and size of the luminous spot decrease. Furthermore, the position of the plasma changes. By decreasing the laser pulse energy, the position of the plasma translates away from the position of the focal lens. In Fig. 9, the relative position of the plasma in relation to the laser pulse energy is plotted. For laser pulse energy smaller than ~ 200 µJ no visible plasma could be detected with the camera.

Fig. 7
figure 7

Etch depth in dependency of the laser pulse energy. The shown red line is a linear fit of the experimental data (Depth [µm] = 0.071*x [µm] – 2 [µm]; with x laser pulse energy). The plasma – surface distance and etch time were fixed at values of 100 µm and 3 min, respectively

Full size image
Fig. 8
figure 8

Images of the laser-induced plasma (called further plasma ellipsoid). The three example images were taken by a fixed camera parameter set. The red arrows indicate the direction of the laser beam. The long white line indicates the reference position and the short lines indicated the relative to the reference position. The pulse energy for used for generation was (left to right) 700 µJ, 630 µJ, 500 µJ, respectively

Full size image
Fig. 9
figure 9

Relative position centre point of the plasma in dependence on the laser pulse energy used. As reference position, the plasma generated with 700 µJ was used. With decreasing the pulse energy values the plasma position translates away from the focal lens position

Full size image

4 Discussion

The etching of SiO2 with a reactive laser-induced CF4 plasma has been demonstrated. Etching of surfaces with reactive CF4 plasma comprises numerous different physical and chemical processes. Additionally, feedback and crossover reactions need to be considered, as well as the typically highly dynamic nature of laser processes. The main processes are excitation and decay of species, transport of different components in the gas phase, and chemical reactions at the surface as well as in the gas phase. The proposed mechanism of laser-plasma etching comprises of the following steps: (I) Laser excitation of plasma in the gas mixture, (II) Decomposition of the gas components forming reactive species, (III) Diffusion of the reactive species to the surface, (VI) Reaction of the different laser plasma-activated species and neutral species at the surface, (V) Detachment of volatile reaction products and diffusion away from the surface. This reaction mechanism results in the removal of the surface material measured as etching pits. Ballistic transport from the plasma to the surface can be neglected. This is because the mean free path length is approximately 100 nm. Collision related random transport needs approximately 106 collisions to occur. Additionally, the concentration gradient needs to be considered in transport, too. The experiments show that the laser pulse energy and plasma-surface distance range analysed result in etching of the SiO2 surface. With increasing etching time, the etching depth increases. The peak etching rate occurs at an etching time range between 1 to 3 min and for longer etching times the etching decreases slightly. The surface of the etching pit appears smooth in the optical microscope, SEM, AFM, and WLI analyses. The plasma for the etching process was generated by an optical breakdown. An accepted definition for optical breakdown is when electron density reaches a value of ~ 1014 cm−3 [15]. This typically corresponds to a laser power density of ~ 2.4*1014 W/cm2 [15] with λ = 807 nm, tp = 45 fs). After exceeding this laser power density, the electron density increases sharply. Electron density increases with a slow rate for laser power densities larger than ~ 1*1015 W/cm3, with values of electron density in a range of 1017 to 1019 cm−3 [15]. The electron generation can be divided into different processes: multiphoton ionization (MPI) and avalanche ionization (AI). MPI electrons were generated by the simultaneous absorption of a sufficient number of photons to ionize an atom or molecule. The MPI process can be described as:

$$M+m*\hbar \omega \to {e}^{-}+{M}^{+}$$
(1)

With \(E=\hbar \omega\) the photon energy and m the number of photons required to strip an electron e− from an atom or molecule M. During AI, free electrons in the focal plane were accelerated due to the electrical field of the laser pulse. The accelerated electrons collide with the neutral atoms and molecules and ionize them.

$${e}^{-}+M\to 2{e}^{-}+{M}^{+}$$
(2)

The MPI process is dominant for high laser intensity and very low gas pressures (< 10 mBar [16]. Whereas for higher pressure, AI is more dominant. Comparison of the electron density values measured in air at atmospheric pressure with the values measured in this study using CF4 as the gas at slightly reduced pressure gives a rough estimation of the processes involved in the plasma etching process. Fluorescence studies of fs-laser excitation of fluorine-containing halocarbons, e.g. CF4, C2F6, show a linear increase of the fluorescence intensity with the concentration of fluorocarbon. This suggests an increase in generated radical density, e.g. reactive species [23]. The pulse energy threshold for etching, obtained from the data shown in Fig. 7, is 280 µJ and the threshold for generation of a visible plasma (see Figs. 8 and 9) is 200 µJ. These values correspond to laser power densities of 1.4*1015 W/cm2 and 1.1*1015 W/cm2, respectively. That value range is close to the value at which the electron density reaches the measured and calculated saturation point [15] were the electron density increases with a lower slew rate.

Interestingly, the etching depth increases almost linearly with the pulse energy as seen in Fig. 7. This is surprising, as the distance of the focal spot from the surface determines the density of the radicals as well as the energy transfer from the plasma to the surface. Therefore, a non-linear dependency can be expected. In relation to the experimental findings, the etching rate increases above the threshold of 280 µJ linearly but a fluorescing plasma can be observed already at 200 µJ. The increase of the etching rate with increasing pulse energy is probably caused by a combination of effects that are not clearly understood. Primarily, the pulse energy results in a denser plasma but due to the nonlinear processes at generation, the energy density in the laser-generated plasma should increase proportionally. With increasing pulse energy, the size of the visible plasma increases as it can be seen in Fig. 8. With a larger active plasma volume, more reactive species can be generated which are additionally closer to the sample surface. The electron density and electron temperature increase with increasing of the pulse energy. This causes an enhancement of the dissociation rate of CF4 resulting in more fluorine and fluoromethane radicals being generated. According to Jin et al. [24], fluorine atoms are mainly produced by electron-impact dissociation of CF4. Simultaneously, F atoms are generated and fluorocarbon radicals CFx (x = 1–3) are ionized. By recombination of the CFx (x = 1–3) with F atoms, CFx+1 can be formed. The dissociation of the CF4 can be written as [25].

$${CF}_{4}+{e}^{-}\to {CF}_{3}+{F}^{-}$$
(3)
$${CF}_{4}+{e}^{-}\to {CF}_{3}^{+}+F+2{e}^{-}$$
(4)
$${CF}_{x=1-3}^{+}+{e}^{-}\to {CF}_{x-1}+F$$
(5)

In addition to the distance, the lifetime of reactive species determines the diffusive flow of laser-plasma activated species to the surface and their concentration there. In comparison to other gases, the lifetime of CF2 is relatively long [23] and can, therefore, be moved for longer distances before decaying. Moreover, by increasing the pulse energy, the kinetic energy of the ions increases which supports the diffusion of these species to the sample surface. The material removal process is mainly driven by chemical processes and not by laser ablation. Indications for chemical etching rather ablation are:

  1. i.

    The high quality, low roughness (1.4 nm rms) of the etched surface exemplary shown in Fig. 4

  2. ii.

    The linear increase of the etching rate with the pulse energy, rather than a logarithmic rise of the rate.

  3. iii.

    The low etching rate of < 1 Å/pulse in contrast to ablation depth in the range of the optical penetration depth.

For laser ablation processes, the laser processed surface is characterized typically by deep ablation craters [2, 26], a rough surface covered [26] with LIPSS [27], and signs of melting and re-solidification. In contrast, common reactive plasma etching methods typically result in surface roughness values in the range from tens of nanometres down to the sub-nanometres range. [28]. The footprint of the etching has a similar shape to the laser-induced plasma, which can be seen by comparison of the footprint in Fig. 3 and the images of the plasma shown in Fig. 8. The exact dimension of the footprint changes with changes to the laser parameters. For example, the footprint decreases with decreasing the laser pulse energy. With the laser parameter used for etching the pit in Fig. 3, a footprint (length × width) of 275 ×  ~ 750 µm can be estimated.

This footprint for SiO2 surface etching is significantly larger in comparison to the laser spot radius and focal length of rg = 6.5 µm and lRy = 685 µm respectively. In particular, the increase of the etching width is a strong indication for the redistribution of the excited species from the core of the laser-induced plasma by diffusion or secondary excitation. Secondary excitation can be also related to the temperature of the plasma after thermalisation. The optical images of the plasma (see Figs. 2 and 8) confirm the larger plasma size compared to the focal region. Hence, etching is not directly related to the interaction of the laser photons with the sample material but to several mediation processes related to the combination of the laser-excitation and material removal.

The footprint for etching the SiO2 sample is large in comparison to laser processing where typical ablation spots have a size in the range of 10–100 µm. However, in comparison to plasma etching methods, the footprint is relatively small [29].

From the etching rate – etching time dependency in Fig. 5b, two distinctive features can be seen. The sharp increase in etching rate for low etching times and a slight decrease in the etching rate with longer etching times. The sharp increase can be caused by various effects. At the beginning of the etching process, a stable equilibrium has to be established between dissociation of the CF4, transport of the reactive species, and chemical reaction at the sample surface. Additionally, it is likely that on the SiO2 surface a modified layer is generated by the intensive UV and soft X-ray radiation generated by the laser plasma in close proximity. It is known that the excimer radiation of SiO2, that SiO2 is subject to structural modification which causes refractive index changes. Additionally, it is known that irradiation of SiO2 with different high energy radiation source like X-rays, protons, EUV, electrons, and photons (multi-photon processes) can all cause a wide range of different defect generation processes. The processes include E’ colour centre formation and non-bridging oxygen hole centre formation [30–32]. The accumulation of these defects during the beginning of the etching process results in higher chemical yields which support the etching process. Etching of the surface supported by plasma heating of the surface cannot be excluded. The etching rate decrease for longer etching times can be explained by geometric effects, accumulation processes, and changing of the near-surface chemical composition.

With longer etching time the etching pit depth increases and in consequence the geometric distance between the surface and the plasma. This increases the diffusion length and diffusion time which causes a reduction of the reactive species density at the surface. Additionally, the interaction of the reactive species with the surface changes the physical–chemical structure of the surface. In principle, the CxFy species are enabled to etch the surface by forming volatile products or molecules with longer chains resulting in fluorocarbon films. These films protect the surface, in part, from the etching attack of the reactive species. Therefore, with increasing etching time a very thin fluorocarbon layer can be formed until an equilibrium that reduces the etching rate by partially reducing the stream of reactive species to the surface. As is shown in Fig. 8, plasma generation translates in the direction of the focal lens. These effects have been found in experimental and theoretical studies investigating the breakdown of ultrashort laser pulses [15]. The effect was due to the critical electron density for an optical breakdown being reached in front of the geometrical focal point position. This effect increases with increasing the laser pulse energy or the focal length of the lens. The nearly linear dependency of the etching depth at the process parameter etching time, pulse energy, and the plasma surface distance make the presented laser-plasma process well controllable for industrial applications. The low etching per applied laser pulse gives precise control of the etching depth which makes the laser-plasma process suitable for application like post-processing and correction of traditionally manufactured complex optics.

5 Conclusions

In the present study, etching of SiO2 samples with reactive plasma generated by the laser-induced optical breakdown in CF4 at near atmospheric pressure was investigated. The results showed that etching of the SiO2 with the laser-induced plasma in a CF4 gas environment near atmospheric pressure is possible. The surface quality of the etching pits was inspected by optical microscopy, SEM and AFM. The found surface quality with the measured surface roughness value of 1.4 nm rms is comparable to other plasma etch techniques such as plasma jet etching. The etching rate increases sharply at low etching times and decreases slightly with increasing etching time. The etching rate was found in a range between 1.53 µm/min and 1.16 µm/min between 1 and 10 min etching time respectively. A linear correlation between the etching depth and the distance of the plasma was found. The etching depth increased linearly with increasing laser pulse energy. The threshold for etching was found at a laser pulse energy value of ~ 280 µJ at a plasma surface distance of 100 µm. The material removal process of the SiO2 surface was explained by a chemical reaction of the SiO2 with fluorine. That chemical reaction was supported by a modification of the SiO2 surface due to the emitted secondary radiation of the plasma.