Chemistry in laser-induced plasmas at local thermodynamic equilibrium

Abstract

The equation of state for plasmas containing negative and positive ions of elements and molecules formed by these elements is modeled under the assumption that all ionization processes and chemical reactions are at local thermal equilibrium and the Coulomb interaction in the plasma is described by the Debye–Hückel theory. The hierarchy problem for constants of molecular reactions is resolved by using three different algorithms for high, medium, and low temperatures: the contraction principle, the Newton–Raphson method, and a scaled Newton–Raphson method, respectively. These algorithms are shown to have overlapping temperature ranges in which they are stable. The latter allows one to use the developed method for calculating the equation of state in combination with numerical solvers of Navier–Stokes equations to simulate laser-induced plasmas initiated in an atmosphere and to study formation of molecules and their ions in such plasmas. The method is applicable to a general chemical network. It is illustrated with examples of Ca–Cl and C–Si–N laser-induced plasmas.

Appendix

1.1 A contraction condition at high temperatures

Here a sufficient condition is obtained for the map $\varvec{\varphi }(\varvec{\nu })$ in (13) to be a contraction. Fix two points $\varvec{\nu }$ and $\varvec{\nu }'$. Consider a straight line segment connecting them. The points of the segment are $\varvec{\nu }_t=t\varvec{\nu }+(1-t)\varvec{\nu }'$, $0\le t\le 1$. Let $\varvec{\phi }(t)=\varvec{\varphi }(\varvec{\nu }_t)$ be the values of $\varvec{\varphi }$ on the segment. Then for each q there is $0\le t_q\le 1$ such that $\phi _q(1)-\phi _q(0)=\phi '_q(t_q)$. For any t and any q,

$$\begin{aligned} |\phi _q'(t)|=|(\varvec{\nabla }\varphi _q(\varvec{\nu }_t),\varvec{\nu }-\varvec{\nu }')| \le |\varvec{\nabla }\varphi _q(\varvec{\nu }_t)||\varvec{\nu }-\varvec{\nu }'| \end{aligned}$$

(21)

by the Schwartz inequality for the dot product of two vectors. The components of the gradient vectors $\varvec{\nabla }\varphi _q$ are nothing but the elements of the Jacobian of the map:

$$\begin{aligned} J_{qq'}=\frac{\partial \varphi _q}{\partial \nu _{q'}}=-\varphi _q \sum _p \frac{C_{pq}C_{pq'}}{\nu _p^H-\sum _{q''}C_{pq''}\nu _{q''}} . \end{aligned}$$

The physical range of $\nu _q$ is the polyhedron $\mathcal{P}$ defined in (15). The elements of the Jacobian are bounded in $\mathcal{P}$ as

$$\begin{aligned} |J_{qq'}|\le \nu _q^{\text {max}}\sum _p \frac{C_{pq}C_{pq'}}{\nu _p^H}\equiv K_{qq'}, \end{aligned}$$

where $\nu _q^{\text {max}}$ is defined in (12). This estimate follows from $\nu _p\le \nu _p^H$ and

$$\begin{aligned} \frac{\varphi _q}{\nu _p}=\frac{1}{\nu _p\Lambda _q^H}\prod _{p'} \nu _{p'}^{C_{pq'}}= \frac{\nu _p^{C_{pq}-1}}{\Lambda _q^H}\, \prod _{p'\ne p}\nu _{p'}^{C_{p'q}}\le \frac{(\nu _p^H)^{C_{pq}-1}}{\Lambda _q^H}\, \prod _{p'\ne p}(\nu _{p'}^H)^{C_{p'q}}=\frac{\nu _q^{\text {max}}}{\nu _p^H} . \end{aligned}$$

Put

$$\begin{aligned} K =\left( {\sum _{q,q'} K_{qq'}^2}\right) ^{1/2} . \end{aligned}$$

(22)

Therefore using the inequality (21) one infers that

$$\begin{aligned}&|\varphi _q(\varvec{\nu })-\varphi _q(\varvec{\nu }')|= |\phi _q(1)-\phi _q(0)|=|\phi '_q(t_q)|\le K_q |\varvec{\nu }-\varvec{\nu }'|,\\&\quad K_q=\left( {\sum _{q'} K_{qq'}^2}\right) ^{1/2} . \end{aligned}$$

Taking the square root of the sum of squares of the above inequality it is concluded that

$$\begin{aligned} |\varvec{\varphi }(\varvec{\nu })-\varvec{\varphi }(\varvec{\nu }')|\le K|\varvec{\nu }-\varvec{\nu }'|, \end{aligned}$$

where K is given in (22). Thus, if $K<1$, then the contraction principle can be used to find the root of the system (13).

1.2 An initial point of the contraction sequence

For any choice of the index p

$$\begin{aligned} \sum _{p'}\frac{C_{p'q}C_{p'q'}}{\nu ^H_{p'}} \ge \frac{C_{pq}C_{pq'}}{\nu ^H_{p}} \end{aligned}$$

because the terms in the sum are non-negative. Therefore, the semi-axes of the ellipsoid in (16) are bounded from above as

$$\begin{aligned} a_q \le \frac{\nu ^H_p}{C_{pq}\sqrt{\sum _{q'}C_{pq'}^2}} ,\quad C_{pq} \ne 0, \end{aligned}$$

(23)

for any p such that $C_{pq}\ne 0$ (the molecule q contains the element p). Let $M_p$ be the total number of molecules containing the element p. Then

$$\begin{aligned} M_p \le \sum _{q}C_{pq}^2 \end{aligned}$$

(24)

because $C_{pq}\ge 1$ (the equality is reached only if $C_{pq}=1$, which means that no molecule contains more than one element of the kind p). Next, consider the function $f(\mathbf{x})=\sum _q x_q$ of M real variables $x_q$. Using the method of Lagrange multipliers is not difficult to prove that the maximal value of f on the unit sphere $\sum _q x_q^2=1$ is $f_{\text {max}}=\sqrt{M}$ which is reached at $x_q=1/\sqrt{M}$. Therefore

$$\begin{aligned} \sum _qx_q\le \sqrt{M}\quad {\text {if}}\quad \sum _qx_q^2\le 1 . \end{aligned}$$

(25)

Put $\nu _q=a_q x_q$, $x_q\ge 0$. The point $\nu _q$ lies in the ellipsoid (16) if and only if $x_q=\nu _q/a_q$ lies in the unit ball $\sum _q x_q^2 \le 1$. The point $\nu _q$ also lies in the polyhedron $\mathcal{P}$ if $x_q$ satisfy the conditions $\nu _p =\nu _p^H-\sum _{q}C_{pq}\nu _q\ge 0$. This is indeed the case for any $x_q$ in the unit ball:

$$\begin{aligned} \nu _p^H-\sum _{q}C_{pq}\nu _q &= \nu _p^H-\sum _{q}C_{pq}a_q x_q \ge \nu _p^H\left( 1-\frac{\sum _q x_q}{\sqrt{\sum _{q'}C_{pq'}^2}} \right) \\ & \ge \nu _p^H\left( 1-\frac{\sqrt{M_p}}{\sqrt{\sum _{q'}C_{pq'}^2}} \right) \ge 0, \end{aligned}$$

where the first inequality follows from (23), the second one from (25), and the last one from (24). Thus, the set (16) lies within the polyhedron $\mathcal{P}$.

1.3 The Jacobian in scaled variables at low temperatures

Let us investigate the limit of the Jacobian in the limit of low temperatures and see that it is not singular after the suggested scaling procedure. Let $\nu _q^*$, $q=1,2,\ldots ,N\le M$, be the values of the molecular number densities in the ground state (here the ordering of the index q is done in accord with the above scaling algorithm). Then by construction of the scaling factors, the scaled reaction constants for these molecules are unit, $\Lambda _q^{sc}=1$, $q=1,2,\ldots ,N$. Let us assume that the ground state does not contain molecules with $q>N$. Then $\nu _q^*$ can be found by solving the mass conservation equation at $T=0$:

$$\begin{aligned} \nu _p^H =\sum _{q=1}^N C_{pq}\nu _q^* . \end{aligned}$$

(26)

The scaled reaction constants for other molecules have the property $\Lambda _q^{sc}\rightarrow \infty$ as $T\rightarrow 0$. Indeed, the new variables $x_p$ tend to some limit values $x_p^*>0$ as $T\rightarrow 0$ which satisfy the system of equations

$$\begin{aligned} \nu _q^*=\prod _{p}(x_p^*)^{C_{pq}}\quad {\mathrm{or}}\quad \sum _{p}C_{pq}\ln (x_p^*)=\ln (\nu _q^*), \end{aligned}$$

(27)

where $q=1,2,\ldots ,N$. The systems (26) and (27) have the same matrix as in (20) and, hence, have unique solutions if the scaling coefficients $\lambda _p$ exist. Since $\nu _q^*\ne 0$ so must be $x_p^*\ne 0$. It follows from (19) that $\Lambda _q^{sc}\rightarrow \infty$ as $T\rightarrow 0$ for any molecule not present in the ground state ($q>N$), while $\Lambda _q^{sc}=1$ for $q\le N$. Therefore the block $(J_{MA})_{qp}$ of the Jacobian contains non-zero elements only for $q\le N$ in the low-temperature limit. Furthermore, the block $J_{AA}$ remains diagonal after the scaling, and $(J_{AA})_{pp'}=\lambda _p\delta _{pp'}\rightarrow 0$ as $T\rightarrow \infty$ because by construction all scaling factors $\lambda _p$ vanish as $T\rightarrow 0$. Therefore in the low-temperature limit

$$\begin{aligned} \det J \approx \det \left( \lambda _p\delta _{pp'}+\sum _{q=1}^N C_{pq}\frac{\partial \nu _q^*}{\partial x_{p'}^*}\right) \approx \det \left( \sum _{q=1}^N C_{pq}C_{p'q}\frac{\nu _q^*}{x_{p'}^*}\right) , \end{aligned}$$

(28)

where the block decomposition of the determinant (17) was used to reduce it to the determinant of an $N\times N$ matrix; here $p,p'=1,2,\ldots ,N$. If the ground state contains free atoms of sort p, then the corresponding $\lambda _p=1$ should be retained when passing to the second equality in (28). Since $\nu _q^*\ne 0$, the Jacobian is not singular for low temperatures, provided the system has the same ground state for all values of $\nu _p^H$.

It turns out that if in the simplex of values of $\nu _p^H$, $\sum _p\nu _p^H=1$, $\nu _p^H\ge 0$, there are different ground states, then $\det J$ can vanish at the interface between two ground states in the limit $T\rightarrow 0$. The calculated values of $x_p$ suffer jump discontinuities across this interface if T is low enough. However, the physical fractions $\nu _s$ are proved to remain smooth everywhere in the simplex so that their values in a vicinity of the interface can accurately be found by a suitable interpolation. An example is provided below with the Ca–Cl system.

1.4 The stability of the scaled Newton–Raphson algorithm

1.4.1 Two elements and their dimers

Consider a system containing two elements A and B, and three molecules $A_2$, $B_2$, and AB. The corresponding fractions are denoted $\nu _a$, $\nu _b$, $\nu _{aa}$, $\nu _{bb}$, and $\nu _{ab}$, respectively, and the elemental number densities are $\nu _a^H$ and $\nu _b^H$. Let $D_{aa}$, $D_{bb}$, and $D_{ab}$ be the dissociation energies of $A_2$, $B_2$, and AB, respectively. The ground state of this system is unique if $2D_{ab}\ne D_{aa}+D_{bb}$. If $2D_{ab}- D_{aa}-D_{bb}$ is negative, then the ground state contains $A_2$ and $B_2$, while if it is positive, a formation of the maximal number of AB becomes energetically favorable. So, the ground state has the form:

$$\begin{aligned}&({\text {I}}): 2D_{ab}-D_{bb}-D_{aa}<0,\quad \quad \left\{ \begin{array}{l} \nu _a^*=\nu _b^*=\nu _{ab}^*=0,\\ \nu _{aa}^*= \frac{1}{2}\nu _a^H,\ \nu _{bb}^*=\frac{1}{2}\nu _b^H \end{array}\right. \\&({\text {II}}): 2D_{ab}-D_{bb}-D_{aa}>0,\quad \quad \left\{ \begin{array}{l} \nu _a^*=\nu _b^*=0,\ \nu _{ab}^*=\min \{\nu _a^H,\nu _b^H\},\\ \nu _{bb}^*=\frac{1}{2}(\nu _b^H-\nu _{ab}^*),\ \nu _{aa}^*= \frac{1}{2}(\nu _a^H-\nu _{ab}^*)\end{array}\right. \end{aligned}$$

In the case (I), the ordering $q=1,2,3$ means $q=aa,bb,ab$, provided $D_{aa}<D_{bb}$ (otherwise, the positions of the indices aa and bb are swapped). In the case (II), the ordering $q=1,2,3$ means $q=ab,aa,bb$, provided $\nu _a^H>\nu _b^{H}$ because $\nu _{bb}^*=0$ (otherwise the positions of the indices aa and bb are swapped because $\nu _{aa}^*=0$ if $\nu _a^H<\nu _b^{H}$).

It should be noted that in the case (II), the system has two ground states $(AB,\,A_2)$ and $(AB,\ B_2)$. In the segment $\nu _a^H+\nu _b^H=1$, $\nu _{a,b}\ge 0$ (a one-dimensional simplex), they are separated by the point $\nu _a^H=\nu _b^H=\frac{1}{2}$. The scaling is done differently for each ground state. The existence of two distinct ground states indicates a potential problem for the scaled Newton–Raphson algorithm at low temperature near the point $\nu _a^H=\nu _b^H=\frac{1}{2}$ as is shown below.

The solutions for scaling coefficients in the change of variables $\nu _a=\lambda _a x_a$ and $\nu _b=\lambda _b x_b$ are found from (20):

$$\begin{aligned} (A_2,B_2) :\quad & \lambda _a=\sqrt{\Lambda _{aa}^H},\quad \lambda _b=\sqrt{\Lambda _{bb}^H}\\ (AB,A_2) :\quad & \lambda _a=\sqrt{\Lambda _{aa}^H},\quad \lambda _b=\frac{\Lambda _{ab}^H}{\sqrt{\Lambda _{aa}^H}}\\ (AB,B_2) :\quad & \lambda _a=\frac{\Lambda _{ab}^H}{\sqrt{\Lambda _{bb}^H}} ,\quad \lambda _b=\sqrt{\Lambda _{bb}^H}. \end{aligned}$$

The corresponding scaled reaction constants in the above three cases are

$$\begin{aligned} (A_2,B_2) :\quad &\Lambda _{aa}^{sc}=\Lambda _{bb}^{sc}=1,\quad \Lambda _{ab}^{sc} =\frac{\Lambda _{ab}^H}{\sqrt{\Lambda _{aa}^H\Lambda_{bb}^H}}\\ (AB,A_2) :\quad &\Lambda _{ab}^{sc}=\Lambda _{aa}^{sc}=1,\quad \Lambda _{bb}^{sc} =\frac{\Lambda _{aa}^H\Lambda _{bb}^H}{(\Lambda _{ab}^H)^2}\\ (AB,B_2) :\quad &\Lambda _{ab}^{sc}=\Lambda _{bb}^{sc}=1,\quad \Lambda _{aa}^{sc} =\frac{\Lambda _{aa}^H\Lambda _{bb}^H}{(\Lambda _{ab}^H)^2} . \end{aligned}$$

In the low-temperature limit, $T\rightarrow 0$, the scaling constants should tend to zero because $\nu _p\rightarrow \nu _p^*=0$ (all atoms are bound into molecules in the ground state). So, the whole purpose of the scaling is to specify how fast the atomic fractions $\nu _p$ tend to zero with decreasing the temperature. In this way, possible round-off problems occurring in calculations of the right sides of the Guldberg–Waage equations can be avoided. For example, if the ground state is $(A_2,B_2)$, then the system to be solved in the new variables has the form

$$\begin{aligned}&\nu _{aa}=x_a^2,\quad \nu _{bb}=x_b^2,\quad \nu _{ab}=\frac{x_ax_b}{\Lambda _{ab}^{ren}},\\&\nu _a^H=\lambda _a x_a+\nu _{ab}+2\nu _{aa},\quad \nu _a^H=\lambda _bx_b+\nu _{ab}+2\nu _{bb}. \end{aligned}$$

In this case $\lambda _a$ and $\lambda _b$ tend to 0 as $T\rightarrow 0$, while $\nu _{aa}\rightarrow \nu _{aa}^*$ and $\nu _{bb}\rightarrow \nu _{bb}^*$, which implies that $x_a\rightarrow \sqrt{\nu _{aa}^*}$ and $x_b\rightarrow \sqrt{\nu _{bb}^*}$. Therefore the system contains no terms that can possibly produce round-off errors, and the Jacobian of the system remains finite in the limit $T\rightarrow 0$ as well. Indeed, it is straightforward to find the four blocks of the Jacobian for the above system:

$$\begin{aligned} J_{AA}= \left( \begin{array}{cc} \lambda _a &{} 0\\ 0 &{}\lambda _b\, \end{array}\right) , \quad J_{AM}=\left( \begin{array}{ccc} 2&{}0&{}1\\ 0&{}2&{}1 \end{array}\right) ,\quad J_{MA}= \left( \begin{array}{cc} -2x_a&{}0\\ 0&{}-2x_b\\ -\frac{x_b}{\Lambda _{ab}^{sc}}&{} -\frac{x_a}{\Lambda _{ab}^{sc}} \end{array}\right) \end{aligned}$$

and $J_{MM}=I$. By construction of the scaling factors, the reciprocal of the scaled reaction constant $\Lambda _{ab}^{sc} \sim \exp \left[ \frac{1}{2}(2D_{ab}-D_{aa}-D_{bb})/(kT)\right] \rightarrow \infty$ as $T\rightarrow 0$ so that

$$\begin{aligned} \det J =\det (J_{AA}-J_{AM}J_{MA})\approx \det \left( \begin{array}{cc} 4x_a&{}0\\ 0 &{} 4x_b\\ \end{array}\right) \approx 16 \sqrt{\nu ^*_{aa}\nu ^*_{bb}}, \end{aligned}$$

in the low-temperature limit. Thus, if the system has a single ground states for all values of $\nu ^H_{a,b}$, the Newton–Raphson algorithm solves the system in the scaled variables.

The other two cases can be analyzed similarly. For instance, if $2D_{ab}-D_a-D_b>0$ and $\nu _a^H> \nu _b^H$ so that the ground state is $(AB,\ A_2)$, the system in the new variables reads

$$\begin{aligned}&\nu _{aa}=x_a^2,\quad \nu _{ab}=x_ax_b,\quad \nu _{bb}=\frac{x_b^2}{\Lambda _{bb}^{sc}},\\&\nu _a^H=\lambda _a x_a+\nu _{ab}+2\nu _{aa},\quad \nu _a^H=\lambda _bx_b+\nu _{ab}+2\nu _{bb}. \end{aligned}$$

In this case, $x_a\rightarrow \sqrt{\nu _{aa}^*}$ and $x_b\rightarrow \nu _{ab}^*/\sqrt{\nu _{aa}^*}$ as $T\rightarrow 0$. Owing to the fact that $\lambda _a$, $\lambda _b$, and $(\Lambda _{bb}^{sc})^{-1}$ tend to zero exponentially as $T\rightarrow 0$ (so that $\nu _{bb}\rightarrow 0$), the determinant of the Jacobian in this limit is

$$\begin{aligned} \det J\approx \det \left( \begin{array}{cc} x_b+4x_a&{}x_a\\ x_b &{} x_a\\ \end{array}\right) = 4x_a^2\approx 4\nu _{aa}^*. \end{aligned}$$

If $\nu _a^H< \nu _b^H$ so that the ground state is $(AB,\ B_2)$, $x_b^*\rightarrow \sqrt{\nu _{bb}^*}$ while $x_a^*\rightarrow \nu _{ab}^*/\sqrt{\nu _{bb}^*}$ because $\lambda _a$, $\lambda _b$, and $(\Lambda _{aa}^{sc})^{-1}$ are exponentially small in the limit $T\rightarrow 0$ so that $\det J\rightarrow 4\nu _{bb}^*$.

Thus, in the limit $T\rightarrow 0$,

$$\begin{aligned} \det J \rightarrow 2|\nu _a^H-\nu _b^H| \end{aligned}$$

the Jacobian becomes singular at the point $\nu _a^H=\nu _b^H=\frac{1}{2}$ separating two ground states. It is also noteworthy that the asymptotic values of $x_a$ and $x_b$ (as $T\rightarrow 0$) suffer a discontinuity at this point:

$$\begin{aligned} x_a \rightarrow \left\{ \begin{array}{ll} \frac{1}{2}(\nu _a^H-\nu _b^H),&{} (AB,A_2)\\ \sqrt{2}\nu _{ab}^*(\nu _b^H-\nu _a^H)^{-1/2},&{} (AB,B_2). \end{array} \right. \end{aligned}$$

At a low temperature, the scaled fraction $x_a$ tends to zero if the point separating two ground states is approached from the side where $\nu _a^H>\nu _b^H$ [from $(AB,B_2)$], while $x_a$ diverges if the point separating two ground states is approached from the other side (from $(AB,B_2)$). The picture for $x_b$ is similar, but $x_b$ tends to zero if the point $\nu _a=\nu _b$ is approached from $(AB,B_2)$, and it diverges when this point is approached from $(AB,A_2)$. For a finite temperature the discontinuity in $x_{a,b}$ has actually a finite jump and becomes infinite only in the limit $T\rightarrow 0$. The jump discontinuity becomes smaller with increasing the temperature. In the next section, a real chemical network exhibiting such a singularity at low temperatures is analyzed and a possible instability of the NR algorithm is shown to be eliminated by a simple interpolating procedure across the singular point.

1.4.2 The Ca–Cl system

Consider a system with two elements A and B that can form molecules $AB_2$, AB, $B_2$, and $A_2$. Let $A={\mathrm{Ca}}$ and $B={\mathrm{Cl}}$. The dissociation energies of ${\mathrm{CaCl}}_2$, ${\mathrm{CaCl}}$, and ${\mathrm{Cl}}_2$ are given in Table 2, while for the dimer ${\mathrm{Ca}}_2$ it is 0.2 eV. This system was studied in our earlier work by analytic methods [20]. It was found that the system reaches its ground states at a room temperature. Owing to a low dissociation energy of $A_2$, this dimer can be excluded from the network. In this case, the ground state may contain free atoms of sort A when all elements of sort B are bound into molecules $AB_2$. The molecules AB and free atoms of sort B can never occur in the ground state because the reactions $2AB\rightarrow AB_2+B_2$ and $2B\rightarrow B_2$ reduce the total energy of the system. The system has two ground states:

$$\begin{aligned} \begin{array}{llll} (AB_2,\ B_2): &{}{\textstyle {\frac{1}{2}}}\nu _b^H-\nu _a^H>0,\\ \quad &{} \nu _{abb}^*=\nu _a^H,\quad &{}\nu _{bb}^*= {\textstyle {\frac{1}{2}}}\nu _b^H -\nu _a^H,\quad &{}\nu _{a}^*=0,\\ (AB_2,\ A): &{} \nu _a^H-{\textstyle {\frac{1}{2}}}\nu _b^H>0\\ \quad &{} \nu _{abb}^*={\textstyle {\frac{1}{2}}}\,\nu _b^H,\quad &{}\nu _{bb}^*=0 ,\quad &{}\nu _{a}^*=\nu _a^H -{\textstyle {\frac{1}{2}}}\nu _b^H. \end{array} \end{aligned}$$

In the interval $\nu _a^H+\nu _b^H=1$, $\nu _{a,b}^H\ge 0$, the point $(\nu _a^H,\nu ^H_b)=\left( \frac{1}{3},\frac{2}{3}\right)$ is the boundary between two ground states. The point is characterized by the “perfect” stoichiometry: all elements are bound into the $AB_2$ molecules, there is neither excess of A nor B to form anything else in the limit $T\rightarrow 0$. This is a general feature. Any point in an interface separating two ground states in the simplex formed by values of $\nu _p^H$ corresponds to a specific stoichiometry at which only molecules common for the two ground states exist in the limit $T\rightarrow 0$, while molecules by which the ground states differ from one another cease to exist in this limit.

The ordering of molecular species in the composition matrix $C_{pq}$ in the case $(AB_2,\ B_2)$ is $q=abb$, bb, ab and $q=abb$, ab, bb in the case $(AB_2,\ A)$. The scaling factors and scaled reaction constants are obtained from (20):

$$\begin{aligned} (AB_2,\ B_2):\quad &\lambda _a=\frac{\Lambda _{abb}^H}{\Lambda _{bb}^H}, \quad \lambda _b=\sqrt{\Lambda _{bb}^H} \\&\Lambda _{abb}^{sc}=\Lambda _{bb}^{sc}=1,\quad \Lambda _{ab}^{sc}=\frac{\Lambda _{ab}^H}{\lambda _a\lambda _b}, \\ (AB_2,\ A):\quad &\lambda _a=1 , \quad \lambda _b= \sqrt{\Lambda _{abb}^H} \\&\Lambda _{abb}^{sc}=1,\quad \Lambda _{ab}^{sc}=\frac{\Lambda _{ab}^H}{\lambda _a\lambda _b},\quad \Lambda _{bb}^{sc}=\frac{\Lambda _{bb}^H}{\lambda _{b}^2}. \end{aligned}$$

Using the dissociation constants, it is not difficult to see that $\Lambda _{ab}^{sc}\sim e^{3.9/kT}\rightarrow \infty$ as $T\rightarrow 0$ in the case $(AB_2,\ B_2)$, where the number in the exponentials are given in eV, while in the second case, $\Lambda _{ab}^{sc}\sim e^{2.2/kT}\rightarrow \infty$ and $\Lambda _{bb}^{sc}\sim e^{6.7/kT}\rightarrow \infty$ as $T\rightarrow 0$ which implies that the molecules AB and $B_2$ would eventually cease to exist with decreasing the temperature as required by the general analysis.

Fig. 8

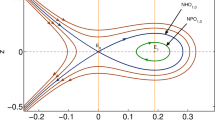
a The scaled atomic number densities $x_a=x_{\mathrm{Ca}}$ and $x_b=x_{\mathrm{Cl}}$ in the Ca–Cl system versus $\nu _a^H=\nu _{\mathrm{Ca}}^H$ at two different temperatures 300 K (dashed lines) and 3000 K (solid lines). The point separating two ground states (${\mathrm{CaCl}}_2$, ${\mathrm{Cl}}_2$) and (${\mathrm{CaCl}}_2$, ${\mathrm{Ca}}$) is at $\nu _{\mathrm{Ca}}^H =\frac{1}{3}$ and $\nu _{\mathrm{Cl}}^H =1-\nu _{\mathrm{Ca}}^H=\frac{2}{3}$. b The physical number densities of all molecular and atomic species versus $\nu _a^H=\nu _{\mathrm{Ca}}^H$ at 3000 K

Since the scaling depends on the ground state, the asymptotic behavior of the scaled atomic number densities at low temperatures exhibit singularities at the point that separates two ground states. Let $x^*_{a,b}$ be the limit values of $x_{a,b}$ in the limit $T\rightarrow 0$. Then

$$\begin{aligned} x_a^*= & {} \left\{ \begin{array}{ll} \nu _{abb}^*(\nu _{bb}^*)^{-1}=\nu _a^H\left( \frac{1}{2}\nu _b^H-\nu _a^H\right) ^{-1}, \quad &{}(AB_2,\ B_2)\\ \nu _a^*=\nu _a^H-\frac{1}{2}\nu _b^H,\quad &{}(AB_2,\ A) \end{array} \right. \\ x_b^*= & {} \left\{ \begin{array}{ll} (\nu _{bb}^*)^{1/2}=\left( \frac{1}{2}\nu _b^H-\nu _a^H\right) ^{1/2}, \quad &{}(AB_2,\ B_2)\\ (\nu _{abb}^*)^{1/2}(\nu _a^*)^{-1/2}=\left( \frac{1}{2} \nu _b^*\right) ^{1/2} \left( \nu _a^H-\frac{1}{2}\nu _b^H\right) ^{-1/2},\quad &{}(AB_2,\ A) . \end{array} \right. \end{aligned}$$

The values of $\nu _{abb}^*$, $\nu _{bb}^*$, and $\nu _a^*$ are obtained from (26)

$$\begin{aligned} \begin{array}{rll} (AB_2,B_2):\quad &{} \nu _a^H=\nu _{abb}^*,\quad &{}\nu _b^H=2\nu _{abb}^*+2\nu _{bb}^*\\ (AB_2,A):\quad &{} \nu _a^H=\nu _a^*+\nu _{abb}^*,\quad &{}\nu _b^H=2\nu _{abb}^* \end{array} \end{aligned}$$

and $x^*_{a,b}$ are the solutions to (27). Using (28), the asymptotic value of the determinant of the Jacobian is calculated:

$$\begin{aligned} \det J=\left\{ \begin{array}{ll}4(x_b^*)^3,&{}\ (AB_2,\ B_2)\\ 4x_a^*x_b^*,&{}\ (AB_2,\ A) \end{array}\right. . \end{aligned}$$

It should be noted that in the ground state $(AB_2,\ A)$, the block $J_{AA}$ does not vanish in the limit $T\rightarrow 0$ because $\lambda _a=1$ (free atoms in the ground state), $(J_{AA})_{pp'}= \lambda _p \delta _{pp'}$. Therefore the limit value of $J_{AA}$ must be added to the matrix whose determinant is given in Eq. (28), when computing $\det J$ in the state $(AB_2,\ A)$.

The limit values of $x_{a,b}^*$ suffer an “infinite” jump discontinuity at the point $(\nu _a^H,\nu _b^H)=\left( \frac{1}{3},\frac{2}{3}\right)$ that separates two ground states. If $(\nu _a^H,\nu _b^H)\rightarrow \left( \frac{1}{3},\frac{2}{3}\right)$ from the state $(AB_2,B_2)$, then $x_a^*\rightarrow \infty$, while $x_b^*\rightarrow 0$, and, if $(\nu _a^H,\nu _b^H)\rightarrow \left( \frac{1}{3},\frac{2}{3}\right)$ from the state $(AB_2,A)$, then $x_a^*\rightarrow 0$, while $x_b^*\rightarrow \infty$. The determinant $\det J$ tends to zero when $(\nu _a^H,\nu _b^H)\rightarrow \left( \frac{1}{3},\frac{2}{3}\right)$ from either state, indicating an instability of the scaled Newton–Raphson algorithm. It should be emphasized that the Jacobian is singular at $(\nu _a^H,\nu _b^H)=\left( \frac{1}{3},\frac{2}{3}\right)$ only at $T=0$, while it remains close to singular for low temperatures and eventually become regular with increasing T.

In panel a of Fig. 8, the values of the scaled atomic number densities $x_a$ and $x_b$ calculated by the scaled Newton–Raphson algorithm are shown as functions of $0\le \nu _a^H\le 1$ at $T=300$ K (dashed lines) and $T=3000$ K (solid lines). The necessary spectroscopic data for all species of the Ca–Cl system can be found in [20] (it includes all molecular and atomic species as well as their positive and negative ions). At $T=300$ K, the system is practically in the ground state. The calculated values of $x_{a,b}$ match the analytic values $x_{a,b}^*$ given above. As one can see the scaled atomic number densities are not continuous across the point $(\nu _a^H,\nu _b^H)=(\frac{1}{3},\frac{2}{3})$ separating two ground states, but the discontinuity jump remains finite for $T>0$ and becomes infinite only in the limit $T\rightarrow 0$. The calculated values of the physical number densities (panel b of Fig. 8) are smooth across the singular point. A small gap in the solid lines in panel b of Fig. 8 at the singular point $\nu _a^H=\frac{1}{3}$ indicates that the scaled Newton–Raphson algorithm can fail to calculate the corresponding $x_{a,b}$. It was found that the window in which such a failure could occur lies within the interval $|\nu _a^H-\frac{1}{3}|<10^{-6}$ for all temperatures at which the scaling was needed in this system to resolve the hierarchy problem ($T<3500$ K). Owing to the smoothness of the physical number densities in a neighborhood of the singular point, their accurate values in the indicated window can be obtained by an interpolation from the left and right sides of the singular point. This is an example of the general (interpolation) approach to deal with possible irregularities of the scaled Newton–Raphson algorithm if the system in question has multiple ground states.