Abstract
We investigate the use of ultra-short laser pulses for the selective melting of Al-Si40-powder to fabricate complex light-weight structures with wall sizes below \(100\,\upmu \text {m}\) combined with higher tensile strength and lower thermal expansion coefficient in comparison to standard Al–Si alloys. During the cooling process using conventional techniques, large primary silicon particles are formed which impairs the mechanical and thermal properties. We demonstrate that these limitations can be overcome using ultra-short laser pulses enabling the rapid heating and cooling in a non-thermal equilibrium process. We analyze the morphology characteristics and micro-structures of single tracks and thin-walled structures depending on pulse energy, repetition rate and scanning velocity utilizing pulses with a duration of \(500\,\text {fs}\) at a wavelength of \(1030\,\text {nm}\). The possibility to specifically change and optimize the microstructure is shown.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the last decade, selective laser melting and sintering (SLM/SLS) of metal powders evolved as one of the most promising tools for the fabrication of three-dimensional freeform elements with highly sophisticated geometries that cannot be processed with conventional machining methods or casting techniques [1, 2]. Nowadays SLM is advanced to the serial production of customized products in a wide range of applications, especially in automotive, aerospace and medicine. One outstanding advantage is a high level of flexibility in the design of tailored and optimized light-weight structures. In this context, aluminium as a major alloy component is predominantly used due to the combination of low density, high thermal conductivity and low material costs. Usually silicon is added to reinforce the material to achieve an improved torsion resistance, ultimate tensile strength, wear resistance and ductility as well as a reduction of the thermal expansion coefficient [3,4,5]. The eutectic point of this binary system is located at a mass fraction of 12.2% silicon and \(577\,^\circ \text {C}\) [6, 7]. A hypereutectic Si content leads to a significant improvement of the ultimate tensile strength and elastic modulus and a decrease of the thermal expansion coefficient [3]. However, utilizing conventional techniques such as extrusion, forging, casting, powder metallurgy and continuous-wave laser (cw laser) treatment, the cooling rate is low, resulting in the formation of large primary silicon plates that deteriorate the mechanical and thermal properties [1, 8]. At a mass fraction of \(40\,\%\) silicon the liquidus temperature is \(350\,\text {K}\) above the eutectic temperature [7]. Up to now only a few methods such as spray deposition and melt spinning allow a rapid cooling that is suitable to achieve a desired fine distribution of silicon particles in an aluminium matrix [9,10,11,12]. However, these techniques only allow the fabrication of semi-finished products without complex designed structures. First SLM investigations of Al-Si40 using cw laser radiation reveal a promising fine grained distribution of silicon as well [13]. Moreover, the smallest sizes that could be achieved with hypereutectic Al–Si powders are above \(150\,\upmu \text {m}\) using laser cladding with a cw laser [14, 15].
To overcome these limitations, we investigate the use of ultra-short laser pulses as an alternative heat source. Ultra-short laser pulses in the range of femtoseconds to picoseconds are commonly used in laser material micro processing for burr free and low-damage ablation with negligible heat-affected zone [16, 17]. Nevertheless, even for ultra-short laser pulses a certain amount of energy remains in the material [18]. When the time between two successive pulses is shorter than the characteristic heat diffusion time the heat is accumulating and temperature rises [19]. This heat accumulation effect is specifically utilized, e.g., for the local welding of glass [20,21,22]. So far, the use of ultra-short laser pulses at high repetition rates has been reported only few times for the SLM of materials with high melting temperatures and high thermal conductivities such as tungsten, zirconium and copper [23,24,25,26,27,28,29]. In the investigations presented here, we make use of the extraordinary short interaction time of the laser pulses with the hypereutectic Al–Si alloy to realize fast controlled heating and cooling cycles for producing samples with optimized microstructure and highly confined geometrical features.
2 Experimental setup
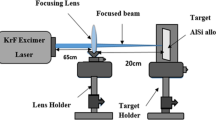
The experiments were realized with a basic SLM-setup that enables the layer-wise melting of powder which is illustrated in Fig. 1.
The irradiation source was a femtosecond fiber laser (Activefiber Systems GmbH) that generates pulses with a central wavelength of \(1030\,\text {nm}\) and a duration of 500 fs. The maximum average power is \(25\,\text {W}\) at a repetition rate of \(20\,\text {MHz}\) that can be modified with an internal acousto-optic modulator (AOM). The pulses were deflected by a computer controlled galvano-mirror scanner (SCANgine from Scanlab). The scanner system was equipped with a \(100\,\text {mm}\)-F-Theta lens that focuses the pulses with a waist diameter (\({d}_{1/\text {e}^2}\)) of \(35\,\upmu \text {m}\) onto the surface of the powder bed. By adjusting the distance between powder bed and focusing lens the beam diameter can be adapted up to \(300\,\upmu \text {m}\). The powder was deposited manually on a standard aluminium building platform with a rubber blade. After illumination the platform was lowered stepwise using the upper lifting axis. The position was controlled with a dial gauge having an accuracy of \(5\,\upmu \text {m}\). With this setup it is possible to fabricate parts with maximum dimensions of \(10\,\text {mm} \times 40\,\text {mm} \times 40\,\text {mm}^3\) (\(H \times W \times D\)). To avoid oxidation a sealed chamber was installed that was flooded with nitrogen to keep the residual oxygen level less than 0.1% as described by Louvis et al. [30]. Additionally, an exhauster was fixed close to the melt pool for removing the strong smoke to protect the exit window of the objective against the deposition of soot. In all the experiments, Al–Si powder with a mass fraction of \(40\,\%\) silicon was used supplied by TLS-Technik. The gas atomized powder grains have a size distribution of \(20{-}63\,\upmu \text {m}\) with a mean diameter of \(38\,\upmu \text {m}\) as can be seen in Fig. 2a.
The additive fabrication of fine structures requires both a small particle size and a low layer thickness. Hence, the sphere-like particles have been sieved again with a strainer mesh size of \(40\,\upmu \text {m}\). The mean particle size obtained is approximately \(25\,\upmu \text {m}\) which nearly fits the focal diameter and ensures a more homogeneous powder deposition at a layer thickness below \(30\,\upmu \text {m}\). In Fig. 2b, a polished cross section of loose powder grains is shown. As already mentioned, large primary silicon plates (gray areas) surrounded by eutectic Si and \(\alpha \)-Al (brighter two-phase area) can be observed.
After SLM, the samples were analyzed by different imaging techniques such as optical microscopy and scanning electron microscopy (SEM) to qualify the melting characteristics and to quantify melt widths and heights. Furthermore, the processed samples were embedded in epoxy resin and polished with \(\text {Al}_{2}\text {O}_{3}\) nano-powder to obtain deeper insight into the microstructure.
3 Results
The interaction of ultra-short laser pulses with matter is different and more complex in comparison to cw lasers. In SLM studies using cw lasers essentially, the applied power (\({P}_{\text {av}}\)), scanning velocity (\({v}_{\text {scan}}\)), wavelength and focal diameter are varied apart from the built orientation and different scan strategies. For ultra-short pulsed lasers, pulse energy (\({E}_{\text {P}}\)), pulse duration (\({t}_{\text {P}}\)) and repetition rate (\({f}_{\text {rep}}\)) are additionally influencing the interaction. Hence, some preliminary studies are required to define an appropriate processing regime.
3.1 Parameter and Morphological Studies
In selective laser melting, ablation should be avoided. To determine the damage/ablation threshold of materials in ultra-short laser pulse processing, the energy density or the so-called fluence
is used. The single pulse ablation threshold fluence of aluminium and silicon at \(1030\,\text {nm}\) is approximately \(0.12\frac{\text {J}}{\text {cm}^2}\) in the sub-picosecond regime [31, 32]. For shorter laser wavelengths, the silicon particles linearly absorb the laser radiation which strongly decreases the threshold for ablation [31]. This could lead to a greater loss of silicon and an undesirable change of the material composition at higher fluences. Additionally, multi-pulse irradiation may reduce the ablation threshold further depending on the repetition rate [33].
To figure out possible limitations caused by such unfavorable ablation effects, we studied the basic pulse-powder interaction depending on pulse energy, spot diameter and repetition rate. Therefore, we deposited a single powder layer with a thickness of \(30\,\upmu \text {m}\) on the building platform and scanned squares with an edge length of \(2\,\text {mm}\) and a hatch distance of \(\frac{1}{3}\) of the spot diameter (\({d}_{\text {S}}\)) to ensure a suitable track overlap. For these investigations, we kept the energy per unit length
constant at \(150\,\frac{\text {J}}{\text {m}}\) to compare results with different pulse energies, repetition rates and scanning velocities. Figure 3 exemplary shows the threshold power and fluence for a repetition rate of \(500\,\text{ kHz }\) for different spot diameters (a) and for a spot diameter of \(35\,\upmu \text {m}\) and varying repetition rate (b).
The threshold values represent the onset of powder blasted away from the underlying platform. This removal can be explained by a strong pressure due to a combination of material vaporization and generated shock waves. Figure 3a shows that the blasting fluence decreases with increasing spot diameter. However, for spot diameters \(>\,150\,\upmu \text {m}\) the threshold fluence practically remains constant. Moreover, the decrease of the blasting threshold with increasing repetition rate at fixed spot diameter indicates also a cumulative effect (see Fig. 3b).
To fully apply the average power of \(25\,\text {W}\) provided by the laser system, the repetition rate and beam diameter were set to \(20\,\text {MHz}\) and \(50\,\upmu \text {m}\), respectively, for the following investigations. This ensures a high spatial resolution without limiting effects of vaporization and blasting. The influence of average power and energy per unit length was investigated by scanning single lines with a length of \(2\,\text {mm}\). All tracks were separated by a minimum distance of \(1\,\text {mm}\) to melt the powder on pristine positions and to avoid any potential interplay between neighboring lines. The average power was altered in the range of 2.5–25 W and energies per unit length were varied between 25 and \(350\,\frac{\text {J}}{\text {m}}\). Seven layers with a thickness of \(30\,\upmu \text {m}\) each and the same line patterns were processed to achieve significant and comparable results. Figure 4a shows a representative selection of SEM images of molten tracks with an approximate height of \(200\,\upmu \text {m}\).
a SEM images of molten tracks with different energies per unit length at a fixed average power of \(25\,\text {W}\) and a repetition rate of \(20\,\text {MHz}\) (left side). Different characteristic morphologies can be observed due to the change in the scanning velocity and the corresponding energies per unit length. The influence of different average powers for \(\text {Q} = 150\,\frac{\text {J}}{\text {m}}\) is shown on the right side. b SEM images of molten tracks at different average powers and a fixed Q-value of \(150\,\frac{\text {J}}{\text {m}}\) using multiple scanning repetitions from 1 to 6
On the left side, the average power was fixed to \(25\,\text {W}\) corresponding to a pulse energy of \(1.25\,\upmu \text {J}\), and on the right side tracks with a constant energy per unit length of \(150\,\frac{\text {J}}{\text {m}}\) are shown. Based on these images one can identify various melting morphologies which yield important insight into the solidification characteristics. At low scanning velocities \({v}_{\text {scan}} <120\,\frac{\text {mm}}{\text {s}}\) (\(Q>210\,\frac{\text {J}}{\text {m}}\)), the amount of heat is too high resulting in melt warps that protrude from the powder bed and consequently disturb the preparation of following layers (see left side of Fig. 4a). The extreme heat flow leads to an extensive heat-affected zone that is several times larger than the irradiated area. Here, the track widths are in the range of 150–200 \(\upmu \text {m}\) with a rough surface and a multitude of attached particles on the side walls. At scanning velocities \({v}_{\text {scan}}> 800\,\frac{\text {mm}}{\text {s}}\) (\(Q<30\,\frac{\text {J}}{\text {m}}\)), irregular structures are formed including interruptions and welding beads. Additionally, when the average power is decreased below \(5\,\text {W}\) (see right side of Fig. 4a) the particles are only surface-sintered. This can be explained by persistent liquid phase sintering [34], which is not sufficient to melt primary silicon to achieve a homogeneous mixture.
In an intermediate regime above \(12\,\text {W}\) and \(40\,\frac{\text {J}}{\text {m}}\) uniform structures with a significantly reduced roughness could be melted. The homogeneity can be significantly improved by re-scanning a single track several times. Figure 4b illustrates this effect for different processing regimes. Between two successive scans a dwell time of \(1\,\text {s}\) was set to cool down the material below the melting point. After three cycles an improved compaction and a decrease of the waviness of the track can be seen. Too frequent re-melting results in ripples and grain agglomerations. At low average powers, no improved uniformity could be obtained.
Figure 5 summarizes the quality characteristics depending on average power and energy per unit length. We determined a suitable processing window in the range of \({P}_\text {av} = 12{-}25\,\text {W}\) and \({Q} = 40{-}170\,\frac{\text {J}}{\text {m}}\).
3.2 Structural investigations
After defining a suitable processing regime, we studied the achievable feature sizes and microstructural morphology of additive manufactured samples. Therefore, we constructed single circles with a diameter of \(1.5\,\text {mm}\), consisting of 50 layers with a thickness of \(30\,\upmu \text {m}\), each. The circle paths were re-scanned three times for each layer. The average laser power and scan velocity were varied, resulting in different values of Q. The thin-walled hollow cylinders are shown in Fig. 6a.
The wall thickness was measured at ten different positions along the circumference to achieve a reliable average value. Therefore, the samples were cleaning in an ultrasonic bath and polished on the topside as can be seen in Fig. 6b. Figure 6c illustrates the wall thickness depending on the energy per unit length and power. In the range of \({Q} = 40{-}150\,\frac{\text {J}}{\text {m}}\), the wall thickness grows almost linearly with Q and slightly increases with average power. The smallest achievable wall thickness was \(54\pm 5\,\upmu \text {m}\) at \(18\,\text {W}\) and \(40\,\frac{\text {J}}{\text {m}}\).
To analyze the phase composition and distribution of Al and Si, the fabricated thin-walled cylinders were embedded in epoxy resin and polished upright on the top edge. In Fig. 7, the micrograph series shows the distribution of primary silicon particles (bulk gray) and the surrounding Al/eutectic Si (bright).
Black sections illustrate boundaries and cracks. The primary silicon particle size is decreasing with increasing average power and energy per unit length. In addition, a more uniform and fine distribution of these particles surrounded by \(\alpha \)-Al and eutectic Si is observed for average powers above \(12\,\text {W}\). Some flaws recognizable in between fine distributed silicon could be based on thin oxide films present on the surface. Below \(10\,\text {W}\), the silicon particles agglomerate in different directions, resulting in deteriorate formation of sintering necks between adjacent powder grains which reduces the stability of the entire structure.
These investigations suggest the use of high average power and energy per unit length as the optimum processing parameters.
3.3 Lightweight sample structures
On the basis of these results different lightweight structures with high aspect ratios of more than 1 : 50 were realized which are shown in Fig. 8.
a Hollow thin-walled hemisphere with a starting overhang angle of \(35^\circ \) on the platform (left) and a SEM image of a molten intersection (right). b Hexagonal wall arrangement with a minimum wall thickness of \(80\,\upmu \text {m}\). c Impeller (right) with a detailed view on the centered hub after polishing the surface (right)
The samples were fabricated with a layer thickness of \(30\,\upmu \text {m}\) using an average power of \(25\,\text {W}\) and an energy per unit length of \(125\,\frac{\text {J}}{\text {m}}\) corresponding to a scan velocity of \(200\,\frac{\text {mm}}{\text {s}}\). Each constructed path was scanned for three times and to increase lateral structure sizes the areas were hatched along the contour with a distance of \(30\,\upmu \text {m}\). The SEM image of the hemisphere in Fig. 8a shows a neat and robust connection between the intersecting walls with a mean thickness of \(80\,\upmu \text {m}\). Here, no external supporting structures are necessary in overhang areas even at angles down to \(35^\circ \). The SEM image of the hexagon in Fig. 8b imparts insight into the wall quality. The appropriate vertical overlap of the molten layers leads to a dense framework with an average roughness of \(10\,\upmu \text {m}\). Furthermore, the lateral connection of the melted areas reveals low porosity as can be seen in the SEM image of the central hub in Fig. 8c after polishing of the top side.
4 Conclusions
These investigations clearly demonstrate the potential of ultra-short laser pulses for additive manufacturing of non-eutectic alloys such as Al-Si40. A controlled energy deposition allows a homogeneous re-solidification of the melted Al-Si40 powder which is necessary for reproducible and stable parts. By appropriate choice of the processing parameters the microstructure can be optimized. High aspect ratio lightweight elements with structure sizes down to \(70\,\upmu \text {m}\) and an average roughness of about \(10\,\upmu \text {m}\) could be realized.
In future work, we will determine the mechanical and thermal properties such as elastic modulus, ultimate tensile strength and hardness as well as the thermal conductivity and thermal expansion coefficient of the produced structures.
References
E.O. Olakanmi, R.F. Cochrane, K.W. Dalgarno, Prog. Mater. Sci. 74, 401 (2015)
D. Buchbinder, H. Schleifenbaum, S. Heidrich, W. Meiners, J. Bültmann, Phys. Proc. 12, 271 (2011)
A. Gebhardt, J. Kinast, R.-R. Rohloff, W. Seifert, M. Beier, S. Scheiding, T. Peschel, ICSO 2014, International conference on space optics (2014)
L. Zhang, D.G. Eskin, A. Miroux, L. Katgerman, M. Beier, S. Scheiding, T. Peschel, in Light Metals 2012, ed. by C.E. Suarez (2012), p. 999
L.Z. Zhao, M.J. Zhao, L.J. Song, J. Mazumder, Mater. Design 56, 542 (2014)
J.L. Murray, A.J. McAlister, Bull. Alloy Phase Diagr. 5, 74 (1984)
M.B. Djurdjevic, S. Manasijevic, Z. Odanovic, N. Dolic, Adv. Mat. Sci. Eng. 2013 (2013)
S. Siddique, M. Imran, E. Wycisk, C. Emmelmann, J. Mater. Process. Technol. 221, 205 (2015)
R.-R. Rohloff, A. Gebhardt, V. Schönherr, S. Risse, J. Kinast, S. Scheiding, T. Peschel, Proc. SPIE 7739 (2014)
F. Alshmri, Adv. Mater. Res. 383–390, 1740 (2014)
E.J. Abed, Int. J. Curr. Eng. Technol. 4(3), 1394 (2014)
O. Uzun, Turk. J. Phys. 25, 455 (2014)
E. Hilpert, S. Risse, in Proc. of MS & T, Columbus, Ohio, USA (2015)
S.N. Grigoriev, T.V. Tarasova, G.O. Gvozdeva, S. Nowotny, J. Mech. Eng. 60, 389 (2014)
S.N. Grigoriev, T.V. Tarasova, G.O. Gvozdeva, S. Nowotny, Surf. Coat. Technol. 268, 303 (2015)
B.N. Chichkov, C. Momma, S. Nolte, F. von Alvensleben, A. Tünnermann, Appl. Phys. A. 63, 109 (1996)
C. Momma, S. Nolte, B.N. Chichkov, F. von Alvensleben, A. Tünnermann, Appl. Surf. Sci. 109–110, 15 (1997)
F. Bauer, A. Michalowski, S. Nolte, JLMN J. Laser Micro Nanoeng. 10(3), 325 (2015)
R. Weber, T. Graf, P. Berger, V. Onuseit, M. Wiedenmann, C. Freitag, A. Feuer, Opt. Express 22(9), 11312 (2014)
E.G. Gamaly, A.V. Rode, B. Luther-Davies, J. Appl. Phys. 85, 4213 (1999)
S.M. Eaton, H. Zhang, P.R. Herman, F. Yoshino, L. Shah, J. Bovatsek, A.Y. Arai, Opt. Express 13(12), 4708 (2005)
S. Richter, S. Döring, A. Tünnermann, S. Nolte, Appl. Phys. A 103(2), 257 (2011)
R. Ebert, F. Ullmann, D. Hildebrandt, J. Schille, L. Hartwig, S. Kloetzer, A. Streek, H. Exner, JLMN J Laser Micro Nanoeng 7,(1) (2012)
R. Ebert, F. Ullmann, U. Loeschner, H. Exner, Proc. SPIE 8607, 86070X (2013)
B. Nie, H. Huang, S. Bai, J. Liu, Appl. Phys. A 118(1), 37 (2015)
B. Nie, L. Yang, H. Huang, S. Bai, P. Wan, J. Liu, Appl. Phys. A 119(3), 1075 (2015)
L. Kaden, G. Matthäus, T. Ullsperger, S. Nolte, in SPIE Photonics West Conference, vol. 10095, no. 7 (2017)
L. Kaden, G. Matthäus, T. Ullsperger, A. Tünnermann, S. Nolte, in WLT—Lasers in Manufacturing Conference (2017)
L. Kaden, G. Matthäus, T. Ullsperger, H. Engelhardt, M. Rettenmayr, A. Tünnermann, S. Nolte, Appl. Phys. A 123, 596 (2017)
E. Louvis, P. Fox, C.J. Sutcliffe, J. Mate. Process. Technol. 211(2), 275 (2011)
R. Le Harzic, D. Breitling, M. Weikert, S. Sommer, C. Föhl, S. Valette, C. Donnet, E. Audouard, F. Dausinger, Appl. Surf. Sci. 249(1–4), 322 (2005)
L. Gallais, D.-B. Douti, M. Commandré, G. Bataviciute, E. Pupka, M. Sciuka, L. Smalakys, V. Sirutkaitis, A. Melninkaitis, J. Appl. Phys. 177, 223103 (2015)
F. Di Niso, C. Gaudiuso, S. Sibillano, F.P. Mezzapesa, A. Ancona, P.M. Lugarà, Phys. Proc. 41, 698 (2013)
R. Tandon, J. Johnson, in ASM Handbook, Powder Metal Technologies and Applications, vol. 7 (1990), pp. 565–573 (9)
Acknowledgements
We acknowledge support by the Deutsche Institut für Luft und Raumfahrttechnik (DLR) and the German Federal Ministry for Economic Affairs and Energy (BMWi) within the project ultraLEICHT (Grant number 50EE1408) and the German Federal Ministry of Education and Research (BMBF) within the project AM-OPTICS (02P15B203). Lisa Kaden acknowledges support by TRUMPF Laser GmbH. Furthermore, we would like to thank Johannes Wilke for preparing the samples for microstructural investigations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ullsperger, T., Matthäus, G., Kaden, L. et al. Selective laser melting of hypereutectic Al-Si40-powder using ultra-short laser pulses. Appl. Phys. A 123, 798 (2017). https://doi.org/10.1007/s00339-017-1337-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00339-017-1337-z