Abstract
Starting from a classic non-local (in space) Cahn–Hilliard–Stokes model for two-phase flow in a thin heterogeneous fluid domain, we rigorously derive by mathematical homogenization a new effective mixture model consisting of a coupling of a non-local (in time) Hele-Shaw equation with a non-local (in space) Cahn–Hilliard equation. We then analyse the resulting model and prove its well-posedness. A key to the analysis is the new concept of sigma-convergence in thin heterogeneous domains allowing to pass to the homogenization limit with respect to the heterogeneities and the domain thickness simultaneously.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Statement of the Problem and the Main Results
Diffuse interface models based on a multiphase approach associated to the balance and constitutive laws and on thermodynamic principles are a useful approach to describing the evolution and interactions of different species or phases. Such models have many applications, especially in filtering (Kozicki and Kuang 1994), blood flow (Aland et al. 2014) and flow of liquid gases in fuel cells (Bazylak et al. 2008). Many models in the literature consist of a mixture of two species and are modelled as a two-phase flow coupled to a reaction–diffusion-type equation, thereby leading to coupled systems of partial differential equations of Cahn–Hilliard type, see e.g. (Jiang et al. 2015; Lowengrub et al. 2013; Wise et al. 2008; Wu and Wang 2012). The classical well-known non-local model in this context is the non-local Cahn–Hilliard–Navier–Stokes system, which reads as follows:
In (1.1), D is a bounded open smooth domain in \(\mathbb {R}^{d}\) (\( d=2,3\)), \(\varvec{u}\) is the velocity, \(\varphi \) is the order parameter (differentiating between the two fluids), \(\mu \) is the chemical potential, p is the pressure, \(\alpha \) is the viscosity of the fluid, and \(\textrm{Re}\) is the Reynolds number. If the Reynolds number is low, e.g. when the characteristic length is small, the convective term \((\varvec{u}\cdot \nabla )\varvec{u}\) can be neglected, in which case (1.1) can be well approximated by the Cahn–Hilliard–Stokes system, see for instance (Han et al. 2013, Section 2.2.3), in which a number of applications are discussed as well, for heterogeneous media in particular.
In the current work, we are interested in two-phase flow in the special case of a Hele-Shaw cell of a fluid in between two rigid parallel walls separated by a very small distance, which naturally implies flow at low Reynolds number. Moreover, the fluid phases in the Hele-Shaw cell are assumed to be mixed on the same small scale so that the problem we address is related to the study of a phase-field model for the evolution of a mixture of two incompressible immiscible fluids modelled by the non-local Cahn–Hilliard–Stokes system evolving in a highly heterogeneous Hele-Shaw cell. To be more precise, the model problem of our study is as follows.
1.1 Geometry of the Domain
We assume that the domain in \(\mathbb {R}^{d}\) (\(d=2,3\)) occupies a bounded region in between two rigid walls. More precisely, let \(\Omega \) be a bounded open Lipschitz domain in \(\mathbb {R}^{d-1}\). For \(\varepsilon >0\), we define the thin heterogeneous domain \(\Omega _{\varepsilon }\) in \(\mathbb {R} ^{d}\) by
The heterogeneity of the domain is implicit in the sense that it stems from the two fluids being mixed at lengthscale \(\varepsilon \). This is reflected in a viscosity oscillating at scale \(\varepsilon \) in a general deterministic way as well as corresponding initial conditions. The distribution function of those microstructures is therefore represented by an assumption made on the fast spatial scale \(\overline{y}=\overline{x}/\varepsilon \) covering a wide range of behaviours such as the uniform (or periodic) distribution, the almost periodic distribution and some more as described in detail later.
1.2 Statement of the Model Equations and the Main Results
In the thin layer \(\Omega _{\varepsilon }\), the flow of two-phase immiscible fluids at the micro-scale is assumed to be described by the non-local Stokes–Cahn–Hilliard system
In (1.2), \(Q_{\varepsilon }=(0,T)\times \Omega _{\varepsilon }\) (we also define \(Q=(0,T)\times \Omega \)), where \(T>0\) is a given fixed real number, and the functions J, \(a_{\varepsilon }\) (which depends on J), \(B^\varepsilon \), F, \(\varvec{u}_{0}^{\varepsilon }\), \(\varphi _{0}^{\varepsilon }\) and \( \varvec{h}\) satisfy the following hypotheses:
-
(H1)
\(J\in W_\textrm{uloc}^{1,1}(\mathbb {R}^{d})\cap \mathcal {C}([ \mathbb {R}^{d-1}\backslash \{0\}]\times \mathbb {R})\) with \(J(y)=J(-y)\), and \( a_{\varepsilon }(x)=\int _{\Omega _{\varepsilon }}J(x-z)\ \textrm{d}z\ge 0\) (\( x\in \Omega _{\varepsilon }\)) satisfies \(\varepsilon ^{-1}a_{\varepsilon }\in L^{\infty }(\Omega _{\varepsilon })\) and there exists \(\beta >0\) such that \( \beta ^{-1}\ge \varepsilon ^{-1}a_{\varepsilon }(x)\ge \beta \) for all \( x\in \Omega _{\varepsilon }\);
-
(H2)
\(F\in \mathcal {C}_{\textrm{loc}}^{2,1}(\mathbb {R})\) and there exists \((c_{i})_{0\le i\le 8}\subset \mathbb {R}\), \(1<r\le 2\) and \(q\ge \frac{1}{2}\) with \(c_{1}>\frac{k_{0}}{2}\left\| J\right\| _{L_{\textrm{ uloc}}^{1}(\mathbb {R}^{d})}\) (where \(k_{0}=k_{0}(d)>0\) is a universal constant given below in (2.2)), \(c_{0},c_{3},c_{5},c_{6}>0\), \( c_{4}\ge 0\) such that for all \(s\in \mathbb {R}\),
- (i):
-
\(F^{\prime \prime }(s)+\beta \ge c_{0}\)
- (ii):
-
\(F(s)\ge c_{1}s^{2}-c_{2}\)
- (iii):
-
\(\left| F^{\prime }(s)\right| ^{r}\le c_{3}\left| F(s)\right| +c_{4}\)
- (iv):
-
\(F^{\prime \prime }(s)+\beta \ge c_{5}\left| s\right| ^{2q}-c_{6}\);
-
(H3)
\(\varvec{u}_{0}^{\varepsilon }\in L^{2}(\Omega _{\varepsilon })^{d}\) and \(\varphi _{0}^{\varepsilon }\in L^{2}(\Omega _{\varepsilon })\) satisfy
$$\begin{aligned} \left\| \varvec{u}_{0}^{\varepsilon }\right\| _{L^{2}(\Omega _{\varepsilon })^{d}}+\left\| \varphi _{0}^{\varepsilon }\right\| _{L^{2}(\Omega _{\varepsilon })}\le c_{7}\varepsilon ^{\frac{1}{2}}\text {, \ }\int _{\Omega _{\varepsilon }}F(\varphi _{0}^{\varepsilon })\ \textrm{d} x\le c_{8}\varepsilon , \end{aligned}$$(1.3)for some positive constants \(c_{7}\) and \(c_{8}\), and further, when \( \varepsilon \rightarrow 0\),
$$\begin{aligned} \varepsilon ^{-\frac{1}{2}}\left\| \varvec{u}_{0}^{\varepsilon }- \varvec{u}^{0}\right\| _{L^{2}(\Omega _{\varepsilon })^{d}}+\varepsilon ^{-\frac{1}{2}}\left\| \varphi _{0}^{\varepsilon }-\varphi ^{0}\right\| _{L^{2}(\Omega _{\varepsilon })}\rightarrow 0, \end{aligned}$$(1.4)where \(\varvec{u}^{0}\in L^{2}(\Omega )^{d}\) and \(\varphi ^{0}\in L^{2}(\Omega )\); finally, \(\varvec{h}\) has the form
$$\begin{aligned} \varvec{h}(t,x)=(\varvec{h}_{1}(t,\overline{x}),0)\text { for a.e. } (t,x=(\overline{x},x_{d}))\in (0,T)\times \Omega \times (-1,1)\equiv Q_{1}, \end{aligned}$$(1.5)where \(\varvec{h}_{1}\in L^{2}(Q)^{d-1}\).
-
(H4)
The oscillating viscosity \(B^{\varepsilon }\) is defined by \( B^{\varepsilon }(x)=B(\overline{x},x/\varepsilon )\) (\(x\in \Omega _{\varepsilon }\)) where \(B\in \mathcal {C}(\overline{\Omega };L^{\infty }( \mathbb {R}_{y}^{d})^{d\times d})\) is a symmetric matrix satisfying
$$\begin{aligned} \alpha \left| \xi \right| ^{2}\le B(\overline{x},y)\xi \cdot \xi \le \alpha ^{-1}\left| \xi \right| ^{2}\text { for all }\xi \in \mathbb {R}^{d}\text {, }\overline{x}\in \overline{\Omega }\text { and a.e. } y\in \mathbb {R}^{d}\text {,} \end{aligned}$$with \(\alpha >0\) being a given constant independent of x, y and \(\xi \).
For the homogenization process, we will furthermore require a structural assumption on B, (H5), given at the beginning of Sect. 4.
Choosing \(\varvec{h}\) as in (1.5) is common and justified when dealing with thin domains. Indeed, as we are interested in the thin-domain limit, the forcing should be independent of the variable \(x_{d}\). Moreover, we note that, from a modelling point of view, it would be desirable to allow the viscosity to depend explicity on the order parameter (similar to Reischmann and Peter 2020, 2022), but this direct coupling would imply a nonlinearity beyond the scope of this work.
Here and henceforth, we adopt notation (1.2)\(_{i}\) to designate the ith equation of system (1.2). The same will also apply for any other system encountered in this work.
Remark 1.1
Since F is bounded from below, it is easy to see that (iii) in (H2) implies that F has polynomial growth of order \( r^{\prime }\) where \(r^{\prime }\in [2,\infty )\) is the conjugate index of r. Namely, there exist \(c_{9}>0\) and \( c_{10}\ge 0\) such that
Conditions (i) and (iv) in (H2) imply, respectively, that \(F^{\prime \prime }(s)+\varepsilon ^{-1}a_{\varepsilon }(x)\ge c_{0}\) and \( F^{\prime \prime }(s)+\varepsilon ^{-1}a_{\varepsilon }(x)\ge c_{5}\left| s\right| ^{2q}-c_{6}\) for all \(s\in \mathbb {R}\) and all \(x\in \Omega \).
Remark 1.2
(1) In Assumptions (H1) and (H2), the spaces \(L_\textrm{uloc}^{1}(\mathbb {R}^{d})\) and \(W_\textrm{uloc}^{1,1}(\mathbb {R} ^{d}) \) are defined in Section 2 together with the universal constant \(k_{0}\), which depends only on d. (2) Assumption (H1) on J generalizes the previous ones made in the literature. The common well-known assumption (see e.g. Colli et al. 2012; Frigeri and Grasselli 2012; Frigeri et al. 2016) on J stipulates that \(J\in W^{1,1}(\mathbb {R}^{d})\). In Bates and Han (2005), J is constrained as follows:
Both assumptions above imply that \(J\in W_\textrm{uloc}^{1,1}(\mathbb { R}^{d})\).
Remark 1.3
Typical well-known examples of functions J and F fulfilling assumptions (H1) and (H2) are the Landau double-well potential defined by \(F(r)=\frac{1}{4}(r^{2}-1)^{2}\) and \( J(x)=\beta _{1}\left| x\right| ^{-1}\) (if \(d=3\)) and \( J(x)=-\beta _{2}\ln \left| x\right| \) (if \(d=2\)), respectively. Here, \(\left| x\right| \) stands for the Euclidean norm of \(x\in \mathbb {R}^{d}\) and \(\beta _{1}\), \( \beta _{2}\) are positive constants.
In (1.2), the Laplace operator acts on \(\varvec{u}_{\varepsilon }=(u_{\varepsilon }^{k})_{1\le k\le d}\) in the following manner: \(\Delta \varvec{u}_{\varepsilon }=(\Delta u_{\varepsilon }^{k})_{1\le k\le d}\), so that
It is worth noticing that in (1.2)\(_{4}\) we use the factor \( 1/\varepsilon \) in front of \((a_{\varepsilon }\varphi _{\varepsilon }-J*\varphi _{\varepsilon })\) to preserve the relative size of the open set \( \Omega _{\varepsilon }=\Omega \times (-\varepsilon ,\varepsilon )\) for small \( \varepsilon \). The above-mentioned term obviously satisfies the equality
where \(J_{\varepsilon }(x)=J(\overline{x},\varepsilon x_{d})\) for \(x=( \overline{x},x_{d})\in \Omega _{1}\) and \(\widetilde{\varphi }_{\varepsilon }(t,x)=\varphi _{\varepsilon }(t,\overline{x},\varepsilon x_{d})\) for \( (t;x)\in Q_{1}\). It is at this level that the assumption \(J\in \mathcal {C}(( \mathbb {R}^{d-1}\backslash \{0\})\times \mathbb {R})\) is essential as it will be seen in Sect. 4.
Remark 1.4
Assumptions (1.3)–(1.4) on \(\varvec{u} _{0}^{\varepsilon }\) and \(\varphi _{0}^{\varepsilon }\) are relevant from the physical standpoint for if we choose \(\varvec{u} _{0}^{\varepsilon }\) to be the solution of the Stokes system
with \(\varvec{g}(x)=(\varvec{g}_{1}(\overline{x}),0)\), \(\varvec{g}_{1}\in L^{2}(\Omega )^{d-1}\), then it is a fact that \( \left\| \varvec{u}_{0}^{\varepsilon }\right\| _{H_{0}^{1}(\Omega _{\varepsilon })^{d}}\le C\varepsilon ^{1/2}\). It comes readily from the two-scale convergence for thin heterogeneous periodic media (see, e.g. Neuss-Radu and Jäger 2007) that there exists \(\varvec{u}^{0}\in L^{2}(\Omega )^{d}\) such that \(\varepsilon ^{-\frac{1}{2}}\left\| \varvec{u}_{0}^{\varepsilon }-\varvec{u}^{0}\right\| _{L^{2}(\Omega _{\varepsilon })^{d}}\rightarrow 0\) when \( \varepsilon \rightarrow 0\). The same process applies to \( \varphi _{0}^{\varepsilon }\) where we instead consider the equation
with \(g_{\varepsilon }\in L^{2}(\Omega _{\varepsilon })\) being such that \(\left\| g_{\varepsilon }\right\| _{L^{2}(\Omega _{\varepsilon })}\le C\varepsilon ^{1/2}\) for some fixed positive constant C.
System (1.2) is a non-local Cahn–Hilliard–Stokes system frequently used in describing the behaviour of multiphase fluids in Hele-Shaw cells (Della Porta et al. 2018; Frigeri and Grasselli 2012). Its local version has been investigated in Cheng and Feng (2017), see also Gurtin et al. (1996) for the derivation of the local version of (1.2), and (Han et al. 2013) for the derivation of a Cahn–Hilliard–Stokes–Darcy model obtained by coupling the Cahn–Hilliard–Stokes system and the Cahn–Hilliard–Darcy system. It is important to note that, in Gurtin et al. (1996), Han et al. (2013)), the authors considered the stationary Stokes system.
In (1.2), instead of taking the Laplace operator, we assume a general linear elliptic operator of order 2 in divergence form with non-constant viscosity \(B(\overline{x},x/\varepsilon )\) depending on the position \(x=(\overline{x},x_{d})\in \Omega _{\varepsilon }\). The distribution function of the microstructures is therefore represented by an assumption made on the fast spatial scale \(\overline{y}=\overline{x} /\varepsilon \) covering a wide range of behaviours such as the uniform (or periodic) distribution, the almost periodic distribution and the asymptotic almost periodic one. This assumption is made on the function \(\overline{y}\mapsto B( \overline{x},y)\) with \(y=(\overline{y},y_{d})\).
The scaling in (1.2)\(_{1}\) is the classic one balancing viscosity effects and leading to memory effects in the homogenized limit, see e.g. (Allaire 1992) in which, with the same scaling, the author obtained the Darcy law with memory. This suggests to envisage obtaining in the limit a coupled system consisting of a Darcy-type equation with memory effects associated to a non-local convective Cahn–Hilliard equation, thus obtaining a doubly non-local system. Therefore, to justify the latter assertion, we aim at investigating the limiting behaviour when \(\varepsilon \rightarrow 0\) of the sequence of solutions of (1.2). This will be achieved through a two-step process: (1) deriving the homogenized system by employing the sigma-convergence concept for thin heterogeneous media. At this level, we shall deal with the non-trivial passage to the limit in the non-local term; (2) analysing the resulting system in order to address its well-posedness.
The homogenization theory in thin periodic structures is now well known, see e.g. (Bhattacharya et al. 2022; Gahn et al. 2017, 2021, 2018; Neuss-Radu and Jäger 2007) for some works in this direction. On the other hand, the general deterministic homogenization theory beyond the periodic setting is in its early stage. To the best of our knowledge, the only works to date in that direction are Cardone et al. (2022), Jäger and Woukeng (2022). It is also worth noting that even in fixed or porous media, the theory of homogenization for multiphase flows is less developed. Nevertheless, we refer to Auriault et al. (1989), Banas and Mahato (2017), Bunoiu et al. (2020), Daly and Roose (2015), Hornung (1997), Schmuck et al. (2012), and Sharmin et al. (2022) in this context.
Highly heterogeneous model problem (1.2) considered in this work is stated in a thin domain, in which the heterogeneities are distributed in a general deterministic manner. Therefore, our study falls within the framework of the sigma-convergence theory for thin heterogeneous domains which has recently been introduced in Jäger and Woukeng (2022) as a generalization of two-scale convergence for thin periodic structures introduced in Neuss-Radu and Jäger (2007). The use of the sigma-convergence concept covers several important special cases. The heterogeneities may be uniformly distributed (leading to the periodic distribution and, hence, to the use of the two-scale convergence for thin domains). They may also be distributed in an almost periodic way or in an asymptotic almost periodic manner. This will be further illustrated in Sect. 7. The expected upscaled model (corresponding to the 3D \(\varepsilon \)-model) is, to the best of our knowledge, new and is stated below as one of the main results of the work.
Theorem 1.1
Assume \(d=3\). For each \(\varepsilon >0\), let \((\varvec{u} _{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon },p_{\varepsilon }) \) be the unique solution of (1.2). Then, up to a subsequence (not relabelled), \((\varvec{u}_{\varepsilon },\mu _{\varepsilon },p_{\varepsilon })_{\varepsilon >0}\) weakly \(\Sigma _{A}\)-converges (as \( \varepsilon \rightarrow 0\)) in \(L^{2}(Q_{\varepsilon })^{3}\times L^{2}(Q_{\varepsilon })\times L^{2}(Q_{\varepsilon })\) towards \((\varvec{ u}_{0},\mu _{0},p_{0})\) and \((\varphi _{\varepsilon })_{\varepsilon >0}\) strongly \(\Sigma _{A}\)-converges in \(L^{2}(Q_{\varepsilon })\) towards \( \varphi _{0}\) with \(\varphi _{0}\in L^{\infty }(0,T;H^{1}(\Omega ))\), \( \varvec{u}_{0}\in L^{2}(Q;\mathcal {B}_{A}^{1,2}(\mathbb {R} ^{2};H_{0}^{1}(I))^{3})\), \(\mu _{0}\in L^{2}(0,T;H^{1}(\Omega ))\) and \( p_{0}\in L^{2}(0,T;L_{0}^{2}(\Omega ))\). Setting
and
one has \(u_{3}=0\) and, up to the same subsequence as above, we have, as \( \varepsilon \rightarrow 0\),
Moreover, it holds that \(\overline{\varvec{u}}\in \mathcal {C}([0,T]; \mathbb {H})\), \(\varphi _{0}\in \mathcal {C}([0,T];L^{2}(\Omega ))\cap L^{2}(0,T;H^{1}(\Omega ))\), \(p_{0}\in L^{2}(0,T;H^{1}(\Omega )\cap L_{0}^{2}(\Omega ))\) and the quadruple \((\overline{\varvec{u}},\varphi _{0},\mu _{0},p_{0})\) is a weak solution of the effective 2D problem
where \(*\) stands for the convolution operator with respect to time in (1.9)\(_{1}\) and with respect to space in (1.9)\( _{4} \), and \(G=(G_{ij})_{1\le i,j\le 2}\) is a symmetric positive definite \( 2\times 2\) matrix defined by its entries \(G_{ij}(t,\overline{x})=\frac{1}{2} \int _{-1}^{1}M(\omega ^{i}(\overline{x},t,\cdot ,\zeta ))e_{j}\ \textrm{d} \zeta \) for \((t,\overline{x})\in \overline{Q}\). Here, \(\omega ^{j}=(\omega _{i}^{j})_{1\le i\le 3}\) is such that, for any fixed \(\overline{x}\in \overline{\Omega }\), \(\omega ^{j}(\overline{x},\cdot )\) is the unique solution in \(\mathcal {C}([0,T];\mathcal {B}_{A}^{2}(\mathbb {R} ^{2};L^{2}(I))^{3})\cap L^{2}(0,T;\mathcal {B}_{A}^{1,2}(\mathbb {R} ^{2};H_{0}^{1}(I))^{3})\) of the auxiliary Stokes system
\(e_{j}\) being the jth vector of the canonical basis in \(\mathbb {R}^{3}\). Furthermore, it holds that \(\omega ^{j}\in \mathcal {C}(\overline{Q};\mathcal {B}_{A}^{2}(\mathbb {R}^{2};L^{2}(I))^{3})\cap L^{2}(Q;\mathcal {B}_{A}^{1,2}( \mathbb {R}^{2};H_{0}^{1}(I))^{3})\), such that \(G\in \mathcal {C}(\overline{Q} )^{2\times 2}\). Moreover, if \(\varphi ^{0}\in L^{\infty }(\Omega )\) and \( \varvec{u}^{0}\in L^{4}(\Omega )^{2}\), then the quadruple \((\overline{ \varvec{u}},\varphi _{0},\mu _{0},p_{0})\) is the unique solution of (1.9), so that the whole sequence \((\varvec{u}_{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon },p_{\varepsilon })_{\varepsilon >0}\) converges in the sense of (1.8).
For the details of the notations and concepts used in the statement of Theorem 1.1, we refer the reader to Sect. 3.
Equation (1.9)\(_{1}\) is a non-local (in time) Hele-Shaw equation. System (1.9) is therefore an interesting alternative to the non-local Hele-Shaw–Cahn–Hilliard system as it requires the initial value for the velocity and it is also non-local in space. Furthermore, the pressure, the velocity, the order parameter and the chemical potential rely on the history of the system and there is no non-physical jump in velocity at \(t=0\). Thus, it is a doubly non-local Hele-Shaw–Cahn–Hilliard (HSCH) system and it can be used e.g. to model tumour growth as in Lowengrub et al. (2013), and Wise et al. (2008). To the best of our knowledge, this is the first time that such a model is obtained.
The mathematical/numerical analysis of the local/non-local version of (1.9) when the velocity in (1.9)\(_{1}\) has the form \(\overline{ \varvec{u}}=\varvec{h}_{1}+\mu _{0}\nabla _{\overline{x}}\varphi _{0}-\nabla _{\overline{x}}p_{0}\) has already been worked out, see e.g. (Feng and Wise 2012; Jiang et al. 2015; Lowengrub et al. 2013; Wang and Zhang 2013; Wise 2010; Wise et al. 2008; Wu and Wang 2012) when the chemical potential \(\mu _{0}\) is local, and Cavaterra et al. (2022); Della Porta and Grasselli (2016); Della Porta et al. (2018) when \(\mu _{0}\) is non-local. More precisely, the local version has been studied numerically in Wise (2010) and analytically in Feng and Wise (2012) where existence and uniqueness of weak solutions in two- or three-dimensional bounded domains were addressed. In Wang and Zhang (2013); Wu and Wang (2012), the well-posedness and long-time behaviour of strong solutions in the two- or three-dimensional torus were considered. In Lowengrub et al. (2013), a systematic analysis of the local version was performed in a 2D rectangle and in a 3D parallelepiped. In Della Porta and Grasselli (2016), it is proved that weak solutions to the non-local Cahn–Hilliard–Brinkman system converge to a weak solution of the non-local Cahn–Hilliard–Hele-Shaw system.
In the light of the results mentioned above, none of them address the case where the Hele-Shaw equation is non-local in time as it is the case in this work. Therefore, we present a systematic analysis of (1.9) in Sect. 5 and prove its well-posedness therein. To the best of our knowledge, this is the first time that this model is derived and analysed.
The second main result of the work corresponds to the 2D \(\varepsilon \) -model posed in \(\Omega _{\varepsilon }=(a,b)\times (-\varepsilon ,\varepsilon )\), and it is stated as follows.
Theorem 1.2
Assume \(d=2\) and \(\varvec{u}^{0}=0\). For each \(\varepsilon >0 \), let \((\varvec{u}_{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon },p_{\varepsilon })\) be the solution to (1.2). Then, the sequence \((\varvec{u}_{\varepsilon },\mu _{\varepsilon },p_{\varepsilon })_{\varepsilon >0}\) weakly \(\Sigma _{A}\)-converges (as \( \varepsilon \rightarrow 0\)) in \(L^{2}(Q_{\varepsilon })^{2}\times L^{2}(Q_{\varepsilon })\times L^{2}(Q_{\varepsilon })\) towards \((\varvec{ u}_{0},\mu _{0},p_{0})\) and the sequence \((\varphi _{\varepsilon })_{\varepsilon >0}\) strongly \(\Sigma _{A}\)-converges in \( L^{2}(Q_{\varepsilon })\) towards \(\varphi _{0}\) with \(\varphi _{0}\in L^{\infty }(0,T;H^{1}(\Omega ))\), \(\varvec{u}_{0}\in L^{2}(Q;\mathcal {B} _{A}^{1,2}(\mathbb {R};H_{0}^{1}(I))^{2})\), \(\mu _{0}\in L^{2}(0,T;H^{1}(\Omega ))\) and \(p_{0}\in L^{2}(0,T;L_{0}^{2}(\Omega ))\). Moreover, setting
one has \(\varvec{u}=0\), and the couple \((\varphi _{0},\mu _{0})\) is the unique solution to the 1D non-local Cahn–Hilliard equation
Furthermore, the pressure \(p_{0}\) is the unique solution of the equation
Very few works deal with the homogenization of the Cahn–Hilliard–Navier–Stokes system. We refer e.g. to Banas and Mahato (2017); Bunoiu et al. (2020); Schmuck et al. (2013). In Bunoiu et al. (2020), the authors deal with the Cahn–Hilliard–Navier–Stokes system in fixed domains, while in Banas and Mahato (2017), Schmuck et al. (2013), the authors deal with the Stokes–Cahn–Hilliard equations in periodically porous domains. It is worth pointing out the following two facts: a) the kernel J in (1.2) is assumed to be locally uniformly integrable. This widens the scope of the applications of our results although (as we will see in the next section) this does not change considerably the proof of the existence result. However, this choice affects the uniform estimates; b) the domain is thin and of a general deterministic type, so that the expected upscaled equation in (1.2)\(_{1}\) will be of Darcy type with memory effects. We also note the recent works on upscaling of the Cahn–Hilliard equation coupled with the equations of linear elasticity, the so-called Cahn–Larché system (Reischmann and Peter 2020, 2022).
1.3 Outline of the Paper
The well-posedness of (1.2) as well as the proof of the uniform estimates for the sequence of its solutions is considered in Sect. 2. We gather in Sect. 3 useful tools about the \(\Sigma \) -convergence method in thin heterogeneous media. Section 4 deals with the limit passage in (1.2) by relying on the results of the previous two sections. In Sect. 5, we prove Theorem 1.1 after a careful analysis of the solutions of the upscaled limit problem. Section 6 is devoted to the proof of Theorem 1.2. Finally, in Sect. 7, we illustrate our results for specific types of heterogeneities.
Throughout the work, C will denote a generic constant independent of \( \varepsilon >0\) which may change from line to line.
2 Existence Result and Uniform Estimates
2.1 Existence Result
We begin with the functional-analytic setup. For a Banach space X, we denote by \(\left\langle \cdot ,\cdot \right\rangle \) the duality pairing between X and its topological dual \(X^{\prime }\). We set \(\mathbb {X}=\) \( X\times \cdots \times X\), d times, and we equip \(\mathbb {X}\) with the product topology. In case X is a real Hilbert space with inner product \( (\cdot ,\cdot )_{X}\), we shall denote by \(\left\| \cdot \right\| _{X}\) the induced norm. We therefore introduce the classical Hilbert spaces for the Navier–Stokes systems with no-slip boundary condition (see e.g. Temam 2001) \(\mathbb {H}_{\varepsilon }\) and \(\mathbb {V}_{\varepsilon }\) defined as the closure of \(\{\varvec{u}\in \mathbb {C}_{0}^{\infty }( \Omega _{\varepsilon }):{{\,\textrm{div}\,}}\varvec{u}=0\) in \(\Omega _{ \varepsilon }\}\) in \(\mathbb {L}^{2}(\Omega _{\varepsilon })\) and in \(\mathbb {H} _{0}^{1}(\Omega _{\varepsilon })\), respectively. We see that \(\mathbb {V} _{\varepsilon }=\{\varvec{u}\in \mathbb {H}_{0}^{1}(\Omega _{\varepsilon }): {{\,\textrm{div}\,}}\varvec{u}=0\) in \(\Omega _{\varepsilon }\}\) and \(\mathbb {H} _{\varepsilon }=\{\varvec{u}\in \mathbb {L}^{2}(\Omega _{\varepsilon }):{{\,\textrm{div}\,}}\) \( \varvec{u}=0\) in \(\Omega _{\varepsilon }\) and \(\varvec{u}\cdot \nu =0\) on \(\partial \Omega _{\varepsilon }\}\), where \(\nu \) is the outward unit normal to \(\partial \Omega _{\varepsilon }\). The space \(\mathbb {H}_{\varepsilon }\) is endowed with the scalar product denoted by \((\cdot ,\cdot )\) whose the associated norm is denoted by \(\left\| \cdot \right\| _{\mathbb {H} _{\varepsilon }}\). The space \(\mathbb {V}_{\varepsilon }\) is equipped with the scalar product
whose associated norm is the norm of the gradient and is denoted by \( \left\| \cdot \right\| \). Owing to the Poincaré inequality, the norm in \(\mathbb {V}_{\varepsilon }\) is equivalent to the \(\mathbb {H} ^{1}(\Omega _{\varepsilon })\)-norm. We also define the space \( L_{0}^{2}(\Omega _{\varepsilon })=\{v\in L^{2}(\Omega _{\varepsilon }):\int _{\Omega _{\varepsilon }}v\ \textrm{d}x=0\}\). We denote by \(\mathbb {V}\) (resp. \(\mathbb {H}\)) the space defined as \( \mathbb {V}_{\varepsilon }\) (resp. \(\mathbb {H}_{\varepsilon }\)) when replacing \(\Omega _{\varepsilon }\) by \(\Omega \).
The Wiener amalgam \((L^{p},\ell ^{\infty })( \mathbb {R}^{d})\) (\(1\le p<\infty \))
We recall that the Wiener amalgam \((L^{p},\ell ^{\infty })(\mathbb {R}^{d})\) (Wiener 1932) (see also Bertrandias et al. 1978; Fournier and Stewart 1985) is defined as the subspace of \(L_{\textrm{loc}}^{p}(\mathbb {R}^{d})\) consisting of functions u such that
where \(B_{R}(x)\) stands for the open ball centred at x and of radius R. Functions in \((L^{p},\ell ^{\infty })(\mathbb {R}^{d})\) are called locally uniformly \(L^{p}\)-integrable, and we therefore use the notation \(L_{\textrm{ uloc}}^{p}(\mathbb {R}^{d})=(L^{p},\ell ^{\infty })(\mathbb {R}^{d})\). We endow \(L_{\textrm{uloc}}^{p}(\mathbb {R}^{d})\) with the norm
which makes it a Banach space. It is important to note that all the \( \left\| \cdot \right\| _{p,R}\) are equivalent to \(\left\| \cdot \right\| _{p,1}\), so that the former is independent of the choice of R, and is henceforth denoted by \(\left\| \cdot \right\| _{L_{\textrm{uloc} }^{p}(\mathbb {R}^{d})}\). The properties of \(L_{\textrm{uloc}}^{p}(\mathbb {R} ^{d})\) are well-known, see e.g. (Bertrandias et al. 1978, Sections 6–7). Nevertheless, let us recall one of its important properties, which will be used in what follows (see Bertrandias et al. 1978, Sections 6-7 for the proof):
-
(P)
There exists a positive constant \(k_{0}=k_{0}(d,p)\) such that for any \(f\in L_\textrm{uloc}^{1}(\mathbb {R}^{d})\) and \(g\in L^{p}(\mathbb {R} ^{d})\) (\(1\le p<\infty \)), one has \(f*g\in L_\textrm{uloc}^{p}(\mathbb {R} ^{d})\) and
$$\begin{aligned} \left\| f*g\right\| _{L_\textrm{uloc}^{p}(\mathbb {R}^{d})}\le k_{0}\left\| f\right\| _{L_\textrm{uloc}^{1}(\mathbb {R} ^{d})}\left\| g\right\| _{L^{p}(\mathbb {R}^{d})}. \end{aligned}$$(2.2)
We define the Sobolev-type space \(W_{\textrm{uloc}}^{1,p}(\mathbb {R }^{d})\) accordingly:
a Banach space with norm \(\left\| u\right\| _{W_{\textrm{uloc}}^{1,p}( \mathbb {R}^{d})}=\left[ \left\| u\right\| _{L_{\textrm{uloc}}^{p}( \mathbb {R}^{d})}^{p}+\left\| \nabla u\right\| _{L_{\textrm{uloc}}^{p}( \mathbb {R}^{d})}^{p}\right] ^{1/p}\).
We proceed with the notion of weak solutions considered in this work.
Definition 2.1
Let \(\varvec{u}_{0}^{\varepsilon }\in \mathbb {H} _{\varepsilon }\) and \(\varphi _{0}^{\varepsilon }\in L^{2}(\Omega _{\varepsilon })\) with \(F(\varphi _{0}^{\varepsilon })\in L^{1}(\Omega _{\varepsilon })\). A function \((\varvec{u} _{\varepsilon },\varphi _{\varepsilon })\) is a weak solution to (1.2) if
-
\((\varvec{u}_{\varepsilon },\varphi _{\varepsilon })\) and \(\mu _{\varepsilon }\) satisfy
-
(i)
\(\varvec{u}_{\varepsilon }\in \mathcal {C}([0,T];\mathbb {H} _{\varepsilon })\cap L^{2}(0,T;\mathbb {V}_{\varepsilon })\) with \(\partial \varvec{u}_{\varepsilon }/\partial t\in L^{2}(0,T;\mathbb {V} _{\varepsilon }^{\prime }),\)
-
(ii)
\(\varphi _{\varepsilon }\in \mathcal {C}([0,T];L^{2}(\Omega _{\varepsilon }))\cap L^{2}(0,T;H^{1}(\Omega _{\varepsilon }))\) with \(\partial \varphi _{\varepsilon }/\partial t\in L^{2}(0,T;H^{1}(\Omega _{\varepsilon })^{\prime });\)
-
(i)
-
Setting \(\rho _{\varepsilon }(x,\varphi _{\varepsilon })=\varepsilon ^{-1}a_{\varepsilon }(x)\varphi _{\varepsilon }+F^{\prime }(\varphi _{\varepsilon })\), one has, for every \(\psi \in H^{1}(\Omega _{\varepsilon })\), \(v\in \mathbb {V}_{\varepsilon }\) and for a.e. \(t\in (0,T)\) that
$$\begin{aligned}{} & {} \left\langle \frac{\partial \varvec{u}_{\varepsilon }}{\partial t},v\right\rangle +\varepsilon ^{2}\left( B^{\varepsilon }\nabla \varvec{u} _{\varepsilon },\nabla v\right) =-\int _{\Omega _{\varepsilon }}(v\cdot \nabla \mu _{\varepsilon })\varphi _{\varepsilon }\ \textrm{d}x+\int _{\Omega _{\varepsilon }}\varvec{h}(t)v\ \textrm{d}x,\\{} & {} \quad \left\langle \frac{\partial \varphi _{\varepsilon }}{\partial t},\psi \right\rangle +(\nabla \rho _{\varepsilon },\nabla \psi )=\int _{\Omega _{\varepsilon }}(\varvec{u}_{\varepsilon }\cdot \nabla \psi )\varphi _{\varepsilon }\ \textrm{d}x+\int _{\Omega _{\varepsilon }}\varepsilon ^{-1}(\nabla J*\varphi _{\varepsilon })\cdot \nabla \psi \textrm{d}x; \end{aligned}$$ -
\(\varvec{u}_{\varepsilon }(0)=\varvec{u}_{0}^{\varepsilon }\) and \(\varphi _{\varepsilon }(0)=\varphi _{0}^{\varepsilon }\).
The following result provides us with the existence and uniqueness of the solution of (1.2) in the sense of Definition 2.1.
Theorem 2.1
Assume that (H1)–(H4) are satisfied. For each \( \varepsilon >0\), there exists a unique solution \((\varvec{u} _{\varepsilon },\varphi _{\varepsilon })\) to (1.2) in the sense of Definition 2.1. Moreover, a unique \(p_{\varepsilon }\in L^{2}(0,T;L_{0}^{2}(\Omega _{\varepsilon }))\) is associated to \((\varvec{ u}_{\varepsilon },\varphi _{\varepsilon })\) such that the first equation in (1.2) is satisfied in the distributional sense.
Proof
Let \(\varepsilon >0\) be fixed. For the existence of \((\varvec{u} _{\varepsilon },\varphi _{\varepsilon })\), we observe that we may follow exactly the lines of the proof of Colli et al. (2012, Theorem 1). Let us however explain some steps where we need further developments. Looking carefully at the proof of Colli et al. (2012, Theorem 1), we notice two important facts:
-
(1)
In our model equation (1.2), we have replaced the function \( \nu (\varphi _{\varepsilon })\) (in Colli et al. (2012)) by the matrix \( \varepsilon ^{2}B^{\varepsilon }\) having coefficients depending only on x. However, the uniform ellipticity of the operator \(-{\text {div}}(\varepsilon ^{2}B^{\varepsilon }\nabla )\) provides us with suitable properties yielding the existence of the approximate solutions as in Colli et al. (2012).
-
(2)
As we assumed low Reynolds number so that the convective term \(( \varvec{u}_{\varepsilon }\cdot \nabla )\varvec{u}_{\varepsilon }\) in Colli et al. (2012) disappeared in our system (1.2), the estimates of the velocity in our case do not depend on the dimension d as in Colli et al. (2012). This being so, checking the validity of the estimates for the approximate solutions in Colli et al. (2012), we notice that estimates (4.9) and (4.10) in Colli et al. (2012) still hold under the general assumption \(J\in W_{\textrm{uloc}}^{1,1}(\mathbb {R}^{d})\) (instead of \(J\in W^{1,1}(\mathbb {R} ^{d})\) considered in Colli et al. (2012)). Indeed, we use the Young inequality for functions in \(L_{\textrm{uloc}}^{p}(\mathbb {R}^{d})\) which reads as (see (2.2)): there is \(k_{0}=k_{0}(d)>0\) such that
$$\begin{aligned} \left\| f*g\right\| _{L_{\textrm{uloc}}^{2}(\mathbb {R}^{d})}\le k_{0}\left\| f\right\| _{L_{\textrm{uloc}}^{1}(\mathbb {R} ^{d})}\left\| g\right\| _{L^{2}(\Omega _{\varepsilon })} \end{aligned}$$for all \(f\in L_{\textrm{uloc}}^{1}(\mathbb {R}^{d})\) and all \(g\in L^{2}(\Omega _{\varepsilon })\), where g is extended by 0 outside of \( \Omega _{\varepsilon }\) and where the norm \(\left\| \cdot \right\| _{L_{\textrm{uloc}}^{p}(\mathbb {R}^{d})}\) is defined by
$$\begin{aligned} \left\| f\right\| _{L_{\textrm{uloc}}^{p}(\mathbb {R}^{d})}=\sup _{x\in \mathbb {R}^{d}}\left( \int _{B_{R_{0}}(x)}\left| f\right| ^{p}\ \textrm{d}y\right) ^{\frac{1}{p}}\ \ (1\le p<\infty ), \end{aligned}$$\(B_{R_{0}}(x)\) being the open ball centred at x and of radius \(R_{0}>0\). For convenience, we choose \(R_{0}\) such that \(\Omega _{1}\subset B_{R_{0}}=B_{R_{0}}(0)\). It readily follows that
$$\begin{aligned}{} & {} \left\| J*\varphi _{\varepsilon }\right\| _{L^{2}(\Omega _{\varepsilon })}\le k_{0}\left\| J\right\| _{L_{\textrm{uloc}}^{1}( \mathbb {R}^{d})}\left\| \varphi _{\varepsilon }\right\| _{L^{2}(\Omega _{\varepsilon })} \end{aligned}$$(2.3)$$\begin{aligned}{} & {} \left\| \nabla J*\varphi _{\varepsilon }\right\| _{L^{2}(\Omega _{\varepsilon })}\le k_{0}\left\| J\right\| _{W_{\textrm{uloc}}^{1,1}( \mathbb {R}^{d})}\left\| \varphi _{\varepsilon }\right\| _{L^{2}(\Omega _{\varepsilon })}. \end{aligned}$$(2.4)We recall that \(k_{0}\) is the same as in assumption (H2), where we choose \( c_{1}>0\) such that \(c_{1}>\frac{k_{0}}{2}\left\| J\right\| _{L_{ \textrm{uloc}}^{1}(\mathbb {R}^{d})}\). We infer from (2.3) that we get the inequality (4.9) in Colli et al. (2012) with the constant \(\alpha _{0}=2c_{1}-k_{0}\left\| J\right\| _{L_{\textrm{uloc}}^{1}(\mathbb {R} ^{d})}>0\), and we obtain inequality (4.10) in Colli et al. (2012) with \( \left\| J\right\| _{W^{1,1}(\mathbb {R}^{d})}\) being replaced by \( \left\| J\right\| _{W_{\textrm{uloc}}^{1,1}(\mathbb {R}^{d})}\) (see (2.4) above). The rest of the proof is therefore copied from that of Colli et al. (2012, Theorem 1).
As for the uniqueness of the solution, Frigeri et al. (2016, Theorem 2) provides us with the uniqueness in the case when \(d=2\). For the case \(d=3\), if we come back to identity (3.4) in the proof of Frigeri et al. (2016, Theorem 2), we notice that it does not involve in our situation, the terms arising from the convective term. Now, sticking on the corresponding equality (3.4) for our case, and using the estimates corresponding to \(d=3\) in the proof of Della Porta and Grasselli (2016, Proposition 2.2), we are led to an estimate similar to estimate (3.8) in the proof of Frigeri et al. (2016, Theorem 2). This also ensures uniqueness in the case \(d=3\). Finally, the existence of a unique pressure \( p_{\varepsilon }\in L^{2}(0,T;L_{0}^{2}(\Omega _{\varepsilon }))\) follows the same lines of reasoning as in the proof of Bunoiu et al. (2020, Theorem 1). \(\square \)
2.2 Uniform Estimates
We are now concerned with some uniform estimates which will be useful in what follows. Before proceeding further, let us first notice that
We also have
where \(\widetilde{\varphi }_{\varepsilon }(t,x)=\varphi _{\varepsilon }(t, \overline{x},\varepsilon x_{d})\) for \((t,x)\in Q_{1}\). We therefore use the dilatation in the vertical variable \(x_{d}\): \(y_{d}=x_{d}/\varepsilon \), and we define the new functions \(\widetilde{\varvec{u}}_{\varepsilon }\), \( \widetilde{\mu }_{\varepsilon }\) and \(\widetilde{p}_{\varepsilon }\) accordingly (see the definition of \(\widetilde{\varphi }_{\varepsilon }\)). In particular, one has \(\widetilde{B}^{\varepsilon }(x)=B^{\varepsilon }( \overline{x},\varepsilon x_{\varepsilon })=B(\overline{x},\overline{x} /\varepsilon ,x_{d})\) for \(x\in \Omega _{1}\).
Next, we set
and we denote by \(H_{\varepsilon }^{1}(\Omega _{1})\) the space \(H^{1}(\Omega _{1})\) endowed with the \(H^{1}\)-norm, where we have replaced the usual gradient operator \(\nabla \) by \(\nabla _{\varepsilon }\):
With all this in mind, system (1.2) becomes
Let us note that, from the equality \(\left\| \widetilde{\phi }\right\| _{L^{p}(\Omega _{1})}=\varepsilon ^{-\frac{1}{p}}\left\| \phi \right\| _{L^{p}(\Omega _{\varepsilon })}\) (\(1\le p<\infty \)), we infer from (1.3) that
We shall need the following result whose proof can be found in Marusić and Marusić-Paloka (2000, Lemmas 8, 10 and Remark 5).
Lemma 2.1
It holds that
and
for any \(u\in H_{0}^{1}(\Omega _{\varepsilon })\), where \(C>0\) is independent of \(\varepsilon \).
Remark 2.1
With the notation above, (2.7) and (2.8) are equivalent to
and
for any \(u\in H_{0}^{1}(\Omega _{\varepsilon })\), where \(C>0\) is independent of \(\varepsilon \).
The following result is the starting point of the uniform estimates obtained in this subsection.
Lemma 2.2
Suppose that \((\varvec{u}_{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon })\) is a solution of (1.2). Then, the following dissipative energy equality holds:
where
Moreover, the following energy inequality holds for almost all \(t>0\):
where \(\widetilde{\varvec{u}}_{\varepsilon }(t)=\widetilde{\varvec{u}} _{\varepsilon }(t,\cdot )\) and \(\varvec{h}(t)=\varvec{h}(t,\cdot )\).
Proof
By using \(\widetilde{\varvec{u}}_{\varepsilon }\) as a test function in the first equation in (2.5), we obtain
Setting \(\rho _{\varepsilon }(\cdot ,\widetilde{\varphi }_{\varepsilon })=a_{\varepsilon }\widetilde{\varphi }_{\varepsilon }+F^{\prime }( \widetilde{\varphi }_{\varepsilon })\), the third equation of (2.5) becomes
and, using \(\widetilde{\mu }_{\varepsilon }\) as test function in (2.14 ), we obtain
where we have used the equality \(\frac{\partial \widetilde{\mu } _{\varepsilon }}{\partial \nu }=0\) on \(\partial \Omega _{1}\). On the other hand, using the expression of \(\widetilde{\mu }_{\varepsilon }\), we have
where \(\widetilde{\varphi }_{\varepsilon }(\zeta )=\widetilde{\varphi } _{\varepsilon }(t,\zeta )\) for \(\zeta =x,\xi \). Since \(\rho _{\varepsilon }(\cdot ,\widetilde{\varphi }_{\varepsilon })=\widetilde{\mu }_{\varepsilon }+J_{\varepsilon }*\widetilde{\varphi }_{\varepsilon }\), we get
Thus, substituting (2.16) and (2.17) in (2.15),
Summing up (2.13) and (2.18) yields
where we have set
Next, appealing to (H4) and integrating (2.19) over (0, t), we obtain the following energy inequality
for all \(t\in [0,T]\). \(\square \)
Proposition 2.1
Under assumptions (H1)–(H4), the weak solution \(( \varvec{u}_{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon })\) of (1.2) in the sense of Definition 2.1 satisfies the following estimates
and
where the positive constant C is independent of \(\varepsilon \).
Proof
First, since \(\varvec{h}(t,x)=(\varvec{h}_{1}(t,\overline{x}),0)\), we have
Thus, going back to (2.12) and using there the series of inequalities above, we get
where the constant C in (2.26) depends on \(\int _{0}^{T}\left\| \varvec{h}_{1}(t)\right\| _{L^{2}(\Omega )^{d-1}}^{2} \ \textrm{d}t\).
Now, using (H1), it holds that
Next, in view of (ii) in (H2), which yields \(F(\widetilde{\varphi } _{\varepsilon })\ge c_{1}\left| \widetilde{\varphi }_{\varepsilon }\right| ^{2}-c_{2}\), we get
where \(\left| \Omega _{1}\right| \) stands for the Lebesgue measure of \(\Omega _{1}\) in \(\mathbb {R}^{d}\). The Young inequality for convolution in \( L_{\textrm{uloc}}^{p}\) gives
so that
where \(\alpha _{1}=2c_{1}-k_{0}\left\| J\right\| _{L_{\textrm{uloc} }^{1}(\mathbb {R}^{d})}>0\), the last inequality of the series of inequalities above stemming from the inequality \(a_{\varepsilon }\ge 0\). Inequality (2.26) therefore gives
Next, in view of the properties of \(a_{\varepsilon }\) and \(J_{\varepsilon }\), one has
in such a way that, appealing to (1.3) (in (H3)), we get at once from (2.27) inequalities (2.21), (2.22) as well as the following ones
From the obvious inequality \(c_{3}\left| F(s)\right| +c_{4}\le c_{3}(\left| F(s)\right| +c_{4}c_{3}^{-1})^{r}\) (recall that \(r>1\)), we infer from (iii) in (H2) that \(\left| F^{\prime }(s)\right| \le C\left| F(s)\right| +C\) for every \(s\in \mathbb {R}\), so that we get (2.25) as a consequence of (2.29). Next, we deduce from (2.28) an estimate for \(\widetilde{\varphi }_{\varepsilon }\in L^{2}(0,T;H^{1}(\Omega _{1}))\). Indeed, we have
and
where we have used part (i) [in (H2)], Young inequality (2.4) and the fact that \(\nabla _{\varepsilon }J_{\varepsilon }(x)=(\nabla J)( \overline{x},\varepsilon x_{d})\). It follows that (setting \(k_{1}=1+k_{0}\))
Using
we get
It follows from (2.28) that
Putting together (2.28) and (2.30) yields
We are now concerned with the estimate of \(\widetilde{\mu }_{\varepsilon }\) in \(L^{2}(0,T;H^{1}(\Omega _{1}))\). To this end, we have
Therefore, applying the Poincaré–Wirtinger’s inequality, we obtain

where  and C is independent of \(\varepsilon \). It follows that
and C is independent of \(\varepsilon \). It follows that
from which (using (2.32) and (2.28)) we get
Inequalities (2.33) and (2.28) therefore yield
which completes the proof of the proposition. \(\square \)
As a consequence of the previous proposition, we obtain the following a priori estimates.
Corollary 2.1
Under assumptions (H1)–(H3), the weak solution \(( \varvec{u}_{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon })\) of (1.2) in the sense of Definition 2.1 satisfies the following estimates
and
where the positive constant C is independent of \(\varepsilon \).
Proof
Estimates (2.35), (2.36), (2.37), (2.38) and (2.40) follow promptly from the obvious equalities \(\left\| \widetilde{\phi }\right\| _{L^{2}(\Omega _{1})}=\varepsilon ^{-\frac{1}{2} }\left\| \phi \right\| _{L^{2}(\Omega _{\varepsilon })}\), \(\left\| \nabla _{\varepsilon }\widetilde{\phi }\right\| _{L^{2}(\Omega _{1})}=\varepsilon ^{-\frac{1}{2}}\left\| \nabla \phi \right\| _{L^{2}(\Omega _{\varepsilon })}\) and \(\left\| \widetilde{\phi } \right\| _{L^{1}(\Omega _{1})}=\varepsilon ^{-1}\left\| \phi \right\| _{L^{1}(\Omega _{\varepsilon })}\). It remains to check (2.39). To that end, let \(\varvec{v}\in \mathbb {V}_{\varepsilon }\), then
where above we have used the continuous embedding \(H^{1}(\Omega _{\varepsilon })\hookrightarrow L^{4}(\Omega _{\varepsilon })\). Indeed for \( d=3\), the continuous embedding \(H^{1}(\Omega _{\varepsilon })\hookrightarrow L^{4}(\Omega _{\varepsilon })\) follows from both the Sobolev embedding \( H^{1}(\Omega _{\varepsilon })\hookrightarrow L^{2^{*}}(\Omega _{\varepsilon })\) (where \(2^{*}=2d/(d-2)=6\)) and the embedding \( L^{6}(\Omega _{\varepsilon })\hookrightarrow L^{4}(\Omega _{\varepsilon })\) (recall that \(\Omega _{\varepsilon }\subset \Omega _{1}\) is bounded) with the embedding constants depending only on \(\Omega _{1}\); the case \(d=2\) is a classical result, the embedding constant being also independent of \( \varepsilon \). Thus,
We integrate the square of \(\sup _{\left| \left| \varvec{v} \right| \right| _{\mathbb {V}_{\varepsilon }}\le 1}\left| \left\langle \frac{\partial \varvec{u}_{\varepsilon }}{\partial t} (t),v\right\rangle \right| \) over (0, T) and deduce from (2.22), ( 2.31) and (2.34) the uniform bound
which completes the proof. \(\square \)
We need the following lemma for estimating the pressure term in (1.2)\( _{1}\) next.
Lemma 2.3
(Marusić and Marusić-Paloka 2000, Lemma 20) Let \(f\in L_{0}^{2}(\Omega _{\varepsilon })\). Then, a function \( \phi \in H_{0}^{1}(\Omega _{\varepsilon })^{d}\) can be found such that \({\text { div}}\phi =f\) in \(\Omega _{\varepsilon }\) and
where \(C>0\) is independent of \(\varepsilon \).
Proposition 2.2
Let \(p_{\varepsilon }\in L^{2}(0,T;L_{0}^{2}(\Omega _{\varepsilon }))\) satisfying (1.2)\(_{1}\). It holds that
for a positive constant C independent of \(\varepsilon \).
Proof
Based on Lemma 2.3, we consider \(\phi _{\varepsilon }\in L^{2}(0,T;H_{0}^{1}(\Omega _{\varepsilon })^{d})\) satisfying \({\text {div}}\phi _{\varepsilon }=p_{\varepsilon }\) in \(Q_{\varepsilon }\) and such that
Multiplying (1.2)\(_{1}\) by \(\phi _{\varepsilon }\) and integrating the resulting equality by parts over \(\Omega _{\varepsilon }\), we get
Taking into account (2.39), (2.43) and noticing that \( \left\| \phi _{\varepsilon }\right\| _{L^{2}(0,T;\mathbb {V} _{\varepsilon })}=\left\| \nabla \phi _{\varepsilon }\right\| _{L^{2}(Q_{\varepsilon })}\), we obtain
Next, using (2.36) and (2.43),
Also, from the definition of \(\varvec{h}\) and (2.43), we deduce that
Making use of (2.8) together with the continuous embedding \( H^{1}(\Omega _{\varepsilon })\hookrightarrow L^{4}(\Omega _{\varepsilon })\) and inequalities (2.37), (2.38) and (2.43), we get
This yields
thereby concluding the proof. \(\square \)
Now, we define the following partial mean integral of \(\varphi _{\varepsilon }\):

Using the Lebesgue theorem about differentiation under the integral sign, we have
This immediately gives \(M_{\varepsilon }\varphi _{\varepsilon }\in L^{2}(0,T;H^{1}(\Omega ))\), and we can prove the following estimate.
Proposition 2.3
Let \(M_{\varepsilon }\varphi _{\varepsilon }\) be defined by (2.24). Then, \(M_{\varepsilon }\varphi _{\varepsilon }\in L^{2}(0,T;H^{1}(\Omega ))\) with \(\partial M_{\varepsilon }\varphi _{\varepsilon }/\partial t\in L^{2}(0,T;H^{1}(\Omega )^{\prime })\), and we further have
where \(C>0\) is independent of \(\varepsilon \).
Proof
We recall that (1.2)\(_{3}\) (with the help of (1.2)\(_{2}\)) is equivalent to
With this in mind, we set, for any function v defined in \(Q_{\varepsilon }\), \(\widetilde{v}(t,\overline{x})=(M_{\varepsilon }v)(t,\overline{x})\) (\((t, \overline{x})\in Q\)). We have
Indeed, let \(v\in \mathcal {C}_{0}^{\infty }(Q)\). Then,
that is, (2.48).
We obtain from (2.37) and (2.38) that
where \(C>0\) is independent of \(\varepsilon \).
Now, for \(\phi \in H^{1}(\Omega )\), we have
Since \(\left\| \nabla _{\overline{x}}\phi \right\| _{L^{2}(\Omega _{\varepsilon })}=\sqrt{2}\varepsilon ^{\frac{1}{2}}\left\| \nabla _{ \overline{x}}\phi \right\| _{L^{2}(\Omega )}\) and by (2.7) associated to the embedding \(H^{1}(\Omega _{\varepsilon })\hookrightarrow L^{4}(\Omega _{\varepsilon })\) (with the Sobolev constant being independent of \(\varepsilon \)), we are led to
Proceeding as for \(\partial \varvec{u}_{\varepsilon }/\partial t\), we integrate the square of \(\sup _{\phi \in H^{1}(\Omega ),\left\| \phi \right\| _{H^{1}(\Omega )}\le 1}\left| \left\langle \frac{\partial \widetilde{\varphi }_{\varepsilon }}{\partial t},\phi \right\rangle \right| \) over (0, T) and take advantage of estimates (2.36) and (2.49) to obtain
where C is independent of \(\varepsilon \). \(\square \)
3 Sigma-Convergence for Thin Heterogeneous Domains
The concept of sigma-convergence relies on the notion of algebra with mean value. Before we can state it, let us first and foremost set some prerequisites about algebras with mean value.
3.1 Fundamentals of Algebras with Mean Value
We begin with the concept of algebra with mean value. Let \(\textrm{BUC}( \mathbb {R}^{N})\) denote the Banach algebra of bounded uniformly continuous real-valued functions defined on \(\mathbb {R}^{N}\). For \(u\in \textrm{BUC}( \mathbb {R}^{N})\) we set

with  , where \( B_{R}=B_{R}(0)\) and \(\left| B_{R}\right| \) denotes the Lebesgue measure of \(B_{R}\). We say that the function u has a mean value if the limit \(\lim _{R\rightarrow \infty }u_{R}\) exists in \(\mathbb {R}\). We set
, where \( B_{R}=B_{R}(0)\) and \(\left| B_{R}\right| \) denotes the Lebesgue measure of \(B_{R}\). We say that the function u has a mean value if the limit \(\lim _{R\rightarrow \infty }u_{R}\) exists in \(\mathbb {R}\). We set

Let \(u\in \textrm{BUC}(\mathbb {R}^{N})\) and assume that M(u) exists. Then
where \(u^{\varepsilon }\in \textrm{BUC}(\mathbb {R}^{N})\) is defined by \( u^{\varepsilon }(x)=u(x/\varepsilon )\) for \(x\in \mathbb {R}^{N}\). This is an easy consequence of the fact that the set of finite linear combinations of the characteristic functions of open balls in \(\mathbb {R}^{N}\) is dense in \( L^{1}(\mathbb {R}^{N})\).
This being so, a closed subalgebra A of \(\textrm{BUC}(\mathbb {R}^{N})\) is said to be an algebra with mean value (Zhikov and Krivenko 1983) (algebra wmv, in short) on \(\mathbb {R}^{N}\) if it contains the constants, is translation invariant (\( \tau _{a}u=u(\cdot +a)\in A\) for any \(u\in A\) and \(a\in \mathbb {R}^{N}\)) and any of its elements possesses a mean value in the sense of (3.1).
Let A be an algebra wmv on \(\mathbb {R}^{N}\). For any integer \(m\ge 0\), we set \(A^{m}=\{\psi \in \mathcal {C}^{m}(\mathbb {R}^{N}):D_{y}^{\alpha }\psi \in A\) \(\forall \alpha =(\alpha _{1},\ldots ,\alpha _{N})\in \mathbb {N}^{N}\) with \(\left| \alpha \right| \le m\}\) with \(D_{y}^{\alpha }\psi = \frac{\partial ^{\left| \alpha \right| }\psi }{\partial y_{1}^{\alpha _{1}}\ldots \partial y_{N}^{\alpha _{N}}}\). Then, \(A^{m}\) is a Banach space if equipped with the norm \(\left\| \left| u\right| \right\| _{m}=\sup _{\left| \alpha \right| \le m}\left\| D_{y}^{\alpha }\psi \right\| _{\infty }\), \(A^{m}\). The space \(A^{\infty }:=\cap _{m\ge 0}A^{m}=\{\psi \in \mathcal {C}^{\infty }(\mathbb {R} ^{N}):D_{y}^{\alpha }\psi \in A\) \(\forall \alpha =(\alpha _{1},\ldots ,\alpha _{N})\in \mathbb {N}^{N}\}\) is a Fréchet space under the family of norms \(\left\| \left| \cdot \right| \right\| _{m}\) (see Nguetseng 2003), and it is dense in any \(A^{m}\).
Throughout this section, we shall need the concept of vector-valued algebra wmv. To that end, let \(\textbf{F}\) be a Banach space. We denote by BUC\((\mathbb {R}^{N};\textbf{F})\) the Banach space of bounded uniformly continuous functions \(u:\mathbb {R}^{N}\rightarrow \textbf{F}\), equipped with the norm
where \(\left\| \cdot \right\| _{\textbf{F}}\) denotes the norm in \( \textbf{F}\). Let A be an algebra with mean value on \(\mathbb {R}^{N}\). We denote by \(A\otimes \textbf{F}\) the usual space of functions of the form
where \((u_{i}\otimes e_{i})(y)=u_{i}(y)e_{i}\) for \(y\in \mathbb {R}^{N}\). We define the vector-valued algebra wmv \(A(\mathbb {R}^{N};\textbf{F})\) as the closure of \(A\otimes \textbf{F}\) in BUC\((\mathbb {R}^{N};\textbf{F})\).
Now, let \(f\in A(\mathbb {R}^{N};\textbf{F})\) (integer \(N\ge 1\)). Then, defining \(\left\| f\right\| _{\textbf{F}}\) by \(\left\| f\right\| _{\textbf{F}}(y)=\left\| f(y)\right\| _{\textbf{F}}\) (\(y\in \mathbb {R} ^{N}\)), we have that \(\left\| f\right\| _{\textbf{F}}\in A\). Similarly, we can define (for \(0<p<\infty \)) the function \(\left\| f\right\| _{\textbf{F}}^{p}\), which belongs to \(\left\| f\right\| _{ \textbf{F}}^{p}\in A\). This allows us to define the Besicovitch seminorm on \( A(\mathbb {R}^{N};\textbf{F})\) as follows: for \(1\le p<\infty \), we define the Marcinkiewicz-type space \(\mathfrak {M}^{p}(\mathbb {R}^{N};\textbf{F})\) to be the vector space of functions \(u\in L_\textrm{loc}^{p}(\mathbb {R}^{N}; \textbf{F})\) such that

where \(B_{R}\) is the open ball in \(\mathbb {R}^{N}\) centred at the origin and of radius R. Under the seminorm \(\left\| \cdot \right\| _{p, \textbf{F}}\), \(\mathfrak {M}^{p}(\mathbb {R}^{N};\textbf{F})\) is a complete seminormed space with the property that \(A(\mathbb {R}^{N};\textbf{F})\subset \mathfrak {M}^{p}(\mathbb {R}^{N};\textbf{F})\) since \(\left\| u\right\| _{p,\textbf{F}}<\infty \) for any \(u\in A(\mathbb {R}^{N};\textbf{F})\). We therefore define the generalized Besicovitch space \(B_{A}^{p}(\mathbb {R}^{N}; \textbf{F})\) as the closure of \(A(\mathbb {R}^{N};\textbf{F})\) in \(\mathfrak {M }^{p}(\mathbb {R}^{N};\textbf{F})\). The following hold true (see e.g. Nguetseng et al. 2010; Sango et al. 2011):
- (i):
-
The space \(\mathcal {B}_{A}^{p}(\mathbb {R}^{N};\textbf{F} )=B_{A}^{p}(\mathbb {R}^{N};\textbf{F})/\mathcal {N}\) (where \(\mathcal {N} =\{u\in B_{A}^{p}(\mathbb {R}^{N};\textbf{F}):\left\| u\right\| _{p, \textbf{F}}=0\}\)) is a Banach space under the norm \(\left\| u+\mathcal {N} \right\| _{p,\textbf{F}}=\left\| u\right\| _{p,\textbf{F}}\) for \( u\in B_{A}^{p}(\mathbb {R}^{N};\textbf{F})\).
- (ii):
-
The mean value \(M:A(\mathbb {R}^{N};\textbf{F} )\rightarrow \textbf{F}\) extends by continuity to a continuous linear mapping (still denoted by M) on \(B_{A}^{p}(\mathbb {R}^{N};\textbf{F})\) satisfying
$$\begin{aligned} L(M(u))=M(L(u))\text { for all }L\in \textbf{F}^{\prime }\text { and }u\in B_{A}^{p}(\mathbb {R}^{N};\textbf{F}). \end{aligned}$$Moreover, for \(u\in B_{A}^{p}(\mathbb {R}^{N};\textbf{F})\), we have
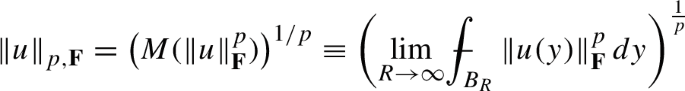
and, for \(u\in \mathcal {N}\), one has \(M(u)=0\).
It is to be noted that \(\mathcal {B}_{A}^{2}(\mathbb {R}^{N};H)\) (when \( \textbf{F}=H\) is a Hilbert space) is a Hilbert space with inner product
where \((\cdot ,\cdot )_{H}\) stands for the inner product in H and \(\left( u,v\right) _{H}\) the function \(y\mapsto \left( u(y),v(y)\right) _{H}\) from \( \mathbb {R}^{N}\) to \(\mathbb {R}\), which belongs to \(\mathcal {B}_{A}^{1}( \mathbb {R}^{N})\).
In what follows, spaces of Sobolev–Besicovitch type defined as follows are of special interest:
Equipped with the seminorm
\(B_{A}^{1,p}(\mathbb {R}^{m};\textbf{F})\) is a complete seminormed space. Its Banach counterpart is denoted by \(\mathcal {B}_{A}^{1,p}(\mathbb {R}^{m}; \textbf{F})\) and is defined by replacing \(B_{A}^{p}(\mathbb {R}^{m};\textbf{F} )\) by \(\mathcal {B}_{A}^{p}(\mathbb {R}^{m};\textbf{F})\) and \( \partial /\partial y_{i}\) by \(\overline{\partial }/\partial y_{i}\), where \( \overline{\partial }/\partial y_{i}\) is defined by
Let us denote by \(\varrho :B_{A}^{p}(\mathbb {R}^{m};\textbf{F})\rightarrow \mathcal {B}_{A}^{p}(\mathbb {R}^{m};\textbf{F})=B_{A}^{p}(\mathbb {R}^{m}; \textbf{F})/\mathcal {N}\), \(\varrho (u)=u+\mathcal {N}\), the canonical surjection. We observe that if \(u\in B_{A}^{1,p}(\mathbb {R}^{m};\textbf{F})\) then \(\varrho (u)\in \mathcal {B}_{A}^{1,p}(\mathbb {R}^{m};\textbf{F})\) and
as seen above in (3.4).
We define a further notion by restricting ourselves to the case \(\textbf{F}= \mathbb {R}\). We say that the algebra A is ergodic if any \(u\in \mathcal {B} _{A}^{1}(\mathbb {R}^{m};\mathbb {R})\) that is invariant under \((\mathcal {T} (y))_{y\in \mathbb {R}^{m}}\) is a constant in \(\mathcal {B}_{A}^{1}(\mathbb {R} ^{m};\mathbb {R})\): this amounts to, if \(\mathcal {T}(y)u=u\) in \(\mathcal {B} _{A}^{1}(\mathbb {R}^{m};\mathbb {R})\) for every \(y\in \mathbb {R}^{m}\), then \( u=c\) in \(\mathcal {B}_{A}^{1}(\mathbb {R}^{m};\mathbb {R})\) in the sense that \( \left\| u-c\right\| _{1}=0\), c being a constant.
The following corrector function space will be useful in the sequel. Let G be an open bounded subset in \(\mathbb {R}^{N}\). We define the corrector function space \(B_{\#A}^{1,p}(\mathbb {R}^{m};W^{1,p}(G))\) by
where, in this case, \(\nabla =(\nabla _{y},\nabla _{\zeta })\), \(\nabla _{y}\) (resp. \(\nabla _{\zeta }\)) being the gradient operator with respect to the variable \(y\in \mathbb {R}^{m}\) (resp. \(\zeta \in \mathbb {R}^{N}\)). We identify two elements of \(B_{\#A}^{1,p}(\mathbb {R}^{m};W^{1,p}(G))\) by their gradients in the sense that \(u=v\) in \(B_{\#A}^{1,p}(\mathbb {R} ^{m};W^{1,p}(G))\) iff \(\nabla (u-v)=0\), i.e. \(\int _{G}\left\| \nabla (u(\cdot ,\zeta )-v(\cdot ,\zeta ))\right\| _{p}^{p}\ \textrm{d} \zeta =0 \). The space \(B_{\#A}^{1,p}(\mathbb {R}^{m};W^{1,p}(G))\) is therefore a Banach space under the norm \(\left\| u\right\| _{\#,p}=\left( \int _{G}\left\| \nabla u(\cdot ,\zeta )\right\| _{p}^{p}d\zeta \right) ^{1/p}\).
3.2 Sigma-Convergence for Thin Heterogeneous Domains
Let \(d\ge 2\) be a given integer and let \(\Omega \subset \mathbb {R}^{d-1}\) be an open set, which will be assumed throughout this section to be not necessarily bounded. For \(\varepsilon >0\) a given small parameter, we define the thin domain by \(\Omega _{\varepsilon }=\Omega \times (-\varepsilon , \varepsilon )\). When \(\varepsilon \rightarrow 0\), \(\Omega _{\varepsilon }\) shrinks to the "interface" \(\Omega _{0}=\Omega \times \{0\}\). We set \( Q_{\varepsilon }=(0,T)\times \Omega _{\varepsilon }\) and \(Q=(0,T)\times \Omega _{0}\equiv (0,T)\times \Omega \) as well as \(I=(-1,1)\).
The space \(\mathbb {R}_{\xi }^{m}\) is the numerical space \(\mathbb {R}^{m}\) of generic variable \(\xi \). In this regard we set \(\mathbb {R}^{d-1}=\mathbb {R}_{ \overline{x}}^{d-1}\) or \(\mathbb {R}_{\overline{y}}^{d-1}\), where \(\overline{x }=(x_{1},...,x_{d-1})\), so that \(x\in \mathbb {R}^{d}\) can be written as \(( \overline{x},x_{d})\) or \((\overline{x},\zeta )\). We identify \(\Omega _{0}\) with \(\Omega \) so that the generic element in \(\Omega _{0}\) is also denoted by \(\overline{x} \) instead of \((\overline{x},0)\).
Let A be an algebra with mean value on \(\mathbb {R}^{d-1}\). We denote by M the mean value on A as well as its extension on the associated generalized Besicovitch spaces \(B_{A}^{p}(\mathbb {R}^{d-1};L^{p}(I))\) and \(\mathcal {B} _{A}^{p}(\mathbb {R}^{d-1};L^{p}(I))\), \(1\le p<\infty \).
Definition 3.1
A sequence \((u_{\varepsilon })_{\varepsilon >0}\subset L^{p}(Q_{\varepsilon })\) is said to
-
(i)
weakly \(\Sigma \)-converge in \(L^{p}(Q_{\varepsilon })\) to \(u_{0}\in L^{p}(Q;\mathcal {B}_{A}^{p}(\mathbb {R} ^{d-1};L^{p}(I))) \) if, as \(\varepsilon \rightarrow 0\),
$$\begin{aligned} \frac{1}{\varepsilon }\int _{Q_{\varepsilon }}u_{\varepsilon }(t,x)f\left( t, \overline{x},\frac{x}{\varepsilon }\right) \ \textrm{d}x\ \textrm{d} t\rightarrow \int _{Q}\int _{I}M(u_{0}(t,\overline{x},\cdot ,y_{d})f(t, \overline{x},\cdot ,y_{d}))\ \textrm{d}y_{d}\ \textrm{d}\overline{x}\ \textrm{ d}t \end{aligned}$$for any \(f\in L^{p^{\prime }}(Q;A(\mathbb {R}^{d-1};L^{p^{\prime }}(I)))\) (\(1/p^{\prime }=1-1/p\)); we denote this by“\( u_{\varepsilon }\rightarrow u_{0}\) in \(L^{p}(Q_{\varepsilon })\) -weak \(\Sigma _{A}\)”;
-
(ii)
strongly \(\Sigma \)-converge in \(L^{p}(Q_{ \varepsilon })\) to \(u_{0}\in L^{p}(Q;\mathcal {B}_{A}^{p}(\mathbb {R} ^{d-1};L^{p}(I)))\) if it is weakly sigma-convergent and
$$\begin{aligned} \varepsilon ^{-\frac{1}{p}}\left\| u_{\varepsilon }\right\| _{L^{p}(Q_{\varepsilon })}\rightarrow \left\| u_{0}\right\| _{L^{p}(Q; \mathcal {B}_{A}^{p}(\mathbb {R}^{d-1};L^{p}(I)))}; \end{aligned}$$(3.5)we denote this by “\(u_{\varepsilon }\rightarrow u_{0}\) in \( L^{p}(Q_{\varepsilon })\)-strong \(\Sigma _{A}\)”.
Remark 3.1
(1) It is easy to see that if \(u_{0}\in L^{p}(Q;A(\mathbb { R}^{d-1};L^{p}(I)))\) then (3.5) is equivalent to
where \(u_{0}^{\varepsilon }(t,x)=u_{0}(t,\overline{x},x/\varepsilon )\) for \((t,x)\in Q_{\varepsilon }\).
(2) In Definition 3.1, the test functions in part (i) may also be taken in the space \(\mathcal {C}(\overline{Q};B_{A}^{^{\prime }}(\mathbb {R }^{d-1};L^{p^{\prime }}(I))\cap L^{\infty }(\mathbb {R}^{d-1}\times I))\); see, e.g. Woukeng (2015).
Throughout the work, the letter E will stand for any ordinary sequence \( (\varepsilon _{n})_{n\ge 1}\) with \(0<\varepsilon _{n}\le 1\) and \(\varepsilon _{n}\rightarrow 0\) when \(n\rightarrow \infty \). The generic term of E will merely denote by \(\varepsilon \) and \(\varepsilon \rightarrow 0\) will mean \( \varepsilon _{n}\rightarrow 0\) as \(n\rightarrow \infty \).
Theorem 3.1
Any sequence \((u_{\varepsilon })_{\varepsilon \in E}\) in \( L^{p}(Q_{\varepsilon })\) \((1<p<\infty )\) satisfying
where \(C>0\) is independent of \(\varepsilon \), possesses a weakly \(\Sigma _{A}\) -convergent subsequence.
The proof of the above theorem follows the same way of proceeding as the one in Jäger and Woukeng (2022).
Remark 3.2
Theorem 3.1 generalizes its periodic counterpart in Neuss-Radu and Jäger (2007), see for instance Proposition 4.2 in Neuss-Radu and Jäger (2007), which corresponds to the special case \(A=\mathcal {C}_\textrm{per}(Y)\) (with \(Y=(0,1)^{d-1}\)) of our result here.
We gather below some important results whose proofs can be found in Cardone et al. (2022) (see also Jäger and Woukeng 2022).
Theorem 3.2
Assume that the algebra with mean value A on \(\mathbb {R}^{d-1}\) is ergodic. Let \((u_{\varepsilon })_{\varepsilon \in E}\) be a sequence in \( L^{p}(0,T;W^{1,p}(\Omega _{\varepsilon }))\) (\(1<p<\infty \)) such that
where \(C>0\) is independent of \(\varepsilon \). Then, there exist a subsequence \(E^{\prime }\) of E and a couple \((u_{0},u_{1})\) with \(u_{0}\in L^{p}(0,T;W^{1,p}(\Omega _{0}))\) and \(u_{1}\in L^{p}(Q;B_{\#A}^{1,p}(\mathbb {R }^{d-1};W^{1,p}(I)))\) such that, as \(E^{\prime }\ni \varepsilon \rightarrow 0\),
and
Remark 3.3
If we set
then (3.9) and (3.10) are equivalent to
The following result provides us with sufficient conditions for which the convergence result in (3.8) is strong.
Theorem 3.3
The assumptions are those of Theorem 3.2. Moreover, suppose that
where \(M_{\varepsilon }\) is defined by (2.28). Assume finally that \(\Omega \) is regular enough so that the embedding \(W^{1,p}(\Omega )\hookrightarrow L^{p}(\Omega )\) is compact. Let \((u_{0},u_{1})\) and \( E^{\prime }\) be as in Theorem 3.2. Then, as \( E^{\prime }\ni \varepsilon \rightarrow 0\), the conclusions of Theorem 3.2 hold and further
The next result and its corollary are proved exactly as their analogues in Sango and Woukeng (2011, Theorem 6 and Corollary 5) (see also Woukeng 2015).
Theorem 3.4
Let \(1<p,q<\infty \) and \(r\ge 1\) be such that \(1/r=1/p+1/q\le 1\). Assume \((u_{\varepsilon })_{\varepsilon \in E}\subset L^{q}(Q_{\varepsilon })\) is weakly \(\Sigma _{A}\)-convergent in \(L^{q}(Q_{\varepsilon })\) to some \( u_{0}\in L^{q}(Q;\mathcal {B}_{A}^{q}(\mathbb {R}^{d-1};L^{q}(I)))\), and \( (v_{\varepsilon })_{\varepsilon \in E}\subset L^{p}(Q_{\varepsilon })\) is strongly \(\Sigma _{A}\)-convergent in \(L^{p}(Q_{\varepsilon })\) to some \( v_{0}\in L^{p}(Q;\mathcal {B}_{A}^{p}(\mathbb {R}^{d-1};L^{p}(I)))\). Then, the sequence \((u_{\varepsilon }v_{\varepsilon })_{\varepsilon \in E}\) is weakly \( \Sigma _{A}\)-convergent in \(L^{r}(Q_{\varepsilon })\) to \(u_{0}v_{0}\).
Corollary 3.1
Let \((u_{\varepsilon })_{\varepsilon \in E}\subset L^{p}(Q_{\varepsilon })\) and \((v_{\varepsilon })_{\varepsilon \in E}\subset L^{p^{\prime }}(Q_{\varepsilon })\cap L^{\infty }(Q_{\varepsilon })\) (\( 1<p<\infty \) and \(p^{\prime }=p/(p-1)\)) be two sequences such that:
-
(i)
\(u_{\varepsilon }\rightarrow u_{0}\) in \(L^{p}(Q_{\varepsilon })\) -weak \(\Sigma _{A}\);
-
(ii)
\(v_{\varepsilon }\rightarrow v_{0}\) in \(L^{p^{\prime }}(Q_{ \varepsilon })\)-strong \(\Sigma _{A}\);
-
(iii)
\((v_{\varepsilon })_{\varepsilon \in E}\) is bounded in \(L^{\infty }(Q_{\varepsilon })\).
Then, \(u_{\varepsilon }v_{\varepsilon }\rightarrow u_{0}v_{0}\) in \( L^{p}(Q_{\varepsilon })\)-weak \(\Sigma _{A}\).
The following result will be very helpful in the next section.
Proposition 3.1
Let \((u_{\varepsilon })_{\varepsilon \in E}\) be a sequence in \( L^{p}(0,T;W^{1,p}(\Omega _{\varepsilon }))\) such that
where \(C>0\) is independent of \(\varepsilon \). Then, there exist a subsequence \(E^{\prime }\) of E and a function \(u_{0}\in L^{p}(Q;\mathcal {B}_{A}^{1,p}( \mathbb {R}^{d-1};W^{1,p}(I)))\) such that, as \(E^{\prime }\ni \varepsilon \rightarrow 0\),
and
Proof
From Theorem 3.1, we can find a subsequence \(E^{\prime }\) from E and a couple \((u_{0},u_{1})\in L^{p}(Q;\mathcal {B}_{A}^{p}(\mathbb {R} ^{d-1};L^{p}(I)))\times L^{p}(Q;\mathcal {B}_{A}^{p}(\mathbb {R} ^{d-1};L^{p}(I)))^{d}\) such that, as \(E^{\prime }\ni \varepsilon \rightarrow 0\),
Let us show that \(u_{1}=\overline{\nabla }_{y}u_{0}\). To that end, let \(\Phi \in (\mathcal {C}_{0}^{\infty }(Q)\otimes A^{\infty }(\mathbb {R}^{d-1};\mathcal {C }_{0}^{\infty }(I)))^{d}\). Then, we have
Letting \(E^{\prime }\ni \varepsilon \rightarrow 0\), we get
This shows that \(u_{1}=\overline{\nabla }_{\overline{y},\zeta }u_{0}\equiv \overline{\nabla }_{y}u_{0}\), so that \(u_{0}\in L^{p}(Q;\mathcal {B}_{A}^{1,p}( \mathbb {R}^{d-1};W^{1,p}(I)))\). \(\square \)
4 Homogenized System
For the homogenization process to be performed, we assume throughout this section and, henceforth, that A is an ergodic algebra with mean value on \( \mathbb {R}^{d-1}\) and that the matrix B satisfies the following structural assumption:
-
(H5)
\(B(\overline{x},\cdot )\in (B_{A}^{2}(\mathbb {R} ^{d-1};L^{2}(I)))^{d\times d}\) for any \(\overline{x}\in \overline{\Omega }\),
where \(B_{A}^{2}(\mathbb {R}^{d-1};L^{2}(I))\) is the vector-valued generalized Besicovitch space defined in Sect. 3.1. It is worth noticing that without such an assumption, the passage to the limit in (1.2)\(_{1}\) is out of reach, as B should be used as test function in the variational form of (1.2)\(_{1}\). It is worth noting that continuity property of B with respect to \(\overline{x}\) yields \(B\in \mathcal {C}(\overline{\Omega };(B_{A}^{2}(\mathbb {R}^{d-1};L^{2}(I)))^{d \times d})\).
4.1 Preliminary Results
The purpose of this subsection is to provide some useful results for the homogenization process. We start with the following result dealing with the non-local part of (1.2).
Proposition 4.1
Let \((v_{\varepsilon })_{\varepsilon >0}\subset L^{2}(Q_{\varepsilon })\) be a sequence such that \(v_{\varepsilon }\rightarrow v_{0}\) in \(L^{2}(Q_{\varepsilon })\)-strong \(\Sigma _{A}\) as \( \varepsilon \rightarrow 0\), where \(v_{0}\in L^{2}(Q)\). Then, as \( \varepsilon \rightarrow 0\), one has
where \(\widehat{J}(\overline{x})=J(\overline{x},0)\) for \(\overline{x}\in \mathbb {R}^{d-1}\).
Proof
A simple computation involving a change of variable gives
where \(\widetilde{v}_{\varepsilon }(t,\xi )=v_{\varepsilon }(t,\overline{\xi },\varepsilon \xi _{d})\) in \(Q_{1}\).
Setting \(U_{\varepsilon }=\varepsilon ^{-1}(J*v_{\varepsilon })\), we have that \(U_{\varepsilon }=J_{\varepsilon }*\widetilde{v}_{\varepsilon }\) in \( Q_{1}\), where \(J_{\varepsilon }(x)=J(\overline{x},\varepsilon x_{d})\) in \( \Omega _{1}\), so that
Let us look at \(I_{2}\) since \(I_{1}\) obviously tends to zero with \( \varepsilon \). First, we know that J is continuous in \((\Omega \backslash \{0\})\times [-1,1]\), so that \(J_{\varepsilon }(x)=J( \overline{x},\varepsilon x_{d})\rightarrow J(\overline{x},0)=\widehat{J}( \overline{x})\) a.e. in \(\Omega _{1}\) as \(\varepsilon \rightarrow 0\). The Lebesgue dominated convergence theorem gives immediately \(\left\| J_{\varepsilon }-\widehat{J}\right\| _{L^{1}(\Omega _{1})}\rightarrow 0\) with \(\varepsilon \). Therefore, we get \(U_{\varepsilon }\rightarrow \widehat{J} *v_{0}\) in \(L^{2}(Q_{1})\)-strong. This is easily seen to conclude the proof. \(\square \)
Now, we consider the following function spaces:
\(V=~\)the closure of \(\mathcal {V}\) in \(\mathcal {B}_{A}^{1,2}(\mathbb {R} ^{d-1};H_{0}^{1}(I))^{d}\) and \(H=\) the closure of \(\mathcal {V}\) in \(\mathcal {B}_{A}^{2}(\mathbb {R}^{d-1};L^{2}(I))^{d}\). We recall (see Cardone et al. 2022, Lemma 4.1) that \(\mathcal {B}_{A}^{1,2}(\mathbb {R}^{d-1};H_{0}^{1}(I))\) is a Hilbert space equipped with the gradient norm \(\left\| \overline{\nabla }.\right\| _{2}\), where \(\overline{\nabla }=(\frac{\overline{\partial }}{ \partial y_{1}},...,\frac{\overline{\partial }}{\partial y_{d-1}},\frac{ \partial }{\partial y_{d}})\). We also recall the definition of the Laplace and divergence operators for functions in \(\mathcal {B}_{A}^{2}(\mathbb {R} ^{d-1};L^{2}(I))\):
Obviously we have \(V=\{u\in \mathcal {B}_{A}^{1,2}(\mathbb {R} ^{d-1};H_{0}^{1}(I))^{d}:\overline{{\text {div}}}u=0\}\). We endow V and H with the relative norm topologies, say
and
where \(\overline{\nabla }\otimes u=\left( \frac{\overline{\partial }u_{i}}{ \partial y_{j}}\right) _{1\le i,j\le d}\) with \(\frac{\overline{\partial }}{ \partial y_{d}}=\frac{\partial }{\partial y_{d}}\) (the usual partial derivative in the distributional sense).
Finally, we consider the subspace \(V_{d}\) of V defined as follows
which is a closed subspace of V with the relative norm.
The following auxiliary result holds.
Proposition 4.2
Assume B satisfies (H4)–(H5). Let \((e_{j})_{1\le j\le d}\) be the canonical basis in \(\mathbb {R}^{d}\). Then, for any fixed \( \overline{x}\in \Omega \), there exists a unique \(\omega ^{j}(\overline{x},\cdot )=(\omega _{i}^{j}(\overline{x},\cdot ))_{1\le i\le d}\in \mathcal {C }([0,\infty );H)\cap L^{2}(0,\infty ;V_{d})\) for \(1\le j\le d-1\) (resp. \( \mathcal {C}([0,\infty );H)\cap L^{2}(0,\infty ;V)\) for \(j=d\)) such that the function \(\omega ^{j}(\overline{x},\cdot )\) solves the system
In addition, we have \(\omega ^{j}\in \mathcal {C}(\overline{\Omega }\times [0,\infty );H)\cap L^{2}(\Omega \times (0,\infty );V_{d})\) for \(1\le j\le d-1\) (resp. \(\mathcal {C}(\overline{\Omega }\times [0,\infty );H)\cap L^{2}(\Omega \times (0,\infty );V)\) for \(j=d\)). Moreover, if we set
then \(G_{ij}\in \mathcal {C}(\overline{Q})\) with \(G_{jd}=G_{dj}=0\) for all \( 1\le j\le d-1\), and the matrix \(G=(G_{ij})_{1\le i,j\le d-1}\) is symmetric, positive definite and has entries which decrease exponentially as t increases.
Proof
This result has been proved in Cardone et al. (2022, Section 4.1) in the case where the operator \(\overline{{\text {div}}}_{y}(B(\overline{x},\cdot )\overline{ \nabla }_{y})\) was replaced by \(\alpha \overline{\Delta }_{y}\). However, since B satisfies (H4) and (H5), the proof of the same results in Cardone et al. (2022, Section 4.1) carries over mutatis mutandis to the present setting. We also recall that the fact for the matrix \((G_{ij})_{1\le i,j\le d-1}\) to be symmetric stems from the symmetric property of the matrix B. The fact that the coefficients \(G_{ij}\) decrease exponentially in time can be shown by proceeding like in Cardone et al. (2022, Section 4.1).
It remains to check the continuity of \(\omega ^{j}\) with respect to \( \overline{x}\), that is, \(\omega ^{j}\in \mathcal {C}(\overline{\Omega }\times [0,\infty );H)\). To this end, we fix \(\overline{x}_{0}\in \overline{ \Omega }\), and we assume for a while that any element of \(\overline{\Omega }\) is denoted without the bar, say \(x,x_{0}\in \overline{\Omega }\). With this in mind, we set \(w(x)=\omega ^{j}(x,\cdot )-\omega ^{j}(x_{0},\cdot )\). Then \(w(x)\in \mathcal {C}([0,\infty );H)\cap L^{2}((0,\infty );V_{d})\) and satisfies a.e. in \(t\in (0,\infty )\) and in the sense of distributions in \( \mathbb {R}^{d-1}\times I\),
where \(\pi =\pi ^{j}(x,\cdot )-\pi ^{j}(x_{0},\cdot )\). Using a classical estimate for linear Stokes system, we get, using w(x) as test function in (4.2),
since
Therefore, the continuity of \(\omega ^{j}\) with respect to x stems from the continuity of \(x\mapsto B(x,\cdot )\). This concludes the proof. \(\square \)
We are now able to move forward in the homogenization process.
4.2 Limit Passage in (1.2)
Owing to Corollary 2.1 and Propositions 2.2 and 2.3, the following uniform estimates hold for any \(\varepsilon >0\):
where the positive constant C is independent of the small positive parameter \(\varepsilon \). Thus, in view of Theorems 3.1, 3.2 and 3.3 and Proposition 3.1, any ordinary sequence E contains a subsequence \(E^{\prime }\) of E and there exist functions \( \varvec{u}_{0}\in L^{2}(Q;\mathcal {B}_{A}^{1,2}(\mathbb {R} ^{d-1};H_{0}^{1}(I)))^{d}\), \((\varphi _{0},\varphi _{1}),(\mu _{0},\mu _{1})\in L^{2}(0,T;H^{1}(\Omega _{0}))\times L^{2}(Q;B_{\#A}^{1,2}(\mathbb {R} ^{d-1};H^{1}(I)))\) and \(p_{0}\in L^{2}(Q;\mathcal {B}_{A}^{2}(\mathbb {R} ^{d-1};L^{2}(I)))\) such that, as \(E^{\prime }\ni \varepsilon \rightarrow 0\),
where \(\nabla _{\overline{x}}\varphi _{0}=(\frac{\partial \varphi _{0}}{ \partial x_{1}},...,\frac{\partial \varphi _{0}}{\partial x_{d-1}},0)\) (the same holds for \(\nabla _{\overline{x}}\mu _{0}\)).
Now, from the equality \({\text {div}}\varvec{u}_{\varepsilon }=0\) in \( Q_{\varepsilon }\), it emerges that \(\overline{{\text {div}}}_{y}\varvec{u} _{0}=0\) in \(Q\times \mathbb {R}^{d-1}\times I\). We set
Then, \(\varvec{u}\in L^{2}(Q)^{d}\). Moreover,
where \(\varvec{n}\) is the outward unit normal to \(\partial \Omega \). Indeed, as in Cardone et al. (2022, Section 4), we may easily show that
so that \(\varvec{u}=(\overline{\varvec{u}},0)\). Therefore, we may easily verify (4.12) for, if \(\varphi \in \mathcal {D}(\overline{Q})\), we use the Stokes formula together with the equality \({\text {div}}\varvec{u }_{\varepsilon }=0\) in \(Q_{\varepsilon }\) to obtain
Passing to the limit after dividing the last equality above by \(\varepsilon \) and letting \(E^{\prime }\ni \varepsilon \rightarrow 0\), we get immediately
This yields (4.12). We also derive the equality \(\int _{\Omega _{0}} \int _{I}M(p_{0}(t,\overline{x},\cdot ,\zeta ))\ \textrm{d}\zeta \ \textrm{d} \overline{x}=0\) from the obvious one \(\int _{\Omega _{\varepsilon }}p_{ \varepsilon }\ \textrm{d}x=0\).
Now we define the function
We may therefore state the following global homogenized result.
Proposition 4.3
The functions \(\varvec{u}_{0},\varphi _{0},\varphi _{1},\mu _{0},\mu _{1}\) and \(p_{0}\) solve system (4.15)–(4.18) below:
for all \(\Psi \in (\mathcal {C}_{0}^{\infty }(Q)\otimes A^{\infty }(\mathbb {R} ^{d-1};\mathcal {C}_{0}^{\infty }(I)))^{d}\) with \({\text {div}}_{y}\Psi =0\), \( (\phi _{0},\phi _{1})\in \mathcal {C}_{0}^{\infty }(Q)\times (\mathcal {C} _{0}^{\infty }(Q)\otimes A^{\infty }(\mathbb {R}^{d-1};\mathcal {C} _{0}^{\infty }(I)))\) and \(\chi _{0}\in \mathcal {C}_{0}^{\infty }(Q)\).
Proof
Let \(\Psi \in (\mathcal {C}_{0}^{\infty }(Q)\otimes A^{\infty }(\mathbb {R} ^{d-1};\mathcal {C}_{0}^{\infty }(I)))^{d}\), \((\phi _{0},\phi _{1})\in \mathcal {C}_{0}^{\infty }(Q)\times (\mathcal {C}_{0}^{\infty }(Q)\otimes A^{\infty }(\mathbb {R}^{d-1};\mathcal {C}_{0}^{\infty }(I)))\) and \(\chi _{0}\in \mathcal {C}_{0}^{\infty }(Q)\). We define, for \((t,x)\in Q_{\varepsilon }\),
Taking \((\Psi ^{\varepsilon },\phi _{\varepsilon },\chi _{0})\in \mathcal {C} _{0}^{\infty }(Q_{\varepsilon })^{d}\times \mathcal {C}_{0}^{\infty }(Q_{\varepsilon })\times \mathcal {C}_{0}^{\infty }(Q)\) as test function in the variational form of (1.2), we obtain
We start with (4.19) and let \(E^{\prime }\ni \varepsilon \rightarrow 0\). Then,
This shows that \(p_{0}\) does not depend on y, i.e. \(p_{0}(t,\overline{x},y)=p_{0}(t,\overline{x})\), and thus \(\int _{\Omega _{0}}p_{0}(t,\overline{x} )\ \textrm{d}\overline{x}=0\), so that \(p_{0}\in L^{2}(0,T;L_{0}^{2}(\Omega ))\).
Now, we consider \(\Psi \) such that \({\text {div}}_{y}\Psi =0\), and we divide both sides of (4.19) by \(\varepsilon \):
We need to pass to the limit in (4.22) as \(E^{\prime }\ni \varepsilon \rightarrow 0\). First of all, we observe that the symmetric property of B gives
Next, we have
Now, from assumptions (H4) and (H5), we see that the matrix B belongs to the space \(\mathcal {C}(\overline{\Omega };(B_{A}^{2}(\mathbb {R} ^{d-1};L^{2}(I))\cap L^{\infty }(\mathbb {R}^{d-1}\times I))^{d\times d})\), so that \(B\nabla _{y}\Psi \) can be taken as test function in (4.23) while letting \(E^{\prime }\ni \varepsilon \rightarrow 0\). Bearing this in mind, we pass to the limit as \(E^{\prime }\ni \varepsilon \rightarrow 0\) in (4.23) using \(B\nabla _{y}\Psi \) as test function, and in (4.24 ) using strong \(\Sigma _{A}\)-convergence (4.7) in conjunction with weak \(\Sigma _{A}\)-convergence (4.10) (both in Corollary 3.1 ) to obtain
and
Hence, we let \(E^{\prime }\ni \varepsilon \rightarrow 0\) in (4.22) and divide both members of the resulting limit by 2 to get (4.15), viz.
As for (4.20), we divide both sides by \(2\varepsilon \) and, accounting for the equality
we obtain in the limit when \(E^{\prime }\ni \varepsilon \rightarrow 0\) (4.16).
Let us now consider (4.21). We start with the term \( \int _{Q_{\varepsilon }}F^{\prime }(\varphi _{\varepsilon })\chi _{0}\ \textrm{d}x\ \textrm{d}t\). We need to check that
First of all, since \(F\in \mathcal {C}_{loc}^{2,1}(\mathbb {R})\), \(F^{\prime }\) is locally Lipschitz continuous. Next, from (4.7), we have \( \varepsilon ^{-\frac{1}{2}}\left\| \varphi _{\varepsilon }-\varphi _{0}\right\| _{L^{2}(Q_{\varepsilon })}\rightarrow 0\) as \(E^{\prime }\ni \varepsilon \rightarrow 0\). But
This shows that the sequence \((\widetilde{\varphi }_{\varepsilon })_{\varepsilon \in E^{\prime }}\) defined by \(\widetilde{\varphi } _{\varepsilon }(t,x)=\varphi _{\varepsilon }(t,\overline{x},\varepsilon x_{d})\) (\((t,x)\in Q_{1}\)) converges strongly to \(\varphi _{0}\) in \( L^{2}(Q_{1})\), and, so, \(\widetilde{\varphi }_{\varepsilon }\rightarrow \varphi _{0}\) a.e.in \(Q_{1}\). The continuity of \(F^{\prime }\) entails \( F^{\prime }(\widetilde{\varphi }_{\varepsilon })\rightarrow F^{\prime }(\varphi _{0})\) a.e. in \(Q_{1}\). Now, the uniform bound \(\left\| F^{\prime }(\varphi _{\varepsilon })\right\| _{L^{1}(Q_{\varepsilon })}\le C\varepsilon \) yields \(\left\| F^{\prime }(\widetilde{\varphi } _{\varepsilon })\right\| _{L^{1}(Q_{1})}\le C\) for all \(\varepsilon >0\). The Lebesgue dominated convergence theorem readily gives
Thus, setting \(x_{d}=\zeta \), we have, as \(E^{\prime }\ni \varepsilon \rightarrow 0\),
which proves (4.26).
Now, concerning the others terms, we appeal to Proposition 4.1 to obtain, when \(E^{\prime }\ni \varepsilon \rightarrow 0\),
since none of the terms involved depends on the microscopic variable \( y=x/\varepsilon \).
With this in mind, we divide both terms involved in (4.21) by \( 2\varepsilon \) and we pass to the limit in the resulting equation to obtain (4.17). Finally, since \(\varvec{u}_{0}^{\varepsilon }\rightarrow \varvec{u}^{0}\) in \(L^{2}(\Omega _{\varepsilon })^{d}\)-strong \(\Sigma _{A}\) and \(\varphi _{0}^{\varepsilon }\rightarrow \varphi ^{0}\) in \(L^{2}(\Omega _{\varepsilon })\)-strong \(\Sigma _{A}\), we conclude by integration by parts that \(\varvec{u}_{0}(0)=\varvec{u}^{0}\) and \(\varphi _{0}(0)= \varphi ^{0}\). We recall that, from (4.13), we have \(\varvec{u} ^{0}=(\overline{\varvec{u}}^{0},0)\) since the last component \(u_{d}\) of \(\varvec{u}_{0}\) is zero. \(\square \)
4.3 Derivation of the Homogenized System
Our goal in this subsection is to find the equivalent problem that is solved by \((\overline{\varvec{u}},\varphi _{0},\mu _{0},p_{0})\). We recall that \( \overline{\varvec{u}}\) is defined by (4.11) and satisfies (4.12). This being so, we first consider (4.17). Since none of the terms in (4.17) depends on the variable \(\zeta \), we readily get that (4.17) is equivalent to
Next, we consider (4.16) and choose there \(\phi _{0}=0\) and take \(\phi _{1}\) to be of the form \(\phi _{1}(t,\overline{x},y)=\phi _{1}^{0}(t, \overline{x})\theta (y)\) with \(\phi _{1}^{0}\in A^{\infty }(\mathbb {R}^{d-1}; \mathcal {C}_{0}^{\infty }(I))\). Then, we obtain
However,
Therefore, (4.28) becomes
Since \(\mu _{0}\) is independent of y, we can easily show that \(\mu _{1}=0\).
Taking into account the equality \({\text {div}}_{\overline{x}}\varvec{u} _{0}=0\), we see that (4.16) (in which we take \(\phi _{1}=0\)) is the variational form of
where once again we recall that \(\overline{\varvec{u}}\) is defined by (4.11).
Let us move on to (4.15). Using Cardone et al. (2022, Proposition 2.1), we derive the existence of \(p_{1}\in L^{2}(Q;\mathcal {B}_{A}^{2}(\mathbb {R} ^{d-1};L^{2}(I)))\) such that
At this level, let \(\omega ^{j}=(\omega _{i}^{j})_{1\le i\le d}\) and \( G=(G_{ij})_{1\le i,j\le d-1}\) be as in Proposition 4.2. It is known from that proposition that G is a \((d-1)\times (d-1)\) symmetric positive definite matrix. This being so, let us fix \((t,\overline{x})\in Q\) and take \( v(\tau ,y)=\varvec{u}_{0}(t-\tau ,\overline{x},y)\) (\((\tau ,y)\in (0,t)\times \mathbb {R}^{d-1}\times I\)) as test function in the weak form of (4.1), i.e.
which amounts to
Integrating (4.31) over (0, t) gives
where the brackets \(\left\langle \cdot ,\cdot \right\rangle \) denote the duality pairings between \(\left[ \mathcal {B}_{A}^{1,2}(\mathbb {R} ^{d-1};H_{0}^{1}(I))^{d}\right] ^{\prime }\) and \(\mathcal {B}_{A}^{1,2}( \mathbb {R}^{d-1};H_{0}^{1}(I))^{d}\).
Next, we multiply the variational form of (4.30) by the function
and then integrate the resulting equality over (0, t), we obtain the following equality in the sense of distributions in \(\Omega \):
From the obvious equality
and comparing (4.32) and (4.33), we get
that is,
or, equivalently,
where \(G=(G_{j})_{1\le j\le d-1}\).
We have just proved the following result.
Theorem 4.1
The quadruple \((\overline{\varvec{u}},\varphi _{0},\mu _{0},p_{0})\) defined by (4.11), (4.7), (4.9) and (4.6) solves in the weak sense homogenized system (4.34), (4.29), (4.27) with appropriate boundary and initial conditions, viz.
Equation (4.35)\(_{1}\) is a Hele-Shaw equation with memory, that is, a non-local (in time) Hele-Shaw equation. Thus, system (4.35) is a doubly non-local Hele-Shaw–Cahn–Hilliard (HSCH) system arising from transient flow through thin domains, and modelling in particular tumour growth. To the best of our knowledge, this is the first time that such a system is obtained in the literature. For this reason, a qualitative analysis of (4.35) is necessary in order to prove some regularity results and its well-posedness. This is the aim of the next section.
5 Analysis of the 2D Homogenized System and Proof of Theorem1.1
Throughout this section we assume that \(\Omega \) is a Lipschitz bounded domain in \(\mathbb {R}^{2}\). For \(\psi \in (H^{1}(\Omega ))^{\prime }\) we set \( \overline{\psi }=\left| \Omega \right| ^{-1}\left\langle \psi ,1\right\rangle \). If in particular \(\psi \in L^{2}(\Omega )\), then  . With this in mind, we define the spaces \(V_{0}=\{v\in H^{1}(\Omega ):\overline{v}=0\}\) and \(V_{2}=\{v\in H^{2}(\Omega ):\partial v/\partial n=0\) on \(\partial \Omega \}\). It is well-known that the unbounded operator \(-\Delta :L^{2}(\Omega )\rightarrow L^{2}(\Omega )\) with dense domain \( V_{2}\) is self-adjoint and nonnegative, becoming strictly positive on \(V_{0}\). Further, it maps \(V_{0}\) onto \(V_{0}^{\prime }=\{\psi \in H^{1}(\Omega ): \overline{\psi }=0\}\).
. With this in mind, we define the spaces \(V_{0}=\{v\in H^{1}(\Omega ):\overline{v}=0\}\) and \(V_{2}=\{v\in H^{2}(\Omega ):\partial v/\partial n=0\) on \(\partial \Omega \}\). It is well-known that the unbounded operator \(-\Delta :L^{2}(\Omega )\rightarrow L^{2}(\Omega )\) with dense domain \( V_{2}\) is self-adjoint and nonnegative, becoming strictly positive on \(V_{0}\). Further, it maps \(V_{0}\) onto \(V_{0}^{\prime }=\{\psi \in H^{1}(\Omega ): \overline{\psi }=0\}\).
This being so, we set, for every \(r\in \mathbb {R}\),
We observe as in Della Porta and Grasselli (2016) that the norm \(\left\| \cdot \right\| _{\#}\) defined by
is equivalent to the usual norm of \((H^{1}(\Omega ))^{\prime }\).
Bearing this in mind, we recall that in this section we are concerned with 2D doubly non-local HSCH system (4.35) derived from the upscaling of \(\varepsilon \)-model (1.2) in 3D. For the sake of simplicity, we rewrite (4.35) in the following form
where we have omitted all the subscripts and the hat and bar on all the unknown functions as well as on the given data. We recall that in (5.2 ) the functions a and J are constrained as follows,
- (H1)\(_{1}\):
-
\(J\in W_{\textrm{uloc}}^{1,1}(\mathbb {R}^{2})\cap \mathcal {C }(\mathbb {R}^{2}\backslash \{0\})\) and \(a(x)=\int _{\Omega }J(x-z)\ \textrm{d} z\ge 0\) (\(x\in \Omega \)),
the function F satisfies (H2) (see Sect. 1.2) and the initial data \(\varvec{u}^{0}\), \(\varphi ^{0}\) and the source term \(\varvec{h}\) are constrained by
- (H3)\(_{1}\):
-
\(\varvec{u}^{0}\in \mathbb {H}=\{\varvec{u}\in L^{2}(\Omega )^{2}:{{\,\textrm{div}\,}}\) \(\varvec{u}=0\) in \(\Omega \) and \(\varvec{u} \cdot \varvec{n}=0\) on \(\partial \Omega \}\), where \(\varvec{n}\) is the outward unit normal to \(\partial \Omega \), \(\varphi ^{0}\in L^{2}(\Omega )\) with \(F(\varphi )\in L^{1}(\Omega )\) and \(\varvec{h}\in L^{2}(Q)^{2}\).
Under assumptions (H1)\(_{1}\), (H2) and (H3)\(_{1}\), we have proved in Sect. 4 that problem (5.2) admits at least a solution \((\varvec{ u},\varphi ,\mu ,p)\) in the class \(L^{2}(0,T;\mathbb {H})\times [\mathcal {C }([0,T];L^{2}(\Omega ))\cap L^{2}(0,T;H^{1}(\Omega ))]\times L^{2}(0,T;H^{1}(\Omega ))\times L^{2}(0,T;L_{0}^{2}(\Omega ))\). Moreover, in the light of (5.2)\(_{1}\), one sees that \(\varvec{u}\in \mathcal {C} ([0,T];\mathbb {H})\).
Finally, when dealing with (5.2), we shall often use the notation \( *_{t}\) (resp. \(*_{x}\)) to denote the convolution operator with respect to time (resp. space) if there is a danger of confusion.
5.1 Continuous Dependence of the Solutions on the Data
Our aim in this subsection is to prove the continuous dependence of the solution to (5.2) on the given data. Before we can do this, we first need an important preliminary result, which is stated as follows.
Proposition 5.1
(i) The pressure p lies in the space \( L^{2}(0,T;H^{1}(\Omega )\cap L_{0}^{2}(\Omega ))\).
(ii) Assume \(\varphi ^{0}\in L^{\infty }(\Omega )\). Then, the order parameter \(\varphi \) belongs to \(L^{\infty }(Q)\). If further \( \varvec{u}^{0}\in L^{s}(\Omega )^{2}\) and \(\varvec{h}\in L^{\infty }(0,T;L^{s}(\Omega )^{2})\) (for a fixed given real number \(s>1\)) then \( \varvec{u}\in \mathcal {C}([0,T];L^{s}(\Omega )^{2})\).
Proof
(i) First we show that \(\mu \nabla \varphi \in L^{2}(0,T;\mathbb {H})\). To this end, we observe that \(\varphi \in L^{4}(Q)\) as from the Gagliardo–Nirenberg inequality (in 2D), say \(\left\| \varphi \right\| _{L^{4}(\Omega )}^{2}\le \left\| \varphi \right\| _{L^{2}(\Omega )}\left\| \nabla \varphi \right\| _{L^{2}(\Omega )}\), and taking into account \(\varphi \in L^{\infty }(0,T;L^{2}(\Omega ))\), it follows that
Now, let \(\textbf{v}\in L^{2}(0,T;\mathbb {H})\) (we may start with smooth \( \textbf{v}\in V_{{\text {div}}_{\overline{x}}}=\{\textbf{v}\in \mathcal {C} _{0}^{\infty }(\Omega )^{2}:{\text {div}}\textbf{v}=0\}\) and next use the density of \(V_{{\text {div}}_{\overline{x}}}\) in \(\mathbb {H}\)). From the obvious equality (stemming from Frigeri et al. 2016, Proof of Theorem 2)
we get, for a.e. \(t\in (0,T)\),
so that using Hölder’s inequality,
We obtain immediately
amounting to \(\mu \nabla \varphi \in L^{2}(0,T;\mathbb {H})\).
We get readily that \(\varvec{h}+\mu \nabla \varphi \in L^{2}(0,T;L^{2}(\Omega )^{2})\). Also \(G(t)\varvec{u}^{0}\in L^{2}(0,T;L^{2}(\Omega )^{2})\). We may therefore proceed as in Mikelić (1994) by using the Laplace transform, which is well-defined in \(\mathcal {D} _{+}^{\prime }((0,\infty );L_{0}^{2}(\Omega ))\) (see for instance Vladimirov 1984, pp. 158–170): we apply it to (5.2)\(_{1}\) and (5.2)\(_{2}\) to obtain the following equation
In (5.4) the hat \(\widehat{\cdot }\) denotes the Laplace transform which is a function of variable \(\tau \in \mathbb {C}\) (the complex field). It is worth recalling that \(\widehat{G}\) is an analytic function of \(\tau \) for \(\textrm{Re}\tau >0\). Also, as G is a symmetric positive definite \( (d-1)\times (d-1)\) matrix, so is \(\widehat{G}(\tau )\). Next, as for each \( \tau \in \mathbb {C}\) with \(\textrm{Re}\tau >0\), the functions \(\widehat{G} (\tau )(\widehat{\varvec{h}}+\widehat{\mu \nabla \varphi })(\tau )\) and \( \widehat{G}(\tau )\varvec{u}^{0}\) belong to \(L^{2}(\Omega )^{2}\), we infer that (5.4) possesses a unique solution \(\widehat{p}(\tau )\in H^{1}(\Omega )\) for such \(\tau \). Therefore, \(p\in L^{2}(0,T;H^{1}(\Omega )\cap L_{0}^{2}(\Omega ))\).
(ii) Assume \(\varphi ^{0}\in L^{\infty }(\Omega )\). Then, proving that \(\varphi \in L^{\infty }(Q)\) uses Alikakos’ iteration method Alikakos (1979), which has been applied in Frigeri et al. (2015, Proof of Theorem 3) to prove a result very similar to the one in this proposition. We recall that this method, originated from Alikakos (1979, Proof of Theorem 2), relies on a Moser-type iteration.
Let us now move on to the proof of the last part of (ii). For this to be achieved, we use an equivalent reformulation of Eq. (5.2)\(_{1}\), where we use equality (5.3) to get
where the extra pressure is given by \(\widetilde{p}=p-(F(\varphi )+a\frac{ \varphi ^{2}}{2})\). Therefore, for each \(v\in \mathbb {H}\) and a.e. \(t\in (0,T)\),
This gives us the following equivalent form of \(\varvec{u}\):
This being so, we set
Then, (5.2)\(_{2}\) amounts to
with the compatibility condition \(\int _{\Omega }\widetilde{q}=0\). This being so, let \(1<s<\infty \) be fixed. Using the \(L^{s}\) estimate of the gradient of the solutions to (5.6), one gets
This gives
Now, since \(\varphi \in L^{\infty }(Q)\) and \(\nabla J\in L_{\textrm{uloc}}^{1}( \mathbb {R}^{2})^{2}\), we get readily from the assumptions \(\varvec{u} ^{0}\in L^{s}(\Omega )^{2}\) and \(\varvec{h}\in L^{\infty }(0,T;L^{s}(\Omega )^{2})\) that \(\varvec{u}\in \mathcal {C} ([0,T];L^{s}(\Omega )^{2})\). This concludes the proof. \(\square \)
We are now able to prove the main result of this subsection.
Theorem 5.1
Assume \(\varphi ^{0}\in L^{\infty }(\Omega )\), \(\varvec{u} ^{0}\in L^{4}(\Omega )^{2}\) and \(\varvec{h}\in L^{\infty }(0,T;L^{4}(\Omega )^{2})\). Let \((\varvec{u}_{1},\varphi _{1})\) and \((\varvec{u}_{2},\varphi _{2})\) be two weak solutions of (5.2) corresponding to initial values \((\varvec{u}_{1}^{0}, \varphi _{1}^{0})\) and \((\varvec{u}_{2}^{0},\varphi _{2}^{0})\), respectively. Then, there exists a positive constant C depending on the norms of the two solutions such that, for all \(t\in [0,T]\),
In particular, the solution of (5.2) is unique.
Proof
We proceed as in (5.3) to rewrite (5.2) in the form
With this in mind, let \((\varvec{u}_{1},\varphi _{1})\) and \((\varvec{u }_{2},\varphi _{2})\) be as in the theorem. We set \(\varvec{u}=\varvec{ u}_{1}-\varvec{u}_{2}\), \(\varphi =\varphi _{1}-\varphi _{2}\), \( \mu =\mu _{1}-\mu _{2}\) and \(\widetilde{p}=\widetilde{p}_{1}-\widetilde{p}_{2}\). Then, \(\varphi (0)=\varphi _{1}^{0}-\varphi _{2}^{0}\equiv \varphi ^{0}\) and \( \varvec{u}(0)=\varvec{u}_{1}^{0}-\varvec{u}_{2}^{0}\equiv \varvec{u}^{0}\). Then, it is a fact that \((\varvec{u},\varphi ,\mu , \widetilde{p})\) satisfies
The variational form of (5.9) reads, for a.e. \(t\in (0,T)\), as
where we use the fact that \((G*_{t}\nabla \widetilde{p},v)=-(G*_{t} \widetilde{p},{\text {div}}v)=0\).
If we take \(\psi =1\) in (5.10), then we see that \(\overline{\varphi } (t)=\varphi ^{0}\) for all \(t\in [0,T]\). With this in mind, we take \( \psi =(-\Delta )^{-1}(\varphi -\overline{\varphi })\) in (5.10) to get
that is,
In (5.11), we choose \(v=\varvec{u}\). Then,
We first notice that
and
It follows from (5.13) that
But
so that
Repeating the same process as to obtain (5.15) for some other terms in (5.14), we get
or, equivalently,
where the constant C in (5.16) depends on the norms of \(\varphi _{i}\), J and a.
Now, coming back to (5.12), we have
and
Next, using part (i) [of assumption (H2)], we see that
For the first term on the right-hand side of (5.12), we have
where we have combined Hölder’s and Young’s inequalities.
Next, as for \(\left| \Omega \right| \overline{\varphi }\overline{\mu }\), we know that \(\left| \Omega \right| \left| \overline{\mu } \right| =\left| \int _{\Omega }(F^{\prime }(\varphi _{1})-F^{\prime }(\varphi _{2}))\ \textrm{d}x\right| \), so that, appealing to the inequality \(\left| F^{\prime }(s)\right| \le C(\left| F(s)\right| +1)\), we find
Recalling (2.26), we see that
Owing to (1.4) (which amounts to \(\left\| \widetilde{\varvec{u}} _{0}^{\varepsilon }-\varvec{u}^{0}\right\| _{L^{2}(\Omega _{1})^{d}}+\left\| \widetilde{\varphi }_{0}^{\varepsilon }- \varphi ^{0}\right\| _{L^{2}(\Omega _{1})}\rightarrow 0\) as \( \varepsilon \rightarrow 0\)), we take the \(\liminf _{E^{\prime }\ni \varepsilon \rightarrow 0}\) in (5.20) to get
This shows that
Collecting (5.17)–(5.21) in (5.12) yields
It follows promptly
Applying Gronwall’s lemma, we get readily
The last inequality above gives rise to
that is, for all \(t\in [0,T]\),
Now, integrating (5.16) over (0, t) for any fixed \(t\in [0,T]\) and using (5.23), we get (5.7), concluding the proof of the theorem. \(\square \)
We are now in a position to prove Theorem 1.1.
5.2 Proof of Theorem 1.1
Proof
Given an ordinary sequence E of positive real numbers converging to zero, we have derived the existence of a subsequence \(E^{\prime }\) from E and of a quadruple \((\varvec{u}_{0},\varphi _{0},\mu _{0},p_{0})\) with \( \varvec{u}_{0}\in L^{2}(Q;\mathcal {B}_{A}^{1,2}(\mathbb {R} ^{2};H_{0}^{1}(I))^{3})\), \(\varphi _{0}\in L^{\infty }(0,T;H^{1}(\Omega ))\), \(\mu _{0}\in L^{2}(0,T;H^{1}(\Omega ))\) and \(p_{0}\in L^{2}(0,T;L_{0}^{2}(\Omega ))\) such that, as \(E^{\prime }\ni \varepsilon \rightarrow 0\),
and
By setting \(\varvec{u}(t,\overline{x})=\frac{1}{2}\int _{I}M(\varvec{u }_{0}(t,\overline{x},\cdot ,\zeta ))\ \textrm{d}\zeta =(\overline{ \varvec{u}}(t,\overline{x}),u_{d}(t,\overline{x}))\), we have shown that \( u_{d}=0\) and that the quadruple \((\overline{\varvec{u}},\varphi _{0},\mu _{0},p_{0})\) solves system (1.9). Furthermore we have \(\overline{ \varvec{u}}\in \mathcal {C}([0,T];\mathbb {H})\), \(\varphi _{0}\in L^{4}(0,T;L^{4}(\Omega ))\) and \(p_{0}\in L^{2}(0,T;H^{1}(\Omega )\cap L_{0}^{2}(\Omega ))\). Next, assuming that \(\varphi ^{0}\in L^{\infty }(\Omega )\), we get that \(\varphi _{0}\in L^{\infty }(Q)\) so that, if further \(\varvec{u}^{0}\in L^{4}(\Omega )^{2}\), the solution of (5.2) is unique thanks to Theorem 5.1. As a result, the whole sequence \((\varvec{u}_{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon },p_{\varepsilon })\) converges in the sense of (1.8) towards the unique solution of (1.9). The theorem is therefore proved. \(\square \)
6 Proof of Theorem 1.2
Proof
The existence of \((\varvec{u}_{0},\varphi _{0},\mu _{0},p_{0})\) is obtained as at the beginning of the proof of Theorem 1.1. So we focus on system (4.35), which reads in the special case \(d-1=1\) as follows:
We note that we have assumed \(\varvec{u}^{0}=0\). From the equality \( \dfrac{\partial \overline{\varvec{u}}}{\partial x_{1}}=0\) in Q, we deduce that \(\overline{\varvec{u}}(t,x_{1})=\overline{\varvec{u}}(t)\) for all \(t\in (0,T)\). Now, since \(\overline{\varvec{u}}(t,a)=0\) in (0, T) , we infer \(\overline{\varvec{u}}=0\) in Q. Therefore, the first equation in (6.1) becomes
and the third one becomes \(\dfrac{\partial \varphi _{0}}{\partial t}-\dfrac{ \partial ^{2}\mu _{0}}{\partial x_{1}^{2}}=0\) in Q. The last four equations in (6.1) amount in the end to the non-local Cahn–Hilliard equation in one spatial dimension, which is known to possess a unique solution in the underlying spaces. Now, applying the Laplace transform to (6.2), we get that \(\varvec{h}_{1}+\mu _{0}\dfrac{\partial \varphi _{0}}{\partial x_{1}}-\dfrac{\partial p_{0}}{\partial x_{1}}=0\). Taking into account the fact that \(p_{0}\in L_{0}^{2}(a,b)\), we deduce that \(p_{0}\) solves (1.11). This completes the proof of Theorem 1.2. \(\square \)
7 Some Concrete Illustrations
The goal of this section is to present some concrete situations leading to the use of sigma-convergence with the underlying algebras with mean value, so that the homogenization problem for (1.2) is solvable.
7.1 Equidistribution of Microstructures in \(\Omega \)
We assume that the heterogeneity is uniformly distributed in \(\Omega \). This means that the distribution function of the microstructures is periodic, so that the function \(\overline{y}\mapsto B(\overline{x}, \overline{y},\zeta )\) is 1-periodic in each of its occurrences. Therefore, the corresponding algebra with mean value on \(\mathbb {R}^{d-1}\) is the algebra of Y-periodic continuous functions \(A=\mathcal {C}_{\textrm{per} }(Y) \), \(Y=(0,1)^{d-1}\). The mean value of a function \(u\in A\) is given by
The corresponding function spaces are defined as follows: \(B_{A}^{p}(\mathbb { R}^{d-1};L^{p}(I))=L_{\textrm{per}}^{p}(Y;L^{p}(I))\) (the space of functions in \(L_{\textrm{loc}}^{p}(\mathbb {R}^{d-1};L^{p}(I))\) that are Y-periodic), \(B_{A}^{1,p}(\mathbb {R}^{d-1};W^{1,p}(I))=W_{\textrm{per} }^{1,p}(Y;W^{1,p}(I))\) (the subspace of \(W_{\textrm{loc} }^{1,p}(Y;W^{1,p}(I)) \) made of periodic Y-periodic functions), and
(where \(Z=Y\times I\) with \(I=(-1,1)\)), a Banach space under the norm
We notice that, here, \(B_{A}^{p}(\mathbb {R}^{d-1};L^{p}(I))=\mathcal {B} _{A}^{p}(\mathbb {R}^{d-1};L^{p}(I))\) (\(L_{\textrm{per}}^{p}(Y;L^{p}(I))\) is a Banach space with the corresponding norm) and, so, \(B_{A}^{1,p}(\mathbb {R} ^{d-1};W^{1,p}(I))=\mathcal {B}_{A}^{1,p}(\mathbb {R}^{d-1};W^{1,p}(I))\).
In this case, the suitable concept of convergence is the two-scale convergence for thin heterogeneous domains, which is defined as follows: A sequence \((u_{\varepsilon })_{\varepsilon >0}\subset L^{p}(Q_{\varepsilon })\) is said to two-scale converge weakly in \(L^{p}(Q_{\varepsilon })\) to \( u_{0}\in L^{p}(Q;L_{\textrm{per}}^{p}(Y;L^{p}(I)))\) if, as \(\varepsilon \rightarrow 0\),
for any \(f\in L^{p^{\prime }}(Q;\mathcal {C}_{\textrm{per}}(Y;L^{p^{\prime }}(I)))\) (\(1/p^{\prime }=1-1/p\)).
In this case, the homogenization result in Theorem 1.1 reads as follows.
Theorem 7.1
Assume \(d=3\). For each \(\varepsilon >0\), let \((\varvec{u} _{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon },p_{\varepsilon }) \) be the unique solution of (1.2). Then, up to a subsequence (not relabelled), \((\varvec{u}_{\varepsilon },\mu _{\varepsilon },p_{\varepsilon })_{\varepsilon >0}\) weakly two-scale converges (as \( \varepsilon \rightarrow 0\)) in \(L^{2}(Q_{\varepsilon })^{3}\times L^{2}(Q_{\varepsilon })\times L^{2}(Q_{\varepsilon })\) towards \((\varvec{ u}_{0},\mu _{0},p_{0})\) and \((\varphi _{\varepsilon })_{\varepsilon >0}\) strongly two-scale converges in \(L^{2}(Q_{\varepsilon })\) towards \(\varphi _{0}\) with \(\varphi _{0}\in L^{\infty }(0,T;H^{1}(\Omega ))\), \(\varvec{u} _{0}\in L^{2}(Q;W_{\textrm{per}}^{1,2}(Y;H_{0}^{1}(I))^{3})\), \(\mu _{0}\in L^{2}(0,T;H^{1}(\Omega ))\) and \(p_{0}\in L^{2}(0,T;L_{0}^{2}(\Omega ))\). Setting
and
one has \(u_{3}=0\) and, up to the same subsequence as above, we have (1.8) as \(\varepsilon \rightarrow 0\). Moreover, it holds that \( \overline{\varvec{u}}\in \mathcal {C}([0,T];\mathbb {H})\), \(\varphi _{0}\in \mathcal {C}([0,T];L^{2}(\Omega ))\cap L^{2}(0,T;H^{1}(\Omega ))\), \( p_{0}\in L^{2}(0,T;H^{1}(\Omega )\cap L_{0}^{2}(\Omega ))\) and the quadruple \((\overline{\varvec{u}},\varphi _{0},\mu _{0},p_{0})\) is a weak solution to (1.9), where \(*\) stands for the convolution operator with respect to time in (1.9)\(_{1}\) and with respect to space in (1.9)\(_{4}\), and \(G=(G_{ij})_{1\le i,j\le 2}\) is a symmetric positive definite \(2\times 2\) matrix defined by its entries \( G_{ij}(t,\overline{x})=\frac{1}{2}\int _{Z}\omega ^{i}(\overline{x},t,y)e_{j}\,\textrm{d}y\). Here, \(\omega ^{j}=(\omega _{i}^{j})_{1\le i\le 3}\) is the unique solution in \(\mathcal {C}(\overline{Q};L_{\textrm{per} }^{2}(Y;L^{2}(I))^{3})\cap L^{2}(Q;W_{\textrm{per} }^{1,2}(Y;H_{0}^{1}(I))^{3})\) of the auxiliary Stokes system
\(e_{j}\) being the jth vector of the canonical basis in \(\mathbb {R}^{3}\). Moreover, if \(\varphi ^{0}\in L^{\infty }(\Omega )\) and \(\varvec{u} ^{0}\in L^{4}(\Omega )^{2}\), then the quadruple \((\overline{\varvec{u}},\varphi _{0},\mu _{0},p_{0})\) is the unique solution of (1.9), so that the whole sequence \((\varvec{u}_{\varepsilon },\varphi _{\varepsilon },\mu _{\varepsilon },p_{\varepsilon })_{\varepsilon >0}\) converges in the sense of (1.8).
Proof
The result is obtained just by identifying the mean value of a periodic function: for \(u\in L_{\textrm{per}}^{2}(Y)\), \(M(u)=\int _{Y}u(y)\, \textrm{d} y\). \(\square \)
7.2 Almost Periodic Distribution of the Microstructures
Now, we assume that the heterogeneity is induced in an almost periodic fashion. This amounts to the function \(\overline{y}\mapsto B( \overline{x},\overline{y},\zeta )\) being almost periodic in the Besicovitch sense (Besicovitch 1954; Bohr 1947). The corresponding algebra with mean value in \(\mathbb {R}^{d-1}\) is then the algebra of Bohr continuous almost periodic functions on \(\mathbb {R}^{d-1}\), say \(A=\textrm{AP}(\mathbb {R}^{d-1})\). We recall that \(\textrm{AP}(\mathbb {R}^{d-1})\) (Besicovitch 1954; Bohr 1947) is defined as the algebra of functions on \(\mathbb {R}^{d-1}\) that are uniformly approximated by finite linear combinations of functions in the set \(\{\cos (k\cdot ),\sin (k\cdot ):k\in \mathbb {R}^{d-1}\}\) where \(\cos (k\cdot )(y)=\cos (2\pi k\cdot y)\) and \(\sin (k\cdot )(y)=\sin (2\pi k\cdot y)\) (\( y\in \mathbb {R}^{d-1}\)). It is known that \(\textrm{AP}(\mathbb {R}^{d-1})\) is an algebra wmv called the almost periodic algebra wmv on \(\mathbb {R}^{d-1}\). The corresponding generalized Besicovitch space \(B_{A}^{p}(\mathbb {R}^{d-1})\) is precisely the Besicovitch space \(\mathcal {B}^{p}(\mathbb {R}^{d-1})\) defined in Besicovitch (1954), Bohr (1947).
Under the almost periodic distribution of microstructures, the main results in Theorems 1.1 and 1.2 are satisfied with the corresponding function spaces. We recall that, in this case, the mean value (Bohr 1947) of a function \(u\in \textrm{AP}(\mathbb {R}^{d-1})\) is defined as the unique constant belonging to the closed convex hull of the set of translates \(\{u(\cdot +a):a\in \mathbb {R}^{d-1}\}\) of u. It also satisfies property (3.1).
7.3 The Perturbed Periodic/Almost Periodic Setting
Some other examples can be considered, namely the asymptotic periodic distribution of microstructures in \(\Omega \), which leads to the use of the algebra wmv \(A=\mathcal {C}_{\textrm{per}}(Y)+\mathcal {C}_{0}(\mathbb {R} ^{d-1})\) (Jäger and Woukeng 2021, Section 5.2.3), where \(\mathcal {C}_{0}(\mathbb {R} ^{d-1})\) is the Banach algebra of continuous functions that vanish at infinity. In that case, assumption (H5) holds with \(A=\mathcal {C}_{\textrm{ per}}(Y)+\mathcal {C}_{0}(\mathbb {R}^{d-1})\). We may also deal with the asymptotic almost periodic distribution of heterogeneities, with the corresponding algebra wmv \(A=\textrm{AP}(\mathbb {R}^{d-1})+\mathcal {C}_{0}(\mathbb {R}^{d-1})\) (Jäger and Woukeng 2021, Section 5.2.3).
References
Aland, S., Egerer, S., Lowengrub, J., Voigt, A.: Diffuse interface models of locally inextensible vesicles in a viscous fluid. J. Comput. Phys. 277, 32–47 (2014)
Alikakos, N.D.: \(L^{p}\) bounds of solutions of reaction-diffusion equations. Commun. Partial Differ. Equ. 4, 827–868 (1979)
Allaire, G.: Homogenization of the unsteady Stokes equations in porous media. In: Progress in Partial Differential Equations: Calculus Of Variations, Applications, Pont-à-Mousson, 1991. Longman Sci. Tech., Harlow, pp. 109–123 (1992)
Auriault, J.-L., Lebaigue, O., Bonnet, G.: Dynamics of two immiscible fluids flowing through deformable porous media. Transp. Porous Media 4, 105–128 (1989)
Banas, L., Mahato, H.S.: Homogenization of evolutionary Stokes–Cahn–Hilliard equations for two-phase porous media flow. Asympt. Anal. 105, 77–95 (2017)
Bates, P.W., Han, J.: The Neumann boundary problem for a nonlocal Cahn–Hilliard equation. J. Differ. Equ. 212, 235–277 (2005)
Bazylak, A., Berejnov, V., Markicevic, B., Sinton, D., Djilali, N.: Numerical and microfluidic pore networks: Towards designs for directed water transport in GDLs. Electrochim. Acta 53, 7630–7637 (2008)
Bertrandias, J.-P., Datry, C., Dupuis, C.: Unions et intersections d’espaces \(L^{p}\) invariantes par translation ou convolution. Ann. Inst. Fourier 28, 53–84 (1978)
Besicovitch, A.S.: Almost Periodic Functions. Dover Publications, Cambridge (1954)
Bhattacharya, A., Gahn, M., Neuss-Radu, M.: Effective transmission conditions for reaction-diffusion processes in domains separated by thin channels. Appl. Anal. 101, 1896–1910 (2022)
Bohr, H.: Almost Periodic Functions. Chelsea, New York (1947)
Bunoiu, R., Cardone, G., Kengne, R., Woukeng, J.L.: Homogenization of 2D Cahn–Hilliard–Navier–Stokes system. J. Elliptic Parabol. Equ. 6, 377–408 (2020)
Cardone, G., Jäger, W., Woukeng, J.L.: Derivation and analysis of a non-local Hele-Shaw–Cahn–Hilliard system for flow in thin heterogeneous layers, Submitted Preprint (2022)
Cavaterra, C., Frigeri, S., Grasselli, M.: Nonlocal Cahn–Hilliard–Hele-Shaw systems with singular potential and degenerate mobility. J. Math. Fluid Mech. 24, 13 (2022)
Cheng, K., Feng, W.: Global well-posedness of strong solution for the three dimensional dynamic Cahn–Hilliard–Stokes model. J. Nonlinear Sci. Appl. 10, 4209–4221 (2017)
Colli, P., Frigeri, S., Grasselli, M.: Global existence of weak solutions to nonlocal Cahn–Hillliard–Navier–Stokes system. J. Math. Anal. Appl. 386, 428–444 (2012)
Daly, K.R., Roose, T.: Homogenization of two fluid flow in porous media. Proc. Roy. Soc. A: Math. Phys. Eng. Sci. 471, 2014056-1–2014056-20 (2015)
Della Porta, F., Grasselli, M.: On the nonlocal Cahn–Hilliard–Brinkman and Cahn–Hilliard–Hele-Shaw systems. Commun. Pure Appl. Anal. 15, 299–317 (2016)
Della Porta, F., Giorgini, A., Grasselli, M.: The nonlocal Cahn–Hilliard–Hele-Shaw system with logarithmic potential. Nonlinearity 31, 4851–4881 (2018)
Feng, X., Wise, S.M.: Analysis of a Darcy–Cahn–Hilliard diffuse interface model for the Hele-Shaw flow and its fully discrete finite element approximation. SIAM J. Numer. Anal. 50, 1320–1343 (2012)
Fournier, J.J.F., Stewart, J.: Amalgams of \(L^{p}\) and \( \ell ^{q}\). Bull. Amer. Math. Soc. (N.S.) 13, 1–21 (1985)
Frigeri, S., Grasselli, M.: Nonlocal Cahn–Hilliard–Navier–Stokes systems with singular potentials. Dyn. Part. Differ. Equ. 9, 273–304 (2012)
Frigeri, S., Gal, C.G., Grasselli, M., Rocca, E.: A diffuse interface model for two-phase incompressible flows with nonlocal interactions and nonconstant mobility. Nonlinearity 28, 1257–1293 (2015)
Frigeri, S., Gal, C.G., Grasselli, M.: On nonlocal Cahn–Hilliard–Navier–Stokes systems in two dimensions. J. Nonlin. Sci. 26, 847–893 (2016)
Gahn, M., Neuss-Radu, M., Knabner, P.: derivation of effective transmission conditions for domains separated by a membrane for different scaling of membrane diffusivity. Discrete Cont. Dyn. Syst. S 10, 773–797 (2017)
Gahn, M., Neuss-Radu, M., Knabner, P.: Effective interface conditions for processes through thin heterogeneous layers with nonlinear transmission at the microscopic bulk-layer interface, Network. Heter. Media 13, 609–640 (2018)
Gahn, M., Neuss-Radu, M., Pop, I.S.: Homogenization of a reaction–diffusion–advection problem in an evolving micro-domain and including nonlinear boundary conditions. J. Differ. Equ. 289, 95–127 (2021)
Gurtin, M.E., Polignone, D., Viñals, J.: Two-phase binary fluids and immiscible fluids described by an order parameter. Math. Mod. Meth. Appl. Sci. 6, 815–831 (1996)
Han, D., Sun, D., Wang, X.: Two-phase flows in karstic geometry. Math. Meth. Appl. Sci. 37, 3048–3063 (2013)
Hornung, U. (ed.): Homogenization and Porous Media, Interdisciplinary Applied Mathematics, vol. 6. Springer, New York (1997)
Jäger, W., Woukeng, J.L.: Sigma-convergence for thin heterogeneous domains and application to the upscaling of Darcy–Lapwood–Brinkman flow, arXiv:2309.09004 (Submitted Preprint ), (2022)
Jäger, W., Woukeng, J.L.: Homogenization of Richards’ equation in multiscale porous media. J. Differ. Equ. 281, 503–549 (2021)
Jiang, J., Wu, H., Zheng, S.: Well-posedness and long-time behavior of anon-autonomous Cahn–Hilliard–Darcy system with mass source modeling tumor growth. J. Differ. Equ. 259, 3032–3077 (2015)
Kozicki, W., Kuang, P.Q.: Cake filtration of suspensions in viscoelastic fluids. Canad. J. Chem. Eng. 72, 828–839 (1994)
Lowengrub, J., Titi, E., Zhao, K.: Analysis of a mixture model of tumor growth. Eur. J. Appl. Math. 24, 691–734 (2013)
Marusić, S., Marusić-Paloka, E.: Two-scale convergence for thin heterogeneous domains and its applications to some lower-dimensional models in fluid mechanics. Asymptot. Anal. 23, 23–58 (2000)
Mikelić, A.: Mathematical derivation of the Darcy-type law with memory effects, governing transient flow through porous medium. Glasnik Matematički 29(49), 57–77 (1994)
Neuss-Radu, M., Jäger, W.: Effective transmission conditions for reaction–diffusion processes in domains separated by an interface. SIAM J. Math. Anal. 39, 687–720 (2007)
Nguetseng, G.: Homogenization structures and applications I. Z. Anal. Anwen. 22, 73–107 (2003)
Nguetseng, G., Sango, M., Woukeng, J.L.: Reiterated ergodic algebras and applications. Commun. Math. Phys. 300, 835–876 (2010)
Reischmann, L., Peter, M.A.: Multiscale modeling and simulation of a Cahn-Larché system with phase separation on the microscale. SIAM J. Appl. Math. 80, 2170–2193 (2020)
Reischmann, L., Peter, M.A.: Analysis and homogenisation of a linear Cahn-Larché system with phase separation on the microscale. J. Appl. Math. Mech. (ZAMM) 102, e202100165 (2022)
Sango, M., Woukeng, J.L.: Stochastic sigma-convergence and applications. Dyn. PDE 8, 261–310 (2011)
Sango, M., Svanstedt, N., Woukeng, J.L.: Generalized Besicovitch spaces and application to deterministic homogenization. Nonlin. Anal. TMA 74, 351–379 (2011)
Schmuck, M., Pradas, M., Pavliotis, G.A., Kalliadasis, S.: Upscaled phase-field models for interfacial dynamics in strongly heterogeneous domains. Proc. R. Soc. A 468, 3705–3724 (2012)
Schmuck, M., Pradas, M., Pavliotis, G.A., Killiadasis, S.: Derivation of effective macroscopic Stokes–Cahn–Hilliard equations for periodic immiscible flows in porous media. Nonlinearity 26, 3259–3277 (2013)
Sharmin, S., Bastidas, M., Bringedal, C., Pop, I.S.: Upscaling a Navier–Stokes–Cahn–Hilliard model for two-phase porous-media flow with solute-dependent surface tension effects. Appl. Anal. 101, 4171–4193 (2022)
Temam, R.: Navier–Stokes Equations. AMS Chelsea Publishing, Providence (2001)
Vladimirov, V.S.: Equations of Mathematical Physics. Mir Publishers, Moscow (1984)
Wang, X., Zhang, Z.: Well-posedness of the Hele-Shaw-Cahn-Hilliard system. Ann. I. H. Poincaré-A.N. 30, 367–384 (2013)
Wiener, N.: Tauberian theorems. Ann. Math. 33, 1–100 (1932)
Wise, S.M.: Unconditionally stable finite difference nonlinear multigrid simulation of the Cahn–Hilliard–Hele-Shaw system of equations. J. Sci. Comput. 44, 38–68 (2010)
Wise, S.M., Lowengrub, J.S., Frieboes, H.B., Cristini, V.: Three-dimensional multispecies nonlinear tumor growth—I: Model and numerical method. J. Theor. Biol. 253, 524–543 (2008)
Woukeng, J.L.: Homogenization in algebras with mean value. Banach J. Math. Anal. 9, 142–182 (2015)
Wu, H., Wang, X.: Long-time behavior for the Hele-Shaw–Cahn–Hilliard system. Asymptot. Anal. 78, 217–245 (2012)
Zhikov, V.V., Krivenko, E.V.: Homogenization of singularly perturbed elliptic operators, Matem. Zametki 33, 571–582 (1983). (english transl.: Math. Notes, 33 (1983) 294–300)
Acknowledgements
The second author would like to acknowledge the kind support of the Alexander von Humboldt Foundation for supporting a research visit to the University of Augsburg during which this research was carried out. The authors thank the Reviewer for his/her helpful comments and suggestions that contributed to the improvement of the initial work.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by George Haller.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Peter, M.A., Woukeng, J.L. On the Doubly Non-local Hele-Shaw–Cahn–Hilliard System: Derivation and 2D Well-Posedness. J Nonlinear Sci 34, 43 (2024). https://doi.org/10.1007/s00332-024-10018-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-024-10018-6
Keywords
- Non-local Cahn–Hilliard–Stokes system
- Sigma-convergence
- Thin domains
- Doubly non-local Hele-Shaw–Cahn–Hilliard system
- Homogenization