Frictional Locomotion of a Radially Symmetric Tripedal Robot

Abstract

This study seeks to provide physical insight into the friction-driven crawling locomotion of systems with radially symmetric bodies. Laboratory experiments with a tripedal robot show that both translation and rotation can be achieved with just three independently actuated rigid limbs, i.e., with 3 degrees-of-freedom. These observations are rationalized using a simple mathematical model, which assumes that the friction at each limb is linearly proportional to the normal force at the contact point, and opposes the direction of motion. This dynamic model reproduces experimental observations across an extensive parametric sweep involving sinusoidal rotation of the limbs with varying amplitudes and phase shifts. Model predictions highlight the role played by time-varying normal forces at the contact points. These predictions are confirmed using embedded force transducers in the limbs. We present a further simplified analysis explaining that a geometric nonlinearity is induced in the dynamics from the radial symmetry and that this nonlinearity is essential to the generation of pure translation. We also show that this nonlinearity can be amplified by a cyclic time-varying limb length variation. These results provide a framework for further study of radially symmetric movers.

1 Introduction

Previous locomotion studies have primarily focused on bilaterally symmetric body arrangements. This is partly because the majority of land-based animals are bilaterally symmetric. However, radially symmetric body arrangements are common in aquatic environments, e.g. Cnidaria (swimming medusae, or jellyfish; Cameron and Fankboner (1989)) and Echinodermata (crawling organisms such as sea stars, brittle stars, and sea urchins; Manuel (2009); Astley (2012)). We are interested in exploring how these predominantly aquatic body arrangements can be used for amphibious or terrestrial locomotion. As a starting point in this endeavor, this study analyzes friction-driven locomotion of tripedal geometries involving three contact points—the minimum number required for stable motion with radially symmetric bodies—via laboratory experiments and the development of simplified mathematical models. The focus on a tripedal geometry allows us to minimize the complexity of the robot used in the experiments and provide simplified analyses for the nonlinear dynamics we observe.

Radially symmetric morphologies offer some benefits over bilaterally symmetric arrangements. First, radially symmetric movers can use any limb to define a lead direction Cole (1913); Astley (2012). For example, pentaradial brittle stars are shown to exhibit bilaterally symmetric motion strategies in which one of the five limbs remains inactive Astley (2012). However, because they are radially symmetric, the inactive limb can be reassigned to change direction immediately Astley (2012). In addition to having no front bias, in the case of radially symmetric body plans with more than 3 limbs, the mover is robust to limb damage due to redundancy Kano et al. (2017, 2019); Sköld and Rosenberg (1996); Carnevali (2006); Matsuzaka et al. (2017). This advantage may be of use in remote environments where loss of motor function or general damage to a limb does not render the mover immobile. Finally, for locomotion in the presence of strong external forces (e.g., aerodynamic or hydrodynamic disturbances), having multiple contact points enables more robust adhesion. This can reduce risk of surface dislodgement and enhance the net adhesive force through distributive attachment Arshavskii et al. (1976).

Several recent efforts have considered the development of radially symmetric robots. Our previous work describing the development of the tripedal test system used in this study showed that the radially symmetric arrangement is controllable using an omnidirectional gait map Hermes et al. (2021). This prior effort also highlighted an advantage of being able to define arbitrary lead limbs for radially symmetric robots: sharp path curves can easily be followed. The Robotics and Mechanisms Laboratory at UCLA has produced many radially symmetric systems: the hexapod robots SiLVIA, HEX, and MARS Showalter et al. (2008); a radially symmetric quadruped, ALPHRED Hooks et al. (2020); and two tripod robots, THALer Webb et al. (2015) and STriDER Heaston et al. (2007). In general, these robots have multi-actuated legs for walking and interacting with their environments. The tripedal STriDER and THALer systems have also demonstrated application of a novel swinging gait allowing for translation in three directions. The Ishikawa lab group Oki et al. (2015); Ishikawa et al. (2018); Masuda and Ishikawa (2017) have also demonstrated controlled crawling using a robot called Martian with similar geometry to STriDER. Unlike STriDER, this robot uses small vertical stepping oscillations coupled with joint rotation driven by a decentralized control scheme using normal force feedback. Locomotion studies for this robot showed natural synchronization to occur from a large set of initial conditions. Bevly et al. (2000) have demonstrated vertical climbing using a radially symmetric tri-arm robot. Several other groups have developed hex-symmetric terrestrial Faigl and Čížek (2019); Žák et al. (2021); Liu et al. (2018); Bjelonic et al. (2018) or aerial Ryll et al. (2017) robots.

Other research efforts have considered the development of robots with close similarity to pentaradial brittle stars. For example, Watanabe et al. (2012) developed a decentralized control scheme to orchestrate limb motion for a pentaradial system. Kano et al. (2012) demonstrated omnidirectional locomotive capabilities using this control scheme on a physical ophiuroid robot. More recently, Kano et al. (2017) demonstrated robust locomotion capabilities in a pentaradial robot by systematically removing appendages and showing the adapted locomotion strategy. This effort built on biological observations that involved removing arms from live brittle stars and observing the resulting locomotion patterns. Lal et al. (2007, 2008) developed motion control algorithms for a pentaradial robot with multisegmented arms using genetic algorithms. This work showed that a nonintuitive complex writhing motion generated the largest net translation.

Given the triradial geometry considered in this study, a related field of research involves controlling the motion of trident robots, which are tripedal robots with wheels at the end effector instead of simple frictional contacts Ishikawa et al. (2009a, 2009b); Jakubiak et al. (2010); Yamaguchi (2012). In general, these studies use nonholonomic kinematic relations to obtain optimal control strategies. Ishikawa et al. Ishikawa et al. (2009a) have also demonstrated the ability to track sharp path trajectories with a geometric mechanics algorithm.

The efforts described in the preceding paragraphs highlight the broad applicability of radially symmetric robots, and emphasize the comparative advantages to systems with bilateral symmetry. The present work seeks to build on these prior efforts and provide insight into the nonlinear dynamics underlying friction-driven sliding (or crawling) locomotion of systems exhibiting triradial symmetry. For this purpose, we have developed an idealized robot with 3 rigid single DOF limbs. We have characterized the motion of this robot in laboratory experiments comprising a systematic parametric sweep involving open-loop sinusoidal actuation of the limbs. We have also developed a simplified physics-based mathematical model that reproduces the experimental observations, and provides insight into the unique locomotive capabilities of this arrangement. Through this effort, we have identified and characterized actuation patterns that lead to pure rotation and pure translation.

The remainder of this paper is structured as follows. Robot design and laboratory experiments are described in Sect. 2. The physics-based model is developed in Sect. 2.3. Experimental results and model predictions are compared in Sect. 3. Actuation patterns that lead to pure rotational and translational motion are also evaluated in this section. We then seek an explanation for answering why the symmetric gait sequence generates net translation in Sect. 4. Concluding remarks are presented in Sect. 5.

2 Experimental Approach and Physics-Based Model

In this section, we provide an overview of the robot design (2.1), our mathematical model (2.3), and normal force validation (2.4).

2.1 Robot Design and Characterization

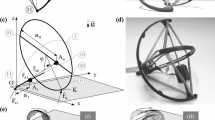
A top and isoview of the simple tripedal robot used in this study is shown in section 1. The tripedal robot comprises 7.5cm long 3D-printed polylactic acid (PLA) arms connected to an stereolithography (SLA) resin motor support structure with an effective radius of 5cm. We used Hitec HS-5646 digital servo motors to drive the arms, which were powered by an external power supply and controlled by an Arduino Uno. The total mass of the structure was measured to be 888g. We also embedded limbs with 5 kg bending-beam load cells (Chenbo CZL635) with an HX-711 amplifier module to measure normal forces with a noise profile of roughly $\pm 1.5\%$FS (approximately $\pm 0.7$N).

Fig. 1

a Top and b iso view of the robot

We varied the friction at the contact points using polymer laminate and 600-grit sandpaper surfaces. We used paper as the test platform surface. The friction coefficients measured were $\mu = 0.33 \pm 0.012$ for the polymer-paper contact and $\mu = 0.85 \pm 0.043$ for the sandpaper-paper contact. As described in Hermes et al. (2021), these values were obtained by releasing a known mass (with appropriate contacts) from rest down a slope and measuring the velocity achieved by the mass after a set distance. The difference between the initial gravitational potential energy and the final kinetic energy of the sliding mass was attributed to friction, and friction coefficients were estimated from this frictional loss. The sliding masses were randomly oriented and produced small deviations in the measured friction coefficients. From this, we concluded that the friction coefficient is nearly isotropic. As discussed below, we ignored high-order friction effects for modeling simplicity. To ensure that the observed robot motion was purely due to limb actuation, we ensured that the dynamic impact of surface imperfections and the power/control tether were minimized. All experiments were carried out on a smooth, level optimal support table with tilt less than $0.2^\circ$. The tether cable was supported externally to minimize tension.

2.2 Motion Experiments and Video Tracking

To characterize the dynamic behavior of the tripedal robot, we pursued a systematic experimental evaluation in which we measured the robot motion resulting from prescribed sinusoidal actuation of each limb. Specifically, the angular position of the $i-$th limb (see Fig. 2) was prescribed as

$$\begin{aligned} \phi _i(t) = \xi \sin (2 \pi f t + i \Delta \psi ), \end{aligned}$$

(1)

where $i = {1,2,3}$. Here, $\xi$ represents rotation amplitude, f is the oscillation frequency, and $\Delta \psi$ is a temporal phase shift in actuation between the limbs. We refer to $\xi$ as sweep and $\Delta \psi$ as phase for the remainder of this paper.

Fig. 2

Abstracted model representation of tripedal robot

The following ranges were tested for each of the three actuation parameters: $f \in [0.4,1.0]Hz$, $\xi \in [20^\circ ,50^\circ ]$, and $\Delta \psi \in [20^\circ ,80^\circ ]$. The ranges for f and $\xi$ were constrained by servomotor limitations and stability considerations. The range of test values for $\Delta \psi$ was chosen to span the configuration space. Table 1 shows the specific parameter combinations tested. In addition to this sinusoidal parametric sweep, we also tested actuation patterns resembling locomotion strategies observed for brittle stars named rowing and reverse rowing Astley (2012). Both of these translation modes involve one unpaired or inactive limb. Rowing and reverse rowing are distinguished by the orientation of this inactive limb and are graphically described in Fig. 9. In the case of rowing, the inactive limb leads the body forward, whereas for reverse rowing, the inactive limb passively trails the body. For both locomotor modes, kinematic observations show that the motion of the active limbs is symmetric with respect to the translation axis Astley (2012). Thus, despite the radial body plan, brittle stars effectively employ coordinated, bilaterally symmetric locomotion; radial symmetry is broken by the presence of an inactive limb.

Table 1 Parametric combinations tested for sinusoidal actuation experiments

The robot was tracked at 30 frames per second from above using a camera mounted on an elevated platform. Because the largest test frequency was 1.2 Hz, the selected frame rate resolves motion completely. The center of mass for the robot in the horizontal plane, $\textbf{x}=[x,y]$, was determined by applying a MATLAB image-filter script to the recorded images. A reference measurement object was used for pixel-to-centimeter calibration in the motion plane. The relative rotation of the robot, $\theta$, was tracked by finding the maximum correlation between the preceding image, rotated in the range $[-3^\circ ,3^\circ ]$, and the frame being considered. The starting position of the robot for each experiment was defined as $\textbf{x}= [0,0]$ and $\theta = 0^\circ$.

2.3 Mathematical Model

We developed a simplified dynamic model for the tripedal robot based on momentum conservation laws with nonlinear friction forces. In our model, we assume rotational and translational intertias for the limbs to be negligible compared to those for the central body. Friction forces are modeled as point forces at the tips of the limbs.

The friction force is simplified in our model to be the signum function of the velocity. In other words, there are no stick–slip effects. Olsson et al. (1998); Pennestrì et al. (2016). We recognize that this friction model constitutes a significant simplification. However, below we show that this simplified model is able to reasonably reproduce experimental observations. The friction force, $\textbf{F}_i = [F_{i,x},F_{i,y}]$, acting at the contact point at the end of each limb in the $x-y$ plane, $\textbf{r}_i = [r_{i,x},r_{i,y}]$, is modeled as

$$\begin{aligned} \textbf{F}_i = - \mu N_i \frac{\dot{\textbf{r}}_i}{|\dot{\textbf{r}}_i|}. \end{aligned}$$

(2)

Here, $N_i$ is the normal force at contact point i, $\mu$ is the measured kinetic friction coefficient, and $\dot{\textbf{r}}_i = [\dot{r}_{i,x},\dot{r}_{i,y}]$ is the velocity of the contact point at the end of each limb. Note that $\textbf{r}_i$ and $\dot{\textbf{r}}_i$ can be expressed in terms of the robot state vector, $\textbf{z}= [\textbf{x}, \dot{\textbf{x}}, \theta , \dot{\theta }]$, the actuation angles and rotation rates, $\phi _i$ and $\dot{\phi _i}$, and the geometric constants, R and l, using simple trigonometric relations (see Fig. 2). To avoid numerical issues for cases in which the velocity at the contact point is zero, we assume $\textbf{F}_i = 0$ for $|\mathbf {\dot{r}}_i| \ll 1$, or that there is no translational friction force for infinitesimally small velocities. Normal forces are computed by combining a vertical force balance ($N_1 + N_2 + N_3 = M g$) with torque balances about the robot center of mass:

$$\begin{aligned} \left[ \begin{array}{c c c} 1 &{} 1 &{} 1 \\ r_{1,x} - x &{} r_{2,x} - x &{} r_{3,x} - x \\ r_{1,y} - y &{} r_{2,y} - y &{} r_{3,y} - y \end{array}\right] \left[ \begin{array}{c } N_1\\ N_2 \\ N_3 \end{array}\right] = \left[ \begin{array}{c } M g \\ 0 \\ 0 \end{array}\right] . \end{aligned}$$

(3)

The second and third lines in the equation above ensure that there are no net torques about the robot center-of-mass due to the normal forces.

Under the assumptions stated above, conservation laws for linear momentum in the horizontal plane can be expressed as

$$\begin{aligned} M \ddot{x} = \sum \limits _{i=1}^{3} F_{i,x} \end{aligned}$$

(4)

and

$$\begin{aligned} M \ddot{y} = \sum \limits _{i=1}^{3} F_{i,y}, \end{aligned}$$

(5)

respectively. The conservation law for angular momentum can be expressed compactly as

$$\begin{aligned} J \ddot{\theta } = \sum \limits _{i=1}^{3} (\mathbf {r_i} - \textbf{x}) \times \textbf{F}_i, \end{aligned}$$

(6)

where J represents the second mass moment of inertia, which is estimated from the mass distribution of the central support structure.

The system of ordinary differential equations shown in (4-6) is solved numerically to yield predictions for robot translation ($\textbf{x}$) and rotation ($\theta$) using the MATLAB ode45 algorithm for an adaptive time-step 4th-order Runge–Kutta solver. Recall that the location of the contact points relative to the robot center, $\textbf{r}_i - \textbf{x}$, depends on the limb angles, $\phi _i(t)$ (Fig. 2). Therefore, the prescribed actuation angles $\phi _i(t)$ appear directly in all three conservation laws via the friction terms dependent on $\textbf{r}_i$ and $\dot{\textbf{r}}_i$. Also, keep in mind that these model simulations involve no tuning parameters. All geometric and dynamic variables appearing in the governing equations (e.g., $M, J, l, R, \mu$) are obtained from independent measurements.

2.4 Normal Force Simulation Predictions and Measurements

As noted earlier, we embedded three load cells into the robot limbs to measure normal forces. In this section we compare the measured normal forces against predictions made using eq. (3). Measured normal forces for $f=0.5$Hz, $\xi = 30^\circ$, and varying phase differences $\Delta \psi =60^\circ$, $\Delta \psi =90^\circ$, and $\Delta \psi =120^\circ$ are plotted with simulation data in Fig. 3. Note that the measured data are phase averaged over 5 oscillation cycles.

Fig. 3

Time series showing model predictions (black) and experiment measurements (red) for the normal forces acting at each contact point for phase shifts: a $\Delta \psi =60^\circ$, b $\Delta \psi =90^\circ$, and c $\Delta \psi =120^\circ$. The oscillation frequency and sweep angle are set to $f = 0.5$ Hz and $\xi = 30^\circ$ for the high-friction sandpaper-paper contact. Shaded red regions represent measurement variability. This is defined as one standard deviation for the phase averaging procedure

Though the measurements are qualitatively similar to the predictions, there are some consistent quantitative discrepancies. First, the amplitude of force oscillation for all limbs is larger for the measurements compared to the simulations. In addition, for $\Delta \psi = 120^\circ$, the normal force profiles of the legs are not equal with a phase shift. Unlike the simulations, the measured normal forces differ in magnitude. These measurements suggest that the robot weight may not be evenly distributed, which is a source of potential modeling error. This error could, in part, explain some of the discrepancies in trajectories between simulation data and experiment results observed in the next section. Nevertheless, the qualitative agreement between model predictions and measured normal forces is promising, especially keeping in mind the expected $\pm 0.7$N noise floor in the load cell measurements, which is comparable to the discrepancy between measurements and predictions.

3 Results

A systematic parametric sweep was performed for the sinusoidal actuation described by (1). Oscillation frequencies (f), sweep angles ($\xi$), and relative phases ($\Delta \psi$) were varied over the ranges shown in Table 1. Comparison between experimental tracking results and model predictions for these cases are shown in Sects. 3.1–3.3. Simulation predictions were interpolated at a rate of 30 Hz, consistent with the experimental imaging results. The total time interval for all the results shown in Figs. 4-6 below was 30 s. Sections 3.4–3.5 build upon these findings to consider actuation patterns that result in pure rotation and translation.

3.1 Frequency Variation

Fig. 4

Comparison between model predictions and experimental results over a period of 30 s for the frequency variation experiments. For all cases, $\xi = 30^\circ$ and $\Delta \psi = 30^\circ$. The actuation frequency is set to be a, e $f=0.4$ Hz, b, f $f= 0.6$ Hz, c, g $f= 0.8$ Hz, d, h $f=1.0$ Hz. Panels a–d correspond to the low-friction tape-paper contact while panels e–h correspond to the high-friction sandpaper-paper contact. Tracking data from the experiments are shown as thin red lines and the simulation data are shown as a thick black lines. Movie 1 in the supplementary materials provides a side-by-side comparison of experimental results and model predictions

Fig. 4 compares model predictions for robot position with tracking results from experiments with varying oscillation frequency, f. The sweep angle and relative phase shift were maintained constant at $\xi = 30^\circ$ and $\Delta \psi = 30^\circ$ for these experiments. Model predictions and experimental results both show the presence of small-scale oscillations in robot center-of-mass as well as a larger-scale orbit or revolution. For the low-friction cases shown in (a)-(d), an increase in frequency led to a contraction in the local oscillation length in the experiments, i.e., the small-scale oscillations clustered closer together. For the high-friction cases shown in (e)-(h), increasing frequency did not significantly change the local oscillation scale or the arc radius of the large-scale revolution. Instead, increasing frequency simply led to an increase in the total distance traveled by the robot, i.e., the arc length traversed by the robot increased.

For the high-friction cases, model predictions (black lines) are in good qualitative and quantitative agreement with experimental observations (red lines). For the low-friction case, the model predictions are in qualitative agreement with the experimental results, though the clustering effect is not reproduced as clearly; only a minor reduction in the oscillation scale is observed from panel (a) to panel (d). Note that the discrepancy between model predictions and experiments is greatest for the lowest-frequency cases considered in (a) and (e). This discrepancy could be attributed to the highly-simplified contact model considered here, which does not distinguish between static and kinetic friction. Transitions between static and kinetic friction (i.e., stick–slip dynamics) are expected to be more important at lower actuation frequencies.

3.2 Sweep Variation

Fig. 5

Comparison between model predictions and experimental results over a period of 30 s for the sweep variation experiments. For all cases, $f = 1.0$ Hz and $\Delta \psi = 30^\circ$. The sweep angles correspond to a, e $\xi =20^\circ$, b, f $\xi =30^\circ$, c, g $\xi =40^\circ$, d, h $\xi =50^\circ$. Panels (a–d) correspond to the low-friction tape-paper contact while panels (e–h) correspond to the high-friction sandpaper-paper contact. Tracking data from the experiments are shown as thin red lines and the simulation data are shown as a thick black lines

Next, we consider robot motion for cases in which the sweep values were varied systematically while the oscillation frequency and phase shift were kept constant at $f = 1.0$ Hz and $\Delta \psi = 30^\circ$. Experimental observations and model predictions of robot trajectory for these cases are shown in Fig. 5. For both the low- and high-friction tests, an increase in sweep angle led to an increase in the local oscillation length. For the high-friction cases, the arc radius for the large-scale revolution also decreased slightly with increasing sweep angles. Together, this increase in oscillation length and reduction in arc radius resulted in a lower revolution period. In other words, for the high-friction cases, the robot completed a large scale revolution faster as the sweep angle increased. This is clear from a comparison between the high-sweep case shown in Fig. 5(h), which shows a complete revolution, and the lower-sweep cases shown in Figs. 5e–g, which do not show a complete revolution. The low-friction cases do not show a clear reduction in arc radius, though the total distance traveled by the robot does increase monotonically with increasing sweep angles.

Once again, the mathematical model generates predictions in good quantitative agreement with the experimental observations for the high-friction cases. For the low-friction contact, the model qualitatively reproduces the observed increase in the local oscillation scale and distance traveled by the robot with increasing sweep. However, there are deviations between the observed trajectories and model predictions.

3.3 Phase Variation

Fig. 6

Comparison between model predictions and experimental results over a period of 30 s for the phase variation experiments. For all cases, $f = 1.0$ Hz and $\xi = 30^\circ$. The phase shift between individual limbs is a, e $\Delta \psi =20^\circ$, b, f $\Delta \psi =40^\circ$, c, g $\Delta \psi =60^\circ$, d, h $\Delta \psi =80^\circ$. Panels (a–d) correspond to the low-friction tape-paper contact while panels (e–h) correspond to the high-friction sandpaper-paper contact. Tracking data from the experiments are shown as thin red lines and the simulation data are shown as a thick black lines

Finally, Fig. 6 shows the effect of varying phase difference, $\Delta \psi$, on robot motion at constant oscillation frequency, $f = 1.0$ Hz, and sweep angle, $\xi = 30^\circ$. For both the low-friction and high-friction cases, an increase in the phase shift led to a decrease in the arc radius for the large-scale revolution. This was accompanied by a marked change in the character or shape of the small-scale oscillation patterns. Specifically, the oscillations became sharper and less rounded with increasing phase separation between limbs. This is in contrast to the results shown in Fig. 5, in which the arc radius decreased slightly with increasing sweep, but the rounded profile of the oscillations remained. As with the sweep and frequency variation experiments, there is very good quantitative agreement between model predictions and experimental trajectories for the high-friction cases, but less so for the low-friction cases.

3.4 Pure Rotation

Fig. 7

Illustration of pure rotation for a phase difference of $\Delta \psi =120^\circ$ for the high-friction sandpaper-paper contact. The left panel confirms that there is minimal net translation. The right panel shows a monotonic increase in rotation angle. The actuation parameters were $f = 1.0$ Hz, and $\xi = 30^\circ$. Once again, experimental data are shown as thin red lines while the simulation predictions are shown as thick black lines. Movie 2 shows model predictions and experimental results for a case with $\Delta \psi = 120 ^\circ$

The observed decrease in arc radius with increasing phase shift observed in Fig. 6 inspired an additional experiment in which the phase shift was set to $\Delta \psi = 120^\circ$. Given the triradial symmetry of the robot, for $\Delta \psi \ne 120^\circ$, the sinusoidal actuation described by (1) leads to a constant phase difference between limbs $i=(1,2)$ and $i=(2,3)$ but not $i=(3,1)$. For $\Delta \psi = 120^\circ$, the phase difference is constant across all limbs. Figure 7 shows the time-variation in the x-location of the robot center of mass (a) and rotation angle $\theta$ (b) for sinusoidal actuation with $\Delta \psi = 120^\circ$. The observed trajectory shows minimal translation ($x \approx 0$ m) and a monotonic increase in the rotation angle, i.e., the robot effectively exhibits pure rotation for $\Delta \psi = 120^\circ$. Model predictions for translation in the x-direction are similar to the experimental observations. However, they differ in predicting both the average rate and nature of the rotation. The model predicts a pronounced acceleration-deceleration cycle in rotation rate at the actuation frequency ($f=1.0$ Hz), whereas the experiment results show a relatively constant rotation rate.

Fig. 8

Curvature for the large-scale revolution (normalized by $l = 0.075$ m), obtained by fitting a parametric circle to model predictions for cases with $\xi = 30^\circ$, $f= 1.0$ Hz and $\Delta \psi = [20:350]^\circ$ for the high-friction sandpaper-paper contact

To provide further insight into the observed rotational — or pivoting — motion, additional simulations were pursued for $\Delta \psi = [20,30,...,350]^\circ$, with the sweep angle and oscillated frequency fixed at $\xi = 30^\circ$ and $f = 1.0$ Hz. The resulting large-scale revolution was characterized by fitting a circle with radius r and center (a, b) in the horizontal plane to the observed trajectories. Specifically, a quasi-Newton gradient optimization method (with tolerance $10^{-6}$) was used in MATLAB to minimize the error function

$$\begin{aligned} e(a,b,r) = \sum _{j} (r - \sqrt{(x_j - a)^2 + (y_j - b)^2}) \end{aligned}$$

(7)

for all data points $(x_j,y_j)$ in the predicted trajectories. The normalized curvature obtained from this procedure, l/r, is plotted in Fig. 8 as a function of the phase different $\Delta \psi$. The predictive curvature is maximum (i.e., fitted radius r is minimum) at $\Delta \psi = 120^\circ$ and $240^\circ$. As noted earlier, given the triradial symmetry of the robot, $\Delta \psi = 120^\circ$ ensures a constant phase difference across all three limbs. This is also true for $\Delta \psi = 240^\circ$. Interestingly, the model also predicts zero curvature (i.e., $r \rightarrow \infty$) for $\Delta \psi =180^\circ$. This particular actuation essentially corresponds to a rowing motion with an oscillating unpaired limb. As we discuss in the following section, this actuation results in translational motion with minimal curvature.

Model predictions shown in Fig. 8 indicate that the large-scale revolution is driven by the inconsistent phase differences resulting from $\Delta \psi \ne 120^\circ$ (or $240^\circ$). The physical mechanism giving rise to this effect is illustrated by Fig. 3, which shows the time-varying normal forces acting at each contact point for phase shifts $\Delta \psi = [60,90,120]^\circ$. As expected, in all cases, the normal forces show periodic variation at the oscillation frequency. However, the cases with $\Delta \psi = 60^\circ$ and $90^\circ$ are characterized by the presence of a single differentiated limb that exhibits a higher-amplitude oscillation (see black lines in Figs. 3a, b). This differentiated limb corresponds to $i=2$ in (1), which maintains the prescribed phase shift, $\Delta \psi$ relative to the other two limbs. Recall that the phase shift between the remaining two limbs, $i=1$ and $i=3$, is not $\Delta \psi$ except for cases in which $\Delta \psi = 120^\circ$ (or a multiple thereof). These differences in relative phase give rise to differences in the frictional forces acting at each limb, which drive the large-scale orbital motion exhibited by the robot. For $\Delta \psi = 120^\circ$, there is no differentiated limb. As shown in Fig. 3c, the normal force waveforms are equal in amplitude and exhibit a constant phase difference relative to one another. In this case, the robot effectively rotates in place.

3.5 Pure Translation: Brittle Star Inspired Rowing Reverse Rowing

In addition to characterizing the motion resulting from the sinusoidal actuation in (1), we were also inspired to reproduce brittle star locomotion patterns observed by Astley Astley (2012), which we interpret as the rowing and reverse-rowing motions shown in Fig. 9. Exact replication of the complex kinematics exhibited by brittle stars is impossible with the idealized rigid robot. However, the rowing and reverse-rowing motions can be simulated qualitatively by making one of the robot limbs inactive, and by altering the neutral position and motion of the remaining two active limbs. To simulate rowing, the neutral position of the limbs was unchanged from the natural state in which the limbs are distributed evenly around the unit circle, i.e., separated by $120^\circ$ from each other. To simulate reverse-rowing, the neutral position of the active limbs was shifted by $30^\circ$ towards the inactive limb. As shown in Fig. 9, this meant that the active limbs were each separated from the inactive limb by $90^\circ$ in the neutral position, and from one another by $180^\circ$. For both rowing and reverse rowing, the active limbs were actuated in anti-phase, i.e., with a phase difference of $180^\circ$.

Figure 9 provides a comparison of experimental tracking results and model predictions for the simulated rowing and reverse-rowing motions with the following actuation parameters: oscillation frequency $f=1.0$ Hz and sweep angle $\xi = 30^\circ$. The rowing results shown in panels (b) and (d) show sustained translation in the positive x-direction. In other words, the robot moves in the direction of the inactive limb, which is consistent with biological observations. Model predictions are also in good agreement with the experimental tracking data. In contrast to the rowing locomotion results presented in Fig. 9b and d, the attempt at simulating reverse-rowing was unsuccessful. As shown in panels (a) and (c), the robot effectively oscillated back and forth in place, with no significant net motion relative to the starting point at $x=0$. Model predictions also show similar behavior. Thus, simply altering the neutral position of the active limbs does not reproduce the reverse-rowing locomotion observed in nature. This issue is discussed in greater in the following section.

Fig. 9

Comparison between model predictions and experimental observations for reverse-rowing (a, c) and rowing (b, d) locomotion over a period of 20 s. Panels (a, b) show results from the low-friction tape-paper experiments, and panels (c, d) show results from the high-friction sandpaper-paper experiments. Experimental data are shown as thin red lines and simulation data are shown as thick black lines. All datasets correspond to oscillation frequency $f=1.0$ Hz and sweep angle $\xi = 30^\circ$. Movie 3 showcases low friction rowing from panel (b)

Fig. 10

Measured and predicted robot translation for the rowing configuration with varying sweep angles. The actuation frequency was $f=1.0$ Hz in all cases. The sweep angle is set to $\xi =20^\circ$ for (a, e), $\xi =30^\circ$ for (b, f), $\xi =40^\circ$ for (c, g) and $\xi =50^\circ$ for (d, h). Panels (a–d) show data for the low-friction tape-paper contact. Panels (e–h) show data for the high-friction sandpaper-paper contact. Experimental data are shown as thin red lines and simulation data are shown as thick black lines

To evaluate the effect of varying actuation parameters on net translation speed for the rowing configuration, we pursued additional experiments and model simulations with sweep angles $\xi = [20,30,40,50]^\circ$ and oscillation frequency $f=1.0$ Hz. In other words, the oscillation amplitude for the active limbs was varied. Figure 10 shows the net translation of the robot center-of-mass as a function of time, x(t). In general, increasing sweep led to an increase in the net translation speed. However, maximum sweep angle was limited by robot stability. For $\xi \ge 60^\circ$, the active limbs moved beyond the center-of-mass of the robot during the actuation cycle, causing the robot to tip over. A comparison of panels (a)-(d) with panels (e)-(h) also indicates a reduction in translation speed with increasing friction. For all cases, model predictions are in good agreement with the experimental tracking data. The model reproduces the back-and-forth nature of the observed motion, in which the oscillation period is determined by the actuation frequency. Moreover, the predicted average translation speeds are consistent with the experimental observations.

Fig. 11

Model predictions for rowing translation speed ($\bar{U}$) as a function of friction coefficient for $f=1.0$ Hz and varying sweep angles $\xi = [20,30,40,50]^\circ$

To provide further insight into the observed reduction in net translation speed for the high-friction sandpaper-paper contact, model predictions were carried out with friction coefficients $\mu \in [0.1,0.9]$ and sweep angles $\xi = [20,30,40,50]^\circ$. The average translation speeds predicted by the model are shown in Fig. 11. Interestingly, for each value of $\xi$, there is an optimal friction coefficient that maximizes translation speed. Beyond this optimum, translation speed decreases monotonically with increasing friction coefficient This is consistent with the experimental observations in Fig. 10, which showed a decrease in average translation speed for the high-friction sandpaper-paper contact. Model predictions also suggest that an increase in the sweep angle increases the maximum translation speed and shifts the optimum friction coefficient higher. Physically, the presence of an optimum could be explained by considering the following limiting scenarios. For $\mu = 0$, the active limbs would simply slide back and forth on the substrate without generating any net friction forces (or translation). However, for very high friction coefficients, the inactive limb may effectively act as an anchor that slows the robot down.

4 Discussion

4.1 Analysis of Translation

Fig. 12

Simplified geometric representation of single active limb

In this section, we pursue a simplified analysis to provide further insight into rowing and reverse rowing locomotion. Specifically, we seek to provide an explanation for why the attempt at replicating reverse rowing was unsuccessful with the rigid-limb tripedal robot used in this study. Without loss of generality, the representation shown in Fig. 12 can be used to describe the kinematics of one active limb for the rowing and reverse rowing modes considered in Sect. 3.5. The horizontal and vertical components of velocity for the active limb, $\dot{\textbf{r}}=[\dot{r}_x,\dot{r}_y]$, can be written as

$$\begin{aligned} \dot{r}_x&= \dot{x} - \ell \dot{\phi } \ \sin (\alpha + \phi ) = \dot{x} - \ell \dot{\phi } (\sin \alpha \ \cos \phi + \cos \alpha \ \sin \phi ), \end{aligned}$$

(8)

$$\begin{aligned} \dot{r}_y&= \ell \dot{\phi } \ \cos (\alpha + \phi ), \end{aligned}$$

(9)

where $\dot{\textbf{x}}=[\dot{x},\dot{y}]$ represents the velocity for the robot center of mass, $\alpha \in (0,\pi )$ represents the constant offset angle for the active limb and $\phi = \xi \sin (\omega t )$ represents the angular actuation with sweep angle $\xi$ and frequency $\omega = 2 \pi f$. Per the model shown in eq. (2), the friction force generated by the active limb in the direction of motion is expected to be proportional to

$$\begin{aligned} F_x \propto -\frac{\dot{r}_x}{\sqrt{\dot{r}_x^2+\dot{r}_y^2}} = -\frac{\dot{x} - \ell \dot{\phi } \sin (\alpha +\phi )}{\sqrt{\dot{x}^2 - 2\dot{x} \ell \dot{\phi } \sin (\alpha + \phi ) + \ell ^2 \dot{\phi }^2}}. \end{aligned}$$

(10)

Given the symmetric actuation of the active limbs in rowing and reverse rowing locomotion, the other active limb would generate an identical frictional force in the direction of motion. The above analysis assumes that the normal force is constant. To test the validity of this assumption, we performed simulations with a constant normal force and found the character of the resulting motion patterns to not change. Modeling the time-varying normal forces is important for the accuracy of the numerical simulations. However, the same trends can be captured with a constant normal force approximation.

For there to be net motion in the horizontal direction, the cycle-averaged value of the friction force must be non-zero, $\bar{F_x} \ne 0$. To evaluate the conditions in which this occurs analytically, we redefine the offeset angle as $\alpha = \pi /2 + \epsilon$ and consider the limit in which the actuation angle is small, $|\phi | \ll 1$. Under this assumption, we have

$$\begin{aligned} \sin (\alpha + \phi ) = \sin (\frac{\pi }{2} + \epsilon + \phi ) = \sin (\frac{\pi }{2}) \cos (\epsilon +\phi ) \approx \cos \epsilon - \phi \sin \epsilon \end{aligned}$$

(11)

such that

$$\begin{aligned} F_x \propto -\frac{\dot{x} - \ell \dot{\phi } (\cos \epsilon - \phi \sin \epsilon )}{\sqrt{\dot{x}^2 - 2\dot{x} \ell \dot{\phi } (\cos \epsilon - \phi \sin \epsilon ) + \ell ^2 \dot{\phi }^2}}. \end{aligned}$$

(12)

To make further analytical progress, we assume that the horizontal motion of the center of mass can be expressed as:

$$\begin{aligned} \dot{x} = A \ell \omega \xi \sin \alpha \cos (\omega t + B), \end{aligned}$$

(13)

in which A and B represent a scaling factor and phase shift in the motion of the center of mass relative to the leading harmonic in the actuation velocity, $\ell \dot{\phi } \sin \alpha = \ell \omega \xi \sin \alpha \cos (\omega t)$. Note that the above expression neglects the (small) cycle-averaged motion of the center of mass as well as any motion at higher harmonics. Substituting the assumed expression for $\dot{x}$ into the simplified friction model and factoring out $\ell \omega \sin \alpha$ yields

$$\begin{aligned} F_x\propto - \frac{A \cos (\omega t + B) - \cos (\omega t)[\cos \epsilon - \xi \sin (\omega t) \sin \epsilon ]}{\sqrt{[A \cos (\omega t + B)]^2 - 2A\cos (\omega t + B)\cos (\omega t)[\cos \epsilon - \xi \sin (\omega t ) \sin \epsilon ] + [\cos (\omega t)]^2}}. \end{aligned}$$

(14)

The above expression indicates that the following three conditions are necessary for the generation of a non-zero cycle-averaged friction force: (1) $\epsilon \ne 0$, (2) $A \ne 0$, and (3) $B \ne n \pi$ with $n \in \mathbb {Z}$. This can be shown by considering each of the three conditions separately.

• (1) If $\epsilon =0$, the friction force expression simplifies to:

  $$\begin{aligned} F_x \propto - \frac{A \cos (\omega t + B) - \cos (\omega t)}{\sqrt{[A \cos (\omega t + B) - \cos (\omega t)]^2}}, \end{aligned}$$

  (15)

  or

  $$\begin{aligned} F_x \propto -sgn(A\cos (\omega t + B) - \cos (\omega t)), \end{aligned}$$

  (16)

  for which $\overline{F_x}=0$ since the signum function for waveforms comprising single Fourier harmonics is positive and negative for the same duration of an oscillation cycle.

• (2) If $A=0$, the friction force expression simplifies to:

  $$\begin{aligned} F_x \propto \frac{\cos (\omega t) [\cos \epsilon - \xi \sin \epsilon \sin (\omega t)]}{\sqrt{[\cos (\omega t)]^2}}, \end{aligned}$$

  (17)

  or

  $$\begin{aligned} F_x \propto sgn(\cos (\omega t)) \ [\cos \epsilon - \xi \sin \epsilon \sin (\omega t)], \end{aligned}$$

  (18)

  since $\overline{sgn(\cos (\omega t))} = 0$ and $\overline{sgn(\cos (\omega t))\sin (\omega t)} = 0$, the above expression also yields $\overline{F_x} = 0$.

• (3) If $B = n\pi$, the $n \in \mathbb {Z}$, the friction force expression simplifies to:

  $$\begin{aligned} F_x \propto sgn(\cos (\omega t)) \frac{\pm A + \cos \epsilon - \xi \sin \epsilon \sin ( \omega t)}{\sqrt{A^2 \pm 2A \cos \epsilon + 1 \pm 2A \xi \sin \epsilon \sin (\omega t)}}. \end{aligned}$$

  (19)

  It can be shown formally (or via simple numerical tests) that the expression above again yields zero cycle-averaged force, $\overline{F_x}=0$.

Condition (1) explains why reverse-rowing, which is characterized by an offset angle $\alpha = \pi /2$ or $\epsilon =0$ in the present work, is unsuccessful. Physically, the geometric nonlinearity in limb motion that arises for $\alpha \ne \pi /2$ and gives rise to a second harmonic in horizontal limb velocity, $\dot{r}_x \propto \sin (2 \omega t)$, is essential to the generation of a cycle-averaged friction force. The results presented in Sect. 4.2 show how this geometric nonlinearity can be reintroduced via a change in limb length over an actuation cycle.

Fig. 13

Simulation (black) vs experiment (red) data of $\dot{r}_x$ (dashed) and $\dot{x}$ (solid) for rowing with $\xi = 30^\circ , f=1$ Hz

Conditions (2) and (3) indicate that there is no cycle-averaged force if the center of mass is held in place ($A=0$) or if the motion of the robot center of mass is exactly in phase or antiphase with the motion of the active limbs. Physically, for dynamics governed by Eq. (4), these conditions are expected to be satisfied naturally. In other words, we expect non-zero motion of the robot center of mass that is out of phase with the motion of the limbs. Indeed, as shown in Fig. 13, the leading harmonic in robot x-direction body velocity is described for simulations by scaling factor $A \approx 0.30$ and phase shift with x-direction limb velocity, $B \approx 0.08$ [rad]. For experiments, the scaling factor is $A\approx 0.57$ and the phase shift is $B \approx 0.23$ [rad]. Note that the experimental velocities were estimated using a first-order derivative of position data obtained from frame-by-frame tracking.

4.2 A Successful Reverse Rowing Gait

Fig. 14

Schematic showing limb length variation l(s, t) for the modified reverse-rowing locomotion strategy. The maximum and minimum limb lengths are set at $l_o = 7.5$ cm and $l_s=2.5$ cm, respectively. The actuation frequency is $f = 1.0$ Hz. Movie 4 provides an illustrative example of reverse-rowing with varying limb length

The results obtained in the previous section showed that reverse-rowing is not possible with the robot developed and tested in this study due to condition (2). This suggests that, in general, rowing locomotion is likely a more effective strategy for radially symmetric crawling robots with fixed limbs. To test if changing limb length could indeed enable crawling with the reverse-rowing mode, we pursued additional simulations with the mathematical model from Sect. 2.3. Note that the results described in the previous sections indicate that this model generates very useful qualitative and quantitative predictions, even if perfect agreement with the experiments is not observed in all cases.

To mimic the reverse-rowing sequence exhibited by brittle stars where arm length varies over a cycle Kano et al. (2017), the length of the active limbs in our model was prescribed to vary as follows over an oscillation cycle:

$$\begin{aligned} l(s,t) = \frac{(l_o-l_{s})}{2} \ (\cos (2 \pi f t) + 1) + l_s. \end{aligned}$$

(20)

The parameter $l_s$ represents the minimum limb length during the cycle, and $l_o = 0.075$ m is the maximum limb length. As shown in Fig. 14, this reproduces a breast stroke-like variation in limb length over a cycle. Model predictions for the net translation speed — away from the inactive limb in this case — are shown in Fig. 15 for varying minimum lengths $l_s = [0.01, 0.03,0.05]$m. For reference, the translation speed for rowing locomotion with rigid arms of length 0.075 m is also reproduced from Fig. 11. The results shown in Fig. 15 confirm that reverse rowing is possible with varying limb length. Further, the translation speed increases monotonically with decreasing $l_s$, i.e., as the relative change in limb length increases. The model also indicates that translation speed for the modified reverse-rowing mode increases initially with increasing friction coefficient, before approaching an asymptotic limit that depends on $l_s$. This is unlike the results obtained for rowing locomotion, which predict that there is an optimal friction coefficient that maximizes translation speed. Further increases in $\mu$ beyond this optimum lead to a decrease in translation speed. These observations suggest that the modified reverse-rowing locomotor mode may be less sensitive to substrate type.

Fig. 15

Predicted translation speeds for rowing and modified reverse-rowing locomotion. In all cases, the sweep angle is $\xi =30^\circ$ and actuation frequency is $f = 1.0$ Hz

In general, model predictions presented in this section indicate that the ability to vary limb length could lead to more robust locomotion capabilities. For robotic systems, variable limb length could be achieved either via the use of soft appendages or by incorporating additional degrees of freedom into rigid limbs, such as in Oki et al. (2015).

4.3 Non-sinusoidal Gait Optimization

This study largely focuses on the analysis of sinusoidal gait patterns. However, there may exist non-sinusoidal gaits that result in faster translation. As a preliminary evaluation of this effect, we revisited the rowing strategy described in §3.5 and pursued parametric optimization of the cyclic actuation of the limbs, i.e., the angular position $\phi (t)$ in (1).

Fig. 16

Isosurfaces of performance metric for parameterized gait using (a) PCHIP splines and (b) piecewise sinusoidal curves

For this optimization, we used a three degree-of-freedom continuous spline that is constrained to be zero at the beginning and end of the cycle, and also constrained to cross the zero axis only once. As a starting point, a Piece-wise Cubic Hermite Interpolating Polynomial (PCHIP) spline was used. We selected PCHIP because it allows for sharper curvatures compared to sinusoidal functions and a more diverse set of allowable functions. Limb oscillation was parameterized using three variables, $\textbf{p} = \{p_1,p_2,p_3\}$, defined as:

$$\begin{aligned} p_1&:= \max _{t \in [0,T]} \ \phi (t)/\xi \end{aligned}$$

(21)

$$\begin{aligned} p_2&:= \min _{t \in [0,T]} \ \phi (t)/\xi \end{aligned}$$

(22)

$$\begin{aligned} p_3&:= \arg _{t \in [0,T]} \ {\phi (t)=0} \quad , \end{aligned}$$

(23)

where $T=2\pi /f$. The variables $p_1$, $p_2$, and $p_3$ represent the maximum angular position, the minimum angular position, and the time corresponding to the zero crossing in the oscillation cycle, respectively. The objective function, $x_f(\textbf{p})$, for the optimization was the final $x-$position of the robot after 5 simulation cycles (i.e., 5 s). We selected 5 cycles to eliminate transient effects, while minimizing simulation time. To maintain consistency with the earlier rowing results, the sweep angle was set to $\xi = 30^\circ$ and the oscillation frequency was fixed at $f = 1.0$ Hz.

Isocontours of $x_f$ are shown in Fig. 16a. The highest performing parameter combination, $p_1 = 0.981$, $p_2 = -0.974$ and $p3 = 0.478$, resulted in nearly sinusoidal gaits. Based on this observation, we also tested similarly parameterized piecewise-sinusoid curves instead of PCHIP curves, and found the resulting $x_f$-map to be similar with a significant computational time reduction (see Fig. 16b). Thus, for additional gait design and optimization, we used the piecewise-sinusoid curve. We applied an adaptive-step gradient search algorithm. The resulting functional was multimodal near the optimum and the optimal parameter sets were found to be near $\textbf{p} \approx \{1,-1,0.456\}$. In other words, the optimal PCHIP and piecewise-sinusoid gaits are both close to sinusoidal (see Fig. 17a). However, by moving the crossover point earlier in the cycle, net translation increases slightly ($\sim 5\%$) for the piecewise-sinusoidal gait compared to a purely sinusoidal gait after 5 cycles (see Fig. 17b). This preliminary evaluation of optimal gaits suggests that the study of harmonic sinusoidal gaits remains a useful starting point for future studies.

Interestingly, the optimization results in Fig. 16 also show that it is possible to get backwards translation ($x_f < 0$) by introducing temporal asymmetry in the gaits ($p_3 > 0.5$). This is consistent with the findings presented in §4.2, which indicate that kinematic asymmetry is required to generate a successful reverse rowing gait.

Fig. 17

Comparison between optimal PCHIP gait (bold black line), piecewise-sinusoid gait (bold gray line), and standard sinusoidal gait (fine dashed line) (a) and resulting distance traveled (b)

5 Conclusion

This study demonstrates that several locomotion strategies are possible for robotic systems with radially-symmetric bodies. Sequential actuation of all limbs can give rise to locomotion along circular orbits with controllable radius. Periodic actuation with a constant phase shift across all limbs ($\Delta \psi = 120^\circ$ for a tripedal robot) leads to rotation in-place. Pure translation is achieved through the presence of an inactive limb that breaks radial symmetry. The ability to move along prescribed curves, rotate in place, and travel in a straight line establishes a framework for future motion planning efforts for radially-symmetric crawling robots. Using the models developed in this paper, we have successfully demonstrated path following for this robot using image-based feedback control Hermes et al. (2021). The primary advantage of radial symmetries highlighted in this work is the omni-directional translation ability. Consequently, robots that require instantaneous omni-directional actuation may benefit most from applying the ideas presented here.

For systems with rigid limbs and sinusoidal actuation, such as the robot developed here, we found only the so-called rowing locomotor mode observed in nature to be effective at locomotion (we cannot comment on feasibility with non-sinusoidal gaits). For this mode, the hind limbs are actuated in anti-phase with one another and the robot moves in the direction of the inactive forelimb. In Sect. 4, we showed via further simplifications to the dynamic model that net translation is only present if certain conditions are met. These conditions establish that a phase shift between the robot center velocity and the limb velocity is generated due to inertial effects, and that this phase shift creates a positive net force over a cycle. Reverse-rowing was only feasible for more complicated systems capable of varying limb length over an actuation cycle. Note that the ability to vary limb length ultimately allows biological and engineered systems to vary the position of the contact points relative to the center of mass. This allows for finer control over the normal and, hence, friction forces acting at each contact point.

The ability to modulate frictional forces can play an important role in crawling locomotion. Indeed, previous studies show that snakes try to maximize normal forces over low-friction surfaces through several different mechanisms; this includes lifting parts of their body off the substrate to enhance normal forces Hu et al. (2009); Marvi and Hu (2012). Predictions made using the simple Coulomb friction model indicate the presence of an optimal sweep-dependent friction coefficient that maximizes translation speed for brittle star inspired rowing locomotion. The optimal friction coefficient values were $\mu < 0.3$ for the range of sweep angles tested here. For higher friction coefficients, translation speed decreased. However, model predictions also suggest that this deterioration of performance can be mitigated by switching to a reverse-rowing strategy, in which limb length varies over an actuation cycle. These differences in crawling efficacy may explain the prevalence of both rowing and reverse-rowing locomotion in nature Astley (2012). The relative performance of these rowing and reverse-rowing locomotor modes in terms of speed and energetic efficiency remains to be evaluated.

Finally, it must be emphasized that the simple model developed here is very much a starting point for further research. More sophisticated frictional models that account for stick–slip dynamics Heslot et al. (1994), or analytical models that take advantage of scale separation between the timescale associated with the fast periodic actuation and the slow macro-scale motion (i.e., translation, large-scale revolution) might provide significant further insight into crawling dynamics. Models grounded in geometric mechanics Kelly and Murray (1995); Ostrowski and Burdick (1998) that can predict motion from periodic shape-space changes for robotic systems could also be valuable.