On the Dynamics of a Heavy Symmetric Ball that Rolls Without Sliding on a Uniformly Rotating Surface of Revolution

Abstract

We study the class of nonholonomic mechanical systems formed by a heavy symmetric ball that rolls without sliding on a surface of revolution, which is either at rest or rotates about its (vertical) figure axis with uniform angular velocity $\Omega$. The first studies of these systems go back over a century, but a comprehensive understanding of their dynamics is still missing. The system has an $\mathrm {SO(3)}\times \mathrm {SO(2)}$ symmetry and reduces to four dimensions. We extend in various directions, particularly from the case $\Omega =0$ to the case $\Omega \not =0$, a number of previous results and give new results. In particular, we prove that the reduced system is Hamiltonizable even if $\Omega \not =0$ and, exploiting the recently introduced “moving energy,” we give sufficient conditions on the profile of the surface that ensure the periodicity of the reduced dynamics and hence the quasiperiodicity of the unreduced dynamics on tori of dimension up to three. Furthermore, we determine all the equilibria of the reduced system, which are classified in three distinct families, and determine their stability properties. In addition to this, we give a new form of the equations of motion of nonholonomic systems in quasi-velocities which, at variance from the well-known Hamel equations, use any set of quasi-velocities and explicitly contain the reaction forces.

1 Introduction

1.1 Motivations

This paper is devoted to the class of nonholonomic mechanical systems formed by a ball that rolls without sliding on a surface of revolution, under the action of gravity, which is assumed to be directed as the surface figure axis. The ball is assumed to be dynamically symmetric, namely, its center of mass coincides with its center and its three moments of inertia relative to the center are equal. The surface may either be at rest ($\Omega =0$) or rotate with constant angular velocity $\Omega \not =0$ about its figure axis. This system has an eight-dimensional phase space, but its $\mathrm {SO(3)}\times \mathrm {SO(2)}$-symmetry (rotate the ball about its center, and the center about the surface figure axis) allows a reduction to dimension 4.

The dynamics of this system with particular—and simple—profiles of the surface (planes, cylinders, cones) is integrable by elementary techniques, and the first results in this direction date back at least to the work of Routh (1955). However, there have been relatively few general studies of these systems, and correspondingly a global comprehension of the dynamics with any profile is still largely missing.

When $\Omega =0$, the nonholonomic constraint is linear in the velocities and the energy is conserved; being $\mathrm {SO(3)}\times \mathrm {SO(2)}$-invariant, the energy is also a first integral of the reduced system. Routh (1955) noticed the existence of two additional $\mathrm {SO(3)}\times \mathrm {SO(2)}$-invariant independent integrals of motion which, together with the energy, imply that the 4-dimensional reduced system is integrable by quadratures. Routh also began the study of some stability questions, mostly for $\Omega =0$.

A breakthrough, in our opinion, came in the mid-1990s when the quasiperiodicity of the system with $\Omega =0$ and any convex profile was proved by Hermans (1995) and Zenkov (1995): The center of the ball rotates around the figure axis and oscillates periodically between two parallels of the surface, and the motion of the ball about its center adds a third frequency. These results use techniques proper to the reconstruction from periodic reduced dynamics; see Field (1990), Krupa (1990), Hermans (1995), and Fassò and Giacobbe (2007). One of the reasons of interest of this result is the fact that it disclosed a class of non-Hamiltonian integrable systems.

Another important achievement in the case $\Omega =0$ was, a few years later, the discovery by Borisov, Mamaev, and Kilin of the existence of a rank-two Poisson structure in the four-dimensional reduced space that makes the reduced system Hamiltonian after a time reparametrization (Borisov et al. 2002).

A non-sporadic study of the case $\Omega \not =0$ began in the early 2000s and led to two main results. Borisov, Mamaev, and Kilin proved the existence of two first integrals of Routh type and of an invariant measure of the four-dimensional reduced system (Borisov et al. 2002). (They considered the case with no gravity, but the generalization is immediate.) From this, they deduced, via the Euler–Jacobi theorem, the integrability by quadratures of the reduced system.

A basic difficulty for a more detailed study of the case $\Omega \not =0$ was the absence of the energy integral, which is due to the fact that if the surface rotates then the nonholonomic constraint is not linear but affine (linear nonhomogeneous) in the velocities (Fassò and Sansonetto 2015). However, two of the present authors proved that, under suitable symmetry hypotheses, nonholonomic systems with affine constraints possess a first integral which is a modification of the energy, and called it a moving energy (Fassò and Sansonetto 2016). The existence of a moving energy for the ball on a rotating surface was proved in Fassò and Sansonetto (2016), and its expression for this and other systems was subsequently given by Borisov et al. (2015) (who referred to it as to the “Jacobi integral”).

Using the moving energy instead of the energy, Fassò and Sansonetto (2016) also proved that the quasiperiodicity of the dynamics of the ball in a convex surface persists if the surface rotates, at least if the angular velocity $\Omega$ is sufficiently small.

Nevertheless, at present, a general comprehension of the dynamics of this class of systems, with any geometry of the profile, seems to be lacking even in the case $\Omega =0$. For instance, important issues, such as a general study of the equilibria of the four-dimensional reduced system (which are key to the comprehension of the reduced—and hence unreduced—dynamics), have never been undertaken. Our purpose in this paper is to begin this study, giving new results, in particular, on its Hamiltonization, integrability and relative equilibria.

1.2 Content and Organization of the Paper

We describe the system in Sect. 2. We limit our treatment to those cases in which the ball rolls on a surface ${\tilde{\Sigma }}$ which is a graph over the horizontal plane and the ball moves on top of it. Following Hermans (1995) and Fassò et al. (2005), and at variance from other treatments (Routh 1955; Zenkov 1995; Borisov et al. 2002), we assign the surface $\Sigma$ to which the center of the ball belongs, not that on which the ball rolls. The smoothness of ${\tilde{\Sigma }}$ puts some conditions on the curvature of $\Sigma$, which are clarified in Proposition 1.

The equations of motion of the system are derived in the “Appendix,” as an instance of a novel form of the equations of motion of nonholonomic systems in quasi-velocities which we derive there. At variance from Hamel equations, that choose the quasi-velocities so as to “hide” the reaction forces (Hamel 1904; Neimark and Fufaev 1972; Bloch et al. 2009), our equations use any set of quasi-velocities and include the explicit expression of the reaction forces as a function on the phase space (Proposition 16). From a general perspective, this might be useful in the study of a number of questions in nonholonomic mechanics in which the reaction forces play a dominant role, such as the existence of first integrals, invariant measures etc.

Since the $\mathrm {SO(2)}$-action given by spatial rotations of the system around the surface figure axis has isotropy, the quotient space $M_4=M_8/(\mathrm {SO(3)}\times \mathrm {SO(2)})$ is a stratified space. It consists of a singular, one-dimensional stratum $M_4^\textrm{sing}$ that contains all reduced kinematical states in which the center of the ball is at the “vertex” of the surface (the point of $\Sigma$ that belongs to the figure axis) with zero velocity, and of a regular four-dimensional stratum $M_4^\textrm{reg}$. Following (Hermans 1995; Fassò et al. 2005) we will embed $M_4$ in ${\mathbb {R}}^{5}$ through the use of a set of 5 invariant polynomials. This will allow us to give some results on the entire reduced space $M_4$. Subsequently, we will specialize the analysis to $M_4^\textrm{reg}$ or even to its subset $M_4^\circ$ obtained by removing all states in which the center of the ball passes (with any velocity) through the vertex. In so doing, when this makes the description more transparent, we will reverse to polar coordinates.

In Sect. 3, we study some general properties of the reduced and unreduced systems. After giving the expressions of the two Routh integrals and of the moving energy, extending a similar analysis in Fassò et al. (2005) we study their independence (Proposition 3). Next, we show that the motions of the reduced system (including those that transit through the vertex) are of four possible types (equilibria, periodic motions, motions asymptotic to equilibria, motions which go to infinity; Proposition 4) and we discuss their reconstruction to the full system (Proposition 5). In particular, the already mentioned results on the reconstruction under compact symmetry groups (Krupa 1990; Field 1990) imply that motions of the full system in relative equilibria and relative periodic orbits are quasiperiodic on tori of dimension up to, respectively, two and three. Lastly, we prove that the level sets of the moving energy in $M_4$ are all compact—so that the reduced dynamics is generically periodic and the unreduced one is generically quasiperiodic—in two cases: if $\Omega =0$ and the surface goes to $+\infty$ at infinity, and if $\Omega \not =0$ and the surface goes to $+\infty$ at infinity sufficiently fast, more than quadratically in the distance (Proposition 7). We stress that it is only the behavior at infinity of the surface—and no other details of it—that plays a role in these two results. The first was in fact proven in Hermans (1995); Zenkov (1995); Fassò et al. (2005), but was there stated only for either convex or compact surfaces. The case $\Omega \not =0$ is new. (A very weak version of it was proven in Fassò and Sansonetto (2016), with a continuation argument from the case $\Omega =0$, for convex surfaces and sufficiently small $\Omega$’s.)

In Sect. 4, we restrict our analysis to the subset $M_4^\circ$ (all states with the ball at vertex removed) and first prove the existence in $M_4^\circ$ of a rank-two Poisson tensor that makes the system Hamiltonian, with the moving energy as Hamilton function (Proposition 8) and the two Routh integrals as Casimirs. This tensor reduces to the ones of Ramos (2004); Fassò et al. (2005) and (up to a factor related to a time reparametrization) of Borisov et al. (2002) for $\Omega =0$. The interest of this Hamiltonization result resides also in the fact that while the Hamiltonizability of nonholonomic systems has been so far extensively studied in the case of linear constraints, very little is known in the case of affine constraints (the only other result we are aware of concerns the Veselova system (García-Naranjo 2007). Next, we show that the restriction of the dynamics to the level sets of the two Routh integrals can be seen as a natural Lagrangian system with one degree of freedom, namely with a Lagrangian which is the difference between the kinetic energy of a point holonomically constrained to the surface $\Sigma$ and of an “effective” potential energy which depends on the value of the two Routh integrals (Proposition 9).

In Sect. 5, we determine the equilibria of the reduced system in $M_4^\circ$, thus excluding those at the vertex (Proposition 10). An equilibrium of the reduced system corresponds to motions of the unreduced system in which the center of the ball either stands still in space or moves along a parallel of the surface $\Sigma$, namely on a horizontal circle, and the component of the angular velocity of the ball normal to the surface is constant. We prove that there are reduced equilibria on any parallel of $\Sigma$, which are different if the parallel is critical (a local maximum or minimum or a saddle point of the radial height) or regular. On each critical parallel there are two families of reduced equilibria, the first for all $\Omega$’s and the second only for $\Omega \not =0$, both parametrized by the vertical component $\omega _\textrm{z}\in {\mathbb {R}}$ of the ball’s angular velocity. In the first family the center of the ball stands still in space; this happens also if the surface $\Sigma$ rotates, with any $\Omega$. In the reduced equilibria of the second family, instead, the center of the ball rotates uniformly on the parallel with nonzero angular velocity $c\Omega$ with a certain $0<c<1$ which depends on the moment of inertia of the ball. On regular parallels, there is, for each $\Omega \in {\mathbb {R}}$, a family of reduced equilibria parametrized by the (nonzero) angular velocity of the center of the ball.

In Sect. 6, we study the stability of the reduced equilibria, regarding them as equilibria of the restriction of the reduced system to a level set of the two Routh integrals, namely, to a symplectic leaf of the rank-two Poisson structure. In order to avoid ambiguities, we thus speak of “leafwise-stability.” This study reduces to the study of the critical points of the effective potential. We first give analytical conditions for the leafwise-(in)stability of the reduced equilibria of the three families (Proposition 11) and then we study these conditions, with particular attention to the effect of the surface rotation. The resulting bifurcation scenario, which is somehow rich, is described in Propositions 12–14, and a number of situations are considered. Overall, we reach a fairly complete understanding of the reduced equilibria’s leafwise-stability.

In Sect. 7, we study in some detail, and partly numerically, the particular case in which the surface is a paraboloid. This has two motivations. First, since the behavior at infinity of the surface is exactly quadratic in the distance from the center, our result about the compactness of the level sets of the moving energy does not apply when $\Omega \not =0$. Nevertheless, using the fact that in this case the two Routh integrals can be explicitly determined, we can prove that the common level sets of the three first integrals are compact, so that the dynamics of the reduced system is generically periodic. This suggests that our integrability results can be improved. Second, we investigate numerically the existence and number of reduced equilibria on the level sets of the two Routh integrals, finding that on each of them there are between one (leafwise-stable) and three (one of which leafwise-unstable) reduced equilibria.

In the very short Conclusions, we point out some open problems and some future research directions.

Fig. 1

Generatrices $\Gamma$ and ${\tilde{\Gamma }}$ of the surfaces $\Sigma$ and ${\tilde{\Sigma }}$

2 The System and Its Reduction

2.1 The System

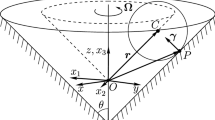
We start with the holonomic system formed by a homogeneous ball of mass m and radius a, the center C of which is constrained to belong to a smooth surface of revolution $\Sigma$ embedded in ${\mathbb {R}}^{3}\ni (\textrm{x},\textrm{y},\textrm{z})$ and produced by the rotation, about the $\textrm{z}$-axis, of the graph $\Gamma$ of a smooth function, see Fig. 1. Precisely, in view of a later rescaling of the coordinates, we assume that $\Sigma$ is described by the equation

$$\begin{aligned} \textrm{z}= a \, f\big (\textstyle { \frac{1}{a} \sqrt{\textrm{x}^2+\textrm{y}^2} }\,\big ) \,,\qquad (\textrm{x},\textrm{y})\in {\mathbb {R}}^{2} \,, \end{aligned}$$

with an even and smooth function $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ that we call the “profile function,” and the curve $\Gamma$ is defined as the graph of the function af. Note that f has either a minimum or a maximum at 0.

The configuration manifold of this holonomic system can be identified with ${\mathbb {R}}^{2}\times \mathrm {SO(3)}\ni (x,{\mathcal {R}})$, where $x=(x_1,x_2)$ are the a-rescaled $(\textrm{x},\textrm{y})$-coordinates of C, so that $OC=(ax_1,ax_2,af(|x|))$, and the matrix ${\mathcal {R}}$ fixes the attitude of the ball. After (right) trivialization of the tangent bundle of $\mathrm {SO(3)}$, the phase space of the system can be identified with the ten-dimensional manifold

$$\begin{aligned} M_{10} = {\mathbb {R}}^{2}\times \mathrm {SO(3)}\times {\mathbb {R}}^{2}\times {\mathbb {R}}^{3}\ni (x,{\mathcal {R}},\dot{x},\omega )\, \end{aligned}$$

where $\omega =(\omega _\textrm{x},\omega _\textrm{y},\omega _\textrm{z})$ is the angular velocity of the ball relative to, and written in, the spatial frame.

We assume that the only active force that acts on the system is weight, directed as the downward $\textrm{z}$-axis. We denote by g the gravity acceleration and by $mka^2$ the moment of inertia of the ball with respect to C; thus, $0<k<1$ ($k=\frac{2}{5}$ for a homogeneous ball). Then, up to an overall factor $ma^2$, the Lagrangian of the system is

$$\begin{aligned} {\mathcal {L}}(x,{\mathcal {R}},\dot{x},\omega ) = \frac{1}{2} |\dot{x}|^2 + \frac{1}{2} \Big ( \frac{x\cdot \dot{x}}{|x|} \,f'(|x|) \Big )^2 + \frac{1}{2} k |\omega |^2 - {\hat{g}}f(|x|) \end{aligned}$$

(1)

with ${\hat{g}}=g/a$.

Next, we introduce the nonholonomic constraint that the ball rolls without sliding on a surface ${\tilde{\Sigma }}$ which lies below $\Sigma$ and rotates with constant angular velocity $\Omega e_\textrm{z}$ about the $\textrm{z}$-axis. The points of ${\tilde{\Sigma }}$ have normal distance a from those of $\Sigma$. The surface ${\tilde{\Sigma }}$ is produced by the rotation of the curve ${\tilde{\Gamma }}$ which is parallel to $\Gamma$, has normal distance a from it, and lies below it. It is necessary to assume that ${\tilde{\Gamma }}$ is a regular curve and that, at each point of contact with ${\tilde{\Sigma }}$, the ball touches ${\tilde{\Sigma }}$ in only that point. The latter condition requires that, at each point at which it is not concave (namely, its signed curvature is nonnegative), the curve ${\tilde{\Gamma }}$ has radius of curvature $>a$.

As it turns out, the latter condition follows from the former, which also ensures that ${\tilde{\Gamma }}$ is diffeomorphic to $\Gamma$:

Proposition 1

${\tilde{\Gamma }}$ is the image of a smooth immersion if and only if

$$\begin{aligned} f''(s) > - (1+f'(s)^2)^{3/2} \qquad \forall s \in {\mathbb {R}}\,. \end{aligned}$$

(2)

In such a case, ${\tilde{\Gamma }}$ is diffeomorphic to $\Gamma$ and has radius of curvature $>a$ at each point at which it is not concave.

Proof

$\Gamma$ is the image of the immersion $\iota :{\mathbb {R}}\rightarrow {\mathbb {R}}^{2}$, $\iota (s)=(as,af(s))$. The downward unit normal to $\Gamma$ at the point $\iota (s)$ is $N(s)=\frac{1}{\sqrt{1+f'(s)^2}}(f'(s),-1)$. Thus, ${\tilde{\Gamma }}$ is the image of the map ${\tilde{\iota }}:{\mathbb {R}}\rightarrow {\mathbb {R}}^{2}$ given by

$$\begin{aligned} {\tilde{\iota }}(s) = \iota (s)+aN(s) = \bigg ( as + \frac{af'(s)}{\sqrt{1+f'(s)^2}} \;,\, af(s) - \frac{a}{\sqrt{1+f'(s)^2}} \bigg )\,. \end{aligned}$$

Since ${\tilde{\iota }}' = a\big (1+\frac{f''}{(1+f'^2)^{3/2}} , \big (1+\frac{f''}{(1+f'^2)^{3/2}}\big )f'\big )$, ${\tilde{\iota }}$ is an immersion if and only if $f''(s)\not =-(1+f'(s)^2)^{3/2}$ for all $s\in {\mathbb {R}}$. The fact that f is defined in all of ${\mathbb {R}}$ rules out the possibility that $f''(s)<-(1+f'(s)^2)^{3/2}$ for all $s\in {\mathbb {R}}$. (By a standard comparison theorem for ODEs, since the solution of $y'=-(1+y^2)^{3/2}$, $y(0)=0$, blows up to $-\infty$ in finite time, if f would satisfy such a condition then its derivative could not be defined in all of ${\mathbb {R}}$.) Thus, ${\tilde{\iota }}$ is an immersion if and only if f satisfies (2).

If the signed curvature of $\Gamma$ at the point $\iota (s)$ is $\kappa (s)$, then that of ${\tilde{\Gamma }}$ at the point ${\tilde{\iota }}(s)$ is $\frac{\kappa (s)}{|1+a\kappa (s)|}=:{\tilde{\kappa }}(s)$ (see, e.g., Abbena et al. 2006). Thus, ${\tilde{\kappa }}(s)<\frac{1}{a}$ at every point s where $\kappa (s)>0$.

Finally, if f satisfies (2) then the map ${\mathcal {C}}:{\mathbb {R}}^{2}\rightarrow {\mathbb {R}}^{2}$, ${\mathcal {C}}(\textrm{x},\textrm{z}) = \big ( \textrm{x}+\frac{af'(\frac{\textrm{x}}{a})}{\sqrt{1+f'(\frac{\textrm{x}}{a})^2}} \,,\, \textrm{z}-\frac{a}{\sqrt{1+f'(\frac{\textrm{x}}{a})^2}}\big )$ is a diffeomorphism, and ${\tilde{\iota }}={\mathcal {C}}\circ \iota$. $\square$

We will assume that (2) is satisfied. This excludes cases such that of a conical $\Sigma$. However, many of our results can be applied to such cases as well after removing the vertex or deforming the surface in a suitable neighborhood of the vertex. Cases in which the profile function is defined only in an open bounded interval, and possibly diverges at its boundary, could be easily treated as well. However, we note that in such cases it might happen that condition (2) is satisfied with the opposite sign, and this might affect the stability analysis of Sect. 6.3.

The nonholonomic constraint forces the velocity $v_P$ of the point P of the ball in contact with the surface ${\tilde{\Sigma }}$ to be equal to $\Omega \,e_\textrm{z}\times OP$. Since $v_P=v_C + \omega \times CP$ and $OP=OC+CP$, the nonholonomic constraint is

$$\begin{aligned} v_C + \omega \times CP - \Omega e_\textrm{z}\times (OC+CP) =0 \,. \end{aligned}$$

(3)

Equation (3) defines an eight-dimensional submanifold $M_8$ of $M_{10}$ which is diffeomorphic to ${\mathbb {R}}^{2}\times \mathrm {SO(3)}\times {\mathbb {R}}^{3}$ and can be globally parametrized with $(x,{\mathcal {R}},\dot{x},\omega _\textrm{z})$. Indeed, since $CP=a\,n(x)$ with¹

$$\begin{aligned} n(x) {:}{=} \left( \frac{x_1}{|x|} \frac{f'}{F} , \frac{x_2}{|x|} \frac{f'}{F} ,-\frac{1}{F} \right) \,, \end{aligned}$$

(4)

where

$$\begin{aligned} F \;:=\; \sqrt{ 1 +f'^2} \,, \end{aligned}$$

(5)

the (downward) normal unit vector to $\Sigma$ at its point $\big (ax_1,ax_2,af\big )$, the first two entries of (3) can be written as

$$\begin{aligned} \omega _\textrm{x}= (\Omega x_1-\dot{x}_2)F + (\Omega -\omega _\textrm{z})\frac{x_1}{|x|}f' \,,\qquad \omega _\textrm{y}= (\Omega x_2+\dot{x}_1)F + (\Omega -\omega _\textrm{z})\frac{x_2}{|x|}f' \,. \end{aligned}$$

(6)

(The third equation in (3) is obviously not independent of the first two.) We thus identify

$$\begin{aligned} M_8 = {\mathbb {R}}^{2}\times \mathrm {SO(3)}\times {\mathbb {R}}^{2}\times {\mathbb {R}}\ni (x,{\mathcal {R}},\dot{x},\omega _\textrm{z}) \,. \end{aligned}$$

Clearly, the functions $\frac{ x\cdot \dot{x}}{|x|} f'$ and $\frac{x_i}{|x|}f'$, $i=1,2$, that enter expressions (1) and (6) are not defined at $x=0$ but extend smoothly to 0 at $x=0$. In order to make smoothness at $x=0$ transparent, following (Fassò et al. 2005) we substitute the profile function f with a smooth function $\psi :{\mathbb {R}}\rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} f(r) = \psi \big ( \textstyle { \frac{1}{2}{r^2}} \big ) \qquad \forall r\in {\mathbb {R}}\,. \end{aligned}$$

The existence of such a function is granted by a result of Whitney (1943) (see also Golubitski and Guillemin 1973, pages 103, 108) on account of the fact that f is even. Note that $f'(r)=r\psi '\big (\frac{r^2}{2}\big )$ and

$$\begin{aligned} \psi '\Big (\frac{r^2}{2}\Big ) = \frac{f'(r)}{r} \qquad \mathrm {for\ } r>0 \,,\qquad \psi '(0) = f''(0) \,. \end{aligned}$$

However, since $f''(r)=\psi '\big (\frac{r^2}{2}\big ) +r^2\psi ''\big (\frac{r^2}{2}\big )$ and

$$\begin{aligned} \psi ''\Big (\frac{r^2}{2}\Big ) = \frac{rf''(r)-f'(r)}{r^3} \quad \mathrm {for\ } r>0 \,, \end{aligned}$$

we will use $f''$ when we need to stress the dependence on the convexity properties of the profile.

The equations of motion of this nonholonomic system are derived in the “Appendix.” We need them only as a tool to deduce those of the reduced system.

2.2 The $\mathbf {\mathrm {SO(3)}\times \mathrm {SO(2)}}$-Reduced System

Consider now the action $\Xi$ of $\mathrm {SO(3)}\times \mathrm {SO(2)}$ on $M_{10}$ given by

$$\begin{aligned} \Xi _{(S,P)}(x,{\mathcal {R}},\dot{x},\omega ) = (Px,P{\mathcal {R}}S,P\dot{x},P\omega ) \,, \end{aligned}$$

namely, $\mathrm {SO(3)}$ acts on the right on itself and $\mathrm {SO(2)}$ acts by rotations about the z axis. From (6), it follows that the constraint manifold $M_8$ is invariant under the action $\Xi$. Therefore, $\Xi$ restricts to an action on $M_8$. Moreover, since the Lagrangian (1) is invariant under $\Xi$, the equations of motion of the nonholonomic system in $M_8$ are invariant under the restriction of $\Xi$ to $M_8$ (Bates and Śniatycki 1993; Bloch et al. 1996) and can be reduced to $M_8/(\mathrm {SO(3)}\times \mathrm {SO(2)})$. Since the actions of $\mathrm {SO(3)}$ and $\mathrm {SO(2)}$ commute, the reduction can be performed in stages.

Since the Lagrangian and the constraint are independent of the attitude ${\mathcal {R}}$ of the ball, the $\mathrm {SO(3)}$-reduction consists in simply cutting off the $\mathrm {SO(3)}$ factor of $M_8$, and the $\mathrm {SO(3)}$-reduced space is the five-dimensional manifold

$$\begin{aligned} M_5 = {\mathbb {R}}^{2}\times {\mathbb {R}}^{2}\times {\mathbb {R}}\ni (x,\dot{x},\omega _\textrm{z}) \,. \end{aligned}$$

The $\mathrm {SO(2)}$-action on $M_{8}$ induces an action on $M_5$ given by $P.(x,\dot{x},\omega _\textrm{z})= (Px,P\dot{x},\omega _\textrm{z})$, which is free at all points of $M_5$ except at those with $x = \dot{x} = 0$ (the kinematical states in which the ball is at the vertex of the surface and the velocity of its center of mass is zero—hence, its angular velocity is vertical).²

The reduction under this action is well known. In fact, $\mathrm {SO(2)}$ does not act on the ${\mathbb {R}}$-factor of $M_5$, while its action on the factor ${\mathbb {R}}^{2}\times {\mathbb {R}}^{2}$ is nothing but the familiar $\mathrm {SO(2)}$-action of the 1:1 oscillator (Hermans 1995; Fassò et al. 2005). Therefore, the reduced space $M_5/\mathrm {SO(2)}=M_8/(\mathrm {SO(3)}\times \mathrm {SO(2)})$ can be identified with the semialgebraic variety

$$\begin{aligned} M_4 = \big \{ (p_0,p_1,p_2,p_3,p_4) \in {\mathbb {R}}^{5} \;:\; 4p_0 p_1 =p_2^2+p_3^2 \,,\; p_0 \ge 0\,,\; p_1 \ge 0 \big \} \end{aligned}$$

immersed in ${\mathbb {R}}^{5} \ni (p_0,p_1,p_2,p_3,p_4)=:p$, with quotient map $M_5\rightarrow M_4$ given by

$$\begin{aligned} p_0 = \frac{1}{2}\, |\dot{x}|^2 \,,\quad p_1 =\frac{1}{2}\,|x|^2 \,,\quad p_2 = x\cdot \dot{x} \,,\quad p_3 = x_1\dot{x}_2 - x_2\dot{x}_1 \,,\quad p_4 = \omega \cdot n(x) \end{aligned}$$

(7)

(a set of generators of the invariant polynomials of the $\mathrm {SO(2)}$-action, see Hermans (1995); Cushman et al. (2010); see also Borisov et al. (2002)).

The last coordinate $p_4$ for ${\mathbb {R}}^{5}$ has been chosen as $\omega \cdot n$, instead of $\omega _\textrm{z}$, because this will somehow simplify the expression, and the analysis, of the moving energy. It also simplifies the equations that define the other two first integrals of the system, $J_1$ and $J_2$ below, but this is actually not that important.

The semialgebraic variety $M_4$ consists of two strata: a “singular” one-dimensional stratum

$$\begin{aligned} M_4^\textrm{sing}= \{p\in {\mathbb {R}}^{5}\; : \; p_0 = p_1 =p_2=p_3 = 0\} \approx {\mathbb {R}}\ni p_4\,, \end{aligned}$$

which is the quotient of the one-dimensional submanifold $M_5^\textrm{sing}= \{(0,0)\}\times \{(0,0)\}\times {\mathbb {R}}$ of $M_5$ left fixed by the $\mathrm {SO(2)}$-action, and can be identified with it, and a four-dimensional “regular” stratum

$$\begin{aligned} M_4^\textrm{reg} = \big \{p\in {\mathbb {R}}^{5} \;:\; 4p_0 p_1 =p_2^2+p_3^2\,,\; p_0 \ge 0\,,\; p_1 \ge 0\,,\; (p_0 ,p_1 )\not =(0,0) \big \} \,, \end{aligned}$$

which is the quotient of the open subset of $M_5$ where the $\mathrm {SO(2)}$-action is free.

We will denote

$$\begin{aligned} \pi :M_8\rightarrow M_4 \end{aligned}$$

the quotient map associated with the $\mathrm {SO(3)}\times \mathrm {SO(2)}$-action in $M_8$. Note that

$$\begin{aligned} M_4^\textrm{reg}=\pi (M_8^\textrm{reg}) \end{aligned}$$

with $M_8^\textrm{reg} = ({\mathbb {R}}^{2}\setminus \{0\}) \times \mathrm {SO(3)}\times ({\mathbb {R}}^{2}\setminus \{0\}) \times {\mathbb {R}}$.

At a certain stage, we will restrict to the submanifold of $M_4^\textrm{reg}$ where $p_1>0$, which is diffeomorphic to ${\mathbb {R}}_+\times {\mathbb {R}}^{3}$ and can be globally parametrized with either $(p_1,p_2,p_3,p_4)$ or $(r,\dot{r},\dot{\theta },\omega _n)$ (or, for that matter, with $(r,\dot{r},\dot{\theta },\omega _\textrm{z})$ as well). In fact, we will switch between these two parametrizations depending on the needs: the former is closely linked to the theory in $M_4$ and $M_4^\textrm{reg}$, the latter has a more direct physical interpretation.

Remark

The manifold $M_4^\textrm{reg}$ is diffeomorphic to $({\mathbb {R}}^{3}\setminus \{0\})\times {\mathbb {R}}$, with global parametrization $({\mathbb {R}}^{3}\setminus \{0\})\!\times \!{\mathbb {R}}\ni \big ((y,p_2,p_3),p_4\big ) \!\mapsto \! \Big (\frac{1}{2}\Big (\sqrt{y^2\!+\!p_2^2\!+\!p_3^2}-y\Big ), \frac{1}{2}\Big (\sqrt{y^2+p_2^2+p_3^2}\,+\,y\Big ), p_2,p_3,p_4 \Big ) \,.$ However, we will prefer using its embedding in ${\mathbb {R}}^{5}$.

2.3 The Equations of Motion of the Reduced System

Following (Hermans 1995; Fassò et al. 2005), we write the equations of motion of the $\mathrm {SO(3)}\times \mathrm {SO(2)}$-reduced system in $M_4$ (from now on, “reduced system”) as the restriction to $M_4$ of a set of equations in ${\mathbb {R}}^{5}$. The deduction of these equations is detailed in the “Appendix.”

The equations of motion of the reduced system are the restriction to $M_4$ of the equation

$$\begin{aligned} \dot{p} = X(p) \,,\qquad p=(p_0 ,p_1,p_2,p_3,p_4) \in {\mathbb {R}}^{5} \, \end{aligned}$$

(8)

where $X=(X_0,X_1,X_2,X_3,X_4)$ is the vector field in ${\mathbb {R}}^{5}$ with components

$$\begin{aligned} \begin{aligned} X_0&= p_2\Big ( \big (\mu p_3 p_4\psi '' -p_2^2\psi '\psi '' - \gamma \psi ' -2p_0 \psi '^2\big ){\mathcal {F}}^2 + \Omega \mu p_3\big (\psi '^2+{\mathcal {F}}\psi '') {\mathcal {F}}^2 \Big ) \\ X_1&= p_2 \\ X_2&= \big ( 2p_0 -\mu p_3 p_4\psi ' -2 \gamma p_1 \psi '- 2p_1 p_2^2 \psi '\psi ''\big ){\mathcal {F}}^2 - \Omega \mu p_3 \big (1+\psi '{\mathcal {F}}\big ){\mathcal {F}}^2 \\ X_3&= p_2\, \big ( G_3 p_4+ \Omega g_3\big ) \\ X_4&= p_2\, \big (G_4 p_3 + \Omega g_4\big ) \end{aligned} \end{aligned}$$

(9)

where

$$\begin{aligned} \mu = \frac{k}{1+k} \,,\qquad \gamma = \frac{{\hat{g}}}{1+k} \,,\qquad {\mathcal {F}}(p_1)=\frac{1}{F(\sqrt{2p_1})} =\frac{1}{\sqrt{1+2p_1\psi '(p_1)^2}} \,, \end{aligned}$$

(10)

and

$$\begin{aligned} \begin{aligned} G_3&= \mu \big (\psi ' + 2 p_1 \psi ''\big ) {\mathcal {F}}^2 \,,&\qquad g_3&= \mu \big ( 1+(\psi ' + 2 p_1 \psi ''){\mathcal {F}}^3 \big ) \\ G_4&= \big (\psi '^3 - \psi ''\big ) {\mathcal {F}}^2 \,,&g_4&= \big (1+{\mathcal {F}}\psi '\big )\, \big ( \psi '+2p_1 \psi ''\big ){\mathcal {F}}^2 \,. \end{aligned} \end{aligned}$$

(11)

Note that $\frac{1}{2}<\mu <1$ and that $\psi$, ${\mathcal {F}}$, $G_3$, $G_4$, $g_3$ and $g_4$ are functions of $p_1$ alone and are independent of $\Omega$. Instead, f and F are functions of r, and $F(r)=1/{\mathcal {F}}(r^2/2)$.

For consistency, we note that $M_4$ is invariant under the flow of the vector field X in ${\mathbb {R}}^{5}$: X vanishes at the points of $M_4^\textrm{sing}$ and is tangent to $M_4^\textrm{reg}$ given that $L_X(p_2^2+p_3^2-4p_0 p_1 )=0$.

From (9), it follows that the equilibria of the reduced system are the points where $p_2=0$ and $X_2=0$. They are all the points of the singular stratum $M_4^\textrm{sing}$ and the points of the set

$$\begin{aligned} {\mathcal {E}}_4^\textrm{reg} = \big \{ p\in M_4^\textrm{reg} \,:\; p_2 = 0\,,\; X_2(p_0 ,p_1,0,p_3,p_4) = 0 \big \} \,. \end{aligned}$$

(12)

The reduced equilibria forming the singular stratum $M_4^\textrm{sing}$ are the projection of relative equilibria in $M_8$ which consist of motions in which the ball stands at the vertex of the surface and uniformly spins with constant, vertical angular velocity. Relative equilibria that project onto reduced equilibria in ${\mathcal {E}}_4^\textrm{reg}$ consist instead of motions of the nonholonomic system in $M_8$ in which the ball uniformly rolls along a horizontal circle in ${\tilde{\Sigma }}$. We will study reduced equilibria in ${\mathcal {E}}_4^\textrm{reg}$ and their stability in Sect. 5. Instead, we will not study in this work the stability of the reduced equilibria in $M_4^\textrm{sing}$, and the related existence of motions asymptotic to/from them. One possible approach to this question is via the analysis of the system in the $\mathrm {SO(3)}$-reduced space $M_5$, which is extraneous to the approach taken here and is left for a separate work.³

Finally, we note that the dynamics of the reduced system relative to a certain $\Omega \not =0$ is conjugate by the reflection

$$\begin{aligned} C:M_4^\textrm{reg}\rightarrow M_4^\textrm{reg}\,, \qquad C(p_0,p_1,p_2,p_3,p_4)=(p_0,p_1,p_2,-p_3,-p_4) \end{aligned}$$

(13)

to that of the reduced system relative to $-\Omega$. In fact, if we make momentarily explicit the dependence of the vector field X on the surface’s angular velocity $\Omega$ by denoting it $X_\Omega$, it follows from (9) that

$$\begin{aligned} C_*X_\Omega = X_{-\Omega } \qquad \forall \Omega \in {\mathbb {R}}\,. \end{aligned}$$

(14)

In particular, the dynamics at $\Omega =0$ is invariant under the reflection C.

3 Reduced and Unreduced Dynamics

In this section, we first describe some general features of the dynamics of the reduced and unreduced systems and then particularize to the case of coercive profile functions.

3.1 The First Integrals

The reduced system (and hence the unreduced one) is known to have three integrals of motion: the moving energy discovered in Fassò and Sansonetto (2015) and two other integrals, whose existence was proven by Routh for $\Omega =0$ (and for the special case of a spherical profile also for $\Omega \not =0$ (Routh 1955, section 224)) and by Borisov, Mamaev and Kilin for $\Omega \not =0$ (Borisov et al. 2002). In order to express the latter two integrals we note that the equations for $p_3$ and $p_4$ are

$$\begin{aligned} \Big ( \begin{array}{l} \dot{p}_3 \\ \dot{p}_4 \end{array} \Big ) = p_2 \Big [ G(p_1 ) \Big (\begin{array}{l} p_3 \\ p_4 \end{array} \Big ) + \Omega g(p_1 ) \Big ] \end{aligned}$$

(15)

where

$$\begin{aligned} G(x) :=\left( \begin{array}{ll} 0 &{} G_3(x) \\ G_4(x) &{} 0 \end{array} \right) \,,\qquad g(x) := \left( \begin{array}{l} g_3(x) \\ g_4(x) \end{array} \right) \end{aligned}$$

(16)

with $G_3$, $G_4$, $g_3$ and $g_4$ as in (11). Let ${\mathbb {R}}\ni x\mapsto U(x)\in \mathrm {GL(2)}$ be the solution of the matrix differential equation

$$\begin{aligned} U' = G(x)U \,, \qquad U(0)={\mathbb {I}} \qquad \big (U\in \mathrm {GL(2)} \big ) \end{aligned}$$

(17)

and ${\mathbb {R}}\ni x\mapsto u(x)\in {\mathbb {R}}^{2}$ the solution of the differential equation

$$\begin{aligned} u'=G(x)u+g(x) \,,\qquad u(0)=0 \qquad \big (u \in {\mathbb {R}}^{2}\big ). \end{aligned}$$

(18)

(Recall that linear (non)homogeneous equations have global existence of the solutions.)

Proposition 2

The restrictions to $M_4$ of the function $E:{\mathbb {R}}^{5}\rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} E(p){} & {} = \gamma \psi (p_1) + p_0 + \frac{1}{2} p_2^2 \psi '(p_1)^2 + \frac{1}{2}\mu p_4^2\nonumber \\{} & {} \quad +\Omega \big (\mu p_4 {\mathcal {F}}(p_1) -p_3\big ) \;+\; \Omega ^2 \mu p_1 \big (1-{\mathcal {F}}(p_1)^2 \psi '(p_1)^2 \big ) \end{aligned}$$

(19)

and of the two components $J_1, J_2$ of the map $J:{\mathbb {R}}^{5}\rightarrow {\mathbb {R}}^{2}$ given by

$$\begin{aligned} J(p) = U(p_1 )^{-1} \Big [ \Big ( \begin{array}{l} p_3 \\ p_4 \end{array} \Big ) -\Omega \,u(p_1 ) \Big ] \end{aligned}$$

(20)

are first integrals of the reduced system (8).

Proof

We show that $E,J_1,J_2$ are first integrals of system (8) in the entire ${\mathbb {R}}^{5}$. That $L_XE=0$ is checked with a computation. If we denote with a dot the derivative with respect to time and with a prime the derivative with respect to $p_1$, then, along a solution of (8)

$$\begin{aligned} \frac{d}{dt}J= \dot{p}_1 (U^{-1})' \Big ( \Big ( \begin{array}{l} p_3 \\ p_4 \end{array} \Big ) - \Omega u \Big ) + U^{-1} \Big ( \Big ( \begin{array}{l} \dot{p}_3 \\ \dot{p}_4 \end{array} \Big ) - \Omega \dot{p}_1 u' \Big ) \,. \end{aligned}$$

The fundamental matrix U satisfies the equation $U'=GU$, which implies $(U^{-1})'=-U^{-1}G$. Using this equality, $u'=Gu+g$ and (15) one verifies that $\frac{d}{dt}J =0$. $\square$

We will refer to $E|_{M_4}$ as to the “reduced moving energy” and to $J_1|_{M_4}$ and $J_2|_{M_4}$ as to “reduced Routh integrals” of the system. The pullbacks of these functions to $M_8$ give three $\mathrm {SO(3)}\times \mathrm {SO(2)}$-invariant first integrals of the unreduced system.

We also note that, if we momentarily make explicit the dependence of the first integrals on $\Omega$ by denoting them $E_\Omega$ and $J_\Omega =(J_{\Omega ,1},J_{\Omega ,2})$, then

$$\begin{aligned} E_\Omega = E_\Omega \circ C \,,\qquad J_\Omega \circ C=-J_{-\Omega } \qquad \forall \Omega \in {\mathbb {R}}\end{aligned}$$

(21)

where C is the reflection (13).

We now prove that the three first integrals are everywhere functionally independent at all points of $M_4$ which are not equilibria. Specifically, we neglect the singular stratum $M_4^\textrm{sing}$ (which consists of equilibria) and prove that $E,J_1,J_2$ are functionally independent at all points of the regular stratum $M_4^\textrm{reg}$ but the equilibria. For $\Omega =0$, this was proven in Fassò et al. (2005) with a direct computation. For $\Omega \not =0$, a direct computation is somewhat cumbersome and we use a somehow different argument. This argument makes explicitly appear in the proof the component $X_2$ of the reduced vector field and in this way sheds some light on why, in $M_4^\textrm{reg}$, the independence is lost exactly at the reduced equilibria.

Let us define two functions ${{\tilde{p}}}_3,\tilde{p}_4:{\mathbb {R}}\times {\mathbb {R}}^{2}\rightarrow {\mathbb {R}}$ as

$$\begin{aligned} \left( \begin{array}{l} {{\tilde{p}}}_3(p_1,j) \\ {{\tilde{p}}}_4(p_1,j) \end{array}\right) \,:=\, U(p_1)j+\Omega \, u(p_1) \end{aligned}$$

(22)

with U and u as in Proposition 2.

Proposition 3

• i. The critical points of the map $(E,J)|_{M_4^\textrm{reg}}:M_4^\textrm{reg}\rightarrow {\mathbb {R}}^{3}$ are the points of the set ${\mathcal {E}}_4^\textrm{reg}$.

• ii. The map $J|_{M_4^\textrm{reg}}:M_4^\textrm{reg}\rightarrow {\mathbb {R}}^{2}$ is a surjective submersion.

Proof

(i.) $M_4^\textrm{reg}\subset {\mathbb {R}}^{5}$ is one of the two components of the zero level set of the function $K:{\mathbb {R}}^{5}\rightarrow {\mathbb {R}}$, $K(p)=\frac{p_2^2+p_3^2}{2} - 2 p_0 p_1$, with the singular stratum $M_4^\textrm{sing}=\{(0,0,0,0)\}\times {\mathbb {R}}$ removed. We determine the critical points of $(E,J_1,J_2)|_{M_4^\textrm{reg}}$ at the points of $K^{-1}(0)$ using Lagrange multipliers $\lambda =(\lambda _1,\lambda _2,\lambda _3,\lambda _4)$. The critical points of $(E,J_1,J_2)|_{M_4^\textrm{reg}}$ in $K^{-1}(0)$ are those at which the equation

$$\begin{aligned} \lambda _1 dJ_1 + \lambda _2 dJ_2 + \lambda _3 dE + \lambda _4 dK = 0 \end{aligned}$$

(23)

has a nontrivial solution $\lambda \not =0$. For notational convenience we introduce the function ${\mathcal {G}}_\lambda := \lambda _1J_1 + \lambda _2J_2 + \lambda _3E + \lambda _4K:{\mathbb {R}}^{5}\rightarrow {\mathbb {R}}$, where the $\lambda _i$’s have to be thought of as parameters (namely, $d{\mathcal {G}}_\lambda$ equals the left-hand side of (23)).

We begin noticing that $\partial _{p_0 }{\mathcal {G}}_\lambda = \lambda _3 - 2p_1 \lambda _4$ and $\partial _{p_2}{\mathcal {G}}_\lambda = p_2\psi '^2 \lambda _3+ p_2\lambda _4$ vanish simultaneously in the following three⁴ cases: (a) $\lambda _3 = \lambda _4=0$, (b) $\lambda _3=0$, $\lambda _4\not =0$, $p_1 =p_2=0$, (c) $\lambda _3 = 2p_1 \lambda _4$, $p_2=0$, $p_1 \not =0$, $\lambda _4\not =0$.

The first two cases do not lead to any critical point in $M_4^\textrm{reg}$. In case (a), (23) reduces to $\lambda _1dJ_1+\lambda _2dJ_2= 0$ and hence admits only the trivial solution because the two functions $J_1,J_2:{\mathbb {R}}^{5}\rightarrow {\mathbb {R}}$ are functionally independent given that the fundamental matrix U is nonsingular. In case (b), since $\lambda _3=0$, $\partial _{p_1 }{\mathcal {G}}_\lambda |_{p_1 =p_2=0} = -2p_0 \lambda _4$ which, for $\lambda _4\not =0$, vanishes only if $p_0 =0$: but there are no points in $M_4^\textrm{reg}$ with $p_0 =p_1 =0$.

We thus consider case (c). We may assume $\lambda _4=1$, $\lambda _3=2p_1$. The vanishing of $\partial _{p_3}{\mathcal {G}}_\lambda \big |_{p_2=0}$ and $\partial _{p_4}{\mathcal {G}}_\lambda |_{p_2=0}$ gives the linear system for $\lambda _1,\lambda _2$

$$\begin{aligned} (DJ)^T \Big (\begin{array} {l} \lambda _1\\ \lambda _2 \end{array}\Big ) = - \nabla _{(p_3,p_4)}\big (\lambda _3E+K)\big |_{p_2=0,\lambda _3=2p_1 } \end{aligned}$$

where DJ stands for the Jacobian matrix of $J=(J_1,J_2)$ with respect to $(p_3,p_4)$. Since $DJ=U^{-1}$ is nonsingular, this system determines the multipliers $\lambda _1,\lambda _2$: $(\lambda _1,\lambda _2)=\ell$ with

$$\begin{aligned} \ell = - U^T\nabla _{(p_3,p_4)}\big (\lambda _3E+K)\big |_{p_2=0,\lambda _3=2p_1 } \,. \end{aligned}$$

Thus, equation (23) reduces to the only condition $\partial _{p_1 }{\mathcal {G}}_\lambda \big |_{p_2=0, \, \lambda =(\ell _1,\ell _2,2p_1 ,1)} =0$, namely

$$\begin{aligned} \ell \cdot \partial _{p_1 }J + \partial _{p_1 } (\lambda _3E+K)\big |_{p_2=0,\,\lambda _3=2p_1 } = 0 \,. \end{aligned}$$

(24)

Let us shorten $(p_3,p_4)=:y$, denote by a prime the derivative with respect to $p_1$ and write $J'$ for $(J'_1,J_2')$. From (20), $J'=(U^{-1})'(y-\Omega u) - \Omega U^{-1} u'$. As already noticed, $(U^{-1})'=-U^{-1}G$ and $u'=Gu+g$. Thus, $J'=-U^{-1}(Gy+\Omega g)$ and so $\ell \cdot J'= (Gy+\Omega g)\cdot \nabla _{(p_3,p_4)}\big (\lambda _3E+K)\big |_{p_2=0,\lambda _3=2p_1 }$. Therefore, condition (24) is

$$\begin{aligned} \big [ (Gy+\Omega g) \cdot \nabla _{(p_3,p_4)}+ \partial _{p_1 }\big ] (\lambda _3E+K)\Big |_{p_2=0,\lambda _3=2p_1 } =0 \,. \end{aligned}$$

(25)

Note now that, since E and K are first integrals of system (9) in ${\mathbb {R}}^{5}$, $L_X(\lambda _3 E+K)=0$ and therefore, for all $p_2$ and $\lambda _3$,

$$\begin{aligned} p_2\big [ (Gy+\Omega g) \cdot \nabla _{(p_3,p_4)}+ \partial _{p_1 }\big ] (\lambda _3E+K) = - \big ( X_0\partial _{p_0 } + X_2\partial _{p_2} \big ) (\lambda _3E+K) \end{aligned}$$

Hence, for all $p_2\not =0$ and all $\lambda _3$,

$$\begin{aligned} \big [ (Gy+\Omega g) \cdot \nabla _{(p_3,p_4)}+ \partial _{p_1 }\big ] (\lambda _3E+K) = - \frac{1}{p_2} \big ( X_0 \partial _{p_0 } + X_2\partial _{p_2} \big ) (\lambda _3E+K) \,. \end{aligned}$$

But $\partial _{p_0 }(\lambda _3E+K) =\lambda _3-2p_1$ vanishes for $\lambda _3=2p_1$ while $\partial _{p_2}(\lambda _3E+K) =p_2(1+\psi '^2)$. Hence, for $p_2\not =0$,

$$\begin{aligned} \big [ (Gy+\Omega g) \cdot \nabla _{(p_3,p_4)}+ \partial _{p_1 }\big ] (\lambda _3E+K)\big |_{\lambda _3=2p_1 } = -(1+\psi '^2) X_2 \,. \end{aligned}$$

By continuity, this equality is satisfied at $p_2=0$ as well. Hence, (25) is equivalent to $p_2=0$, $X_2|_{p_2=0}=0$, which defines the zeroes of X in $M_4^\textrm{reg}$, see (12).

(ii.) Surjectivity of $J|_{M_4^\textrm{reg}}:M_4^\textrm{reg}\rightarrow {\mathbb {R}}^{2}$ is obvious. In order to verify that it is a submersion, put $\lambda _3=0$ in the previous computations. The vanishing of $\partial _{p_0 }{\mathcal {G}}_\lambda = - 2p_1 \lambda _4$ and $\partial _{p_2}{\mathcal {G}}_\lambda = p_2\lambda _4$ gives either $\lambda _4=0$ (hence, as before, $\lambda _1=\lambda _2=0$) or $p_1 =p_2=0$ (which is not satisfied at any point in $M_4^\textrm{reg}$). $\square$

Remarks

(i) The pullback of $E|_{M_4}$ differs by a factor $k+1$ from the reduced moving energy of the (unreduced) system as defined in Fassò and Sansonetto (2015). The existence of this first integral was proven in Fassò and Sansonetto (2015), and its expression was then computed in Borisov et al. (2015).

(ii) With reference to the theory developed in Fassò and Sansonetto (2015) and Fassò et al. (2018), we note that the reduced moving energy of the (unreduced) system is the difference between the energy $E_0={\mathcal {L}}+2{\hat{g}} f$ and the “momentum” of the vector field $Y=\big (-\Omega \frac{x_2}{|x|},\Omega \frac{x_1}{|x|},0,0,\Omega \big )$ on the configuration manifold ${\mathbb {R}}^{2}\times \mathrm {SO(3)}$ of the system. This is a “kinematically interpretable” moving energy in the sense of Fassò et al. (2018) and its conservation follows from Proposition 8 of Fassò et al. (2018).

(iii) As shown in Fassò et al. (2009), when $\Omega =0$ the Routh integrals are “gauge momenta” (Fassò et al. 2008). In the case of the rotating cylinder, the two Routh integrals are gauge momenta as well (Fassò and Sansonetto 2015). In analogy with the case of linear constraints (Fassò et al. 2012), the fact that, being $\mathrm {SO(3)}\times \mathrm {SO(2)}$-invariant, the Routh integrals are “weakly Noetherian” (in the sense of Fassò et al. (2008)) might suggest that they are always gauge momenta.

3.2 Some Results on the Reduced and Unreduced Dynamics

The existence of three independent integrals of motion makes the reduced dynamics in $M_4$ very simple.

Proposition 4

Assume that $p\in M_4$ is not an equilibrium point of X and let $\eta _p$ be the connected component of the fiber of $(E,J)|_{M_4}$ that contains p.

• i. If $\eta _p$ does not contain any equilibrium, then the integral curve of X through p either is periodic or leaves any compact subset of $M_4$ for both positive and negative times.

• ii. If $\eta _p$ contains an equilibrium, then for positive times the integral curve of X through p either leaves any compact subset of $M_4$ or is asymptotic to an equilibrium. The same happens for negative times.

Proof

(i.) Not containing equilibria, $\eta _p$ is a subset of $M_4^\textrm{reg}\setminus {\mathcal {E}}_4^\textrm{reg}$ and, by Proposition 3, is a component of a regular fiber of $(E,J)|_{M_4}$. As such, $\eta _p$ is a closed embedded one-dimensional submanifold of $M_4^\textrm{reg}$, which is moreover invariant under the flow of X and does not contain any equilibrium. Thus, $\eta _p$ is the image of the maximal integral curve of X through p. If $\eta _p$ is diffeomorphic to $S^1$, then the integral curve of X through p is periodic. If $\eta _p$ is diffeomorphic to ${\mathbb {R}}$, then it is parametrized by the maximal integral curve of X through p, say $\varphi :(T_-,T_+)\rightarrow M_4$ with $\varphi (0)=p$ and some $-\infty \le T_-<0<T_+\le +\infty$. Assume now, by contradiction, that $\eta _+:=\varphi ([0,T_+))$ is contained in a compact subset K of $M_4$. Then, $T_+=+\infty$ and, since $\eta _p$ is an embedded submanifold, $\lim _{t\rightarrow +\infty }\varphi (t)=:p_+$ exists in K. Elementary facts about ODEs imply that then $X(p_+)=0$. But this is impossible because $p_+\in \eta _p$, given that $\eta _p$ is closed, and $\eta _p$ does not contain equilibria. Similarly for $\eta _-:=\varphi ((T_-,0])$.

(ii.) Let $\eta ^\textrm{eq}$ be the set of points of $\eta _p$ at which X vanishes. Thus $\eta ^\textrm{eq} = \eta _p\cap (M_4^\textrm{sing}\cup {\mathcal {E}}_4^\textrm{reg})$ and $\eta _p\setminus \eta ^\textrm{eq} \subset M_4^\textrm{reg} \setminus {\mathcal {E}}_4^\textrm{reg}$. Let $\eta _p^*$ be the connected component of $\eta _p\setminus \eta ^\textrm{eq}$ that contains p. $\eta _p^*$ is X-invariant and is a connected component of a fiber of $(E,J)|_{M_4^\textrm{reg} \setminus {\mathcal {E}}_4^\textrm{reg}}$. Since $M_4^\textrm{reg} \setminus {\mathcal {E}}_4^\textrm{reg}$ is an open subset of $M_4^\textrm{reg}$, $\eta _p^*$ is a one-dimensional immersed submanifold of $M_4$. Being X-invariant, $\eta _p^*$ is the image of the maximal integral curve of X through p. At variance from case (i), however, now $\eta _p^*$ is not closed. Thus, the integral curve through p either leaves every compact set or tends to an equilibrium point. $\square$

We note that reduced motions may leave any compact set in $M_4$ in two ways: either the center of the ball goes to infinity or some components of the velocity go to infinity. The conservation of the moving energy, together with the “Hamiltonization” of the reduced system which shows that it is a family of one-degree-of-freedom Hamiltonian (or Lagrangian) systems of mechanical type (Proposition 9), will imply that the latter possibility can only take place with motions that tend to the vertex. Because of the singularity of the reduced space at the vertex, it seems to us that an investigation of motions asymptotic to them is more naturally performed in the $\mathrm {SO(3)}$-reduced system in $M_5$, and we leave it for a future work.$^{3}$

The knowledge of the reduced dynamics in $M_4$ gives some information on the properties of the motions of the unreduced system in $M_8$. In particular, a rather complete description can be given for motions that project over equilibria and periodic orbits of the reduced system. Assume that a compact Lie group G acts freely on a manifold ${\hat{M}}$ and that ${\hat{X}}$ is a G-invariant vector field on ${\hat{M}}$. Let $\pi :{\hat{M}}\rightarrow M:={\hat{M}}/G$ be the quotient map and X the reduced vector field, which is $\pi$-related to ${\hat{X}}$. The preimage under $\pi$ of an equilibrium of X is called relative equilibrium of ${\hat{X}}$ and the preimage of a periodic orbit of X is called relative periodic orbit of ${\hat{X}}$. The work of Field (1990) and Krupa (1990) proves that for each relative equilibrium (resp. the relative periodic orbit) there exist an integer $0\le k\le \mathrm {rank\,}G$ (resp. $1\le k\le 1+\mathrm {rank\,}G$) and a vector $\omega \in {\mathbb {R}}^{k}$ such that the relative equilibrium (resp. relative periodic orbit) is fibered by X-invariant submanifolds diffeomorphic to ${\mathbb {T}}^{k}$, and the restriction of the flow of ${\hat{X}}$ to each of these submanifolds is conjugate to the linear flow $\alpha \mapsto \alpha +t\omega$ $\textrm{mod}(2\pi )$ on ${\mathbb {T}}^k$. We say that the flow in the relative equilibrium or relative periodic orbit is quasiperiodic with k frequencies.

Proposition 5

In $M_8$:

• i. $\pi ^{-1}(M_4^\textrm{sing})$ is a union of relative equilibria in each of which the flow of the unreduced system is periodic (unless $p_4=0$ in which case the relative equilibrium consists of equilibria).

• ii. $\pi ^{-1}({\mathcal {E}}_4^\textrm{reg})$ is a union of relative equilibria in each of which the flow of the unreduced system is quasiperiodic with $0\le k \le 2$ frequencies.

• iii. In every relative periodic orbit, the flow of the unreduced system is quasiperiodic with $1\le k\le 3$ frequencies.

Proof

(i.) We have already remarked that in motions that project onto the equilibria of the reduced system in the singular stratum $M^\textrm{sing}$ the ball stands on the vertex of the surface ${\tilde{\Sigma }}$ and may have any vertical angular velocity. (ii.) and (iii.) follow from the fact that the rank of $\mathrm {SO(3)}\times \mathrm {SO(2)}$ is 2. $\square$

In view of Propositions 4 and 5, in order to reach a complete picture of the dynamics of the (reduced or unreduced) system it is necessary to determine the reduced equilibria in ${\mathcal {E}}_4^\textrm{reg}$, the motions asymptotic to them, and the regions of the reduced space $M_4^\textrm{reg}\setminus {\mathcal {E}}_4^\textrm{reg}$ in which the (connected components of the) level sets of (E, J) are compact and those in which they are not. In the next section we make a first step in this direction, looking for situations in which all the level sets of (E, J) are compact and hence the reduced dynamics in the complement of the set of the reduced equilibria and of their stable and unstable sets is periodic, and the unreduced dynamics in the complement of the set of relative equilibria and of their stable and unstable sets is quasiperiodic.

Remarks

• (i) The integrability by quadratures of the reduced system was proved in Borisov et al. (2002) by exploiting the existence of an invariant measure and of the two Routh integrals and applying the Euler–Jacobi theorem. However, this method cannot prove the periodicity of the reduced dynamics. (At best, after replacing one of the Routh integrals with the moving energy, it gives the weaker result that the reduced dynamics is, after a time reparametrization, linear on tori of dimension two.)

• (ii) For the dynamics in relative equilibria and relative periodic orbits in the presence of a non-compact symmetry group, which also is of interest in nonholonomic mechanics, see Ashwin and Melbourne (1997), Fassò et al. (2020).

• (iii) The conclusions of Proposition 4 may also be obtained using the Lagrangian formulation of Proposition 9, but only restricted to the subset $M_4^\circ$ of $M_4$ where such a formulation is defined; this excludes all motions passing through, or tending to, the vertex.

3.3 Coercive Profiles and Quasiperiodicity of the Unreduced Dynamics

The simplest case in which all the level sets of $(E,J)|_{M_4}$ are compact is when those of $E|_{M_4}$ are compact. Extending a result in Fassò et al. (2005) for the case $\Omega =0$ and for a convex profile, we give some conditions that ensure this fact.

Definition 6

We say that the profile function f is coercive if

$$\begin{aligned} \lim _{r\rightarrow +\infty } f(r) = +\infty \end{aligned}$$

and that it is asymptotically superquadratic if

$$\begin{aligned} \lim _{r\rightarrow +\infty } \frac{f(r)}{r^2} = +\infty \,. \end{aligned}$$

(Equivalently, $\lim _{p_1 \rightarrow +\infty } \psi (p_1)=+\infty$ in the first case and $\lim _{p_1 \rightarrow +\infty } \frac{\psi (p_1 )}{p_1 } = +\infty$ in the second.)

Proposition 7

The reduced moving energy $E|_{M_4}$ has all its level sets compact in any one of the following two cases:

• (H1) $\Omega =0$ and f is coercive.

• (H2) f is asymptotically superquadratic.

Proof

Since $E:{\mathbb {R}}^{5}\rightarrow {\mathbb {R}}$ is continuous, its level sets are closed and we prove that their intersection with $M_4$ is bounded. Note that $\frac{1}{2}p_2^2\psi '^2\ge 0$ in all of ${\mathbb {R}}^{5}$ while, in $M_4$,

$$\begin{aligned} p_1 {\mathcal {F}}^2\psi '^2=\frac{p_1 \psi '^2}{1+2p_1 \psi '^2}\le \frac{1}{2} \end{aligned}$$

and hence $-\Omega ^2\mu p_1 {\mathcal {F}}^2\psi '^2\ge -\frac{1}{2} \mu \Omega ^2$. Moreover, in $M_4$, $p_2^2+p_3^2=4p_0 p_1$ and hence $-|\Omega p_3|\ge -2|\Omega |\sqrt{p_0 p_1 }$. Thus, in $M_4$,

$$\begin{aligned} \begin{aligned} E&\ge \gamma \psi + p_0 + \frac{1}{2}\mu p_4^2 + \mu \Omega p_4 {\mathcal {F}}-2\Omega \sqrt{p_0 p_1 } + \Omega ^2 \mu p_1 -\frac{1}{2}\mu \Omega ^2 \\&= \gamma \psi -\frac{1}{2}\mu \Omega ^2 -(1-\mu )\Omega ^2p_1 + \mu \Big (\frac{1}{2}p_4^2+ \Omega p_4{\mathcal {F}}\Big ) + \big (\sqrt{p_0 }-\Omega \sqrt{p_1 }\,\big )^2 \\&= P + \mu Q + \big (\sqrt{p_0 }-\Omega \sqrt{p_1 }\,\big )^2 \\&\ge P + \mu Q \end{aligned} \end{aligned}$$

where

$$\begin{aligned} P= \gamma \psi -\frac{1}{k+1}\Omega ^2p_1 -\frac{1}{2}\mu \Omega ^2 \,,\qquad Q=\frac{1}{2}p_4^2+ \Omega p_4{\mathcal {F}}\end{aligned}$$

(recall that $1-\mu =\frac{1}{1+k}$). In $M_4$, $0<{\mathcal {F}}\le 1$ and $Q\ge \frac{1}{2}p_4^2-|\Omega p_4|\ge -\frac{1}{2}\Omega =:Q_m$ is bounded from below and goes to $+\infty$ for $|p_4|\rightarrow +\infty$. Similarly, in $M_4$, $p_1 \ge 0$ and P is bounded from below by a constant $P_m\in {\mathbb {R}}$. Moreover, if either $\lim _{p_1\rightarrow +\infty }\psi (p_1)/p_1=+\infty$ (which happens if f is asymptotically superquadratic) or $\Omega =0$ and $\lim _{p_1\rightarrow +\infty }\psi (p_1)=+\infty$ (which happens if f is coercive), then P goes to $+\infty$ for $p_1 \rightarrow +\infty$.

Hence, in any level set $L_E$ of E, both P and Q are bounded from below and from above. It easily follows from this that, in $L_E$, both $p_1$ and $p_4$ are bounded, so that $0\le p_1 \le c_1(E)$ and $|p_4|\le c_4(E)$ for some positive $c_1(E)$ and $c_4(E)$. Since $(\sqrt{p_0 }-\Omega \sqrt{p_1 })^2\le E-P-\mu Q \le E-P_m-\mu Q_m$, $p_0$ is bounded as well in $L_E$. Finally, from $p_2^2+p_3^2=4p_0 p_1$ it follows that, in $L_E$, $p_2$ and $p_3$ are bounded as well. $\square$

Since the map J is continuous, under either of the two hypotheses of Proposition 7 the level sets of the map $(E,J)|_{M_4}$ are compact and, as already pointed out, the reduced dynamics is generically periodic and the unreduced dynamics is generically quasiperiodic on tori of dimensions up to three.

Remarks

(i) For $\Omega =0$, Proposition 7 was stated in Fassò et al. (2005) for convex profile functions, but a simple inspection to the proof shows that what is there used is only the coercivity of f, not its convexity.

(ii) When $\Omega \not =0$, the asymptotic superquadraticity of the profile function is likely to be not only sufficient but also necessary for the compactness of the level sets of $E|_{M_4}$. Indeed, for $p_2=p_4=0$ and large $p_1$, $E|_{M_4}$ is approximately equal to $\gamma \psi + \frac{p_3^2}{4p_1}-\Omega p_3+\mu \Omega ^2p_1$ and hence, if $\psi$ goes to $+\infty$ not faster than $p_1$, to $\frac{p_3^2}{4p_1}-\Omega p_3+\mu \Omega ^2p_1$ whose level sets are hyperbolas (recall that $\mu <1$). The level sets of the map $(E,J)|_{M_4}$ might nevertheless be compact. In fact, in Sect. 7 we will show that this happens for the parabolic profile $f(r)=b r^2$ with $b>0$; the same argument could be easily applied to the case of the conic profile $f(r)=br$ with $b>0$. A study of the compactness of the map $(E,J)|_{M_4}$ for a generic profile is difficult because the functions $J_1$ and $J_2$ are not explicitly known.

4 Hamiltonization of the Reduced System

4.1 A Rank-Two Poisson Structure

The system formed by a sphere that rolls without sliding on a surface of revolution which is at rest, namely our system for $\Omega =0$ and a convex profile, has been one of the first—if not even the very first—nonholonomic system with linear constraints and a symmetry group for which it has been shown that the reduced system is Hamiltonian with respect to a Poisson structure of rank two, with the reduced energy as Hamiltonian (Borisov et al. 2002; Ramos 2004; Fassò et al. 2005; Balseiro and Yapu 2021).

We show here that the same remains true when $\Omega \not =0$, but with the reduced moving energy, instead of the reduced energy, as Hamiltonian. This is of interest for two reasons: From a geometrical perspective, the very existence of Poisson structures for systems with affine (rather than linear) constraints was so far unknown, except in the very special case of the Veselova system (García-Naranjo 2007). And from a dynamical perspective, it helps enlightening some aspects of the dynamics of the reduced system, which turns that of a (family of) Hamiltonian systems with one degree of freedom which are of mechanical type (hence, also Lagrangian).

We limit ourselves to consider the reduced system in the subset of the regular stratum $M_4^\textrm{reg}$ where $p_1\not =0$. As we have already noticed, $M_4^\textrm{reg} \setminus \{p_1=0\}$ is diffeomorphic to

$$\begin{aligned} M_4^\circ := {\mathbb {R}}_+\times {\mathbb {R}}^{3} \ni (p_1,p_2,p_3,p_4) \,, \end{aligned}$$

with diffeomorphism $M_4^\circ \rightarrow M_4^\textrm{reg}\setminus \{p_1=0\}$ given by $(p_1,p_2,p_3,p_4) \mapsto \Big (\frac{p_2^2+p_3^2}{4p_1},p_1,p_2,p_3,p_4\Big )$. We thus pull back the entire description to $M_4^\circ$, and we denote with a superscript ${}^\circ$ the pullbacked objects on $M_4^\circ$. In this way, the restriction to $M_4^\textrm{reg}\setminus \{p_1=0\}$ of the vector field $X=(X_0,X_1,\dots ,X_4)$ in ${\mathbb {R}}^{5}$ given by (9) becomes the vector field $X^\circ$ in $M_4^\circ$ with components

$$\begin{aligned} X^\circ _i = X_i\big |_{p_0=\frac{p_2^2+p_3^2}{4p_1}} \,,\qquad i=1,\ldots ,4 \,. \end{aligned}$$

(26)

Similarly, the reduced moving energy (19) becomes the function $E^\circ :M_4^\circ \rightarrow {\mathbb {R}}$ given by

$$\begin{aligned} E^\circ \;=\; \frac{p_2^2}{4p_1{\mathcal {F}}^2} + \gamma \psi + \frac{p_3^2}{4p_1} + \frac{1}{2}\mu p_4^2 \;+\; \Omega \big (\mu p_4 {\mathcal {F}}-p_3\big ) \;+\; \Omega ^2 \mu p_1 \big (1-{\mathcal {F}}^2 \psi '^2 \big ) \,. \end{aligned}$$

The representative $J^\circ :M_4^\circ \rightarrow {\mathbb {R}}^{2}$ of $J|_{M_4^\textrm{reg} \setminus \{p_1=0\}}$ has the same expression (20) as J, but we prefer using the symbol $J^\circ$ to stress that we are working in a subset of $M_4^\textrm{reg}$, and with a different parametrization.

Proposition 8

Consider the bivector

$$\begin{aligned} \Lambda \;:=\; 2p_1{\mathcal {F}}^2 \partial _{p_2}\wedge \Big ( \partial _{p_1} + (G_3p_4+\Omega g_3) \partial _{p_3} + (G_4p_3+\Omega g_4) \partial _{p_4} \Big ) \end{aligned}$$

on $M_4^\circ$. Then:

• i. $X^\circ =\Lambda (dE^\circ ,\cdot )$.

• ii. $\Lambda$ is a rank-two Poisson tensor on $M_4^\circ$.

• iii. The two components of $J^\circ$ are Casimirs of $\Lambda$.

Proof

(i.) In the dense subset of $M_4^\circ$ where $p_2\not =0$, $\Lambda = \frac{2p_1}{p_2} {\mathcal {F}}^2 \partial _{p_2}\wedge X^\circ$. Since $L_{X^\circ }E^\circ =0$, in such a subset $\Lambda (dE^\circ ,\cdot ) = (\frac{2p_1}{p_2}{\mathcal {F}}^2\partial _{p_2}E^\circ )X^\circ = \frac{2p_1}{p_2}{\mathcal {F}}^2\big ( \frac{p_2}{2p_1} + p_2\psi '^2\big )X^\circ = X^\circ$. By continuity, this is true in all of $M_4^\circ$.

(ii.) The characteristic distribution of the bivector $\Lambda$ is spanned by the two vector fields $\partial _{p_2}$ and $\partial _{p_1} + (G_3p_4+\Omega g_3) \partial _{p_3} + (G_4p_3+\Omega g_4) \partial _{p_4}$, which are everywhere linearly independent. Thus, $\Lambda$ has everywhere rank two and the associated Poisson brackets trivially satisfy the Jacobi identity, so that it is Poisson.

(iii.) From (20), $J^\circ =U^{-1}({\hat{p}}+\Omega g)$ with ${\hat{p}}=\Big (\begin{array}{l} p_3\\ p_4 \end{array}\Big )$. Recalling that $\partial _{p_1}U^{-1} = -U^{-1}G$ we have, for each $i=1,2$,

$$\begin{aligned} \partial _{p_1}J_i^\circ= & {} -[U^{-1}G{\hat{p}}+\Omega U^{-1}g]_i\\= & {} -[U^{-1}Gp_3e_1+U^{-1}Gp_4e_2 + \Omega U^{-1}g_3e_1 + \Omega U^{-1}g_4e_2]_i \end{aligned}$$

where $e_1=\Big (\begin{array}{l} 1\\ 0 \end{array}\Big )$ and $e_2=\Big (\begin{array}{l} 0\\ 1 \end{array}\Big )$. Moreover,

$$\begin{aligned} (G_3p_4+\Omega g_3)\partial _{p_3}J^\circ _i= & {} (G_3p_4+\Omega g_3)[U^{-1}e_1]_i = [U^{-1}p_4 G_3 e_1+\Omega U^{-1}g_3 e_1]_i\\= & {} [U^{-1}Gp_4 e_2+\Omega U^{-1}g_3 e_1]_i \end{aligned}$$

and, similarly, $(G_4p_3+\Omega g_4)\partial _{p_4}J^\circ _i = [U^{-1}Gp_3 e_1+\Omega U^{-1}g_4 e_2]_i$. Hence $\Lambda (dJ^\circ _i,\cdot )=0$. $\square$

We point out that, for $\Omega \not =0$, the origin of the rank-two Poisson structure $\Lambda$ is not clear. There are two possible approaches:

1. There exists an almost-Poisson formulation of nonholonomic mechanical systems with linear (or more generally homogeneous) constraints and Lagrangian without gyrostatic terms (Bates and Śniatycki 1993; Cantrijn et al. 1999; van der Schaft and Maschke 1994). In the presence of symmetry—and under suitable hypotheses—this almost-Poisson structure induces a Poisson structure on the reduced space, that makes the reduced system Hamiltonian with the energy as Hamiltonian (Balseiro and García-Naranjo 2012; Balseiro 2014; García-Naranjo and Montaldi 2018; Balseiro 2017; Balseiro and Yapu 2021). A similar theory for the case of affine constraints (or, equivalently, for Lagrangians with gyrostatic terms) does not exist yet. We speculate that such an extension might exist, particularly if the reduced moving energy is “kinematically interpretable” in the sense of Fassò et al. (2018).

2. In Fassò et al. (2005), it is shown that every dynamical system with periodic flow possesses (infinitely many) rank-two Poisson formulations, suggesting a dynamical origin of these structures. This point of view may account for the existence of $\Lambda$ in the case of coercive profiles, but not in general. It is possible that the approach of Fassò et al. (2005) could be extended by using the existence of three first integrals, even if their level sets are not compact.

4.2 The $J^\circ$-Restricted Reduced Systems

The symplectic leaves of the Poisson manifold $(M_4^\circ ,\Lambda )$ are the level sets of the Casimir map $J^\circ :M_4^\circ \rightarrow {\mathbb {R}}^{2}$. Clearly, this map is surjective and, for any $j\in {\mathbb {R}}^{2}$, the level set $M_2^j:=(J^\circ )^{-1}(j)$ is given by

$$\begin{aligned} M_2^j \,=\, \big \{(p_1,p_2,p_3,p_4) \in M_4^\circ \,:\, p_3= {{\tilde{p}}}_3(p_1,j),\, p_4={{\tilde{p}}}_4(p_1,j) \big \} \,, \end{aligned}$$

with ${{\tilde{p}}}_3$ and ${{\tilde{p}}}_4$ defined by (22), and is a submanifold of $M_4^\circ$ diffeomorphic to ${\mathbb {R}}_+\times {\mathbb {R}}\ni (p_1,p_2)$. The Poisson structure $\Lambda$ induces a symplectic form $\omega _j$ on each symplectic leaf $M_2^j$, and the restriction of $X^\circ$ to $M_2^j$ equals the vector field $\omega _j^\flat \big (dE^\circ |_{M_2^j}\big )$, namely, the $\omega _j$-Hamiltonian vector field whose Hamiltonian is the restriction of the reduced moving energy $E^\circ$ to $M_2^j$.

If we use $(p_1,p_2)$ as coordinates on $M_2^j$, then

$$\begin{aligned} \omega _j(p_1,p_2) = \frac{1}{2p_1{\mathcal {F}}^2}\, dp_2\wedge dp_1 \end{aligned}$$

and $E^\circ |_{M_2^j}(p_1,p_2)= \frac{1}{2}\,\frac{p_2^2}{2p_1{\mathcal {F}}(p_1)^2} + W_{j}(p_1)$ with “effective potential”

$$\begin{aligned} W_{j} = \gamma \psi + \frac{{{\tilde{p}}}_{3,j}^2}{4p_1} + \frac{1}{2}\mu {{\tilde{p}}}_{4,j}^2 +\Omega \big (\mu {{\tilde{p}}}_{4,j}{\mathcal {F}}- {{\tilde{p}}}_{3,j}\big ) +\Omega ^2 \mu p_1(1-{\mathcal {F}}^2\psi '^2) \,. \end{aligned}$$

where ${{\tilde{p}}}_{3,j}$ and ${{\tilde{p}}}_{4,j}$ stand for $\tilde{p}_3(\cdot ,j)$ and ${{\tilde{p}}}_4(\cdot ,j)$. If we pass to the (Darboux) coordinates $(Q,P)=\big (p_1,\frac{p_2}{2p_1{\mathcal {F}}^2}\big ) \in {\mathbb {R}}_+\times {\mathbb {R}}$ on $M_2^j$, then the symplectic 2-form $\omega _j$ becomes $dP\wedge dQ$ and $E^\circ |_{M_2^j}$ becomes $\frac{1}{2} {2p_1{\mathcal {F}}^2} {p_2^2}+ W_{j}(p_1)$. Thus, the restriction of the reduced system to each symplectic leaf can be regarded as a Hamiltonian system that describes a one-degree-of-freedom mechanical (holonomic) system on the cotangent bundle $T^*{\mathbb {R}}_+\ni (Q,P)$ of the configuration space ${\mathbb {R}}_+\ni Q=p_1=r^2/2$. Equivalently, this can be regarded as a Lagrangian system on $T{\mathbb {R}}_+\ni (Q,\dot{Q})=(p_1,\dot{p}_1)$ with “natural” Lagrangian $\frac{1}{2} \frac{\dot{p}_1^2}{2p_1{\mathcal {F}}^2}-W_{j}(p_1)$. To allow for easier interpretation, we prefer switching to the coordinates $(r,\dot{r})$. Correspondingly, we reverse to the original profile function f(r) and we use the two functions

$$\begin{aligned} {\overline{p}}_{i,j}(r):={{\tilde{p}}}_{i,j}\Big (\frac{r^2}{2}\Big ) \,,\qquad i=3,4 \,. \end{aligned}$$

Proposition 9

The restriction of the reduced equations (8) to any level set $M_2^j$ of the two reduced Routh integrals, written in coordinates $(r,\dot{r})\in T{\mathbb {R}}_+$, is the Lagrangian system with Lagrangian

$$\begin{aligned} \frac{1}{2} F(r)^2\dot{r}^2 - V_{j}(r) \end{aligned}$$

(27)

with the effective potential

$$\begin{aligned} V_{j} = \gamma f + \frac{{\overline{p}}_{3,j}^2}{2r^2} + \frac{1}{2}\mu {\overline{p}}_{4,j}^2 +\Omega \Big (\mu \frac{\overline{p}_{4,j}}{F}-{\overline{p}}_{3,j}\Big ) +\frac{1}{2} \mu \Omega ^2 \Big (r^2 -\frac{f'^2}{F^2}\Big ) \,. \end{aligned}$$

(28)

5 Reduced Equilibria in ${\mathcal {E}}_4^\textrm{reg}$

5.1 The Reduced Equilibria in ${\mathcal {E}}_4^\textrm{reg}$

In this section, we study the reduced equilibria in ${\mathcal {E}}_4^\textrm{reg}$. Since at an equilibrium with $p_1=0$ (namely $r=0$) it is necessarily $p_0=p_2=p_3=0$, all equilibria with $p_1=0$ belong to $M_4^\textrm{sing}$. Therefore, ${\mathcal {E}}_4^\textrm{reg}\subset M_4^\textrm{reg}\setminus \{p_1=0\}$ and for easier interpretation we may work in $M^\circ _4$ with the coordinates $(r,v_r,v_\theta ,\omega _n)$ (which in the “Appendix” is called ${\widehat{M}}_4^\circ$; recall that $p_1=\frac{r^2}{2}$, $p_2=rv_r$, $p_3=2p_1v_\theta$, $p_4=\omega _n$). Obviously, $v_r=0$ at all reduced equilibria.

Proposition 10

For any $\Omega \in {\mathbb {R}}$ and ${\bar{r}}>0$, the reduced equilibria with $r={\bar{r}}$ form three families:

• (RE1) If $f'({\bar{r}})=0$, the one-parameter family ${\mathcal {P}}_1({\bar{r}}, \omega _n,\Omega ) = ({\bar{r}},0,\Omega \mu ,\omega _n)$, $\omega _n\in {\mathbb {R}}$.

• (RE2) If $f'({\bar{r}})=0$, the 1-parameter family ${\mathcal {P}}_2({\bar{r}}, \omega _n,\Omega ) = ({\bar{r}},0,0,\omega _n)$, $\omega _n\in {\mathbb {R}}$.

• (RE3) If $f'({\bar{r}})\not =0$, the 1-parameter family ${\mathcal {P}}_3({\bar{r}},v_\theta ,\Omega ) = \big ({\bar{r}},0,v_\theta , {\tilde{\omega }}_n({\bar{r}},v_\theta ,\Omega )\big )$, $v_\theta \not =0$, where

  $$\begin{aligned} {\tilde{\omega }}_n(r,v_\theta ,\Omega ) := \frac{r v_\theta }{\mu f'(r)} - \frac{\gamma }{\mu v_\theta } - \Omega \Big (\frac{r}{f'(r)}+\frac{1}{F(r)}\Big ) \,. \end{aligned}$$

  (29)

Proof

The equilibria of the reduced vector field $X^\circ$ in $M_4^\circ$ are the points $(p_1,p_2,p_3,p_4)$ where $p_2=0$ and $X_2\big (\frac{p_3^2}{4p_1},p_1,0,p_3,p_4\big )=0$. Since ${\mathcal {F}}$ never vanishes, the latter condition is

$$\begin{aligned} \frac{p_3^2}{2p_1} -\mu p_3p_4\psi '(p_1) -2\gamma p_1\psi '(p_1) -\Omega \mu p_3\big (1+\psi '(p_1){\mathcal {F}}(p_1)\big ) = 0 \,. \end{aligned}$$

(30)

If $\psi '(p_1)=0$, this condition becomes

$$\begin{aligned} \frac{p_3^2}{2p_1} -\Omega \mu p_3 = 0 \end{aligned}$$

and has the solutions $p_3=2\Omega \mu p_1$ and $p_3=0$, which give the reduced equilibria of types RE1 and RE2, respectively. If $\psi '(p_1)\not =0$, then (30) does not have any solution with $p_3=0$. Equation (30) can then be solved for $p_4$, obtaining

$$\begin{aligned} p_4 = -\frac{2\gamma }{\mu }\,\frac{p_1}{p_3} + \frac{p_3}{2\mu p_1\psi '(p_1)} -\frac{\Omega }{\psi '(p_1)}-\Omega {\mathcal {F}}(p_1) \,. \end{aligned}$$

(31)

In the coordinates $(r,v_r,\dot{\theta },\omega _n)$ this is $\omega _n={\tilde{\omega }}_n(r,v_\theta ,\Omega )$. $\square$

When $\Omega =0$, ${\mathcal {P}}_1(r,\omega _n,0)={\mathcal {P}}_2(r,\omega _n,0)$ for all r and $\omega _n$; hence, the two families RE1 and RE2 coincide for $\Omega =0$, but they are disjoint for all $\Omega \not =0$. Thus, for each $r>0$ and $\Omega \in {\mathbb {R}}$ there are either one (RE1$=$RE2 if $f'(r)=0$ and $\Omega =0$, RE3 if $f'(r)\not =0$) or two (RE1$\not =$RE2 if $f'(r)=0$, $\Omega \not =0$) 1-parameter families of reduced equilibria with those r and $\Omega$. Families RE1 and RE2 are parametrized by $\omega _n\in {\mathbb {R}}$, while family RE3 is parametrized by $v_\theta \not =0$.

For fixed r and $\Omega$, the curve $\omega _n={\tilde{\omega }}_n(r,v_\theta ,\Omega )$ in the plane $(v_\theta ,\omega _n)$ has two branches, one in the half-plane $v_\theta >0$ and one in the half-plane $v_\theta <0$. When $\Omega =0$ these two branches are symmetrical with respect to the origin. The qualitative properties of these curves depend on the sign of $f'(r)$, and are shown in Fig. 2 for $\Omega =0$; a nonzero $\Omega$ shifts both branches up or down, depending on the signs of $\Omega$ and of the quantity $\frac{r}{f'(r)}+ \frac{1}{F(r)}$ and has no effect on them if the latter quantity vanishes. Curiously, if $f'(r)>0$ then there are exactly two reduced equilibria with $\omega _n=0$.

Fig. 2

Two branches of the RE3 equilibria ${\mathcal {P}}_3(r,v_\theta ,0)$ in the plane $(v_\theta ,\omega _n)$ for $\Omega =0$. The dotted line is the asymptote $\omega _n=\frac{r}{\mu f'(r)}v_\theta$

A more difficult question is which reduced equilibria are present for any given value of $J^\circ =(J^\circ _1, J^\circ _2)$. This depends in a non-obvious way on the profile of the surface $\Sigma$ and on $\Omega$, given that the map $J^\circ$ depends on them, and can be investigated, numerically if not analytically, on a case by case basis. The case of an upward half-cone was studied in Borisov et al. (2019). The case of an upward paraboloid is studied in Sect. 7.

Remarks

(i) Even though the reduced equilibria $({\bar{r}},0,0,\omega _n)$ of type RE2 are independent of $\Omega$ their stability properties do depend on $\Omega$, and this is why we denote them ${\mathcal {P}}_2(\bar{r},\omega _n,\Omega )$.

(ii) It follows from (14) that, if $(r,0,v_\theta ,\omega _n)$ is an equilibrium of the reduced system for a certain value of $\Omega$, then $(r,0,-v_\theta ,-\omega _n)$ is an equilibrium of the reduced system for $-\Omega$, and they have the same stability properties. (This can also be checked with (30) and with the formulas of Proposition 11.) We may therefore restrict our study of the reduced equilibria to the case $\Omega \ge 0$.

(iii) When $\Omega =0$, the invariance of X under the reflection C as in (13) implies that if $(r,0,v_\theta ,\omega _n)$ is a reduced equilibrium then so is $(r,0,-v_\theta ,-\omega _n)$ and they have the same stability properties. Note that, by (21), if one of them belongs to $M_2^j$, then the other belongs to $M_2^{-j}$. When $\Omega =0$ we may thus restrict ourselves to study reduced equilibria for $j_1\in {\mathbb {R}}$, $j_2\ge 0$.

5.2 Motions in Relative Equilibria

Motions in all relative equilibria in $M_8$ consist of a uniform rotation of the center of mass of the ball on a parallel (hence, a horizontal circle) of the surface $\Sigma$, and of a uniform rotation of the ball around the axis normal to $\Sigma$ (which changes periodically with the same frequency as the center of mass). See also Proposition 5.

By Proposition 10, there are three families of relative equilibria, which we call with the same names of the reduced equilibria onto which they project, and there is at least one such family on any parallel of $\Sigma$. For each $\Omega \in {\mathbb {R}}$:

• Relative equilibria of type RE1 consist of motions in which the center of mass of the ball uniformly moves (if $\Omega \not =0$) or stands (if $\Omega =0$) on a horizontal “critical” parallel of the surface $\Sigma$. At these points the normal vector n is vertical. Note that, since $\frac{1}{2}<\mu <1$, the angular velocity $v_\theta =\Omega \mu$ of the center of mass is smaller than that of the surface. Thus, the ball either rolls (if $\Omega \not =0$) or stands (if $\Omega =0$) on the corresponding critical parallel of the surface ${\tilde{\Sigma }}$, and at the same time rotates around its vertical axis with any constant angular velocity $\omega _\textrm{z}=\omega _n$.

• In relative equilibria RE2, $v_\theta =0$ and the center of mass of the ball stands still in space. Correspondingly, the ball rolls uniformly on a critical parallel of the surface ${\tilde{\Sigma }}$. Here too, the ball may rotate with any constant angular velocity $\omega _n=\omega _\textrm{z}$ around its vertical axis.

• In relative equilibria of type RE3, the ball rolls along a non-critical parallel of the surface ${\tilde{\Sigma }}$, with any nonzero $v_\theta$.

Example

The case of a ball on a plane ($\psi =0$) is well known and elementary (Earnshaw 1844; Neimark and Fufaev 1972). The equations of motion for the $\mathrm {SO(3)}$-reduced system in $M_5\ni (x,y,\dot{x},\dot{y},\omega _\textrm{z})$ are $\ddot{x} = -\mu \Omega \dot{y}$, $\ddot{y} = \mu \Omega \dot{x}$, $\dot{\omega }_\textrm{z}= 0$ (Equations (5.44) in Neimark and Fufaev (1972)). $\omega _\textrm{z}=\omega _n$ is constant. If $\Omega =0$ the center of mass moves on a straight line or stands still. For $\Omega =0$, the solution with initial conditions $(x_0,y_0,\dot{x}_0,\dot{y}_0)$ is

$$\begin{aligned}{} & {} x(t) = x_0 - \frac{\dot{y}_0}{\mu \Omega } + \frac{\dot{y}_0}{\mu \Omega } \cos (\mu \Omega t) + \frac{\dot{x}_0}{\mu \Omega } \sin (\mu \Omega t), \\{} & {} \quad y(t) = y_0 + \frac{\dot{x}_0}{\mu \Omega } + \frac{\dot{y}_0}{\mu \Omega }\sin (\mu \Omega t) - \frac{\dot{x}_0}{\mu \Omega } \cos (\mu \Omega t) \end{aligned}$$

and the center of mass moves along a circle. According to Proposition 10, the $\mathrm {SO(2)}$-reduction to $M_4$ of this system in $M_5$ has two families of reduced equilibria at any distance r from the origin, one of type RE1 and one of type RE2. The lift to $M_5$ of the reduced equilibria of type RE1 are motions with $\dot{x}_0=-\mu \Omega y_0$, $\dot{y}_0=\mu \Omega x_0$ with nonzero $(x_0,y_0)$: the ball spins with any $\omega _\textrm{z}$ around its center of mass, that moves along a circle centered at the origin. The lift to $M_5$ of the reduced equilibria of type RE2 are motions with initial conditions $\dot{x}_0=\dot{y}_0=0$: the ball spins with any $\omega _\textrm{z}$ around its center of mass, that stands still in space.

Remarks

(i) Relative equilibria of type RE2 resemble certain motions of a ball on a rotating umbrella produced in the Japanese “turning umbrella” (kasamawashi) art. In some of these performances, an umbrella is kept in uniform rotation about its inclined axis, and a ball rolls on its surface in such a way to remain fixed in space. At each instant, the ball touches a point of the umbrella whose tangent plane is horizontal. The difference with our treatment is that, due to the inclination of the umbrella, that system is not invariant under rotation about the vertical. We will come back on this system in a future work (see footnote 3).

(ii) In view of the example of the ball on the rotating plane, the existence of the reduced equilibria of types RE1 and RE2 can be regarded as obvious. However, the stability of these equilibria depends on the surface profile, see next section.

6 (Leafwise) Stability of the Reduced Equilibria

6.1 Leafwise-Stability

We study now the stability of the reduced equilibria—where ‘stability’ is relative to the restriction of the reduced system to a level set $M_2^j$ of the map $J^\circ$. In order to avoid ambiguities on this point, we introduce the following terminology:

We say that an equilibrium of the reduced system is leafwise-stable (leafwise-unstable) if it is a Lyapunov-stable (Lyapunov unstable) equilibrium of the restriction of the reduced system to the level set $M_2^j$ of the map $J^\circ$ to which it belongs. (“Leafwise” refers, of course, to the symplectic leaves of the Poisson structure of $M_4^\textrm{reg}$.)

Leafwise-stability of a reduced equilibrium does not imply its stability as equilibrium of the reduced system in $M_4^\textrm{reg}$, because motions nearby might run away with small but nonzero $v_\theta$. However, it implies the $\mathrm {SO(3)}\times \mathrm {SO(2)}$-orbital stability of the motion in the corresponding relative equilibria of the unreduced system.

By Proposition 9, a reduced equilibrium in $M_2^j$ is a point $(r,\dot{r}=0)\in M_2^j$ with r a critical point of $V_{j}$ and, given the Lagrangian nature of the restriction of the reduced system to $M^j_2$, it is leafwise-stable if $V''_j(r)>0$, leafwise-unstable if $V''_j(r)<0$. This leads to the following conditions:

Proposition 11

For any $r>0$ and $\Omega \in {\mathbb {R}}$:

• i. A reduced equilibrium ${\mathcal {P}}_1(r,\omega _n,\Omega )$ of type RE1 is leafwise-stable if $S_1(r,\Omega )>0$ and leafwise-unstable if $S_1(r,\Omega )<0$, where

  $$\begin{aligned} S_1(r,\Omega ):=\mu ^2\Omega ^2+\gamma f''(r) \,. \end{aligned}$$

  (32)

• ii. A reduced equilibrium ${\mathcal {P}}_2(r,\omega _n,\Omega )$ of type RE2 is leafwise-stable if $S_2(r,\omega _n,\Omega )>0$ and leafwise-unstable if $S_2(r,\omega _n,\Omega )<0$, where⁵

  $$\begin{aligned} S_2(r,\omega _n,\Omega ) := \mu ^2\Omega ^2+\big (\gamma +\mu ^2\omega _n\Omega +\mu ^2\Omega ^2\big )f''(r) \,. \end{aligned}$$

  (33)

• iii. A reduced equilibrium ${\mathcal {P}}_3(r,v_\theta ,\Omega )$ of type RE3 is leafwise-stable if $S_3(r,v_\theta ,\Omega )>0$ and leafwise-unstable if $S_3(r,v_\theta ,\Omega )<0$ where

  $$\begin{aligned} S_3(r,v_\theta ,\Omega ) := \Delta _0(r,v_\theta ) + \Omega \Delta _1(r,v_\theta ) \end{aligned}$$

  (34)

  with

  $$\begin{aligned} \Delta _0(r,v_\theta ) = \Delta _{00}(r) + \Delta _{02}(r)v_\theta ^2 + \Delta _{04}(r)v_\theta ^4 \,,\qquad \Delta _{1}(r,v_\theta ) = \Delta _{11}(r)v_\theta \end{aligned}$$

  and

  $$\begin{aligned} \Delta _{00} \!\!= & {} \!\!\gamma ^2 f'f'' \,,\qquad \Delta _{02} = 2\gamma F^2 f' \,,\qquad \Delta _{04} = (1+\mu f'^2)rF^2 + (1-\mu )r^2f'f'' \,, \\ \Delta _{11} \!\!= & {} \!\!\gamma \mu \big (rf'' - F^2 f'\big ) \,. \end{aligned}$$

Proof

Let $p_1=r^2/2$. The equilibrium belongs to a level set $M_2^j$ of J and, as remarked, it is leafwise-stable if $W''_j(p_1)>0$ and leafwise-unstable if $W''_j(p_1)<0$. Computing $W''_j(p_1)$ using ${{\tilde{p}}}_{3,j}'=G_3{{\tilde{p}}}_{4,j}+\Omega g_3$ and $\tilde{p}_{4,j}'=G_4{{\tilde{p}}}_{3,j}+\Omega g_4$, we obtain $W''_j=D_0+\Omega D_1+\Omega ^2 D_2$ with

$$\begin{aligned} D_0 \,\!\!= & {} \!\!\, \gamma \psi '' + \mu ^2p_4^2\Big (\frac{\psi '}{2p_1}+\psi ''\Big ) {\mathcal {F}}^2 \psi ' + \mu \frac{p_3p_4}{2p_1^2} \big (p_1 (1-2{\mathcal {F}}^2)\psi ''-(1+{\mathcal {F}}^2)\psi '\big ) \\{} & {} +\frac{p_3^2}{2p_1^3} \big ( 1 + 2p_1\psi '^2 + \mu p_1^2(\psi '^3-\psi '')\psi '\big ) {\mathcal {F}}^2 \,, \\ D_1 \,\!\!= & {} \!\!\, \mu ^2\frac{p_4}{p_1} \Big ( \big (1+{\mathcal {F}}\psi '+p_1\psi '^2\big )\psi ' + p_1\big (1+2{\mathcal {F}}\psi '\big )\psi '' \Big ) {\mathcal {F}}^2 \\ \ \quad{} & {} +\mu \frac{p_3}{2p_1} \Big ( \big (1 + 2p_1{\mathcal {F}}\psi ' -2{\mathcal {F}}^2 \big ){\mathcal {F}}\psi '' - \frac{1}{p_1}(1+{\mathcal {F}}^2)(1+{\mathcal {F}}\psi ') - {\mathcal {F}}^2 \psi '^2 \Big )\,, \\ D_2 \,\!\!= & {} \!\!\, \frac{\mu ^2}{2p_1} \big (1+{\mathcal {F}}\psi '\big ) \big (1+{\mathcal {F}}^3\psi '+2p_1{\mathcal {F}}^3\psi ''\big ) \,. \end{aligned}$$

(Here and below in this proof, $p_3$ and $p_4$ stand, respectively, for ${{\tilde{p}}}_{3,j}$ and ${{\tilde{p}}}_{4,j}$.)

(i.) If $\psi '(p_1)=0$, then ${\mathcal {F}}(p_1)=1$ and, if moreover $p_3=2\Omega \mu p_1$, then $W''_j(p_1)= \gamma \psi ''(p_1) + \frac{\mu ^2\Omega ^2}{2p_1}$. If $\psi '(p_1)=0$ then $\psi ''(p_1)=\frac{f''(r)}{2p_1}$ and reversing to the coordinate r this gives the stated result.

(ii.) If $\psi '(p_1)=0$ and $p_3=0$ then $W''_j(p_1)= \frac{1}{2p_1}\mu ^2\Omega ^2 + \big (\gamma + \mu ^2 p_4\Omega +\mu ^2\Omega ^2\big )\psi ''(p_1)$.

(iii.) At the reduced equilibria of type RE3, $p_3\not =0$ and $p_4$ is given by (31). Inserting this expression in the formulas above gives $W''_j(p_1)=d_0+\Omega d_1$ with

$$\begin{aligned} d_0 \!\!= & {} \!\!2\gamma ^2\frac{p_1}{p_3^2}\big (\psi '+2p_1\psi '')\psi '{\mathcal {F}}^2 + \gamma \frac{\psi '}{p_1}\\{} & {} +\frac{p_3^2}{2p_1}\Big (\frac{1}{4p_1^2}+\frac{\psi '^2+\mu p_1\psi '^4}{p_1} + (1-\mu )\psi '\psi ''\Big ) {\mathcal {F}}^2\\ d_1 \!\!= & {} \!\!2\gamma \mu \frac{p_1}{p_3} \big (\psi ''-\psi '^3){\mathcal {F}}^2 \,. \end{aligned}$$

Up to the change of coordinates, $\Delta _0=F^2 r^3v_\theta ^2d_0$ and $\Delta _1 = F^2 r^3v_\theta ^2 d_1$. $\square$

We now draw some consequences from Proposition 11. Of special interest is the effect of the rotation of the surface on the properties of leafwise-stability of the reduced equilibria. However, also the case $\Omega =0$ is of interest because it has been so far investigated only very partially (Routh 1955; Hermans 1995; Zenkov 1995). As remarked, we may restrict the analysis to the case $\Omega \ge 0$.

6.2 Leafwise-Stability of RE1 Reduced Equilibria

The properties of leafwise-stability of the reduced equilibria of type RE1 are read without any difficulty from the expression of the function $S_1$ as in (32). Assume $f'(r)=0$.

As it might be expected, when $\Omega =0$ all reduced equilibria ${\mathcal {P}}_1(r,\omega _n,0)$, $\omega _n\in {\mathbb {R}}$, are leafwise-stable if $f''(r)>0$ and leafwise-unstable if $f''(r)<0$. For a given $\Omega \not =0$, ${\mathcal {P}}_1(r,\omega _n,\Omega )$ is leafwise-stable if $f''(r)>-\frac{\mu ^2}{\gamma }\Omega ^2$ and leafwise-unstable if $f''(r)<-\frac{\mu ^2}{\gamma }\Omega ^2$.

Since (2) implies $f''(r)>-1$ at any critical point r of f, for $\Omega >\frac{\sqrt{\gamma }}{\mu }$ all reduced equilibria of type RE1 are leafwise-stable. The rotation of the surface has thus a stabilizing effect on reduced equilibria of type RE1 (a sort of “gyrostatic stabilization”).

Note that the properties of leafwise-stability of reduced equilibria of type RE1 are independent of the angular velocity $\omega _n=\omega _z$ of the ball.

6.3 Leafwise-Stability of RE2 Reduced Equilibria

We consider the reduced equilibria of type RE2 only for $\Omega >0$ given that for $\Omega =0$ they coincide with the already considered RE1. Proposition 11 implies that

Proposition 12

Assume $f'(r)=0$. Then, for any $\Omega >0$:

• i. If $f''(r)=0$, all reduced equilibria ${\mathcal {P}}_2(r,\omega _n,\Omega )$, $\omega _n\in {\mathbb {R}}$, are leafwise-stable.

• ii. If $f''(r)>0$, ${\mathcal {P}}_2(r,\omega _n,\Omega )$ is leafwise-stable if

  $$\begin{aligned} \omega _n > -\frac{1+f''(r)}{f''(r)}\Omega - \frac{\gamma }{\mu ^2\Omega } \end{aligned}$$

  and leafwise-unstable if $\omega _n$ satisfies the opposite inequality.

• iii. If $f''(r)<0$ (hence $|f''(r)|<1$), ${\mathcal {P}}_2(r,\omega _n,\Omega )$ is leafwise-stable if

  $$\begin{aligned} \omega _n < \frac{1-|f''(r)|}{|f''(r)|}\Omega - \frac{\gamma }{\mu ^2\Omega } \end{aligned}$$

  and leafwise-unstable if $\omega _n$ satisfies the opposite inequality.

Thus, the rotation of the surface has a stabilizing effect also on the reduced equilibria of type RE2: they all become leafwise-stable for $\Omega \rightarrow +\infty$.

The regions of leafwise-stability and leafwise-instability of these reduced equilibria in the half-plane $(\Omega ,\omega _n)\in {\mathbb {R}}_+\times {\mathbb {R}}$ are depicted in Fig. 3 for the cases in which $f''(r)\not =0$. Note that, in these cases, the stability properties depend also on the angular velocity $\omega _n=\omega _\textrm{z}$ with which the ball rotates about its vertical axis.

Fig. 3

Bifurcation diagrams for the reduced equilibria of type RE2. Reduced equilibria are leafwise-stable in the shaded regions and leafwise-unstable in the unshaded regions. The boundary of the two regions is the curve $\omega _n=-\frac{1+f''(r)}{f''(r)}\Omega - \frac{\gamma }{\mu ^2\Omega }$. The dashed curve is the asymptote $\omega _n=-\frac{1+f''(r)}{f''(r)}\Omega$

6.4 Leafwise-Stability of RE3 Reduced Equilibria

Reduced equilibria of type RE3 exhibit more complex bifurcation scenarios than those of types RE1 and RE2. As above, we may assume $\Omega \ge 0$.

First, we note that, for large $\Omega$, the surface rotation may have either a stabilizing or a destabilizing effect on these reduced equilibria, depending on the direction in which the ball moves along the surface’s parallel, or even (in nongeneric but nontrivial cases) no effect at all:

Proposition 13

Consider $r>0$ such that $f'(r)\not =0$ and $v_\theta \not =0$.

• i. If $\Delta _{11}(r)=0$, then the properties of leafwise-stability of ${\mathcal {P}}_3(r,v_\theta ,\Omega )$ are independent of $\Omega$.

• ii. If $\Delta _{11}(r)>0$, then for $\Omega$ large enough ${\mathcal {P}}_3(r,v_\theta ,\Omega )$ is leafwise-stable if $v_\theta >0$ and leafwise-unstable if $v_\theta <0$.

• iii. If $\Delta _{11}(r)<0$, then for $\Omega$ large enough ${\mathcal {P}}_3(r,v_\theta ,\Omega )$ is leafwise-stable if $v_\theta <0$ and leafwise-unstable if $v_\theta >0$.

Proof

(i.) is obvious. If $\Delta _{11}(r)\not =0$ then, for $\Omega >\big |\frac{\Delta _0(r,v_\theta )}{v_\theta \Delta _{11}(r)}\big |$, $\textrm{Sign}(S_3) = \textrm{Sign}(\Omega v_\theta )\textrm{Sign}(\Delta _{11})$ and the other two statements follow from Proposition 11. $\square$

Next, we investigate the leafwise-stability and instability of the reduced equilibria of type RE3 with given r, as a function of $\Omega$ and $v_\theta$. Recall that for given r and $\Omega$ there are two branches of these equilibria in the plane $(v_\theta ,\omega _n)$, one with $v_\theta >0$ and one with $v_\theta <0$, which are given by (29) and are shown in Fig. 2.

For any $\Omega \ge 0$, the condition $S_3(r,v_\theta ,\Omega )>0$ of leafwise-stability (resp. $S_3(r,v_\theta ,\Omega )<0$ of leafwise-instability) of the reduced equilibrium ${\mathcal {P}}_3(r,v_\theta ,\Omega )$ is:

• If $\Delta _{11}(r)=0$

  $$\begin{aligned} \Delta _{00}(r) + \Delta _{02}(r)v_\theta ^2 + \Delta _{04}(r)v_\theta ^4 >0 \qquad \mathrm {\big (resp.}\ <0 \big ) \,. \end{aligned}$$

  (35)

• If $\Delta _{11}(r)\not =0$

  $$\begin{aligned} {\tilde{\Omega }}(r,v_\theta )< & {} \Omega \quad \mathrm {\big (resp.}\ {\tilde{\Omega }}(r,v_\theta )> \Omega \big ) \quad \textrm{if}\quad v_\theta \Delta _{11}(r)>0 \end{aligned}$$

  (36)
  $$\begin{aligned} {\tilde{\Omega }}(r,v_\theta )> & {} \Omega \quad \mathrm {\big (resp.}\ {\tilde{\Omega }}(r,v_\theta )<\Omega \big ) \quad \textrm{if}\quad v_\theta \Delta _{11}(r)<0 \end{aligned}$$

  (37)

  with

  $$\begin{aligned} {\tilde{\Omega }}(r,v_\theta ) \,:=\, -\frac{\Delta _{00}(r)}{\Delta _{11}(r)}\frac{1}{v_\theta } -\frac{\Delta _{02}(r)}{\Delta _{11}(r)}{v_\theta } -\frac{\Delta _{04}(r)}{\Delta _{11}(r)}{v_\theta ^3} \,. \end{aligned}$$

  (38)

When $\Delta _{11}(r)\not =0$, for $\Omega =0$ conditions (36) and (37) coincide with (35). Thus, (35) can be regarded as the condition for leafwise-stability or instability when $\Omega =0$. For the case $\Omega =0$, a condition equivalent to (35) is given by Routh (1955), who, however, does not study or apply it, and appears also in Hermans (1995) and Zenkov (1995).

(In some of the computations below, we prefer using (36) and (37) also for $\Omega =0$).

Proposition 14

For any $r>0$ and any $\Omega \ge 0$:

• i. In each of the two branches of reduced equilibria of type RE3 in the plane $(v_\theta ,\omega _n)$ there are at most two zeroes of the function $S_3$. These zeroes divide the branch in up to three connected components, in each of which all reduced equilibria are either leafwise-stable or leafwise-unstable (and if there are three, the properties of leafwise-stability alternate among them).

• ii. In each branch, the reduced equilibria in the closest component to $v_\theta =0$ are leafwise-stable if $f'(r)f''(r)>0$ and leafwise-unstable if $f'(r)f''(r)<0$.

• iii. In each branch, the reduced equilibria in the farthest component from $v_\theta =0$ are leafwise-stable if $rf''(r)>F(r)^2f'(r)$ and leafwise-unstable if $rf''(r)<F(r)^2f'(r)$.

Proof

(i.) Fix $\Omega$ and r. If $\Delta _{11}(r)=0$, then $S_3(r,v_\theta ,\Omega )=\Delta _{0}(r,v_\theta )$ is an even polynomial in $v_\theta$ and we may study it only for $v_\theta >0$. Since it has degree four, it has at most two positive roots. And if it has two positive roots, none of them is an extremal point. If $\Delta _{11}(r)\not =0$, then the zeroes of $S_3(r,v_\theta ,\Omega )$ are the values of $v_\theta$ at which ${\tilde{\Omega }}(r,v_\theta )=\Omega$. This is an odd function of $v_\theta$, and again we may study it only for $v_\theta >0$. The positive zeroes of ${\tilde{\Omega }}(r,v_\theta )$ are the positive roots of the even polynomial of degree four $v_\theta {\tilde{\Omega }}(r,v_\theta )$. Hence, they are at most two and $v_\theta \mapsto {\tilde{\Omega }}(r,v_\theta )$ can have at most one extremal point on the positive axis. It follows that, for $v_\theta >0$, its graph intersects in at most two points any horizontal line. And if there are two intersections, none of them is at an extremal of $v_\theta \mapsto {\tilde{\Omega }}(r,v_\theta ,\Omega )$. (ii.) For small $|v_\theta |$, the sign of $S_3(r,v_\theta ,\Omega )$ is the same as that of $\Delta _{00}(r)$. (iii.) This follows from items ii. and iii. of Proposition 13. $\square$

We detail now a few situations, not with the purpose of being exhaustive (which would require too many cases and subcases, and can be done on a case by case basis) but with that of covering a few typical situations and disclosing some general patterns. In particular, we neglect almost all nongeneric cases. We define

$$\begin{aligned} {\tilde{\Omega }}_{m}(r) \;:=\; \inf _{v_\theta \not =0}|{\tilde{\Omega }}(r,v_\theta )| \end{aligned}$$

Case 1: $f'(r)>0$, $f''(r)>0$. The three coefficients of the polynomial $\Delta _0(r,v_\theta )$ are all positive (recall that $\mu <1$). Thus, $\Delta _0(r,v_\theta )>0$ for all $v_\theta \not =0$ and it follows that all RE3 reduced equilibria with this r are leafwise-stable when $\Omega =0$. This has already been proved by Hermans (1995).

The situation for $\Omega >0$ depends on the sign of $\Delta _{11}(r)$. If $\Delta _{11}(r)>0$, then the graph of ${\tilde{\Omega }}(r,v_\theta )$ is shown in Fig. 4a, with ${\tilde{\Omega }}_{m}(r)$ finite and positive. For $v_\theta >0$, the condition of leafwise-stability is $\tilde{\Omega }(r,v_\theta )< \Omega$ and is satisfied by all reduced equilibria because ${\tilde{\Omega }}(r,v_\theta )<0$ if $v_\theta >0$. For $v_\theta <0$, ${\mathcal {P}}_3(r,v_\theta ,\Omega )$ is leafwise-stable if ${\tilde{\Omega }}(r,v_\theta )> \Omega$ and leafwise-unstable if $\tilde{\Omega }(r,v_\theta )<\Omega$. Thus, for $\Omega <{\tilde{\Omega }}_{m}(r)$, all the reduced equilibria with $v_\theta <0$ are leafwise-stable. If instead $\Omega >{\tilde{\Omega }}_{m}(r)$ there are two values $v_2<v_1<0$, which depend on r, such that ${\mathcal {P}}_3(r,v_\theta ,\Omega )$ is leafwise-stable for $v_\theta <v_2$ and for $v_1<v_\theta <0$ and is leafwise-unstable for $v_2<v_\theta <v_1$. See Fig. 4b, c.

As $\Omega \rightarrow \infty$, $v_2\rightarrow -\infty$ and $v_1\rightarrow 0$ and the entire branch of reduced equilibria with $v_\theta <0$ becomes leafwise-unstable, in agreement with Proposition 13.

If $\Delta _{11}(r)<0$, then ${\tilde{\Omega }}$ has the opposite sign of that of the case $\Delta _{11}(r)>0$; the resulting situation is depicted in Fig. 4b, d.

Fig. 4

Leafwise-stability of the two branches of reduced equilibria of type RE3 in the plane $(v_\theta ,\omega _n)$ when $f'(r)>0$ and $f''(r)>0$ for various values of $\Omega$. a Graph of ${\tilde{\Omega }}(r,v_\theta )$ for $\Delta _{11}(r)>0$. b–d Leafwise-stable (solid) and leafwise-unstable (dotted) RE3 reduced equilibria for $\Omega >0$ and $\Delta _{11}(r)\not =0$

We now study a few other cases. The analysis is similar to that of Case 1, and we may limit ourselves to a few comments—mostly, to draw the graph of the function ${\tilde{\Omega }}$. Instead of plotting the bifurcation diagrams in the plane $(\omega _n,v_\theta )$ we may describe them by specifying the type and the order (left to right) of the components of leafwise-stability (“S”) and of leafwise-instability (“U”) in each branch $v_\theta <0$ and $v_\theta >0$. We write the resulting strings between brackets, with a comma that separates the branch $v_\theta <0$ (first) from the branch $v_\theta >0$. Thus, for instance, the bifurcation diagrams of Fig. 4b–d are, respectively, of types (S, S), (SUS, S), (S, SUS).

Case 2: $f'(r)>0$, $f''(r)<0$. In this case, $\Delta _{00}(r)$ and $\Delta _{11}(r)$ are negative, $\Delta _{02}(r)$ is positive and $\Delta _{04}(r)$ may have any sign. If $\Delta _{04}(r)>0$, then the graph of ${\tilde{\Omega }}(r,v_\theta )$ is as in Fig. 5a and the bifurcation diagram is of type (SU, US). If $\Delta _{04}(r)<0$, there are two (generic) cases, depending on the sign of the discriminant

$$\begin{aligned} D(r) := \Delta _{02}(r)^2 - 4|\Delta _{00}(r)\Delta _{04}(r)| \,. \end{aligned}$$

If $D(r)>0$, then the graph of ${\tilde{\Omega }}(r,v_\theta )$ is as in Fig. 5b, with ${\tilde{\Omega }}_m(r)$ finite and positive, and the (generic) bifurcation diagrams are of type (USU, USU) if $0\le \Omega <{\tilde{\Omega }}_m(r)$ and of type (USU, U) if $0>{\tilde{\Omega }}_m(r)$. The graph of ${\tilde{\Omega }}(r,v_\theta )$ when $D(r)<0$ is as in Fig. 5c and the (generic) bifurcation diagrams are of type (U, U) if $0\le \Omega <{\tilde{\Omega }}_m(r)$ and of type (USU, U) if $\Omega >{\tilde{\Omega }}_m(r)$.

Fig. 5

Graphs of ${\tilde{\Omega }}(r,v_\theta )$ at fixed r when $f'(r)>0$, $f''(r)<0$: a $\Delta _{04}(r)>0$, b $\Delta _{04}(r)<0$ and $D(r)>0$, c $\Delta _{04}(r)<0$ and $D(r)<0$

Case 3: $f'(r)>0$, $f''(r)=0$. This case is nongeneric, but it is worth mentioning because it is the case of a cone, for which the existence and stability of reduced equilibria has been investigated in Borisov et al. (2019).

In this case $\Delta _{00}(r)=0$, $\Delta _{02}(r)>0$, $\Delta _{04}(r)>0$ and $\Delta _{11}(r)<0$. Thus $\Delta _0(r,v_\theta )>0$ for all $v_\theta \not =0$ and for $\Omega =0$ all RE3 reduced equilibria are leafwise-stable. Moreover, ${\tilde{\Omega }} = \frac{\Delta _{02}}{|\Delta _{11}|}v_\theta +\frac{\Delta _{04}}{|\Delta _{11}|}v_\theta ^3$. It follows that, for $\Omega >0$, all reduced equilibria with $v_\theta <0$ are leafwise-stable while those with $v_\theta >0$ are leafwise-stable for $v_\theta <v_1$ and leafwise-unstable for $v_\theta >v_1$ with a certain $v_1>0$ that depends on r and $\Omega$ and goes to 0 for $\Omega \rightarrow 0$ and to $+\infty$ for $\Omega \rightarrow +\infty$.

The bifurcation diagram is of type (S, S) for $\Omega =0$ and of type (S, SU) for $\Omega >0$.

Case 4: $f'(r)<0$, $f''(r)<0$. $\Delta _{00}(r)$ and $\Delta _{04}(r)$ are positive, $\Delta _{02}(r)$ is negative and $\Delta _{11}(r)$ may have any sign. Let D(r) be the discriminant defined in Case 2.

• If $\Delta _{11}(r)>0$ and $D(r)>0$, then the graph of ${\tilde{\Omega }}$ is as in Fig. 5b and the bifurcation diagram is of type (SUS, SUS) if $0\le \Omega \le {\tilde{\Omega }}_{m}$ and of type (SUS, S) if $\Omega >{\tilde{\Omega }}_{m}$.

• If $\Delta _{11}(r)>0$ and $D(r)<0$, then the graph of ${\tilde{\Omega }}$ is as in Fig. 5c and the bifurcation diagram is of type (S, S) if $0\le \Omega \le {\tilde{\Omega }}_{m}$ and of type (SUS, S) if $\Omega >{\tilde{\Omega }}_{m}$.

• If $\Delta _{11}(r)<0$ and $D(r)>0$, then the graph of ${\tilde{\Omega }}$ is the reflection about the $v_\theta$ axis of that shown in Fig. 5b. The bifurcation diagram is of type (SUS, SUS) if $0\le \Omega \le {\tilde{\Omega }}_{m}$ and of type (S, SUS) if $\Omega >{\tilde{\Omega }}_{m}$.

• If $\Delta _{11}(r)<0$ and $D(r)<0$, then the graph of ${\tilde{\Omega }}$ is the reflection about the $v_\theta$ axis of that shown in Fig. 5c. The bifurcation diagram is of type (S, S) if $0\le \Omega \le {\tilde{\Omega }}_{m}$ and of type (S, SUS) if $\Omega >{\tilde{\Omega }}_{m}$.

Other cases can be studied similarly.

7 Example: The Ball on an Upward Paraboloid

7.1 The Parabolic Surface

We investigate now some aspects of the dynamics for the parabolic profile

$$\begin{aligned} f = \frac{1}{2}br^2 \end{aligned}$$

(39)

with a constant $b>0$. This has two purposes. One is to prove that, even if the profile is not superquadratic, all motions which do not pass through the vertex are bounded, and hence generically quasiperiodic, even for $\Omega \not =0$ (Proposition 15; this had been previously proven only for small values of $|\Omega |$, see Fassò and Sansonetto 2015). The other is to investigate, numerically, the presence and number of (particularly leafwise-unstable) reduced equilibria on each level set of the map J. We give all expressions in polar coordinates. Note that

$$\begin{aligned} f' = br \,,\qquad f''=b \,,\qquad F=\sqrt{1+b^2r^2} \,. \end{aligned}$$

7.2 Reduced Equilibria

The system has only reduced equilibria of type RE3, with

$$\begin{aligned} {\tilde{\omega }}_n(r,v_\theta ,\Omega ) = -\frac{\gamma }{\mu }\frac{1}{v_\theta } + \frac{1}{\mu b}v_\theta -\Omega \Big (\frac{1}{b}+\frac{1}{F}\Big ) \,,\qquad v_\theta \not =0 \,. \end{aligned}$$

The two branches they form are independent of r if $\Omega =0$, but for $\Omega >0$ they are shifted below by an amount which decreases with r and varies between $\Omega (1+\frac{1}{b})$ and $\frac{\Omega }{b}$.

All these reduced equilibria pertain to Case 1 of Sect. 6.4, with $\Delta _{11}=-\gamma \mu b^2 r^3<0$. For $\Omega =0$ they are all leafwise-stable and for $\Omega >0$ all those with negative $v_\theta$ are leafwise-stable. We thus focus on the reduced equilibria with $\Omega >0$ and $v_\theta >0$.

For $v_\theta >0$, the possible situations are those of Fig. 4b, d. The function ${\tilde{\Omega }}$ is given by

$$\begin{aligned} {\tilde{\Omega }}(r,v_\theta ) = \frac{\gamma }{b\mu r^2 v_\theta } + \frac{2}{\mu }\Big (\frac{1}{b^2r^2}+1\Big ) v_\theta + \frac{1}{b\gamma \mu }\Big (\frac{1}{b^2r^2}+2+\mu b^2r^2\Big )v_\theta ^3 \end{aligned}$$

and some of its level curves (with values increasing from top to bottom) are shown in Fig. 6 for three different values of the parameter b. For each ${\bar{r}}>0$, the level curve ${\tilde{\Omega }}({\bar{r}},v_\theta )={\tilde{\Omega }}_{m}({\bar{r}})$ is the one tangent to the (horizontal) line $r={\bar{r}}$. Therefore, the function $r\mapsto {\tilde{\Omega }}_{m}(r)$ is a strictly decreasing function which tends to $+\infty$ for $r\rightarrow 0$ and to 0 for $r\rightarrow +\infty$ and its graph resembles that of a branch of a hyperbola. Its inverse $\Omega \mapsto {{\tilde{r}}}_{m}(\Omega )$, which gives the r-coordinate of the minimum of the level curves of ${\tilde{\Omega }}$, has these same properties. We stress that, for each $\Omega >0$, $\tilde{r}_m(\Omega )>0$.

Fig. 6

Level curves of ${\tilde{\Omega }}$ for the parabolic profile (39). Each panel shows (from bottom to top) the level curves ${\tilde{\Omega }}=100,60,30,15,6,2,1$ for the indicated values of b. The first panel is an enlargement of the third

This provides the following picture for the stability of the reduced equilibria ${\mathcal {P}}_3(r,v_\theta ,\Omega )$ with $v_\theta >0$. For each $\Omega >0$, they are all leafwise-stable if $r<{{\tilde{r}}}_m(\Omega )$. For $r>{{\tilde{r}}}_m(\Omega )$ there are the three intervals “SUS” of values of $v_\theta$ as in Fig. 4d. As r increases, the first “S” interval, the one closest to $v_\theta =0$, becomes extremely narrow while the amplitude of the middle “U” interval reaches a maximum and then goes (slowly) to zero as $r\rightarrow +\infty$. We stress that all reduced equilibria become stable for $v_\theta$ large enough.

Concerning the dependence on the parameters, Fig. 6 indicates that as b increases, namely, as the paraboloid becomes steeper, the amplitude of the “U” interval decreases at small r but increases at large r. We mention that increasing $\gamma$ expands the instability region at all r, while increasing $\mu$ expands it at small r and seems to have little effect at large r.

7.3 The J-Restricted Reduced Systems

In order to understand the dynamics we investigate now the $J^\circ$-restricted systems. For the parabolic profile the integration of the differential equations that give the two first integrals $J_1$ and $J_2$ can be done explicitly. Expressed as functions of r instead of $p_1$, the solutions of equations (17) and (18) are

$$\begin{aligned}{} & {} {\overline{U}} = \left( \begin{array}{ll} c &{} \frac{\sqrt{\mu }}{b} s\\ \frac{b}{\sqrt{\mu }}s &{} c \end{array} \right) \,,\\{} & {} \qquad {\overline{u}} = \left( \begin{array}{l} \frac{1}{(4-\mu )b^2} \big ( (4-3\mu )(c-1)+(4b-(b+1)\mu )\sqrt{\mu }\,s + 2 \mu b^2r^2 \big ) \\ \frac{1}{(4-\mu )b} \big ( (4b-(b+1)\mu )c + \frac{4-3\mu }{\sqrt{\mu }}s - b \frac{4-\mu }{F}+\mu F^2 \big ) \end{array} \right) \end{aligned}$$

where

$$\begin{aligned}{} & {} c(r) := \cosh \Big (\frac{\sqrt{\mu }}{2}\log F(r) \Big ) = \frac{F(r)^{\sqrt{\mu }}+1}{2F(r)^{\sqrt{\mu }/2}} \,,\\{} & {} \quad s(r) := \sinh \Big (\frac{\sqrt{\mu }}{2}\log F(r) \Big ) = \frac{F(r)^{\sqrt{\mu }}-1}{2F(r)^{\sqrt{\mu }/2}} \,. \end{aligned}$$

The effective potential $V_j$ is given by (28) with

$$\begin{aligned} \left( \begin{array}{l} {\overline{p}}_{3,j}(r) \\ {\overline{p}}_{4,j}(r) \end{array} \right) = {\bar{U}}(r)j+\Omega {\bar{u}}(r) \end{aligned}$$

see (22).

Proposition 15

If $f(r)=\frac{1}{2}br^2$, $b>0$, then for any $j_1\not =0$ and $\Omega \ge 0$, $V_j(r)$ goes to $+\infty$ for $r\rightarrow 0^+$ and for $r\rightarrow +\infty$.

Proof

Since ${\overline{p}}_3(0,j)=j_1$ and ${\overline{p}}_4(0,j)=j_2$, for $r\rightarrow 0^+$ the function $V_j$ is asymptotic to $\frac{j_1^2}{2r^2}+\frac{1}{2}\mu j_2^2+\Omega (\mu j_2-j_1)-\frac{1}{2}\mu \Omega ^2$. For $r\rightarrow +\infty$, c(r) and s(r) are both asymptotic to $r^{\sqrt{\mu }/2}$ and the same is true for the matrix ${\overline{U}}(r)$. Instead, ${\overline{u}}(r)$ is asymptotic to $r^2$. Thus, both ${\overline{p}}_{3j}$ and ${\overline{p}}_{4j}$ are asymptotic to $r^2$. This implies that, if $\Omega >0$, then $V_j$ is asymptotic for $r\rightarrow +\infty$ to $\frac{1}{2}\mu {\overline{p}}_{4j}(r)^2$ and hence to $r^4$. $\square$

This implies that, for all $j_1\not =0$, the dynamics of the reduced system is periodic (and hence that of the unreduced one is quasiperiodic) except for the equilibria and the motions asymptotic to and from the unstable ones. We do not investigate here motions in the level set $j_1=0$ because it contains the vertex.

7.4 The Equilibria of the J-Restricted Reduced Systems

Proposition 15 implies that, for any $j_1\not =0$ and $\Omega \ge 0$, the effective potential has at least one minimum, and hence the restriction of the reduced system to $M_2^j$ has at least one stable equilibrium. In fact, since $V_j$ is a real analytic nonconstant function, its minima are all isolated and, since the system has one degree of freedom, they are the only stable equilibrium configurations. Generically, there is obviously an odd number of equilibria on each $M^2_j$, but their exact number—and the numbers of the stable and unstable ones—is of special interest because gives global information on the dynamics in $M_2^j$.

We already know that, when $\Omega =0$, all reduced equilibria are leafwise-stable. This implies that, for each $j\not =0$, $V_j$ has a single critical point, which is a minimum, and the reduced system in $M_2^j$ has only one equilibrium. Figure 7a shows, for a typical choice of the values of the parameters $\mu$, b, j, the value of the r-coordinate of the reduced equilibrium on $M^2_j$ as a function of $j=(j_1,j_2)$. This is a single-valued surface. At fixed $j_2$, the r-coordinate of the reduced equilibrium tends to a constant value when $|j_1|\rightarrow \infty$ and there is a single maximum of r, which goes to $+\infty$ when $|j_2|\rightarrow \infty$. Not surprisingly, when $j_1\rightarrow 0$ the coordinate the reduced equilibrium tends to the vertex ($r\rightarrow 0$). Note the symmetry of the surface S under reflections of $(j_1,j_2)$.

In order to determine the number of unstable equilibria for $\Omega \not =0$, we resorted to a numerical analysis, whose results are illustrated by Fig. 7b–d. As soon as $\Omega \not =0$, two (or exceptionally, at the bifurcations, one) other reduced equilibria are created for $j=(j_1,j_2)$ in about half of the $(j_1,j_2)$-plane, one of which is leafwise-unstable and the other (if present) is leafwise-stable. The figures show the equilibria surface for different values of $\Omega$ and in different ranges of $j_1,j_2$. Even though the figures cannot show it clearly, the shape of the surface is similar for all values of $\Omega$ but, as one sees observing that the figures have different scales, as $\Omega \rightarrow 0$ the two additional equilibria go to infinity in r and/or $v_\theta$.

Fig. 7

Value of the r coordinates at the reduced equilibria for the parabolic profile (39) ($b=\gamma =1$, $\mu =2/7$)

8 Conclusions

We have provided a general analysis of the dynamics of a heavy dynamically symmetric ball that rolls without sliding on a uniformly rotating surface of revolution. Even though this study has clarified a number of aspects of this class of systems, some questions remain open.

• 1. The possibility and the properties of motions through—or asymptotic to—the vertex have not been studied. The possibility of motions in which the point of contact tends to the vertex and (some component of) the angular velocity grows unbounded is not ruled out by our analysis and should be investigated. One natural possibility is to analyze these motions in the five-dimensional $\mathrm {SO(3)}$-reduced system. (As already mentioned in footnote $^{3}$, a study of this question has been performed while the present article was under review Fassò and Sansonetto (2022).)

• 2. When $\Omega \not =0$, we have only proven the boundedness of motions under the hypothesis that the profile of the surface goes superquadratically to $+\infty$ at infinity. We have proven this fact using the compactness of the level sets of the moving energy. However, as pointed out in Sect. 3.3, what is necessary is the compactness of all the level sets of the map (E, J) which, as the example of the (upward) paraboloid of Sect. 7 shows, might be satisfied under the assumption alone of coercivity of the profile. A general study of this question might require a careful analysis of the asymptotic properties of the functions $J_1$ and $J_2$ defined by the differential equations (15).

• 3. When $\Omega =0$, if the profile goes asymptotically to $-\infty$, or to a constant, then there are certainly unbounded motions, in which the ball goes to infinity. Even though some particular statements are made in Routh (1955), a characterization of the initial conditions which lead to bounded or unbounded motions is essentially missing.

• 4. In connection with point 3, we remark that the example of the ball that rolls on a horizontal plane suggests that the rotation of the surface may have a “stabilizing” effect on the dynamics. In fact, in all motions of such a system but the equilibria the ball runs away to infinity if $\Omega =0$, but as soon as $\Omega \not =0$ the center of the ball either stands still or moves on circles! Preliminary investigations show that such a stabilizing effect of the rotation is present in other profiles, e.g., in the downward paraboloid and cone, and we conjecture that, as soon as $\Omega \not =0$, all motions in any profile are bounded (with the possible exception of those asymptotic to the vertex).

• 5. Also the (local and global) structure of the foliation by the invariant tori of the unreduced system (in integrable cases) is still not studied. This study would require some comprehension of the frequencies of motions. Some results on this, for the case of a coercive profile and $\Omega =0$, are given by Hermans (1995).

Appendix: The Equations of Motion

1.1 The Nonholonomic Equations of Motion in Quasi-Velocities with the Reaction Forces

The equations of motion of mechanical systems subject to nonholonomic constraints can be written in several ways. Particularly, when the configuration space involves a Lie group it is customary to employ a technique originally developed by Poincaré for holonomic systems (Poincaré 1901), which is based on the use of coordinates and quasi-velocities—namely linear combinations of the velocities. For instance, for rigid bodies this allows to use the components of the angular velocity (with respect to a fixed or moving frame) instead of the velocities of the Euler angles or other local coordinates on $\mathrm {SO(3)}$. The nonholonomic case was first considered by Hamel (1904).

However, in Hamel’s approach the quasi-velocities are chosen so that the nonholonomic constraint is given as zero of some of them. This leads to a set of equations on the constraint manifold—Hamel equations—in which the reaction forces are not explicitly identified (see, e.g., Neimark and Fufaev 1972; Bloch et al. 2009; Cortés et al. 2009; Bloch 2015; Zenkov 2016 for some treatments and applications). In our opinion, instead, the explicit consideration of the reaction forces is under several respects important, e.g., in determining the conservation of momenta and energy (Fassò and Sansonetto 2015, 2016; Fassò et al. 2018).

We thus derive here a form of the equations of motion of nonholonomic systems that employs quasi-velocities and contains, in an explicit way, the reaction forces. Specifically, we write these equations as the restriction to the nonholonomic constraint manifold $M\subset TQ$ of a set of equations in the tangent bundle of the configuration manifold Q that leave M invariant (namely, as a vector field which is tangent to M). This is a generalization of an analogous form of the equations that uses Lagrangian coordinates and velocities, which is our starting point and for which we refer to Fassò and Sansonetto (2015).

We consider a nonholonomic system $(Q,{\mathcal {L}},{\mathcal {M}})$ with an n-dimensional configuration manifold Q, a mechanical Lagrangian ${\mathcal {L}}:TQ\rightarrow {\mathbb {R}}$, and an affine distribution ${\mathcal {M}}$ on Q with constant rank that describes the nonholonomic constraint. More specifically:

• i. By a mechanical Lagrangian, we mean a function of the form ${\mathcal {L}}={\mathcal {L}}_2+{\mathcal {L}}_1+{\mathcal {L}}_0$, where ${\mathcal {L}}_2$ is a Riemannian metric on Q, ${\mathcal {L}}_1$ is a function whose restriction to each fiber of TQ is linear, and ${\mathcal {L}}_0$ is a basic function, hence constant on the fibers of TQ.

• ii. We write the affine distribution as ${\mathcal {M}}=\xi +{\mathcal {D}}$, with ${\mathcal {D}}$ a non-integrable distribution on Q of constant rank r, $1<r<n$, and $\xi$ a vector field on Q. Clearly, the vector field $\xi$ is defined up to a section of ${\mathcal {D}}$. We denote by M the $(n+r)$-dimensional subbundle of TQ formed by the fibers of ${\mathcal {M}}$.

• iii. Lastly, we assume that the nonholonomic constraint is ideal, namely, that the reaction forces it exerts satisfy d’Alembert principle, see (Agostinelli 1956; Fassò and Sansonetto 2015) for details.

It is well known that, under these hypotheses, there is a unique function $R_{{\mathcal {L}},M}:M\rightarrow {\mathcal {D}}^\circ$ with the property that the restriction to M of Lagrange equations with the reaction forces,

$$\begin{aligned}{}[{\mathcal {L}}]\big |_{M} = R_{{\mathcal {L}},M} \,, \end{aligned}$$

(40)

defines a vector field on M, and hence a dynamical system on M (Agostinelli 1956; Fassò and Sansonetto 2015). Here, $[{\mathcal {L}}]$ is the usual Euler–Lagrange operator. The expression of these equations using lifted coordinates $(q,\dot{q})$ in TQ is given in Fassò and Sansonetto (2015), and can be recovered as a particular case of the present treatment.

Consider now a set of local coordinates $q:Q_U\rightarrow U$ defined in an open set $Q_U \subseteq Q$ and taking values in an open set U of ${\mathbb {R}}^{n}$. We call “lifted coordinates” the coordinates $(q,\dot{q})$ in $TQ_U$. Consider a smooth function $B:U\rightarrow \mathrm {GL(n)}$. Then, the change of coordinates

$$\begin{aligned} (q,\dot{q}) \mapsto \big (q,B(q)\dot{q}\big ) =:(q,v) \end{aligned}$$

defines a new set of bundle-like coordinates in $TQ_U$. The expression of the Euler–Lagrange operator $[{\mathcal {L}}]$ in these coordinates is well known (Lagrange–Poincaré equations Poincaré 1901), and we need only compute $R_{{\mathcal {L}},M}$.

The local representative L of the Lagrangian ${\mathcal {L}}$ has the form $L=L_2+L_1+L_0$ with $L_0$ independent of the v’s, $L_1$ linear in the v’s, and $L_2(q,v)=\frac{1}{2} v\cdot A(q)v$ with

$$\begin{aligned} A= \frac{\partial ^2L}{\partial v\partial v} \end{aligned}$$

a positive definite matrix that depends only on q. The fibers of the distribution ${\mathcal {D}}$ based in $Q_U$ can be represented as the kernel of a q-dependent $(n-r)\times n$ matrix S(q) of rank $n-r$: The fiber of ${\mathcal {M}}$ based at the point of $Q_U$ of coordinates q is given by the equation

$$\begin{aligned} S(q)v+s(q)=0 \,, \end{aligned}$$

where $q\mapsto s(q)\in {\mathbb {R}}^{n}$ is a smooth map that depends on the vector field $\xi$ (specifically, $s(q)=-S(q)\xi ^\textrm{loc}(q)$ if $\xi |_{Q_U}=\sum _i\xi ^\textrm{loc}_i\partial _{q_i}$). The image of $M\cap TQ_U$ under the coordinate map (q, v) is the $(n+r)$-dimensional submanifold

$$\begin{aligned} M_U := \big \{ (q,v)\in U\times {\mathbb {R}}^{n}\,:\; S(q)v+s(q)=0\big \} \end{aligned}$$

of $U\times {\mathbb {R}}^{n}$.

Define now maps $\ell :U\times {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}$, $\sigma :U\times {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n-r}$ and $R:U\times {\mathbb {R}}^{n}\rightarrow {\mathbb {R}}^{n}$ as follows: $\ell (q,v)$ has components⁶

$$\begin{aligned} \ell _i = \frac{\partial ^2L}{\partial v_i\partial q_j} \,B^{-1}_{jh}\,v_h + \gamma _{ijh} \,\frac{\partial L}{\partial v_j} \,v_h - B^{-T}_{ij}\frac{\partial L}{\partial q_j} \,,\qquad i=1,\ldots ,n\,, \end{aligned}$$

(41)

where $\gamma _{ijh} = B^{-T}_{ik}\big (\frac{\partial B^T_{kj}}{\partial q_l} - \frac{\partial B^T_{lj}}{\partial q_k}\big ) B^{-1}_{lh}$ are the so-called transpositional symbols, $\sigma (q,v)\in {\mathbb {R}}^{k}$ has components

$$\begin{aligned} \sigma _a = \Big ( \frac{\partial S_{ai}}{\partial q_j}v_i + \frac{\partial s_a}{\partial q_j}\Big ) B^{-1}_{jh}v_h \,,\qquad a=1,\ldots ,n-r \,, \end{aligned}$$

(42)

and

$$\begin{aligned} R = S^T (SA^{-1}S^T)^{-1} (SA^{-1}\ell -\sigma ) \,. \end{aligned}$$

(43)

Proposition 16

The representative of equation (40) in the coordinates (q, v) is the restriction to $M_U$ of the equation

$$\begin{aligned} \dot{q} = B(q)^{-1} v \,,\qquad A(q)\,\dot{v}+ \ell (q,v) = R(q,v) \end{aligned}$$

(44)

in $U\times {\mathbb {R}}^{n}$.

Proof

The representative ${{\tilde{L}}}$ of ${\mathcal {L}}$ in the coordinates $(q,\dot{q})$ is ${{\tilde{L}}}(q,\dot{q}) = L(q,B(q)\dot{q})$ and so $\tilde{A}:=\frac{\partial ^2{{\tilde{L}}}}{\partial \dot{q}\partial \dot{q}}= B^TAB$. The constraint manifold in lifted coordinates is given by ${{\tilde{S}}}(q)\dot{q}+s(q)=0$ with ${{\tilde{S}}} = SB$. The equations of motion in lifted coordinates are known (Fassò and Sansonetto 2015) to be the restriction to ${{\tilde{M}}}_U = \{(q,\dot{q})\in U\times {\mathbb {R}}^{n} \,:\; {{\tilde{S}}}(q)\dot{q} + s(q)=0\big \}$ of the equation ${{\tilde{A}}}\ddot{q} + {\tilde{\ell }}=\tilde{R}$, where ${\tilde{\ell }}$, ${\tilde{\sigma }}$ and ${{\tilde{R}}}$ are defined by formulas (41)–(43) with L, A and S replaced, respectively, by ${{\tilde{L}}}$, ${{\tilde{A}}}$ and ${{\tilde{S}}}$, v replaced by $\dot{q}$, and B replaced by the unit matrix (hence all $\gamma _{ijh}$ vanish). A computation gives

$$\begin{aligned} {{\tilde{A}}}(q)\ddot{q}= & {} B(q)^T\big [ A(q)\dot{v} - A(q)\dot{B}(q,\dot{q})\dot{q} \big ] \\ {\tilde{\ell }}(q,\dot{q})= & {} B(q)^T\big [\ell (q,v) + A(q)\dot{B}(q,\dot{q})\dot{q}\big ] \\ {\tilde{\sigma }}(q,\dot{q})= & {} \sigma (q,v) + S(q)\dot{B}(q,\dot{q})\dot{q} \end{aligned}$$

where v stands for $B(q)\dot{q}$ and $\dot{B}(q,\dot{q})$ is the matrix with entries $\dot{B}_{ij}=\frac{\partial B_{ih}}{\partial \dot{q}_j}\dot{q}_h$. Thus ${{\tilde{A}}} \ddot{q}+{\tilde{\ell }}-{{\tilde{R}}} = B^T\big (A\dot{v}+\ell -R)$. $\square$

1.2 The (Reduced) Equations of Motion of Our System

We write now the equations of motion of the ball on the rotating surface of revolution considered in this paper and of its $\mathrm {SO(3)}\times \mathrm {SO(2)}$-reduction.

In order to facilitate the reduction under the $\mathrm {SO(2)}$-action we restrict at first to the subset $M_8^\circ$ of $M_8={\mathbb {R}}^{2}\times \mathrm {SO(3)}\times {\mathbb {R}}^{2}\times {\mathbb {R}}\ni (x,{\mathcal {R}},\dot{x}, \omega _\textrm{z})$ where $x\not =0$ and use polar coordinates $(r,\theta )\in {\mathbb {R}}_+\times S^1$ in its factor ${\mathbb {R}}^{2}\setminus \{0\}\ni x=(x_1,x_2)$, with $x_1= r\cos \theta$, $x_2=r\sin \theta$. Correspondingly, we restrict the holonomic system to the submanifold $M_{10}^\circ$ of $M_{10}={\mathbb {R}}^{2}\times \mathrm {SO(3)}\times {\mathbb {R}}^{2}\times {\mathbb {R}}^{3} \ni (x,{\mathcal {R}},\dot{x}, \omega )$ where $x\not =0$ and here too we use polar coordinates in the factor ${\mathbb {R}}^{2}\times \{0\}$, thus working in

$$\begin{aligned} \widehat{M}_8^\circ = {\mathbb {R}}_+\times S^1 \times \mathrm {SO(3)}\times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}\ni (r,\theta ,{\mathcal {R}},v_r,v_\theta , \omega _\textrm{z}) \,. \end{aligned}$$

Furthermore, in $M_{10}^\circ$ we use the quasi-velocities

$$\begin{aligned} v = (v_r,v_\theta ,\omega _\textrm{x},\omega _\textrm{y},\omega _\textrm{z}) \,, \end{aligned}$$

thus identifying $M_{10}^\circ$ with ${\mathbb {R}}_+\times S^1\times \mathrm {SO(3)}\times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}^{3}$. The representative of the Lagrangian (1) of the system is

$$\begin{aligned} L(r,\theta ,{\mathcal {R}},v_r,v_\theta ,\omega ) = \frac{1}{2}F(r)^2v_r^2 + \frac{1}{2}r^2v_\theta ^2 + \frac{1}{2} k |\omega |^2 - {\hat{g}} f(r) \end{aligned}$$

(45)

and the nonholonomic constraint (6) becomes $\omega _\textrm{x}={\tilde{\omega }}_\textrm{x}(r,\theta ,v_r,v_\theta ,\omega _\textrm{z})$, $\omega _\textrm{y}={\tilde{\omega }}_\textrm{y}(r,\theta ,v_r,v_\theta ,\omega _\textrm{z})$ with

$$\begin{aligned} \begin{aligned} {\tilde{\omega }}_\textrm{x}&= (\Omega -\omega _\textrm{z})f' \cos \theta + (\Omega r\cos \theta -v_r\sin \theta -r v_\theta \cos \theta )F \\ {\tilde{\omega }}_\textrm{y}&= (\Omega -\omega _\textrm{z})f'\sin \theta + (\Omega r\sin \theta +v_r\cos \theta -r v_\theta \sin \theta ) F \,. \end{aligned} \end{aligned}$$

(46)

Accordingly, we identify $M_8^\circ$ with

$$\begin{aligned} \widehat{M}_8^\circ := {\mathbb {R}}_+\times S^1\times \mathrm {SO(3)}\times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}\ni (r,\theta ,{\mathcal {R}},v_r, v_\theta , \omega _\textrm{z}) \,. \end{aligned}$$

In this identification, $\mathrm {SO(3)}\times \mathrm {SO(2)}$ acts on the factor ${\mathbb {R}}_+\times S^1$ by translations in $S^1$ and $M_8^\circ /(\mathrm {SO(3)}\times \mathrm {SO(2)})$ can be identified with

$$\begin{aligned} \widehat{M}_4^\circ := {\mathbb {R}}_+\times {\mathbb {R}}\times {\mathbb {R}}\times {\mathbb {R}}\ni (r,v_r, v_\theta , \omega _\textrm{z}) \,. \end{aligned}$$

Proposition 17

(i) The equations of motion in $\widehat{M}_8^\circ$ are

$$\begin{aligned} \dot{r}= & {} v_r \\ \dot{\theta }= & {} v_\theta \\ \dot{\mathcal {R}}= & {} {\mathcal {R}}^T \big ({\tilde{\omega }}_\textrm{x},{\tilde{\omega }}_\textrm{y},\omega _\textrm{z}\big )^T \\ \dot{v}_r= & {} -\gamma f'F^{-2} - f'f''F^{-2}v_r^2 + r(1+\mu f'^2)F^{-2}v_\theta ^2 +\mu f'F^{-1} {-v}_\theta \omega _\textrm{z}\\{} & {} - \Omega \mu (r+f'F^{-1})v_\theta \\ \dot{v}_\theta= & {} -\frac{v_r}{r}\Big [ \big (2+\mu r f'f''F^{-2}\big )v_\theta + \mu f''F^{-1} \omega _\textrm{z}- \Omega \mu (1 +f''F^{-1} + r f'f''F^{-2}) \Big ] \\ \dot{\omega }_\textrm{z}= & {} -v_r\frac{1}{1+k} f'F^{-1}\Big [ rf'f''F^{-2}v_\theta + f'' F^{-1} \omega _\textrm{z}- \Omega \big (1+ f''F^{-1} + rf'f''F^{-2}\big ) \Big ] \end{aligned}$$

with $\mu =\frac{k}{k+1}$, $\gamma =\frac{{\hat{g}}}{k+1}=\frac{g}{(k+1)a}$ and $F=(1+f'^2)^{1/2}$ (see (10)).

(ii) The equations of motion of the reduced system in $\widehat{M}_4^\circ$ are given by the first and the last three equations in (i).

Proof

(i) In order to invoke Proposition 16, we need to introduce local coordinates $\alpha =(\alpha _1,\alpha _2,\alpha _3)$ in $\mathrm {SO(3)}$. Due to the $\mathrm {SO(3)}$-symmetry, the choice of these coordinates is irrelevant, but in order to be able to consider a single chart it is convenient to choose them so that their domain is open and dense in $\mathrm {SO(3)}$. For instance, we could use three Euler angles.

Thus, we use the coordinates $q=(r,\theta ,\alpha _1,\alpha _2,\alpha _3)$ and the quasi-velocities $v=(v_r,v_\theta ,\omega _\textrm{x},\omega _\textrm{y},\omega _\textrm{z})$. The Lagrangian is (45), and $A = \mathrm {diag\,}(F^2,r^2,k,k,k)$. The matrix that gives the quasi-velocities is

$$\begin{aligned} B(r,\theta ,\alpha ) = \textrm{diag}\big (1,1,b(\alpha )\big ) \end{aligned}$$

with a certain $3\times 3$ invertible matrix $b(\alpha )$ whose expression is irrelevant.

The function $\ell$ can be computed, instead of using its expression (41), using the Lagrange equations of the holonomic system. Indeed, the first two components of the quantity $A\ddot{q} +\ell =0$ are $\frac{d}{dt}\frac{\partial L}{\partial v_r}-\frac{\partial L}{\partial r}$ and $\frac{d}{dt}\frac{\partial L}{\partial v_\theta }-\frac{\partial L}{\partial \theta }$, and detailing them gives the first two components of $\ell$. Since $\omega$ is a first integral of the holonomic system, the last three components of $\ell$ are all zero. In this way, using also $FF'=f'f''$, we get

$$\begin{aligned} \ell = \big ( f'f'' v_r^2 - r v_\theta ^2 + {\hat{g}} f', 2r v_r v_\theta , 0, 0, 0 \big ) \,. \end{aligned}$$

The nonholonomic constraint (6) can be written as $S(r,\theta )v+s(r,\theta )=0$ with

$$\begin{aligned} S(r,\theta ) = \left( \begin{array}{lllll} F \cos \theta &{} -r F\sin \theta &{} 0 &{} -1 &{}-f'\sin \theta \\ F \sin \theta &{} r F\cos \theta &{} 1 &{}0 &{}f'\cos \theta \end{array} \right) \,,\quad s(r,\theta ) = \Omega \left( \begin{array}{l} (r F+f')\sin \theta \\ -(r F+f')\cos \theta \end{array} \right) \,. \end{aligned}$$

A direct computation gives

$$\begin{aligned} (SAS^T)^{-1} = \mu {\mathcal {F}}^2 \left( \begin{array}{ll} 1+f'^2(\cos \theta )^2 &{} f'^2 \cos \theta \,\sin \theta \\ f'^2 \cos \theta \,\sin \theta &{} 1+f'^2(\sin \theta )^2 \end{array} \right) \,. \end{aligned}$$

Since S and s are independent of the $\alpha$’s, the sum over the index j in the expression (42) of $\sigma$ reduces to $j=1,2$. Since $B^{-1}_{jh}=\delta _{jh}$ for $j=1,2$ and $h=1,\ldots ,5$, we have

$$\begin{aligned} \sigma _a = \frac{\partial S_{ah}}{\partial r} v_r v_h + \frac{\partial s_a}{\partial r} v_r + \frac{\partial S_{ah}}{\partial \theta }v_\theta v_h + \frac{\partial s_a}{\partial \theta }v_\theta \,,\qquad a = 1,2 \,, \end{aligned}$$

and in fact, since the third and fourth component of S are constant, all sums over the index h restrict to $h=1,2,5$. (This implies that $\sigma$, as all other terms, is independent of $\omega _\textrm{x}$ and $\omega _\textrm{y}$; this will make the restriction to the constraint manifold trivial.) Putting the various terms together, and using again the identity $F'=f'f''/F$, we eventually find from (43)

$$\begin{aligned} R= & {} \mu \left( \begin{array}{l} {\hat{g}} f' + (r f' v_\theta ^2 + F\omega _\textrm{z}v_\theta ) f' \\ -(r f'v_r v_\theta + F\omega _\textrm{z}v_\theta )r f''F^{-2} \\ * \\ * \\ -(r f'F^{-1} v_rv_\theta + v_r\omega _\textrm{z})f' f'' F^{-2} \end{array}\right) \nonumber \\{} & {} + \Omega \mu \left( \begin{array}{l} -(r F + f')Fv_\theta \\ \big (1+f''F^{-1}+r f'f''F^{-2} \big )r v_r \\ * \\ * \\ \big (1+f''F^{-1} +r f' f'' F^{-2} ) f' F^{-1} v_r \end{array}\right) \end{aligned}$$

(47)

where the third and fourth components are not detailed because they will not be present in the restriction to the constraint manifold.

In conclusion, the equations of motion (44) in the ten-dimensional manifold $\widehat{M}_{10}^\circ$ are given by the equations of Proposition 17 with the third one replaced by

$$\begin{aligned} \dot{\alpha }= b(\alpha )^{-1}\omega \end{aligned}$$

and with the two equations for $\dot{\omega }_\textrm{x}$ and $\dot{\omega }_\textrm{y}$ added. Obviously, the equation for $\dot{\alpha }$ is the representative in the chosen coordinates of the equation $\dot{\mathcal {R}}={\mathcal {R}}^T\omega$. Since we have assumed that the domain of the coordinates $\alpha$ is dense in $\mathrm {SO(3)}$, by continuity we may conclude that the equations of motion (44) are given by this set of equations with that for $\dot{\alpha }$ replaced by $\dot{\mathcal {R}}= {\mathcal {R}}^{-1}\omega$. The restriction to $\widehat{M}_8^\circ$ is performed by ignoring the equations for $\dot{\omega }_\textrm{x}$ and $\dot{\omega }_\textrm{y}$ and replacing $\omega _\textrm{x}$ and $\omega _\textrm{y}$ with ${\tilde{\omega }}_\textrm{x}$ and ${\tilde{\omega }}_\textrm{y}$ wherever they appear in the others (namely, in the equation for $\dot{\mathcal {R}}$).

(ii) This is obvious. $\square$

We can now deduce the reduced equations (9). In the subset $M_4^\circ$ of the phase space we may use as (global) coordinates the four functions $p_1,p_2,p_3,p_4$ as in (7), whose expression in polar coordinates is

$$\begin{aligned} p_1 = \frac{r^2}{2} \,,\quad p_2 = r v_r \,,\quad p_3 = r^2 v_\theta \,,\quad p_4 = -\big (F \omega _\textrm{z}+rf'v_\theta \big ) + \Omega \big ( r +f'F^{-1} \big )f' \,, \end{aligned}$$

where the latter is obtained by observing that, in $\widehat{M}_8^\circ$, $\omega \cdot n=(f'\tilde{\omega }_\textrm{x}\cos \theta +f'{\tilde{\omega }}_\textrm{y}\sin \theta - \omega _\textrm{z})F^{-1}$ with ${\tilde{\omega }}_\textrm{x}$ and ${\tilde{\omega }}_\textrm{y}$ as in (46). The inverse change of coordinates, which uses $\psi$ and ${\mathcal {F}}$ instead of f and F, is given by

$$\begin{aligned}{} & {} r = \sqrt{2p_1} \,,\qquad v_r = \frac{p_2}{\sqrt{2p_1}} \,,\qquad v_\theta = \frac{p_3}{2p_1} \,,\\{} & {} \quad \omega _\textrm{z}= -\big (p_4+\psi 'p_3) {\mathcal {F}}+ \Omega \big (1+\psi '{\mathcal {F}}\big )2p_1\psi '{\mathcal {F}}\,. \end{aligned}$$

From here, a computation shows that, in $M_4^\circ$, the first and the last three of the equations of Proposition 17 become the four equations $\dot{p}_i=X_i|_{M_4^\circ }$, $i=1,\ldots ,4$, with $X_1,X_2,X_3,X_4$ as in (9) but with $p_0$ replaced by $\frac{p_2^2+p_3^2}{4p_1}$. Furthermore, differentiating the function $p_0:=\frac{p_2^2+p_3^2}{4p_1}$ in $M_4^\circ$ we find $\dot{p}_0=X_0|_{M_4^\circ }$ with $X_0$ as in (9). This shows that the restriction to $M_4^\circ$ of the reduced equations of motion is the restriction to $M_4^\circ$ of the equations $\dot{p}=X(p)$ with X as in (9). Since the reduced equation of motion is a vector field in $M_4$, the vector field X is continuous in ${\mathbb {R}}^{5}$ and $M_4^\circ$ is dense in $M_4$; by continuity, the same is true in $M_4$.