Abstract
Deciding whether a given function is quasiconvex is generally a difficult task. Here, we discuss a number of numerical approaches that can be used in the search for a counterexample to the quasiconvexity of a given function W. We will demonstrate these methods using the planar isotropic rank-one convex function
where \(\lambda _\textrm{max}\ge \lambda _\textrm{min}\) are the singular values of F, as our main example. In a previous contribution, we have shown that quasiconvexity of this function would imply quasiconvexity for all rank-one convex isotropic planar energies \(W:{\text {GL}}^+(2)\rightarrow {\mathbb {R}}\) with an additive volumetric-isochoric split of the form
with a concave volumetric part. This example is therefore of particular interest with regard to Morrey’s open question whether or not rank-one convexity implies quasiconvexity in the planar case.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The question of whether or not rank-one convexity implies quasiconvexity in the planar case is considered one of the major open problems in the calculus of variations (Pedregal 2019; Casadio-Tarabusi 1993; Parry 1995; Kawohl and Sweers 1990). Morrey (Morrey 1952, 2009) conjectured that this is not the case in general. Of course, in order to demonstrate that these convexity properties are indeed distinct, it is sufficient to identify a single rank-one convex function which is not quasiconvex, as was done by Šverák in the nonplanar case (Šverák 1992). While numerous viable criteria are known for rank-one convexity, it remains highly difficult to explicitly show that a function is not quasiconvex. It is therefore common to apply numerics to the problem (Dacorogna and Haeberly 1998; Pedregal 1996; Bartels et al. 2004).
In this article, we discuss different numerical approaches for demonstrating the non-quasiconvexity of a given function. We will primarily apply our methods to a single example, which has been the subject of a previous article (Voss et al. 2021b): The planar isotropic energy function \(W_{\textrm{magic}}^+\) is defined via

with  as the ordered singular values of the deformation gradient
as the ordered singular values of the deformation gradient  . While it has already been shown that this function is rank-one convex but nowhere strictly elliptic and not polyconvex (Voss et al. 2021b), it remains open whether or not \(W_{\textrm{magic}}^+\) is quasiconvex.
. While it has already been shown that this function is rank-one convex but nowhere strictly elliptic and not polyconvex (Voss et al. 2021b), it remains open whether or not \(W_{\textrm{magic}}^+\) is quasiconvex.
The energy candidate (1.1) is very compelling: It emerged from the investigation of planar isotropic elastic energies with a so-called additive volumetric-isochoric split, i.e., of energies that can be written as the sum of an isochoric part depending only on the product  and a volumetric part depending only on
and a volumetric part depending only on  . Details of this structure and its characteristics are discussed in Sect. 2.1. It can be shown (Voss et al. 2021b) that \(W_{\textrm{magic}}^+(F)\) is a limit case in the investigation of “least rank-one convex” candidates in the family of energy functions with an additive volumetric-isochoric split. In this specific setting, it was demonstrated that the question of quasiconvexity for \(W_{\textrm{magic}}^+(F)\) also determines whether or not any other rank-one convex function with an additive volumetric-isochoric split and a concave volumetric part is quasiconvex.
. Details of this structure and its characteristics are discussed in Sect. 2.1. It can be shown (Voss et al. 2021b) that \(W_{\textrm{magic}}^+(F)\) is a limit case in the investigation of “least rank-one convex” candidates in the family of energy functions with an additive volumetric-isochoric split. In this specific setting, it was demonstrated that the question of quasiconvexity for \(W_{\textrm{magic}}^+(F)\) also determines whether or not any other rank-one convex function with an additive volumetric-isochoric split and a concave volumetric part is quasiconvex.
This work is primarily meant to serve as a guideline towards numerical investigations in the context of Morrey’s conjecture. In particular, while the general methods described here are mostly applicable to a large class of energy functions,Footnote 1 we utilize a number of specific invariance properties exhibited by the particular example \(W_{\textrm{magic}}^+\), as discussed in Sect. 2. Exploiting such properties can vastly improve the efficiency of numerical approaches and, when investigating other types of functions, it should be kept in mind that similar invariances could be identified and used to simplify the more general numerical algorithms for finding counterexamples to quasiconvexity.
The methods we describe reliably find such counterexamples for functions which are known to be non-elliptic and therefore non-quasiconvex. For the rank-one convex energy candidate \(W_{\textrm{magic}}^+\), a number of microstructures with the same energy level as the homogeneous deformation were (re-)discovered. However, we were unable to demonstrate the non-quasiconvexity of \(W_{\textrm{magic}}^+\) with any numerical approach. Although inconclusive, these numerical results certainly suggest that the function \(W_{\textrm{magic}}^+\) is in fact quasiconvex and therefore not suited for answering Morrey’s conjecture.
1.1 Convexity properties of energy functions
We start by recalling the classical definitions of generalized convexity properties (Dacorogna 2008; Šilhavý 1997; Schröder and Neff 2010).
Definition 1.1
The energy function  is quasiconvex if and only if
is quasiconvex if and only if

for any domain \(\Omega \subset {\mathbb {R}}^n\) with Lebesgue measure \(|\Omega |\). The energy function is strictly quasiconvex if the inequality in (1.2) is strict for all \(\vartheta \ne 0\).
While quasiconvexity, together with suitable growth conditions, is sufficient to ensure weak lower semi-continuity of the energy functional, it has the disadvantage of being notoriously difficult to prove or disprove directly. This led to the introduction of various sufficient and necessary conditions for quasiconvexity.
Definition 1.2
(Ball 1976) The energy function  is polyconvex if and only if there exists a convex function
is polyconvex if and only if there exists a convex function  with
with

with  as the matrix of the determinants of all \(i\times i\)–minors of F and \(m(n) :=\sum _{i=1}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) ^2\). The energy function is strictly polyconvex if such a P exists which is strictly convex.
as the matrix of the determinants of all \(i\times i\)–minors of F and \(m(n) :=\sum _{i=1}^n \left( {\begin{array}{c}n\\ i\end{array}}\right) ^2\). The energy function is strictly polyconvex if such a P exists which is strictly convex.
For the planar case \(n=2\), an energy \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) is polyconvex if and only if there exists a convex mapping \(P:{\mathbb {R}}^{2\times 2}\times {\mathbb {R}}\cong {\mathbb {R}}^5\rightarrow {\mathbb {R}}\cup \{+\infty \}\) with
Whereas polyconvexity provides a sufficient criterion for quasiconvexity, a necessary condition is given by the rank-one convexity of a function.
Definition 1.3
The energy function  is rank-one convex if for
is rank-one convex if for  ,
,

If the energy function is twice differentiable, rank-one convexity is equivalent to the Legendre-Hadamard ellipticity condition

which expresses the ellipticity of the Euler-Lagrange equation \({\mathrm{Div\,\,}} DW({\nabla }{\varphi })=0\) corresponding to the variational problem

The energy function is strictly rank-one convex if inequality (1.4) is strict.
Overall, for any  we have the well known hierarchy (Ball 1976, 1987; Dacorogna 2008)
we have the well known hierarchy (Ball 1976, 1987; Dacorogna 2008)
with none of the reverse implications holding in general for \(n\ge 3\). The remaining question whether rank-one convexity implies quasiconvexity for \(n=2\) is known as Morrey’s problem.
In continuum mechanics and related applications, energy functions are often more naturally defined on the group  instead of
instead of  since a deformation gradient F with non-positive determinant would imply local self-intersection. For such functions we introduce:
since a deformation gradient F with non-positive determinant would imply local self-intersection. For such functions we introduce:
Definition 1.4
A function  is called quasi-/poly-/rank-one convex if the function
is called quasi-/poly-/rank-one convex if the function

is quasi-/poly-/rank-one convex.
1.2 Periodic boundary conditions
The definition of quasiconvexity (1.2) can be reformulated in terms of deformations with periodic boundary conditions. As will be demonstrated in Sect. 4, this can be helpful to find periodic microstructures numerically. In the context of planar elasticity, periodic boundary conditions have the form
with a homogeneous deformation  and a periodic superposition \(\vartheta _\#\in W_{\text {per}}^{1,\infty }(\Omega )\). The domain \(\Omega \) has to be in such a geometrical shape that \({\mathbb {R}}^2\) can be covered by periodic replications of \(\Omega \) and the superposition \(\vartheta _\#\) must be \(\Omega \)-periodic (cf. Fig. 1). Seemingly, periodic boundary conditions are a more general concept than Dirichlet boundary conditions with test functions \(\vartheta \subset W_0^{1,\infty }(\Omega ;{\mathbb {R}}^{n})\) because they also allow for changes on the boundary itself.Footnote 2
and a periodic superposition \(\vartheta _\#\in W_{\text {per}}^{1,\infty }(\Omega )\). The domain \(\Omega \) has to be in such a geometrical shape that \({\mathbb {R}}^2\) can be covered by periodic replications of \(\Omega \) and the superposition \(\vartheta _\#\) must be \(\Omega \)-periodic (cf. Fig. 1). Seemingly, periodic boundary conditions are a more general concept than Dirichlet boundary conditions with test functions \(\vartheta \subset W_0^{1,\infty }(\Omega ;{\mathbb {R}}^{n})\) because they also allow for changes on the boundary itself.Footnote 2
However, for the notion of quasiconvexity, the two can be used interchangeably.
Proposition 1.5
Dacorogna (2008, Proposition 5.13) An energy function  is quasiconvex if and only if
is quasiconvex if and only if

for any domain \(\Omega \subset {\mathbb {R}}^n\) with Lebesgue measure \(|\Omega |\) such that \({\mathbb {R}}^2\) can be covered by periodic replications of \(\Omega \). The energy function is strictly quasiconvex if the inequality in (1.9) is strict for all \(\vartheta \ne 0\).
Proof
Inequality (1.9) directly implies quasiconvexity, because \(W_0^{1,\infty }(\Omega )\subset W_{\text {per}}^{1,\infty }(\Omega )\). For the reverse direction see (Dacorogna 2008, p. 173). \(\square \)
In the context of planar elasticity, it is sufficient to consider \(\Omega =[0,1]^2\), and without loss of generality, we can assume \(\vartheta _\#(0,0)=(0,0)\). The periodic replication of \(\Omega \) to cover \({\mathbb {R}}^2\) implies that the values of \(\vartheta _\#\) coincide on opposite edges, i.e., every point at the boundary belongs to two separate unit squares (four at the corners of the square). Thus we can write \(\Omega \)-periodicity as
in particular,
1.3 Previous results related to Morrey’s conjecture
Morrey’s conjecture has long been considered one of the most important open questions in the calculus of variations, and the remaining problem of the planar case has been the subject of extensive research. For the nonplanar case, the problem has been conclusively solved by Šverák (1992), and further examples of rank-one convex, non-quasiconvex functions have been found for dimension \(n>2\) since then (Grabovsky 2018). However, it has also been demonstrated that Šverák’s original counterexample (Pedregal and Šverák 1998; Sebestyén and Székelyhidi 2015) is not directly adaptable to the two-dimensional case.
The Dacorogna and Marcellini (1988) function \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\) with

is a homogeneous polynomial of degree four; here,  denote the signed singular valuesFootnote 3 of F. It has been shown (Dacorogna and Marcellini 1988) that the function is rank-one convex if \(\gamma \in [0,\frac{4}{\sqrt{3}}\approx 2.309]\), but polyconvex only if \(\gamma \le 2\). This result can be extended to the more general class
denote the signed singular valuesFootnote 3 of F. It has been shown (Dacorogna and Marcellini 1988) that the function is rank-one convex if \(\gamma \in [0,\frac{4}{\sqrt{3}}\approx 2.309]\), but polyconvex only if \(\gamma \le 2\). This result can be extended to the more general class

At present, it is not known whether this expression is quasiconvex for \(\gamma \in (2,\frac{4}{\sqrt{3}}]\). However, extensive numerical calculations suggest that it is quasiconvex (Dacorogna and Haeberly 1998, 1996). In the same works, Dacorogna et al. study several rank-one convex functions, including an example by Ball and Murat (1984); Dacorogna et al. (1990):

Together with an example by Aubert (1987), the Dacorogna–Marcellini function has been the first example given in the literature of a planar function which is rank-one convex but not polyconvex.
Many planar functions used in the context of Morrey’s conjecture have the structure  for which additional numerical optimization is available (Gremaud 1995; Grabovsky and Truskinovsky 2019) or are composed of polynomials up to the degree four (Gutiérrez and Villavicencio 2007; Bandeira and Pedregal 2009).
for which additional numerical optimization is available (Gremaud 1995; Grabovsky and Truskinovsky 2019) or are composed of polynomials up to the degree four (Gutiérrez and Villavicencio 2007; Bandeira and Pedregal 2009).
Guerra and da Costa (2021) recently employed a systematic numerical approach towards the question of Morrey’s conjecture. Their findings suggest that in the planar case, rank-one convexity implies N-wave quasiconvexity for \(N\le 5\). Since any function which is N-wave quasiconvex for all \({N\in \mathbb {N}}\) is quasiconvex (Guerra and da Costa 2021, Proposition 3.6) (cf. Sebestyén and Székelyhidi (2017)), these results provide some evidence for the conjecture that rank-one convexity indeed implies quasiconvexity for planar energies.
Previous applications of machine learning in nonlinear elasticity, as we consider in Sect. 4.1, have mostly focused on the energy function itself (Fernández et al. 2021; Klein et al. 2022). The application to deformation functions presented here is based on the concept of physics-informed neural networks, which have recently been employed for finding approximate solutions to various partial differential equations (Raissi et al. 2019; Karniadakis et al. 2021).
2 Exploitable Properties of Functions
Before employing numerical methods to investigate whether a function is quasiconvex, it is generally useful to identify invariances and similar properties of the specific function that may allow for an improvement of the efficiency of the numerical approach. In the following, we will focus on the particular energy function \(W_{\textrm{magic}}^+\), which exhibits three important properties that can be exploited numerically: isotropy, scaling invariance and the specific form of a volumetric-isochoric split.
2.1 The volumetric-isochoric split
The energy \(W_{\textrm{magic}}^+\) emerged from the investigation of the family of planar isotropic energies  with an additive volumetric-isochoric split
with an additive volumetric-isochoric split
We will motivate both the additional structure one can achieve with this type of energy functions as well as the candidate \(W_{\textrm{magic}}^+\) itself. By (Martin et al. 2017, Lemma 3.1) , energies of the type (2.1) can be written as

where \(\lambda _1,\lambda _2>0\) denote the singular values of F and h, f are real-valued functions. In nonlinear elasticity theory, energy functions with an additive volumetric-isochoric split are widely used, primarily to model the behaviour of slightly compressible materials (Ciarlet 1988; Hartmann and Neff 2003; Ogden 1978; Neff et al. 2016).
For a further representation of W, we introduce the (nonlinear) distortion function or outer distortion

where  denotes the Frobenius matrix norm with
denotes the Frobenius matrix norm with  . The distortion function \(\mathbb {K}\) is conformally invariant, i.e.,
. The distortion function \(\mathbb {K}\) is conformally invariant, i.e.,

Additionally, we consider the linear distortion or (large) dilatation

where  denotes the operator norm (i.e., the largest singular value) of F.
denotes the operator norm (i.e., the largest singular value) of F.
We can then express every conformally invariant energy W on  as
as  with
with  (Martin et al. 2017). Note that in general,
(Martin et al. 2017). Note that in general,

In a previous paper (Voss et al. 2021b), we motivated the reduction to the case  for arbitrary additive volumetric-isochoric split energies with a newly developed rank-one convexity criterion (Voss et al. 2021a). More specifically, we showed that if there exists a rank-one convex energy function with an additive volumetric-isochoric split that is not quasiconvex, then we can find such a function in the set
for arbitrary additive volumetric-isochoric split energies with a newly developed rank-one convexity criterion (Voss et al. 2021a). More specifically, we showed that if there exists a rank-one convex energy function with an additive volumetric-isochoric split that is not quasiconvex, then we can find such a function in the set

as well. It is therefore sufficient to consider \({\mathfrak {M}}^*\) instead of the general class of volumetric-isochoric split energies when discussing Morrey’s conjecture.
2.2 Scaling invariance
In general an arbitrary energy \(W\in {\mathfrak {M}}^*\) is neither simply scaling invariant, i.e., \(W(\alpha F)\ne W(F)\) for all \(\alpha \in {\mathbb {R}}\) and  , nor tension-compression symmetric, i.e.,
, nor tension-compression symmetric, i.e.,  for all
for all  . However, \({\mathfrak {M}}^*\) provides additional invariance properties that hold for rank-one convexity and quasiconvexity which we will use to simplify numerical calculations in the following sections by reducing the number of deformation gradients
. However, \({\mathfrak {M}}^*\) provides additional invariance properties that hold for rank-one convexity and quasiconvexity which we will use to simplify numerical calculations in the following sections by reducing the number of deformation gradients  that we must consider.
that we must consider.
Lemma 2.1
Let \(W\in {\mathfrak {M}}^*\) be twice differentiable. Then the ellipticity domain of W is scaling invariant, i.e., a cone: if W is elliptic at  , then W is elliptic at \(\alpha F_0\) for every \(\alpha >0\).
, then W is elliptic at \(\alpha F_0\) for every \(\alpha >0\).
Proof
Let \(\alpha >0\). The isochoric part \(W_{\textrm{iso}}(F)=h\bigl (\frac{\lambda _1}{\lambda _2}\bigr )\) of W is conformally invariant by definition, which implies \(W_{\textrm{iso}}(\alpha F)=W_{\textrm{iso}}(F)\), and therefore

for all \(H\in {\mathbb {R}}^{2\times 2}\). For the volumetric part  we calculate
we calculate

for all \(H\in {\mathbb {R}}^{2\times 2}\). For ellipticity of W, we can assume \(\mathrm{rank\,\,H=1}\) and note that the determinant is affine linear in direction of rank-one matrices (Dacorogna 2008, Theorem 5.20), and thus \(D^2\det [\alpha F].(H,H)=0\) if \(\mathrm rank(H)=1\). Therefore,

Together with (2.8) this implies
for all \(F,H\in {\mathbb {R}}^{2\times 2}\) with \(\mathrm rank(H)=1\) and all \(\alpha >0\), which implies the scaling invariance of the ellipticity domain of \(W\in {\mathfrak {M}}^*\). \(\square \)
Lemma 2.2
Let \(W\in {\mathfrak {M}}^*\) be twice differentiable. The ellipticity domain of W is invariant under inversion, i.e., if W is elliptic at  , then it is elliptic at
, then it is elliptic at  .
.
Proof
Due to the isotropy of every \(W\in {\mathfrak {M}}^*\), and since the singular values of F and \(F^T\) are identical, \(W(F)=W(F^T)\) and therefore
thus ellipticity at F and \(F^T\) are equivalent (cf. Kruzik (1999)). Moreover, Lemma 2.1 states that the ellipticity domain of W is scaling invariant, i.e., ellipticity at F implies W is elliptic for all \(\alpha F\) with \(\alpha >0\). Combining both lemmas and choosing \(\alpha =\frac{1}{\det F}>0\), we find that ellipticity at \({\mathrm{Cof\,\,}}{F}\) would imply ellipticity at  . Therefore, it remains to show that W is elliptic at \({\mathrm{Cof\,\,}} F\).
. Therefore, it remains to show that W is elliptic at \({\mathrm{Cof\,\,}} F\).
In the planar case, the singular values of F and \({\mathrm{Cof\,\,}} F\) are identicalFootnote 4 and thus \(W({\mathrm{Cof\,\,}} F)=W(F)\) for all  due to the isotropy of the energy. Furthermore, because of the simple shape of the cofactor matrix in the planar case
due to the isotropy of the energy. Furthermore, because of the simple shape of the cofactor matrix in the planar case  we find
we find
Note carefully that these properties do not hold for dimension \(n>2\). Thus

which completes the proof because \(\textrm{rank}(H)=1\) impliesFootnote 5\(\textrm{rank}({\mathrm{Cof\,\,}} H)=1\). \(\square \)
Lemma 2.3
Let \(W\in {\mathfrak {M}}^*\) be twice differentiable. Then the quasiconvexity domain of W is scaling invariant: if W is quasiconvex at  , i.e., if
, i.e., if

for any domain \(\Omega \subset {\mathbb {R}}^2\), then the energy is quasiconvex at \(\alpha F_0\) for all \(\alpha >0\).
Proof
We show that the so-called energy gap

i.e., the difference between the energy of \(\varphi (x)=F_0 x+\vartheta (x)\) and the homogeneous solution \(\varphi _0(x)=F_0 x\), is scaling invariant. Note that quasiconvexity at \(F_0\),

implies that the energy gap is always nonnegative. We write \(F=\nabla \varphi \) and compute

\(\square \)
Remark 2.4
With Lemmas 2.1 and 2.3, we showed that both rank-one convexity and quasiconvexity are scaling invariant for any energy \(W\in {\mathfrak {M}}^*\). Regarding Morrey’s question for planar isotropic energies with volumetric-isochoric split, we can therefore assume \(\det F_0=1\) without loss of generality. More specifically, for arbitrary \(W\in {\mathfrak {M}}^*\) we just need to prove the rank-one convexity for all  with \(\det F_0=1\) to obtain rank-one convexity at all
with \(\det F_0=1\) to obtain rank-one convexity at all  . Likewise, it is sufficient to only check for quasiconvexity starting with a homogeneous deformation \(x\mapsto F_0 x\) with \(\det F_0=1\) in place of arbitrary
. Likewise, it is sufficient to only check for quasiconvexity starting with a homogeneous deformation \(x\mapsto F_0 x\) with \(\det F_0=1\) in place of arbitrary  (cf. Fig. 2).
(cf. Fig. 2).
Visualization of a possible [ellipticity/quasiconvexity] domain (shaded blue) of a planar isotropic energy function in terms of the singular values \(\lambda _1,\lambda _2>0\). Left: for an energy \(W\in {\mathfrak {M}}^*\): the scaling invariance implies that [ellipticity/quasiconvexity] on a point (black dots) of an arbitrary curve of the type \(\det F=\lambda _1\lambda _2=c\) (black lines) always entail [ellipticity/quasiconvexity] for the corresponding ray (green line). Right: for an arbitrary volumetric-isochoric split energy, this invariance is lost (Color figure online)
2.3 The least rank-one convex candidate \(W_{\textrm{magic}}^+(F)\)
Continuing with the class \({\mathfrak {M}}^*\), i.e., with energy functions with \(c\log \det F\) as volumetric part, we focus on positive \(c>0\). As multiplying a function by a scalar does not change its convexity behavior, we can consider \(c=1\) without loss of generality and assume that the isochoric part is convex.Footnote 6 Thus we consider the class
Using sharp rank-one convexity conditions (Voss et al. 2021a), it is possible to identify “least” rank-one convex candidates by searching for functions that satisfy those conditions by equality. Surprisingly (Voss et al. 2021b), it is possible to show that the question of quasiconvexity reduces to the single energy function

Hence, if \(W_{\textrm{magic}}^+\) were quasiconvex, then every function in the class \({\mathfrak {M}}_+^*\) and thus every rank-one convex planar isotropic energy function with an additive volumetric-isochoric split whose isochoric part h(t) is convex would be quasiconvex as well. A first analytic observation (see Appendix A) could not conclusively answer this question, but opens the possibility to interesting microstructures having the same energy value as the homogeneous deformation. This motivates us to proceed numerically and try to falsify the quasiconvexity of \(W_{\textrm{magic}}^+\).
3 The Classical Finite Element Approach
A first way to show that a given energy density is not quasiconvex is the finite element method. For this, we discretize the displacement field \(\vartheta \) by Lagrange finite elements (Ciarlet 2002). We use triangle grids and first-order finite elements only. That way, the deformation gradient and hence the integrand are piecewise constant and the hyperelastic energy  can be computed without quadrature error which is important in view of exactly calculating the energy gap (2.14). Our implementation is based on the Dune libraries (Bastian 2021; Sander 2020).
can be computed without quadrature error which is important in view of exactly calculating the energy gap (2.14). Our implementation is based on the Dune libraries (Bastian 2021; Sander 2020).
3.1 Testing for Quasiconvexity
We perform tests on two domains: The square \([-1,1]^2\) and the unit disk \(B_1(0)\). Both are filled with coarse triangle grids as shown in Fig. 3. For ease of implementation, we approximate the boundary of the disk by six quadratic arcs (dashed lines). The finite elements grids are then constructed by uniform refinement of the coarse grids. For the disk grid, new boundary vertices are placed not at edge midpoints but on the curved arcs approximation the boundary. The final grids consist of 16,641 vertices and 32,768 elements for the square and 12,481 vertices and 24,576 elements for the disk. Due to the scaling invariance (the results of Sect. 2.2) it is sufficient to test with an \(F_0\) such that \(\det F_0=1\), thus due to isotropy we consider only  with arbitrary \(a>0\). For the result shown here, we select \(a=2\).
with arbitrary \(a>0\). For the result shown here, we select \(a=2\).
We minimize the hyperelastic energy  with a trust-region algorithm. These algorithms have been thoroughly studied in the literature, and they can be shown to always converge to stationary points of the energy (Conn et al. 2000). As trust-region methods are descent methods, maximizers and saddle-points are not attractive points, and convergence is therefore typically towards (local) minimizers only.
with a trust-region algorithm. These algorithms have been thoroughly studied in the literature, and they can be shown to always converge to stationary points of the energy (Conn et al. 2000). As trust-region methods are descent methods, maximizers and saddle-points are not attractive points, and convergence is therefore typically towards (local) minimizers only.
Trust-region methods perform sequences of quadratic minimization problems with convex inequality constraints. We use a trust-region defined in terms of the maximum norm, and therefore the convex constraints are a set of independent bound constraints. For the quadratic bound-constrained minimization problem we then use a monotone multigrid method (Kornhuber 1994) as suggested in Sander (2012). Such methods achieve multigrid convergence rates even for bound-constrained problems. We solve each inner problem until the maximum-norm of the correction drops below \(10^{-5}\). The large but sparse tangent matrices are computed using the ADOL-C algorithmic differentiation system (Walther and Griewank 2012).
When looking for global minimizers with a descent method, the question of initial iterates is of central importance. As shown exemplary in the next section, when the energy is not quasiconvex, imperfections caused by the finite-precision arithmetic are sufficient to drive the system towards microstructures even starting from the homogeneous configuration. For the particular energy \(W_{\textrm{magic}}^+\), however, this did not lead to any energy decrease. We obtained the same negative results for some other “obvious” initial iterates, such as random perturbations of the homogeneous state. More involved constructions of non-homogeneous initial iterates are described in Sects. 3.2 and 5.
3.2 Non-Elliptic Microstructure
In the following, we introduce several additional ideas to search for microstructures with energy levels below the homogeneous state with more adept methods.
In order to better understand the shape of a possible microstructure, we ensured its existence by considering slightly modified problems. We start with the weakened energy

which is not rank-one convex anymore but satisfies \(\displaystyle \lim _{c\rightarrow 1}W_c(F)=W_{\textrm{magic}}^+(F)\) for all  . We are interested in the resulting microstructures especially if they do not appear to be simple laminations caused by the loss of ellipticity (Ball and James 1987; Dolzmann 1999; Li 2000). Any local minimizer found for \(W_c\) can then be used as an initial deformation for minimizing \(W_{\textrm{magic}}^+\) again with the hope of maintaining the non-homogeneous structure and thereby disproving quasiconvexity of the energy \(W_{\textrm{magic}}^+\) itself.
. We are interested in the resulting microstructures especially if they do not appear to be simple laminations caused by the loss of ellipticity (Ball and James 1987; Dolzmann 1999; Li 2000). Any local minimizer found for \(W_c\) can then be used as an initial deformation for minimizing \(W_{\textrm{magic}}^+\) again with the hope of maintaining the non-homogeneous structure and thereby disproving quasiconvexity of the energy \(W_{\textrm{magic}}^+\) itself.
While our material \(W_c\) indeed shows microstructures that contain a lamination structure, we observe radially symmetric contracting regions as well (cf. Fig. 4). However, we already know that deformations of this kind cannot lower the energy value of \(W_{\textrm{magic}}^+\) (see Appendix A) and thus they are not suited for finding a new microstructure by using them as an initial configuration for minimizing \(W_{\textrm{magic}}^+(F)\) again. This is confirmed by direct numerical experiments: when letting the trust-region solver of the previous section minimize \(W_{\textrm{magic}}^+\) starting from the configurations shown in Fig. 4, all we obtain is convergence to the homogeneous state.
Therefore, we continue with an alternative numerical experiment to produce more convoluted microstructures. For this we place three disjoint balls \(B_{r_i}(x_i)\), \(i=1,2,3\) with radius 0.2 and center \(x_1=(-0.5,0)\), \(x_2=(0.35,0.35)\), and \(x_3=(0.35,-0.35)\) inside the unit disk domain. We then set \(c>1\) inside each circles \(B_{r_i}(x_i)\) but fix \(c=1\) elsewhere, i.e.,

For values slightly larger than \(c=1\) we observe that all three circles contract in a radially symmetric fashion (cf. Fig. 5). Again, we note that Appendix A shows that radial symmetric contracting deformations have the same energy value for the limit case \(c=1\). Increasing the weighting of \(\log \det F\) by raising c results in lower energy values compared to the homogeneous deformation. For higher values of c, the microstructure becomes more convoluted but keeps its contraction structure (cf. Fig. 5).
We note that both microstructures are primarily located inside these circles (where ellipticity is lost), while for the rest of the material with \(c=1\), the deformation remains mostly homogeneous. In particular, the borders of the inner circles maintain their shape to a certain extent, even though we do not impose additional internal boundary conditions to ensure this. We interpret these observations as a first indicator towards our energy candidate \(W_{\textrm{magic}}^+\) being quasiconvex since the response of \(W_{\textrm{magic}}^+\) is “stable” toward the assumed non-elliptic perturbation in the circle.
4 Deep Neural Networks
One may conjecture that minimizing \(W_{\textrm{magic}}^+\) in a finite element space fails to find microstructure because each finite element coefficient influences only a very local part of the deformation function. Additionally, when the strain energy density lacks quasiconvexity (which we consider possible for \(W_\text {magic}^+\)), FEM-methods generally fail (Kumar et al. 2020) due to the non-uniqueness of the solution, i.e., the microstructures. In this chapter, we experiment with an alternative approach where this relationship is more global.
4.1 Physics-Informed Neural Networks
We use a numerical scheme which is based on deep neural networks as an ansatz for solving partial differential equations, an idea also referred to as physics-informed neural networks (Raissi et al. 2019; Karniadakis et al. 2021). In principle, this is similar to the ansatz constructed classically using finite element functions. However, deep neural networks generally lead to highly nonlinear and more efficient (in terms of number of parameters) approximation spaces with considerable approximation properties even for low numbers of coefficients.
In the following, we consider periodic deformations only (cf. Sect. 1.2). Consider the following ansatz for the periodic superposition:
where \({\mathcal {F}}_{\omega _f},{\mathcal {G}}_{\omega _g}:[0,1]\rightarrow {\mathbb {R}}^2\) and \({\mathcal {H}}_{\omega _h}:[0,1]^2\rightarrow {\mathbb {R}}^2\) are feedforward neural networks (Schmidhuber 2015) parameterized by parameters \(\omega _f\), \(\omega _g\), and \(\omega _h\), respectively. The ansatz is intentionally constructed this way to identically satisfy the periodic boundary conditions (1.10). Feedforward neural networks are essentially just highly nonlinear functions constructed by repeated composition of successive high-dimensional linear and nonlinear transformations. The specific neural network architecture (or simply, the choice of linear and nonlinear transformations) is a modeling choice without any specific rules as long as sufficient model complexity and nonlinearity is ensured. In this context, we choose the following neural network architectures:
Here, \({\mathcal {L}}^{i \rightarrow j}_{\omega _{\square ,k}}\), \(k=1,\ldots ,5\) (\(\square \) is a placeholder for ‘f’, ‘g’, and ‘h’) denotes the kth-linear transformation parameterized by the set of weights and biases \(\omega _{\square ,k} = \{A_{\square ,k},b_{\square ,k}\}\) (with \(\omega _{\square } = \{\omega _{\square ,k}\}\)) such that any \(z\in {\mathbb {R}}^i\) is transformed via
The linear transformations are interleaved with element-wise nonlinear transformations \({\mathcal {R}}(\cdot ) = \tanh (\cdot )\).
Since each layer of a neural network is a differentiable operation, the gradient of the superposition field \(\vartheta _\#\) can be computed using the chain rule. This is efficiently implemented using an automatic differentiation engine (Baydin et al. 2018). Note that, unlike numerical differentiation by, e.g., finite differences, the gradients computed via automatic differentiation are analytically exact.
For numerical integration of the strain energy density over the domain \(\Omega \) we discretize the domain with a uniform grid \(\{(x_1^\alpha ,x_2^\beta )\,|\, \alpha ,\beta =1,\dots ,N\}\) of \(N \times N\) points. For a given \(\nabla \vartheta _{\#,\omega }\), the total strain energy is approximated via the trapezoidal integration rule as

where the integration weights \(\xi (\alpha )\) are

Whether the trapezoidal integration rule over- or underestimates the integral depends on whether the integrand is convex or concave, respectively, in the interval of the integration. However, if the integrand exhibits an inflection point (which is also observed here), over-/underestimation of the integral cannot be guaranteed with this rule.
The optimal parameters \(\omega =\{\omega _f,\omega _g,\omega _h\}\) of the neural networks are then obtained as minimizers of the total energy
The minimization problem is solved iteratively using Adam (Kingma and Adam 2017), an efficient first-order gradient-based stochastic optimization method. The derivatives of the objective function with respect to the parameters \(\omega \) are computed via automatic differentiation again. Following the minimization, the periodic superposition field \(\vartheta _\#=\vartheta _{\#,\omega ^\star }\) is given by (4.1). The Adam optimizer was used for 2000 iterations with an initial learning rate of \(10^{-3}\) which was decayed by a factor of 0.1 after the 700th, 1400th, and 1800th iterations. The numerical scheme was implemented in Paszke (2019).
Figure 6 illustrates the representative microstructures obtained via the numerical scheme for \(F_0\) equal to  and
and  on a grid of resolution \(N=128\). For both values of \(F_0\) the microstructure has the form of a smooth laminate and its energy seems to equal the one of the corresponding homogeneous deformation up to machine precisionFootnote 7 which motivates the search for a precise form of the analytical solution.
on a grid of resolution \(N=128\). For both values of \(F_0\) the microstructure has the form of a smooth laminate and its energy seems to equal the one of the corresponding homogeneous deformation up to machine precisionFootnote 7 which motivates the search for a precise form of the analytical solution.
Neural network minimizers of the energy \(W_{\textrm{magic}}^+\) under periodic boundary conditions with two different \(F_0\). (Left) The microstructures are visualized using \((\nabla \vartheta _\#)_{11}\). (Right) \((\nabla \vartheta _\#)_{11}\), \((\vartheta _\#)_{1}\), and \((\vartheta _\#)_{2}\) are plotted against \(x_1\) for constant \(x_2=0.5\). The relevance of \(a_2-a_1\) is discussed in Sect. 4.2
4.2 Smooth laminates
Guided by the numerical findings of the previous section, it turned out that the smooth laminates can be explained analytically as well.
Lemma 4.1
Let \(\Omega =[0,1]^2\) be the unit square and consider  with the ordered singular values
with the ordered singular values  of
of  . For any homogeneous deformation \(\varphi _0(x)=F_0 x\) with
. For any homogeneous deformation \(\varphi _0(x)=F_0 x\) with  and \(a_1\ge a_2>0\), the elastic energy
and \(a_1\ge a_2>0\), the elastic energy  is equal to \(I(\varphi _0)\) for all periodical deformations \(\varphi (x)=F_0 x+\vartheta _\#(x)\) of the type
is equal to \(I(\varphi _0)\) for all periodical deformations \(\varphi (x)=F_0 x+\vartheta _\#(x)\) of the type

Proof
Let \(\vartheta _\#\) be as in (4.7). We find that

is diagonal with \(a_1+f'_\#(x_1)\ge a_2\). This implies  and
and  . Periodic boundary conditions as defined by (1.10) imply \(f(0)=f(1)\) as well as \(f'(0)=f'(1)\). Thus
. Periodic boundary conditions as defined by (1.10) imply \(f(0)=f(1)\) as well as \(f'(0)=f'(1)\). Thus

\(\square \)
We also show explicitly that any \(\varphi \) as defined in Lemma 4.1 is indeed an equilibrium point of I by direct computation. For the corresponding Euler-Lagrange equations we must compute the first Piola-Kirchhoff stress \(S_1(F)=DW_{\textrm{magic}}^+(F)\). We start by considering the restriction to deformations of the type (4.7) as an a priori constraint and verify that the single resulting reduced Euler-Lagrange equation holds: Since

in the class of deformations of the type (4.7), all functions are stationary points of this constrained problem. This is a necessary condition for the general problem (Voss et al. 2020, 2021). It remains to show that any such function is also a stationary point of the full Euler-Lagrange equations \(S_1(F)=DW_{\textrm{magic}}^+(F)\) as well. For this we identify
and start with the first derivative of the nonlinear distortion function \(\mathbb {K}(F)\):

Furthermore, using the notation from (4.10), we make use of
as well as


Altogether, we find

Next, we insert deformations of the type (4.7) as an a posteriori constraint (Voss et al. 2020):

Thus we arrive at

The full Euler-Lagrange equations are therefore satisfied since

Note that the case \(f_\#\equiv 0\) corresponds to the homogeneous solution and that this is the only superposition which also complies with Dirichlet boundary conditions given by \(F_0\). As deformations of the type (4.7) only allow for a smooth displacement in one coordinate direction, we refer to them as smooth laminates (cf. Fig. 6).
Remark 4.2
We can construct a continuous map remaining in the class of smooth laminates (which only contains stationary points of \(W_{\textrm{magic}}^+\)) from one candidate \(f_\#\) to the identity \(f_\#\equiv 0\) and from there to another solution  at constant energy value \(I(\varphi )\). Therefore, neither the homogeneous solution nor any of these smooth laminates are stable , since they are not locally unique minimizers of the energy potential. A similar argument holds for the radially symmetric deformations considered in Voss et al. (2021b).
at constant energy value \(I(\varphi )\). Therefore, neither the homogeneous solution nor any of these smooth laminates are stable , since they are not locally unique minimizers of the energy potential. A similar argument holds for the radially symmetric deformations considered in Voss et al. (2021b).
Remark 4.3
If we allow \(\vartheta _\#\) to be non-smooth (cf. Fig. 7), we can obtain various (classical) lamination patterns as well. For example, as a limit of a smooth laminate microstructure of the type (4.7), we may consider

which yields the simple two-phase laminate

Recall that we can only construct laminations that satisfy the constraint \(f_\#'(x)+a_1\ge -a_2\) (cf. Lemma 4.1).
5 Relaxation to Non-Gradient Fields with a Curl-Based Penalty
While the smooth laminates discussed in Sect. 4 as well as the contracting deformations in Voss et al. (2021b) (cf. Appendix A) allow for non-homogeneous deformations whose energy level for \(W_{\textrm{magic}}^+\) is as low as the homogeneous one, we have yet failed to find strictly lower energy values.
For a new attempt, we expand our set of possible deformations \(\varphi \). To this end, we extend the energy functional from gradient fields \(F=\nabla \varphi \) to more general matrix fields P, but control the distance of P to the set of compatible mappings (i.e., gradient fields) with the \({{\,\mathrm{Curl_{2D}}\,}}\) operator. This approach is commonly used when dealing with local dislocations in gradient plasticity with plastic spin (Neff and Münch 2008; Neff et al. 2009) and with relaxed micromorphic continua (Neff et al. 2014). We expect to obtain new microstructures numerically and, in order to gain additional insight into our original variational problem, we will observe the material behavior as a function of the weight parameter on the penalty term \({{\,\mathrm{Curl_{2D}}\,}}P\). The hope is that when such new microstructures are used as initial iterates, the optimization algorithm of Sect. 3 will converge to an energy level below the homogeneous one.
More specifically, instead of the classical minimization problem in the space \(W^{1,2}(\Omega ,{\mathbb {R}}^2)\), i.e.,

with \(W_{\textrm{magic}}^+\) as in (2.17), we consider

in the larger space  . Here, the vector field \(\tau \) is the unit tangent vector to \(\partial \Omega \)Footnote 8 and
. Here, the vector field \(\tau \) is the unit tangent vector to \(\partial \Omega \)Footnote 8 and  is a penalty parameter. The planar operator \({{\,\mathrm{Curl_{2D}}\,}}\) is discussed in Appendix B. Note that the mapping \(P:\Omega \subset {\mathbb {R}}^2\rightarrow {\mathbb {R}}^{2\times 2}\) does not need to be a gradient field, i.e., P may be incompatible, but that
is a penalty parameter. The planar operator \({{\,\mathrm{Curl_{2D}}\,}}\) is discussed in Appendix B. Note that the mapping \(P:\Omega \subset {\mathbb {R}}^2\rightarrow {\mathbb {R}}^{2\times 2}\) does not need to be a gradient field, i.e., P may be incompatible, but that
since we are considering contractible domains only, and on such domains \({{\,\mathrm{Curl_{2D}}\,}}P=0\) if and only if  for some weakly differentiable \(\varphi \).
for some weakly differentiable \(\varphi \).
We minimize the functional \(I_2\) of (5.2) numerically by approximating the matrix field P by piecewise polynomial functions \(P_n\) such that each row of \(P_n\) is a first-order Nédélec finite element of the first kind Kirby et al. (2012) which are elements of the space  by construction. As the domain, we use the unit ball \(\Omega =B_1(0)\) and the same grid as in Sect. 3.2. The algorithm used to minimize the discretized functional is the same trust-region multigrid algorithm as in Sect. 3.2 as well.
by construction. As the domain, we use the unit ball \(\Omega =B_1(0)\) and the same grid as in Sect. 3.2. The algorithm used to minimize the discretized functional is the same trust-region multigrid algorithm as in Sect. 3.2 as well.
We consider the minimization problem (5.2) for different parameters \(L_c\) and choose the boundary deformation  . We must note that for the range of parameters \(L_c\) considered here, the trust-region algorithm of Sect. 3 would not converge to a stationary point. Rather, due to the severe degeneracy of the energy function (5.2) for low \(L_c\), the solver would get stuck eventually. In such situations, the trust-region control would decrease the trust-region radius further and further, without ever finding an acceptable new iterate. In view of the finite-precision arithmetic used in actual simulation, this is not a contradiction to the trust-region theory, which claims that such a new iterate will always be found.
. We must note that for the range of parameters \(L_c\) considered here, the trust-region algorithm of Sect. 3 would not converge to a stationary point. Rather, due to the severe degeneracy of the energy function (5.2) for low \(L_c\), the solver would get stuck eventually. In such situations, the trust-region control would decrease the trust-region radius further and further, without ever finding an acceptable new iterate. In view of the finite-precision arithmetic used in actual simulation, this is not a contradiction to the trust-region theory, which claims that such a new iterate will always be found.
All figures show the last step computed. For \(L_c=0.5,1,2\) we observe different non-trivial microstructures with significantly lower energy value than the homogeneous solution (cf. Fig. 8). The larger \(L_c\), the closer the energy approaches the energy of the homogeneous state.
After calculating  from \(I_2(P)\rightarrow \min \) by the above numerical method, we construct a deformation field \({\widehat{\varphi }}:\Omega \rightarrow {\mathbb {R}}^2\) with a deformation gradient close to
from \(I_2(P)\rightarrow \min \) by the above numerical method, we construct a deformation field \({\widehat{\varphi }}:\Omega \rightarrow {\mathbb {R}}^2\) with a deformation gradient close to  by computing
by computing

in the space of first-order Lagrange finite elements. While the compatible deformations \({\widehat{\varphi }}\) all look similar to their corresponding incompatible matrix fields  (cf. Fig. 9), the energy value \(I_1({\widehat{\varphi }})\) is always higher then the homogeneous one \(I_1(\varphi _0)\). Starting the minimization algorithm for \(I_1\) from \({\widehat{\varphi }}\) always results in the homogeneous configuration.
(cf. Fig. 9), the energy value \(I_1({\widehat{\varphi }})\) is always higher then the homogeneous one \(I_1(\varphi _0)\). Starting the minimization algorithm for \(I_1\) from \({\widehat{\varphi }}\) always results in the homogeneous configuration.
Compatible deformation \({\widehat{\varphi }}\) from  for the matrix field
for the matrix field  shown in the Fig. 8. Colors show determinant (left) and the distortion
shown in the Fig. 8. Colors show determinant (left) and the distortion  (right) (Color figure online)
(right) (Color figure online)
As a further attempt to reach low values of \(I_2(P)\), we also started the optimization from a non-compatible matrix field instead of the homogeneous deformation gradient \(P=F_0\) we used for the numerical methods before. For this, we chose a checkerboard pattern with squares of size \(\frac{1}{b}\times \frac{1}{b}\) and alternately set the values \(F_1=(1-\delta ) F_0\) and \(F_2=(1+\delta ) F_0\) with \(\delta =0.5\) (cf. Fig. 10).
This pattern has a lower energy value without considering the regularization term  as it only activates the concave volumetric part \(\log \det F\) of \(W_{\textrm{magic}}^+(F)\). As shown in Fig. 11, we indeed arrive at different microstructures. However, the compatible deformations obtained from minimizing
as it only activates the concave volumetric part \(\log \det F\) of \(W_{\textrm{magic}}^+(F)\). As shown in Fig. 11, we indeed arrive at different microstructures. However, the compatible deformations obtained from minimizing  again have higher energy values than the homogeneous state. Furthermore, minimizing the original energy \(I_1\) from there lead back to the homogeneous configuration once again.
again have higher energy values than the homogeneous state. Furthermore, minimizing the original energy \(I_1\) from there lead back to the homogeneous configuration once again.
6 Gradient Young Measures and Laminates
More recently, the problem of Morrey’s conjecture has been approached from the point of view of gradient Young measures and laminates (Kinderlehrer and Pedregal 1991a, b, 1994; Guerra and da Costa 2021; Guerra 2019; Müller 1999; Faraco and Székelyhidi 2008; Harris et al. 2018). In the following, we give a brief overview of this alternative approach and its relation to the optimization methods used above.
Throughout this section, let \(\Omega =[0,1]^2\) denote the unit square.Footnote 9 In order to positively answer Morrey’s conjecture, we would need to find a rank-one convex function \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\) that is not quasiconvex. More explicitly, this task can be stated as follows:
-
(I)
Find a rank-one convex function \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\), a Lipschitz mapping \(\varphi :\Omega \rightarrow {\mathbb {R}}^2\) and \(F_0\in {\mathbb {R}}^{2\times 2}\) with \(\varphi (x)=F_0.x\) for all \(x\in \partial \Omega \) such that
 (6.1)
(6.1)
In particular, such a full solution to Morrey’s problem requires both an energy function \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\) and a mapping \(\varphi :\Omega \rightarrow {\mathbb {R}}^2\).
The classical approach to this problem, as followed in the previous sections, consists of choosing a plausible candidate W first before trying to find a mapping \(\varphi \) that satisfies (6.1) in order to prove the non-quasiconvexity of W. However, recent investigations of Morrey’s conjecture have often taken a slightly different point of view, emphasizing the search for a suitable mapping \(\varphi \) instead. More specifically, these approaches try to establish the existence of a Lipschitz mapping \(\varphi :\Omega \rightarrow {\mathbb {R}}^2\) such that the pushforward measure induced by  violates a Jensen-type inequality.
violates a Jensen-type inequality.
This change in perspective is mainly based on the seminal results by Kinderlehrer and Pedregal (1991a, 1991b, 1994) on the relation between quasiconvexity and gradient Young measures. In particular, these results allow for Morrey’s conjecture (I) to be rephrased in terms of properties of probability measures.
6.1 Equivalent Formulations of Morrey’s Conjecture
First, we consider the following rephrasing, which is obtained by a simple substitution on the left-hand side of (6.1).
-
(II)
Find a rank-one convex function \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\), a Lipschitz mapping \(\varphi :\Omega \rightarrow {\mathbb {R}}^2\) and \(F_0\in {\mathbb {R}}^{2\times 2}\) with \(\varphi (x)=F_0.x\) for all \(x\in \partial \Omega \) such that
$$\begin{aligned} \int _{{\mathbb {R}}^{2\times 2}} W(A)\,{\textrm{d}\nu }_{\varphi }(A) < W(F_0) \,, \end{aligned}$$where \(\nu _{\varphi }\) denotes the pushforward measure of the Lebesgue measure with respect to
 , i.e.,
, i.e., 
This phrasing of Morrey’s problem in terms of probability measuresFootnote 10 is closely related to its formulation in terms of homogeneous gradient Young measures. The exact relation between pushforward measures of gradients and homogeneous gradient Young measures can be established by the Averaging Theorem (Kinderlehrer and Pedregal 1991b, Theorem 2.1), which directly implies the following lemma as a corollary.
Lemma 6.1
Cf. Kinderlehrer and Pedregal (1991b) Let \(\varphi \in W^{1,\infty }(\Omega ;{\mathbb {R}}^2)\) with \(\varphi (x)=F_0.x\) for all \(x\in \partial \Omega \). Then \(\nu _{\varphi }\) is a homogeneous gradient Young measure on \(\Omega \) with barycenter \(\overline{\nu }_{\varphi }=F_0\).
By virtue of Lemma 6.1, if (II) can be solved, so can the following problem:
-
(III)
Find a rank-one convex function \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\) and a homogeneous gradient Young measure \(\nu \) such that
$$\begin{aligned} \int _{{\mathbb {R}}^{2\times 2}} W(A)\,{\textrm{d}\nu }(A) < W(\overline{\nu }) \,, \end{aligned}$$(6.2)where \(\overline{\nu }\) denotes the barycenter of \(\nu \).
In order to see that (III) is also sufficient for (and thus equivalent to) solving (II), recall that for any homogeneous gradient Young measure \(\nu \) there exists a sequence \((\varphi _k)_{k\in \mathbb {N}}\subset W^{1,\infty }(\Omega ;{\mathbb {R}}^2)\) with affine linear boundary values induced by the barycenter \(F_0=\overline{\nu }\) of \(\nu \) such that
for any continuous function \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\). In particular, this implies \(\int _{{\mathbb {R}}^{2\times 2}} W(A)\,{\textrm{d}\nu }_{\varphi _k}(A) < W(\overline{\nu })=W(F_0)\) for sufficiently large k if \(\nu \) satisfies (6.2).
Finally, we can rephrase (III) by employing the notion of a laminate. In the planar case, a laminate can be characterized as a probability measure \(\nu \) on \({\mathbb {R}}^{2\times 2}\) such that the Jensen-type inequality
holds for any rank-one convex function \(W:{\mathbb {R}}^{2\times 2}\rightarrow {\mathbb {R}}\) (Pedregal 1993). Since \(\nu \) is a homogeneous gradient Young measure if and only if (6.3) holds for any quasiconvex energy W according to the Kinderlehrer–Pedregal Theorem (Kinderlehrer and Pedregal 1991b, 1994), the following problem is equivalent to (III):
-
(IV)
Find a homogeneous gradient Young measure \(\nu \) which is not a laminate.
Note that (IV) seems to make no reference to any energy function W. In practice, however (approximately), rank-one convex energy functions need to be applied to a given measure \(\nu \) in order to numerically establish whether it is a laminate (Guerra and da Costa 2021). On the other hand, it is often obvious by construction that \(\nu \) is a homogeneous gradient Young measure. In particular, due to Lemma 6.1, this is the case if \(\nu \) is obtained as the pushforward measure with respect to the gradient of a mapping \(\varphi :\Omega \rightarrow {\mathbb {R}}^2\).
6.2 The Numerical Search for Non-Laminate Gradient Young Measures
A specific numerical method for finding non-laminate homogeneous gradient Young measures numerically has been suggested by Guerra and da Costa (2021). This approach is based on selecting a dense subset \(K(\Omega )\subset W^{1,\infty }(\Omega ;{\mathbb {R}}^2)\) such that each \(\varphi \in K(\Omega )\) induces a discrete-valued gradient field  . Then the following problem needs to be solved numerically:
. Then the following problem needs to be solved numerically:
-
(V)
Find \(\varphi \in K(\Omega )\) such that \(\nu _{\varphi }\) with
 is not a laminate, where \(K(\Omega )=\bigcup _{N\in \mathbb {N}}K_N\) with
is not a laminate, where \(K(\Omega )=\bigcup _{N\in \mathbb {N}}K_N\) with  (6.4)
(6.4)
Both the barycenter \(\overline{\nu }_\varphi \) and the energy value \(\int _{{\mathbb {R}}^{2\times 2}} W(A)\,{\textrm{d}\nu }(A)\) can be easily computed numerically for the measure \(\nu _{\varphi }\) corresponding to any \(\varphi \in K(\Omega )\) and a given energy function W on \({\mathbb {R}}^{2\times 2}\). However, in order to demonstrate that a given measure \(\nu _{\varphi }\) is not a laminate, it is necessary to find a rank-one convex energy W for which (6.3) is violated. The numerical approach suggested by Guerra and da Costa (2021) consists of generating a large number of (approximately) rank-one convex energy functions by computing the rank-one convex envelope for a specific class of functions based on earlier considerations by Šverák (1992).
6.2.1 Application to \(W_{\textrm{magic}}^+\)
In contrast, based on our results in Voss et al. (2021b), we conjecture that the functional \(W_{\textrm{magic}}^+\) defined in 2.17 is a good candidate energy to detect non-laminate measures. Therefore, we do not need to perform the computationally expensive calculations of multiple rank-one convex envelopes. Instead, we directly include the class \(K(\Omega )\) of deformations in our search for a counterexample to the quasiconvexity inequality (1.2). Since the energy values of the inhomogeneous deformations \(\varphi \in K(\Omega )\) and of the corresponding homogeneous deformations given as the energy at the barycenter \(W(F_0)=W(\overline{\nu _{\varphi }})\) are easily computed numerically (without the need of FEM), we can thereby test \(W_{\textrm{magic}}^+\) with a large number of additional deformations with periodic boundary conditions. We call these inhomogeneous deformations \(\varphi \in K(\Omega )\) combined laminates.
For a given homogeneous deformation gradient \(F_0\) and given number N of laminates to combine (cf. (6.4)), our implementation selects random parameter values for \(\eta _i,\xi _i,c_i\) with \(i\in \{1,\ldots ,N\}\), validating that \(\det F>0\) for all such combinations, and computes the energy value of the resulting combined laminate. Figures 12 and 13 show examples of such deformations with \(N=3\) and  ; the “phases” of the superimposed deformations, i.e., the local values of
; the “phases” of the superimposed deformations, i.e., the local values of  , are indicated by \((+/-)\).
, are indicated by \((+/-)\).
Our numerical tests focused on the case \(N\ge 5\).Footnote 11 After testing slightly more than one million combinations with a routine written in Python, where we started with different  with \(a\in [1,10]\) and tried \(N=4,5,6,7\), we were once more unable to obtain an energy level below \(W_{\textrm{magic}}^+(F_0)\). As with our previous approaches, we always find non-trivial microstructures when we change our energy function to be non-rank-one convex. Figure 14, for example, shows such a microstructure for the energy \(W_c\) defined in (3.1) with a modified volumetric part \(c \log \det F\) in place of \(W_{\textrm{magic}}^+\); for \(c>1\), this method once more finds random configurations with lower energy than the homogeneous state.
with \(a\in [1,10]\) and tried \(N=4,5,6,7\), we were once more unable to obtain an energy level below \(W_{\textrm{magic}}^+(F_0)\). As with our previous approaches, we always find non-trivial microstructures when we change our energy function to be non-rank-one convex. Figure 14, for example, shows such a microstructure for the energy \(W_c\) defined in (3.1) with a modified volumetric part \(c \log \det F\) in place of \(W_{\textrm{magic}}^+\); for \(c>1\), this method once more finds random configurations with lower energy than the homogeneous state.
A combined laminate consisting of five parts of the reference configuration (left) and the deformed configuration (right). The deformation is homogeneous for each area with the coloring showing the corresponding value of \(\det F\). The energy value is lower than the homogeneous one for the non-elliptic energy density \(W_c\) defined in (3.1) with \(c=1.5\)
7 Discussion
We have presented several different numerical approaches to check for quasiconvexity of a given function W.
-
In Sect. 3, we demonstrated a classical finite element approach that can find easily microstructures if we perturb the energy candidate to be slightly non-rank-one convex. In addition, we showed a method of disturbing the homogeneous structure of the solution by modifying the energy values on a subdomain and computing the microstructure resulting from this material inhomogeneity.
-
In Sect. 4, under the assumption of periodic boundary conditions, we introduced a numerical scheme that is based on deep neural networks and thereby discovered a new non-trivial microstructure (smooth laminates) with the same energy value as the homogeneous deformation for the considered energy function, which we then investigated analytically.
-
For the relaxation technique considered in Sect. 5, we extended our numerical calculations from gradient fields F to general matrix field P by introducing a penalty term based on
 . This approach resulted in various non-compatible fields with lower energy value than the energy of the homogeneous deformation, even for a quasiconvex energy candidate. The fields found this way were then used as new starting configurations for the finite elements approach. This, unfortunately, did never lead to energies below the one of the homogeneous state.
. This approach resulted in various non-compatible fields with lower energy value than the energy of the homogeneous deformation, even for a quasiconvex energy candidate. The fields found this way were then used as new starting configurations for the finite elements approach. This, unfortunately, did never lead to energies below the one of the homogeneous state. -
In Sect. 6, we discussed an alternative numerically straightforward way of checking for quasiconvexity connected to the theory of gradient Young measures rather than to optimization. Several rank-one laminations were combined so that the resulting deformation remained piece-wise homogeneous and their energy value were compared to the homogeneous deformation. Again, we only found lower values for a non-rank-one convex energy density.
We tested all these methods with the energy \(W_{\textrm{magic}}^+\) from Voss et al. (2021b). If we change this energy to be non-elliptic and thus non-quasiconvex, the presented methods were all able to produce non-trivial microstructures, i.e., deformations that are neither homogeneous nor a simple first-order laminate. This demonstrates their viability as numerical tests for quasiconvexity. On the other hand, while non-quasiconvexity of an energy W can conceivably be proven by numerical methods (since identifying a single suitable deformation would be sufficient), no amount of numerical testing can be considered an actual proof that a given function is quasiconvex. However, if all the described methods fail to yield a deformation energetically more optimal than the homogeneous one—as was the case for the energy  considered here—then this should be interpreted as a strong indication that the function is indeed quasiconvex and therefore not a viable candidate for answering Morrey’s conjecture.
considered here—then this should be interpreted as a strong indication that the function is indeed quasiconvex and therefore not a viable candidate for answering Morrey’s conjecture.
Change history
18 November 2022
Missing Open Access funding information has been added in the Funding Note.
Notes
While a periodic superposition \(\vartheta _\#\in W_{\text {per}}^{1,\infty }([a,b])\) allows for more modifications of the homogeneous deformation \(F_0 x\) than a test function \(\vartheta \in W_0^{1,\infty }([a,b])\) , the average rate of change of \(\varphi (x)=F_0 x+\vartheta _\#(x)\) remains constant, i.e.,

Note that \(\det F=\lambda _1\lambda _2\) if and only if \(\det F > 0\), i.e., if
 . Expressing \(\det F\) for all \(F\in {\mathbb {R}}^{2\times 2}\) requires the signed singular values
. Expressing \(\det F\) for all \(F\in {\mathbb {R}}^{2\times 2}\) requires the signed singular values  ,
,  .
.For arbitrary \(F\in {\mathbb {R}}^{2\times 2}\) we find

Hence the eigenvalues of B and \({\mathrm{Cof\,\,}} B=({\mathrm{Cof\,\,}} F)({\mathrm{Cof\,\,}} F)^T\) and thus the singular values of F and \(\mathrm{Cof\,\,}F\) are identical. In addition, the same holds for the eigenvalues of F and \(\mathrm{Cof\,\,}F\) in the planar case.
The rank of a matrix
 is equal to the maximal size of nonzero minors. The cofactor \({\mathrm{Cof\,\,}} M\) is formed by \((n-1)\times (n-1)-\) minors of M and consequently \(\textrm{rank}({\mathrm{Cof\,\,}} M)=0\) if \(\mathrm{rank\,\,} M<n-1\). In the case \(\mathrm rank\,\,M=n-1\), at least one \((n-1)\times (n-1)-\) minor is nonzero which ensures \(\textrm{rank}({\mathrm{Cof\,\,}} M)>0\). Because
is equal to the maximal size of nonzero minors. The cofactor \({\mathrm{Cof\,\,}} M\) is formed by \((n-1)\times (n-1)-\) minors of M and consequently \(\textrm{rank}({\mathrm{Cof\,\,}} M)=0\) if \(\mathrm{rank\,\,} M<n-1\). In the case \(\mathrm rank\,\,M=n-1\), at least one \((n-1)\times (n-1)-\) minor is nonzero which ensures \(\textrm{rank}({\mathrm{Cof\,\,}} M)>0\). Because  , the image of \(({\mathrm{Cof\,\,}} M)^T\) is in the kernel of M which is of dimension 1 and therefore \(\textrm{rank}({\mathrm{Cof\,\,}} M)=1\).
, the image of \(({\mathrm{Cof\,\,}} M)^T\) is in the kernel of M which is of dimension 1 and therefore \(\textrm{rank}({\mathrm{Cof\,\,}} M)=1\).If the isochoric part h(t) is not convex, the combined function \(h\bigl (\frac{\lambda _1}{\lambda _2}\bigr )+\log (\lambda _1\lambda _2)\) will not correspond to a rank-one convex function (Voss et al. 2021b).
Due to the underestimation of integration using the trapezoidal rule, the total strain energy was observed to be slightly below the energy of the homogeneous deformation. However, under grid-refinement with \(N\gg 1\), this error converges to zero and the total strain energy was observed to equal the energy via homogeneous deformation up to machine precision.
In the three-dimensional case, we can use \(P\times \nu |_{\partial \Omega }=F_0\times \nu \) with \(\nu \in {\mathbb {R}}^3\) as the unit normal vector to \(\partial \Omega \) as equivalent alternative, since \(\displaystyle (P-F_0)\times \nu |_{\partial \Omega }=0\iff (P-F_0).\tau _{1/2}|_{\partial \Omega }=0\) where \(\tau _1,\tau _2\) are the tangent vectors to \(\partial \Omega \).
Note that the term \(|\Omega |=1\) will often be omitted in the following, but would need to be taken into account carefully for a more general choice of \(\Omega \subset {\mathbb {R}}^2\).
Note that \(\nu _{\varphi }\) is indeed a probability measure on \({\mathbb {R}}^{2\times 2}\) due to the choice \(1=|\Omega |=\nu _{\varphi }({\mathbb {R}}^{2\times 2})\).
Configurations with \(N>3\) are usually too convoluted to properly visualize, especially with the addition \((+/-)\) to indicate the “phases”.
The question whether the Burkholder function is quasiconvex or not is discussed extensively in the literature with numerical evidence in favor of the former (Baernstein and Montgomery-Smith 2011). Furthermore, Guerra and Kristensen give a new interesting discussion about \(B_p\) being extremal in the class of p-homogeneous functions (Guerra and Kristensen 2021).
Note that we use
 and
and  for both row and column vectors.
for both row and column vectors.You arrive at the same expression (B.12) by computing \(\left( \nabla \textrm{Div}[P Q]\right) Q^T\) directly.
For the modified energy
 (B.20)
(B.20)it is possible to achieve
 .
.
References
Astala, K., Iwaniec, T., Prause, I., Saksman, E.: Burkholder integrals, Morrey’s problem and quasiconformal mappings. J. Am. Math. Soc. 25(2), 507–531 (2012)
Aubert, G.: On a counterexample of a rank 1 convex function which is not polyconvex in the case \(N= 2\). Proc. R. Soc. Edinb. Sect. A: Math. 106(3–4), 237–240 (1987)
Baernstein, A., Montgomery-Smith, S.: Some conjectures about integral means of \(\partial \)f and \(\partial \)f . Mathematics Publications (MU) (2011). arXiv:math/9709215
Ball, J.M.: Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63(4), 337–403 (1976)
Ball, J.M., James, R.D.: Fine phase mixtures as minimizers of energy. Arch. Ration. Mech. Anal. 100, 13–52 (1987)
Ball, J., Murat, F.: W\(^{1,p}-Quasiconvexity and variational problems for multiple integrals\). J. Funct. Anal. 58, 225–253 (1984)
Ball, J.M.: Does rank-one convexity imply quasiconvexity? In: Antman, S.S., Ericksen, J., Kinderlehrer, D., Müller, I. (eds.) Metastability and Incompletely Posed Problems, vol. 3, pp. 17–32. Springer (1987)
Ball, J.M., Kirchheim, B., Kristensen, J.: Regularity of quasiconvex envelopes. Calc. Var. Part. Differ. Equ. 11(4), 333–359 (2000)
Bandeira, L., Pedregal, P.: Finding new families of rank-one convex polynomials . In: Annales de l’Institut Henri Poincaré. Analyse Non Linéaire, vol. 26, no. 5, pp. 1621–1634. Elsevier, Masson (2009)
Bartels, S., Carstensen, C., Hackl, K., Hoppe, U.: Effective relaxation for microstructure simulations: algorithms and applications. Comput. Methods Appl. Mech. Eng. 193(48–51), 5143–5175 (2004)
Bastian, P., et al.: The DUNE framework: basic concepts and recent developments. Comput. Math. Appl. 81, 75–112 (2021)
Baydin, A.G. , Pearlmutter, B.A., Radul, A.A., Siskind, J.M.: Automatic differentiation in machine learning: a survey. J. Mach. Learn. Res. 18(153), 1–43 (2018). http://jmlr.org/papers/v18/17- 468.html
Burkholder, D.L.: Sharp inequalities for martingales and stochastic integrals. Astérisque 157(158), 75–94 (1988)
Casadio-Tarabusi, E.: An algebraic characterization of quasi-convex functions. Ric. Mat. 42(1), 11–24 (1993)
Ciarlet, P. G.: Mathematical Elasticity. Volume I: Three-Dimensional Elasticity. Studies in Mathematics and its Applications, vol. 20. Elsevier Science (1988)
Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. SIAM (2002)
Conn, A., Gould, N., Toint, P.: Trust-Region Methods. SIAM (2000)
Conti, S., Faraco, D., Maggi, F., Müller, S.: Rank-one convex functions on \(2\times 2\) symmetric matrices and laminates on rank-three lines. Calc. Var. Part. Differ. Equ. 24(4), 479–493 (2005)
Dacorogna, B.: Direct Methods in the Calculus of Variations, Applied Mathematical Sciences, vol. 78, 2nd edn. Springer, Berlin (2008)
Dacorogna, B., Douchet, J., Gangbo, W., Rappaz, J.: Some examples of rank one convex functions in dimension two. Proc. R. Soc. Edinb. Sect. A: Math. 114(1–2), 135–150 (1990)
Dacorogna, B., Haeberly, J.-P.: Remarks on a numerical study of convexity, quasiconvexity, and rank one convexity . In: Variational Methods for Discontinuous Structures, pp. 143–154. Springer, (1996)
Dacorogna, B., Haeberly, J.-P.: Some numerical methods for the study of the convexity notions arising in the calculus of variations. ESAIM: Math. Model. Numer. Anal. 32(2), 153–175 (1998)
Dacorogna, B., Marcellini, P.: A counterexample in the vectorial calculus of variations. In: Ball, J.M. (eds.) Material Instabilities in Continuum Mechanics, pp. 77–83. Oxford Science Publications (1988)
Dolzmann, G.: Numerical computation of rank-one convex envelopes. SIAM J. Numer. Anal. 36(5), 1621–1635 (1999)
Faraco, D., Székelyhidi, L., et al.: Tartar’s conjecture and localization of the quasiconvex hull in \({\mathbb{R}}^{2\times 2}\). Acta Math. 200(2), 279–305 (2008)
Fernández, M., Jamshidian, M., Böhlke, T., Kersting, K., Weeger, O.: Anisotropic hyperelastic constitutive models for finite deformations combining material theory and data-driven approaches with application to cubic lattice metamaterials. Comput. Mech. 67(2), 653–677 (2021)
Grabovsky, Y.: From microstructure-independent formulas for composite materials to rank-one convex, non-quasiconvex functions. Arch. Ration. Mech. Anal. 227(2), 607–636 (2018)
Grabovsky, Y., Truskinovsky, L.: When rank-one convexity meets polyconvexity: an algebraic approach to elastic binodal. J. Nonlinear Sci. 29(1), 229–253 (2019)
Gremaud, P.-A.: Numerical optimization and quasiconvexity. Eur. J. Appl. Math. 6(1), 69–82 (1995)
Guerra, A.: Extremal rank-one convex integrands and a conjecture of Šverák. Calc. Var. Part. Differ. Equ. 58(6), 1–19 (2019)
Guerra, A., da Costa, R. T.: Numerical evidence towards a positive answer to Morrey’s problem . Rev. Mat.Iberoamer. 38(2), 601–614 (2021)
Guerra, A., Kristensen, J.: Automatic quasiconvexity of homogeneous isotropic rank-one convex integrands . arXiv preprint arXiv:2112.10563 (2021)
Gutiérrez, S., Villavicencio, J.: An optimization algorithm applied to the Morrey conjecture in nonlinear elasticity. Int. J. Solids Struct. 44(10), 3177–3186 (2007)
Harris, T.L., Kirchheim, B., Lin, C.-C.: Two-by-two upper triangular matrices and Morrey’s conjecture. Calc. Var. Part. Differ. Equ. 57, 1–12 (2018)
Hartmann, S., Neff, P.: Polyconvexity of generalized polynomial-type hyperelastic strain energy functions for nearincompressibility. Int. J. Solids Struct. 40(11), 2767–2791 (2003). https://doi.org/10.1016/S0020-7683(03)00086-6
Karniadakis, G.E., Kevrekidis, I.G., Lu, L., Perdikaris, P., Wang, S., Yang, L.: Physics-informed machine learning. Nat. Rev. Phys. 3(6), 422–440 (2021)
Kawohl, B., Sweers, G.: On Quasiconvexity, Rank-one Convexity and Symmetry, vol. 14, pp. 251–263. Delft Progress Report (1990)
Kinderlehrer, D., Pedregal, P.: Caractérisation des mesures de Young associées à un gradient. Compt. Rendus l’Acad. Sci. Sér. 1, Math. 313(11), 765–770 (1991a)
Kinderlehrer, D., Pedregal, P.: Characterizations of Young measures generated by gradients. Arch. Ration. Mech. Anal. 115(4), 329–365 (1991b)
Kinderlehrer, D., Pedregal, P.: Gradient Young measures generated by sequences in Sobolev spaces. J. Geom. Anal. 4(1), 59 (1994)
Kingma, D.P., Adam, J.B.: a method for stochastic optimization . arXiv preprint arXiv:1412.6980 (2017)
Kirby, R.C., Logg, A., Rognes, M.E., Terrel, A.R.: Common and unusual finite elements. In: Automated Solution of Differential Equations by the Finite Element Method, pp. 95–119. Springer (2012)
Klein, D., Fern’andez, M., Martin, R.J., Neff, P., Weeger, O.: Polyconvex anisotropic hyperelasticity with neural networks . J. Mech. Phys. Solids (2022). arXiv:2106.14623
Kornhuber, R.: Monotone multigrid methods for elliptic variational inequalities I. Numer. Math. 69(2), 167–184 (1994)
Kruzik, M.: On the composition of quasiconvex functions and the transposition. J. Convex Anal. 6(1), 207–213 (1999)
Kumar, S., Vidyasagar, A., Kochmann, D.M.: An assessment of numerical techniques to find energy-minimizing microstructures associated with nonconvex potentials. Int. J. Numer. Meth. Eng. 121(7), 1595–1628 (2020)
Li, Z.-P.: Finite order rank-one convex envelopes and computation of microstructures with laminates in laminates. BIT Numer. Math. 40(4), 745–761 (2000)
Martin, R.J., Ghiba, I.-D., Neff, P.: Rank-one convexity implies polyconvexity for isotropic, objective and isochoric elastic energies in the two-dimensional case . Proc. R. Soc. Edinb. A 147A, 571–597 (2017). arXiv:1507.00266
Morrey, C.B.: Quasi-convexity and the lower semicontinuity of multiple integrals. Pac. J. Math. 2(1), 25–53 (1952)
Morrey, C. B.: Multiple Integrals in the Calculus of Variations. Springer (2009)
Müller, S.: Rank-one convexity implies quasiconvexity on diagonal matrices. Int. Math. Res. Not. 1999(20), 1087–1095 (1999)
Neff, P., Chelmiński, K., Alber, H.-D.: Notes on strain gradient plasticity: finite strain covariant modelling and global existence in the infinitesimal rate-independent case. Math. Models Methods Appl. Sci. 19(02), 307–346 (2009). https://doi.org/10.1142/S0218202509003449
Neff, P., Eidel, B., Martin, R.J.: Geometry of logarithmic strain measures in solid mechanics . Arch. Ration. Mech. Anal. 222(2), 507–572 (2016). https://doi.org/10.1007/s00205-016-1007-x. arXiv:1505.02203
Neff, P., Ghiba, I.-D., Madeo, A., Placidi, L., Rosi, G.: A unifying perspective: the relaxed linear micromorphic continuum. Contin. Mech. Thermodyn. 26(5), 639–681 (2014). https://doi.org/10.1007/s00161-013-0322-9
Neff, P., Münch, I.: Curl bounds Grad on SO(3). ESAIM: Control Optim. Calc. Variat. 14(1), 148–159 (2008). https://doi.org/10.1051/cocv:2007050
Ogden, R.: Nearly isochoric elastic deformations: application to rubberlike solids. J. Mech. Phys. Solids 26(1), 37–57 (1978)
Parry, G.: On the planar rank-one convexity condition. Proc. R. Soc. Edinb. Sect. A: Math. 125(2), 247–264 (1995)
Paszke , A., et al.: PyTorch: an imperative style, high-performance deep learning library. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’Alchë-Buc, F., Fox, E., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 32, pp. 8024–8035. Curran Associates, Inc. (2019)
Pedregal, P.: Laminates and microstructure. Eur. J. Appl. Math. 4(2), 121–149 (1993)
Pedregal, P.: Some remarks on quasiconvexity and rank-one convexity. Proc. R. Soc. Edinb. Sect. A: Math. 126(5), 1055–1065 (1996)
Pedregal, P.: Rank-one convexity implies quasiconvexity for two-component maps. arXiv preprint arXiv:1905.06571 (2019)
Pedregal, P., Šverák, V.: A note on quasiconvexity and rank-one convexity for \(2 \times 2\) matrices. J. Convex Anal. 5, 107–118 (1998)
Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)
Sander, O.: Geodesic Finite Elements on simplicial grids. Int. J. Numer. Methods Eng. 92(12), 999–1025 (2012)
Sander, O.: DUNE—The Distributed and Unified Numerics Environment. Springer (2020)
Schmidhuber, J.: Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015)
Schröder, J., Neff, P.: Poly-, Quasi-and Rank-one Convexity in Applied Mechanics. Springer (2010). https://doi.org/10.1007/978-3-7091-0174-2
Sebestyén, G., Székelyhidi, Jr., L.: Laminates supported on cubes. arXiv preprint arXiv:1504.06516 (2015)
Sebestyén, G., Székelyhidi, L., Jr.: Laminates supported on cubes. J. Convex Anal. 24(4), 1217–1237 (2017)
Šilhavý, M.: The Mechanics and Thermodynamics of Continuous Media. In: Texts and Monographs in Physics. Springer (1997)
Šverák, V.: Rank-one convexity does not imply quasiconvexity. Proc. R. Soc. Edinb. Sect. A: Math. 120(1–2), 185–189 (1992)
Voss, J., Baaser, H., Martin, R.J., Neff, P.: More on anti-plane shear. J. Optim. Theory Appl. 184(1), 226–249 (2020)
Voss, J., Baaser, H., Martin, R.J., Neff, P.: Anti-plane Shear in Hyperelasticity. In: Mariano, P.M. (eds.) Variational Views in Mechanics, pp. 255–284. Springer (2021)
Voss, J., Ghiba, I.-D., Martin, R.J., Neff, P.: Sharp rank-one convexity conditions in planar isotropic elasticity for the additive volumetric-isochoric split. J. Elast. 143(2), 301–335 (2021). arXiv:2008.04188
Voss, J., Martin, R.J., Ghiba, I.-D., Neff, P.: Morrey’s conjecture for the planar volumetric-isochoric split: least rank-one convex energy functions. J. Nonlinear Sci. (2021) (to appear). arXiv:2106.11887
Walther, A., Griewank, A.: Getting started with ADOL-C. In: Naumann, U., Schenk, O. (eds.) Combinatorial Scientific Computing, pp. 181–202. Chapman-Hall CRC Computational Science (2012)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Alain Goriely.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Contracting Deformations
In a previous article (Voss et al. 2021b), we found a surprising connection of \(W_{\textrm{magic}}^+\) to the work of Burkholder (1988); Astala et al. (2012); Guerra and Kristensen (2021) in the field of complex analysis with the so-called Burkholder functionFootnote 12
where  denotes the operator norm (i.e., the largest singular value) of F. There, we showed the existence of a first non-trivial example for the energy \(W_{\textrm{magic}}^+(F)\) for which equality with the homogeneous solution holds. We considered the radial symmetric deformation, i.e., functions which can be described by a mapping \(v:[0,\infty )\rightarrow {\mathbb {R}}\) such that
denotes the operator norm (i.e., the largest singular value) of F. There, we showed the existence of a first non-trivial example for the energy \(W_{\textrm{magic}}^+(F)\) for which equality with the homogeneous solution holds. We considered the radial symmetric deformation, i.e., functions which can be described by a mapping \(v:[0,\infty )\rightarrow {\mathbb {R}}\) such that

and its subclasses of expanding and contracting deformations


In addition to the proof given in Voss et al. (2021b), we can verify that these deformations are equilibrium states of \(B_p\) and \(W_{\textrm{magic}}^+\) by directly computing the Euler-Lagrange equations with restriction to radial deformations. It is important to note that the Euler-Lagrange equations given in this section are only a necessary but not a sufficient condition to check for stationary points because they assume the restriction to radial deformations as an a priori constraint. For the full system of Euler-Lagrange equations, we have to compute the divergence of the full first Piola-Kirchhoff tensor \(S_1(F)=DW(F)\) (4.15) and insert radial deformations as a posteriori constraint afterward which would go beyond the scope here but has been verified with the support of Mathematica.
We start with the Burkholder functional in the class of expanding deformations \(v\in {\mathcal {V}}_R\)

and compute the corresponding Euler-Lagrange equation

which is always true. Thus any \(v\in {\mathcal {V}}_R\) is an equilibrium with respect to the restricted class of radial deformations. Now we do the same computation for the energy density \(W_{\textrm{magic}}^+\) in the opposite class of contracting deformations 

and compute the corresponding Euler-Lagrange equation

which is always true. Thus any  is an equilibrium with respect to the restricted class of radial deformations.
is an equilibrium with respect to the restricted class of radial deformations.
Appendix B: Euler-Lagrange Equations with Curvature Terms
In the three-dimensional case, we have

Thus in the planar case we may introduce the operator

In addition, in three dimensions, taking  row-wise, it holds
row-wise, it holds

Accordingly, in the planar case we may define the operator

In order to mimic the behavior of the curl in the three-dimensional case ( ) we define moreover the operator
) we define moreover the operator

which is the relevant \(2\times 2\) block of the three-dimensional expression

and ensures the common condition \(\mathrm{Div\,\,}{{\,\mathrm{CCurl_{2D}}\,}}(P)=0\). We calculate the weak form of the Euler-Lagrange equations


where we used that  is a linear operator. With the fundamental lemma of the calculus of variations we obtain the strong form of the Euler–Lagrange equations for the respective cases
is a linear operator. With the fundamental lemma of the calculus of variations we obtain the strong form of the Euler–Lagrange equations for the respective cases
Because of \(\mathrm{Div\,\,}{{\,\mathrm{CCurl_{2D}}\,}}(P)=0\) the Euler–Lagrange equation (B.8) always implies
where

denotes the row-wise divergence of \()\).
Since in the planar case,  can be seen as a rotated \(\div \), i.e.,
can be seen as a rotated \(\div \), i.e.,

we haveFootnote 13

Thus lookingFootnote 14 at Eq. (B.5)

Therefore,

which corresponds to the Euler-Lagrange equation in strong \(\nabla \textrm{Div}\)-form
which is equivalent to (B.8). The corresponding minimization problem (5.2) can hence be rewritten using \({{\,\mathrm{Curl_{2D}}\,}}P=\textrm{Div}[P Q]\) as

We may now substitute  . Then it holds
. Then it holds

because of the isotropy \((\star )\) of \(W_{\textrm{magic}}^+\). Altogether,

which now corresponds to the Euler-Lagrange equation in strong 

and the new minimization problem

with \(\tau \in {\mathbb {R}}^2\) as the unit tangent vector to \(\partial \Omega \). With \(\tau =Q.\nu \) (since  in the planar case) we compute
in the planar case) we compute

and transform the tangential boundary conditions in the curl-formulation to the Neumann-boundary conditions for  in the div-formulation
in the div-formulation

with \(\nu \in {\mathbb {R}}^2\) as the unit normal vector to \(\partial \Omega \).
For numerical experiments we may then also use the space

Because of the involved nonlinear form of \(W_{\textrm{magic}}^+(P)\) it is, however, not clear whether or not \(P\in L^2(\Omega )\) holds.Footnote 15
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Voss, J., Martin, R.J., Sander, O. et al. Numerical Approaches for Investigating Quasiconvexity in the Context of Morrey’s Conjecture. J Nonlinear Sci 32, 77 (2022). https://doi.org/10.1007/s00332-022-09820-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-022-09820-x
Keywords
- Nonlinear elasticity
- Hyperelasticity
- Planar elasticity
- Rank-one convexity
- Quasiconvexity
- Ellipticity
- Isotropy
- Volumetric-isochoric split
- Finite elements
- Physics-informed neural networks



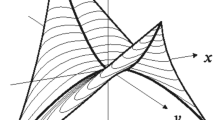





 . The color shows the determinant (left) and the distortion
. The color shows the determinant (left) and the distortion  (right)
(right)
 . The colors encode the determinant (left) and the distortion
. The colors encode the determinant (left) and the distortion  (right)
(right)


 computed for
computed for  . The colors encode the determinant (left) and the distortion
. The colors encode the determinant (left) and the distortion  (right)
(right)


 . This pattern remains visible for the first calculation because as explained in the text, the trust-region algorithm did not find a local minimizer for
. This pattern remains visible for the first calculation because as explained in the text, the trust-region algorithm did not find a local minimizer for 
 , i.e.,
, i.e., 
 is not a laminate, where
is not a laminate, where 



 . This approach resulted in various non-compatible fields with lower energy value than the energy of the homogeneous deformation, even for a quasiconvex energy candidate. The fields found this way were then used as new starting configurations for the finite elements approach. This, unfortunately, did never lead to energies below the one of the homogeneous state.
. This approach resulted in various non-compatible fields with lower energy value than the energy of the homogeneous deformation, even for a quasiconvex energy candidate. The fields found this way were then used as new starting configurations for the finite elements approach. This, unfortunately, did never lead to energies below the one of the homogeneous state.
 . Expressing
. Expressing  ,
,  .
.
 is equal to the maximal size of nonzero minors. The cofactor
is equal to the maximal size of nonzero minors. The cofactor  , the image of
, the image of  and
and  for both row and column vectors.
for both row and column vectors.
 .
.