Abstract
We present two meaningful and effective non-ideal constitutive characterizations for a multiple impulsive constraints \({\mathcal {S}}\) comprising a finite number of non-ideal frictionless constraints of codimension 1, described in the geometric setup given by the space–time bundle \({\mathcal {M}}\) of a mechanical system in contact/impact with \({\mathcal {S}}\). Thanks to the geometric structures associated to the elements of \({\mathcal {S}}\), we introduce a symmetric characterization, that does not distinguish the elements forming \({\mathcal {S}}\) as regards mechanical behavior, and an asymmetric one that makes this distinction. Both the characterizations provide a generalization of the characterization of ideal multiple constraints presented in Pasquero (Q Appl Math 76(3):547–576, 2018). The iterative nature of these characterizations allows the introduction of two algorithms determining the right velocity of the system in case of single or multiple contact/impact with symmetric or asymmetric constraints \({\mathcal {S}}\), once the elements forming \({\mathcal {S}}\) and the left velocity of the system are known. We show the effectiveness of the two possible choices with explicit implementations of these algorithms in two significant examples: a simplified Newton’s cradle system for the symmetric characterization and a disk in multiple contact/impact with two walls of a corner for the asymmetric one.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Jet bundle theory found fruitful application in the study of Classical Mechanics of systems with a finite number n of degrees of freedom since the late 1900 (see e.g., Pommaret 1988; Massa and Pagani 1991) and more specifically in classical impulsive mechanics since the early 2000 (see e.g., Pasquero 2005).
One of the best assets of jet bundle theory applied to classical mechanics consists in its natural framing of time-dependent description and frame independent description of the Lagrangian representation of mechanical phenomena. Frame independence is particularly important in impulsive mechanics, where the concept of velocity, intrinsically dependent on the choice of a frame of reference, plays a crucial role in the laws that govern the motion both for free and constrained systems.
The jet bundle geometric context are especially suitable to frame the so-called event-driven algebraic approach to impulsive systems, where every impact happening in the time evolution of the system is considered as an isolated event with the system in a fixed configuration in contact with the constraints and where the kinematic state of the system after the impact can be expressed as function of the kinematic state before the impact. In particular, the jet bundle context allows a very simple definition of constitutive characterization of impulsive and/or unilateral constraints, that is, roughly speaking, the rule to which the reactive impulse is subject in order to restore determinism. On the understanding that the only compulsory condition for a characterization is to restore determinism of classical mechanics, the choice of a characterization can be based on several different requirements: for instance geometric properties of the constraint itself, frame independence, ideality, extremality, generalization of known cases, physical meaningfulness, agreement with experimental data and so on. The following different cases of impulsive constraints and characterizations have found a satisfactory description in the geometric context of jet bundle theory:
-
Ideal single positional constraints of codimension 1 and of codimension greater than 1 (see Pasquero 2005);
-
Ideal constraints of mixed nature (positional with additional permanent and/or instantaneous kinetic constraints; see Pasquero 2006);
-
Non-ideal single constraints of mixed nature (this case can be divided into non-ideal constraints without or with friction; see Pasquero 2008);
-
Ideal multiple positional constraints formed by \(2 \le r<n\) constraints of codimension 1 (see Pasquero 2018).
The relationships between the cases listed above are illustrated by the following diagram that shows, starting from the “progenitor” case of ideal single positional constraint of codimension 1, the increasing refinement of the modeling and the essential distinction between single and multiple constraints.

Multiple contact/impact, that is the situation when a mechanical system is simultaneously in contact with two o more constraints and impacts with one or more of them, occurs for many mechanical systems, from scholarly cases such as billiard balls to more up to date and applicable cases such as granular matter and kinematic chains.
The aim of this paper is to present one step further in the left column of the diagram above by defining and analyzing two possible constitutive characterizations of non-ideal frictionless multiple positional constraints in symmetric and asymmetric cases. In the symmetric case, the characterization consists in a direct generalization of the ideal one by introducing a suitable global coefficient of restitution (COR) applicable to each element of the multiple constraint. In the asymmetric case, the characterization differentiates the single constraints by considering a (possibly) different COR for each element of the multiple constraint. Of course, the asymmetric characterization comes down to the symmetric one when the CORs of the single constraints are all the same.
The geometric context to which we refer in this paper is the same of Pasquero (2018), fit to manage multiple positional constraints formed by \(2 \le r<n\) constraints of codimension 1. In order to avoid the technicalities of multiple indexes, and without significant loss of generality, we will consider \(r=2\), then modeling simultaneous contact/impact of the mechanical system with two positional constraints of codimension 1. Moreover, we restrict our attention to systems subject only to positional (and not kinetic) constraints.
With the intention of getting the paper closer to self-consistency, and also in order to fix notation, a very concise description of the geometry of the Lagrangian setup of constrained impulsive mechanical systems subject to multiple positional constraints is presented in Sect. 2. It is a short version of that presented in Pasquero (2018). The reader interested in a wider survey on the argument can also refer to Pasquero (2018).
The main known ideas about the concept of impulsive constitutive characterization and the application to single constraints and ideal multiple constraints are presented in Sects. 3.1 and 3.2, respectively. The characterizations of symmetric and asymmetric non-ideal frictionless multiple constraints, that constitute the innovative part of the paper, are presented in Sects. 3.3 and 3.4. The general procedure applicable when \(r >2\) is sketched in Sect. 3.5.
The iterative nature of the procedure giving the characterizations allows the implementation of algorithms effectively applicable to study impacting mechanical systems: Sect. 4 presents two examples of these applications. In Sect. 4.1, we illustrate the behavior of the symmetric characterization applied to a simplified version of the Newton’s cradle, formed by three equal balls. This is a case of “multiple contact with repeated single impacts in a symmetric constraint” (different to the case “multiple impact in a symmetric constraint,” an example of which is analyzed in Fassino and Pasquero (2019)). In Sect. 4.2, we illustrate the behavior of the asymmetric characterization applied to a “multiple impact in an asymmetric constraint,” analyzing the multiple impact of a disk in a corner formed by two walls having different CORs.
The list of references is based on the minimality criterion of making the paper self-consistent and then is focussed on the specific approach given by the jet bundle framework. Different choices, even if restricted to the works pertaining only multiple impacts, could draw away the attention of the reader from the peculiar approach of this paper and moreover could give rise to reasonable criticisms and concern (Saracco 2020). However, the reader interested in classical approach to contact/impact mechanics can find foundations, main results and a huge bibliography in Johnson (1985), Stronge (2000), Brogliato (1996). A different approach to frictionless multiple impacts can be found in Liu et al. (2008, 2009). Different but still heavily based on geometric techniques approaches to unilateral and impulsive constraints can be found in Ibort and De Leon (1998), Cortés and Vinogradov (2006).
2 Geometry of the Lagrangian Setup
In this part, we concisely describe the Lagrangian geometric setup suited to study impulsive mechanics of systems subject to positional constraints, and we recall the main definitions and results about the characterization of impulsive constraints in this context. With few exceptions, the material is not new (for a more detailed discussion we refer to Pasquero (2018) and the references within).
2.1 Free Systems
The configuration space–time of a mechanical system with a finite number n of degrees of freedom is a fiber bundle \(\pi _t: {\mathcal {M}}\rightarrow {\mathbb {E}}\) where \({\mathcal {M}}\) is a \((n+1)\)-dimensional differentiable manifold, \({\mathbb {E}}\) is the 1-dimensional euclidean space representing the time axis, and \(\pi _t\) is the projection implementing the absolute time axiom. We usually refer \({\mathcal {M}}\) to fibred coordinates \((t,x^1,\ldots ,x^n)\), where t is a global euclidean coordinate on \({\mathbb {E}}\). A motion of the system is a section \(\gamma :{\mathbb {E}}\rightarrow {\mathcal {M}}\), locally represented by a map \(\gamma =\gamma (t)\) such that \(t \rightsquigarrow (t, x^1(t), \ldots , x^n(t))\).
The \((2n+1)\)-dimensional vector bundle \(\pi : V({\mathcal {M}})\rightarrow {\mathcal {M}}\) of the vertical (with respect to \(\pi _t\)) vectors that are tangent to the fiber of \({\mathcal {M}}\) is the subbundle of the tangent bundle \(\pi : T({\mathcal {M}})\rightarrow {\mathcal {M}}\) given by the space-like vectors. The elements of \(V({\mathcal {M}})\) have local representation \(\mathbf{V} \, = \, V^1 \frac{\partial }{\partial x^1}+ \cdots + V^n \frac{\partial }{\partial x^n}\).
The \((2n+1)\)-dimensional affine bundle \(\pi : J_1({\mathcal {M}})\rightarrow {\mathcal {M}}\) of the vectors that are tangent to any possible motion of the system in any point is the subbundle of the tangent bundle \(\pi : T({\mathcal {M}})\rightarrow {\mathcal {M}}\) given by the time-like vectors, also called absolute velocities. The elements of \(J_1({\mathcal {M}})\) have local representation \(\mathbf{p} \, = \, \frac{\partial }{\partial t} + p^1 \frac{\partial }{\partial x^1}+ \cdots + p^n \frac{\partial }{\partial x^n}\).
The vertical vector bundle \(V({\mathcal {M}})\) is endowed with a positive definite metric that is a space-like scalar product \(\Phi : V({\mathcal {M}}) \times _{{\mathcal {M}}} V({\mathcal {M}}) \rightarrow {\mathbb {R}}\) locally expressed by \(\Phi (\mathbf{V}_1 , \mathbf{V}_2) = g_{ij} \, V_1^i \, V_2^j\), where the (mass) matrix \(g_{ij}\) takes into account of the massive properties of the system.
The (fibred) action of \(V({\mathcal {M}})\) on \(J_1({\mathcal {M}})\) given by \( + : J_1({\mathcal {M}})\times V({\mathcal {M}}) \rightarrow J_1({\mathcal {M}})\) such that, locally
shows that \(J_1({\mathcal {M}})\) is an affine subbundle of \(T({\mathcal {M}})\) modeled on the vector bundle \(V({\mathcal {M}})\).
A frame of reference for \({\mathcal {M}}\) is a time-like vector field \(\mathbf{h} \, = \, \frac{\partial }{\partial t} + H^1 (t, x^i) \frac{\partial }{\partial x^1}+ \cdots + H^n (t, x^i) \frac{\partial }{\partial x^n}\). Every frame \(\mathbf{h}\) determines a diffeomorphism \(\Delta _\mathbf{h} : J_1({\mathcal {M}})\rightarrow V({\mathcal {M}})\) of \(J_1({\mathcal {M}})\) with \(V({\mathcal {M}})\) such that \(\Delta _\mathbf{h}(\mathbf{p}) = \mathbf{p} \, - \, \mathbf{h}(\pi (\mathbf{p}))\). For every absolute velocity \(\mathbf{p}\) of the system, the space-like vector \(\Delta _\mathbf{h}(\mathbf{p}) = \mathbf{p} \, - \, \mathbf{h}(\pi (\mathbf{p}))\) is the relative velocity \( \mathbf{V}_\mathbf{h}(\mathbf{p})\) of \(\mathbf{p}\) with respect to the frame \(\mathbf{h}\). The function \({\mathcal {K}}_\mathbf{h} : J_1({\mathcal {M}})\rightarrow {\mathbb {R}}\) such that \({\mathcal {K}}_\mathbf{h}(\mathbf{p}) = \frac{1}{2} \, \Phi \left( \mathbf{V}_\mathbf{h}(\mathbf{p}), \mathbf{V}_\mathbf{h}(\mathbf{p}) \right) \) is the kinetic energy of the system with respect to the frame \(\mathbf{h}\).
An impulse acting on the system is an element \(\mathbf{I} \in V({\mathcal {M}})\). The mechanical law governing the impulsive phenomenon is simply the action \(+: J_1({\mathcal {M}})\times V({\mathcal {M}}) \rightarrow J_1({\mathcal {M}})\): given a left velocity \(\mathbf{p}_L\) of the system and an impulse \(\mathbf{I}\) such that \(\pi (\mathbf{p}_L) = \pi (\mathbf{I}) \in {\mathcal {M}}\), we can determine the right velocity \(\mathbf{p}_R \, = \, \mathbf{p}_L + \mathbf{I}\). Given a frame \(\mathbf{h} \in {\mathcal {H}}\), the action \(\Delta _\mathbf{h}\) such that \((\mathbf{p}_R - \mathbf{h}) \, = \, (\mathbf{p}_L - \mathbf{h})+ \mathbf{I}\) or, that is the same, \((\mathbf{V}_\mathbf{h})_R - (\mathbf{V}_\mathbf{h})_L \, = \, \mathbf{I}\), shows the independence by the frame of reference of the jump of velocities given by \(\mathbf{I}\).
2.2 Positional Constraints
A positional constraint \({\mathcal {S}}\) is a (s+1)-dimensional fibred subbundle \(i:{\mathcal {S}}\rightarrow {\mathcal {M}}\) without boundary. The bundle \({\mathcal {S}}\) determines the following additional geometric objects and structures relative to the system:
-
The contact condition of the system with the constraint. The system is in contact with the constraint if its configuration \(x\in i({\mathcal {S}}) \subset {\mathcal {M}}\). Since we adopt the event-driven approach; later on the system will be always considered in contact with the constraint;
-
The affine subbundle \(i_*:J_1({\mathcal {S}})\rightarrow J_1({\mathcal {M}})\) of the absolute velocities that are tangent to \({\mathcal {S}}\) and the vector subbundle \(i_*:V({\mathcal {S}}) \rightarrow V({\mathcal {M}})\) of the vertical vectors that are tangent to the fibers of \({\mathcal {S}}\);
-
The pull-back bundles \(\pi : (i_*)^*(J_1({\mathcal {M}})) \rightarrow {\mathcal {S}}\) and \(\pi : (i_*)^*(V({\mathcal {M}})) \rightarrow {\mathcal {S}}\), representing the bundles of time-like and space-like vectors of the system when the system is in contact with the constraint \({\mathcal {S}}\);
-
The splitting \((i_*)^*(V({\mathcal {M}})) \, = \, i_*(V({\mathcal {S}}))\oplus V^{\perp }({\mathcal {S}})\) with its associated projection operators \({\mathcal {P}}_{V({\mathcal {S}})}, {\mathcal {P}}_{V({\mathcal {S}})}^{\perp }\) induced by the vertical metric \(\Phi \) and the splitting \((i_*)^*(J_1({\mathcal {M}})) \, = \, i_*(J_1({\mathcal {S}})) \oplus V^{\perp }({\mathcal {S}})\) with its associated projection operators \({\mathcal {P}}_{J_1({\mathcal {S}})}, {\mathcal {P}}^{\perp }_{J_1({\mathcal {S}})}\);
-
The set \({\mathcal {H}}_{{\mathcal {S}}}\) of the rest frames of \({\mathcal {S}}\), that is those frames \(\mathbf{h}_{{\mathcal {S}}}\) of \({\mathcal {M}}\) such that \(\left( \mathbf{h}_{{\mathcal {S}}}\right) _{\rfloor _{{\mathcal {S}}}}\) is tangent to \({\mathcal {S}}\).
Some comments are in order to apply these structures in the context of impulsive mechanics.
Heuristically, the pull-back bundle \((i_*)^*(J_1({\mathcal {M}}))\) is formed by the absolute velocities of the system \(\mathbf{p} \in J_1({\mathcal {M}})\) applied in points of \({\mathcal {S}}\) but not necessarily tangent to \({\mathcal {S}}\): then \((i_*)^*(J_1({\mathcal {M}}))\) is the natural geometric framework fit to analyze the behavior of \({\mathcal {S}}\) viewed as a unilateral positional constraint. Since the system is always supposed in contact with the constraint, focussing mainly on the fibers of the bundles, later on we make the identifications \(i_*(J_1({\mathcal {S}})) \simeq J_1({\mathcal {S}})\), \(i_*(V({\mathcal {S}})) \simeq V({\mathcal {S}})\), and the identifications \((i_*)^*(J_1({\mathcal {M}})) \simeq J_1({\mathcal {M}})\), \((i_*)^*(V({\mathcal {M}})) \simeq V({\mathcal {M}})\) (even though these last identify bundles that are structurally different since they have different base manifolds).
Given an absolute velocity \(\mathbf{p} \in J_1({\mathcal {M}})\) of the system in contact with \({\mathcal {S}}\), the vertical vector \(\mathbf{V}^{\perp }_{{\mathcal {S}}}(\mathbf{p}) \, = \, {\mathcal {P}}^{\perp }_{J_1({\mathcal {S}})}(\mathbf{p})\) assumes the “frame invariant” meaning of orthogonal component of the absolute velocity \(\mathbf{p}\) with respect to \({\mathcal {S}}\). We recall, however, that the concept of tangent component of \(\mathbf{p}\) with respect to \({\mathcal {S}}\) has not a frame invariant meaning (see Pasquero 2005).
A positional constraint \({\mathcal {S}}\) is called unilateral if two sets \(\lambda ({\mathcal {S}}) \subset J_1({\mathcal {M}})\) and \(\rho ({\mathcal {S}})\subset J_1({\mathcal {M}})\) are assigned so that \(J_1({\mathcal {M}})\) can be written as the disjoint union
The set \({\mathcal {L}}_{{\mathcal {S}}}(J_1({\mathcal {M}})) \, = \, \lambda ({\mathcal {S}})\cup J_1({\mathcal {S}})\) is the set of the admissible left velocities (or incoming or entrance velocities) for the system (in contact with \({\mathcal {S}}\)). The set \(R_{{\mathcal {S}}}(J_1({\mathcal {M}})) \, = \, J_1({\mathcal {S}})\cup \rho ({\mathcal {S}})\) is the set of the admissible right velocities (or outgoing or exit velocities. See Pasquero 2018). The system with absolute velocity \(\mathbf{p}\) has an impact with the constraint \({\mathcal {S}}\) if and only if \(\mathbf{p} \in \lambda ({\mathcal {S}})\).
If \(codim({\mathcal {S}})=1\), then \({\mathcal {S}}\) has a natural structure of unilateral constraint. Since \(J_1({\mathcal {M}})\, = \, J_1({\mathcal {S}})\otimes V^{\perp }({\mathcal {S}})\) with \(V^{\perp }({\mathcal {S}})\) of dimension 1, let \(\mathbf{U}^{\perp }_{{\mathcal {S}}}\) be such that \(V^{\perp }({\mathcal {S}}) \, = \, \mathrm{Lin}\{\mathbf{U}^{\perp }_{{\mathcal {S}}} \}\). Then, for instance, we can define
and of course we have \(J_1({\mathcal {S}})\, = \, \{ \mathbf{p} \in J_1({\mathcal {M}})\, | \, \Phi \left( \mathbf{V}^{\perp }_{{\mathcal {S}}}(\mathbf{p}) ,\mathbf{U}^{\perp }_{{\mathcal {S}}}\right) = 0 \}\). If \(F_{{\mathcal {S}}}(t, x^1, \ldots ,x^n) =0\) is a local Cartesian representation of \({\mathcal {S}}\), then (for a suitable choice of \(\mathbf{U}^{\perp }_{{\mathcal {S}}}\)) we have (see Pasquero 2018)
2.3 Multiple Positional Constraints
A multiple positional constraint \({\mathcal {S}}\) is the assignment of two (or possibly more) positional constraints \({\mathcal {S}}_1, {\mathcal {S}}_2\) satisfying
-
(i)
Both \({\mathcal {S}}_1, {\mathcal {S}}_2\) are of codimension 1;
-
(ii)
\({\mathcal {S}}\, = \, {\mathcal {S}}_1 \cap {\mathcal {S}}_2 \ne \emptyset \), and it is a regular subbundle of \({\mathcal {M}}\);
-
(iii)
if \(V^{\perp }({\mathcal {S}}_i) \, = \, Lin\{\mathbf{U}^{\perp }_{{\mathcal {S}}_i}\}_{\rfloor _{i=1,2}} \), then \(\mathbf{U}^{\perp }_{{\mathcal {S}}_1}, \mathbf{U}^{\perp }_{{\mathcal {S}}_2}\) are independent vectors.
The system has a (multiple) contact with \({\mathcal {S}}\) if its space-time configuration \(x\in {\mathcal {S}}\). Due to condition (iii) above, a multiple positional constraint can also be considered as unilateral. For instance, labeling for simplicity with the indexes 1, 2, 12 the objects relative to \({\mathcal {S}}_1, {\mathcal {S}}_2, {\mathcal {S}}\), respectively, we can set:
For every \(\mathbf{p} \in J_1({\mathcal {M}})\), we have then three different orthogonal velocities: \(\mathbf{V}^{\perp }_{12}(\mathbf{p}), \mathbf{V}^{\perp }_{1}(\mathbf{p}), \mathbf{V}^{\perp }_{2}(\mathbf{p})\). The following result clarifies the relation between these velocities.
Proposition 1
For every \(\mathbf{p} \in J_1({\mathcal {M}})\), we have that
-
i)
\(\mathbf{V}^{\perp }_{12}(\mathbf{p}) \, = \, \mathbf{V}^{\perp }_{i}(\mathbf{p}) \,\) if and only if \(\, \mathbf{V}^{\perp }_{j}(\mathbf{p}) \, = \, 0\) for \(i\ne j\);
-
ii)
\(\mathbf{V}^{\perp }_{12}(\mathbf{p}) \, = \, \mathbf{V}^{\perp }_{1}(\mathbf{p}) + \mathbf{V}^{\perp }_{2}(\mathbf{p}) \,\) if and only if \( \, \Phi ( \mathbf{V}^{\perp }_{1}(\mathbf{p}), \mathbf{V}^{\perp }_{2}(\mathbf{p})) \, = \, \Phi ( \mathbf{U}^{\perp }_{1}, \mathbf{U}^{\perp }_{2}) \, = \, 0\).
Proof
Since \(J_1({\mathcal {S}})\subset J_1({\mathcal {S}}_{\alpha }), \, \alpha =1,2\), we have \(V^{\perp }({\mathcal {S}}_{\alpha }) \subset V^{\perp }({\mathcal {S}}), \, \alpha = 1,2\). Then, due to the independence condition (iii) and the dimensions of the spaces, we have \(V^{\perp }({\mathcal {S}}) \, = \, V^{\perp }({\mathcal {S}}_1) \oplus V^{\perp }({\mathcal {S}}_2)\). In particular, for every \(\mathbf{p} \in J_1({\mathcal {M}})\) we have \(\mathbf{V}^{\perp }_{12}(\mathbf{p}) \, = \, \lambda \mathbf{V}^{\perp }_{1}(\mathbf{p}) + \mu \mathbf{V}^{\perp }_{2}(\mathbf{p})\). Moreover, we have that
with
Since \( {\mathcal {P}}_{12}(\mathbf{p}) = {\mathcal {P}}_{12}({\mathcal {P}}_{1}(\mathbf{p})) = {\mathcal {P}}_{12}({\mathcal {P}}_{2}(\mathbf{p})) \), we have that
Therefore, by orthogonality, we have \(\lambda = \mu = 1\) and so the first statement. About the second statement, we have that:
- “\(\Rightarrow \)”:
-
if \(\mathbf{V}^{\perp }_{12}(\mathbf{p}) \, = \, \mathbf{V}^{\perp }_{1}(\mathbf{p}) + \mathbf{V}^{\perp }_{2}(\mathbf{p})\), then \(\mathbf{V}^{\perp }_{12}({\mathcal {P}}_{1}(\mathbf{p}))\, = \, \mathbf{V}^{\perp }_{2}(\mathbf{p})\) and so \(\Phi ( \mathbf{V}^{\perp }_{1}(\mathbf{p}), \mathbf{V}^{\perp }_{2}(\mathbf{p})) \, = \, 0\).
- “\(\Leftarrow \)”:
-
if \(\Phi ( \mathbf{V}^{\perp }_{1}(\mathbf{p}), \mathbf{V}^{\perp }_{2}(\mathbf{p})) \, = \, 0\), then \(\mathbf{V}^{\perp }_{12}({\mathcal {P}}_{1}(\mathbf{p}))\, = \, \mu \mathbf{V}^{\perp }_{2}(\mathbf{p})\) and \(\mathbf{V}^{\perp }_{12}({\mathcal {P}}_{2}(\mathbf{p}))\, = \, \lambda \mathbf{V}^{\perp }_{1}(\mathbf{p})\), so that \(\lambda =\mu =1\) and \(\mathbf{V}^{\perp }_{12}(\mathbf{p}) \, = \, \mathbf{V}^{\perp }_{1}(\mathbf{p}) + \mathbf{V}^{\perp }_{2}(\mathbf{p})\).
\(\square \)
The absolute velocity \(\mathbf{p}\) determines a multiple impact if \(\mathbf{p} \in \lambda ({\mathcal {S}}_1)\) and \(\mathbf{p} \in \lambda ({\mathcal {S}}_2)\) (and of course it determines a single impact with multiple contact if the space–time configuration \(\pi (\mathbf{p})\in {\mathcal {S}}\) and \(\mathbf{p} \in \lambda ({\mathcal {S}}_1)\) “exor” \(\mathbf{p} \in \lambda ({\mathcal {S}}_2)\)).
3 Constitutive Characterizations of Impulsive Constraints
In the frame independent context of Lagrangian systems, a characterization for an impulsive constraint (not necessarily positional and/or of codimension 1) is a map \(\mathbf{I} : J_1({\mathcal {M}})\rightarrow {\mathcal {V}}({\mathcal {M}})\) assigning to every absolute (left) velocity \(\mathbf{p}_L\in J_1({\mathcal {M}})\) of the system in contact with the constraint a uniquely determined reactive impulse, that is a space-like vector \(\mathbf{I}(\mathbf{p}_L) \in V({\mathcal {M}})\). Once \(\mathbf{I}(\mathbf{p}_L)\) is known, an absolute (right) velocity \(\mathbf{p}_R\in J_1({\mathcal {M}})\) is determined by the rule \(\mathbf{p}_R\, = \, \mathbf{p}_L+ \mathbf{I}(\mathbf{p}_L)\) (see e.g., Pasquero 2018). Later on the constraints will be always considered as unilateral.
3.1 Single Constraints
The simplest case of positional constraint \({\mathcal {S}}\) with \(codim({\mathcal {S}})=1\) is emblematic: The only requirements of frame independence and ideality, in the form of conservation of kinetic energy for all the rest frames of \({\mathcal {S}}\), univocally determine the characterization as the “reflection rule” \(\mathbf{I}(\mathbf{p}_L) \, = \, -2 \, \mathbf{V}^{\perp }_{{\mathcal {S}}}(\mathbf{p}_L)\) (see Pasquero 2005). An analogous characterization turns out to be significant also in more complex cases, such as ideal constraints of \(codim({\mathcal {S}})>1\) or in presence of ideal kinetic constraints of both permanent or instantaneous kind (see Pasquero 2005, 2006). The introduction of a (Newtonian) COR \(\varepsilon \in [0,1]\) allows to generalize the “reflection rule” also in case of non-ideal frictionless constraints, in the form \(\mathbf{I}(\mathbf{p}_L) \, = \, -(1+\varepsilon ) \, \mathbf{V}^{\perp }_{{\mathcal {S}}}(\mathbf{p}_L)\) (see Pasquero 2008). Of course, the condition \(\varepsilon =1\) returns the case of ideal constraint, while the condition \(\varepsilon = 0\) gives in this case the totally inelastic impact, with the annihilation of the normal (with respect to \({{\mathcal {S}}}\)) component of the impact velocity and the maximum possible loss of kinetic energy of the system (with respect to every frame \(\mathbf{h}_{{\mathcal {S}}} \in {\mathcal {H}}_{{\mathcal {S}}}\)). Note, however, that this does not imply the rest of the system after the impact, since this concept has a clear meaning only if a frame of reference is fixed.
To give a physical meaning to the unilaterality of the constraint \({\mathcal {S}}\), the characterizations above must be detailed in the form (with \(\varepsilon \in [0,1]\))
This assignment naturally gives an outgoing right velocity \(\mathbf{p}_R\) starting from an incoming left velocity \(\mathbf{p}_L\).
3.2 Multiple Ideal Constraints
Due to the presence of three different orthogonal velocities, the same ideas are not analogously appropriate to model a multiple constraint \({\mathcal {S}}= {\mathcal {S}}_1 \cap {\mathcal {S}}_2\). Once again labeling for simplicity with the indexes 1, 2, 12 the objects relative to \({\mathcal {S}}_1, {\mathcal {S}}_2, {\mathcal {S}}\), respectively, the simplest rule \(\mathbf{I}(\mathbf{p}_L) \, = \, -2 \, \mathbf{V}^{\perp }_{12}(\mathbf{p}_L)\) does not take into account the multiple nature of the constraint, while a rule combining \(\mathbf{V}^{\perp }_{1}(\mathbf{p}_L)\) and \(\mathbf{V}^{\perp }_{2}(\mathbf{p}_L)\) must take into account several details, for instance:
-
The “incoming” nature of \(\mathbf{p}_L\), that could be incoming for \({\mathcal {S}}_1\) alone, or for \({\mathcal {S}}_2\) alone (in case of single impact), or for both (in case of multiple impact);
-
The symmetric or asymmetric behavior of the constraints \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) (that is if the two constraints have or not the same COR);
-
The verification of the outgoing nature of \(\mathbf{p}_R\).
An ideal characterization for multiple constraints \(\mathbf{p} \in \lambda ({\mathcal {S}}_1)\) and \(\mathbf{p} \in \lambda ({\mathcal {S}}_2)\). See Pasquero 2018) can be assigned on the basis of the rule
where the coefficient \(\beta \) is
Note that, since by Prop. (1) we have \(\beta = 1\) if \(\mathbf{V}^{\perp }_{1}(\mathbf{p}_L) =0 \) “exor” \(\mathbf{V}^{\perp }_{2}(\mathbf{p}_L) =0\), the rule restores the usual reflection law in case of single constraint. Moreover, the rule restores also the usual characterization \(\mathbf{I}(\mathbf{p}_L) \, = \, - \, 2 \, \mathbf{V}^{\perp }_{12}(\mathbf{p}_L)\) of single constraints of codimension greater than 1 (see Pasquero 2005) in case of orthogonality \(\Phi \left( \mathbf{V}^{\perp }_{1}(\mathbf{p}_L) , \mathbf{V}^{\perp }_{2}(\mathbf{p}_L) \right) \, = \, 0\). Thirdly, note that the coefficient \(\beta \) has a “kinematic” dependence on \(\mathbf{p}_L\), and not only a “geometric” dependence on \(\mathbf{U}^{\perp }_{1}, \mathbf{U}^{\perp }_{2}\).
However, even in case of single impact with multiple contact, the absolute velocity \(\mathbf{p}_L+ \mathbf{I}(\mathbf{p}_L)\) could be not an exit velocity, so that, in order to have an outgoing \(\mathbf{p}_R\), the evaluation of the reactive impulse could (possibly) be iterated starting from the new entrance velocity \(\mathbf{p}_L+ \mathbf{I}(\mathbf{p}_L)\) (see Pasquero 2018).
3.3 Symmetric Multiple Non-ideal Frictionless Constraints
The ideal characterization (5) allows, once a COR \(\varepsilon \) is assigned, a natural generalization in the form
Such a rule models the symmetric non-ideal behavior of the constraint \({\mathcal {S}}\): In fact the rule, handling symmetrically the two constraints, restores the usual non-ideal frictionless characterization in case of single impact for both the single impacts with \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\).
Once again the absolute velocity \(\mathbf{p}_L+ \mathbf{I}(\mathbf{p}_L)\) could be not an exit velocity, so that the evaluation of the reactive impulse could (possibly) be iterated.
In the next section, we will analyze the well-known system given by a simplified Newton’s cradle formed by three equal balls. This is an example of system subject to multiple contact and (iterated) single symmetric impact. The application of this rule in the case of a disk impacting with two equal walls forming a corner, that is a case of a system subject to multiple contact and multiple symmetric impact, is analyzed in details in Fassino and Pasquero (2019).
3.4 Asymmetric Multiple Non-ideal Frictionless Constraints
Both the characterizations (5, 6) can be generalized, once two possibly different CORs \(\varepsilon _1, \varepsilon _2\) for \({\mathcal {S}}_1, {\mathcal {S}}_2\), respectively, are assigned in the form
Such a rule models the asymmetric non-ideal behavior of the constraint \({\mathcal {S}}\). The rule restores the usual non-ideal frictionless characterization in case of single impact with CORs \(\varepsilon _i\) for the single impacts with \({\mathcal {S}}_i\). Moreover, it restores the previous characterization (6) in the case \(\varepsilon _1 = \varepsilon _2\) and the ideal one (5) for \(\varepsilon _1 = \varepsilon _2 = 1\). Once more, however, the absolute velocity \(\mathbf{p}_L+ \mathbf{I}(\mathbf{p}_L)\) thus obtained could be not an exit velocity and the evaluation of the reactive impulse could (possibly) be iterated.
The application of this rule to the case of a disk impacting with two walls (having different CORs) forming a corner is analyzed in details in the next section.
3.5 Remarks on the Characterizations
The (iterative) line of reasoning traced above to assign the right velocity \(\mathbf{p}_R\) starting from a left velocity \(\mathbf{p}_L\) can be formalized also for a multiple constraint \({\mathcal {S}}\, = \, \bigcap _{i=1}^r \, {\mathcal {S}}_i\) formed by \(2\le r < n\) single constraints with the following step by step procedure. Given a left velocity \(\mathbf{p}_L^0 \in J_1({\mathcal {M}})\) and the CORs \(\varepsilon _1, \ldots , \varepsilon _r \in [0,1]\):
-
a)
Select the set of “contact” indexes \(\{i_1, \ldots , i_k\} \subset \{ 1, \ldots , r\}\) such that the configuration \(\pi (\mathbf{p}_L^0) \in {\mathcal {M}}\) is such that \(\pi (\mathbf{p}_L^0) \in {\mathcal {S}}_{i_m} \, \forall \, m=1, \ldots , k\). If \(\{i_1, \ldots , i_k\} = \emptyset \) then let \(\mathbf{p}_R:= \mathbf{p}_L^0\) (the system is not in contact with the constraint). Otherwise
-
b)
Select the set of “impact” indexes \(\{j_1, \ldots , j_h\} \subset \{i_1, \ldots , i_k\}\) such that the orthogonal velocities \(\mathbf{V}^{\perp }_{j_q}(\mathbf{p}_L^0)\) are such that \((\mathbf {p}_L^0 \in \lambda ({\mathcal {S}}_{j_q}) \, \forall \, q=1, \ldots , h)\);
-
c)
If \(h\ge 2\), calculate the “global” orthogonal velocity \(\mathbf{V}^{\perp }_{j_1 \ldots j_h}\) and the corresponding coefficient
$$\begin{aligned} \beta = \dfrac{\Phi \left( \mathbf{V}^{\perp }_{j_1 \ldots j_h} , \mathbf{V}^{\perp }_{j_1} + \cdots + \mathbf{V}^{\perp }_{j_h}\right) }{\Vert \mathbf{V}^{\perp }_{j_1} + \cdots + \mathbf{V}^{\perp }_{j_h}\Vert ^2 } \, ; \end{aligned}$$ -
d)
Calculate
$$\begin{aligned} \mathbf{I}(\mathbf{p}_L^0) = \left\{ \begin{array}{ll} - \beta \displaystyle \sum _{q=1}^{h} (1+\varepsilon _{j_q}) \, \mathbf{V}^{\perp }_{j_q}(\mathbf{p}_L^0) &{}\quad \text {if} \,\,\, h\ge 2 \\ \\ - (1+\varepsilon _{j_1}) \, \mathbf{V}^{\perp }_{j_1}(\mathbf{p}_L^0) &{}\quad \text {if} \,\,\, h = 1 \\ \\ 0 &{}\quad \text {if} \,\,\, \{j_1, \ldots , j_h\} \, = \, \emptyset ; \end{array} \right. \end{aligned}$$(8) -
e)
Calculate \(\mathbf{p}_L^1 := \mathbf{p}_L^{0} + \mathbf{I}(\mathbf{p}_L^{0})\). If \(\mathbf{p}_L^1 = \mathbf{p}_L^{0}\) then let \(\mathbf{p}_R:= \mathbf{p}_L^0\), otherwise iterate the procedure restarting from b) to obtain a sequence \(\mathbf{p}_L^w := \mathbf{p}_L^{w-1} + \mathbf{I}(\mathbf{p}_L^{w-1})\);
-
f)
If and when \(\mathbf{p}_L^w \, = \, \mathbf{p}_L^{w+1}\), then let \(\mathbf{p}_R:= \mathbf{p}_L^w\).
4 Examples
4.1 Example 1. The Simplified Newton Cradle
Three equal disks of radius R and unitary mass can move in a plane. Labeling the disks with the numbers 1, 2, 3, the space–time configuration is described by 10 coordinates \((t, x^i, y^i, \vartheta ^i), i=1,\ldots ,3\) where \((x^i,y^i)\) are the coordinates of the center of the ith disk and \(\vartheta ^i\) is its orientation. The set of constraints is given (with obvious notation) by the functions
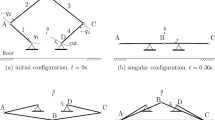
We consider the particular case when disks 2 and 3 are at rest and in contact, while disk 1 moves in the straight line direction given by the centers of 2 and 3 and collides with disk 2 (see the upper part of Fig. 1), so that at the impact instant we have \(x^2 - x^1 = x^3 - x^2 =2R\) and \(y^j - y^i =0, \, \forall \, i,j =1,\ldots ,3\). Then the positional constraints involved in the impact are \(S_{(1,2)}\) and \(S_{(2,3)}\), and the system is subject to multiple contact.
Starting with left velocity \({\mathbf{p}}^0_L = \frac{\partial }{\partial t} + {v_0} \frac{\partial }{\partial x^1}\) with \({v_0} >0\), it is easy to show that, due to the nature of the constraints involved in the impact, all the velocities evaluated by the theoretical algorithm do not have components in the \(\frac{\partial }{\partial y^i}\) directions. Moreover, due to the absence of friction between the disks, a possible initial spin \({\omega _0} \, \frac{\partial }{\partial \vartheta ^1}\) of disk 1 (or even disks 2 and 3) does not have significant effect on the impact. (It will be found unchanged in the final result of the algorithm.) Then the system has only \((t,x^1,x^2,x^3)\) as significant coordinates, the terms \({\dot{x}}^i\) of the velocity \((\mathbf {p} = \frac{\partial }{\partial t} + \, \dot{x}^i \frac{\partial }{\partial x^i})\) represents the horizontal component of the velocity of the ith disk, and the impact conditions could be easily checked in the form \({\dot{x}}^{r+1} - {\dot{x}}^r < 0\) for some \(r=1,2\). Anyway, recalling (2), we have
so that the velocity \({\mathbf{p}}^0_L\) is an incoming velocity only for the constraints \({\mathcal {S}}_{(1,2)}\), and the system is subject to a single impact. The standard calculation of \(\mathbf{V}^{\perp }_{(1,2)}({\mathbf{p}}_L)\) gives
Applying the (first step of the iterative) method described in the previous section, the “new” left velocity is
and we have to determine the nature of the new left velocity \({\mathbf{p}}^1_L\) with respect to the set of constraints. We have:
so that the new left velocity is an outgoing velocity for \(S_{(1,2)}\) and an incoming velocity for \(S_{(2,3)}\). Once again, the system is subject to a single impact. The standard calculation of \(\mathbf{V}^{\perp }_{(2,3)}({\mathbf{p}}^1_L)\) gives
from which we obtain the “new” left velocity
and we have to restart. We have:
Then, \({\mathbf{p}}^2_L\) in an exit velocity for the system if and only if \(\varepsilon =1\). Otherwise, \({\mathbf{p}}^2_L\) is an outgoing velocity for \(S_{(2,3)}\), but it is once again an incoming velocity for \(S_{(1,2)}\). This “second impact” between disks 1 and 2 is a significant difference with respect to the behavior of the ideal Newton’s cradle (see Pasquero 2018).
Further iterations of the algorithm then present different possibilities depending on the value of \(\varepsilon \): the next step gives
that is an exit velocity for the system if and only if \(\varepsilon \ge 3 - 2\sqrt{2} \simeq 0,17157\); otherwise, we have a “second impact” between disks 2 and 3 and the procedure must be further iterated.
With the intent to exit from a completely theoretical presentation (similar to that of Pasquero (2018)) of the characterization (6) applied to the Newton’s cradle with three equal balls with initial velocity \({\mathbf{p}}^0_L \, = \, \frac{\partial }{\partial t} \, + \, {v_0} \, \frac{\partial }{\partial x^1}\), the algorithm for the determination of the exit velocity of the system has been implemented using the software PariGP (The PARI Group (2019). The PariGP implementation of the algorithm for the simplified Newton’s cradle is available as Electronic Supplementary Material). In order to avoid to delve into the technicalities of the robustness of the algorithm (such as in Fassino and Pasquero 2019), the termination was ensured by fixing a maximum number \(N=10^4\) of iterations and a minimum threshold \(\sigma = 10^{-9}\Vert v_0\Vert \) for the differences of the velocities of the three disks. Moreover, a test checking the possible presence of multiple impacts was included, always giving negative result for these initial data.
Since the term \(v_0\) can be factored in the output velocity, Table 1 lists the output of the algorithm (the last rows rounded to the tenth significant digit) for the fixed value \(v_0 = 100\) and for different CORs \(\varepsilon \). The data show a meaningful physical behavior of the system. For instance, the number of iterations increases for decreasing CORs, and the exit velocities of the three disks are increasingly similar for decreasing CORs. In particular, the acronym AEEV in the last three rows stands for “Almost Equal Exit Velocities” followed by the number of iterations before checking the almost equalities of the velocities of the disks (note in fact that the impact conditions \({\dot{x}}^{r+1} - {\dot{x}}^r < 0\) for some \(r=1,2\) is still verified).
The lower part of Fig. 1 illustrates the behavior of the system after the impact for the three cases \(\varepsilon = 0.9,\varepsilon = 0.5,\varepsilon = 0.1\).
4.2 Example 2. The Disk in the Corner
A rigid disk of radius R and unitary mass moves in the part of a horizontal plane delimited by two walls \({\mathcal {S}}_1, {\mathcal {S}}_2\) forming an angle \(2\alpha \in (0, \pi )\). The system can be described using local coordinates \((t,x,y,\vartheta )\) where x, y are the coordinates of the center of the disk and \(\vartheta \) is the orientation of the disk. If \(k = \tan \alpha > 0\), the walls can be described by the Cartesian relations \({\mathcal {S}}_1: kx-y=0, \, {\mathcal {S}}_2: kx+y=0\). We assume that the disk is in contact with both the walls, so that \((x,y)=(-\frac{R}{\sin \alpha },0)\) (see Fig. 2).
Given an absolute velocity \( {\mathbf{p}} \, = \, \frac{\partial }{\partial t} \, + \, {\dot{x}} \, \frac{\partial }{\partial x} \, + \, {\dot{y}} \, \frac{\partial }{\partial y} \, + \, {\dot{\vartheta }} \, \frac{\partial }{\partial \vartheta }\), we have
with corresponding coefficient \(\beta \, = \, \dfrac{1+k^2}{2} \, \dfrac{k^2 {\dot{x}}^2 + {\dot{y}}^2}{k^4 {\dot{x}}^2 + {\dot{y}}^2}\).
In analogy with Fassino and Pasquero (2019), we divide the space of absolute velocities of the system into four different zones \({\mathcal {Z}}_0, {\mathcal {Z}}_1, {\mathcal {Z}}_2, {\mathcal {Z}}_{12}\) with \(\mathbf{p} \in {\mathcal {Z}}_i\) if it determines an impact with \({\mathcal {S}}_i\). Taking into account (3), we have
Once the CORs \(\varepsilon _1, \varepsilon _2\) of \({\mathcal {S}}_1, {\mathcal {S}}_2\), respectively, and an initial velocity
are assigned (once again the component of the velocity in the direction \(\frac{\partial }{\partial \vartheta }\) is irrelevant), the asymmetric constitutive characterization (3.4) is synthesized by the iterative rule
Once again with the intent to exit from a completely theoretical presentation, the algorithm for the determination of the exit velocity of the disk from the angle has been implemented using the software PariGP. (The PariGP implementation of the algorithm for the disk in the corner is available as Electronic Supplementary Material). Once again, the termination was ensured by fixing a maximum number \(N=10^4\) of iterations and a minimum threshold \(\sigma = 10^{-9}\Vert v_0\Vert \) (with \(v_0 = 100\)) for the norm of exit velocity of the disk. Moreover, since the coefficient \(\beta \) changes with the iterations of the algorithm, a test checking the possible excessive downsizing of the denominator of \(\beta \) was included.
The analysis of the output given by the implemented algorithm for different angles \(\alpha \), different impact angles \(\varphi \) and for different CORs \(\varepsilon _i\) shows that
-
The results in case of \(\varepsilon _1 \, = \, \varepsilon _2\) coincide with those presented in Fassino and Pasquero (2019) (up to the different rounding of the implementations of the algorithm);
-
The results present the correct symmetry with respect to the horizontal axis;
-
The results show natural behaviors of the system, such as decreasing norm of the final velocity for decreasing values of the CORs or an increasing number of iterations (i.e., “rebounds”) as the angle \(\alpha \) between the walls becomes narrower.
A very significant difference of the asymmetric case with respect to the behavior of the symmetric corner is about the possibility of repeated multiple impacts. In fact in the (symmetric) ideal case, the fact that the system can have a multiple impact no more than once is theoretically proved, and in the symmetric non-ideal case, although a theoretical result is not proved, the extensive numerical analysis performed supports the same result (see Fassino and Pasquero 2019). Differently, in the asymmetric non-ideal case the numerical analysis shows the presence of repeated multiple impacts when the CORs are very different. For example, this happens even in the simple case \(\alpha =\frac{\pi }{6}, \varphi =\frac{\alpha }{2}=\frac{\pi }{12}\), for \(\varepsilon _1=0.999, \varepsilon _2=0.001\).
Appendix (available as Electronic Supplementary Material) presents some (but very few) of the output data of the implementation of the algorithm (once again with the fixed value \(v_0 = 100\)), together with some visualizations of the exit velocity of the disk from the corner compared with the entrance velocity.
References
Brogliato, B.: Nonsmooth Impact Mechanics, Models, Dynamics and Control. Lecture Notes in Control and Inform, vol. 220. Springer, New York (1996)
Cortés, J., Vinogradov, A.M.: Hamiltonian theory of constrained impulsive motion. J. Math. Phys. 47(4), 042905 (2006)
Fassino, C., Pasquero, S.: An algorithmic approach to the multiple impact of a disk in a corner. Multidiscip. Model. Mater. Struct. 16(3), 476–500 (2019)
Ibort, A., De Leon, M., et al.: Geometric formulation of mechanical systems subjected to time-dependent one-sided constraints. J. Phys. A: Math. Gen. 31, 2655–2674 (1998)
Johnson, K.L.: Contact Mechanics. Cambridge University Press, Cambridge (1985)
Liu, Caishan, Zhao, Zhen, Brogliato, Bernard: Frictionless multiple impacts in multibody systems. i. theoretical framework. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 464, pp. 3193–3211. The Royal Society (2008)
Liu, C., Zhao, Z., Brogliato, B.: Frictionless multiple impacts in multibody systems. ii. numerical algorithm and simulation results. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 465, pp. 1–23. The Royal Society (2009)
Massa, E., Pagani, E.: Classical dynamics of non-holonomic systems: a geometric approach. Ann. Inst. H. Poincarè 55, 511–544 (1991)
Pasquero, S.: Ideal characterizations of multiple impacts: A frame-independent approach by means of jet-bundle geometry. Q. Appl. Math. 76(3), 547–576 (2018)
Pasquero, S.: Ideality criterion for unilateral constraints in time-dependent impulsive mechanics. J. Math. Phys. 46(11), 112904–112920 (2005)
Pasquero, S.: On the simultaneous presence of unilateral and kinetic constraints in time-dependent impulsive mechanics. J. Math. Phys. 47(8), 082903 (2006). 19 pp
Pasquero, S.: Nonideal unilateral constraints in time-dependent impulsive mechanics: a geometric approach. J. Math. Phys. 49(4), 042902 (2008). 17 pp
Pasquero, S.: Framing the bases of impulsive mechanics of constrained systems into a jet-bundle geometric context. Riv. Mat. Univ. Parma 9, 227–254 (2018)
Pommaret, J.F.: Lie Pseudogroups and Mechanics, vol. 16. CRC Press, Florida (1988)
Saracco, A.: Dr. Strangelove or: how i learned to stop worrying and love the citations (2020). arXiv e-print arXiv:2002.09371
Stronge, W.J.: Impact Mechanics. Cambridge University Press, Cambridge (2000)
The PARI Group, PARI/GP version 2.11.2, Univ. Bordeaux (2019). http://pari.math.u-bordeaux.fr/
Acknowledgements
The author is very grateful to Prof. Alessandro Languasco of the University of Padova (Italy) for his valuable help in the use of the software PariGP to implement the algorithms for the analysis of the examples. Moreover, the author would like to thank Dr. Claudia Fassino of the University of Genova (Italy) for her help in the preparation of the figures about Example 2 presented in the Appendix.
Funding
Open access funding provided by Universitá degli Studi di Parma within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pasquero, S. Symmetric and Asymmetric Multiple Impulsive Constraints Without Friction and Their Characterization. J Nonlinear Sci 31, 61 (2021). https://doi.org/10.1007/s00332-021-09718-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00332-021-09718-0