Abstract
In this paper, we investigate the influence of the bulk Dzyaloshinskii–Moriya interaction on the magnetic properties of composite ferromagnetic materials with highly oscillating heterogeneities, in the framework of \(\Gamma \)-convergence and 2-scale convergence. The homogeneous energy functional resulting from our analysis provides an effective description of most of the magnetic composites of interest nowadays. Although our study covers more general scenarios than the micromagnetic one, it builds on the phenomenological considerations of Dzyaloshinskii on the existence of helicoidal textures, as a result of possible instabilities of ferromagnetic structures under small relativistic spin–lattice or spin–spin interactions. In particular, we provide the first quantitative counterpart to Dzyaloshinskii’s predictions on helical structures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Composite ferromagnetic materials are the subject of growing interest, as they often display unusual properties which turn out to be strikingly different from the corresponding ones of their constituents. For this reason, it is possible to engineer ferromagnetic composites exhibiting physical and chemical behaviors which rarely, if ever, emerge in bulk materials (Milton 2009).
A systematic study of composite materials, and more generally of media with microstructures, is the primary source of inspiration for the mathematical theory of homogenization. The theory aims at a description of composite materials with highly oscillating heterogeneities, through a simplified homogeneous model whose material-dependent properties are now related to specific averages of the physical and geometrical parameters of the constituents (cf., e.g., Braides and Defranceschi 1998; Bensoussan et al. 2016). The origins of homogenization in micromagnetics date back to 1824, when Poisson, in his Mémoire sur la théorie du magnétisme (Poisson 1824), laid the foundations of the theory of induced magnetism, proposing a model in which a ferromagnet is composed of conducting spheres embedded in a non-conducting material.
The homogenization analysis performed in our paper is motivated by recent technological advances in the field of spintronics, first and foremost, by the observation, in magnetic systems lacking inversion symmetry, of chiral spin textures known as magnetic skyrmions (Ferriani et al. 2007; Bogdanov and Hubert 1999), whose origin is ascribed to the Dzyaloshinskii–Moriya interaction (DMI) (Dzyaloshinsky 1958; Fields 1956). We refer to Melcher (2014), Muratov and Slastikov (2017), as well as Li and Melcher (2018) and the references therein, for a mathematical analysis of micromagnetic models including DMI [see also (Cicalese and Solombrino 2015; Cicalese et al. 2016; Cicalese 2019) for a study of effective theories and chirality transitions in the discrete-to-continuous setting, and Hrkac et al. (2019) for recent results on the numerics of chiral magnets]. More precisely, our work builds on Dzyaloshinskii’s observations in Dzyaloshinskii (1964), Dzyaloshinskii (1965) where, based on the Landau theory of second-order phase transitions, the emergence of helicoidal structures is predicted (see also Bak and Jensen 1980). According to Dzyaloshinskii, the appearance of these textures is the result of possible instabilities of the ferromagnetic structure created by relativistic spin–lattice or spin–spin forces, or by a sharp anisotropy in the exchange interaction. The results of our paper, based on the continuum theory of micromagnetics, make Dzyaloshinskii predictions quantitative (cf. Theorem 1.2).
From the mathematical point of view, magnetic skyrmions emerge as topological defects in the magnetization texture that carry a specific topological charge, also referred to as the skyrmion (winding) number. If \(\mathcal {H}\) is a compact smooth hypersurface of \({\mathbb {R}}^{n + 1}\) and \(m : \mathcal {H} \rightarrow \mathbb {S}^n\) is a sufficiently smooth vector field on \(\mathcal {H}\), the skyrmion number of m is defined by the Kronecker integral (Nagaosa and Tokura 2013)
with \(\omega _n (x) := \sum _{j = 1}^n (- 1)^{j - 1} x_j \mathrm{d}x_1 \wedge \ldots \wedge \widehat{\mathrm{d}x_j} \wedge \ldots \wedge \mathrm{d}x_n\) the volume form on \(\mathbb {S}^n\), and \(m^{*} \omega _n\) the pull-back of \(\omega _n\) by m on \(\mathcal {H}\). In local coordinates \(x := (x_1, \ldots , x_n)\) this gives:
According to Hadamard (Outerelo and Ruiz 2009), \(N_{\mathrm{sk}} (m)\) is always an integer number and coincides with the topological degree of m. By Hopf’s theorem (Milnor 1965), skyrmions with different topological charges belong to different homotopy classes and, therefore, from the physical point of view, skyrmions are expected to be topologically protected against external perturbations and thermal fluctuations (Cortés-Ortuño et al. 2017).
Since their discovery, magnetic skyrmions have been the object of intense research work in condensed matter physics. Their stability, the reduced size, and the small current densities sufficient to control them make skyrmions extremely attractive for applications in modern spintronics (Fert 2008; Fert et al. 2013; Kang et al. 2016).
In this paper, in the framework of \(\Gamma \)-convergence and 2-scale convergence, we investigate the influence of the bulk Dzyaloshinskii–Moriya interaction (Dzyaloshinsky 1958; Fields 1956) on the magnetic properties of composite ferromagnetic materials with highly oscillating heterogeneities. The homogeneous energy functional resulting from our analysis provides an effective description of most of the magnetic composites of interest nowadays. Indeed, although the homogenized coefficients of the limiting energy functional involve the solution of a system of PDEs, chiral multilayers are essentially one-dimensional structures, and this allows us for a complete characterization of the minimal configurations and their topological degree, at least under some simplified hypotheses on the distribution of the constituents. Precisely, we show that depending on the effective DMI constant of the homogeneous model, two Bloch-type chiral skyrmions with opposite topological charges can arise. Our results provide a solid ground to the experimental observations that ground states with a non-trivial topological degree do exist here in a stable state (Yu et al. 2010; Fert et al. 2017; Chen et al. 2017) (see Remark 3.1).
To describe our main contributions, we first collect below some preliminary notation and results. Readers who are already acquainted with the theory of micromagnetics might skip the following two subsections and proceed directly with the statement of the main results in Sect. 1.3.
1.1 The Micromagnetic Theory of (Single-Crystal) Chiral Magnets
In the continuum theory of micromagnetism (Brown 1963; Hubert and Schäfer 2008), which dates back to the seminal work of Landau–Lifshitz (Landau and Lifshitz 2012) on fine ferromagnetic particles, the observable states of a rigid ferromagnetic body, filling a region \(\Omega \subseteq {\mathbb {R}}^3\), are described by the magnetization \(M : \Omega \rightarrow {\mathbb {R}}^3\), a vector field subject to the fundamental constraint of micromagnetism: the existence of a material-dependent constant \(M_s\) such that \(| M | =M_s\) in \(\Omega \). For single-crystal ferromagnets (cf. Acerbi et al. 2006; Alouges and Di Fratta 2015), the saturation magnetization \(M_s := M_s (T)\) depends only on the temperature T and vanishes above a critical value \(T_c\), characteristic of each crystal type, known as the Curie temperature. When the specimen is at a fixed temperature well below \(T_c\), the function \(M_s\) is constant in \(\Omega \) and the magnetization takes the form \(M := M_s m\), where \(m : \Omega \rightarrow \mathbb {S}^2\) is a vector field with values in the unit sphere of \({\mathbb {R}}^3\) (cf. Brown 1963; Hubert and Schäfer 2008).
Although the length of m is constant in space, this is, in general, not the case for its direction, and the observable states of the magnetization result as the local minimizers of the micromagnetic energy functional, which, for non-centrosymmetric (chiral) magnets, reads as
for every \(m \in H^1( \Omega , {\mathbb {R}}^3 )\), \(m (x) \in \mathbb {S}^2\) a.e. in \(\Omega ,\) where \(m \chi _{\Omega }\) denotes the extension by zero of m to the whole space.
The exchange energy\(\mathcal {E}_{\Omega }\) penalizes spatial variations of the magnetization. The quantity \(a_{\mathrm{ex}} > 0\) represents a phenomenological (material-dependent) constant that summarizes the effect of short-range exchange interactions.
The second term, \(\mathcal {K}_{\Omega } (m)\), represents the bulk Dzyaloshinskii–Moriya interaction (DMI) and accounts for possible lacks of inversion symmetry in the crystal structure of the magnetic material. The material-dependent constant \(\kappa \in {\mathbb {R}}\) is the bulk DMI constant; its sign affects the chirality of the ferromagnetic system (Thiaville et al. 2012; Sampaio et al. 2013).
The third term, \(\mathcal {W}_{\Omega }\), is the magnetostatic self-energy, that is, the energy due to the demagnetizing (or stray) field \(\varvec{h}_{\mathsf {{\mathrm{d}}}}\) generated by m. The stray field \(- \varvec{h}_{\mathsf {{\mathrm{d}}}} [ M_s m \chi _{\Omega } ]\) is characterized as the projection of \(m \chi _{\Omega } \in L^2( {\mathbb {R}}^3, {\mathbb {R}}^3 )\) on the closed subspace of gradient vector fields
The physical constant \(\mu _0\) denotes the vacuum permeability.
The competition among the contributions in (3) explains most of the striking pictures of the magnetization observable in ferromagnetic materials (Hubert and Schäfer 2008), in particular, the emergence of chiral spin textures with a non-trivial topological degree, i.e., magnetic skyrmions (Fert et al. 2013, 2017).
We note that, usually, the micromagnetic energy includes two additional energy contributions: the magnetocrystalline anisotropy energy\(\mathcal {A}_{\Omega }\) and the Zeeman energy\(\mathcal {Z}_{\Omega }\):
The energy density \(\varphi _{\mathrm{an}} : \mathbb {S}^2 \rightarrow {\mathbb {R}}_+\) accounts for the existence of preferred directions of the magnetization: It vanishes on a finite set of directions, called easy axes, that depend on the crystallographic structure of the material. Instead, \(\mathcal {Z}_{\Omega }\) models the tendency of a specimen to have the magnetization aligned with the external applied field \(\varvec{h}_a \in L^2 ( \Omega , {\mathbb {R}}^3 )\), assumed to be unaffected by variations of m. Although both \(\mathcal {A}_{\Omega }\) and \(\mathcal {Z}_{\Omega }\) are of fundamental importance in ferromagnetism, in a homogenization setting, they behave like \(\Gamma \)-continuous perturbations, and their analysis has already been performed in Alouges and Di Fratta (2015). Therefore, to shorten notation, they will be neglected in our investigation.
1.2 The Micromagnetic Theory of Periodic Chiral Magnets
When considering a ferromagnetic body composed of several magnetic materials, the material-dependent parameters \(a_{\mathrm{ex}}\), \(\kappa \), \(M_s\), are no longer constant in the region \(\Omega \) occupied by the ferromagnet. Moreover, one has to describe the local interactions of two grains with different magnetic properties at their touching interface (Acerbi et al. 2006). There are different ways to take into accounts interfacial effects, and we will follow the approach of Alouges and Di Fratta (2015), Alouges et al. (2019): We will assume a strong coupling condition, meaning that the direction m of the magnetization does not jump through an interface, and only the magnitude \(M_s\) is allowed to be discontinuous. This assumption allows for the analysis of the homogenized problem under the standard requirement that the magnetization direction m is in \(H^1 (\Omega , \mathbb {S}^2)\), i.e., that m belongs to the topological subspace of \(H^1 (\Omega , {\mathbb {R}}^3)\) consisting of vector-valued functions taking values on \(\mathbb {S}^2\).
The previous considerations lead to consider, for every \(\varepsilon > 0\), the family of energy functionals
where the exchange constant \(a_{\mathrm{ex}}\), the DMI constant \(\kappa \), and the saturation magnetization \(M_s\) are now replaced by \(Q\)-periodic functions in \({\mathbb {R}}^3\) of period \(Q:= (0, 1)^3\), and where \(a_{\varepsilon } (x) := a_{\mathrm{ex}} (x / \varepsilon )\), \(\kappa _{\varepsilon } (x) := \kappa (x / \varepsilon )\), \(M_{\varepsilon } (x) := M_s (x / \varepsilon )\) for almost every \(x \in {\mathbb {R}}^3\).
Note that, \(a_{\varepsilon }\), \(\kappa _{\varepsilon }\), and \(M_{\varepsilon }\) are \(\varepsilon \)-periodic functions that describe the oscillations of the material-dependent parameters of the composite. The main object of this paper is the asymptotic \(\Gamma \)-convergence analysis of the family of functionals \(\left( \mathcal {F}_{\varepsilon } \right) _{\varepsilon \in {\mathbb {R}}_+}\) in the highly oscillating regime, i.e., when \(\varepsilon \rightarrow 0\).
1.3 State of the Art
Although the periodic homogenization of Dirichlet-type energies has been the focus of several studies (see, e.g., Sanchez-Palencia 1974; Marcellini 1978; Allaire 1992), it is only recently that the analysis has been extended to the case of manifold-valued Sobolev spaces by means of \(\Gamma \)-convergence techniques (Dacorogna et al. 1999; Babadjian and Millot 2009). In Babadjian and Millot (2009), a general result is proven for Caratheodory integrands of the type \(f \left( x / \varepsilon , \nabla m \right) \), with f being \(Q\)-periodic in the first variable, and subject to classical growth conditions, and where \(m \in H^1 \left( \Omega , \mathcal {M} \right) \) is constrained to take values in a connected smooth submanifold \(\mathcal {M}\) of \({\mathbb {R}}^n\). Under these assumptions, it is shown that the behavior of \(f (x / \varepsilon , \nabla m)\) as \(\varepsilon \rightarrow 0\) can be described by a suitable tangentially homogenized energy density defined on the tangent bundle of \(\mathcal {M}\).
However, the analysis in Babadjian and Millot (2009) being purely local does not cover long-range interactions such as the magnetostatic ones; this motivated the work in Alouges and Di Fratta (2015) (recently generalized to the stochastic setting in Alouges et al. (2019)). Two main novelties were introduced therein:
- (1)
The identification of the \(\Gamma \)-limit of the family of magnetostatic self-energies \(\mathcal {W}_{\Omega }^{\varepsilon }\), and the proof that it constitutes a \(\Gamma \)-continuous perturbation of the micromagnetic energy functional.
- (2)
While the analysis of the exchange energy density was already covered by the general results in Babadjian and Millot (2009), the treatment of the manifold-valued constraint in Alouges and Di Fratta (2015), via 2-scale convergence, allowed to obtain the result in a more concise and direct way, however under a bothering convexity assumption on \(\mathcal {M}\) that in this paper we are going to remove.
For what concerns the statement in i., we recall the following result which we state here (without proof) in the slightly more general setting of a bounded, \(C^2\) orientable hypersurface \(\mathcal {M}\) of \({\mathbb {R}}^3\).
Proposition 1.1
(Prop. 4.4 in Alouges and Di Fratta (2015)) The family of magnetostatic self-energies \(\left( \mathcal {W}_{\Omega }^{\varepsilon } \right) _{\varepsilon \in {\mathbb {R}}_+}\ \Gamma \)-continuously converges in \({\mathbb {R}}_+ \times L^2 \left( \Omega , \mathcal {M} \right) \) to the functional
where for almost every \(x \in \Omega \) the scalar potential \(v_m (x, \cdot )\) is the unique solution in \(H^1_{\sharp } \left( Q\right) \) of the cell problem \(\Delta _y v_m (x, y) = m (x) \cdot \nabla _y M_s (y)\).
In particular, this guarantees that \(\mathcal {W}_{\Omega }^{\varepsilon }\) can be treated as a continuous perturbation [cf. (Dal Maso 1993, Prop. 6.20, p. 62)]. Namely, \(\Gamma \text {-} \lim _{\varepsilon \rightarrow 0} \mathcal {F}_{\varepsilon } = \Gamma \text {-} \lim _{\varepsilon \rightarrow 0} \left( \mathcal {E}^{\varepsilon }_{\Omega } +\mathcal {K}_{\Omega }^{\varepsilon } \right) +\mathcal {W}_0\). For this reason, in the sequel, our analysis will be focused on the family
Regarding point ii., we observe that the energy densities in \(\left( \mathcal {E}^{\varepsilon }_{\Omega } +\mathcal {K}_{\Omega }^{\varepsilon } \right) _{\varepsilon \in {\mathbb {R}}_+}\) explicitly depend on m and cannot be expressed in the form \(f (x / \varepsilon , \nabla m)\) for some Caratheodory integrand f fitting the analysis in Babadjian and Millot (2009).
1.4 Contribution of the Present Work
Moving beyond (Babadjian and Millot 2009) and departing from the observations in Alouges and Di Fratta (2015), our analysis tackles the more general setting of periodic chiral magnets, that is, composite chiral magnets in which the heterogeneities are evenly distributed inside the media.
The contribution of the present work is threefold, and it goes both in the mathematical direction of advancing the theory of homogenization in manifold-valued Sobolev spaces, and in the modellistic direction of studying skyrmions in composite materials. First, we provide a characterization of the asymptotic behavior of the energy functionals \(\left( \mathcal {G}_{\varepsilon }\right) _{\varepsilon \in {\mathbb {R}}_+}\) (see (7)) in terms of \(\Gamma \)-convergence in the weak \(H^1 \left( \Omega , \mathcal {M} \right) \)-topology. Our homogenization result reads as follows (see Proposition 2.1 and Theorem 2.1).
Theorem 1.1
Let \(\mathcal {M}\) be a bounded, \(C^2\) orientable hypersurface of \({\mathbb {R}}^3\) that admits a tubular neighborhood of uniform thickness. Then, the family \(\left( \mathcal {G}_{\varepsilon }\right) _{\varepsilon \in {\mathbb {R}}_+} \ \Gamma \)-converges with respect to the weak topology in \(H^1 ( \Omega , \mathcal {M})\), to the energy functional
for every \(m \in H^1 \left( \Omega , \mathcal {M} \right) \), where \(\varvec{\chi }\) is the map
and \(\phi [ m, \nabla ^{\mathsf {T}} m ]\) is the unique solution of the cell problem described in Proposition 2.1.
We point out that the range of surfaces included in our study is quite broad. Indeed, any compact and smooth surface is orientable and admits a tubular neighborhood (of uniform thickness) (cf. (Do Carmo 2018, Prop. 1, p. 113)). In particular, our analysis covers the class of bounded surfaces that are diffeomorphic to an open subset of a compact surface (e.g., a finite cylinder, or the graph of a \(C^2\) function). The proof strategy relies on a characterization of the two-scale asymptotic behavior of sequences in \(H^1 \left( \Omega , \mathcal {M} \right) \) (see Proposition 2.2), on an application of the theory of two-scale convergence (see Allaire 1992; Nguetseng 2005; Lukkassen et al. 2002), and on a careful projection argument guaranteeing the optimality of \(\mathcal {G}_0\) as a lower bound for the energies \(\mathcal {G}_{\varepsilon }\), as \(\varepsilon \) converges to zero.
Our second main result concerns the case in which \(\mathcal {M}=\mathbb {S}^2\) and \(\Omega \subseteq {\mathbb {R}}^3\) has a laminated structure (see Fig. 1). In this micromagnetic setting of chiral multilayers, we provide an explicit identification of minimizers of the functional \(\mathcal {G}_0\). Our theorem reads as follows (see Theorem 3.1).
Theorem 1.2
Assume that \(\Omega := \omega \times I_{\lambda }\) with \(\omega \subset {\mathbb {R}}^2\), \(| \omega | = 1\), \(\lambda > 0, I_{\lambda } = (0, \lambda )\) and that the material-dependent functions \(a, \kappa \in L^{\infty }_{\sharp } \left( Q, {\mathbb {R}}\right) \) depend only on the third coordinate: \(a (y) = a (y \cdot e_3)\) and \(\kappa (y) = \kappa (y \cdot e_3)\). Then, for \(\int _{Q} \kappa (y) \mathrm{d}y = 0\), the only energy minimizers are the helical textures
with \(\theta _0 \in {\mathbb {R}}\) arbitrary, and the minimum value of the energy is \(\mathcal {G}_0 (m_{*}) = - \frac{\lambda }{2} \int _{Q} \frac{\kappa ^2 (y)}{a (y)} \mathrm{d}y.\)
The arising of helical magnetic structures in composite alloys had been originally theorized by Dzyaloshinskii in Dzyaloshinskii (1964, 1965) (see also Rybakov et al. 2013), as a result of possible instabilities of ferromagnetic structures with respect to small relativistic spin–lattice or spin–spin interactions. A concrete realization of Dzyaloshinskii’s conjecture has been shown in Bak and Jensen (1980), where the authors exhibited long-period structures in MnSi and FeGe alloys stemming from the phenomenon described in Dzyaloshinskii (1964), Dzyaloshinskii (1965). Helical textures in chiral models for director fields have been analyzed in the setting of liquid crystals in the two seminal works (Ericksen 1959; Wright and Mermin 1989). Multilayered chiral magnets have been the subject of a growing interest in the Physics literature (see, e.g., (Moreau-Luchaire et al. 2016; Legrand et al. 2018, 2018)).
Theorem 1.2 provides a mathematical evidence of Dzyaloshinskii’s conjectures in multilayers when long-range effects are neglected (see Remark 3.3).
Our third main contribution consists of an extension of the characterization in Theorem 1.1 to the higher-dimensional setting. To be precise, we consider the family of energy functionals
where for every \(i = 1, \ldots , n\) the maps \(A^i, K^i \in L^{\infty }_{\sharp } ( {\mathbb {R}}^n, {\mathbb {R}}_{\mathrm{sym}}^{n \times n} )\) are \(Q\)-periodic functions, taking values in the set \({\mathbb {R}}_{\mathrm{sym}}^{n \times n}\) of symmetric matrices, and where \(J^i \in L^{\infty }_{\sharp } ( {\mathbb {R}}^n, {\mathbb {R}}^{n \times n})\) is a \(Q\)-periodic function, taking values in the set of \(n \times n\)-matrices. Additionally, we assume that each map \(A^i\) is uniformly positive definite, namely that for every \(i = 1, \ldots , n\) there exists \(c_i > 0\) such that
As highlighted in Remark 4.1, the class of energies densities as above includes the setting in which both the exchange energy coefficient and the material-dependent DMI constant are anisotropic. In Theorem 4.1, we prove the following.
Theorem 1.3
The family \(\left( \mathcal {G}_{\varepsilon ,v} \right) _{\varepsilon \in {\mathbb {R}}_+}\ \Gamma \)-converges with respect to the weak topology in \(H^1 ( \Omega , \mathcal {M})\), to the energy functional
for every \(m \in H^1 \left( \Omega , \mathcal {M} \right) \), where \(\phi _v [m, \nabla m]\) solves the cell problem in Proposition 4.1.
We stress that Theorems 1.1 and 1.3 are formulated in the general setting of \(H^1 (\Omega , \mathcal {M})\) for mathematical interest in the study of homogenization problems for manifold-valued Sobolev spaces. The application to the micromagnetic chiral setting is obtained by considering their restriction to the case in which \(\mathcal {M}= \mathbb {S}^2\).
The paper is organized as follows: In Sect. 2, we introduce the setting of the problem and prove some first preliminary results. In Sect. 2.1, we characterize the two-scale limits of \(H^1 \left( \Omega , \mathcal {M} \right) \)-maps. Sections 2.2 and 2.3 are devoted to the proof of Theorem 1.1. The study of chiral multilayers and the higher-dimensional setting are the subject of Sect. 3 and Sect. 4, respectively.
2 The Three-Dimensional Setting
In what follows, \(\Omega \) will be an open bounded domain of \({\mathbb {R}}^3\). Our analysis will focus on vector-valued functions taking values on surfaces \(\mathcal {M}\) in \({\mathbb {R}}^3\). We will always assume that \(\mathcal {M}\) is a bounded, \(C^2\) orientable hypersurface of \({\mathbb {R}}^3\) that admits a tubular neighborhood of uniform thickness.
The normal field associated with the choice of an orientation for \(\mathcal {M}\) will be denoted by \(n : \mathcal {M} \rightarrow \mathbb {S}^2\). For every \(m \in \mathcal {M}\) and every \(\delta \in {\mathbb {R}}\), we denote by \(\ell _{\delta } (m) := \left\{ m + t n (m) : \, - \delta< t < \delta \right\} \) the normal segment to \(\mathcal {M}\) having radius \(\delta \) and centered at m. We recall that if \(\mathcal {M}\) admits a tubular neighborhood (of uniform thickness), then there exists a \(\delta \in {\mathbb {R}}_+\) such that the following properties hold [cf. (Do Carmo 2018, p. 112)]:
- (1)
For every \(m_1, m_2 \in \mathcal {M}\), there holds \(\ell _{\delta } (m_1) \cap \ell _{\delta } (m_2) = \emptyset \) whenever \(m_1 \ne m_2\), and the union \(\mathcal {M}_{\delta } := \cup _{m \in \mathcal {M}} \ell _{\delta } (m)\) is an open set of \({\mathbb {R}}^3\) containing \(\mathcal {M}\).
- (2)
The nearest-point projection
$$\begin{aligned} \pi _{\mathcal {M}} : \mathcal {M}_{\delta } \rightarrow \mathcal {M}, \end{aligned}$$(12)which maps every \(p \in \mathcal {M}_{\delta }\) onto the unique \(m \in \mathcal {M}\) such that \(p \in \ell _{\delta } (m)\), is a \(C^1\) map.
The open set \(\mathcal {M}_{\delta }\) is called the tubular neighborhood of \(\mathcal {M}\) of thickness \(\delta \).
We denote by \(T\mathcal {M}\) the tangent bundle of \(\mathcal {M}\), and by \(\varvec{T}\mathcal {M} :=\bigcup _{s \in \mathcal {M}} \{ s \} \times \varvec{T}_s \mathcal {M}\) the vector bundle, with \(\varvec{T}_s \mathcal {M} := (T_s \mathcal {M})^3\). We will indicate by \(\xi ^{\mathsf {T}} := ( \xi _1^{\mathsf {T}}, \xi _2^{\mathsf {T}}, \xi _3^{\mathsf {T}})\) a generic element of \(\varvec{T}_s \mathcal {M}\). The notation is motivated by the fact that if \(\xi : = \nabla m\), with \(m \in H^1 \left( \Omega , \mathcal {M} \right) \) and \(\nabla m\) is the transpose of the Jacobian matrix of m, the columns \(( \xi _1^{\mathsf {T}}, \xi _2^{\mathsf {T}}, \xi _3^{\mathsf {T}} ) := (\partial _1 m (x), \partial _2 m (x), \partial _3 m (x))\) of \(\left( \nabla m (x) \right) ^{\mathsf {T}}\) are in \(T_{m (x)} \mathcal {M}\) for almost every \(x \in \Omega \).
In what follows, \(Q\) will be the unit cube in \({\mathbb {R}}^3\). We will denote by \(H^1_{\sharp } \left( Q\right) \) the set of corresponding periodic \(H^1\)-maps, namely the collection of functions \(u \in H^1 \left( {\mathbb {R}}^3 \right) \) such that \(u (x + k e_i) = u (x)\) for every \(k \in {\mathbb {N}}\), and for almost every \(x \in {\mathbb {R}}^3\), \(i = 1, 2, 3\). With a slight abuse of notation, we will identify \(H^1_{\sharp } \left( Q\right) \) with \(H^1_{\sharp } \left( Q\right) / {\mathbb {R}}\) and for \(\phi , \psi \in H^1_{\sharp } \left( Q\right) \)we will write \(\phi = \psi \) if \(\phi - \psi \in {\mathbb {R}}\). Throughout the paper, the symbol \(\twoheadrightarrow \) will denote weak two-scale convergence. The symbol \(\mathcal {D} \left( \Omega \right) \) will represent the class of smooth functions having compact support in \(\Omega \). Also, to shorten notation, for every map \(\psi \in L^1 \left( Q\right) \) we will denote by \(\langle \psi \rangle _{Q}\) the average of \(\psi \) on \(Q\).
We consider the energy density
where \(\kappa \in L^{\infty }_{\sharp } ( {\mathbb {R}}^3 )\) is a Q-periodic function, representing the material-dependent DMI constant, and \(a \in L^{\infty }_{\sharp } ( {\mathbb {R}}^3, {\mathbb {R}}_+)\) is a 1-periodic positive function accounting for the range of exchange interactions. For every \(\varepsilon > 0\), we set \(a_{\varepsilon } (x) := a (x / \varepsilon )\), and \(\kappa _{\varepsilon } (x) := \kappa (x / \varepsilon )\) for almost every \(x \in {\mathbb {R}}^3\). For every \(m \in H^1 \left( \Omega , \mathcal {M} \right) \), we define the family of energy functionals
with \(\varvec{\chi }\) given by (9). We aim at identifying a homogenized functional capturing the limiting behavior of minimizers of \(\mathcal {G}_{\varepsilon }\) as \(\varepsilon \rightarrow 0\), that is, as the period over which the heterogeneities are evenly distributed inside the media shrinks to zero.
Before stating our main result, we introduce the so-called tangentially homogenized energy density \(T_{\hom } : ( s, \xi ^{\mathsf {T}}) \in \varvec{T}\mathcal {M} \rightarrow {\mathbb {R}}\), defined by the minimization problem
for every \(s \in \mathcal {M}\) and \(\xi ^{\mathsf {T}} \in \varvec{T}_s \mathcal {M}\). We first show an explicit characterization of solutions to (15), guaranteeing, as a by-product, the measurability of the map \(x \rightarrow T_{\hom } (m (x), \nabla m (x))\) for every \(m \in H^1 \left( \Omega , \mathcal {M} \right) \).
Proposition 2.1
For every \(( s, \xi ^{\mathsf {T}} ) \in \varvec{T}\mathcal {M}\), the minimization problem (15) has a unique solution. Specifically, let \(\tau _1 (s), \tau _2 (s)\) be an orthonormal basis at \(s \in \mathcal {M}\). Let \(\varphi _a, \varphi _k \in H^1_{\sharp } ( Q, {\mathbb {R}}^3 )\) be the unique solutions to the cell equations
Here the operator \(\mathbf {div}\) acts on columns. Then, the unique solution \(\phi [ s, \xi ^{\mathsf {T}} ] \in H^1_{\sharp } ( Q, T_s \mathcal {M})\) of the minimization problem (15) is given by
with \(\mu _j (s) := s \times \tau _j (s)\), for every \(s \in \mathcal {M}\), and for almost every \(y \in Q\). Additionally,
Proof
We first observe that for every \(\phi \in H^1_{\sharp } \left( Q, T_s \mathcal {M} \right) \) there holds \(\phi (y) = \sum _{j = 1}^2 \phi ^j (y) \tau _j (s)\) for almost every \(y \in Q\). Analogously, \(\xi _i^{\mathsf {T}} = \sum _{j = 1}^2 ( \xi _i^{\mathsf {T}} \cdot \tau _j (s) ) \tau _j (s), \, i = 1, 2, 3,\) because \(\xi ^{\mathsf {T}} \in \varvec{T}_s \mathcal {M}\). Therefore
where we set \(\xi _{\tau } (s) := (\xi \tau _1 (s), \xi \tau _2 (s)) \in {\mathbb {R}}^{3 \times 2}\) and \( \phi _{\tau } (y) = (\phi ^1 (y), \phi ^2 (y))\), for every \(s \in \mathcal {M}\) and for almost every \(y\in Q\). Additionally, we have
with \(\mu (s) := (\mu _1 (s), \mu _2 (s)) \in {\mathbb {R}}^{3 \times 2}\) and \(\mu _j (s) := s \times \tau _j (s), \, j = 1, 2\), for every \(s \in \mathcal {M}\).
Summarizing, the minimization problem in (15) can be restated under the form
which in turn can be rephrased as the combination of two scalar infimization procedures. Indeed, for every \(\sigma , \omega \in {\mathbb {R}}^3\) we consider the minimization problem
By Lax–Milgram’s lemma, for every \(\sigma , \omega \in {\mathbb {R}}^3\) problem (22) admits a unique solution in \(H^1_{\sharp } \left( Q, {\mathbb {R}}\right) ,\) denoted henceforth by \(\psi [\sigma , \omega ]\). In particular, \(\psi [\sigma , \omega ]\) coincides with the unique solution to the Poisson equation
Accordingly, the unique solution of the main minimization problem (15) reads as
where
for every \(s \in \mathcal {M}\), and almost every \(y \in Q\). The expression of \(\phi [ s, \xi ^{\mathsf {T}} ]\) can be further simplified. Indeed, by (16) and (17) we have \(- \mathrm{div}\left( a \nabla (\varvec{\varphi }_a \cdot \sigma ) \right) =-\mathbf {div} (a \nabla \varvec{\varphi }_a) \cdot \sigma =\nabla a \cdot \sigma \) and \(- \mathrm{div}\left( a \nabla (\varvec{\varphi }_{\kappa } \cdot \omega ) \right) = - \nabla \kappa \cdot \omega \). Therefore \(\psi [\sigma , \omega ] =\varvec{\varphi }_a \cdot \sigma +\varvec{\varphi }_{\kappa } \cdot \omega \), and we deduce the following identities:
for every \(s \in \mathcal {M}\) and almost every \(y \in Q\). This completes the proof of (18).
To prove (19), we observe that \(\phi (y) := \phi [ s, \xi ^{\mathsf {T}} ] (y) \in H^1_{\sharp }( Q, T_s \mathcal {M} )\) satisfies the Euler–Lagrange equations
In particular, choosing \(\varphi = \phi \) we get
This implies that
which yields (19). \(\square \)
Corollary 2.1
For every \(m_0 \in H^1 \left( \Omega , \mathcal {M} \right) \), the map
is measurable.
Proof
From the proof of Proposition 2.1, we find that the tangentially homogenized energy density in (15) can be written as
with \(\phi _{\tau } [ s, \xi ^{\mathsf {T}} ] = \left( \phi ^1 [ s, \xi ^{\mathsf {T}} ], \phi ^2 [ s, \xi ^{\mathsf {T}} ] \right) \), and \(\xi _{\tau } (s) := (\xi \tau _1 (s), \xi \tau _2 (s))\), for every \(s \in \mathcal {M}\) and for almost every \(y \in Q\). Note that, when \(s := m (x)\) and \(\xi := \nabla m (x)\) we have \(\xi _{\tau } (x) := \nabla _{\tau } m (x) = \left( \nabla m (x) \tau _1 (m (x)), \nabla m (x) \tau _2 (m (x)) \right) \).
The measurability of the map \(x \in \Omega \mapsto T_{\hom } \left( m_0 (x), \nabla m_0 (x) \right) \) follows from (28), the regularity of \(\mathcal {M}\), and the explicit expressions of \(\phi _{\tau } [ s, \xi ^{\mathsf {T}} ]\) in (18). \(\square \)
Our main result is to show that \(T_{\hom } \) represents the effective energy density associated with our homogenization problem.
Theorem 2.1
The family \(\left( \mathcal {G}_{\varepsilon }\right) _{\varepsilon \in {\mathbb {R}}_+} \ \Gamma \)-converges with respect to the weak topology in \(H^1( \Omega , \mathcal {M})\), to the energy functional
for every \(m \in H^1 \left( \Omega , \mathcal {M} \right) \).
Proof
The proof of Theorem 2.1 is subdivided into two main steps: the compactness of sequences with equibounded energies and the liminf inequality are the subject of Theorem 2.2; the optimality of the upper bound follows from Theorem 2.3. The second equality in (29) is a direct consequence of Proposition 2.1. \(\square \)
2.1 Two-Scale Limits of Fields in \(H^1 ( \Omega , \mathcal {M})\)
In this section, we characterize the two-scale asymptotic behavior of sequences in \(H^1 \left( \Omega , \mathcal {M} \right) \).
Proposition 2.2
Let \(\mathcal {M}\) be a \(C^2\) orientable hypersurface in \({\mathbb {R}}^3\), and let \((u_{\varepsilon })_{\varepsilon \in {\mathbb {R}}_+}\ \subset \, H^1 \left( \Omega , \mathcal {M} \right) \). Assume that there exist \(u_0 \in H^1( \Omega , {\mathbb {R}}^3 )\) and \(u_1 \in L^2 ( \Omega , H^1_{\sharp } ( Q, {\mathbb {R}}^3 ) )\) such that
Then, \(u_0 \in H^1 ( \Omega , \mathcal {M} )\) and \(u_1 (x, y) \in T_{u_0 (x)} \mathcal {M}\) for almost every \((x, y) \in \Omega \times Q\).
Proof
Since \(\mathcal {M}\) is a \(C^2\) orientable hypersurface, there exist an open tubular neighborhood \(U \subseteq {\mathbb {R}}^3\) of \(\mathcal {M},\) and a \(C^2\) function \(\gamma : U \rightarrow {\mathbb {R}}\), which has zero as a regular value, and is such that \(\mathcal {M}= \gamma ^{- 1} (0)\). In view of (29), we have, up to the extraction of a (not relabeled) subsequence, \(0 = \gamma (u_{\varepsilon } (x)) \rightarrow \gamma (u_0 (x)) = 0\) for almost every \(x \in \Omega \); therefore \(u_0 (x) \in \mathcal {M}\) for almost every \(x \in \Omega \). Additionally, for every \(\varepsilon > 0\) there holds,
By (29), it follows that \(\nabla \gamma (u_{\varepsilon }) \rightarrow \nabla \gamma (u_0)\) strongly in \(L^2 \left( \Omega , {\mathbb {R}}^3 \right) \). Thus, by (30) we obtain, for every \(\psi \in \mathcal {D} [ \Omega , C_{\sharp }^{\infty } \left( Q, {\mathbb {R}}^3 \right) ]\),
Since \(\gamma (u_0) = 0\), we conclude that \(\nabla u_0 \nabla \gamma (u_0) = 0\) in \(\Omega \). Thus, from (31) we infer that
Hence, \(u_1 (x, y) \cdot \nabla \gamma (u_0 (x)) = c (x)\) for almost every \((x, y) \in \Omega \times Q\), for some function \(c \in L^2 \left( \Omega \right) \). As \(\int _{Q} u_1 (x, y) \mathrm{d}y = 0\) for almost every \(x \in \Omega \), it follows that \(c \equiv 0\). Thus, \(u_1 \cdot \nabla \gamma (u_0) \equiv 0.\) The thesis follows by observing that the vector \(\nabla \gamma (u_0 (x))\) is orthogonal to \(T_{u_0 (x)} \mathcal {M}\) for almost every \(x \in \Omega \). \(\square \)
Remark 2.1
The proposition holds if we assume, more generally, that \(\mathcal {M}\) is the inverse image of a regular value of a \(C^2\) function \(\gamma : U \subseteq {\mathbb {R}}^N \rightarrow {\mathbb {R}}^M\) with \(M <N\). Indeed, in this case, there exist M linearly independent normal vector fields, \((n_j)_{j \in {\mathbb {N}}^M}\), which at every point \(p \in \mathcal {M}\) span the orthogonal complement of \(T_p \mathcal {M}\). Repeating the same argument, one then finds that \(u_1 \cdot n_j (u_0) = 0\) for every \(j \in {\mathbb {N}}^M\), and therefore \(u_1 (x, y) \in T_{u_0 (x)} \mathcal {M}\).
2.2 Compactness and \(\Gamma \)-Liminf Inequality in the 3d-Setting
This section is devoted to the identification of a lower bound for the limiting behavior of the energy functionals \(\mathcal {E}_{\varepsilon }\). In what follows, as suggested by Lemma 2.2, we will denote by \(L^2 ( \Omega , H^1_{\sharp } ( Q, T_{m_0} \mathcal {M} ) )\) the set of maps \(\phi \in L^2 ( \Omega , H^1_{\sharp } ( Q, {\mathbb {R}}^3 ) )\) such that \(\phi (x) \in T_{m_0 (x)} \mathcal {M}\) for almost every \(x \in \Omega \).
Theorem 2.2
Let \((m_{\varepsilon })_{\varepsilon } \subset H^1 \left( \Omega , \mathcal {M} \right) \) be such that \(\sup _{\varepsilon > 0} \mathcal {G}_{\varepsilon }(m_{\varepsilon }) < + \infty \). Then, there exists \(m_0 \in H^1 ( \Omega , \mathcal {M} )\) and \(m_1 \in L^2 ( \Omega , H^1_{\sharp } ( Q, T_{m_0} \mathcal {M} ))\) such that
Additionally,
Proof
The compactness result is a direct consequence of Proposition 2.2, the assumptions on a and \(\kappa \), and the boundedness of \(\mathcal {M}\). First, we observe that the energy density (13) can be rearranged as follows:
with \(\varvec{\chi }\) given by (9). Therefore
where
and
For \(\psi _{0, n} \in C^{\infty } ( \bar{\Omega }, {\mathbb {R}}^3 )\) and \(\psi _{1, n} \in \mathcal {D} ( \Omega , H_{\sharp }^{1} ( Q, {\mathbb {R}}^3 ) )\), we define
We then have
because the difference of the integrand on the left-hand side with the integrand on the right-hand side is a perfect square. Since \(\psi _{0, n}\) and \(\psi _{1, n}\) are smooth in the x-variable, the functions \(a (y) | \varphi _n (x, y) |^2\), \(a (y) \varphi _n (x, y)\), and \(\kappa (y) \varphi _n (x, y)\) are admissible test functions. Therefore, by standard properties of two-scale convergence, we obtain the inequality
Next, we choose \((\psi _{0, n})_{n \in {\mathbb {N}}}\) in \(C^{\infty } (\bar{\Omega }, {\mathbb {R}}^3 )\) an \((\psi _{1, n})_{n \in {\mathbb {N}}}\) in \(\mathcal {D} ( \Omega , H_{\sharp }^{1}( Q, {\mathbb {R}}^3 ) )\) such that \(\psi _{0, n} \rightarrow m_0\) in \(H^1 ( \Omega , {\mathbb {R}}^3 )\) and \(\psi _{1, n} \rightarrow m_1\) in \(L^2 ( \Omega , H^1_{\sharp }(Q) )\). Passing to the limit for \(n \rightarrow \infty \) into (40), we get that
On the other hand, since \(\kappa _{\varepsilon }^2 / a_{\varepsilon } \rightharpoonup ^{*} \langle \kappa ^2 / a \rangle _{Q}\) weakly\(^{*}\) in \(L^{\infty } ( Q),\) we conclude that
By combining (36), (41), and (42), we obtain (34). \(\square \)
2.3 The Limsup Inequality in the 3d-Setting
In this section, we show that the lower bound identified in Theorem 2.2 is optimal. To be precise, we prove the following result.
Theorem 2.3
Let \(\mathcal {M}\) be a \(C^2\) orientable hypersurface of \({\mathbb {R}}^N\) such that \(\mathcal {M}\) has a tubular neighborhood of uniform thickness \(\delta > 0\). Let \(m_0 \in H^1 ( \Omega , \mathcal {M} ) .\) Then, there exists a sequence \((m_{\varepsilon })_{\varepsilon > 0}\) in \(H^1 (\Omega , \mathcal {M})\) such that, as \(\varepsilon \rightarrow 0\),
and
Proof
Denote by \(U_{\delta }\) the tubular neighborhood of size \(\delta \) around \(\mathcal {M}\), and let
be the pointwise projection operator. Note that, since \(\mathcal {M}\) is \(C^2\), the projection satisfies \(\pi _{\mathcal {M}} \in C^1 (U_{\delta }, \mathcal {M})\). Clearly, we can choose \(\delta \) small enough so that \(\pi _{\mathcal {M}} \in C^1 ( \bar{U}_{\delta }, \mathcal {M} )\). For the convenience of the reader, we subdivide the proof into two steps.
Step 1. Given \(\psi \in C^{\infty } ( \bar{\Omega }, W_{\sharp }^{1, \infty } ( Q, {\mathbb {R}}^3 ) )\), for every \(\varepsilon > 0\) and almost every \(x \in \Omega \) we set
We note that
Given the regularity of \(\psi \), for \(\varepsilon \) small enough there holds \(\hat{m}_{\varepsilon } \in U_{\delta }\) for almost every \(x \in \Omega \). By the regularity of \(\pi _{\mathcal {M}}\), there exists a constant \(c_{\mathcal {M}} > 0\) depending only on \(\mathcal {M}\), such that
By (46) and the boundedness of \((\nabla \hat{m}_{\varepsilon })\) in \(L^2 ( \Omega , {\mathbb {R}}^{3 \times 3} )\), we deduce that, up to the extraction of a not relabeled subsequence,
Moreover, by Proposition 2.2, we infer that, up to the extraction of a not relabeled subsequence, there holds
for some \(\phi \in L^2 ( \Omega , H^1_{\sharp } ( Q, T_{m_0} \mathcal {M} ) )\) with \(\int _{Q} \phi (x, y) \mathrm{d}y = 0\) for almost every \(x \in \Omega \).
Next, a direct computation shows that
for almost every \(x \in \Omega \). By (49), and by the regularity of \(\psi \) and \(\pi _{\mathcal {M}}\), it follows that
By combining the above convergences and (52), we conclude that
Since \(\pi _{\mathcal {M}} [m_0] = m_0\) in \(\Omega \), by differentiating we obtain that \(\nabla m_0 \nabla \pi _{\mathcal {M}} [m_0] = \nabla m_0\) for almost every \(x \in \Omega \). Thus, by (56) we infer that
To see that the previous convergence is actually stronger, we observe that
and
Now, we observe that the first term in the right-hand side of (59) converges to zero in \(L^2 \left( \Omega , {\mathbb {R}}^{3 \times 3} \right) \). Indeed, the regularity of \(\mathcal {M}\) provides an \(L^{\infty }\)-bound on \(\nabla \pi _{\mathcal {M}}\); moreover, owing (45), we have that \(\nabla \hat{m}_{\varepsilon } -(\nabla m_0 + \nabla _y \psi ) = \varepsilon \nabla \psi (x, x / \varepsilon )\). Thus, we conclude by Lebesgue’s dominated convergence theorem. The very same proves that \((\nabla m_0 + \nabla _y \psi ) (\nabla \pi _{\mathcal {M}} [\hat{m}_{\varepsilon }] - \nabla \pi _{\mathcal {M}} [m_0]) \rightarrow 0\) strongly in \(L^2 ( \Omega , {\mathbb {R}}^{3 \times 3} )\). Overall,
In view of (60) and of the regularity of \(\psi \), we directly obtain that
with \(\varvec{\chi }\) given by (9).
Step 2. Let now \(m_0 \in H^1 \left( \Omega , \mathcal {M} \right) \), and let
where \(\phi [ x, \xi ^{\mathsf {T}} ] (y)\) is the map defined in Proposition 2.1. We observe that \(m_1\) has the same regularity in y as the maps \(\varvec{\varphi }_a (y), \varvec{\varphi }_{\kappa } (y)\) defined in (16), (17), and the same regularity in x as \(\nabla m_0\). Thus, in particular, \(m_1 \in \, L^2 ( \Omega , H^1_{\sharp } ( Q, T_{m_0} \mathcal {M} ) )\). By density, and by means of a mollification procedure in the y variable, we find a sequence \(\psi _k \in \mathcal {D} ( \Omega , W_{\sharp }^{1, \infty } ( \bar{Q}, {\mathbb {R}}^3 ) )\) such that
Setting
for every \(\psi \in \, L^2 ( \Omega , H^1_{\sharp } ( Q, T_{m_0} \mathcal {M} ))\), we have
Additionally, we observe that
This follows from the fact that for every \(s \in \mathcal {M}\), and for every \(v \in T_s \mathcal {M}\), \({\nabla ^{\mathsf {T}} \pi _{\mathcal {M}} (s) v = v}\). Indeed, since \(m_1 (x) \in T_{m_0 (x)} \mathcal {M}\) for almost every \(x \in \Omega \), we conclude that \({\nabla ^{\mathsf {T}}_y m_1 = \nabla ^{\mathsf {T}} \pi _{\mathcal {M}} [m_0] \nabla ^{\mathsf {T}}_y m_1}\).
In view of (64) and (65), for every \(\delta >0\) there exists \(\psi _{k_{\delta }} \in \mathcal {D} ( \Omega , W_{\#}^{1, \infty } ( \bar{Q}, {\mathbb {R}}^3 ) )\) such that
By Step 1 and (61), there exists an associated sequence \((m_{\varepsilon }^{\delta })_{\varepsilon > 0}\) in \(H^1 (\Omega , \mathcal {M} )\) such that
and hence
By the arbitrariness of \(\delta \), the limsup inequality follows then from classical properties of \(\Gamma \)-convergence [see Section 1.2 in Braides (2002)]. \(\square \)
3 The Micromagnetic Setting: Applications to Multilayers
In this section, we specify the characterization of the effective energy to the micromagnetic setting of chiral multilayers. In this case, \(\mathcal {M}=\mathbb {S}^2\) and \(\Omega \subseteq {\mathbb {R}}^3\) has a laminated structure as in Fig. 1. We have the following result.
We consider here a chiral multilayer having a laminated structure, namely \(\Omega := \omega \times I_{\lambda }\) with \(\omega \subset {\mathbb {R}}^2\), \(| \omega | = 1\), \(\lambda > 0,\) and \(I_{\lambda } = (0, \lambda )\). We assume that the material-dependent functions \(a_{\varepsilon } (y) = a (y / \varepsilon )\) and \(\kappa _{\varepsilon } (y) = \kappa (y / \varepsilon )\) depend only on the third coordinate: \(a (y) = a (y \cdot e_3) =: a (t)\) and \(\kappa (y) = \kappa (y \cdot e_3) =: \kappa (t)\)
Theorem 3.1
Assume that \(\Omega := \omega \times I_{\lambda }\) with \(\omega \subset {\mathbb {R}}^2\), \(| \omega | = 1\), \(\lambda > 0, I_{\lambda } = (0, \lambda )\), and that the material-dependent functions \(a, \kappa \in L^{\infty }_{\sharp }( Q, {\mathbb {R}})\) depend only on the third coordinate: \(a (y) = a (y \cdot e_3)\) and \(\kappa (y) = \kappa (y \cdot e_3)\). Then, the homogenized energy functional (29) is given, for every \(m \in H^1 ( \Omega , \mathbb {S}^2 )\), by
where the effective parameters are defined by
Additionally, for \(\langle \kappa \rangle _{Q} = 0\) the only energy minimizers are the helical textures
with \(\theta _0 \in {\mathbb {R}}\) arbitrary, and the minimum value of the energy is \(\mathcal {G}_0 (m_{*}) = - \frac{\lambda }{2} \langle \kappa ^2 / a \rangle _{Q}\).
Remark 3.1
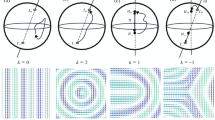
It is interesting to note that the DMI layers contribute to an increase in the crystal anisotropy of the magnetic system. When \(\langle \kappa \rangle _{Q} = 0\), the minimizers of \(\mathcal {G}_0\) are always planar and constant on each layer. Moreover, depending on the effective DMI constant \(\gamma _0\) of the homogeneous model, two Bloch-type chiral skyrmions with opposite (and possibly non-integral) topological charges can arise. Indeed, the sign of \(\gamma _0\), equivalently the sign of \(\langle \kappa / a \rangle _{Q}\), controls the chirality of the system: the minimizers describe right-handed helices when \(\gamma _0 > 0\) and left-handed helices when \(\gamma _0 < 0\) (cf. Fig. 2). Additionally, identifying \(m_{*}\) with the curve
in the complex plane, for
one can interpret \(\tilde{m}_{*}\) as a map from \(\mathbb {S}^1\) to \(\mathbb {S}^1\), whose skyrmion number (cf. (2)) coincides with the winding number of \(\tilde{m}_{*}\) around the origin:
In other words, for the values of \(\lambda \) specified in (69), the sign of \(\langle \kappa / a \rangle _{Q}\) determines that of the topological degree of \(m_{*}\).
A schematic representation of the minimizers of \(\mathcal {G}_{\bot }\). A posteriori, they completely characterize the profiles of the minimizers of \(\mathcal {G}_0\). The minimizers of \(\mathcal {G}_0\) are always planar and constant on every layer. According to the sign of \(\gamma _0\), equivalently on the sign of \(\langle \kappa / a \rangle _{Q}\), they describe right-handed (left) or left-handed helices (right)
Remark 3.2
Note that the shape of the minimizers does not depend on the height \(\lambda \) of the multilayer. Instead, the minimum value of the energy scales linearly in \(\lambda \).
Remark 3.3
Our analysis in Theorem 3.1 does not take into account long-range effects such as the ones originating from magnetostatic interaction, as well as magnetocrystalline effects. As already pointed out, these contributions can be superimposed to our energy functional because, from the variational point of view, they play the role of a continuous perturbation. For example, to include magnetostatic interaction, one has to consider the augmented energy functional (cf. Proposition 1.1) \(\mathcal {G}_0 +\mathcal {W}_0\) ,with \(\mathcal {W}_0\) given by (6). In this case, although we expect similar qualitative considerations, an explicit characterization of the minimizing profiles of \(\mathcal {G}_0 +\mathcal {W}_0\) will be hardly achievable.
Proof
We denote by t the third coordinate in \(Q\), we write \(Q= Q' \times I\), and we consider the setting in which \(a (y) = a (y \cdot e_3) =: a (t)\) and \(\kappa (y) = \kappa (y \cdot e_3) =: \kappa (t)\) for almost every \(y \in Q\). In this framework, the two functions \(\varphi _{\kappa }\) and \(\varphi _a\) can be computed explicitly in terms of \(\kappa \) and a. Indeed, consider the equation
Testing (70) against vector fields \(\psi \in H^1_{\sharp } ( Q, {\mathbb {R}}^3 )\) that do not depend on t we get that, for a.e. \(t \in I_{\lambda }\), the distribution \(\varphi _{\kappa } (\cdot , t)\) is harmonic:
where we set \(\Delta _{\omega } \varphi _{\kappa } (\cdot , t) :=\partial ^2_{y_1} \varphi _{\kappa } (\cdot , t) + \partial ^2_{y_2} \varphi _k (\cdot , t)\). Hence, by Weyl’s lemma, \(\varphi _k (\cdot , t) \in C^{\infty }_{\sharp } ( Q', {\mathbb {R}}^3 )\). Also, for a.e. \(t \in I_{\lambda }\), \(\varphi _k (\cdot , t) \equiv 0\) is the unique solution of (71) in \(H^1_{\sharp } ( Q', {\mathbb {R}}^3 ) / {\mathbb {R}}\supseteq C^{\infty }_{\sharp } ( Q', {\mathbb {R}}^3 ) / {\mathbb {R}}\). We conclude that \(\varphi _{\kappa } (y)\) depends only on the t-variable. Therefore, we set \(\varphi _{\kappa } (y) = \varphi _{\kappa } (y \cdot e_3) =: \varphi _{\kappa } (t)\).
In view of (70), it follows that \(\varphi _{\kappa } (t)\) solves the ordinary differential equation
Integrating in [0, t] yields the equation
where we set \(a_0 := a (0), \kappa _0 := \kappa (0)\). Integrating again in I and imposing periodicity, we deduce that
The previous relation implies that \(\varphi _{\kappa }' (0) \cdot e_1 = 0\), \(\; \varphi _{\kappa }' (0) \cdot e_2 = 0\), and
Therefore, for every \(t \in I\)
Noting that \(\varphi _a\) solves an analogous differential equation as \(\varphi _{\kappa }\), in which \(\kappa \) is replaced by \(- a\), we conclude that \(\varphi _a' (0) \cdot e_1 = 0\), \(\varphi _a' (0) \cdot e_2 = 0\), and \(\varphi _a' (0) \cdot e_3 = - 1 + (a_0 \langle a^{- 1} \rangle _I)^{- 1}\). Thus, for every \(t \in I\),
We stress that \(\mathfrak {K} (t)\) and \(\mathfrak {a} (t)\) in (72) and (73) have been introduced because they are the only quantities of interest for the tangentially homogenized energy density \(T_{\hom }\).
We recall in fact that \(T_{\hom }\) reads as (cf. (19))
where, for every \(s \in \mathcal {M}\) and \(\xi ^{\mathsf {T}} \in T_s \mathcal {M}\), the map \(\phi (y) := \phi [ s, \xi ^{\mathsf {T}} ] (y)\) is given by
In the micromagnetic setting, in which the vector field m take values in \(\mathcal {M} := \mathbb {S}^2,\)an explicit identification of \(| \nabla \phi |^2\) is available. Indeed, we find that \(\mu _1 (s) = \tau _2 (s)\) and \(\mu _2 (s) = - \tau _1 (s)\) for every \(s \in \mathbb {S}^2\). Hence, recalling that \(\varphi _a\) and \(\varphi _k\) depend only on the t-variable, for almost every \(y \in Q\), \(s \in \mathcal {M}\) and \(\xi ^{\mathsf {T}} \in T_s \mathcal {M}\), we deduce
with \(\mathfrak {K} (t)\) and \(\mathfrak {a} (t)\) given by (72) and (73). A direct computation shows that
Thus, for almost every \(y \in Q\), \(s \in \mathcal {M}\), and \(\xi ^{\mathsf {T}} \in T_s \mathcal {M}\), we have
Substituting the previous expression in (19) gives
with \(\alpha _0 := \langle a\mathfrak {a}^2 \rangle _{Q}\), \(\beta _0 := \langle a\mathfrak {K}^2 \rangle _{Q}\), and \(\gamma _0 := \langle a\mathfrak {a}\mathfrak {K} \rangle _{Q}\) explicitly given by
and
This yields (66). To complete the proof of the theorem, it remains to show that when \(\langle \kappa \rangle _{Q} = 0\) the energy minimizers depend on \(y \cdot e_3\) only and can be fully characterized. We proceed in two steps:
- 1.:
We assume that any minimizer \(m_{*}\) of \(\mathcal {G}_0\) is of the form \(m_{*} (x) = u (x \cdot e_3)\) for some planar one-dimensional profile \(u : I_{\lambda } \rightarrow \mathbb {S}^1 \times \{0\}\), and we characterize the minimizers in this class.
- 2.:
We prove that every minimizer of \(\mathcal {G}_0\) satisfies the assumptions in step 1.
Step 1. We start noting that under the symmetry assumptions in 1. the minimization problem for the micromagnetic energy functional reduces to the minimization in \(H^1 ( I_{\lambda } ; \mathbb {S}^2)\) of the functional
where \(\tilde{\alpha }_0 := \langle a \rangle _{Q} - \alpha _0 =\langle a^{- 1} \rangle ^{- 1} > 0\). Since \(u (t) \in \mathbb {S}^1 \times \{ 0 \}\) for almost every \(t \in I\), we have that \(u (t) \cdot \dot{u} (t) = 0\), and therefore, for almost every \(t \in I_{\lambda }\) there holds
with \(\sigma (u (t), \dot{u} (t)) = 1\) if the couple \((u, \dot{u})\) induces a positively oriented basis of \({\mathbb {R}}^2\), and \(\sigma (u (t), \dot{u} (t)) = - 1\) otherwise. In particular, if \(u^+\) is a critical point of the energy for \(\gamma _0 > 0\), then for every \(R \in \mathrm{SO} (3)\), the profile \(R u^+\) is again a critical point. By contrast, if \(R_- \in O (3)\) and \(\det R_- = - 1\), then \(u^- := R_- u^+\) is a critical point of the energy for \(\gamma _0 = - | \gamma _0 |\). Therefore, without loss of generality, we can assume that \(\gamma _0 > 0\).
The Euler–Lagrange equations associated with (76) read as
with \(\tilde{\alpha }_0 := \langle a \rangle _{Q} - \alpha _0 =\langle a^{- 1} \rangle ^{- 1} > 0\). In particular, parameterizing u in polar coordinates, we obtain that the general solution of (77) is given by
with \(\theta _0 := \theta (0), \theta _{\lambda } := \theta (\lambda )\) arbitrary real numbers. The corresponding values of the energy depend on \(\theta _{\lambda } - \theta _0\) and on the height \(\lambda \) of the multilayer. Precisely, evaluating \(\mathcal {G}_{\bot }\) on the family (78) we find that
Minimizing with respect to \((\theta _{\lambda } - \theta _0)\), and taking into account (74) and (75), we deduce that the corresponding minimum value of \(\mathcal {G}_{\bot }\) is achieved when \((\theta _{\lambda } - \theta _0) = \lambda \gamma _0 / \tilde{\alpha }_0 = \lambda \langle \kappa / a \rangle _{Q}\), it is strictly negative, and it is given by
Summarizing, the energy \(\mathcal {G}_{\bot }\) is minimized by all profiles of the form
As we were expecting, depending on the sign of \(\gamma _0\), equivalently on the sign of \(\langle \kappa / a \rangle _{Q}\), the rotation is clockwise or counter-clockwise (cf. Fig. 2).
Note that the structure of optimal profiles does not depend on the height \(\lambda \) of the multilayer. The length \(\lambda \) affects only the minimal energy value, which is a decreasing function of \(\lambda \).
Step 2. We decompose each element \(m \in H^1 (\Omega , \mathbb {S}^2 )\) as \(m = u + m_3 e_{3,}\) with \(u : \Omega \rightarrow {\mathbb {R}}^3\) being the projection of m on \({\mathbb {R}}^2 \times \{ 0 \}\). We expand the energy \(\mathcal {G}_0\) as
with
Note that \(\mathcal {I}_2 (m_3) \geqslant 0\) for every \(m \in H^1 (\Omega , \mathbb {S}^2 )\). Additionally, for every \(\delta > 0\) there holds
Therefore, neglecting the contribution of \(\frac{1}{2} \left| \delta \partial _3 u - \frac{\gamma _0}{\delta } e_3 \times u \right| ^2\) leads to the lower bound
for every \(m \in H^1 ( \Omega , \mathbb {S}^2 )\) and every \(\delta > 0\). Choosing \(\delta ^2 := \tilde{\alpha }_0\), and neglecting the contribution of \(\langle a \rangle _{Q} (| \partial _1 u |^2+| \partial _2 u |^2)\) we obtain
for every \(m \in H^1 ( \Omega , \mathbb {S}^2 )\). Recall that (cf. (74) and (75)) \(\beta _0 + \gamma _0^2 / \tilde{\alpha }_0 = \langle \kappa ^2 / a \rangle _{Q} > 0\). Hence, since \(| u | \leqslant 1\) and \(\left| \Omega \right| = \lambda | \omega | = \lambda \), we deduce the estimate
for every \(m \in H^1 ( \Omega , \mathbb {S}^2 )\), which in turn implies that
From step 1, we know that there exist configurations \(m_{*} : \Omega \rightarrow \mathbb {S}^2\) for which the equality holds in (85). Indeed, it is sufficient to set \(m_{*} (x) = u (x \cdot e_3)\) with u given by (79):
and \(\theta _0 \in {\mathbb {R}}\) arbitrary. Hence
To conclude the proof, we observe that the right-hand side of (85) is attained if and only if
Hence, if m is a minimizer of \(\mathcal {G}_0\), then necessarily \(m_3 \equiv 0\), and \(\partial _1 u = \partial _2 u = 0\). Therefore, every minimizer \(m_{*}\) of \(\mathcal {G}_0\) is of the form \(m_{*} (x) =u(x\cdot e_3)\) for some one-dimensional profile \(u : I_{\lambda } \rightarrow \mathbb {S}^2\), with \(u \cdot e_3 \equiv 0\), i.e., due to step 1, u is of the form described in (86). \(\square \)
4 The Higher-Dimensional Case
This section is devoted to a higher-dimensional counterpart of the results presented so far in \({\mathbb {R}}^3\). Since many arguments follow along the same lines as in the 3d-setting, we only highlight here the main changes. Fix \(n \in {\mathbb {N}}\). In this section, \(\Omega \) will be an open bounded domain of \({\mathbb {R}}^n\), and \(\mathcal {M}\) will be a bounded, \(C^2\) orientable \(n - 1\)-dimensional surface of \({\mathbb {R}}^n\) that admits a tubular neighborhood of uniform thickness. We consider the energy density
where for every \(i = 1, \ldots , n\) the maps \(A^i, K^i \in L^{\infty }_{\sharp } ( {\mathbb {R}}^n, {\mathbb {R}}_{\mathrm{sym}}^{n \times n} )\) are \(Q\)-periodic functions, taking values in the set \({\mathbb {R}}_{\mathrm{sym}}^{n \times n}\) of symmetric matrices, and where \(J^i \in L^{\infty }_{\sharp } ( {\mathbb {R}}^n, {\mathbb {R}}^{n \times n} )\) is a \(Q\)-periodic function, taking values in the set of \(n \times n\)- matrices. Additionally, we will assume that each map \(A^i\) is uniformly positive definite, namely that for every \(i = 1, \ldots , n\) there exists \(c_i > 0\) such that
Remark 4.1
The motivation for taking into account the class of energy densities having the structure in (87) is the observation that, in the case in which the exchange energy coefficient and the material-dependent DMI constant are anisotropic, then the natural generalization of the energy density in (13) to an n-dimensional setting would be the following:
with \(\mathcal {A}_i \in L^{\infty }_{\sharp } ( {\mathbb {R}}^n, {\mathbb {R}}_{\mathrm{sym}}^{n \times n})\) and \(\mathcal {K}_i \in L^{\infty }_{\sharp } ({\mathbb {R}}^n, {\mathbb {R}}_{\mathrm{skew}}^{n \times n} )\), and where \({\mathbb {R}}_{\mathrm{skew}}^{n \times n}\) denotes the set of skew-symmetric matrices, \({\mathbb {R}}_{\mathrm{skew}}^{n \times n} := \left\{ M \in {\mathbb {R}}^{n \times n} : \, M^{\mathrm{T}} = - M \right\} .\) An algebraic manipulation yields the identity:
for almost every \(x \in {\mathbb {R}}^n\), and for all \(( s, \xi ^{\mathsf {T}} ) \in \varvec{T}\mathcal {M}\), where we have used the symmetry of \(\mathcal {A}_i\) and the skew symmetry of \(\mathcal {K}_i\). We point out that
for almost every \(x \in \Omega \). For this reason, the analysis of energy densities \(\widetilde{f}_v\) as in (88) is naturally encompassed by the study of functions \(f_v\) as in (87).
For every \(\varepsilon > 0\), we set \(A^i_{\varepsilon } (x) := A^i (x / \varepsilon )\), \(J^i_{\varepsilon } (x) := J^i (x / \varepsilon )\), and \(K^i_{\varepsilon } (x) := K^i (x / \varepsilon )\) for almost every \(x \in {\mathbb {R}}^n\). For every \(m \in H^1 \left( \Omega , \mathcal {M} \right) \), we define the family of energy functionals
The main result of this section is the proof that the effective functional,
encodes the asymptotic behavior of \(\mathcal {G}_{\varepsilon , v}\) as the periodicity scale converges to zero. In the expression above, \(T_{\hom }^v:( s, \xi ^{\mathsf {T}}) \in \varvec{T}\mathcal {M} \rightarrow {\mathbb {R}}\) is the tangentially homogenizedn-dimensional energy density, defined as
for every \(s \in \mathcal {M}\) and \(\xi ^{\mathsf {T}} \in \varvec{T}_s \mathcal {M}\).
We first provide the counterpart to Proposition 2.1 in the higher-dimensional setting.
Proposition 4.1
For every \(( s, \xi ^{\mathsf {T}} ) \in \varvec{T}\mathcal {M}\), the minimization problem (93) has a unique solution. Specifically, let \(\varphi _{J}, \varphi _{ A}^{\ell } \in H^{-1}_{\sharp }( Q, {\mathbb {R}}^{n \times n}), \, \ell = 1, \ldots , n\) be the unique solutions to the cell elliptic systems
and
Then, the unique solution \(\phi _v [ s, \xi ^{\mathsf {T}} ] \in H^1_{\sharp } ( Q, T_s \mathcal {M} )\) of the minimization problem (93) is given by
for every \(s \in \mathcal {M}\), and for almost every \(y \in Q\).
Proof
The characterization of \(\phi _v [ s, \xi ^{\mathsf {T}} ]\) follows by computing the Euler–Lagrange equations associated with the minimum problem in (93), by the fact that \(A^i\) is uniformly positive definite for every \(i = 1, \ldots , n\), and by the linearity of (93) with respect to s and \(\xi \). \(\square \)
We are now in a position to state our main result.
Theorem 4.1
The family \(\left( \mathcal {G}_{\varepsilon , v} \right) _{\varepsilon \in {\mathbb {R}}_+}\ \Gamma \)-converges with respect to the weak topology in \(H^1 (\Omega , \mathcal {M} )\), to the energy functional
for every \(m \in H^1 ( \Omega , \mathcal {M} )\).
Proof
We provide here a sketch of proof for the liminf inequality. Let \((m_{\varepsilon })_{\varepsilon }\) in \(H^1 ( \Omega , \mathcal {M} )\) be such that
Then, by the uniform positive definiteness of the maps \(A^i\) for every \(i = 1, \ldots , n\) and by the boundedness of \(\mathcal {M}\), the sequence \((m_{\varepsilon })_{\varepsilon }\) is uniformly bounded in \(H^1 \left( \Omega , \mathcal {M} \right) .\) By standard properties of two-scale convergence and by Proposition 2.2, there exists \(m_0 \in H^1 ( \Omega , \mathcal {M} )\) and \(m_1 \in L^2 (\Omega , H^1_{\sharp } ( Q, T_{m_0} \mathcal {M} ) )\) such that
We proceed by showing that,
Arguing as in the scalar case, we decompose \(\mathcal {G}_{\varepsilon , v} (m_{\varepsilon })\) as
where
and
For \(\psi _{0, n} \in C^{\infty } ( \bar{\Omega }, {\mathbb {R}}^3 )\) and \(\psi _{1, n} \in \mathcal {D} ( \Omega , H_{\sharp }^{1} ( Q, {\mathbb {R}}^3 ) )\), we define
We have
owing to the fact that the difference of the integrand on the left-hand side with the integrand on the right-hand side is a perfect square. By the smoothness of \(\psi _{0, n}\) and \(\psi _{1, n}\) in the x-variable, the maps \(A^i (y) \Psi ^i_n (x, y):\Psi ^i_n (x, y)\), \(A^i (y) \Psi ^i_n (x, y)\), and \(A^i (y) J^i (y) \Psi ^i_n (x, y)\) are admissible test functions. Thus, by standard properties of two-scale convergence, and owing to the regularity of \(\psi \), we deduce
By a density argument, the previous inequality yields
Finally, since \(K^{i}_{\varepsilon } \rightharpoonup \int _{Q} K^i (y) \mathrm{d}y\) weakly\(^{*}\) in \(L^{\infty } ( Q, {\mathbb {R}}^{n \times n}),\) we get
Combining (102) and (103), we deduce (98). The optimality of the lower bound is a straightforward adaptation of the arguments in Theorem 2.3. \(\square \)
References
Acerbi, E., Fonseca, I., Mingione, G.: Existence and regularity for mixtures of micromagnetic materials. Proce. R. Soc. A Math. Phys. Eng. Sci. 462, 2225–2243 (2006). https://doi.org/10.1098/rspa.2006.1655
Allaire, G.: Homogenization and two-scale convergence. SIAM J. Math. Anal. 23, 1482–1518 (1992)
Alouges, F., De Bouard, A., Merlet, B., Nicolas, L.: Stochastic homogenization of the Landau–Lifshitz–Gilbert equation (2019). arXiv preprint arXiv:1902.05743
Alouges, F., Di Fratta, G.: Homogenization of composite ferromagnetic materials. Proc. R. Soc. A Math. Phys. Eng. Sci. 471, 20150365 (2015). https://doi.org/10.1098/rspa.2015.0365
Babadjian, J.-F., Millot, V.: Homogenization of variational problems in manifold valued Sobolev spaces. ESAIM: Control Optim. Calc. Var. 16, 833–855 (2009). https://doi.org/10.1051/cocv/2009025
Bak, P., Jensen, M.H.: Theory of helical magnetic structures and phase transitions in MnSi and FeGe. J. Phys. C: Solid State Phys. 13, 0 (1980)
Bensoussan, A., Lions, J.-L., Papanicolaou, G.: Asymptotic Analysis for Periodic Structures, vol. 374. American Mathematical Society, Providence (2016). https://doi.org/10.1090/chel/374
Bogdanov, A., Hubert, A.: Stability of vortex-like structures in uniaxial ferromagnets. J. Magn. Magn. Mater. 195, 182–192 (1999). https://doi.org/10.1016/S0304-8853(98)01038-5
Braides, A., Defranceschi, A.: Homogenization of Multiple Integrals, vol. 263. Clarendon Press, Oxford (1998)
Braides, A.: \(\Gamma \)-convergence for beginners, vol. 22 of Oxford Lecture Series in Mathematics and its Applications, Oxford University Press, Oxford (2002)
Brown, W.F.: Micromagnetics. Interscience Publishers, London (1963)
Chen, G., Zang, J., te Velthuis, S.G., Liu, K., Hoffmann, A., Jiang, W.: Skyrmions in magnetic multilayers. Phys. Rep. 704, 1–49 (2017). https://doi.org/10.1016/j.physrep.2017.08.001
Cicalese, M., Ruf, M., Solombrino, F.: Chirality transitions in frustrated \(S^{2}\)-valued spin systems. Math. Mod. Methods Appl. Sci. 26(08), 1481–1529 (2016)
Cicalese, M., Solombrino, F.: Frustrated ferromagnetic spin chains: a variational approach to chirality transitions. J. Nonlinear Sci. 25(2), 291–313 (2015)
Cicalese, M.F.M.O.G.: Variational analysis of a two-dimensional frustrated spin system: emergence and rigidity of chirality transitions (2019). Preprint arXiv:1904.07792
Cortés-Ortuño, D., Wang, W., Beg, M., Pepper, R.A., Bisotti, M.A., Carey, R., Vousden, M., Kluyver, T., Hovorka, O., Fangohr, H.: Thermal stability and topological protection of skyrmions in nanotracks. Sci. Rep. 7, 4060 (2017). https://doi.org/10.1038/s41598-017-03391-8
Dacorogna, B., Fonseca, I., Malý, J., Trivisa, K.: Manifold constrained variational problems. Calc. Var. Partial. Differ. Equ. 9, 185–206 (1999). https://doi.org/10.1007/s005260050137
Dal Maso, G.: Introduction to \(\Gamma \)-convergence, vol. 8. Birkhauser, Boston (1993)
Do Carmo, M.: Differential geometry of curves and surfaces, 2nd edn. Prentice-Hall, Englewood Cliffs (2018). https://doi.org/10.1201/b18913
Dzyaloshinskii, I.: Theory of helicoidal structures in antiferromagnets. I. nonmetals. Soviet Phys. JETP 19, 960–971 (1964)
Dzyaloshinskii, I.: The theory of helicoidal structures in antiferromagnets. II. metals. Soviet Phys. JETP 20, 223–231 (1965)
Dzyaloshinsky, I.: A thermodynamic theory of weak ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958). https://doi.org/10.1016/0022-3697(58)90076-3
Ericksen, J.L.: Anisotropic fluids. Arch. Ration. Mech. Anal. 4(1), 231–237 (1959)
Ferriani, P., Bihlmayer, G., Pietzsch, O., Heinze, S., von Bergmann, K., Blügel, S., Bode, M., Wiesendanger, R., Kubetzka, A., Heide, M.: Chiral magnetic order at surfaces driven by inversion asymmetry. Nature 447, 190–193 (2007). https://doi.org/10.1038/nature05802
Fert, A.: Origin, development, and future of spintronics (Nobel lecture). Angew. Chem. Int. Ed. 47, 5956–5967 (2008). https://doi.org/10.1002/anie.200801093
Fert, A., Cros, V., Sampaio, J.: Skyrmions on the track. Nat. Nanotechnol. 8, 152–156 (2013). https://doi.org/10.1038/nnano.2013.29
Fert, A., Reyren, N., Cros, V.: Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2 (2017). https://doi.org/10.1038/natrevmats.2017.31
Fields, C.: Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 249, 91 (1956)
Hrkac, G., Pfeiler, C.-M., Praetorius, D., Ruggeri, M., Segatti, A., Stiftner, B.: Convergent tangent plane integrators for the simulation of chiral magnetic skyrmion dynamics. Adv. Comput. Math. 45, 1329–1368 (2019)
Hubert, A., Schäfer, R.: Magnetic Domains: The Analysis of Magnetic Microstructures. Springer, Berlin (2008)
Kang, W., Huang, Y., Zhang, X., Zhou, Y., Zhao, W.: Skyrmion-electronics: an overview and outlook. Proc. IEEE 104, 2040–2061 (2016)
Landau, L., Lifshitz, E.: On the theory of the dispersion of magnetic permeability in ferromagnetic bodies. Perspect. Theor. Phys. 8, 51–65 (2012). https://doi.org/10.1016/b978-0-08-036364-6.50008-9
Legrand, W., Chauleau, J.-Y., Maccariello, D., Reyren, N., Collin, S., Bouzehouane, K., Jaouen, N., Cros, V., Fert, A.: Hybrid chiral domain walls and skyrmions in magnetic multilayers. Sci. Adv. 4, 1–10 (2018)
Legrand, W., Ronceray, N., Reyren, N., Maccariello, D., Cros, V., Fert, A.: Modeling the shape of axisymmetric skyrmions in magnetic multilayers. Phys. Rev. Appl. 10(6), 64042 (2018)
Li, X., Melcher, C.: Stability of axisymmetric chiral skyrmions. J. Funct. Anal. 275(10), 2817–2844 (2018)
Lukkassen, D., Nguetseng, G., Wall, P.: Two-scale convergence. Int. J. Pure Appl. Math. 2(1), 35–86 (2002)
Marcellini, P.: Periodic solutions and homogenization of non linear variational problems. Annali di Matematica Pura ed Applicata, Series 4(117), 139–152 (1978). https://doi.org/10.1007/BF02417888
Melcher, C.: Chiral skyrmions in the plane. Proc. R. Soc. A Math. Phys. Eng. Sci. 470, 20140394 (2014). https://doi.org/10.1098/rspa.2014.0394
Milnor, J.W.: Topology from the Differentiable Viewpoint. Princeton University Press, Princeton (1965)
Milton, G.W.: The Theory of Composites, vol. 6. Cambridge University Press, Cambridge (2009). https://doi.org/10.1017/cbo9780511613357
Moreau-Luchaire, C., Moutafis, C., Reyren, N., Sampaio, J., Vaz, C.A.F., Horne, N.V., Bouzehouane, K., Garcia, K., Deranlot, C., Warnicke, P., Wohlhüter, P., George, J.-M., Weigand, M., Raabe, J., Cros, V., Fert, A.: Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotechnol. 11, 444–448 (2016). https://doi.org/10.1038/nnano.2015.313
Muratov, C.B., Slastikov, V.V.: Domain structure of ultrathin ferromagnetic elements in the presence of Dzyaloshinskii–Moriya Interaction. Proc. R. Soc. A: Math. Phys. Eng. Sci. 473, 20160666 (2017). https://doi.org/10.1098/rspa.2016.0666
Nagaosa, N., Tokura, Y.: Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013). https://doi.org/10.1038/nnano.2013.243
Nguetseng, G.: A general convergence result for a functional related to the theory of homogenization. SIAM J. Math. Anal. 20, 608–623 (2005). https://doi.org/10.1137/0520043
Outerelo, E., Ruiz, J.: GSM-108 Mapping Degree Theory, vol. 108. American Mathematical Society, Providence (2009). https://doi.org/10.1090/gsm/108
Poisson, S.D.: Mémoire sur la théorie du magnétisme, Mémoires de l’Académie des Sciences (1824)
Rybakov, F., Borisov, A., Bogdanov, A.: Three-dimensional skyrmion states in thin films of cubic helimagnets. Phys. Rev. B 87, 94424 (2013)
Sampaio, J., Cros, V., Rohart, S., Thiaville, A., Fert, A.: Nucleation, stability and current-induced motion of isolated magnetic skyrmions in nanostructures. Nat. Nanotechnol. 8, 839–844 (2013). https://doi.org/10.1038/nnano.2013.210
Sanchez-Palencia, E.: Comportament local et macroscopique d’un type de milieux physiques hétéroènes. Int. J. Eng. Sci. 12, 331–351 (1974)
Thiaville, A., Rohart, S., Jué, É., Cros, V., Fert, A.: Dynamics of Dzyaloshinskii domain walls in ultrathin magnetic films. EPL (Europhys. Lett.) 100, 57002 (2012). https://doi.org/10.1209/0295-5075/100/57002
Wright, D.C., Mermin, N.D.: Crystallin liquids: the blue phases. Rev. Mod. Phys. 61, 385–432 (1989)
Yu, X., Onose, Y., Kanazawa, N., Park, J., Han, J., Matsui, Y., Nagaosa, N., Tokura, Y.: Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901 (2010)
Acknowledgements
Open access funding provided by Austrian Science Fund (FWF). Both authors acknowledge support from the Austrian Science Fund (FWF) through the special research program Taming complexity in partial differential systems (Grant SFB F65). The research of E.D. has been supported from the Austrian Science Fund (FWF) through the grants V 662-N32 High contrast materials in plasticity and magnetoelasticity and I 4052 N32 Large Strain Challenges in Materials Science and from BMBWF through the OeAD-WTZ project CZ04/2019 Mathematical Frontiers in Large Strain Continuum Mechanics. G. Di F. would like to thank the Isaac Newton Institute for Mathematical Sciences for support and hospitality during the program “The design of new materials programme” when part of the work on this paper was undertaken. G. Di F. acknowledges the support of the Vienna Science and Technology Fund (WWTF) through the research project Thermally controlled magnetization dynamics (Grant MA14-44).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Dr.Paul Newton.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Davoli, E., Di Fratta, G. Homogenization of Chiral Magnetic Materials: A Mathematical Evidence of Dzyaloshinskii’s Predictions on Helical Structures. J Nonlinear Sci 30, 1229–1262 (2020). https://doi.org/10.1007/s00332-019-09606-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00332-019-09606-8
Keywords
- Chiral magnetic materials
- Micromagnetics
- Dzyaloshinskii–Moriya interaction
- Homogenization
- Manifold-valued Sobolev spaces