Retrieval optimization in a warehouse with multiple input/output-points

Abstract

Optimizing retrieval requests in warehouses is essential for maintaining a smooth flow of products. Most studies on warehouse retrieval optimization have considered no more than two input/output-points for product retrieval. In this paper, we study different variants of a new stacker crane scheduling problem, where pallets have to be retrieved in a warehouse with multiple input/output-points. The goal is to minimize the total travel time of the stacker crane to perform all retrievals. The problem variants we consider require determining either the pallet retrieval sequence, the assignment of pallets to input/output-points, or both. We prove NP-hardness results and identify cases that can be solved in strongly polynomial time. Additionally, we propose transformations to the traveling salesman problem, enabling the application of a vast collection of existing solution techniques. Finally, in an extensive computational study, we compare different problem variants, assess their gain of optimization, and experimentally analyze the impact of various instance parameters.

1 Introduction

The storage and subsequent retrieval of items in warehouses is crucial for ensuring a smooth flow of products in supply chains. To increase the efficiency, warehouses often use automated storage/retrieval systems (AS/RS), where all incoming items are transferred on uniform pallets. In such storages, there are two types of requests: storage requests and retrieval requests. For a storage request, a pallet is moved by an automatically controlled stacker crane from an input/output-point (I/O-point) to a location within the warehouse. Moreover, for a retrieval request, the stacker crane returns a pallet to an I/O-point. To obtain more details on warehouses with AS/RS, we refer to the survey papers by Boysen and Stephan (2016) as well as Roodbergen and Vis (2009).

1.1 Motivation

Our work was initially motivated by a problem setting we encountered at an industrial company operating a high-bay warehouse with AS/RS. Nevertheless, the scope of our findings reaches beyond this specific context. The problem we identified and subsequently studied has broad applicability across a range of settings, even those that do not involve warehouses, as we will illustrate later. For clarity and ease of understanding, we will keep using terminology related to warehouses.

At the aforementioned industrial company, we discovered a warehouse with three different I/O-points and the following stacker crane scheduling problem. Initially and finally, the stacker crane is located at a specific depot I/O-point. A given set of retrieval requests has to be processed, where each pallet to be retrieved can be returned to an arbitrary I/O-point. When approaching an I/O-point, the stacker crane drops the pallet to be retrieved there and picks up a pallet to be stored. It then moves to the next pallet to be retrieved in the warehouse and swaps it with the pallet to be stored currently loaded on the stacker crane (it has an additional buffer location to perform such swaps).

Each pallet to be retrieved will be returned to the storage after an employee has removed specific parts from it used in a further production process. Consequently, at each I/O-point, exactly the pallet that was previously retrieved there is available as a storage request. This means that the retrieval requests are automatically synchronized with the number of storage requests waiting at the I/O-points. Therefore, for a processing sequence of retrieval requests and their assignment to I/O-points, the storage requests result implicitly and do not have to be considered explicitly. Moreover, to optimize storage locations based on the retrieval frequencies of the pallets, the company regularly rearranges the assignment of pallets to storage locations, for instance during breaks or at night. The described process is called warehouse reshuffling (Pazour and Carlo 2015; Buckow and Knust 2023a, b), and it ensures that high frequency retrieval requests can be performed fast without considering the selection of storage locations for storage requests.

The goal is to minimize the makespan, i.e., the total travel time of the stacker crane to perform all retrieval requests of the current shift. However, even if the travel time is the key performance measure in the company’s problem setting, our approaches can also handle other performance measures instead, such as the stacker crane’s energy consumption or its wear and tear. In the following, we hence use the more general term travel costs instead of travel time, highlighting that we simply can use another performance measure without affecting the correctness of our proposed methodology.

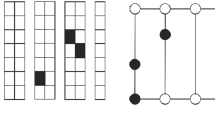
For example, Fig. 1 shows a feasible stacker crane tour processing four pallet retrieval requests in a warehouse with three I/O-points (the leftmost I/O-point serves as depot where the stacker crane tour starts and ends). The numbers indicate the sequence in which the stacker crane traverses the tour.

Fig. 1

Stacker crane tour processing four pallet retrieval requests. Numbers indicate the order of movements

The industrial company mentioned operates a large high-bay racking using a stacker crane equipped with an additional buffer location. This device is designed to swap the pallet currently loaded on the stacker crane with a pallet at a storage location. We know from the stacker crane’s manufacturer that other companies operate similar warehouses. These firms are predominantly engaged in sectors such as the metal industry or the production of windows and doors. Since they handle heavy pallets, it is not feasible to use the stacker crane’s increased capacity to transport two pallets at once. Therefore, pallet swaps are the operating mode of choice in such warehouses (Buckow and Knust 2023b, a).

Note that this setting can also be used to model other problems. For example, besides the scenario discussed above, it also applies to warehouses with stacker cranes of capacity one when only retrieval requests have to be performed. This is possible because the stacker crane can simply omit picking up a pallet when reaching an I/O-point, while still visiting pallets and I/O-points alternately in the tour. Furthermore, the described problem can be used to model specific transportation problems outside of warehouses, such as transporting patients to health care facilities. In this scenario, different patients are located in different places and a single ambulance, capable of transporting only one patient at a time, must transport each patient to one of several healthcare facilities. The ambulance starts and ends its tour at a given facility, and the goal is to minimize the time it takes to complete the transport of all patients. This can be modeled by our problem, with the patients corresponding to retrieval requests and the facilities corresponding to I/O-points.

Our problem can also be interpreted as a new variant of the bipartite traveling salesman problem (${{\text {TSP}}}$). In the bipartite ${{\text {TSP}}}$, two node sets of equal size and travel costs between the nodes are given, and the goal is to find a minimum cost tour that visits each node exactly once, where nodes from the two sets must be visited alternately. For more details on the bipartite ${{\text {TSP}}}$, we refer to García and Tejel (2017), Kovács et al (2018) and Frank et al (1998). In the case of our problem, we also aim to find a minimum cost tour that alternately visits pallets and I/O-points. However, in contrast to the bipartite ${{\text {TSP}}}$, I/O-points are allowed to be visited any number of times, while each pallet must be visited exactly once.

Depending on the real-world scenario to be modeled, each pallet may only be allowed to be retrieved at a specific I/O-point. This is the case, for example, if the pallet has to be processed on a machine that is located in a production hall which can only be reached via a specific I/O-point. Similarly, each pallet may need to be retrieved at a specific I/O-point because there a specific truck is loaded. In addition, a sequence may be given in which the pallets have to be retrieved. For example, the machines in the production process may require the pallets in a specific order. Besides the basic problem scenario described above, we hence also study the problem scenarios that the pallet retrieval sequence and/or the assignment of pallets to I/O-points is fixed.

1.2 Literature review

A lot of literature has tackled stacker crane scheduling problems to optimize storage and retrieval requests in warehouses with a single I/O-point (Boysen and Stephan 2016). These problems mainly deal with finding an appropriate sequence in which the storage and retrieval requests are processed by the stacker crane. The stacker crane can thereby be operated in two different ways, namely in a single command cycle or in a dual command cycle. In a single command cycle, the stacker crane performs either a single storage or a single retrieval request. In a dual command cycle, the stacker crane performs a combined storage and retrieval request. First, the stacker crane picks up a pallet to be stored at an I/O-point and brings it to an empty location. Afterwards, the stacker crane moves unloaded to the location of a retrieval request and returns the pallet there to an I/O-point.

Some modern warehouses (e.g., the industrial company mentioned above) are equipped with a stacker crane classified as a twin shuttle or sometimes also called dual shuttle (Keserla and Peters 1994; Malmborg 2000; Meller and Mungwattana 1997). Because a twin shuttle has an additional buffer, it can perform swap moves where the stacker crane directly swaps the pallet at a storage location with the pallet currently stored in its buffer (Buckow and Knust (2023b, 2023a)). By using swap moves when performing dual command cycles, the unloaded travel can be completely eliminated by directly swapping the pallet to be stored with the pallet to be retrieved. Moreover, note that the handling effort of the dual command cycles only depends on the retrieval requests when using swap moves, because the pallet retrieval locations are used to store the next pallets. However, recall that in the problem setting of the company mentioned above, they are handling heavy pallets, and it is hence not possible to combine two storage and two retrieval requests to one command cycle, even with two pallet positions on the stacker crane.

There are few studies on the optimization of storage and retrieval requests in warehouses with more than one I/O-point. Nonetheless, the publications on the stacker crane scheduling problems most similar to ours are summarized in Table 1, including a brief description of the problem characteristics, their complexity and the solution methods applied. Other complexity results for related problems are presented by Boysen and Stephan (2016). Van den Berg and Gademann (1999) consider a specialized scenario where the input and the output point are separated locations, i.e., all storage requests start at the input point, and all retrieval requests have to be brought to the output point. They assume that the arrival sequence of the storage requests is fixed, and present a polynomial-time algorithm to solve their problem optimally. Both Vis and Roodbergen (2009) as well as Vis and Carlo (2010) consider a container storage with multiple rows each having two I/O-points. On the one hand, Vis and Roodbergen (2009) study the case with a single stacker crane, and they decompose their problem into single-row blocks where all requests are located on a line. Moreover, they combine a linear assignment and a dynamic programming approach to solve their problem efficiently. On the other hand, Vis and Carlo (2010) extend the described setting to the case with two coorperating stacker cranes, and they developed a simulated annealing heuristic for their problem.

Table 1 Overview of publications with similar stacker crane scheduling problems

In the case of two I/O-points and arbitrary positions of the requests, Gharehgozli et al (2014b) present polynomial-time algorithms to minimize the total travel time of the stacker crane. Man et al (2021) study a bi-objective stacker crane scheduling problem to optimize storage and retrieval requests in a warehouse with two I/O-points. They consider the two objectives of minimizing the total travel time and the total tardiness. Yu et al (2022) present models for the expected travel time in warehouses with two I/O-points and a class-based storage policy, i.e., the storage is partitioned into different classes where only specific pallets are allowed to be stored in each class. Nevertheless, Yu et al (2022) concentrate on warehouse design, and no algorithms for scheduling storage and retrieval requests are presented.

Gharehgozli et al (2014a) consider a yard crane scheduling problem with multiple I/O-points arranged linearly both on the landside and seaside. They prove that their problem is NP-hard, but the proof assumes that storage requests have to be scheduled in addition to retrieval requests. Nonetheless, the complexity status when only scheduling retrieval requests in a warehouse with multiple I/O-points remains unclear. Gharehgozli et al (2014a) formulate their problem as a ${{\text {TSP}}}$ and introduce a branch-and-bound algorithm that utilizes patching techniques to solve it. However, the approach presented by Gharehgozli et al (2014a) primarily exploits the specific distances in container yards, making it unsuitable for our problem setting. Moreover, their algorithm is not designed to handle the specific case that the retrieval I/O-points are fixed.

1.3 Contribution

In this paper, we study different variants of a new stacker crane scheduling problem, which we call the retrieval optimization problem (${{\text {ROP}}}$). In the ${{\text {ROP}}}$, we are given a warehouse with multiple I/O-points, and a set of retrieval requests to be processed. The goal of the ${{\text {ROP}}}$ is to schedule all retrieval requests with minimum total travel costs of the stacker crane. As already described above, the ${{\text {ROP}}}$ has several applications, including the problem setting of the company, which initially motivated our work.

In order to schedule the retrieval requests, we have to determine a sequence in which the pallets are retrieved, and it must be decided which pallet is retrieved at which I/O-point. We also consider different problem variants with a fixed pallet retrieval sequence and/or a fixed assignment of pallets to retrieval I/O-points. Even if there are typically two-dimensional warehouses in practice, our approach is more general and can handle arbitrary costs as long as they are symmetric and fulfill the triangle inequality. In contrast to the existing literature, we consider an arbitrary number of I/O-points, arbitrary positions of the requests, and dual command cycles in connection with swap moves are used to pair storage and retrieval tasks. Since swap moves are used, only the scheduled retrieval requests determine the handling effort.

Our results show that the ${{\text {ROP}}}$ is strongly NP-hard as long as the number of I/O-points is part of the input and the pallet retrieval sequence has to be determined. In contrast, if the number of I/O-points is fixed or the pallet retrieval sequence is already given, the problem becomes polynomially solvable. Moreover, we present efficient transformations of the ${{\text {ROP}}}$ to the ${{\text {TSP}}}$, which opens a rich arsenal of existing solution approaches in the literature, enabling to effectively solve the ${{\text {ROP}}}$. The computational study reveals several managerial implications and insights, such as that the stacker crane’s total travel costs can be reduced considerably by allowing the pallets to be retrieved at arbitrary I/O-points instead of fixing them.

The remainder of this paper is structured as follows. First, in Sect. 2, we provide a formal definition of the ${{\text {ROP}}}$ and introduce the used notations. Section 3 is devoted to theoretical properties: we prove NP-hardness of two variants of the ${{\text {ROP}}}$, consider the case that the number of I/O-points is fixed, and investigate the gain of flexible retrieval I/O-points. Next, in order to solve the ${{\text {ROP}}}$, we present efficient transformations to the ${{\text {TSP}}}$ in Sect. 4. In Sect. 5, we reveal extensive computational results for different problem variants. Finally, Sect. 6 concludes the paper.

2 Problem definition

The ${{\text {ROP}}}$ can be stated as follows. In a warehouse, n pallets $P=\{p_1,\ldots ,p_n\}$ have to be retrieved, and there are m different I/O-points $\Theta =\{\theta _1,\ldots ,\theta _m\}$, where $\theta _{depot} \in \Theta$ denotes the depot I/O-point. Each pallet $p \in P$ and each I/O-point $\theta \in \Theta$ is associated with a location $\ell (p)$ and $\ell (\theta )$, respectively. For the resulting $\mu =n+m$ locations $L=\{\ell _1,\ldots ,\ell _{\mu }\}$, we have symmetric travel costs $c[\ell _i,\ell _j]=c[\ell _j,\ell _i]$, fulfilling the triangle inequality $c[\ell _i,\ell _j] \le c[\ell _i,\ell _k]+c[\ell _k,\ell _j]$ for all locations $\ell _i,\ell _j,\ell _k \in L$. To express the travel costs between the locations of pallets $p,p' \in P$ and I/O-points $\theta ,\theta ' \in \Theta$, we also use the simpler notations $c[p,\theta ]$, $c[\theta ,p]$, $c[p,p']$, and $c[\theta ,\theta ']$ instead of $c[\ell (p),\ell (\theta )]$, $c[\ell (\theta ),\ell (p)]$, $c[\ell (p),\ell (p')]$, and $c[\ell (\theta ),\ell (\theta ')]$, respectively.

Let $\Pi$ denote the set of permutations of all pallets P, and $\pi =(\pi _1,\ldots ,\pi _n) \in \Pi$ be a specific sequence in which the n pallets are retrieved. Moreover, $\alpha =(\alpha (p_1),\ldots ,\alpha (p_n)) \in \Theta ^n$ represents an assignment of the pallets to I/O-points (where $\alpha (p) \in \Theta$ denotes the I/O-point at which pallet $p \in P$ is retrieved). The goal of the ${{\text {ROP}}}$ is to find a pallet retrieval sequence $\pi \in \Pi$ as well as an assignment $\alpha \in \Theta ^n$ of the pallets to I/O-points such that the total travel costs ${{\text {TTC}}}: \Pi \times \Theta ^n\rightarrow \mathbb {R}_+$ of the resulting stacker crane tour are minimized, i.e.,

$$\begin{aligned} \min _{(\pi ,\alpha ) \in \Pi \times \Theta ^n}{{\text {TTC}}}(\pi ,\alpha ), \end{aligned}$$

where the objective function is defined as

$$\begin{aligned} \begin{aligned} {{\text {TTC}}}(\pi ,\alpha ) ={}&c[\theta _{depot},\pi _1] + c[\pi _1,\alpha (\pi _1)] + c[\alpha (\pi _1),\pi _2] + \ldots \\ {}&+ c[\pi _n,\alpha (\pi _n)] + c[\alpha (\pi _n),\theta _{depot}]\\ ={}&c[\theta _{depot},\pi _1]+c[\alpha (\pi _n),\theta _{depot}]+\sum _{i=2}^{n} c[\alpha (\pi _{i-1}),\pi _{i}]+\sum _{i=1}^{n} c[\pi _{i},\alpha (\pi _{i})].\\ \end{aligned} \end{aligned}$$

Here, it is assumed that the stacker crane tour starts and ends at the depot I/O-point $\theta _{depot}$. For a solution $S \in \Pi \times \Theta ^n$, we denote by $\pi (S)$ its pallet sequence, by $\alpha (S)$ the tuple $(\alpha (p_1),\ldots ,\alpha (p_n))$, and by $c(S)={{\text {TTC}}}(\pi (S),\alpha (S))$ its costs. In the stacker crane tour corresponding to a solution $S \in \Pi \times \Theta ^n$, pallets and I/O-points are visited alternately. It is sufficient to consider only such tours, as the costs cannot decrease by visiting additional locations in between due to the triangle inequality. In particular, we can assume that $\alpha (\pi _n)=\theta _{depot}$ in an optimal solution, as we need to return to the depot I/O-point at the end of the tour.

Example 1

Consider the instance of the ${{\text {ROP}}}$ shown in Fig. 2 with $n=3$ pallets, $m=2$ I/O-points, $\theta _{depot}=\theta _1$, and costs $c[\ell _i,\ell _j]$ as displayed in Fig. 2a. A feasible solution S for this instance with $\pi (S)=(p_1,p_2,p_3)$, $\alpha (S)=(\theta _1,\theta _1,\theta _2)$, and total costs $c(S)=2+2+2+2+6+1+5=20$ is shown in Fig. 2b. Note that in solution S, the stacker crane additionally needs to traverse the arc $(\theta _2,\theta _1)$ in order to return to the depot I/O-point $\theta _1$. A better feasible solution $\overline{S}$ with $\pi (\overline{S})=(p_2,p_3,p_1)$, $\alpha (\overline{S})=(\theta _1,\theta _2,\theta _2)$, and $c(\overline{S})=13$ is displayed in Fig. 2c. In solution $\overline{S}$, the last pallet $p_1$ is already retrieved at the depot I/O-point $\theta _1$, eliminating an additional stacker crane movement.

Fig. 2

Example of the ${{\text {ROP}}}$

Since the pallet sequence $\pi$ and/or the assignment $\alpha$ of pallets to I/O-points may be fixed or not, we consider the following four problem variants:

• (i) both $\pi$ and $\alpha$ are fixed,

• (ii) the permutation $\pi$ is fixed, whereas the assigned I/O-points $\alpha (p) \in \Theta$ for all pallets $p \in P$ have to be determined,

• (iii) the assigned I/O-points $\alpha (p) \in \Theta$ for all pallets $p \in P$ are fixed, whereas the permutation $\pi$ has to be determined, or

• (iv) both the permutation $\pi$ and the assigned I/O-points $\alpha (p) \in \Theta$ for all pallets $p \in P$ have to be determined.

In case (i), a solution is already fully determined and there is no room for optimization, as the stacker crane’s tour is fixed due to the known permutation $\pi$ and the known assignment of the pallets $p \in P$ to I/O-points $\alpha (p) \in \Theta$. Case (ii) is also easy to solve, because the pallet permutation $\pi$ is fixed, and the I/O-points to be assigned can be chosen independently of each other, as they are always approached between two fixed locations. Therefore, for all $i=1,\ldots ,n-1$, we set the I/O-points to

$$\begin{aligned} \alpha (\pi _i)= \text {arg min}_{\theta \in \Theta }\{c[\pi _i,\theta ]+c[\theta ,\pi _{i+1}]\}, \end{aligned}$$

(1)

meaning that an I/O-point $\theta \in \Theta$ is chosen such that the costs $c[\pi _i,\theta ]+c[\theta ,\pi _{i+1}]$ of moving from the current pallet $\pi _i$ over I/O-point $\theta$ to its fixed successor pallet $\pi _{i+1}$ are minimized. Moreover, we set $\alpha (\pi _n)=\theta _{depot}$ as the stacker crane needs to return to the depot I/O-point $\theta _{depot}$.

As only the assignment $\alpha$ of pallets to I/O-points has to be determined in case (ii), we refer to this problem variant as ${{\text {ROP}}_{{{\text {A}}}}}$. However, the cases (iii) and (iv) require to find an appropriate sequence in which the pallets are retrieved; these cases are both more complex to consider. We refer to the problem variant of case (iii) as ${{\text {ROP}}_{{{\text {P}}}}}$, since only the permutation $\pi$ needs to be determined. Similarly, the problem variant of case (iv) is called ${{\text {ROP}}_{{{\text {AP}}}}}$ because both the assignment $\alpha$ and the permutation $\pi$ must be determined. In the following sections of this paper, the problem variants ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ are discussed in more detail. For the sake of completeness and to better illustrate the original research problem, a complete mathematical model for the ${{\text {ROP}}}$ can be found in Appendix A.

3 Theoretical results

In this section, we present some theoretical results of the ${{\text {ROP}}}$. First, in Sect. 3.1, we prove that both ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$ are strongly NP-hard. Afterwards, it is shown in Sect. 3.2 that these two problem variants become solvable in strongly polynomial time if the number of I/O-points is fixed. Finally, in Sect. 3.3, we analytically investigate the difference between ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$, i.e., the gain when the retrieval I/O-points are not fixed but flexible.

3.1 NP-hardness

The variant ${{\text {ROP}}_{{{\text {AP}}}}}$ aims to find a minimum cost tour that alternately visits pallets and I/O-points. In contrast to the well-known ${{\text {TSP}}}$, which aims to find a minimum cost tour of nodes containing each node exactly once, each pallet must be visited exactly once, whereas the I/O-points do not require a given number of visits. The ${{\text {TSP}}}$ is known to be NP-hard in the strong sense, even if the distances are restricted to the Chebyshev, Euclidean and Manhattan metric, respectively (Garey and Johnson 1979). In Theorem 1, we show that ${{\text {ROP}}_{{{\text {AP}}}}}$ is also strongly NP-hard by giving a reduction from the ${{\text {TSP}}}$. Note that the provided reduction exploits the fact that the number m of I/O-points is part of the input. In Sect. 3.2, we show that ${{\text {ROP}}_{{{\text {AP}}}}}$ becomes polynomially solvable for a fixed number m. Furthermore, note that the costs of the resulting ${{\text {ROP}}_{{{\text {AP}}}}}$ instance correspond to the same metric as the costs of the original ${{\text {TSP}}}$ instance. Therefore, even for the specific cost types (mainly Chebyshev, Euclidean and Manhattan) typically occurring in real warehouses, ${{\text {ROP}}_{{{\text {AP}}}}}$ remains NP-hard.

Theorem 1

${{\text {ROP}}_{{{\text {AP}}}}}$ is NP-hard in the strong sense.

Proof

We reduce from the decision variant of the metric ${{\text {TSP}}}$, where we are given a complete, undirected graph $G=(V,E)$, costs $c'[v,w]=c'[w,v]$ for all $v,w \in V$ (which are symmetric and fulfill the triangle inequality), and a threshold value $k \ge 0$. The aim is to decide whether there exists a Hamiltonian cycle on G with total costs that are less than or equal to k.

For a given ${{\text {TSP}}}$ instance, we construct an ${{\text {ROP}}_{{{\text {AP}}}}}$ instance with $n=|V|$ pallets and $m=|V|$ I/O-points (note that $n=m$), where each node $v_i \in V$ corresponds to both a pallet $p_i$ and an I/O-point $\theta _i$. The costs are set to $c[\theta _i,p_i]=c[p_i,\theta _i]=0$ for all $i=1,\ldots ,n$, and $c[\theta _i,p_j]=c[p_i,\theta _j]=c'[v_i,v_j]$ for all $i,j=1,\ldots ,n$ with $i \ne j$. Next, we show that there exists a ${{\text {TSP}}}$ solution $S_{{{\text {TSP}}}}$ with costs $c(S_{{{\text {TSP}}}}) \le k$ if and only if there is an ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S_{{{\text {AP}}}}$ with costs $c(S_{{{\text {AP}}}}) \le k$.

“$\Rightarrow$”: We start having a solution $S_{{{\text {TSP}}}}$ with costs $c(S_{{{\text {TSP}}}}) \le k$. W.l.o.g., we assume that the nodes are processed in the sequence $(v_1,v_2,\ldots ,v_n)$, and $\theta _{depot}=\theta _{\mu }$ for one $\mu \in \{1,\ldots ,n\}$. We construct a solution $S_{{{\text {AP}}}}$ for our problem, where the pallets are processed in the sequence $\pi (S_{{{\text {AP}}}})=(p_{\mu +1},p_{\mu +2},\ldots ,p_n,p_1,\ldots ,p_{\mu })$. The assignment to I/O-points is given by $\alpha (p_i)=\theta _i$ for all $i=1,\ldots ,n$, resulting in the overall tour

$$\begin{aligned} (\theta _{\mu },p_{\mu +1},\theta _{\mu +1},p_{\mu +2},\theta _{\mu +2},\ldots ,p_n,\theta _n,p_1,\theta _1,\ldots ,p_{\mu },\theta _{\mu }), \end{aligned}$$

with total costs

$$\begin{aligned} c(S_{{{\text {AP}}}})=\sum _{i=1}^{n}(c[p_i,\theta _i]+c[\theta _i,p_{i+1}])=\sum _{i=1}^{n}c[\theta _i,p_{i+1}]=\sum _{i=1}^{n}c'[v_i,v_{i+1}]=c(S_{{{\text {TSP}}}}) \le k, \end{aligned}$$

where $p_{n+1}=p_1$ and $v_{n+1}=v_1$.

“$\Leftarrow$”: We start having a solution $S_{{{\text {AP}}}}$ with costs $c(S_{{{\text {AP}}}}) \le k$, where we can assume $\alpha (p_i)=\theta _i$ for all $i=1,\ldots ,n$, since otherwise a solution that is not worse can be constructed because of the triangle inequality and the fact that $c[p_i,\theta _i]=0$ for all $i=1,\ldots ,n$. We assume w.l.o.g. that the pallets are processed in the sequence $\pi (S_{{{\text {AP}}}})=(p_1,p_2,\ldots ,p_n)$, resulting in the overall tour $(\theta _{depot},p_{1},\theta _{1},p_{2},\theta _{2},\ldots ,p_n,\theta _n,\theta _{depot})$. We then construct the ${{\text {TSP}}}$ solution $S_{{{\text {TSP}}}}=(v_1,v_2,\ldots ,v_n)$, with total costs of

$$\begin{aligned} \begin{aligned} c(S_{{{\text {TSP}}}}) ={}& c^{\prime} [v_n,v_1]+\sum _{i=1}^{n-1} c^{\prime} [v_i,v_{i+1}]&\\ ={}&c[\theta _n,p_1]+\sum _{i=1}^{n-1}c[\theta _i,p_{i+1}]+\sum _{i=1}^{n}c[p_i,\theta _i]&\\ \le {}& c[\theta _n,\theta _{depot}]+c[\theta _{depot},p_1]+\sum _{i=1}^{n-1}c[\theta _i,p_{i+1}]+\sum _{i=1}^{n}c[p_i,\theta _i]&\\ ={}&c(S_{{{\text {AP}}}}) \le k.&\\ \end{aligned} \end{aligned}$$

Note that in this calculation, we have $c[\theta _n,p_1] \le c[\theta _n,\theta _{depot}]+c[\theta _{depot},p_1]$ due to the triangle inequality. $\square$

Similar to ${{\text {ROP}}_{{{\text {AP}}}}}$, variant ${{\text {ROP}}_{{{\text {P}}}}}$ also seeks a minimum cost tour that alternately visits pallets and I/O-points, and in which every pallet is visited exactly once. However, ${{\text {ROP}}_{{{\text {P}}}}}$ additionally requires each pallet $p \in P$ to be retrieved at a specific I/O-point $\alpha (p) \in \Theta$. Despite this additional constraint, ${{\text {ROP}}_{{{\text {P}}}}}$ is also strongly NP-hard, as shown in Theorem 2 by slightly changing the NP-hardness proof of ${{\text {ROP}}_{{{\text {AP}}}}}$ for Theorem 1. Again, note that the provided reduction exploits the fact that the number m of I/O-points is part of the input. Also, the costs of the resulting ${{\text {ROP}}_{{{\text {P}}}}}$ instance correspond to the same metric as the costs of the original ${{\text {TSP}}}$ instance, and hence ${{\text {ROP}}_{{{\text {P}}}}}$ remains NP-hard even if the costs are restricted to the Chebyshev, Euclidean and Manhattan metric, respectively.

Theorem 2

${{\text {ROP}}_{{{\text {P}}}}}$ is NP-hard in the strong sense.

Proof

This can be proven in a similar way as Theorem 1, with the only change that in the constructed instance of our problem, we set the I/O-points corresponding to the pallets to $\alpha (p_i)=\theta _i$ for all $i=1,\ldots ,n$. Since we have $c[p_i,\theta _i]=0$ for all $i=1,\ldots ,n$, the arguments remain the same as in the proof of Theorem 1. $\square$

3.2 A fixed number of I/O-points

The NP-hardness proofs of ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$ according to Theorems 1 and 2 rely on the fact that an arbitrary number m of I/O-points is allowed to be created since m is part of the input. Nonetheless, for example, both ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$ are trivial to solve if we have a single I/O-point, because in this case, the pallet retrieval sequence has no impact on the objective function. Next, we consider the question whether ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$ can be solved efficiently if the number m of I/O-points is not part of the input, but a fixed constant.

As shown in Theorem 3, even ${{\text {ROP}}_{{{\text {AP}}}}}$ is solvable in strongly polynomial time if m is a fixed constant. The key observation to construct a polynomial algorithm is that the required travel cost to retrieve a pallet depends on exactly two I/O-points. The problem can therefore be solved by determining n appropriate pairs of I/O-points (which we call dominos in the following), and the n pallets must be assigned to these pairs of I/O-points.

Theorem 3

${{\text {ROP}}_{{{\text {AP}}}}}$ is solvable in $\mathcal {O}(n^{m^2+2m+3})$.

Proof

We define $D=D_{start} \cup D_{main} \cup D_{target}$ as the set of all domino types, where $D_{start}=\{s\} \times \Theta$ represents the start dominos (where the tour starts), $D_{main}=\Theta \times \Theta$ represents the main dominos (pairs of two I/O-points $\theta ,\theta ' \in \Theta$), and $D_{target}=\Theta \times \{t\}$ represents the target dominos (where the tour ends). To construct all possible tours, we enumerate all n-element multi-subsets of D that contain at least one start domino and one end domino, check if a feasible tour can be constructed with the current combination of dominos, and determine a matching of the pallets to the dominos incurring minimum costs. The proof is illustrated with Fig. 3 using an instance with $n=4$ pallets and $m=3$ I/O-points. Figure 3a shows a feasible ordering of a combination of n dominos and the assigned pallets, while Fig. 3b displays the resulting stacker crane tour.

Fig. 3

Illustration of the domino approach

Since exactly n pallets have to be retrieved and exactly one start as well as one end domino have to be selected, each type of domino occurs between 0 and $n-1$ times in any feasible domino combination. In total, there are $|D|=m^2+2m$ different types of dominos, and hence we have to check at most $\mathcal {O}(n^{m^2+2m})$ possible domino combinations. To determine a corresponding tour for the current domino combination, the following steps need to be performed:

• 1. Check if there is an ordering of the n current dominos such that for all adjacent dominos $(\theta _{j},\theta _{\nu })$ and $(\theta _{\mu },\theta _{\lambda })$, we have $\nu =\mu$. Such an ordering can be determined in $\mathcal {O}(n)$ by finding an Eulerian path in a multi-graph, where we have a node for each element in $\Theta \cup \{s,t\}$, and for each of the n chosen dominos we create an edge between the two corresponding nodes. Discard the current combination of dominos if there does not exist such an ordering (there exists a feasible tour for the combination if and only if there exists such an ordering, since the I/O-point at which a pallet is brought to defines the position where the stacker crane is located before handling the next pallet). Any Eulerian path results in the same objective value.

• 2. It remains to find a minimum cost matching between the n pallets and the n current dominos. The costs of the arcs are chosen as follows: Matching pallet $p \in P$ with (i) domino $(s,\theta ) \in D_{start}$ incurs costs $c[\theta _{depot},p]+c[p,\theta ]$, (ii) domino $(\theta _{j},\theta _{j'}) \in D_{main}$ incurs costs $c[\theta _{j},p]+c[p,\theta _{j'}]$, and (iii) domino $(\theta ,t) \in D_{target}$ incurs costs $c[\theta ,p]+c[p,\theta _{depot}]$. By finding such a matching, the total cost for the given combination of dominos is minimized. This can be done in $\mathcal {O}(n^3)$ by using the Hungarian method (Kuhn and Yaw 1955).

From all combinations of dominos checked as described above, a best solution found is stored. This solution must be optimal, because all possible combinations of dominos are checked, and for each combination, a cheapest matching of pallets with dominos is calculated. The total runtime of the described procedure is $\mathcal {O}(n^{m^2+2m+3})$ as checking a combination can be done in $\mathcal {O}(n^3)$ (this runtime is determined by calculating the matching), and at most $\mathcal {O}(n^{m^2+2m})$ combinations need to be checked. $\square$

The proof of Theorem 3 for ${{\text {ROP}}_{{{\text {AP}}}}}$ can easily be adapted to ${{\text {ROP}}_{{{\text {P}}}}}$ by removing some arcs in the matching part and further restricting the allowed combinations of dominos. As shown in Theorem 4, it follows that ${{\text {ROP}}_{{{\text {P}}}}}$ also becomes solvable in strongly polynomial time for any fixed value of m.

Theorem 4

${{\text {ROP}}_{{{\text {P}}}}}$ is solvable in $\mathcal {O}(n^{m^2+2m+3})$.

Proof

This can be proven in a similar way as Theorem 3, except the following changes in the matching part performed for each domino combination. Only arcs which are compatible with the given assignment $\alpha$ of pallets to I/O-points have to be considered in the matching part, i.e., we only have an arc from pallet $p \in P$ to a start domino $(s,\theta ) \in D_{start}$ if $\alpha (p)=\theta$, and similarly, we only have an arc from pallet p to a main domino $(\theta ,\theta ') \in D_{main}$ if $\alpha (p)=\theta '$. From pallet p, we still have an arc to each target domino $(\theta ,t) \in D_{target}$, but we change the arc costs to $c[\theta ,p]+c[p,\alpha (p)]+c[\alpha (p),\theta _{depot}]$ (it is thus ensured that the costs for returning to the depot I/O-point are considered properly). If there does not exist a perfect matching, the given domino combination is discarded, since it is infeasible. $\square$

The computational runtimes of the algorithms provided for ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$ depend strongly on the number m of I/O-points. However, despite the polynomial runtime for any fixed value of m, this approach is not practical, due to the large degree of the polynomial. It remains open if there exist fixed parameter tractable (FPT) algorithms for ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$ with respect to the parameter m, where the resulting polynomial runtime is independent of the parameter m.

3.3 Gain of flexible retrieval I/O-points

In contrast to ${{\text {ROP}}_{{{\text {AP}}}}}$, the assignment of pallets to retrieval I/O-points is already fixed in the case of ${{\text {ROP}}_{{{\text {P}}}}}$. Thus, algorithms have less flexibility to find good solutions when considering ${{\text {ROP}}_{{{\text {P}}}}}$ instead of ${{\text {ROP}}_{{{\text {AP}}}}}$. In this subsection, we study how much can be gained by choosing arbitrary retrieval I/O-points compared to fixed retrieval I/O-points.

In Theorem 5, we compare the costs of optimal solutions when the retrieval I/O-points are fixed or not, i.e., we compare ${{\text {ROP}}_{{{\text {P}}}}}$ with ${{\text {ROP}}_{{{\text {AP}}}}}$. It shows that the optimal costs can be arbitrarily larger when having fixed instead of non-fixed retrieval I/O-points. On the other hand, the optimal costs when having non-fixed retrieval I/O-points are at most as large as having fixed retrieval I/O-points, because the solution space of ${{\text {ROP}}_{{{\text {AP}}}}}$ is a superset of ${{\text {ROP}}_{{{\text {P}}}}}$.

Theorem 5

For a given ${{\text {ROP}}}$ instance, let $S^*_{{{\text {P}}}}$ and $S^*_{{{\text {AP}}}}$ be optimal solutions in the case of  ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$, respectively. Then, we have

• (i) $c(S^*_{{{\text {P}}}})/c(S^*_{{{\text {AP}}}})$ can be arbitrarily large,

• (ii) $c(S^*_{{{\text {AP}}}})/c(S^*_{{{\text {P}}}}) \le 1$.

Proof

(i) We construct an ${{\text {ROP}}}$ instance as displayed in Fig. 4. We have $n=2\lambda$ pallets $P=\{p_1,\ldots ,p_{2\lambda }\}$ for some constant $\lambda \in \mathbb {N}$, and $m=2$ I/O-points $\Theta =\{\theta _1,\theta _2\}$, where $\theta _1$ serves as depot. Moreover, given a constant $d>0$, we have the costs

• $c[p_i,\theta _1]=0$ for $i=1,\ldots ,\lambda$, and $c[p_i,\theta _1]=d$ for $i=\lambda +1,\ldots ,2\lambda$,

• $c[p_i,\theta _2]=d$ for $i=1,\ldots ,\lambda$, and $c[p_i,\theta _2]=0$ for $i=\lambda +1,\ldots ,2\lambda$.

In other words, the locations of $\theta _1$ and $p_1,\ldots ,p_{\lambda }$ coincide, the locations of $\theta _2$ and $p_{\lambda +1},\ldots ,p_{2\lambda }$ also coincide, and there is a distance d separating the two resulting places. For ${{\text {ROP}}_{{{\text {P}}}}}$, we additionally set the retrieval I/O-points to $\alpha (p_i)=\theta _2$ for $i=1,\ldots ,\lambda$ and $\alpha (p_i)=\theta _1$ for $i=\lambda +1,\ldots ,2\lambda$.

Fig. 4

Worst-case example of ${{\text {ROP}}_{{{\text {P}}}}}$

In the case of ${{\text {ROP}}_{{{\text {P}}}}}$, the retrieval I/O-points of the pallets are each fixed to the I/O-point on the opposite side, and hence an optimal solution $S^*_{{{\text {P}}}}$ processes the pallets assigned to both I/O-points alternately, i.e., it traverses the path $(\theta _1,p_1,\theta _2,p_{\lambda +1},\theta _1,\ldots ,p_{\lambda },\theta _2,p_{2\lambda },\theta _1)$ with costs $c(S^*_{{{\text {P}}}})=2 \lambda d$. In contrast, in the case of ${{\text {ROP}}_{{{\text {AP}}}}}$, there are no fixed retrieval I/O-points, and an optimal solution $S^*_{{{\text {AP}}}}$ first processes the pallets $p_1,\ldots ,p_{\lambda }$ located closely to depot I/O-point $\theta _1$ and then processes the pallets $p_{\lambda +1},\ldots ,p_{2\lambda }$ located closely to I/O-point $\theta _2$ before returning to the depot I/O-point $\theta _1$, i.e., it traverses the path $(\theta _1,p_1,\theta _1,\ldots ,p_{\lambda },\theta _1,p_{\lambda +1},\theta _2,\ldots ,p_{2\lambda },\theta _2,\theta _1)$ incurring costs $c(S^*_{{{\text {AP}}}})=2d$. Then, we have $\lim _{\lambda \rightarrow \infty } c(S^*_{{{\text {P}}}})/c(S^*_{{{\text {AP}}}})=\infty$.

(ii) We start with an optimal ${{\text {ROP}}_{{{\text {P}}}}}$ solution $S^*_{{{\text {P}}}}$ and create an ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S_{{{\text {AP}}}}$ by processing the pallets in the same sequence, and choosing the same retrieval I/O-points. Thus, we obtain an ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S_{{{\text {AP}}}}$ incuring costs $c(S_{{{\text {AP}}}})=c(S^*_{{{\text {P}}}})$. An optimal ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S^*_{{{\text {AP}}}}$ can incur even smaller costs, i.e., $c(S^*_{{{\text {AP}}}}) \le c(S_{{{\text {AP}}}})=c(S^*_{{{\text {P}}}})$, which completes the proof. $\square$

4 Transformations to the ${{\text {TSP}}}$

We have already seen from the NP-hardness proofs of Theorems 1 and 2 that the ${{\text {ROP}}}$ is structurally similar to the ${{\text {TSP}}}$. We aim to exploit these similarities in order to use the rich toolbox of ${{\text {TSP}}}$ algorithms to solve the ${{\text {ROP}}}$. In this section, we present two transformations of the ${{\text {ROP}}}$ to the ${{\text {TSP}}}$. Our computational results in Sect. 5 show that these transformations enable to effectively solve the ${{\text {ROP}}}$, outperforming intuitive nearest neighbor heuristics.

First, we transform ${{\text {ROP}}_{{{\text {AP}}}}}$ to the metric ${{\text {TSP}}}$ (i.e., the costs in the resulting ${{\text {TSP}}}$ instance are symmetric and the triangle inequality holds). The key idea is to create a node for each pallet, and only determine a retrieval sequence $\pi$ of the pallets by solving the corresponding ${{\text {TSP}}}$ instance, while an assignment $\alpha$ of pallets to their retrieval I/O-points results implicitly. For each pair of pallets $p_i,p_j \in P$, we denote by $\beta (p_i,p_j)$ an I/O-point $\theta \in \Theta$ that minimizes the cost of retrieving pallet $p_i$ if pallet $p_j$ is processed directly afterwards, i.e., minimizing the cost $c[p_i,\theta ]+c[\theta ,p_j]$. We also call $\beta (p_i,p_j)$ an optimal I/O-point to be placed between pallets $p_i$ and $p_j$. Based on this, we next define the set of solutions

$$\begin{aligned} \mathcal {S}_{{{\text {AP}}}}=\{(\pi ,\alpha ) \in \Pi \times \Theta ^n \mid \alpha (\pi _i)=\beta (\pi _{i},\pi _{i+1}) \; \text {for } \; i=1,\ldots ,n-1 \; \text {and} \; \alpha (\pi _n)=\theta _{depot} \}, \end{aligned}$$

where an optimal I/O-point $\beta (\pi _{i},\pi _{i+1})$ is always placed between all successive pallets $\pi _{i}$ and $\pi _{i+1}$ ($i=1,\ldots ,n-1$), and the last pallet $\pi _n$ in the pallet retrieval sequence is retrieved at the depot I/O-point $\theta _{depot}$. For ${{\text {ROP}}_{{{\text {AP}}}}}$, note that each solution $S \in \Pi \times \Theta ^n$ can be transformed into a solution $S' \in \mathcal {S}_{{{\text {AP}}}}$ with costs $c(S') \le c(S)$ by replacing the current retrieval I/O-points with the corresponding optimal I/O-points to be placed between all two pairs of pallets in the given pallet retrieval sequence, and retrieving the last pallet at the depot I/O-point $\theta _{depot}$. In order to solve ${{\text {ROP}}_{{{\text {AP}}}}}$, it is therefore sufficient to consider only the solution set $\mathcal {S}_{{{\text {AP}}}}$, as it contains in particular an optimal solution.

A transformation of ${{\text {ROP}}_{{{\text {AP}}}}}$ to the metric ${{\text {TSP}}}$ is formulated in Theorem 6. Moreover, each ${{\text {TSP}}}$ solution of the transformed instance corresponds to an ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S_{{{\text {AP}}}} \in \mathcal {S}_{{{\text {AP}}}}$ with the same total costs. In particular, the set of all corresponding ${{\text {TSP}}}$ solutions must contain a solution which is optimal for ${{\text {ROP}}_{{{\text {AP}}}}}$. Consequently, it is sufficient to solve ${{\text {ROP}}_{{{\text {AP}}}}}$ indirectly by using algorithms for the ${{\text {TSP}}}$ applied to the transformed instance.

Theorem 6

There is a polynomial-time transformation of  ${{\text {ROP}}_{{{\text {AP}}}}}$ to the metric ${{\text {TSP}}}$, and we have a bijection between the set $\mathcal {S}_{{{\text {AP}}}}$ of  ${{\text {ROP}}_{{{\text {AP}}}}}$ solutions and the set $\mathcal {S}_{{{\text {TSP}}}}$ of ${{\text {TSP}}}$ solutions. Moreover, each ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S_{{{\text {AP}}}} \in \mathcal {S}_{{{\text {AP}}}}$ has the same total costs as its corresponding ${{\text {TSP}}}$ solution $S_{{{\text {TSP}}}} \in \mathcal {S}_{{{\text {TSP}}}}$, i.e., $c(S_{{{\text {AP}}}})=c(S_{{{\text {TSP}}}})$.

Proof

We are given an ${{\text {ROP}}_{{{\text {AP}}}}}$ instance with n pallets $P=\{p_1,\ldots ,p_n\}$, m I/O-points $\Theta =\{\theta _1,\ldots ,\theta _m\}$, a specific depot I/O-point $\theta _{depot} \in \Theta$, and the corresponding $\mu =n+m$ locations $L=\{\ell _1,\ldots ,\ell _{\mu }\}$ with metric travel costs $c[\ell _i,\ell _j]$ for all $\ell _i,\ell _j \in L$. We construct a ${{\text {TSP}}}$ instance with the complete, undirected graph $G=(V,E)$ having $n'=n+1$ nodes and edge costs $c'[v,w]$ for all $v,w \in V$ as follows.

• We have the node set $V=\{v_0,v_1,\ldots ,v_n\}$, where node $v_0$ corresponds to the depot I/O-point $\theta _{depot}$, and for all $i=1,\ldots ,n$, the node $v_{i}$ corresponds to pallet $p_{i} \in P$.

• The edge costs between pallet nodes and the depot node remain the same as in the ${{\text {ROP}}_{{{\text {AP}}}}}$ instance, i.e., for all $i=1,\ldots ,n$, we have $c'[v_0,v_{i}]=c[\theta _{depot},p_{i}].$

• The edge costs between two different pallet nodes correspond to the cheapest possible way to place an I/O-point in between, i.e., for all $i,j=1,\ldots ,n$ with $i \ne j$, we have

  $$\begin{aligned} c^{\prime} [v_i,v_j]=\min _{\theta \in \Theta }\{c[p_i,\theta ]+c[\theta ,p_j]\}. \end{aligned}$$

The resulting ${{\text {TSP}}}$ costs are symmetric due to the definition above. Moreover, the original ${{\text {ROP}}_{{{\text {AP}}}}}$ costs fulfill the triangle inequality, and as discussed next, this property remains also valid for the resulting ${{\text {TSP}}}$ costs, i.e., $c'[v_i,v_j] \le c'[v_i,v_k]+c'[v_k,v_j]$ for all different $i,j,k=0,\ldots ,n$.

• For $i=0$ and $j,k=1,\ldots ,n$ (similarly the case $j=0$ and $i,k=1,\ldots ,n$), we have

  $$\begin{aligned} \begin{aligned} c'[v_0,v_j] ={}&c[\theta _{depot},p_j]&\\ \le {}&c[\theta _{depot},p_k]+c[p_k,\beta (p_k,p_j)]+c[\beta (p_k,p_j),p_j]&\\ ={}&c'[v_0,v_k]+c'[v_k,v_j].&\\ \end{aligned} \end{aligned}$$

• For $k=0$ and $i,j=1,\ldots ,n$, we have

  $$\begin{aligned} \begin{aligned} c'[v_i,v_j] ={}&c[p_i,\beta (p_i,p_j)]+c[\beta (p_i,p_j),p_j]&\\ \le {}&c[p_i,\theta _{depot}] + c[\theta _{depot},p_j]&\\ ={}&c'[v_i,v_0]+c'[v_0,v_j].&\\ \end{aligned} \end{aligned}$$

• For $i,j,k=1,\ldots ,n$, we have

  $$\begin{aligned} \begin{aligned} c'[v_i,v_j] ={}&c[p_i,\beta (p_i,p_j)] + c[\beta (p_i,p_j),p_j]&\\ \le {}&c[p_i,\beta (p_i,p_k)] + c[\beta (p_i,p_k),p_j]&\\ \le {}&c[p_i,\beta (p_i,p_k)] + c[\beta (p_i,p_k),p_k] + c[p_k,\beta (p_k,p_j)] + c[\beta (p_k,p_j),p_j]&\\ ={}&c'[v_i,v_k] + c'[v_k,v_j].&\\ \end{aligned} \end{aligned}$$

Next, we show that there is a bijection between the set $\mathcal {S}_{{{\text {AP}}}}$ of ${{\text {ROP}}_{{{\text {AP}}}}}$ solutions and the set $\mathcal {S}_{{{\text {TSP}}}}$ of ${{\text {TSP}}}$ solutions, and that each ${{\text {TSP}}}$ solution has the same total costs as its corresponding ${{\text {ROP}}_{{{\text {AP}}}}}$ solution. On the one hand, each ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S_{{{\text {AP}}}} \in \mathcal {S}_{{{\text {AP}}}}$ can uniquely be described by its pallet retrieval sequence $\pi$, as the assignment of pallets to I/O-points results implicitly (for all $i=1,\ldots ,n-1$, pallet $\pi _i$ is retrieved at I/O-point $\beta (\pi _{i},\pi _{i+1})$, and the last pallet $\pi _n$ is retrieved at the depot I/O-point $\theta _{depot}$). On the other hand, each ${{\text {TSP}}}$ solution $S_{{{\text {TSP}}}} \in \mathcal {S}_{{{\text {TSP}}}}$ can uniquely be described by its pallet node sequence, as the position of the depot node $v_0$ in the tour can be assumed to be fixed. Therefore, we have $|\mathcal {S}_{{{\text {AP}}}}|=|\mathcal {S}_{{{\text {TSP}}}}|=n!$, and for each ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S_{{{\text {AP}}}} \in \mathcal {S}_{{{\text {AP}}}}$, we can construct a corresponding ${{\text {TSP}}}$ solution $S_{{{\text {TSP}}}} \in \mathcal {S}_{{{\text {TSP}}}}$ and vice versa, just by considering the pallet retrieval sequence. Moreover, we have $c(S_{{{\text {AP}}}})=c(S_{{{\text {TSP}}}})$ for corresponding solutions, because in both cases, the tour starts and ends at a depot I/O-point or depot node, and the costs between two pallet nodes $v_i,v_j \in V \setminus \{v_0\}$ also consider the cost of placing an optimal I/O-point $\beta (p_i,p_j)$ between the two corresponding pallets $p_i$ and $p_j$.

The corresponding ${{\text {TSP}}}$ instance of an ${{\text {ROP}}_{{{\text {AP}}}}}$ instance can be computed in $\mathcal {O}(n^2 \cdot m)$, as mainly for each pair of two pallets, an optimal I/O-point to be placed between them has to be calculated. Converting an ${{\text {ROP}}_{{{\text {AP}}}}}$ solution to the corresponding ${{\text {TSP}}}$ solution and vice versa can be done in $\mathcal {O}(n)$, since only the pallet retrieval sequence $\pi$ needs to be considered (assuming optimal I/O-points to be placed between the pallets are stored in the previous step). We hence conclude that the transformation can be done in polynomial time. $\square$

Example 2

Reconsider the ${{\text {ROP}}_{{{\text {AP}}}}}$ instance shown in Fig. 2a with $n=3$ pallets and $m=2$ I/O-points. The corresponding ${{\text {TSP}}}$ instance is shown in Fig. 5a, where we have $\beta (p_1,p_2)=\beta (p_2,p_1)=\theta _1$, $\beta (p_1,p_3)=\beta (p_3,p_1)=\theta _2$, and $\beta (p_2,p_3)=\beta (p_3,p_2)=\theta _2$. For the ${{\text {TSP}}}$ solution $S_{{{\text {TSP}}}}=(v_0,v_2,v_3,v_1)$ with costs $c(S_{{{\text {TSP}}}})=13$, we obtain the corresponding ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $\overline{S}$ shown in Fig. 2c with costs $c(\overline{S})=13$.

Fig. 5

Example of the costs $c'{[v_i,v_j]}$ of the resulting ${{\text {TSP}}}$ instances according to the transformations presented in Theorems 6 and 7

Since the transformation presented in Theorem 6 is polynomial, and we have a bijection between the set $\mathcal {S}_{{{\text {AP}}}}$ of ${{\text {ROP}}_{{{\text {AP}}}}}$ solutions and the set $\mathcal {S}_{{{\text {TSP}}}}$ of ${{\text {TSP}}}$ solutions, each approximation algorithm for the metric ${{\text {TSP}}}$ also yields the same performance guarantee for ${{\text {ROP}}_{{{\text {AP}}}}}$. From Theorem 6, it hence follows immediately Corollary 1.

Corollary 1

There is a $\frac{3}{2}$-approximation for ${{\text {ROP}}_{{{\text {AP}}}}}$.

Proof

We apply the transformation from Theorem 6 to the given ${{\text {ROP}}_{{{\text {AP}}}}}$ instance and get the corresponding instance of the metric ${{\text {TSP}}}$, which in turn is solved by using the algorithm presented by Christofides (1976). For the resulting ${{\text {TSP}}}$ solution, we compute the corresponding ${{\text {ROP}}_{{{\text {AP}}}}}$ solution of the original instance. This procedure yields the same performance guarantee of $\frac{3}{2}$ for ${{\text {ROP}}_{{{\text {AP}}}}}$ as the algorithm presented by Christofides (1976) for the metric ${{\text {TSP}}}$, since we have a bijection between the set $\mathcal {S}_{{{\text {AP}}}}$ of ${{\text {ROP}}_{{{\text {AP}}}}}$ solutions and the set $\mathcal {S}_{{{\text {TSP}}}}$ of ${{\text {TSP}}}$ solutions, and each ${{\text {ROP}}_{{{\text {AP}}}}}$ solution $S_{{{\text {AP}}}} \in \mathcal {S}_{{{\text {AP}}}}$ has the same total costs as its corresponding ${{\text {TSP}}}$ solution $S_{{{\text {TSP}}}} \in \mathcal {S}_{{{\text {TSP}}}}$. Furthermore, the procedure can be applied in polynomial time, because creating the corresponding metric ${{\text {TSP}}}$ instance can be done in $\mathcal {O}(n^2 \cdot m)$, and converting the resulting ${{\text {TSP}}}$ solution into an ${{\text {ROP}}_{{{\text {AP}}}}}$ solution can be done in $\mathcal {O}(n)$, as shown in the proof of Theorem 6. $\square$

In the case of ${{\text {ROP}}_{{{\text {P}}}}}$, only the pallet retrieval sequence has to be determined, and we define $\mathcal {S}_{{{\text {P}}}}=\Pi$ as the set of all possible solutions. As stated in Theorem 7, we present a transformation of ${{\text {ROP}}_{{{\text {P}}}}}$ to the asymmetric ${{\text {TSP}}}$ (${{\text {ATSP}}}$) with valid triangle inequality. In addition, for each ${{\text {ATSP}}}$ solution $S_{{{\text {ATSP}}}} \in \mathcal {S}_{{{\text {ATSP}}}}$ of the transformed instance, we have a corresponding ${{\text {ROP}}_{{{\text {P}}}}}$ solution $S_{{{\text {P}}}} \in \mathcal {S}_{{{\text {P}}}}$ with the same total costs and vice versa. The main idea of this transformation is to create a ${{\text {TSP}}}$ node for each pallet $p \in P$, and the cost of moving from pallet p to $p' \in P$ considers the cost of moving to the specific I/O-point $\alpha (p)$ approached in between to retrieve pallet p before moving to $p'$. Note that the resulting costs are asymmetric, since the fixed retrieval I/O-points $\alpha (p)$ and $\alpha (p')$ may differ.

Unlike in the case of ${{\text {ROP}}_{{{\text {AP}}}}}$, there does not seem to be an efficient transformation of ${{\text {ROP}}_{{{\text {P}}}}}$ to the symmetric ${{\text {TSP}}}$, since the assigned pallet I/O-points are given as input. Nevertheless, each possible pallet retrieval sequence of the ${{\text {ROP}}_{{{\text {P}}}}}$ instance can be expressed as an ${{\text {ATSP}}}$ solution for the corresponding transformed instance, and this solution has the same costs as a solution with the same sequence of the original instance. It is thus also sufficient to solve ${{\text {ROP}}_{{{\text {P}}}}}$ indirectly by using algorithms for the ${{\text {TSP}}}$ applied to the transformed instance.

Theorem 7

There is a polynomial-time transformation of ${{\text {ROP}}_{{{\text {P}}}}}$ to the ${{\text {ATSP}}}$ fulfilling the triangle inequality, and we have a bijection between the set $\mathcal {S}_{{{\text {P}}}}$ of ${{\text {ROP}}_{{{\text {P}}}}}$ solutions and the set $\mathcal {S}_{{{\text {ATSP}}}}$ of ${{\text {ATSP}}}$ solutions. Moreover, each ${{\text {ROP}}_{{{\text {P}}}}}$ solution $S_{{{\text {P}}}} \in \mathcal {S}_{{{\text {P}}}}$ has the same total costs as its corresponding ${{\text {ATSP}}}$ solution $S_{{{\text {ATSP}}}} \in \mathcal {S}_{{{\text {ATSP}}}}$, i.e., $c(S_{{{\text {P}}}})=c(S_{{{\text {ATSP}}}})$.

The proof follows a similar idea as the proof for Theorem 6 and is presented in Appendix B.

Example 3

Reconsider the ${{\text {ROP}}_{{{\text {P}}}}}$ instance shown in Fig. 2a with $n=3$ pallets, $m=2$ I/O-points, $\alpha (p_1)=\alpha (p_2)=\theta _1$, and $\alpha (p_3)=\theta _2$. The corresponding ${{\text {ATSP}}}$ instance is shown in Fig. 5b. For the ${{\text {ATSP}}}$ solution $S_{{{\text {ATSP}}}}=(v_0,v_1,v_2,v_3)$ with costs $c(S_{{{\text {ATSP}}}})=20$, we obtain the corresponding ${{\text {ROP}}_{{{\text {P}}}}}$ solution S shown in Fig. 2b with costs $c(S)=20$.

Again, each approximation algorithm for the ${{\text {ATSP}}}$ fulfilling the triangle inequality also yields the same performance guarantee for ${{\text {ROP}}_{{{\text {P}}}}}$, because the transformation presented in Theorem 7 is polynomial, and we have a bijection between the set $\mathcal {S}_{{{\text {P}}}}$ of ${{\text {ROP}}_{{{\text {P}}}}}$ solutions and the set $\mathcal {S}_{{{\text {ATSP}}}}$ of ${{\text {ATSP}}}$ solutions where corresponding solutions have the same total costs. For the ${{\text {ATSP}}}$ fulfilling the triangle inequality, Asadpour et al (2010) presented an approximation algorithm with an $\mathcal {O}(\log n / \log \log n)$ performance guarantee. We therefore immediately conclude Corollary 2.

Corollary 2

There is an approximation algorithm with an $\mathcal {O}(\log n / \log \log n)$ performance guarantee for ${{\text {ROP}}_{{{\text {P}}}}}$.

5 Computational results

This section presents extensive computational results for the ${{\text {ROP}}}$. First, in Sect. 5.1, we describe the test instances used in our experiments. Optimal results determined by a branch-and-cut solver for the ${{\text {ATSP}}}$ are presented in Sect. 5.2, where we analyze the effect of different instance parameters on the solution quality. In Sect. 5.3, the results determined by four different heuristics are presented. Finally, Sect. 5.4 provides insights on the gain of optimization for different ${{\text {ROP}}}$ variants.

We implemented all algorithms in C++, and our experiments were performed on an Intel Core i9-10920X 3.5GHz machine with 64 Bit Ubuntu 20.04 LTS and 64GB RAM. To solve the ${{\text {TSP}}}$ instances resulting from the transformations presented in Sect. 4, we implemented a branch-and-cut solver using CPLEX 20.1 and the graph library LEMON 1.3.1 (Dezső et al 2011). Our experiments with the branch-and-cut solver were multi-threaded, allowing for simultaneous use of up to ten cores, and we set a time limit of one hour for each instance. However, for the heuristics, the experiments were single-threaded, and average gaps to the best lower bound values of the corresponding instances are reported. For a given solution S, the percentage gap is calculated according to the formula $100 \cdot \frac{c(S)-LB}{LB}$, where LB denotes the best lower bound of the corresponding instance obtained by CPLEX. All instances and the raw data of all results can be found at http://www2.informatik.uos.de/kombopt/data/rop/.

5.1 Test data

To properly evaluate our solution approaches, we randomly generated instances with various parameters based on data provided by the company we collaborate with. This company operates a high-bay warehouse using AS/RS where around $n=100$ pallets need to be retrieved during a single shift by using $m=3$ different I/O-points. Their stacker crane can move independently of each other in horizontal and vertical directions, and hence the travel costs between two locations are based on the Chebyshev metric (i.e., the maximum of the vertical and horizontal costs).

To gain deeper insights on the ${{\text {ROP}}}$, we also generated instances that are more general than the company’s specific problem setting, allowing to examine the influence of some instance parameters. First, the number of pallets to be retrieved or the number of I/O-points may differ in other problem settings. Moreover, in warehouses without AS/RS, stacker cranes typically cannot move independently in horizontal and vertical directions, and therefore other travel cost measures apply. Besides the Chebyshev metric, other realistic travel cost measures in warehouses include the Euclidean (i.e., the length of the direct connection line) and the Manhattan (i.e., the total horizontal plus vertical costs) metric. For example, in unit-load warehouses with forklifts and rectilinear ordered racks positioned on the ground, travel costs can be accurately modeled by the Manhattan metric. In contrast, for warehouses with human pickers and few items stored on the ground, the Euclidean metric seems to be a suitable choice as nearly the direct connection line between two locations can be traversed.

In practice, the ordering of I/O-points may be linear, for example, if they are located at the bottom of a shelf for easy accessibility. However, we know from the company we collaborate with that they plan to build a new warehouse on a hill, and to accommodate the different ground levels, the I/O-points need to be ordered at different heights instead of being located on a line. Additionally, there are warehouses located above production or logistic facilities where the I/O-points may possibly be ordered arbitrarily on the ground, such as a carpet manufacturer mentioned by Gharehgozli et al (2014b). Thus, from a practical perspective, both linear and arbitrary orderings of the I/O-points seem to make sense.

Based on the previous discussion, we generated a total of 160 instances with four parameters. In line with the notation used above, parameter n corresponds to the number of pallets to be retrieved, and parameter m describes the number of I/O-points in the warehouse. The ordering parameter specifies whether the locations corresponding to the I/O-points are chosen randomly or are ordered on a line. The metric parameter describes how the travel costs between two locations are calculated, where we consider the Chebyshev, Manhattan and Euclidean metric, respectively.

All locations are randomly chosen within a square area having an edge length of $1\,000$ and are sampled as integer values. To ensure that the instances can be used not only for ${{\text {ROP}}_{{{\text {AP}}}}}$, but also for ${{\text {ROP}}_{{{\text {A}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$, we also randomly sampled an assignment $\alpha$ of pallets to I/O-points as well as a pallet retrieval sequence $\pi$. Depending on the problem variant considered, the values of $\alpha$ and $\pi$ may be not required. In these cases they are simply ignored.

To investigate the influence of specific parameters and to cover a wide range of problem settings, we grouped the instances into three sets $I_{n}$, $I_{m}$ and $I_{Costs}$. These instance sets are all based on the company’s problem setting, except that certain parameters are varied. Instance set $I_{n}$ varies the number of pallets to be retrieved $n \in \{20,50,100,200,500,1\,000\}$, while assuming $m=3$ different I/O-points ordered randomly and travel costs resulting from the Chebyshev metric. Instance set $I_{m}$ varies the number of I/O-points $m \in \{1,2,3,5,10,20\}$, while assuming $n=100$ pallets to be retrieved, a random ordering of the I/O-points and travel costs resulting from the Chebyshev metric. Finally, instance set $I_{Costs}$ varies both the ordering and the metric parameter, considering all possible combinations of these two parameters while assuming $n=500$ and $m=3$ (note that larger instances are needed to get meaningful differences between varying travel costs). For each specified combination of parameters, ten random instances were created.

5.2 Optimal results

In a first experiment, we aimed to determine optimal solutions for both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ to examine how different instance parameters affect the difficulty of solving these problems. In preliminary experiments, the mathematical model presented in Appendix A turned out to be inappropriate to solve ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$. In order to still obtain optimal solutions, we hence transformed the ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ instances into their corresponding ${{\text {TSP}}}$ instances according to Theorems 6 and 7, respectively. Unfortunately, hardly any exact solvers are freely available to solve the resulting ${{\text {TSP}}}$ instances, with the Concorde solver developed by Applegate et al (2006) apparently being the only exception. However, it is limited to handle symmetric ${{\text {TSP}}}$ instances. Since only transformed ${{\text {ROP}}_{{{\text {AP}}}}}$ instances are guaranteed to be symmetric, while transformed ${{\text {ROP}}_{{{\text {P}}}}}$ instances may result in asymmetric ${{\text {TSP}}}$ instances, a general ${{\text {ATSP}}}$ solver is required to solve all instances properly and to enable a fair comparison between all results. To address this issue, we implemented our own branch-and-cut ${{\text {ATSP}}}$ solver using CPLEX to solve all resulting ${{\text {TSP}}}$ instances.

Our branch-and-cut solver is based on the well-known two-index formulation originally proposed by Dantzig et al (1954). Further details can be found in survey papers such as the one by Roberti and Toth (2012). Moreover, we separate subtour elimination constraints by calculating minimum cuts with the LEMON library implementation of the algorithm proposed by Hao and Orlin (1994). We conducted tests on our branch-and-cut solver to evaluate the impact of a warm-start, i.e., initializing CPLEX with a given solution determined by a heuristic. In Sect. 5.3, we evaluate various heuristics to solve the resulting ${{\text {ATSP}}}$ instances. The modified Karp-Steele patching heuristic presented by Glover et al (2001) proved to be the most effective on our transformed instances, and we therefore use it for the warm-start of our branch-and-cut solver. In all experiments with our branch-and-cut solver, a time limit of one hour per instance was applied.

Table 2 presents the results of the impact of the warm-start on our branch-and-cut solver for all 160 instances $I_{n} \cup I_{m} \cup I_{Costs}$ combined. The first column indicates whether a warm-start was applied. The remaining columns show the number of feasible solutions, the number of solutions verified as optimal within the time limit, and the actual average computing times in seconds, distinguished by ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$.

Table 2 Impact of the warm-start on the branch-and-cut solver for instances $I_{n} \cup I_{m} \cup I_{Costs}$

As shown in Table 2, more instances were verified as optimally solved and the average computation times were lower for ${{\text {ROP}}_{{{\text {P}}}}}$ compared to ${{\text {ROP}}_{{{\text {AP}}}}}$, regardless whether a warm-start was used. Although ${{\text {ROP}}_{{{\text {P}}}}}$ may result in asymmetric ${{\text {TSP}}}$ instances in contrast to ${{\text {ROP}}_{{{\text {AP}}}}}$, they seem to be easier to solve. A plausible explanation is that in ${{\text {ROP}}_{{{\text {P}}}}}$ only a pallet retrieval sequence $\pi$ has to be determined, whereas in ${{\text {ROP}}_{{{\text {AP}}}}}$ additionally an assignment $\alpha$ of the pallets to I/O-points has to be calculated. Since the assignment $\alpha$ is already fixed in ${{\text {ROP}}_{{{\text {P}}}}}$, a sequence $\pi$ can be better determined.

Note that without a warm-start, not for all 160 instances feasible solutions could be found for both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ as listed in Table 2. This is due to the insufficient solving time available to separate all subtour elimination constraints on these instances. In contrast, when using a warm-start, the solver is guaranteed to find feasible solutions for all instances because it has already been initialized with one. Furthermore, the number of instances verified as optimally solved is much larger with a warm-start for both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$, while the average computation times decrease considerably. Even if the gaps reported by CPLEX are at most $2\%$ on any instance solved to feasibility, the compelling positive impact of a warm-start emphasizes the value of considering heuristics for ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$. Due to the high effectiveness of a warm-start, only results with a warm-start are shown below.

In Sect. 3.1, we proved that both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ are strongly NP-hard. Thus, it can be expected that the instance size, measured by parameters n and m, strongly determines the difficulty of solving these problems. Therefore, we investigated how the number of pallets to be retrieved (parameter n) and the number of I/O-points (parameter m) impact the results. Tables 3 and 4 present the results of our branch-and-cut solver for instances $I_{n}$ and $I_{m}$, distinguished by parameters n and m, respectively. For both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ and each value of n or m, the number of instances verified as optimally solved, the maximum percentage gap reported by CPLEX, and the average computing times in seconds are shown. Recall that there are a total of ten instances for each value of n or m.

Table 3 Results of the branch-and-cut solver for instances $I_{n}$ distinguished by parameter n

According to the results shown in Table 3, all instances were verified as optimally solved for ${{\text {ROP}}_{{{\text {P}}}}}$, regardless of the value of parameter n. In contrast, in the case of ${{\text {ROP}}_{{{\text {AP}}}}}$, the time limit of one hour was insufficient to verify some instances for values of $n \ge 500$. However, the gap reported by CPLEX on any instance is far below $0.01\%$, indicating that the corresponding solutions are at least nearly optimal. Furthermore, the average computing times increase sharply with rising values of n for both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$. These results validate that the parameter n has a major impact on the difficulty of solving the problem, even if the given instances are well solvable. Additionally, the values in Table 3 confirm that in practice ${{\text {ROP}}_{{{\text {AP}}}}}$ is more difficult to solve than ${{\text {ROP}}_{{{\text {P}}}}}$.

Table 4 Results of the branch-and-cut solver for instances $I_{m}$ distinguished by parameter m

As can be seen in Table 4, all instances were verified as optimally solved in the case of ${{\text {ROP}}_{{{\text {P}}}}}$, independent of the parameter m. Moreover, for ${{\text {ROP}}_{{{\text {P}}}}}$, the computing times are negligible, being far below one second even for larger values of m. In contrast, for ${{\text {ROP}}_{{{\text {AP}}}}}$, there is a sharp increase in computing times with rising values of m. Additionally, while all solutions were verified as optimal in the case of ${{\text {ROP}}_{{{\text {AP}}}}}$ for $m \le 10$, two instances with $m=20$ could not be verified within the time limit of one hour. However, the gaps reported by CPLEX are at most $1.5\%$. These results show that the parameter m has a large influence on the difficulty of solving ${{\text {ROP}}_{{{\text {AP}}}}}$, while it appears to have less impact on ${{\text {ROP}}_{{{\text {P}}}}}$. Additionally, ${{\text {ROP}}_{{{\text {AP}}}}}$ seems to be much more difficult to solve compared to ${{\text {ROP}}_{{{\text {P}}}}}$.

Next, we evaluated the impact of different orderings of the I/O-points and travel cost metrics on the difficulty of solving ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$. For different orderings and metrics, Table 5 shows the number of instances verified as optimally solved and the average computing times in seconds for the instances $I_{Costs}$, distinguished by ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$. Instances with a linear ordering appear to be easier to solve than those with a random ordering, particularly for ${{\text {ROP}}_{{{\text {AP}}}}}$. For a random ordering, the metric has little influence on the results for both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$. However, if the I/O-points are ordered linearly, there are still few differences in the case of ${{\text {ROP}}_{{{\text {P}}}}}$, while the metric has a considerable impact for ${{\text {ROP}}_{{{\text {AP}}}}}$. With ${{\text {ROP}}_{{{\text {AP}}}}}$, when considering linearly ordered I/O-points, instances with Chebyshev metric take the smallest computing times with just a few seconds, whereas instances with Euclidean and Manhattan metric take more than one thousand seconds on average.

Table 5 Results of the branch-and-cut solver for instances $I_{Costs}$ distinguished by different metrics and orderings of the I/O-points

Due to the special structure of instances with linearly ordered I/O-points, these are easier to solve, mainly because the travel costs between pallets and different I/O-points are more similar. This is particularly the case for the Chebyshev metric, where either the horizontal or vertical direction dominates the distance, enabling to reach several I/O-points from a pallet with the same travel costs. In contrast, with the Euclidean and Manhattan metrics and a linear ordering, there are more differences in travel costs between pallets and I/O-points, as these are never completely dominated by either horizontal or vertical distance. However, the results generally reveal the insight that the ${{\text {ROP}}}$ can be solved well regardless of the cost metric used or the given order of I/O-points.

5.3 Heuristics

In a second experiment, we compared some heuristics to solve ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$. Despite the previously shown good results of our branch-and-cut solver, recall that its sound performance is largely tied to the warm-start with heuristic solutions. Furthermore, the heuristics we used are not only easier to implement than the branch-and-cut solver, but also require much less computational time.

First, we implemented an intuitive heuristic that solves ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ by greedily selecting the next pallets and I/O-points to be visited. For ${{\text {ROP}}_{{{\text {P}}}}}$, starting at the depot I/O-point, in each step we choose a pallet with the smallest travel cost from the current I/O-point until all pallets have been visited. When visiting a pallet, the next I/O-point to be traversed is implicitly determined by the fixed assignment $\alpha$ in the case of ${{\text {ROP}}_{{{\text {P}}}}}$. In contrast, for ${{\text {ROP}}_{{{\text {AP}}}}}$, the only difference of the intuitive heuristic is that an I/O-point minimizing the travel costs from the current pallet is chosen as next I/O-point to be traversed. Note that the intuitive heuristics for both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ can be seen as a special nearest neighbor heuristic, since in each step, a nearest available location is approached. In our experiment, these intuitive heuristics serve as simple baseline approaches that a warehouse planner might employ. We also implemented three ${{\text {TSP}}}$ heuristics, which can be applied to ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ instances transformed according to Theorems 6 and 7, respectively.

• Nearest neighbor (TSP-NN): Starting at the node corresponding to the depot I/O-point, a nearest unvisited node is appended to the tour until all nodes have been visited.

• Cheapest insertion (TSP-CI): The solution is initialized with a tour consisting only of the node corresponding to the depot I/O-point. Iteratively, an unvisited node that can be inserted with the cheapest insertion costs is inserted at a cheapest insertion position until all nodes have been visited.

• Modified Karp-Steele patching (TSP-MKSP): At first, a minimum-cost cycle cover of all nodes is calculated (we solved the corresponding matching problem by using the network simplex algorithm implemented in the LEMON library). Afterwards, the resulting cycles are iteratively patched until only a single cycle remains by evaluating all possible patching options and applying one with the smallest cost increase (Glover et al 2001).

We tested the four heuristics on the instance sets $I_{n}$ and $I_{m}$ for both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$. Figs. 6 and 7 show the average percentage gaps to lower bounds for the four heuristics in the case of ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$, respectively. The results are distinguished by parameter n (left) and parameter m (right). The computing times are not shown in detail as they are negligible, taking less than half a second on any given instance.

Fig. 6

Average gaps [%] of the heuristics in the case of ${{\text {ROP}}_{{{\text {P}}}}}$ for instances $I_{n}$ (left) and $I_{m}$ (right) distinguished by parameters n and m. Note that the gaps of TSP-MKSP are zero in all combinations shown

The results shown in Figs. 6 and 7 indicate that the gaps of all heuristics are generally rather small, being below 12% in any configuration. As the value of n increases, the gaps decrease, while as the value of m rises, the gaps increase. For instances with large values of n, the increased number of pallets provides more flexibility in finding good solutions. In contrast, for instances with large values of m, it becomes even harder to find good solutions because the processing sequence of the pallets plays an increasingly important role.

Fig. 7

Average gaps [%] of the heuristics in the case of ${{\text {ROP}}_{{{\text {AP}}}}}$ for instances $I_{n}$ (left) and $I_{m}$ (right) distinguished by parameters n and m

As shown in Figs. 6 and 7, the intuitive heuristic and TSP-NN have the largest gaps because sections of the tours that have already been determined are not changed later on. However, for ${{\text {ROP}}_{{{\text {AP}}}}}$, TSP-NN performs slightly better than the intuitive heuristic because cheapest I/O-points to be placed between two consecutively retrieved pallets are automatically chosen due to the transformation according to Theorem 6. For both ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$, TSP-CI has smaller gaps because it searches more globally for possibilities to insert nodes into the tours. Overall, heuristic TSP-MKSP has the smallest gaps in all tested combinations. For ${{\text {ROP}}_{{{\text {P}}}}}$, the gaps are $0\%$ on any given instance, meaning that the determined solutions are optimal. In contrast, the gaps of heuristic TSP-MKSP for ${{\text {ROP}}_{{{\text {AP}}}}}$ are slightly larger, but still very small at below $2\%$ on average. The good results of the patching heuristic TSP-MKSP can be explained by the fact that many subtours resulting from the minimum cost cycle cover can be merged with zero costs, as they often contain the same I/O-points.

The results shown above highlight the benefits of the transformations from ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$ to the ${{\text {TSP}}}$, as certain ${{\text {TSP}}}$ heuristics such as the patching-based TSP-MKSP can be applied, beating simple nearest neighbor strategies, such as the intuitive heuristics and TSP-NN. This additionally provides the insight that the heuristics commonly used for the ${{\text {TSP}}}$ are also well suited to solve the ${{\text {ROP}}}$, making it affordable to transcribe good solution approaches in practice.

5.4 Gain of optimization

A crucial question of practical relevance is how large the gain of optimization for the ${{\text {ROP}}}$ actually is, i.e., the percentage reduction of travel costs compared to the case where both the assignment $\alpha$ of pallets to I/O-points and the pallet retrieval sequence $\pi$ are fixed. In our last experiment, we analyzed the gain of optimization for ${{\text {ROP}}_{{{\text {A}}}}}$, ${{\text {ROP}}_{{{\text {P}}}}}$, and ${{\text {ROP}}_{{{\text {AP}}}}}$, where the assignment $\alpha$, the sequence $\pi$, or both have to be determined.

For the case without optimization, we assumed that $\alpha$ and $\pi$ are fixed as specified in the instances. Recall that in the generated instances, both $\alpha$ and $\pi$ are chosen randomly, and they are simply ignored if these values have to be determined in a specific variant of the ${{\text {ROP}}}$. Moreover, for fixed $\alpha$ and $\pi$, solutions are already fully determined, meaning that we have optimal objective values to compare with in the case without optimization. In contrast, optimal objective values for ${{\text {ROP}}_{{{\text {A}}}}}$ were determined in polynomial time by finding an optimal assignment $\alpha$ according to equation (1). However, for ${{\text {ROP}}_{{{\text {P}}}}}$ and ${{\text {ROP}}_{{{\text {AP}}}}}$, which are NP-hard, optimal objective values were determined by our branch-and-cut solver if possible. For instances not verified as optimally solved, we used the best known upper bounds found during all experiments we performed.

Fig. 8

Average cost reductions [%] of different ${{\text {ROP}}}$ variants compared to the case without optimization for instances $I_{n}$ (left) and $I_{m}$ (right) distinguished by parameters n and m

Figure 8 shows the average percentage cost reductions for ${{\text {ROP}}_{{{\text {A}}}}}$, ${{\text {ROP}}_{{{\text {P}}}}}$, and ${{\text {ROP}}_{{{\text {AP}}}}}$ compared to the case without optimization for the instances $I_n$ and $I_m$, distinguished by parameters n and m. Overall, there are remarkable cost reductions in all combinations, with even up to $80\%$. It is noteworthy that parameter n has little impact on the results, whereas the relative gains increase considerably with rising values of m. This suggests to warehouse managers that large cost reductions are possible by optimizing the pallet retrieval, regardless of the number of pallets. As expected, there is no gain at all for $m=1$, since in that case just one possible assignment $\alpha$ exists, and thus the pallet retrieval sequence has no impact on the costs. However, note that even in warehouses with $m=2$ different I/O-points, the possible gain is considerable with at least $10\%$ on average for each considered ${{\text {ROP}}}$ variant. For $m=20$, the cost reductions are largest with at least $30\%$ on average, as there are many different possible assignments $\alpha$, and hence the impact of the pallet retrieval sequence is bigger. This gives practitioners the insight that optimization is particularly worthwhile in warehouses with many I/O-points.

It can also be seen in Fig. 8 that the cost reductions for ${{\text {ROP}}_{{{\text {AP}}}}}$ are largest in all combinations, as both $\alpha$ and $\pi$ can be optimized. In contrast, ${{\text {ROP}}_{{{\text {A}}}}}$ has the second largest cost reductions, while ${{\text {ROP}}_{{{\text {P}}}}}$ has the smallest cost reductions. The reason for this is that for ${{\text {ROP}}_{{{\text {P}}}}}$, the travel costs from the pallets to the I/O-points are already fixed by the given assignment $\alpha$. In contrast, for ${{\text {ROP}}_{{{\text {A}}}}}$, there are no fixed travel costs, providing greater flexibility to find good solutions. This demonstrates that optimizing the assignment $\alpha$ of pallets to I/O-points results in a larger gain than optimizing the pallet retrieval sequence $\pi$. If possible, decision makers in the industry should therefore ensure that pallets do not necessarily have to be retrieved at fixed I/O-points when setting up a warehouse.

In Sect. 3.3, we analytically examined the gain of flexible I/O-points compared to fixed ones by considering the cost ratios of optimal solutions for ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$. We proved in Theorem 5 that for any instance, the ratio of optimal costs for ${{\text {ROP}}_{{{\text {AP}}}}}$ to ${{\text {ROP}}_{{{\text {P}}}}}$ is at most one, while there is no such bound in the opposite direction. In the following, we examine the cost ratios of the best known upper bounds between ${{\text {ROP}}_{{{\text {AP}}}}}$ and ${{\text {ROP}}_{{{\text {P}}}}}$ experimentally. Note that most considered solutions were verified as optimal as shown in Sect. 5.2, and the average gaps of the remaining cases are very small.

Fig. 9

Average cost ratios ${{\text {ROP}}_{{{\text {AP}}}}}/{{\text {ROP}}_{{{\text {P}}}}}$ for instances $I_{n}$ (left) and $I_{m}$ (right) distinguished by parameters n and m

Figure 9 shows the average cost ratios of ${{\text {ROP}}_{{{\text {AP}}}}}$ to ${{\text {ROP}}_{{{\text {P}}}}}$ for the instance sets $I_n$ and $I_m$, differentiated by parameters n and m. As expected, the results show that the ratios are at most one in all tested combinations. For all tested values of n, the ratios range between 0.7 and 0.8, indicating that the number of pallets to be retrieved does not considerably impact these ratios. Conversely, this means that regardless of the number of pallets, the total travel costs can be reduced by at least $20\%$ if assignment $\alpha$ is optimized in addition to sequence $\pi$. Furthermore, the ratios sharply decrease with rising values of m, as the gain of flexible I/O-points can better unfold with more I/O-points. For $m=20$, the average ratio is below 0.4, meaning that the cost reduction is more than $60\%$ on average when additionally optimizing $\alpha$. Overall, the results show that optimizing assignment $\alpha$ in addition to sequence $\pi$ can largely reduce travel costs, particularly when there are a large number of I/O-points.

6 Conclusions

In this paper, we studied, analyzed, and evaluated several variants of the ${{\text {ROP}}}$, where different pallets have to be retrieved in a warehouse with multiple I/O-points. The problem variants we considered required determining either the pallet retrieval sequence, the assignment of pallets to I/O-points, or both.

If only the assignment of pallets to I/O-points has to be determined and the pallet retrieval sequence is fixed, the problem can be solved in strongly polynomial time. Moreover, we proved that the problem becomes strongly NP-hard if the pallet retrieval sequence must be determined, regardless of whether the assignment of pallets to I/O-points is fixed or not. However, if the number of I/O-points is fixed and not part of the input, we have shown that the problem can be solved in polynomial time even when the pallet retrieval sequence must be determined.

To solve the NP-hard problem variants of the ${{\text {ROP}}}$, we formulated them as a ${{\text {TSP}}}$, giving access to highly developed pre-existing methods of the ${{\text {TSP}}}$. When only the pallet retrieval sequence must be determined and the assignment of pallets to I/O-points is fixed, we formulated the problem as an ${{\text {ATSP}}}$ fulfilling the triangle inequality. In contrast, when both the pallet retrieval sequence and the assignment of pallets to I/O-points must be determined, we formulated the problem as a symmetric ${{\text {TSP}}}$ fulfilling the triangle inequality.

Our extensive computational study reveals that the two NP-hard ${{\text {ROP}}}$ variants can be effectively solved by applying algorithms to the transformed ${{\text {TSP}}}$ instances, surpassing the performance of the intuitive nearest neighbor heuristics. Most instances can be verified as optimally solved using a branch-and-cut solver for the ${{\text {ATSP}}}$, where a warm-start with heuristic solutions is particularly effective. The problem variants considered can be solved by heuristics with small gaps to lower bounds within a negligible amount of computing time.

Overall, the problem is easier to solve if only the pallet retrieval sequence must be determined, rather than also the assignment of pallets to I/O-points. Moreover, instances with more pallets to be retrieved and more I/O-points tend to be more difficult to solve, particularly when both the pallet retrieval sequence and the assignment of pallets to I/O-points must be determined. Our computational results also show that the gain from optimization for the ${{\text {ROP}}}$ is generally quite high, with the optimization of the assignment of pallets to I/O-points having a larger influence than the optimization of the pallet retrieval sequence.

Our results particularly disclose the following managerial implications and insights. First, standard heuristics for the ${{\text {TSP}}}$ are already well suited to solve the ${{\text {ROP}}}$ appropriately, permitting convenient access to good existing algorithms. Our numerical results additionally unveil that considerable cost savings are achieved by applying our solution approaches compared to not optimizing at all, particularly when having many I/O-points. Eventually, the stacker crane’s total travel costs can be reduced considerably by allowing the pallets to be retrieved at arbitrary I/O-points instead of fixing them. This suggests that decision makers in the industry should enable the retrieval of pallets at arbitrary I/O-points whenever possible in order to exploit the whole optimization potential.

In conclusion, optimizing retrieval requests in warehouses with multiple I/O-points has a large impact compared to the common scenario with just a single I/O-point. Both exact and heuristic methods have proven suitable for solving our new problem variants. Future research could also explore selecting storage locations for storage requests to ensure that high frequency retrievals still incur low retrieval costs even if the time during breaks is not sufficient to perform warehouse reshuffling strategies. Additionally, the operations at the I/O-points can be modeled in more detail by taking processing times for pallet retrievals into account. Moreover, it can be examined whether there exist FPT algorithms for the two NP-hard ${{\text {ROP}}}$ variants with respect to the number of I/O-points.

Appendix

1.1 A. Mathematical model

In order to better illustrate the original research problem, we also present a complete mathematical model for the ${{\text {ROP}}}$, including the objective function, the decision variables, and the constraints. The way the stacker crane travel costs are modeled is based on the mathematical model presented by Goerigk et al (2013) for a bus evacuation problem. Overall, we have two different variable types, and the binary decision variables $x_{jki}$ obtain the value 1 if pallet $p_j \in P$ is retrived at position $k \in \{1,\ldots ,n\}$ at I/O-point $\theta _i \in \Theta$, and 0 otherwise. In addition, for $k \in \{1,\ldots ,n\}$, the continuous variables $d_{\text {to}}^{k}$ and $d_{\text {from}}^{k}$ represent the stacker crane’s travel costs to approach the kth pallet retrieved and bringing it from there to its chosen I/O-point, respectively.

Given the variable types defined above, we formulated the complete mathematical model (A1)-(A8). First, the objective function (A1) minimizes the total travel costs, including the stacker crane’s travel costs to return to the I/O-point. Equation (A2) guarantees that the travel costs to approach the first pallet retrieved are properly defined, while constraints (A3) consider the travel costs to approach all remaining pallets. Furthermore, it is ensured by equations (A4) that the travel costs to bring each pallet to its chosen I/O-point are computed properly. Equations (A5) and (A6) enforce that exactly one pallet is retrieved at each position, and that each pallet is retrieved exactly once, respectively. Eventually, constraints (A7) and (A8) define the domains of the variables.

$$\begin{aligned} \min \quad&\sum _{k=1}^{n} (d_{\text {to}}^{k}+d_{\text {from}}^{k}) + \sum _{j=1}^{n} \sum _{i=1}^{m} (c[\theta _i,\theta _{depot}] \cdot x_{jni}) \end{aligned}$$

(A1)

$$\begin{aligned} \text {s.t.}\quad&d_{\text {to}}^{1} = \sum _{j=1}^{n} \sum _{i=1}^{m} (c[\theta _{depot},p_j] \cdot x_{j1i}){} & {} \end{aligned}$$

(A2)

$$\begin{aligned}&d_{\text {to}}^{k} \ge c[\theta _i,p_j] \cdot \left( \sum _{j'=1}^{n}x_{j',k-1,i}+\sum _{i'=1}^{m}x_{jki'}-1\right){} & {} {k=2,\ldots ,n;\; j=1,\ldots ,n;\; i=1,\ldots ,m} \end{aligned}$$

(A3)

$$\begin{aligned}&d_{\text {from}}^{k} = \sum _{j=1}^{n}\sum _{i=1}^{m} (c[p_j,\theta _i] \cdot x_{jki}){} & {} k=1,\ldots ,n \end{aligned}$$

(A4)

$$\begin{aligned}&\sum _{j=1}^{n} \sum _{i=1}^{m} x_{jki} = 1{} & {} k=1,\ldots ,n \end{aligned}$$

(A5)

$$\begin{aligned}&\sum _{i=1}^{m} \sum _{k=1}^{n} x_{jki} = 1{} & {} j=1,\ldots ,n \end{aligned}$$

(A6)

$$\begin{aligned}&x_{jki} \in \{0,1\}{} & {} {j,k=1,\ldots ,n;\; i=1,\ldots ,m} \end{aligned}$$

(A7)

$$\begin{aligned}&d_{\text {to}}^{k}, d_{\text {from}}^{k} \ge 0{} & {} k=1,\ldots ,n \end{aligned}$$

(A8)

The formulation (A1)-(A8) models the general variant ${{\text {ROP}}_{{{\text {AP}}}}}$ where both the pallet retrieval sequence $\pi$ and the assignment $\alpha$ of pallets to I/O-points have to be determined. In order to use that model also for variant ${{\text {ROP}}_{{{\text {P}}}}}$ where $\pi$ has to be determined and $\alpha$ is already fixed, the equations (A9) need to be additionally inserted into the model. A similar modification can also be performed for variant ${{\text {ROP}}_{{{\text {A}}}}}$, but we omit specifying it explicitly since the variant can be solved trivially in polynomial time.

$$\begin{aligned} \sum _{k=1}^{n} x_{jki} = 1{} & {} \qquad j=1,\ldots ,n;\; i=\alpha (j) \end{aligned}$$

(A9)

1.2 B. Proof of Theorem 7

Proof

We are given an ${{\text {ROP}}_{{{\text {P}}}}}$ instance with n pallets $P=\{p_1,\ldots ,p_n\}$, m I/O-points $\Theta =\{\theta _1,\ldots ,\theta _m\}$, a specific depot I/O-point $\theta _{depot} \in \Theta$, for each pallet $p \in P$ a specific retrieval I/O-point $\alpha (p) \in \Theta$, and $\mu =n+m$ corresponding locations $L=\{\ell _1,\ldots ,\ell _{\mu }\}$ with metric travel costs $c[\ell _i,\ell _j]$ for all $\ell _i,\ell _j \in L$. We construct an ${{\text {ATSP}}}$ instance with the complete, directed graph $G=(V,A)$ having $n'=n+1$ nodes and arc costs $c'[v,w]$ for all $v,w \in V$ as follows.

• We have the node set $V=\{v_0,v_1,\ldots ,v_n\}$, where node $v_0$ corresponds to the depot I/O-point $\theta _{depot}$, and for all $i=1,\ldots ,n$, the node $v_{i}$ corresponds to pallet $p_{i} \in P$.

• The arcs connecting the depot node with the pallet nodes have the same cost as in the ${{\text {ROP}}_{{{\text {P}}}}}$ instance, i.e., for all $i=1,\ldots ,n$, we have $c'[v_0,v_{i}]=c[\theta _{depot},p_{i}]$.

• The arcs connecting the pallet nodes with the depot node have the cost corresponding to move from the pallet’s specific retrieval I/O-point to the depot I/O-point, i.e., for all $i=1,\ldots ,n$, we have $c'[v_{i},v_0]=c[p_{i},\alpha (p_{i})]+c[\alpha (p_{i}),\theta _{depot}]$.

• The arc costs between two different pallet nodes correspond to the costs of retrieving the first pallet at its specific I/O-point and moving forward to the second pallet, i.e., for all $i,j=1,\ldots ,n$ with $i \ne j$, we have $c'[v_i,v_j]=c[p_i,\alpha (p_i)]+c[\alpha (p_i),p_j]$.

As discussed next, the triangle inequality remains also valid, i.e., $c'[v_i,v_j] \le c'[v_i,v_k]+c'[v_k,v_j]$ for all different $i,j,k=0,\ldots ,n$.

• For $j=0$ and $i,k=1,\ldots ,n$ (similarly the case $k=0$ and $i,j=1,\ldots ,n$), we have

  $$\begin{aligned} \begin{aligned} c'[v_i,v_0] ={}&c[p_i,\alpha (p_i)]+c[\alpha (p_i),\theta _{depot}]&\\ \le {}&c[p_i,\alpha (p_i)]+c[\alpha (p_i),p_k]+c[p_k,\alpha (p_k)]+c[\alpha (p_k),\theta _{depot}]&\\ ={}&c'[v_i,v_k]+c'[v_k,v_0].&\\ \end{aligned} \end{aligned}$$

• For $i=0$ and $j,k=1,\ldots ,n$, we have

  $$\begin{aligned} \begin{aligned} c'[v_0,v_j] ={}&c[\theta _{depot},p_j]&\\ \le {}&c[\theta _{depot},p_k] + c[p_k,\alpha (p_k)]+c[\alpha (p_k),p_j]&\\ ={}&c'[v_0,v_k]+c'[v_k,v_j].&\\ \end{aligned} \end{aligned}$$

• For $i,j,k=1,\ldots ,n$, we have

  $$\begin{aligned} \begin{aligned} c'[v_i,v_j] ={}&c[p_i,\alpha (p_i)] + c[\alpha (p_i),p_j]&\\ \le {}&c[p_i,\alpha (p_i)] + c[\alpha (p_i),p_k] + c[p_k,\alpha (p_k)] + c[\alpha (p_k),p_j]&\\ ={}&c'[v_i,v_k] + c'[v_k,v_j].&\\ \end{aligned} \end{aligned}$$

Next, we prove that there is a bijection between the set $\mathcal {S}_{{{\text {P}}}}$ of ${{\text {ROP}}_{{{\text {P}}}}}$ solutions and the set $\mathcal {S}_{{{\text {ATSP}}}}$ of ${{\text {ATSP}}}$ solutions, and that each ${{\text {ATSP}}}$ solution has the same total costs as its corresponding ${{\text {ROP}}_{{{\text {P}}}}}$ solution. On the one hand, each ${{\text {ROP}}_{{{\text {P}}}}}$ solution $S_{{{\text {P}}}} \in \mathcal {S}_{{{\text {P}}}}$ can uniquely be described by its pallet retrieval sequence $\pi$, as the assignment of pallets to I/O-points is fixed. On the other hand, each ${{\text {ATSP}}}$ solution $S_{{{\text {ATSP}}}} \in \mathcal {S}_{{{\text {ATSP}}}}$ can uniquely be described by its pallet node sequence, as the position of the depot node $v_0$ in the tour can be assumed to be fixed. We hence have $|\mathcal {S}_{{{\text {P}}}}|=|\mathcal {S}_{{{\text {ATSP}}}}|=n!$, and for each ${{\text {ROP}}_{{{\text {P}}}}}$ solution $S_{{{\text {P}}}} \in \mathcal {S}_{{{\text {P}}}}$, we can construct a corresponding ${{\text {ATSP}}}$ solution $S_{{{\text {ATSP}}}} \in \mathcal {S}_{{{\text {ATSP}}}}$ and vice versa, just by considering the pallet retrieval sequence. In addition, $c(S_{{{\text {P}}}})=c(S_{{{\text {ATSP}}}})$ holds for corresponding solutions, because in both cases, the tour starts and ends at the depot I/O-point or depot node, and the costs between two pallet nodes $v_i,v_j \in V \setminus \{v_0\}$ also consider the cost of placing the retrieval I/O-point $\alpha (p_i)$ between the two corresponding pallets $p_i$ and $p_j$.

The resulting ${{\text {ATSP}}}$ instance corresponding to an ${{\text {ROP}}_{{{\text {P}}}}}$ instance can be computed in $\mathcal {O}(n^2)$, as mainly for each pair of two pallets the travel costs have to be calculated and the corresponding retrieval I/O-points are fixed. Converting an ${{\text {ROP}}_{{{\text {P}}}}}$ solution to the corresponding ${{\text {ATSP}}}$ solution and vice versa can be done in $\mathcal {O}(n)$, since only the pallet retrieval sequence $\pi$ needs to be considered. We hence conclude that the transformation can be done in polynomial time. $\square$