Machine learning techniques for cross-sectional equity returns’ prediction

Abstract

We compare the performance of the linear regression model, which is the current standard in science and practice for cross-sectional stock return forecasting, with that of machine learning methods, i.e., penalized linear models, support vector regression, random forests, gradient boosted trees and neural networks. Our analysis is based on monthly data on nearly 12,000 individual stocks from 16 European economies over almost 30 years from 1990 to 2019. We find that the prediction of stock returns can be decisively improved through machine learning methods. The outperformance of individual (combined) machine learning models over the benchmark model is approximately 0.6% (0.7%) per month for the full cross-section of stocks. Furthermore, we find no model breakdowns, which suggests that investors do not incur additional risk from using machine learning methods compared to the traditional benchmark approach. Additionally, the superior performance of machine learning models is not due to substantially higher portfolio turnover. Further analyses suggest that machine learning models generate their added value particularly in bear markets when the average investor tends to lose money. Our results indicate that future research and practice should make more intensive use of machine learning techniques with respect to stock return prediction.

1 Introduction

Recently, Gu et al. (2020) conducted a much noted comparative analysis of machine learning methods for stock return prediction by synthesizing the body of empirical asset pricing literature within the field of machine learning. They provide evidence for a clear rejection of the ordinary least squares (OLS) benchmark in favor of machine learning methods in terms of statistical performance and investors’ economic performance. The OLS benchmark represents the typical approach in one of two basic strands of the empirical literature on stock return prediction. Specifically, cross-sectional stock return predictability research (e.g., Fama and French 2008; Lewellen 2015; Gu et al. 2020) runs cross-sectional regressions of future stock returns on a handful of lagged stock characteristics. The second strand of literature, i.e., time-series stock return predictability research, does not forecast the cross-section but the time-series of returns. This literature typically tries to forecast stock indices employing macroeconomic predictors.¹ Attributable to the underperformance of the linear benchmark in their study, Gu et al. (2020) recommend using machine learning techniques to overcome the severe limitations of commonly applied methods.

The paper from Gu et al. (2020) is the first to comprehensively use ML methods in cross-sectional predictability research. Following this seminal paper, numerous concurrent papers have emerged that contribute to the literature by investigating the generality of the conclusions derived in Gu et al. (2020). This is achieved by applying their research design to other stock markets (see, e.g., Tobek and Hronec 2021; Drobetz and Otto 2021; Leippold et al. 2022; Liu et al. 2022; Rubesam 2022; Lalwani and Meshram 2022, for international applications and applications to individual regions or countries) or other asset classes (see, e.g., Bianchi et al. 2021, for applications to bond returns). Another strand of the literature (see, e.g., Leippold et al. 2022, for a list of exemplary papers) is dedicated to numerous additional refinements of the basic algorithms surveyed in Gu et al. (2020).² Our empirical analysis contributes to the line of research featured in the aforementioned papers by deviating from their research design in several key aspects to further investigate the generality of the conclusion to reject the OLS benchmark in favor of machine learning methods in cross-sectional predictability research. More specifically, we devote our attention to three distinct issues: (1) overfitting and irrelevant predictors, (2) missing data, and (3) a U.S. bias. In the following, we discuss these issues and how they can be overcome. First, the aforementioned literature typically relies on large predictor sets. For example, the predictor set in Gu et al. (2020) includes 94 firm characteristics and interactions of each firm characteristic with eight macroeconomic time-series from Welch and Goyal (2008) and 74 industry sector dummy variables. This results in a set of 900+ predictors. Following (Gu et al. 2020; Leippold et al. 2022) even extend this predictor set (i.e., 1160 predictors) while relying on a smaller cross-section (i.e., 3,900 stocks) and time-series (i.e., a study period from 2000 to 2020). Tobek and Hronec (2021) and Bianchi et al. (2021) also use more than 100 predictors when investigating stocks internationally and bonds, respectively. Such large predictor sets and the enhanced flexibility of machine learning methods over more traditional prediction techniques such as the OLS benchmark come at the risk of overfitting the data, which may put machine learning methods at a disadvantage. However, one can also argue that some machine learning methods can handle irrelevant predictors while OLS cannot, which may put (some) machine learning methods at an advantage. For a comparison at eye level, we provide the OLS benchmark and machine learning methods with the same and a relatively sparse set of only relevant predictor variables to prevent overfitting and avoid irrelevant predictors.³ Our set of predictors consists of beta (Sharpe 1964), market capitalization (Banz 1981), the book-to-market-equity ratio (Rosenberg et al. 1985), momentum (Jegadeesh and Titman 1993), investment (Titman et al. 2004) and operating profitability (Novy-Marx 2013), all of which form the basis for well-known factor models such as the Fama and French (1993) three-factor model, the Carhart (1997) four-factor model and the Fama and French (2015) five-factor model. Second, the treatment of missing data is another potential problem affecting the findings derived in the previous literature. More specifically, if a characteristic is missing, then it is typically replaced by the cross-sectional mean or median, which is zero as stock characteristics are rank-transformed and mapped into a [− 1,1] interval.⁴ In this vein, Cismondi et al. (2013) argue that in cases where missing data can range up to 50% or more, imputing the data is incorrect, as it might create unrealistic states of the process being modeled. Afifi and Elashoff (1966) even argue that imputing the mean yields unbiased estimates if and only if the data follow a multivariate normal distribution and the data are missing at random. Given that this is likely not the case for financial market and accounting data, imputing missing data has received much attention in recent research by Freyberger et al. (2021); Cahan et al. (2022); Bryzgalova et al. (2022); Beckmeyer and Wiedemann (2022). To reduce the unintended impact of missing data, we select the aforementioned predictors so that they are available over the entire period and there are no large deviations in missing data between the predictors in the cross-section. Finally, another potential issue is related to the U.S. bias (and, therefore, lack of external validity) in research in economics (e.g., Das et al. 2013) and finance (e.g., Karolyi 2016).⁵ Specifically, Karolyi (2016) finds that only 16% (23%) of all empirical studies published in the top four (fourteen) finance journals examine non-U.S. markets, a fraction that is well below the measures reflecting their economic importance. This is problematic in two respects. First, generalizing conclusions solely from U.S. data can be dangerous, as research has shown that such conclusions do not necessarily hold internationally (see, e.g., Goyal and Wahal 2015; Woodhouse et al. 2017; Jacobs and Müller 2020). Therefore, every replication makes a contribution when extending existing studies out of sample (see, e.g., Harvey 2017; Hou et al. 2018). Second, a disproportionately high use of U.S. data poses the danger of widespread p-hacking, as argued by Harvey et al. (2016); Harvey (2017); Hou et al. (2018). Harvey et al. (2016) outline three ways to deal with the bias introduced by multiple testing: (1) using out-of-sample validation, (2) using a statistical framework that allows for multiple testing⁶, and (3) looking across multiple asset classes. In this paper, we choose the first approach and conduct the empirical analysis based on all European countries that are part of the MSCI Developed Europe Index. More specifically, we investigate nearly 12,000 individual stocks from 16 countries over almost 30 years from 1990 to 2019. To summarize, we contribute to the cross-sectional predictability research (e.g., Fama and French 2008; Lewellen 2015; Gu et al. 2020) by investigating whether recently derived conclusions (see, e.g., Gu et al. 2020; Tobek and Hronec 2021; Drobetz and Otto 2021; Leippold et al. 2022; Liu et al. 2022; Rubesam 2022; Lalwani and Meshram 2022; Bianchi et al. 2021) hold when we minimize or eliminate the influence of overfitting, irrelevant predictors, missing values, and U.S. bias.

We find confirmation for the results from the previous literature in the sense that the use of machine learning methods appears promising. This is also true if we exclude influences that could potentially distort the results, such as overfitting, irrelevant predictors, missing values, and U.S. bias, and compare the methods on an equal footing. Specifically, the outperformance of the best-performing individual machine learning method is approximately 0.6% per month based on the entire cross-section. This figure is impressive, given that only six predictor variables are considered. The outperformance shrinks to 0.1% per month when only the stocks of the largest ten percent of firms are considered, revealing that the outperformance of the machine learning methods is higher among stocks that are more difficult and costlier to trade. Given that the information environment on these stocks is arguably worse (e.g., in terms of media coverage or analyst following), our results are of great importance to investors seeking guidance. Additionally, we find that the superior performance of machine learning models is not due to substantially higher portfolio turnover. The analysis of bull and bear markets suggests that machine learning models generate their added value particularly in bear markets when the average investor tends to lose money. Lastly, we find that forecast combinations provide the most robust forecasts, on average. More specifically, forecast combinations consisting of only nonlinear methods consistently outperform forecast combinations that also consider linear models. Thus, we find that investors and researchers alike should prioritize machine learning techniques over the commonly applied benchmark approach when engaging in stock return predictions.

The remainder of the paper is organized as follows. Section 2 discusses the differences between time-series and cross-sectional stock return predictability. Section 3 formulates the OLS benchmark and the machine learning methods applied. Section 4 describes the data and provides descriptive statistics on the predictor variables and the dependent variable (stock returns) from the approximately 12,000 European firms included in this study. Sections 5 and 6 report the main and additional results of the performance comparisons based on statistical (model $R^2$) and economic (economic gains to investors from portfolio strategies) analyses. Section 7 concludes the paper.

2 Related literature

In finance research, and even more so in non-finance research such as operations research, the time-series approach dominates the cross-sectional approach when it comes to forecasting asset returns. Against this background, in this section, we aim to shed light on the differences between the two approaches discussed in recent literature:

• Engelberg et al. (2022): “Financial researchers have examined the predictability of stock returns for over a century (e.g., Gibson 1906) and a large literature has documented evidence of predictability in the cross-section of stock returns. A separate literature has examined the predictability of the equity risk-premium using time-series predictive variables. To date, these two literatures have evolved relatively independently.”

• Dong et al. (2022): “The first examines whether firm characteristics can predict the cross-sectional dispersion in stock returns. These studies identify numerous equity market anomalies (e.g., Fama and French 2015; Harvey et al. 2016; McLean and Pontiff 2016; Hou et al. 2018). The second line of research investigates the time-series predictability of the aggregate market excess return based on a variety of economic and financial variables, such as valuation ratios, interest rates, and inflation (Nelson 1976; Campbell 1987; Fama and French 1988, 1989; Pástor and Stambaugh 2009). Studies in this vein attempt to shed light on the variables that affect the equity risk premium.”

• Gu et al. (2020): “The first strand models differences in expected returns across stocks as a function of stock-level characteristics, and is exemplified by Fama and French (2008) and Lewellen (2015). The typical approach in this literature runs cross-sectional regressions of future stock returns on a few lagged stock characteristics. The second strand forecasts the time-series of returns and is surveyed by Welch and Goyal (2008), Koijen and van Nieuwerburgh (2011), and Rapach and Zhou (2013).”

In summary, prediction of the time-series of a single asset such as the aggregate market returns is related to the time-series predictability research. The typical approach is to forecast a single time-series (e.g., a specific MSCI index) based on other time-delayed time-series (e.g., economic and financial variables, such as valuation ratios, interest rates, and inflation). Predicting the cross-sectional dispersion in stock returns is related to cross-sectional predictability. The main approach is to forecast the returns of multiple assets at once and at one point in time (e.g., returns from all stocks in the US at time t) using other, time-delayed, cross-sectional information (e.g., market equity, momentum, market beta from all stocks in the US at time t-1). Following (Rapach and Zhou 2020) and based on a linear regression model, one can also make a more formal distinction between the two approaches:

• The time-series predictability approach considers the following time-series multiple regression model for an individual asset

  $$\begin{aligned} r_{t}=\alpha +\sum _{j=1}^{J}\beta _{j}x_{j,t-1}+\epsilon _{t}, \end{aligned}$$

  (1)

  for $t = 1, . . . , T$, where r is the return on a broad stock market index in excess of the risk-free return, T is the number of time-series observations, $x_{j,t-1}$ are the lagged predictor variables, and $\epsilon _{t}$ is a zero-mean disturbance term.

• The cross-sectional predictability approach considers the following cross-sectional multiple regression model for a certain month

  $$\begin{aligned} r_{i}=\alpha + \sum _{j=1}^{J}\beta _{j}z_{i,j}+\epsilon _{i}, \end{aligned}$$

  (2)

  for $i = 1, . . . , N$, where $z_{i,j}$ is the jth lagged characteristic of firm i and N is the number of available firms.⁷

In this paper, we are interested in predicting the cross-sectional dispersion in stock returns. However, in terms of cross-sectional predictability, Gu et al. (2020) is the first paper to comprehensively use ML methods and compare them against the standard OLS benchmark in this line of research (e.g., Fama and French 2008; Lewellen 2015; Gu et al. 2020). Against this background, we also rely on OLS as our “natural” benchmark.

3 Methodology

In our empirical study, we are dealing with a panel of stocks, where months are indexed as $t=1,...,T$ and stocks are indexed as $i=1,...,N$. Accordingly, the future stock return r of asset i at month $t+1$ can be defined in general terms as:⁸

$$\begin{aligned} r_{i,t+1} = E_t\left( r_{i,t+1}\right) +\epsilon _{i,t+1}, \end{aligned}$$

(3)

with

$$\begin{aligned} E_t\left( r_{i,t+1}\right) = g\left( x_{i,t}\right) , \end{aligned}$$

(4)

where current expectations about future returns are expressed as a function $g\left( \cdot \right)$ of a vector of predictor variables $x_{i,t}$ (i.e., firm characteristics). Specifically, the predictor variables are defined as a P-dimensional vector $x_{i,t}=\left( x_{i,t,1},\ldots ,x_{i,t,P}\right)$. Hence, the aim of the following methods is to provide an estimate $\hat{g}\left( \cdot \right)$ of $g\left( \cdot \right)$.

3.1 Simple and penalized linear regression

Throughout the recent decades of cross-sectional asset pricing research, the common strand in the literature on stock return predictability has been to model conditional expectations about future returns $g\left( \cdot \right)$ as a linear function of stock-level characteristics and a parameter vector $\beta =\left( \beta _1,\ldots ,\beta _P\right)$ (e.g., Fama and French 2008; Lewellen 2015; Green et al. 2017):

$$\begin{aligned} \hat{g}\left( x_{i,t};\beta \right) =x_{i,t}^\prime \beta . \end{aligned}$$

(5)

The parameter vector $\beta$ can be obtained by (pooled) OLS, minimizing the $l_2$ objective function:

$$\begin{aligned} {\mathop {\mathrm{min}}\limits _{\beta }}\,\,{\mathcal {L}\left( \beta \right) =\frac{1}{N(T-1)}\sum _{i=1}^{N}\sum _{t=1}^{T-1} \left( r_{i,t+1}-\hat{g}\left( x_{i,t};\beta \right) \right) ^2,} \end{aligned}$$

(6)

where N is the number of stocks in the cross-section and T is the number of months in the estimation period. We refer to this approach as the OLS benchmark. To reduce the impact of overfitting, we also add a penalty term to the objective function:

$$\begin{aligned} {\mathop {\mathrm{min}}\limits _{\beta }}\,\,{\mathcal {L}\left( \beta ;\cdot \right) =\mathcal {L}\left( \beta \right) +\phi (\beta ;\cdot )}. \end{aligned}$$

(7)

Regularization techniques, such as penalty terms, are most commonly used in the context of large feature spaces. Although the problem of overfitting is only of minor importance for the linear model given the small feature set, it can still occur and affect performance. For the sake of completeness, we follow prior literature and append the linear model by the popular elastic net penalty, which takes the form:

$$\begin{aligned} \phi (\beta ;\lambda ;\rho )=\lambda (1\ -\ \rho )\sum _{p=1}^{P}\left| \beta _p\right| +\frac{1}{2}\lambda \rho \sum _{p=1}^{P}\beta _p^2. \end{aligned}$$

(8)

The two nonnegative hyperparameters of the elastic net penalty, $\lambda$ and $\rho$, nest some special cases. $\lambda$ controls the penalty strength; hence, for $\lambda =0$, the model reduces to the standard OLS. The parameter $\rho$ controls the ratio of lasso versus ridge penalty, where the cases $\rho =\ 0$ and $\rho =\ 1$ correspond to lasso and ridge regression, respectively. Lasso imposes sparsity in the coefficients and may lead to some coefficients being exactly zero. Ridge regression is a dense modeling technique that prevents coefficients from becoming unduly large in magnitude by shrinking them closer to zero without imposing a weight of exactly zero. In addition to lasso ($\rho =0$) and ridge regressions ($\rho =1$), we consider elastic net ($\rho =\ 0.5$), which represents a compromise between the two.

In our empirical application, we determine the parameter $\lambda$ using grid search (see Table 11 in appendix for the ranges) on the validation data.

3.2 Support vector machine

Support vector regression (SVR) is an extension of the basic principle underlying support vector machines developed by Vapnik (1995), originally designed for classification. SVR generally estimates a linear regression function of the following form:

$$\begin{aligned} \hat{g}\left( x_{i,t};w,b\right) =x_{i,t}^\prime w+b, \end{aligned}$$

(9)

where w is a vector of weights and b is a constant. The objective of SVR is to estimate a function that provides a good balance between model complexity and goodness of fit by introducing an error margin ($\epsilon$-insensitive tube) to which the cost function is insensitive in approximating the returns. This may be interpreted as the tolerance for minuscule deviations up to $\epsilon$. The $\epsilon$-insensitive loss is defined as (cf. Vapnik 1995):

$$\begin{aligned} \mathcal {L}(r_{i,t+1},\hat{g}(x_{i,t}))= {\left\{ \begin{array}{ll} 0 &{} \text {if} \left| r_{i,t+1}-\hat{g}\left( x_{i,t}\right) \right| \le \epsilon \\ \left| r_{i,t+1}-\hat{g}\left( x_{i,t}\right) \right| -\epsilon &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

(10)

By introducing two slack variables $\xi _{i,t+1}$ and $\xi _{i,t+1}^*$ for positive and negative deviations from the $\epsilon$-insensitive loss function, respectively, the objective function can be written in primal form as:

$$\begin{aligned}&{\mathop {\mathrm{min}}\limits _{w,b}}\,\,{\mathcal {L}\left( w,b\right) =C\sum _{i=1}^{N}\sum _{t=1}^{T-1}{(\xi _{i,t+1}+\xi _{i,t+1}^*)} +\frac{1}{2}\sum _{p=1}^{P}w_p^2}\nonumber \\&\text {s.t.}\,\, {r_{i,t+1}-\left( w^\prime x_{i,t}-b\right) }{\le \epsilon +\xi _{i,t+1}},\nonumber \\&\quad {\left( w^\prime x_{i,t}+b\right) -r_{i,t+1}}{\le \epsilon +\xi _{i,t+1}^*},\nonumber \\&\quad {\xi _{i,t+1},\xi _{i,t+1}^*}{\ge 0}, \end{aligned}$$

(11)

where the optimization problem is defined as the sum of aggregate errors exceeding the $\epsilon$-boundary plus $l_2$ regularization that encourages a simple model to prevent overfitting of the data. The nonnegative constant C controls how strong deviations from $\epsilon$ should be penalized.⁹ Note that C can be interpreted as an inverse regularization parameter, as it controls the tradeoff between error tolerance and complexity. Two notable cases are $C=0$, for which SVR approximates a constant function, and $C\rightarrow \infty$, $\epsilon =0$, for which SVR essentially estimates an $l_1$-regression.

By means of Lagrangian theory, the above minimization problem can be represented in dual form as:

$$\begin{aligned}&{\mathop {\mathrm{min}}\limits _{\alpha ,\alpha ^*}}\,\,{\mathcal {L}\left( \alpha ,\alpha ^*\right) =\frac{1}{2}\sum _{\left( i,t\right) \in SV}\sum _{\left( j,k\right) \in SV}\left( \alpha _{i,t} -\alpha _{i,t}^*\right) \left( \alpha _{j,k}-\alpha _{j,k}^*\right) x_{i,t}^\prime x_{j,k}}\nonumber \\&{\qquad \qquad \qquad \quad -\epsilon \sum _{\left( i,t\right) \in SV}\left( \alpha _{i,t} -\alpha _{i,t}^*\right) +\sum _{\left( i,t\right) \in SV}y_{i,t}\left( \alpha _{i,t}-\alpha _{i,t}^*\right) }\\& \text {s.t.}\,\,{\sum _{\left( i,t\right) \in SV}\left( \alpha _{i,t}-\alpha _{i,t}^*\right) =0,} {\quad 0 \le \alpha _{i,t}, a_{i,t}^*\le C}, \end{aligned}$$

(12)

where $\alpha _{i,t}$ and $\alpha _{i,t}^*$ are nonnegative Lagrangian multipliers for each observation $x_{i,t}$. SV are the indices of nonzero Lagrangian multipliers, where the corresponding $x_{i,t}$ are the support vectors. Accordingly, the first line of equation (12) considers pairwise combinations of panel observations if they are in the set of support vectors. Support vectors are observations that correspond to nonzero Lagrangian multipliers, i.e., either $\alpha _{i,t}$ or $\alpha _{i,t}^*$ is nonzero.

The dual form enables the introduction of nonlinearity by replacing the inner product $x_{i,t}^\prime$ $x_{j,k}$, i.e., a linear mapping, with a kernel function $K(x_{i,t},x_{j,k})$, which performs a nonlinear mapping of the inputs. Figure 1 illustrates a SVR with a linear (a) and a nonlinear (b) kernel. Conveniently, the introduction of a kernel function allows all calculations to be performed in the original feature space. We apply the most popular radial basis function (RBF), which takes the form Lu et al. (2009), Rasekhschaffe and Jones (2019):

$$\begin{aligned} K(x_{i,t},x_{j,k})=exp(-\gamma \Vert x_{i,t}-x_{j,k}\Vert ^2). \end{aligned}$$

(13)

This kernel function measures the similarity of firm characteristics between firm-observations and, consequently, how they affect the regression function. Here, $\gamma$ is a bandwidth parameter that controls the influence of observations. In our empirical application, we determine parameters $\epsilon$, $\lambda$ and $\gamma$ using grid search (see Table 11 in appendix for the ranges) on the validation data.

Fig. 1

This figure visualizes an exemplary SVR with a linear and a nonlinear kernel in (a) and (b), respectively. $\xi$ and $\xi ^*$ denote errors with magnitude greater than the $\left| \epsilon \right|$ threshold

3.3 Tree-based methods: random forest and gradient boosted regression trees

Regression trees are fully nonparametric and based on recursive binary splits, which enables them to account for high-level interactions. With respect to our application, regression trees group observations based on firm characteristics such that observations within a group are similar in terms of future returns. A tree ‘grows’ by performing a series of binary splits based on cutoffs of the firm characteristics at each branching point. Consequently, each split adds an additional layer of depth capable of incorporating more complex interaction effects. Starting with all observations, the tree successively divides the feature space into two rectangular partitions. The firm characteristic and its cutoff value are chosen to provide the best fit in terms of forecasting error. The resulting rectangular regions in the predictor space approximate the unknown function $g\left( \cdot \right)$ as the mean of the respective partition. The splitting procedure continues on one or both regions, resulting in increasingly smaller rectangles until a stopping criterion is met, e.g., depth of the tree (J) or no improvement by additional splits.

Fig. 2

This figure shows the structure of an example regression tree (a) with two characteristics (char1 and char2) and its equivalent representation as sliced partitions of the predictor space (b)

Figure 2 illustrates a regression tree of depth $J=2$ based on exemplary firm characteristics char1 and char2.¹⁰ Figure 2a presents the tree architecture, and Fig. 2b shows the representation in the rectangular feature space. Initially, all observations are divided based on the firm characteristic char1 with a cutoff value of 0.7. Firm-month observations with a value below that threshold are assigned to the left branch, while all other observations are assigned to the right branch. The left node is not split up any further, resulting in $R_1$, which is also called the “leaf node”. The right node represents another decision node, where the remaining firm-month observations are additionally divided on firm characteristic char2 with a threshold value of 0.6, resulting in $R_2$ and $R_3$. Thus, the observations are divided into regions $R_1$, $R_2$ and $R_3$, as shown in Fig. 2b. The prediction of a tree is the simple average of the response within a leaf node.

Formally, the unknown function $g\left( \cdot \right)$ is approximated by a regression tree as:

$$\begin{aligned} \hat{g}^{tree}\left( x_{i,t};M\right) =\sum _{m=1}^{M}{c_mI\left( x_{i,t}\in R_m\right) ,} \end{aligned}$$

(14)

where $R_m$ is one of the M leaf nodes, I is an indicator function of the firm characteristics identifying observations that belong to a particular region and $c_m$ is the associated average response. At each decision node, the algorithm aims to find the firm characteristic and its respective value that minimize the forecasting error. Finding a global optimal solution is generally computationally infeasible (cf. Hastie et al. 2017). Therefore, we follow (Breiman et al. 1984) and proceed with a greedy algorithm, in which the optimization is only performed locally at each individual decision node, i.e., solving the following optimization problem:

$$\begin{aligned} {\mathop {\mathrm{min}}\limits _{j,s}}{\left[ \sum _{x_{i,t}\in R_{l}\left( j,s\right) }\left( r_{i,t+1}-c_{l}(j,s)\right) ^2 + \sum _{x_{i,t}\in R_{r}\left( j,s\right) }\left( r_{i,t+1}-c_{r}(j,s)\right) ^2 \right] }, \end{aligned}$$

(15)

with

$$\begin{aligned} c_{l}\left( j,s\right)&=ave(r_{i,t+1}|x_{i,t}\in R_{l}(j,s)) \\ \text {and}~c_{r}\left( j,s\right)&=ave(r_{i,t+1}|x_{i,t}\in R_{r}(j,s)), \end{aligned}$$

where $c_{l}$ and $c_{r}$ are the average responses of the left and right partitions, which are conditional on variable j and its value s subject to the minimization. Put differently, at each decision node, the split variable j and its associated split value s are to be found with the aim of locally minimizing the forecasting error on each split.

Regression trees are widely adopted in the ML literature because (as visualized in Fig. 2) the sequence of binary decision rules allows a very simple and intuitive interpretation. Additionally, the inherent structure is ideal for representing multiway interaction effects and nonlinearities. However, regression trees are rarely used individually, as they are unstable with respect to changes in the input data and subject to severe overfitting problems. Unlike OLS, a regression tree can heavily overfit even with few variables, and with sufficient depth, a perfect fit can be achieved. In the limiting case, each leaf node contains only one observation. To alleviate the drawbacks of individual regression trees, we consider popular ensemble algorithms, i.e., random forests and gradient boosting, each of which combines many individually weak trees.

Random forest (RF) is based on the concept of bootstrap aggregation, in which the variance of an estimator is reduced by averaging over multiple independent and identically distributed (i.i.d.) bootstrapped samples. Thus, in the random forest, several B trees are trained independently on bootstrapped samples. In addition, at each decision node of a tree, only a random subset of $p < P$ predictors is considered, reducing both the correlation and variance of the estimator (cf. Breiman 2001). The output of a random forest is provided by:

$$\begin{aligned} \hat{g}\left( x_{i,t};B,M\right) =\frac{1}{B}\sum _{b=1}^{B}{\hat{g}^{tree}_b(x_{i,t};M)}. \end{aligned}$$

(16)

While trees are fit independently in the random forest algorithm, gradient boosted regression trees (GBRT) are estimated in an adaptive manner to reduce the bias. Therefore, B trees are estimated sequentially and combined additively to form an ensemble prediction. At each iteration b, a new tree $\hat{g}^{tree}_b$ is fit on the residuals from the previous iteration and added to the ensemble. However, the contribution of each individual tree is controlled by the learning rate $0< \nu < 1$ (shrinkage) to prevent overfitting of the residuals. Finally, the estimation function of GBRT is given by:

$$\begin{aligned} \hat{g}\left( x_{i,t};B,M,\nu \right) =\sum _{b=1}^{B}\nu \hat{g}^{tree}_b\left( x_{i,t};M\right) . \end{aligned}$$

(17)

In our empirical application, we determine parameters $\left( J,p\right)$ and $\left( J,\nu ,B\right)$ for RF and GBRT, respectively using grid search (see Table 11 in the appendix for the ranges) on the validation data.

3.4 Neural networks

Neural networks are successfully applied in numerous scientific and practical applications. Their flexibility draws from the concept to derive features from linear combinations of the input space and to model the response as a (nonlinear) function of these features (cf. Hastie et al. 2017). We focus on traditional feedforward neural networks, which generally consist of an input layer, one or more hidden layers, and an output layer. Each layer is represented by (computational) units called neurons. Figure 3a gives a graphical representation of a general feedforward neural network. Starting with the input layer, which represents the firm characteristics, the information is carried through the hidden layers via interconnected neurons and finally aggregated to form an estimate of the future returns (represented by the output layer). Each of the neurons performs very simple operations individually, i.e., combining information from the previous layer and applying an (nonlinear) activation function to the aggregate signal (see Fig. 3b).

Fig. 3

This figure provides a graphical representation of the general architecture of a feedforward neural network (a) and the information processing within a hidden neuron (b)

More generally, the output of an L-layer neural network (including the output layer) with $K^l\ \forall 1 \le l \le L$ neurons per layer can be thought of as a chain of functions (cf. Goodfellow et al. 2016), which recursively calculates the activations. Accordingly, the l-th layer’s activations $\alpha ^{l}$, which is a vector of length equal to the number of nodes, are given by:

$$\begin{aligned} a^l=f^l\left( \alpha ^{\left( l-1\right) }\right) =f^l\left( W^l\alpha ^{\left( l-1\right) }+b^l\right) ,\quad \forall 1 \le l \le L, \end{aligned}$$

(18)

where $W^l$ is a $K^{l}\times K^{\left( l-1\right) }$ matrix of weights transmitting the outputs from layer $\left( l-1\right)$ to layer l, where they then aggregate to form the activation a. Accordingly, $l=0$ corresponds to the input layer with $a^0$ being the raw vector of firm characteristics, $x_{i,t}$, and $f^1,\ldots ,f^L$ are univariate transformations of the weighted signal from the previous layer plus a bias. $W=\left\{ W^1,\ldots ,W^L\right\}$ and $b=\left\{ b^1,\ldots ,b^L\right\}$ are parameter sets of weight matrices and bias vectors, respectively, determined in the model calibration.

In a regression task, the output layer L performs a linear combination, yielding the final output:

$$\begin{aligned} \hat{g}\left( x_{i,t};W,b\right) =f^L\left( \alpha ^{\left( L-1\right) };W^L,b^L\right) =W^L\alpha ^{\left( l-1\right) }+b^l. \end{aligned}$$

(19)

There are numerous architectural design options when structuring a neural network, e.g., number of neurons, number of layers, and activation functions. Zhang et al. (1998, p. 42) state that “[...] the design of an ANN is more of an art than a science”. However, there is no clear guidance on how to determine an appropriate network architecture. Therefore, we take a pragmatic approach by choosing a single hidden layer and the hyperbolic tangent as an activation function:

$$\begin{aligned} f^l\left( \cdot \right) =\frac{e^x-e^{-x}}{e^x+e^{-x}},\quad \forall 1\le l \le L-1. \end{aligned}$$

(20)

Hornik et al. (1989) and Cybenko (1989) proved universal approximator properties for single hidden layer feedforward neural networks with sigmoid activations. The number of hidden neurons is chosen based on a rule-of-thumb for single hidden layer neural networks derived by Wong (1991), i.e., twice the number of input nodes.

As stated before, in a neural network, W and b are the parameters of interest. Their estimates, however, are solutions of a nonconvex optimization problem. One of the most widely used algorithms for training neural networks are variants of stochastic gradient descent (SGD). SGD iteratively approaches the (local) minimum of the $l_2$ objective function by approximating its gradient on random subsets of the training data and adapting the parameters accordingly. We use the popular Adaptive Moment estimation (Adam) by Kingma and Ba (2014). A critical tuning parameter in the learning algorithm is the learning rate lr, which controls the step size of each parameter update. First, to mitigate the risk of overfitting, we impose an $l_2$ penalty (weight decay), which shrinks the weights between neurons toward zero without imposing exact zero. Second, we stop the training of our network early if the error on the validation set does not improve for ten consecutive iterations. Third, we build ensembles of size ten and average their outcome, as the parameter initialization and stochastic training introduce sources of randomness. Hansen and Salamon (1990) provide evidence that ensembles not only stabilize results but also improve generalization. In our empirical application, we determine the learning rate lr and $l_2$ penalty strength $\lambda$ using grid search (see Table 11 in the appendix for the ranges) on the validation data.

3.5 Estimation, tuning and testing

We provide all models with the same data, i.e., a ten-year rolling period of monthly data, and predict returns for the months of the subsequent year for every firm. Stated differently, we use only past information to predict future (out-of-sample) returns. Unlike the OLS model, the performance of most machine learning algorithms depends heavily on the choice of hyperparameters. A commonly used strategy is to divide the in-sample data into disjoint subsets (training and validation) to mimic a pseudo out-of-sample setting. The hyperparameters are then chosen to maximize the performance on the validation set. Therefore, we split each in-sample window into seven years of training and three years of validation and perform a grid search to find an appropriate set of hyperparameters.¹¹

Fig. 4

This figure illustrates the rolling estimation scheme employed in this study

Figure 4 illustrates our sample splitting scheme. More precisely, we estimate the respective model with a set of hyperparameters from the parameter grid (see Table 11) on the training set. Then, we generate predictions for the validation set and evaluate the performance. After determining the best set of hyperparameters, we re-estimate the model on the full ten-year period of training and validation data to incorporate the most recent information. However, data for actual forecasting never enter the model during the estimation procedure.

To assess the predictive performance of our models, we evaluate them in three ways. We first deploy a statistical analysis to quantify the models’ predictive accuracy, i.e., how well predicted returns reflect realized returns. A common metric to do so is the out-of-sample (pseudo) $R^2$, which is defined as:

$$\begin{aligned} R^2 = 1 - \frac{\sum _{(i,t)\in OOS}(r_{i,t} - \hat{r}_{i,t})^2}{\sum _{(i,t)\in OOS}(r_{i,t}-\bar{r}_{i,t})^2}, \end{aligned}$$

(21)

where $\hat{r}_{i,t}$ denotes the model’s prediction and $\bar{r}_{i,t}$ denotes the historical average for asset i at time t. This definition measures the proportional reduction in forecasting errors of the predictive model relative to the historical average. Thus, $R^2 > 0$ indicates that the predictive model is more accurate than the historical average in terms of forecasting errors. Note that unlike the conventional $R^2$, this formulation can also be negative. While the historical average is appropriate in terms of a time-series analysis, it leads to an inflated $R^2$ in the case of a panel of stock returns. Therefore, we set $\bar{r}$ to zero, which yields a stricter threshold for proper forecasting models, and we follow this suggestion.¹²

$R^2$ represents a measure that provides information about the quality of forecasts from a predictive model compared to that from a constant model. However, if we want to compare among different models, then examining $R^2$ alone does not allow us to infer whether one model is significantly superior to another. Therefore, we perform the popular (Diebold and Mariano 1995) (DM) test, which is designed to compare the predictive accuracy of two models. More precisely, it tests for the null of equal prediction errors $H_0: E[d_t] = 0$, where $d_t$ is the loss differential between two forecasts at time t. The DM test is applicable in the case of serial correlation. However, stock returns are prone to be strongly correlated in the cross-section while only being weakly correlated across time. To alleviate this issue, we average loss differential $d_t$ across assets, thus resulting in a time-series with weak serial correlation. The test statistic is defined as follows:

$$\begin{aligned} \begin{aligned} DM&= \frac{\bar{d}_{1,2}}{\hat{\sigma }_{\hat{d}}} \sim \mathcal {N}(0,1),\quad \text {with} \\ \bar{d}_{1,2}&= \frac{1}{T}\sum _{t=1}^{T}\hat{d}_{1,2,t}, \\ \hat{d}_{1,2,t}&= \frac{1}{N}\sum _{i=1}^{N}(\hat{e}_{1,i,t}^2-\hat{e}_{2,i,t}^2),\quad \text {and} \\ \hat{\sigma }_{\hat{d}}&= \sqrt{\frac{\frac{1}{T}\sum _{t=1}^{T}(\hat{d}_t - \bar{d})^2}{T}}. \end{aligned} \end{aligned}$$

(22)

Second, we analyze our forecasts in terms of economic gains. Leitch and Tanner (1991) argue that traditional statistical metrics are only loosely related to a forecast’s achievable profit. Thus, we consider forecast-based portfolio sorts to assess the economic performance of our models. At the end of each month in the testing period (January 2001 to December 2019), we assign all available stocks with equal weight to ten portfolios using cross-sectional decile breakpoints based on the return prediction for the next month. In addition, we construct a long-short portfolio reflecting a zero-net investment by buying the top decile portfolio and selling the bottom decile portfolio to capture the aggregate effect.

Third, we use the entire cross-section of stocks to estimate our models. Stocks of small firms, however, follow different dynamics in terms of their covariances, liquidity, and expected returns (cf. Kelly et al. 2019). More specifically, Hou et al. (2018) show that much of the predictability detected in the previous literature is found in the smallest stocks. While microcaps represent only approximately 3% of the total market capitalization of the NYSE/Amex/NASDAQ universe, they account for approximately 60% of the number of stocks. Due to high costs in trading these stocks (e.g., Israel and Moskowitz 2013), predictability (in terms of economic performance) in small stocks is more apparent than it is real. To investigate the degree to which the performance depends on firm size, we successively remove stocks below the respective deciles of the cross-sectional market capitalization.

4 Data

Previous studies have documented the existence of a U.S. bias in research in economics (e.g., Das et al. 2013) and finance (e.g., Karolyi 2016). In this regard, recent literature (e.g., Harvey et al. 2016) argues for a higher statistical threshold (t-statistic of 3 rather than 2) in empirical studies on the U.S. stock market as well as a stronger focus on other asset classes and stock markets. We follow this demand by investigating the European stock market. More specifically, we use all stocks (approximately 12,000) from the countries in the MSCI Developed Markets Europe Index¹³. We retrieve monthly data from January 1990 to December 2019 from Datastream and Worldscope. The data retrieval starts with the identification of common equity stocks using Datastream’s constituent lists (research lists, Worldscope lists and dead lists). Specifically, for every country in the MSCI Developed Europe Index, we use its constituent lists and eliminate any duplicates. As a result, we obtain one remaining list for every country. To each of these lists, we apply generic as well as country-specific screens to eliminate noncommon equity stocks. Moreover, to all stocks remaining from this screening procedure, we then apply dynamic screens to account for data errors. The procedure described above is established in the academic literature and described extensively (e.g., in Ince and Porter 2006; Campbell et al. 2010; Griffin et al. 2010, 2011; Karolyi et al. 2012; Annaert et al. 2013; Fong et al. 2017).

Our predictors are beta, market capitalization, the book-to-market equity ratio, momentum, investment, and operating profitability. These predictors are calculated from the Datastream and Worldscope variables (datatype in brackets) total return index (RI), market equity (MV), book equity (WC03501), total asset growth (WC08621) and operating income (WC01250). We assume that accounting data are available to the public six months after the fiscal year ends to avoid look-ahead bias. Beta (beta) is the exposure of a stock to the market factor as derived from the capital asset pricing model (CAPM). According to the CAPM, stock returns are expected to increase as the stock’s beta increases. For each month, we estimate the beta of a stock based on the daily stock returns from the previous 12 months to avoid any look-ahead bias. Following the established literature, returns are expected to exhibit an inverse relationship with firms’ market capitalization (size) (Banz 1981) and a positive association with the book-to-market-equity ratio (be2me) (Rosenberg et al. 1985). Momentum (mom) is defined as the total return over the prior 12 months, excluding the last month. Prior literature finds evidence of a positive relation between momentum and stock returns (Jegadeesh and Titman 1993; Carhart 1997). Investment (inv) is growth in total assets, and operating profitability (op) is operating income scaled by the book value of equity. Following (Titman et al. 2004) and (Novy-Marx 2013), stock returns are expected to increase as investment decreases and operating profitability increases, respectively. In addition to exposure to the market factor (beta), market capitalization and the book-to-market-equity ratio are proxies for sensitivities to common unobservable risk factors in the Fama and French (1993) three-factor model. Furthermore, momentum is a surrogate for the sensitivity to a common unobservable risk factor in the Carhart (1997) four-factor model. Lastly, investment and operating profitability proxy for sensitivities to common unobservable risk factors in the Fama and French (2015) five-factor model.

Table 1 Descriptive statistics and characteristics of quantile portfolios formed from monthly sorts of stocks on predictor variables

We report time-series averages of cross-sectional statistics, specifically, the mean, standard deviation, and number of observations, of the monthly predictor variables and stock returns in Panel A of Table 1. For comparability, we include only firm-month observations with nonmissing returns in our analysis, resulting in an average sample size of 1,755 firms per month. We find that the average monthly stock return is 0.88% and the average cross-sectional standard deviation in monthly stock returns is 8.86%. To investigate the predictive ability of an individual variable, we further assign all stocks to five portfolios for each month from 1990 to 2019 using quintile breakpoints from the cross-section of monthly predictor variable values and calculate the equal-weighted monthly percent returns for the next month. Panel B of Table 1 reports the average monthly returns of the five portfolios. To analyze the aggregate effect of the predictor variable on stock returns, we take a long position in portfolio 5 and a short position in portfolio 1. Column “pVal (5-1)” reports the p-value (as a percentage) from a t-test against the null hypothesis of zero average return of the “5-1” portfolio. As expected, we find a positive relation between stock returns and momentum, the book-to-market-equity ratio and operating profitability and a negative relation between stock returns and investment for the European stock market. Contradicting the CAPM, we find a negative relation between stock returns and beta, which is consistent with empirical evidence provided by previous studies (e.g., Frazzini and Pedersen 2014). Similarly, we find no relationship between firm size and stock returns, which is also consistent with recent empirical findings (e.g., van Dijk 2011).

In our empirical study, we further account for missing values, different scales and extreme observations. To address missing values and maintain the number of return observations, we replace missing characteristics with their cross-sectional median if the respective returns are available. However, in contrast to much of the current cross-sectional predictability literature, we have observations on each characteristic in every month of our sample and do not fill entire cross-sections with values of zero. Different scales and extreme observations are dealt with by cross-sectionally rank normalizing firm characteristics.

5 Results

5.1 Predictive accuracy

Table 2 presents monthly out-of-sample $R^2$ for the employed methods and different levels of market liquidity. Column 1 displays the levels of market liquidity established by removing stocks with the prior month’s market values below the cross-sectional decile breakpoints corresponding to q. Columns 2 to 9 correspond to the $R^2$ values as a percentage achieved by each individual model. Positive values indicate better predictive accuracy compared to a naive constant zero forecast.

Table 2 This table reports monthly predictive panel $R^2$ as a percent

For the full cross-section of stocks (first row), OLS generates an $R^2$ of 0.43%. After dropping firms with market values below cross-sectional thresholds in increments of ten percent, the predictive power gradually decreases to − 0.32% for the largest stocks. Penalized linear methods, i.e., Lasso, Ridge and Enet, perform on a very similar, yet slightly worse, level than OLS. This result is not surprising, as we are using only a small set of well-established, and essentially uncorrelated firm characteristics. The predictive accuracy of SVR is consistently below that of OLS. A potential source of this underperformance is that distance-based algorithms such as kernel SVR are particularly fragile in the presence of low-impact predictors. Panel B of Table 1 indicates that this may be the case for size, as the return differences across portfolios are only of minuscule amplitude. Additionally, SVRs are highly sensitive to the choice of hyperparameters, as Probst et al. (2019) identify a much higher tunability of SVR compared to that of RF or GBRT. RF, GBRT and NN, however, exhibit a remarkable improvement over OLS for the broad market (0.58%, 0.60% and 0.67%, respectively). With respect to persistence, they exhibit a diminishing pattern in predictability toward larger stocks similar to that of OLS. This pattern is in line with Hou et al. (2018) showing that much of the predictability detected in the previous literature is attributable to the smallest stocks. GBRT and NN, however, are able to achieve both (1) consistently greater $R^2$ than OLS and (2) consistently positive values for $R^2$. The differences range between 0.46 and 0.56 percentage points for GBRT and NN, respectively, indicating that the predictive accuracy can be improved by (choosing the appropriate) machine learning methods.

Table 3 presents the p values for the DM test on the full sample of stocks (Panel A) and for the top decile of market capitalization (Panel B). We display the lower triangle only, in which row models correspond to forecast errors $\hat{e}_1$ in equation (22); thus, significant p-values indicate that the row model outperforms the column model.¹⁴

Table 3 This table reports p values of pairwise Diebold-Mariano (DM) tests comparing stock-level return forecasts of various models against the null hypothesis of equal predictive accuracy

The DM test provides support for the empirical results derived from the $R^2$ values presented in Table 2. The first conclusion from Panel A of Table 3 is that predictions from penalized linear methods and SVR do not provide statistically significant improvements over OLS. More specifically, SVR and Enet even exhibit a significantly inferior predictive ability at the 5% level. Tree-based methods and NN produce statistically significant improvements over linear methods and SVR at least at the 5% level. For any pairwise comparison among tree-based methods and NN, the null of equal predictive accuracy cannot be rejected. For Panel B of Table 3, we find that the p-values of penalized linear methods and SVR generally decrease compared to OLS, indicating that they experience relative improvement when predicting returns of large cap stocks. Conversely, the superiority of RF over linear models and SVR disappears, indicating that its predictive performance is driven by picking up small-scale inefficiencies present in microcap dynamics. For GBRT and NN, the null hypothesis against not only OLS but also against all other models can still be rejected, indicating that their outperformance is present throughout all market segments.

5.2 Economic gains

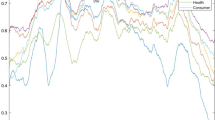
From an investor’s perspective, statistical performance is only of subordinate importance. In addition, Leitch and Tanner (1991) argue that statistical metrics are only loosely related to a forecast’s achievable profit. Next, we assess the economic performance of our models by portfolio sorts. At the end of each month, we generate return forecasts for the next month with each model. After that, we assign stocks to one of ten portfolios based on decile breakpoints of the forecasts. Finally, to capture the aggregate effect, we construct a zero-net-investment portfolio that simultaneously buys (sells) the stocks with the highest (lowest) expected returns, i.e., decile 10 and 1, respectively. Table 4 depicts the results using the full sample. Note that all models share a monotonically increasing relationship in realized returns (column ‘Avg’) and in the Sharpe ratio (column ‘Shp’), which is statistically significant at the 1% level after testing for monotonicity between portfolios 1 to 10 using the Patton and Timmermann (2010) test (row ‘pVal(MR)’). From an investor’s perspective, this property is highly desirable, as higher returns are, thus, relatively cheaper in terms of risk than low returns. Moreover, we see significantly positive spreads (row ‘H-L’) at the 1% significance level for all models, indicating that, generally, all models are effective in capturing the cross-sectional dispersion of returns (row ‘pVal(H-L)’). Upon examining the return spreads, we find penalized linear methods and SVR to be on eye-level with OLS, with Lasso, Enet and SVR resulting in slightly larger spreads. NN and tree-based methods outperform OLS by a quite substantial margin, with a surplus in return spreads of up to 64 basis points for RF. The zero-net-investment strategy for the predictions of RF yields an extraordinary return of 2.38% per month (32.61% annualized), while GBRTs provide the best risk-return-tradeoff with a Sharpe ratio of 0.56 per month (1.94 annualized). Even if SVR exhibits a negligible improvement in terms of return spread, it has a unique characteristic from a risk perspective, as it is the only model with a significantly monotonic increasing relationship in returns while having a significantly monotonic decreasing relationship with risk, i.e., higher returns are associated with lower risk, which is extremely compelling from an investor’s perspective. Figure 5 presents cumulative performance plots corresponding to the long portfolios (portfolio ‘H’) of Table 4 along with the cumulative market return. The market return for Europe is retrieved from Kenneth French’s website.¹⁵ Note that all models outperform the market index and that tree-based methods dominate all other models by a large margin. Consistent with Leitch and Tanner (1991), we find that the statistical performance reported in the previous subsection does not necessarily translate into economic performance.

Table 4 This table reports the performance characteristics of prediction-based decile portfolios formed from different models

Fig. 5

This figure shows cumulative logarithmic returns of prediction-based portfolios for different models and the market (Mkt). The strategy is implemented as follows: In every month of our testing sample from January 2000 to December 2019, we sort all stocks by their expected return for the next month and take a long position in stocks corresponding to the top decile of expected returns

Table 5 presents return spreads analogous to row ‘H-L’ in Table 4 for the different levels of market capitalization. In Table 2, the predictive accuracy gradually decreases for larger stocks. For the return spreads we generally find a similar pattern; however, most models exhibit a peak (economic) performance after cutting off the smallest 20%. This level of market liquidity is often considered free of microcaps (e.g., Lewellen 2015). A possible interpretation might be that the dynamics of those stocks are neither very persistent nor predictable. Tree-based methods, on the other hand, experience a sharp drop in economic performance after cutting off the bottom decile of market capitalization, again indicating that their outperformance, to a large extent, relies on capturing microcap dynamics. Further increasing levels of market capitalization are accompanied by decreasing return spreads, a pattern consistent with the concept of market efficiency, assuming that the information environment for large firms is richer and more efficient than that for small firms. Penalized linear methods are again close to OLS. The outperformance of tree-based methods is mostly present when considering the full sample. While outperformance vanishes for RF afterward, GBRTs maintain a slight surplus over OLS toward reducing the sample to the largest stocks. NN and SVR consistently achieve higher return spreads than OLS across all market segments. While the results for NN are in line with the previous findings, the results for SVR come as quite of a surprise given its low predictive accuracy (cf. Table 2). Specifically, after cutting off the bottom decile of market capitalization, it exhibits the highest returns for the zero-net-investment strategy overall with remarkable stability. The evaluation thus far provides evidence that machine learning can lead to better results than the traditional OLS model, not only statistically but also economically.

Table 5 This table reports the return of a prediction-based zero-investment strategy formed from different models

6 Additional results

6.1 Transaction costs

Transaction costs impair the profitability of any investment. Higher turnover rates of investment strategies can easily nullify their overperformance in terms of raw returns. Therefore, we aim to examine whether the stronger performance of machine learning models compared to OLS is driven by substantially higher turnovers. However, realistic transaction costs are not always available, cumbersome to use or expensive to acquire (cf. Lesmond et al. 1999). Additionally, Collins and Fabozzi (1991) state that true transaction costs are inherently unobservable. Consequently, any good-faith estimate of transaction costs would probably be wrong. We consider the average monthly turnover of the spread portfolios (‘H-L’) calculated as:¹⁶

$$\begin{aligned} Turnover=\frac{1}{T}\sum _{t=1}^{T}{\left( \sum _{i}\left| w_{i,t+1}-\frac{w_{i,t}\left( 1+r_{i,t+1}\right) }{\sum _{j}{w_{j,t}\left( 1+r_{j,t+1}\right) }}\right| \right) ,} \end{aligned}$$

(23)

where $w_{i,t}$ is the weight of stock i in the portfolio at time t.

Table 6 This table reports average monthly percentage changes in holdings, i.e., turnover, for different models and levels of market liquidity in terms of market capitalization (Size)

Table 6 reports the average monthly turnover in percent for all models and levels of market liquidity. In line with Gu et al. (2020), we find that turnover rates for tree-based methods are generally approximately 20% higher than those for OLS. As the outperformance of tree-based methods appeared to be meaningful only when including microcaps, we conclude that their potential is limited by the higher turnover since microcaps are inherently more difficult and costlier to trade. Penalized linear methods, SVR and NN, on the other hand, have turnover rates comparable to those of OLS. Especially on the largest stocks, where transaction costs are generally smaller, SVR and NN still achieve a spread of up to 20 basis points above OLS. We conclude that the marginally higher turnovers are unlikely to explain the pronounced outperformance or, to put it differently, outperformance is unlikely to disappear in the light of transaction costs.

6.2 Performance within subperiods

Inspired by a number of studies suggesting that returns may differ across market states (e.g., Cooper et al. 2004; Wang and Xu 2015), we evaluate the performance of the models separately for bull and bear markets. Following (Zaremba et al. 2020), we define these states as subperiods of positive (bull market) and negative (bear market) total excess return on the market portfolio during the last 12 months. The results for the predictive accuracy and economic gains from the individual models are reported in Tables 7 and 8, respectively.

Table 7 This table reports monthly predictive panel $R^2$ as a percent

The first conclusion from Table 7 is that return predictability is generally higher in bull markets (Panel A) than in bear markets (Panel B). While we encounter decreasing predictability with firm size in the full panel (cf. Table 2), we find that in bull markets, the predictability in terms of $R^2$ is greater when excluding very small stocks. For bear markets, the $R^2$ values are generally negative and monotonically decreasing in firm size. Among the machine learning methods, NN produces the highest $R^2$ and shows the highest outperformance compared to OLS in both bull and bear markets.

Table 8 This table reports the return of a prediction-based zero-investment strategy from the models

With regard to the economic gains reported in Table 8, we find that differences are visible, although not dramatic, during times of a general upward trend (Panel A). In bear markets, however, the differences become more apparent. In particular, SVR and NN exhibit consistently higher returns compared to OLS. Even for the 10% largest stocks, the difference of approximately 40 basis points is quite staggering. The results presented here suggest that machine learning does not add exceptional value over OLS during periods of a general upward trend. However, in downward markets—which is when investors usually lose money—these models generate considerable value.

6.3 Forecast combinations

Lastly, we consider forecast combinations. In general, forecast combination acts as a tool for risk diversification across individual models while, in many cases, simultaneously improving performance (Timmermann 2006). Some of the models presented herein (i.e., RF, GBRT, and NN) utilize the benefits of building ensembles as an integral part of the model definition itself. Several studies have highlighted the benefits of forecast combinations and proposed different methods with respect to choosing optimal model weights (e.g., Bates and Granger 1969; Winkler and Makridakis 1983). However, here, we use the forecast combinations as a simple proxy to test whether linear methods contain information complementary to that of the machine learning models. To do this, we form combinations from 1) all models and 2) only nonlinear methods (SVR, RF, GBRT, NN). If there is additional value, we would expect 1), i.e., the combination of all models, to provide superior predictions. Therefore, we restrict ourselves to simple combination schemes that often show better results than more sophisticated methods involving additional parameter estimates (Timmermann 2006).

The forecast combination takes the general form:

$$\begin{aligned} \hat{r}_{i,t+1}^{\text {COMB}} = \sum _{h=1}^{H}w^{h}_{t}\hat{r}_{i,t+1}^h, \end{aligned}$$

(24)

with

$$\begin{aligned} w^{h}_t = {\left\{ \begin{array}{ll} \frac{1}{H} &{} \text {Equal-weighted (EW)} \\ \frac{1/MSE_t^h}{\sum _{m=1}^{M} 1/MSE_t^m} &{} \text {Inverse MSE-weighted (IMSE)} \\ \frac{1/R_t^h}{\sum _{m=1}^{M} 1/R_t^m} &{} \text {Inverse MSE rank-weighted (IRANK),} \end{array}\right. } \end{aligned}$$

(25)

where $w_t^h$ is the weight of model h at time t and H is the total number of models. MSE refers to the in-sample mean-squared error, and R refers to the ranking of MSE (ascending order) among all models.

Table 9 reports results on the predictive accuracy of forecast combinations. The left-hand panel considers all models in the combination, while the right-hand panel excludes linear methods. We find that the predictive accuracy is consistently higher when relying only on nonlinear methods, irrespective of the concrete combination scheme used. With respect to the weighting-schemes, inverse rank-weighting appears to provide slightly worse results, while the other two are on equal footing. Most importantly, we exhibit two key take-aways: First, all combinations outperform the single use of OLS. Second, and in contrast, none of the combinations is superior to the strongest machine learning model, NN. However, the best model may not be known ex ante; thus, the combination of various models might still reduce model selection risk.

Table 9 This table reports monthly predictive panel $R^2$ as a percent

Table 10 reports return spreads based on the forecast combinations. The results generally support the statistical findings. However, we find that the economic performance improves over the best individual model, SVR, up to $Size > 0.7$. Overall, the performance of the conventional OLS approach can be improved when combined with models from the machine learning literature. Moreover, our results raise the question of whether the commonly applied purely linear model is even necessary for building expectations about future stock returns, as the combination of nonlinear methods provides superior performance both statistically and economically while individual model selection risk is reduced.

Table 10 This table reports the return of a prediction-based zero-investment strategy formed from different forecast combination schemes, i.e., simple averaging (‘EW’), inverse rank-weighting (‘IRANK’) and inverse MSE-weighting (‘IMSE’)

7 Conclusion

In this paper, we provide an eye-level comparison of the commonly applied linear regression approach in stock return predictions (Lewellen 2015) and machine learning methods, i.e., penalized linear methods, support vector regression, tree-based methods, and neural networks. We find that the nonlinear machine learning methods in particular can provide both statistically and economically meaningful performance gains over the conventional OLS approach, thereby revealing that machine learning methods are not more vulnerable than OLS to model breakdowns.¹⁷ In our analysis, GBRTs exhibit the highest outperformance, of approximately 0.6% per month, based on the entire cross-section of European stocks, which decreases to 0.1% per month when only stocks of the largest ten percent of firms are considered. Overall, we find that NN provides the most reliable predictions in terms of both statistical and economic performance, as its superior performance is robust over all market segments. In addition, we find that the economic performance gains are not attributable to substantially higher turnover of stocks. Analyzing bull and bear markets separately, we find that the value of NN is mostly generated in downward trending markets when investors generally lose money. As forecast combinations have frequently been found to produce better forecasts than methods based on the ex ante best individual forecasting models (Timmermann 2006), we investigate the performance of forecast combinations and find that the combination of only nonlinear models exhibits the performance of the best individual model, which is good news, as it allows investors to reduce model selection risk by diversification. We further find that all forecast combinations in this study outperform the sole use of OLS. Our results are derived based on a small set of well-established predictor variables borrowed from the asset pricing literature. However, as the performance of the (nonlinear) machine learning methods is generally higher than that of OLS, we strongly recommend a more intensive use of machine learning models to predict stock returns in future research and practice. Beyond our considerations, future research should also examine the use of machine learning techniques with respect to long-term stock returns (as considered in Kyriakou et al. 2021; Mammen et al. 2019) more closely.

Appendix

See Table 11.

Table 11 This table describes the parameter ranges considered in the grid search