1 Introduction

The following work is motivated by a practical application in the label printing industry. The printing company’s customers are consumer goods manufacturers. They typically require labels of several sorts of a single product family like, for example, different sorts (strawberry, pineapple etc.) of the product family yogurt. These labels show different imprints, but share the same form and size.

Thus, from the printing company’s point of view, a customer order comprises several order lines with varying demands \(d_j\) for different sorts \(j = 1, \ldots {}, J\), which have to be delivered together in a batch. The printer can print several printing lanes \(l = 1, \ldots {}, L\) of equal width in parallel on a single roll of paper of sufficient length. The maximum number of lanes L can easily be calculated because of the labels’ common size.

To set up the printer, a printing plate has to be designed incurring fixed costs sc. Let us temporarily assume \(J = L\). Then all different sorts j could be printed in parallel on a single plate and the sort \({\hat{j}}\) with the maximum demand \({\hat{d}} := \max _{j}{\{d_j\}}\) would define how long the printer has to run. Thus, surplus quantities \(({\hat{d}} - d_{j})\) would have to be generated for the other sorts \(j \ne {\hat{j}}\). Because customers frequently change their labels’ inscriptions, such surplus production quantities, which exceed the actual customer demand, are not held in stock. They have either to be disposed or can be sent to the customer as some free-of-charge bonus quantity. Both alternatives are not desired from the company’s point of view. Thus, these surplus quantities are in the following denoted as “scrap”. Each unit of scrap causes variable costs vc. The overall costs of scrap could, e.g., be decreased by only allowing a single sort j per plate and printing \(\left\lceil {} d_{j}/L \right\rceil {}\) units of this sort in parallel. However, this would necessitate J printing plates and thus imply setup costs \(J \cdot sc\) instead of just \(sc\).

Generalizing the above example to arbitrary J (not necessarily equaling L), the planning problem arises how to assign the sorts j to and spread their demands \(d_j\) over the lanes l of different printing plates \(s = 1, \ldots {}, {\hat{S}}\) so that the sum of setup costs for designing and installing plates and variable costs of surplus scrap are minimized. A sort j could also be produced on more than one and less than L lanes in parallel, but should not involve several printing plates. Printing the same sort on several plates might lead to slight differences in the printed impression. This is not desired by the company and its customers. Since paper is much more expensive than color, the company would rather prefer the “free-of-charge-sending” than disposing empty paper. However, the company does not want to express these preferences by further detailing the costs of scrap vc. Instead, as a general rule of planning, it does not allow a lane to remain empty. The production lot of a printing plate is called a “printing block”. Thus, for ease of notation, this practical optimization problem the company is faced with will in the following be named the “block building problem” (BBP).

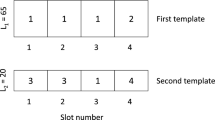
An illustrative example of different solutions of a BBP with \(L = 2\), \(J = 4\) and \(d_{1} = 10\,000, d_{2} = d_{3} = 20\,000\) and \(d_{4} = 30\,000\) is shown in Fig. 1. The intuitive solution (a)—using one lane per sort—requires the minimum of two plates, but necessitates 20 000 units of scrap. The other intuitive solution (b)—using L parallel lanes per sort—does avoid scrap, but needs the maximum number of four plates. As the less intuitive solution (c) demonstrates, solution (b) is inefficient because scrap can also be avoided when using just three printing plates. However, solution (a) has to be preferred to solution (c) as long as \(20\,000 vc < sc\) holds.

Fig. 1
figure 1

Three different solutions of a BBP with \(L=2\), \(d_{1} = 10\,000, d_{2} = d_{3} = 20\,000\) and \(d_{4} = 30\,000\)

Full size image

Up to the authors’ knowledge, this special type of practical application has not yet been considered in the scientific literature. Therefore, the intended contribution of this paper is

  • to formalize the practical problem BBP sketched above as a mixed integer programming (MIP) model in order to ease understanding and allow comparisons with related problem settings, model formulations and solutions approaches known from scientific literature,

  • to present a solution heuristic for this problem that has successfully been introduced in the label printing company some years ago and since then is sustainably used there, and

  • to compare this heuristic with the exact solution of the MIP model and with further, alternative heuristic approaches.

Thus, Sect. 2 discusses closely related problems and shows how the BBP differs. An MIP model of the BBP, which is an extension of a so-called job splitting problem, is introduced in Sect. 3. This MIP model allows a more precise and more formal problem definition than the examples used in the introduction. It is followed by a decomposition approach in Sect. 4, which is tailored to and takes advantage of the special needs and characteristics of the BBP. This decomposition scheme allows to define several heuristics. One of them is used by the above-mentioned printing company. The other ones will serve as benchmarks. The numerical tests of Sect. 5 compare these decomposition heuristics with further intuitive solution approaches and with exact and heuristic solutions of the MIP solver for problem instances of different sizes. Finally, Sect. 6 summarizes the most important results and proposes directions of future research.

2 Literature review

Obviously, the BBP is related to cutting, scheduling and lot-sizing problems. The former tries to avoid the waste or scrap resulting from some cutting process as good as possible. On contrary, the latter minimize setup costs by optimizing the sequence of changeovers or by bundling several demands for the same or (in terms of the setup effort involved) “similar” products to bigger production lots.

Wäscher et al. (2007) introduce a typology of and give an overview over cutting (and packing) problems in general. It is hard to classify the BBP according to this typology. Since the width and number of lanes are fixed, but the length of the paper roll can be assumed as infinite, the BBP could be seen as a one-dimensional “input minimization” problem, where a high number of identically shaped small items (the labels) have to be placed on one large object (the paper roll) with a variable length. This would classify the BBP as a so-called open dimension problem (ODP). However, according to Wäscher et al. (2007, Sect. 7.8), ODPs are only possible in two or more dimensions. This apparent contradiction is due to the fact, that the labels are identically shaped, but nevertheless heterogeneous in terms of the imprint (different sorts) and that the necessity of building blocks introduces a sort of additional “virtual” dimension.

Teghem et al. (1995) describe the “mating problem” (MP), an optimization problem closely related to the BBP, which has unfortunately not been discussed and categorized by Wäscher et al. (2007). Here book covers j have to be grouped (mated) on offset plates s with \(L = 4\) different rectangular compartments l per offset plate and thus per sheet of paper printed. A given demand \(d_{j}\) has to be fulfilled with minimum total costs for the different offset plates involved and for overall sheets of paper printed. Contrary to the BBP, a single book cover can be assigned to several plates. All four compartments have to be used. The authors propose a nonlinear and a linear MIP formulation together with a simulated annealing-based solution heuristic. An overview of further solution approaches to and extensions of this problem is given by Baumann et al. (2015) who denote this class of problems as the cover-printing problem (CPP).

One of these extensions is the so-called label printing problem (LPP) of Yiu et al. (2007). As for the BBP the intended application is printing labels. However, the technology used is different. The labels are not printed on quasi endless rolls of paper, but—alike the MP—on discrete rectangular sheets of paper consisting of L rectangular compartments. Thus, the role of the lanes of the BBP is the same as the role of the compartments of the MP/LPP (or CPP in general). But the lanes are only arranged in one dimension, whereas the compartments are arranged in two dimensions. As opposite to the MP, the LPP is not restricted to \(L = 4\) and a sort j can only be assigned to a single offset plate s. In contrast to the BBP and MP, compartments of the LPP may remain empty. The authors formulate a nonlinear IP which minimizes the amount of printed scrap and empty compartments. Costs are not considered. A solution heuristic decomposes the LPP into two subproblems, one of which is solved by simulated annealing again.

Degraeve and Vandebroek (1998) describe and model a layout problem in the fashion industry, which is a variant of the one-dimensional cutting stock problem (see Gilmore and Gomory 1961, 1963). Transferring its basic idea to the BBP would mean that a maximum of \(J^{L}\) combinations to place sorts j on lanes l has to be enumerated. These “patterns” define the set of potential printing plates \(s = 1,\ldots {}, J^{L}\) which could be designed. Among them (or at least some reasonably pre-defined subset), the ones need to be selected that should actually be used. Additionally, the corresponding production lot-sizes have to be determined that finally establish the printing blocks. Again, Baumann et al. (2015) give an overview over this stream of the literature.

Motivated by practices in the printing industry, Ekici et al. (2010) introduce the “job splitting problem” (JSP). Here J different product types j with demands \(d_{j}\) (“jobs”) have to be produced on a single machine which has L slots l. Each slot l can produce each type j, but only one at a time. The slots need to be set up for the types in a joint setup process with costs sc. Then, all slots do produce simultaneously during a “run” s until the next setup process and the next run \(s+1\) start. If total production exceeds total demand, each unit of waste produced incurs costs vc. The problem is to split the demands into feasible production quantities per slot and per run so that the total costs for setups and waste are minimized.

The authors transform the original objective function into a (w.l.o.g. equivalent) substitute where scaled setup costs \(c: = \frac{{{sc}}}{{vc \cdot L}}\) plus the total run length of the machine (makespan) are minimized. They show that the JSP is strongly NP-hard and present a nonlinear and two linear IP formulations called IP1 and IP2. Whereas IP1 is rather intuitive, IP2 is more efficient because it avoids unnecessary symmetries and allows further improvements. Empty slots could basically occur, but would (in the objective function) be accounted for as if they were producing waste. A job can be split over several runs. The authors propose a polynomial time (\(O(L\log {}J)\)) algorithm for solving the special case \(J \le L\), which they call the “single run problem” (SRP). The basic idea of this “single run algorithm” is to iteratively allocate the type which currently determines the run length to the next free slot. If necessary, a fractional run length is rounded up to the next higher integer number. This algorithm is a major building block to design two heuristic solution procedures for the original JSP where J can also exceed L.

Baumann et al. (2015) present a practical application where customer-specific designs j of napkin pouches are printed using a single machine with \(L = 7\) slots l per offset printing plate s. Alike the JSP, the setup costs for the necessary runs of the different printing plates s have to be minimized together with the run-time-dependent costs of waste. However, in extension to the JSP, several further technical constraints have to be considered like, for example, that colors of napkins and the potential occurrence of white borders restrict the allocation of designs to slots, that slots must not remain empty and that a single design may not be allocated to several plates. The authors present a linear MIP formulation and a savings-based heuristic to solve the problem.

Obviously, the BBP is most closely related to the JSP. It is another extension of the JSP, but with less restrictions than Baumann et al. (2015). In addition to the JSP, merely the further constraints that a slot may not remain empty and that a single item can only be produced in a single run are necessary.

Note that there is a close relationship between the problems discussed until now and so-called multi-period or integrated lot-sizing and cutting-stock problems, as recently reviewed by Melega et al. (2018). While the former ones assume that overproduction is scrap incurring one-time costs of waste, the latter ones assume that overproduction can be stored for later usage, thus causing inventory holding costs for every period of storage. The main difference is that the multi-period versions have additional degrees of freedom to save setups by bringing forward some demand of later periods. Two examples for this type from the molded pulp packaging industry are Martínez et al. (2018) and Martínez et al. (2019). The molding machines described there show similar characteristics as assumed in the BBP and JSP. Instead of lanes or slots, various molds l do simultaneously produce different sorts of packages j in parallel. Several molds require a joint setup because together they constitute a replaceable molding pattern s. The authors describe nonlinear and linearized multi-period MIPs which have to consider some further, very challenging constraints.

These molding models basically build on the single-machine general lot-sizing and scheduling problem (GLSP), introduced by Fleischmann and Meyr (1997). Here, the overall planning horizon is subdivided into rather long, discrete, non-overlapping “macro-periods” \(t = 1,\ldots , T\) of fixed lengths (e.g. weeks), which help to model the time-varying, dynamic demand and the holding of inventory. Each macro-period t again consists of a pre-determined number S of shorter “micro-periods” \(s = (t-1)S+1,\ldots {}, tS\) whose lengths are decision variables. Subsequent micro-periods producing the same product constitute a production run with its corresponding lot-size. Setups can only occur when changing from one product to another between two subsequent micro-periods s and \(s+1\).

Therefore the BBP could also be modeled by reducing the GLSP to a single macro-period \(T = 1\) with \(s = 1, \dots {}, S\) being the micro-periods of this single macro-period. However, unlike the molding models, the BBP needed to build on multi-machine GLSP formulations using a “common time grid” \(w_{s}\) for all machines l involved, where the variables \(w_{s} \ge 0\) denote the starting times of the micro-periods s. Such a common time grid was introduced by Meyr (2004) and later on used by, e.g., Seeanner and Meyr (2013) for the GLSP with multiple production stages (GLSPMS) and by Wörbelauer et al. (2019) for considering secondary resources on the parallel machines of a single stage of production. Note that, according to the classification of Wörbelauer et al. (2019), a printing plate of the BBP can be interpreted as a cumulative secondary resource (with sufficient capacity, but causing setup costs), whereas the printing lanes constitute the parallel primary resources.

This is worth mentioning because these analogies show that the BBP-model of Sect. 3, which is an adaption of a single-period JSP, could be extended to a multi-period integrated lot-sizing and cutting stock problem in a quite straightforward manner if stockable standard products were produced instead of non-storable customized products.

3 Model formulation

Before introducing this model formulation, the printing company’s planning problem BBP and its basic assumptions are briefly summarized:

  1. i

    Demands \(d_j\) of different sorts j of labels have to be satisfied by printing them on a single machine, the “printer”.

  2. ii

    The printer consists of L parallel printing lanes l, which always have to be used simultaneously. It can be decided how long the printer runs. If it runs, all lanes have to be utilized (“empty” lanes are not allowed) and exactly one sort j has to be produced per lane l. Since all labels have the same size and shape, the length of such a run can be determined by counting the labels of a single lane and needs to be an integer number. All labels produced in parallel in a single run are called a “printing block”.

  3. iii

    By designing so-called printing plates, it can be decided which sort j is produced on which lane l in a single block. Several different printing plates s can be designed and installed one after each other on the printer. However, designing and installing (“setting up”) a certain plate s incurs fixed setup costs sc.

  4. iv

    A single sort j can be assigned to several lanes l of the same plate, but not to several plates.

  5. v

    If more labels are produced than actually needed, each surplus label is assumed to be “scrap” and incurs per unit costs vc.

The planning problem BBP is to assign sorts j to lanes l of different plates s and to determine the run length \(Q_{s}\) of each block s so that the overall costs of setups and scrap are minimized while meeting the above assumptions. Obviously, in an optimal solution of the BBP each plate s will exactly be used once, i.e., for a certain printing block of a single run using this plate s. Thus the terms plate, block and run s will be used interchangeably in the remainder.

The following model IP2ext represents the practical problem BBP as a linear MIP-model. It is an extension of the JSP-model IP2 of Ekici et al. (2010), briefly introduced in Sect. 2. Sorts, printing lanes and printing blocks of the BBP correspond with product types, slots and runs of the JSP, respectively. As compared to the original IP2 formulation of Ekici et al. (2010), its BBP-extension IP2ext needs additional constraints forbidding that a lane may remain empty (see assumption ii above) and that a product type can be produced in several runs (see assumption iv). An overview of all indices, data and variables necessary to formulate IP2ext is given in Table 1. Note that Ekici et al. (2010) have shown that \(\left\lceil {} \frac{J}{L} \right\rceil {}\) and J are lower and upper bounds to the number of blocks used in an optimal solution. Thus S is typically initialized by \(S := J\).

Table 1 Indices, data and variables of IP2ext, an extension of IP2 of Ekici et al. (2010)
Full size table

IP2 of Ekici et al. (2010) is more efficient than their IP1 because—instead of explicitly assigning the sorts j to each lane l of a block s—only the aggregate number of lanes per sort is counted. Thus, binary variables \(x_{jsl} \in \{0; 1\}\) indicate whether l printing lanes are set up for sort j in block s or not. Only in case of a setup, the corresponding production quantities \(q_{jsl} \ge 0\) can take on positive values. The variables \(r_{s} \in \{0; 1\}\) show value 1 if block s is needed and thus setup costs have to be incurred. The production quantity of a single lane of block s and thus the length of run s is then measured by the non-negative integer variable \(Q_{s} \in {\mathbb {Z}}^{\ge 0}\). IP2ext is defined by its objective function (1) and the constraints (2)–(13).

IP2ext (modeling the BBP as an extension of IP2 of Ekici et al. (2010)):

$$\begin{aligned} \text {minimize} \quad sc \sum _{s} r_{s} + vc \left( L \sum _{s}{Q_s} - \sum _{j}{d_j} \right) \end{aligned}$$
(1)

subject to

$$\begin{aligned}&\sum _{s}\sum _{l}{ q_{jsl} } = d_{j} \quad \forall j \end{aligned}$$
(2)
$$\begin{aligned}&\sum _{j}\sum _{l}{ l \cdot x_{jsl} } = L \cdot r_{s} \quad \forall s \end{aligned}$$
(3)
$$\begin{aligned}&q_{jsl} \le l \cdot Q_{s} \quad \forall j,s,l \end{aligned}$$
(4)
$$\begin{aligned}&q_{jsl} \le d_{j} \cdot x_{jsl} \quad \forall j ,s,l \end{aligned}$$
(5)
$$\begin{aligned}&\sum _{l}{x_{jsl}} = 1 \quad \forall j,s \end{aligned}$$
(6)
$$\begin{aligned}&Q_{s} \ge Q_{s+1} \quad \forall s \end{aligned}$$
(7)
$$\begin{aligned}&\sum _{j}\sum _{l}q_{jsl} \le L \cdot Q_{s} \quad \forall s \end{aligned}$$
(8)
$$\begin{aligned}&\sum _{s}\sum _{l \ge 1}x_{jsl} = 1 \quad \forall j \end{aligned}$$
(9)
$$\begin{aligned}&x_{jsl} \in \{0; 1\} \quad \forall j,s,l \end{aligned}$$
(10)
$$\begin{aligned}&q_{jsl} \ge 0 \quad \forall j,s,l \end{aligned}$$
(11)
$$\begin{aligned}&r_{s} \in \{0; 1\} \quad \forall s \end{aligned}$$
(12)
$$\begin{aligned}&Q_{s} \in {\mathbb {Z}}^{\ge 0} \quad \forall s \end{aligned}$$
(13)

The objective function (1) minimizes BBP’s overall costs of setup and scrap. There, the term in brackets represents the total amount of scrap. Note that the IP2 formulation of Ekici et al. (2010) prefers to minimize the transformed objective \(\frac{{{sc}}}{{vc \cdot L}}\sum\limits_{s} {r_{s} } + \sum\limits_{s} {Q_{s} }\), i.e., some scaled setup costs plus the makespan. Although the optimal objective values differ, the optimal solutions obtained by this transformation are equivalent to the ones that result from minimizing the original setup and scrap costs directly. With respect to the real-world application, it will be more convenient to use the original costs in the following.

Constraints (2) ensure that the demand for each sort j is satisfied. Constraints (3) differ from the original IP2 of Ekici et al. (2010) by using an \(=\) instead of a \(\le\) sign. They guarantee that all L printing lanes are assigned to the sorts in each block, so that there is no empty lane allowed (see assumption ii). Thus, IP2ext extends the original IP2 by some additional constraints

$$\begin{aligned} \sum _{j}\sum _{l}{ l \cdot x_{jsl} } \ge L \cdot r_{s} \quad \forall s. \end{aligned}$$
(14)

Constraints (4) and (5) determine the quantity \(q_{jsl}\) of sort j in block s if l printing lanes are assigned to j in this block. (4) set an upper bound to \(q_{jsl}\) with respect to the length of run s. In contrast, (5) force that \(q_{jsl}\) can only be positive if its corresponding binary indicator \(x_{jsl}\) is set to 1 and has to be 0 otherwise. These constraints together with constraints (6) ensure that exactly l printing lanes are assigned to a sort j in a block s if \(q_{jsl} > 0\), where l has to be a unique number between 0 and L.

Constraints (7) and (8) are “symmetry-breaking constraints” proposed by Ekici et al. (2010), which help to strengthen the formulation. Alike (14), constraints (9) also extend the original IP2 of Ekici et al. (2010). They ensure that a sort j can only be produced in exactly one block (see assumption iv). Constraints (10)–(13) define the domains of the variables. Note that the variables \(q_{jsl}\) only denote the actually intended share of the total production quantity \(\sum \limits_{s,l}{(l \cdot x_{jsl} \cdot Q_{s}})\) of sort j. Their values will automatically become integer in a feasible solution. It is not necessary to claim \(q_{jsl} \in {\mathbb {Z}}^{\ge 0}\).

The single block special case of IP2ext with \(J \le L\) and \(S = 1\) will in the remainder of this paper be called IP2ext1. There, the index s and constraints (7) are not necessary any longer. IP2ext1 does not completely equal the single run problem SRP of Ekici et al. (2010) (see also Sect. 2) because for SRP empty lanes were basically allowed. For example, if \(S=J=1\), \(L=2\) and \(d_1 = 1\,000\), the solution \(q_{111} = q_{112} = 500\) would be optimal for both IP2ext1 and SRP, but the solution \(q_{111} = 1\,000, q_{112} = 0\) would only be feasible for SRP. Nevertheless, the single run algorithm of Ekici et al. (2010, Algorithm 1) does produce optimal solutions for both special cases because it anyway avoids empty lanes. Note that the first solution shows a makespan \(Q_1 = 500\) in contrast to a makespan \(Q_1 = 1\,000\) of the second solution. This later completion time is less attractive from a practical point of view and thus further justifies assumption ii.

4 Decomposition heuristics

In general, a solution of the BBP is characterized by an ordered sequence \((j) = (j_1, \ldots {}, j_J)\) of sorts, an ordered partitioning of this sequence into \({\hat{S}} \le J\) printing blocks \([s] = [s_1, \dots {}, s_{{\hat{S}}}] = [(j_1, \ldots , j_i), \ldots {}, (j_k, \ldots {}, j_{J} )]\) and a solution of IP2ext1 for each of these blocks. For example, solution c) of Fig. 1 could be represented by the sequences (1, 2, 3, 4) or (1, 3, 2, 4), respectively, and their corresponding partitions [(1), (2, 3), (4)] and [(1), (3, 2), (4)], both with \({\hat{S}} = 3\) printing blocks.

In Section 4 five different solution heuristics for the BBP will be introduced, which base on a common solution approach: They exploit the above characteristics in order to decompose the overall planning problem into the three subroutines

  1. I.

    “determining a sequence of sorts”,

  2. II.

    “partitioning this sequence into printing blocks”, and

  3. III.

    “solving IP2ext1 for potential printing blocks”.

These subroutines are executed successively and iteratively, as illustrated by the flowchart of Fig. 2. In order to come up with a single solution of the BBP, subroutine I first generates a sequence of sorts. Subroutine II then determines the number of printing blocks \({\hat{S}}\) to be used and uniquely assigns each sort to a single block (see assumption iv) without changing the sequence that has been defined by subroutine I. For all potential printing blocks considered by subroutine II, subroutine III is called. There, for each block separately, the sorts of the printing block are assigned to the different lanes and the run length of the block is determined so that these sorts’ demand is met and the block’s costs of scrap can be calculated. Thus, subroutine III corresponds with solving an IP2ext1 for each printing block individually. After subroutine II, the sequence of subroutine I has been partitioned, i.e., it has been converted to a feasible solution of the BBP. The overall setup and scrap costs of the finally used printing blocks of this sequence are known after this step.

Fig. 2
figure 2

Flowchart of the decomposition approach

Full size image

This procedure is repeated \(L \cdot J\) times (see dashed arc of Fig. 2) in order to generate a pool of solutions, from which the best one is then selected in the end. Subroutine I has to ensure that different sequences and thus (at least usually) various solutions of the BBP will result.

As the flowchart indicates, for each of the three subroutines two different alternatives will be proposed how to solve the subroutine’s planning problem. The two alternatives for subroutine I will be described in Subsect.  4.3.1 and  4.3.2 of Sect.  4.3. Similarly, the two alternatives of subroutine II will be explained in Subsect.  4.2.1 and  4.2.2 of Sect.  4.2. Since the single run algorithm of Ekici et al. (2010) is the second way to solve the models IP2ext1 of subroutine III, only one solution method needs to be introduced in Sect.  4.1. Note that the order of description—subroutine III first in Sect.  4.1, followed by II and I in Sect.  4.2 and 4.3—has been reversed in order to be able to re-use earlier definitions and thus to ease understanding for the reader.

Not all eight heuristics that could result from combining two alternatives for three subroutines will be implemented and compared later on. We will concentrate on five of them and justify this selection in Sect.  4.4 after the subroutines’ alternatives have been explained in further detail.

4.1 Solving IP2ext1 for potential printing blocks

IP2ext1 is limited to a single block and single run, respectively. Thus, for the remainder of this subsection, \(J \le L\) can be assumed and the index s can be omitted. The optimal solutions for \(J = 1\) and \(J = L\) are obvious. For \(1< J < L\), the MIP formulation of Sect. 3 could be solved or the single run algorithm of Ekici et al. (2010, Algorithm 1) could be applied. Because the label printing company was not aware of Ekici et al. (2010) at the time of implementation and did not want to use an MIP solver, the dynamic programming formulation (DP) defined by (15) had been chosen as an alternative. Such a DP seemed promising because the number of lanes L is usually rather small in real-world applications (see Sect. 5.1).

Let j denote the sort j considered in stage \(j = 1, \ldots {}, J\) of the recursion. Furthermore, \(l_{j}\) defines the first lane on which sort j is produced. Thus, \(l_{j+1}-1\) represents the last lane on which sort j is produced and \(l_{j+1}-l_{j}\) calculates the total number of lanes, on which sort j is produced. At any stage j of the recursion, \(F(j; l_{j})\) denotes the minimum costs if production of sort j starts on lane \(l_{j}\) when the lanes \(l_{j}, \ldots {}, L\) are left to produce the remaining sorts \(j, j+1, \ldots {}, J\). By initializing \(T_{0} := 0\), \(F(J+1; l) := 0\) for \(l = 1,\ldots {}, L+1\) and \(l_{1} := 1\), the recursion starts and stops at stage 1 with F(1; 1) representing the total minimum costs to produce all J sorts on the given L lanes:

$$\begin{aligned} F(j; l_{j})&:= \min _{1 \le h \le L-J+j-l_{j}+1}\left\{ \left\{ \left[ \frac{d_{j}}{h} - T_{j-1} \right] \cdot vc \cdot (l_{j}-1) \right\} ^{+} \right. \nonumber \\&\qquad + \left\{ h \cdot vc \cdot \left[ T_{j-1} - \frac{d_{j}}{h} \right] \right\} ^{+} \nonumber \\&\qquad \left. + F(j+1; l_{j} + h)\right\} \end{aligned}$$
(15)

\(T_{j-1}\) represents the overall production time that is needed until stage \(j-1\) to produce the sorts \(1, \ldots {}, j-1\) on the lanes \(1,\dots {}, l_{j}-1\). Since a sort i is produced on \(l_{i+1} - l_{i}\) lanes in parallel, \(T_{j-1}\) can be computed by \(T_{j-1} := \max _{1 \le i \le j-1}{\frac{d_i}{l_{i+1} - l_{i}}}\).

On stage j, the DP has to decide on which lanes k the sort j has to be produced. Since at least the last \(J-j\) lanes have to be reserved for the remaining sorts \(j+1, \ldots {}, J\), the index k may only vary between \(l_{j}\) and \(L-J+j\) with the cheapest alternative to be chosen. Thus, depending on k, sort j is produced on \(k - l_{j} + 1\) lanes in parallel and the next sort \(j+1\) starts on lane \(k+1\), incurring cumulated costs \(F(j+1,k+1)\) for the remaining products. For ease of readability, in (15) the substitution \(h := k - l_{j} + 1\) takes place.

The first summand of (15) is relevant if the production time \(\frac{d_j}{h}\) of sort j is longer than the production time \(T_{j-1}\) of the preceding sorts \(j = 1,\ldots {}, j-1\). In this case, additional scrap costs for all these preceding sorts on the lanes \(l = 1, \ldots {}, l_{j}-1\) have to be accounted for the corresponding time delta. Otherwise, scrap costs for sort j have to be accounted for the time difference by which \(T_{j-1}\) is exceeding the sort’s production time on all h lines where j is produced (second summand). The third summand \(F(j+1; l_{j}+h)\) recursively adds the minimum costs of all subsequent sorts \(j+1,\ldots {}, J\) on the subsequent lanes \(l_{j} + h, \ldots {}, L\).

Finally, the total run length \(T_J\) of the printing block is rounded up to \(\left\lceil {} T_J \right\rceil {}\).

4.2 Partitioning a given sequence into printing blocks

Now let us consider a general BBP with \(S = J\) and possibly \(J > L\), but the sequence \((j) = (j_1, \ldots {}, j_S)\) of sorts is assumed to be known in advance. Then, a partitioning of this sequence into \(s = 1, \dots {}, {\hat{S}}\) printing blocks is looked for. However, the partitioning can only group \(1 \le k-i+1 \le L\) subsequent sorts \((j_{i}, j_{i+1}, \ldots , j_{k-1}, j_{k})\) into a single block (\(i \le k\)). Since a sort’s complete demand has to be satisfied by a single printing block, i.e., since \(j_{i} \ne j_{k}\) for all \(1 \le i, k \le S\) with \(i \ne k\), a sort can only be assigned to a single block. Then, the costs of this block can be computed by solving the DP of Sect. 4.1 and by using the single run algorithm of Ekici et al. (2010), respectively, and adding the setup costs sc once. We will denote these costs of a block \((j_{i}, \ldots , j_{k})\) as \(F^{B}_{i-1,k}\) in the following.

Note that this type of problem is quite similar to an uncapacitated, dynamic lot-sizing problem as introduced by Wagner and Whitin (1958). The pre-defined sequence of sorts of the BBP corresponds with the given sequence of periods of the lot-sizing model. A building block corresponds with a production lot, both of them necessitating fixed setup costs. Demand of different sorts cannot be split, resembling the so-called Wagner and Whitin (W&W) property that in an optimal solution of the lot-sizing problem only a period’s complete demand can be pre-produced. However, the BBP incurs variable costs of scrap instead of inventory holding costs.

In Subsect.  4.2.1, a dynamic program will be proposed that solves this problem optimally in a shortest-path-like manner. To have some benchmark algorithm available, in Subsect.  4.2.2 the same planning problem is heuristically solved by distributing the printing blocks more or less evenly over the given sequence \((j) = (j_1, \ldots {}, j_S)\) of sorts.

4.2.1 Using a dynamic program of the shortest path type

To adapt the well-known shortest path algorithm for W&W models (see, e.g., Pochet and Wolsey 2006, Sect. 7.3) to the planning problem of subroutine II we assume that the indexes \(j_1, \ldots {}, j_S\) of the BBP’s given sequence define the nodes of a graph. The graph can be sorted topologically, i.e., an arc from node \(j_i\) to node \(j_k\) does only exist if \(i < k\). The arc from \(j_{i - 1}\) to \(j_k\) represents the printing block \((j_{i}, \ldots , j_{k})\) with \(F^{B}_{i-1,k}\) being the cost of the arc. By introducing a dummy node \(j_0\) with costs \(F^{N}_{0} := 0\), the costs \(F^{N}_{k}\) of node \(j_k\) can be computed in the order \(k = 1, \ldots , S\) according to the forward recursion:

$$\begin{aligned} F^{N}_{k} := \min _{ { \{ k-L \}^{+} } \le i < k}{ \{ F^{N}_{i} + F^{B}_{i,k} \} } \end{aligned}$$
(16)

Since maximally L sorts can be grouped into a printing block, it is sufficient to limit the search to \(i \ge \{ k-L \}^{+}\) instead of \(i \ge 0\). Thus, \(\sum _{l=1}^{L}{(J - l +1)} = \frac{L}{2}(2J-L+1)\) instances of the type IP2ext1 have to be solved at a maximum in order to initialize the scrap costs of the potential building blocks of a given sequence (see Fig. 2 for an example with \(J = 4\) and \(L = 2\)). \(F^{N}_{S}\) are then the costs of the shortest path from node \(j_{1}\) to node \(j_{S}\) and of the cost-optimal partitioning of BBP’s given sequence, respectively. Walking the shortest path backwards, from node \(j_{S}\) to node \(j_{1}\), allows to reconstruct the building blocks of this partitioning.

The reader is referred to the rich literature on W&W models if ideas for more efficient implementations of such recursions are desired (see, e.g., Aggarwal and Park 1993; Federgruen and Tzur 1991 ; Wagelmans et al. 1992).

4.2.2 Evenly distributing the blocks over the sequence

A simpler alternative to get a partitioning of a given sequence \((j) = (j_1, \ldots {}, j_S)\) is to more or less evenly distribute these sorts over a predefined number of printing blocks. Ekici et al. (2010) have shown that a minimum number \(S_{l} := \left\lceil J/L \right\rceil\) and a maximum number \(S_{u} :=J\) of printing blocks can be defined. In case of \(S_{l}\), almost all sorts will be produced on a single printing lane, what results in minimum setup costs. On the other hand, in case of \(S_{u}\), each sort will be produced on L printing lanes, so that every printing block just involves a single sort. To get a partitioning of a given sequence \((j) = (j_1, \ldots {}, j_S)\), the number \({\hat{S}}\) of actually used printing blocks can be varied in the interval \(\left[ S_{l}, \ldots {},S_{u}\right]\).

Let, for a given \({\hat{S}}\), the variable \(s_i\) define the number of sorts assigned to printing block i where \(i=1, \ldots {}, {\hat{S}}\). Then, the Eqs (17) and (18) allow an (almost) even distribution of sorts over the \({\hat{S}}\) printing blocks of the sequence:

$$\begin{aligned} s_{1}&:= \left\lceil \frac{J}{{\hat{S}}} \right\rceil \end{aligned}$$
(17)
$$\begin{aligned} s_{i}&:= \left\lceil \frac{J-\sum _{k=1}^{i-1}{s_{k}}}{{\hat{S}}-(i-1)} \right\rceil \quad i=2, \ldots {},{\hat{S}} \end{aligned}$$
(18)

We enumerate all potential even distributions for \({\hat{S}} = S_{l}, \ldots {},S_{u}\) and calculate their corresponding setup costs \(sc \cdot {\hat{S}}\) and costs of scrap by solving each involved IP2ext1 with subroutine III. Thus, in the end, there are \(\left( S_{u}-S_{l}+1\right)\) solutions for the given sequence, the best of which will be chosen.

As an example assume \(L = 2\), \(J = 4\) and the sequence (1, 3, 2, 4) as given. We get \(S_{l} := 2\) and \(S_{u} := 4\) so that \({\hat{S}}\) has to be varied in the interval [2, 3, 4]. For \({\hat{S}} = 2\), the values \(s_1 = s_2 = 2\) and the partitioning [(1, 3), (2, 4)] result. Additionally, \({\hat{S}} = 3\) leads to \(s_1 = 2\), \(s_2 = s_3 = 1\) and the partitioning [(1, 3), (2), (4)]. Finally, \({\hat{S}} = 4\) comes up with \(s_1 =s_2 = s_3 = s_4 = 1\) and the partitioning [(1), (3), (2), (4)]. Among these three solutions the one with lowest total costs is finally selected.

4.3 Determining the sequence of the sorts

Finally, it has to be explained how promising sequences are generated by repeatedly executing subroutine I. Subsection 4.3.1 tries to support the basic idea of the single run algorithm of Ekici et al. (2010) that the sort with the highest remaining demand should be split and additionally be allocated to a further lane (see Sect. 2). In contrast, Subsect. 4.3.2 assumes that random sequences suffice.

4.3.1 Demand-oriented sorting

The basic idea to generate promising sequences is that at best those sorts should be pooled together in a block whose production times are as equal as possible. Thus, the sorts are sorted with respect to their demands. However, a single sort can be split over several parallel lanes of a printing block. Therefore, the property that the production time \(t_{j}\) of sort j depends on the number \(h_{j}\) of parallel lanes per sort j according to \(t_{j} := \frac{d_{j}}{h_{j}}\) will be used to vary the sequences:

A starting sequence is determined by setting \(h_{j} := 1 \,\, \forall j\) and sorting all sorts j with respect to descending \(t_{j}\). The costs of this sequence are determined using the partitioning algorithm of Sect. 4.2. Altogether, \(L \cdot J\) iterations are executed in the following. In each iteration, the sort k with the currently longest production time is searched for, i.e., \(k := argmax_{j}{ \{ \frac{d_{j}}{h_{j}} \} }\) is determined. This sort’s counter \(h_{k}\) is increased by 1. Thus, the production time \(t_{k}\) of this single sort k has been decreased from \(\frac{d_{k}}{h_{k}}\) to \(\frac{d_{k}}{h_{k}+1}\). All sorts are re-sorted again with respect to descending production times. The costs of the resulting (typically new) sequence are determined using subroutines II and III. If these costs improve the currently best solution, the sequence is stored. No matter whether the best solution has been improved or not, the new value \(h_{k}\) of sort k and the old values \(h_{j}\) of the remaining sorts j build the starting point for the next iteration.

Note that the auxiliary variables \(h_{j}\)—counting the number of parallel lanes per sort j—are only used to determine the next sequence of sorts within subroutine I. These variables are not relevant at all when partitioning the new sequence during subroutine II.

Applying this principle to the example of Fig. 1 leads to sequence (4, 2, 3, 1) with \(h_{j} = 1 \,\, \forall j\) in iteration 1, sequence (2, 3, 4, 1) with \(h_1 = h_2 = h_3 = 1\) and \(h_4 = 2\) in iteration 2, sequence (3, 4, 1, 2) with \(h_1 = h_3 = 1\) and \(h_2 = h_4 = 2\) in iteration 3, etc. Note that in subroutines II and III symmetric sequences cause identical costs so that the sorting could also be ascending instead of descending.

4.3.2 Random sorting

To find out whether the above effort of sorting really pays back, a very simple and stupid alternative sequencing algorithm will be used as a benchmark: Within each of the \(L \cdot J\) iterations, the natural sequence \((1, 2, \ldots {}, J)\) of the sorts will be shuffled randomly to get a new sequence \((j_1, j_2, \ldots {}, j_J)\).

4.4 Definition of the decomposition heuristics

Note that computation times can be decreased if the solutions of IP2ext1 are stored in tree-like data structures whose levels are defined by an ordered sequence of the subset of sorts which is input to a IP2ext1. For example, the second printing block of solution c) of Fig. 1 could alternatively be represented by the sub-sequences (2, 3) and (3, 2), which both are equivalent and show the same objective value \(sc + 0 \cdot vc\). If an increasing sorting was used, for both sub-sequences the parent node 2 would form the root of such a tree and the child node 3 would contain the objective value sc of this printing block’s sub-sequence. These trees remain rather small because IP2ext1 is limited to maximally L sorts. The sequencing algorithms of subroutine I and the partitioning algorithms of subroutine II necessitate that many equivalent IP2ext1s have to be evaluated. Thus, retrieving the objectives of already solved instances from the trees’ database instead of every time computing them from scratch promises to reduce computation times considerably. This general principle is applied to all decomposition heuristics.

As already mentioned only five out of all eight heuristics that would result from combining each two alternatives for the three subroutines of Fig. 2 have been implemented. Table 2 shows which ones these are. The bold capital letters of Fig. 2 and of columns 2-4 in Table 2 define the heuristic’s name according to the sequence of the subroutines’ occurrence. For example, heuristic SDD determines a sequence “Sorted by demands” as described in Subsect. 4.3.1, partitions this sequence into blocks using the “Dynamic program” of Subsect. 4.2.1 and solves IP2ext1 with the “Dynamic program” of Sect. 4.1. SDD has been selected because it is in practical use by the label printing company. It shall be compared with SDA in order to check the effects of the single run algorithm against the DP of Sect. 4.1. As some pre-tests have revealed and Sect. 5.2 will demonstrate, both show the same solution quality, but the single run algorithm runs faster. Thus, the two alternatives for the two subroutines I and II are only tested with the quicker option for subroutine III.

Table 2 Overview of the decomposition heuristics
Full size table

Summing up, SDD denotes the algorithm that is in use by the label printing company. SDA represents an alternative where in subroutine III the single run algorithm of Ekici et al. (2010) is used instead to solve IP2ext1. SDA will serve as some sort of “base algorithm” to check how the alternatives of only subroutine I (RDA), only subroutine II (SEA) and both simultaneously (REA) behave.

Since all of these heuristics decompose the overall planning problem into three subproblems which are solved successively instead of simultaneously, it cannot be expected that (always) global optima are found. Nevertheless, the dynamic programming subroutines and the single run algorithm should help to find good solutions in a short computation time because they at least solve subproblems optimally. The next section evaluates to which extent this is really true.

5 Computational results

As mentioned above, the solution heuristic SDD has been implemented and is still being used by the company. Only a few real-world problem instances have been made available to the authors. Unfortunately, these cannot be published for reasons of confidentiality. SDD led to an average cost saving of 8 % for these instances when compared to the company’s own solutions. Furthermore, the company reported that SDD was superior to their previous manual solution approach for all problem instances that have been tested there. An automated planning using SDD is considered as particularly beneficial if \(J \ge 8\) holds. Since the preparation of the printing plates etc. is time-consuming anyway, a computation time of several hours would be acceptable to solve the really big problem instances.

To allow a systematic evaluation of BBP’s complexity and the performance of the different heuristics of Sect. 4.4, in Sect. 5.1 artificial test instances are generated. Although drawn at random, their overall parameter setting bases on the experiences made in practice. Section 5.2 compares how BBP can be solved exactly and heuristically for a small base scenario. In Sect.  5.3 the influence of the variation of different problem parameters on solution quality and computation time is tested (also for small problem instances). Section 5.4 finally evaluates the running time behavior of the heuristics for larger instances.

Besides the heuristics of Sect. 4.4 the MIP model IP2ext of Sect. 3 is solved by Gurobi (GUR; Gurobi Optimization LLC 2021) either exactly or heuristically by aborting after a pre-defined maximum time limit. However, for very large instances, Gurobi might not be able to find a feasible solution at all within such a time limit. Thus, to have some other benchmark available, the intuitive solution methods illustrated in Fig. 1 have been implemented too: Similar to solution a) the sorts are sorted according to increasing demands and each sort is assigned to a single lane. If some unused lanes remain for the last printing block, this printing block’s largest sort is distributed equally on the remaining lanes. Second, all sorts are sorted according to decreasing demands and the same procedure is repeated. Third, in analogy to solution b) of Fig. 1, a schedule avoiding scrap, but generating maximum setup costs is computed. Finally, the best solution of all three methods is selected. This solution method will be called “Intuitive Solution Method” (ISM) in the following.

All computational tests have been executed in a virtual machine of an Intel Xeon E5-2630 v2 2.6GHz QC server with 16 GB RAM, using the Ubuntu 20.04.2 LTS operating system and Python 3.8.10 or Gurobi 9.0.3, respectively.

5.1 Scenario generation

In the real-world application, the number of lanes L typically varies between 2 and 7. The number of sorts per order J typically varies between 4 and 9 with J/L in a range between 1.0 and 2.5. However, L may grow to 15 and J may grow to 100. Thus, J/L can reach 7 or even more. Nevertheless, the majority of orders show \(J \le 15\). An order with \(L = 15\) and \(J = 30\), i.e., with \(L\cdot {}J = 450\), is already considered as “big” by the company.

Thus, for the computational tests L is varied in the range \(2, \ldots {}, 10\) if small instances and additionally in the range \(11, \ldots {}, 15\) if larger instances are to be tested. J will be varied from 1 to 10 with step size 1 for small and then up to 100 with step size 10 for large instances.

The mean demand \({\bar{d}}\) is 80 000 units for all scenarios. Upper and lower bounds for demand are set to \(d^{min} := {\bar{d}} (1 - HET)\) and \(d^{max} := {\bar{d}} (1 + HET)\), respectively. Demand \(d_{j}\) of sort j is then drawn at random from a discrete uniform distribution over the interval \([d^{min}; d^{max}]\). In order to represent scenarios with low, average and high heterogeneity of customer demand, the parameter \(HET\) is set to 0.1, 0.5 and 0.9, respectively.

The cost relation \(\frac{vc \cdot {\bar{d}}}{sc \cdot L}\) varies between 16% and 90% in the practical cases. Thus we choose a CR of 10%, 50% and 100% to represent a low, average and high influence of variable costs. In order to generate such scenarios, the setup costs are normalized to \(sc := 800\) and the variable costs are set according to \(vc := \frac{CR \cdot sc \cdot L}{{\bar{d}}} = 0.01 \cdot CR \cdot L.\)

The maximum time limit will be set to 600 seconds for all problem instances. We will build problem classes where J, L, HET and CR are varied. For each problem class, \(R=10\) or \(R=30\) replications are drawn at random in the way described above.

We measure the aggregate performance over all replications of a class. For example, \(\%nOpt\) denotes the percentage of replications of a class where Gurobi has not been able to find an optimal solution within the given time limit. Furthermore, \(\%m1/m2\) measures the percentage deviation of solution method m1 from solution method m2 for each problem instance (replication) of the problem class and averages these deviations over all instances of the class. For example, \(\mathrm \%SDD/GUR\) calculates the average percentage deviation of the objective values found by heuristic SDD from the corresponding objective values found by Gurobi. In analogy \(\%m1/best\) denotes the percentage deviation of the solution found by method m1 from the best solution found at all for this problem instance, averaged over all instances of the respective class. Finally, “aSec m1” averages the computation times (in seconds) of solution method m1 over all replications of the respective problem class.

5.2 Exact solution of base scenarios

In order to get some impression how difficult it is to solve BBP exactly and to get an idea how the company’s heuristic SDD compares, L and J are varied systematically in the ranges \(L, J = 2, \ldots {}, 10\). We use a base setting with mean values \(\mathrm{HET} = 0.5\) and \(CR = 0.5\) and draw \(R = 30\) replications per problem class (combinations of J and L) at random. Gurobi was able to solve all instances of the base setting to optimality with the time limit of 600 seconds. Table 3 lists the corresponding average computation times aSec Gur for \(L \ge 2\) and \(J \ge 2\).

Table 3 Average computation times (aSec GUR) of Gurobi in seconds (no entry means: 0.0; \({\text {R}}=30\), \({\text {HET}} = 0.5\), \({\text {CR}} = 0.5\))
Full size table

Obviously increasing J is more crucial than increasing L. This is not surprising since the number of binary variables \(x_{jsl}\) of IP2ext grows with the factor \(J \cdot J \cdot L\). All computation times remain below 17 seconds and are thus negligibly small. Since for typical practical problems \(2 \le L \le 7\), \(4 \le J \le 9\) and \(1.0 \le J/L \le 2.5\) hold (see Sect. 5.1), solving practical problems to optimality seems reasonable in most cases. Whether this is also true for larger practical problems will be checked in Sect. 5.4.

Therefore, heuristics like SDD, SDA or ISM were actually not necessary for small problem instances. Nevertheless, Tables 4 and 5 also show how those behave. Table 4 goes into detail for the company’s heuristic SDD. In contrast, Table 5 shows aggregate results for all heuristics.

Table 4 Average percentage deviation (%SDD/GUR) of the solutions of heuristic SDD from the optimal solutions (no entry means: 0.0; \({\text {R}}=30\), \({\text {HET}} = 0.5\), \({\text {CR}} = 0.5\))
Full size table

Table 4 shows the average percentage deviation \({\% SDD/GUR}\) of SDD from Gurobi. For ease of readability, values 0.0 have been left blank. As can be seen in the left-hand part of the table, SDD can solve all problem instances to optimality if \(L \le 2\) or \(J \le 5\). Usually the deviation of the SDD solutions from the MIP-solutions is not worse than 3 percent. The only exceptions are \((L,J) = (7,10)\) with \({\% SDD/GUR = 5.4}\), \((L,J) = (7,9)\) with \({\% SDD/GUR = 3.2}\) and \((L,J) = (9,10)\) with \(\%SDD/GUR = 3.2\).

The upper part of Table 5 aggregates the results for the average percentage deviation %heuristic/GUR with respect to the number of binary variables JJL and additionally shows the performance of the remaining heuristics. Comparing SDD and SDA does not show any differences and thus lets suspect that not only the single run algorithm of Ekici et al. (2010), but also the dynamic program of Sect. 4.1 with its final rounding procedure solve IP2ext1 to optimality. A formal proof that this hypothesis is indeed true can be found in the Appendix.

Table 5 Average percentage deviation (%heuristic/GUR) of the heuristic solutions from Gurobi solutions for \(L=1,\ldots {}, 10\) and \(J=1,\ldots {}, 10\), further aggregated with respect to the number of binary variables JJL of BBP (no entry means: 0.0; \({\text {R}}=30\), \({\text {HET}} = 0.5\), \({\text {CR}} = 0.5\))
Full size table

Looking at all heuristics reveals the advantages of SDD and SDA. For the base instances, the next best solutions are delivered by the heuristic RDA, which uses a random sequence of the sorts, but also the shortest-path-like dynamic program for partitioning the sequence. Since SEA and REA both perform worse, solving the sub-problem of subroutine II optimally instead of evenly distributing the blocks clearly pays back in terms of overall solution quality. Comparing SDA with RDA and SEA with REA shows that —yet to a smaller extent—the same is true when sorting sequences by demand during subroutine I. ISM performs worst in all cases. Obviously, decomposing BBP into successively and iteratively solved sub-problems is always better than just applying simple intuition.

The lower part of Table 5 demonstrates the effects of relaxing the integer domain of the blocks’ run lengths to a continuous one. Let \(\text{ GUR}^{{\mathbb {R}}}\) denote the solution method that uses Gurobi to solve the IP2ext model of Sect. 3 with \(Q_{s} \in {\mathbb {Z}}^{\ge 0}\) (13) being replaced by \(Q_s \ge 0\). (Note that \(x_{jsl}\) and \(r_s\) are still binary.) When solved to optimality, this relaxation provides a lower bound to IP2ext so that \(\%\text{ GUR}^{{\mathbb {R}}}/GUR \le 0\). As can be seen the resulting relative gaps are extremely small. The Appendix again helps to explain why this is the case. For each individual printing block s, the continuously optimal run length \(Q_s\) can simply be rounded up to the next higher integer \(\lceil Q_s \rceil\) in order to achieve the optimal integer run length. Because typical practical demands \(d_j\) comprise several thousands of labels per sort, the resulting cost differences are almost negligible.

Table 6 finally presents the average computation times of the exact method, the decomposition heuristics and the relaxation in an aggregate manner. ISM is not shown at all because its running times even fall below 50 milliseconds.

Table 6 Average computation times for \(L=1,\ldots {}, 10\) and \(J=1,\ldots {}, 10\), further aggregated with respect to the number of binary variables JJL of BBP (no entry means: 0.0; \({\text {R}}=30\), \({\text {HET}} = 0.5\), \({\text {CR}} = 0.5\))
Full size table

All heuristics are faster than solving BBP exactly. However, at least for these small base problems, this does not really matter. Obviously, the single run algorithm of Ekici et al. (2010) runs quicker than the DP implementation of Sect. 4.1. Thus SDA should be preferred to SDD. Since also all other decomposition heuristics cannot beat SDA in terms of solution quality, but show similar computation times, SDA can be recommended as the number one heuristic—at least for the base scenario’s instances. For obvious reasons, we abstain from further experiments with SDD and REA in the following sections.

Interestingly, relaxing the integer variables \(Q_{s} \in {\mathbb {Z}}^{\ge 0}\) to continuous \(Q_{s} \ge 0\) does not decrease, but increase the computation times of the large instances with \(JJL \ge 750\). Apparently, insisting on only complete labels to be printed makes IP2ext rather easier than more difficult to solve.

5.3 Variation of selected problem parameters

Before evaluating the heuristics’ performance for even larger problem sizes, we want to find out whether and how selected problem characteristics like heterogeneity of demand or the relation between setup and scrap costs influence the “hardness” to solve a certain problem instance.

In a first step, we vary demand heterogeneity, i.e., we decrease and increase the variance of the order sizes for different sorts j of some single product family. As explained in Sect.  5.1, this can be reached by varying the parameter HET. Assuming \({HET = 0.5}\), underlying the experiments of Sect.  5.2, was a medium heterogeneity of some base scenario, the values \({HET = 0.1}\) and \({HET = 0.9}\) allow a comparison with rather low and rather high heterogeneity of demand. Table 7 shows the results of corresponding experiments where R and CR are kept alike the base scenario.

Table 7 Variation of demand heterogeneity HET, grouped with respect to the number of binary variables JJL of BBP (\({\text {R}}=30\), \({\text {CR}} = 0.5\))
Full size table

Apparently, problems with small heterogeneity are easier to solve to optimality than problems with medium or high heterogeneity. As given in Table 7 both aSec GUR and \({\% SDA/GUR}\) are clearly lower if \(HET = 0.1\) than if \({HET = 0.5}\). However, differences are less obvious between \({HET = 0.5}\) and \({HET = 0.9}\). Computation times are quite similar or might even improve a little when changing from medium to high heterogeneity. The solution heuristic SDA seems to get (monotonically) worse when heterogeneity grows, whereas ISM does not show a clear picture.

Table 8 varies the relation between the fix costs for designing and installing printing plates and the variable costs of scrap. Let us again assume that \(CR = 0.5\), used in Sect. 5.2, is some sort of base relation. Then \(CR = 0.1\) and \(CR = 1.0\) represent situations with a low and high influence of variable costs for scrap.

Table 8 Variation of the relation CR between fix and variable costs (\({\text {R}}=30\), \({\text {HET}} = 0.5\))
Full size table

Table 8 reveals that problems with low variable and high fix costs can easily be solved to optimality. Similar to Table 7 and \({HET = 0.1}\), for \(CR = 0.1\) instances can be solved fastest, with a more pronounced difference the larger the instances are. The problems also seem to be the harder to be solved optimally, the higher CR gets. The average computation times aSec GUR of Gurobi increase when the influence of scrap costs grows.

The picture is less clear for the other solution heuristics SDA and ISM. SDA also seems to behave worse if CR grows, but the picture changes if \(JJL \ge 625\). Then SDA’s results are worst if \(CR = 0.5\). If \(JJL \ge 375\), ISM also behaves worst for \(CR = 0.5\). Please remember that ISM always chooses the best of the two extreme solutions, which offer lowest setup costs or lowest variable costs. Thus there has to be some value of CR where ISM switches from one extreme to the other.

5.4 Heuristic solution of big problems

Finally it is of interest how Gurobi and the proposed heuristics perform for large problem instances. Therefore, we choose GUR’s best solution found after the time limit of 600 seconds and compare it with the best solutions of the other heuristics using the same time limit. As mentioned in Sect.  5.1, L may grow to 15 and J may grow to 100 in industrial practice. In the following, we thus vary L from 2 to 15 with step size 1 and J from 10 to 100 with step size 10. To restrict the computational burden, the number of replications is reduced to \(R = 10\).

Table  9 shows average computation times of SDA and GUR for these problem sizes when \(HET = 0.5\) and \(CR = 0.5\) of the base scenario are used again. If detailed results of GUR are omitted, GUR has reached its time limit of 600 seconds. As can be seen, this is the case if \(J \ge 20\) and \(L \ge 7\) or \(J \ge 30\) and \(L \ge 3\). Thus, one cannot expect to solve large problem instances to optimality.

Table 9 Average computation times [sec.] of SDA/GUR or SDA only for big problems with \(10 \le J \le 100\) (all other results of GUR \(\ge 600\); \({\text{R}} = 10\), \({\text {HET}} = 0.5\), \({\text {CR}} = 0.5\))
Full size table

In contrast, SDA stays well below the time limit for all instances tested. It can be seen that the dynamic program and the single run approach used as subroutines of SDA indeed are sensitive with respect to the problem dimensions. Fortunately—also for large problem instances—the decomposition of BBP into three subsequently solved sub-problems keeps computations times in an acceptable range although two of the three sub-problems are solved to optimality.

Further results are again only presented in an aggregate manner. Table  10 summarizes the comparison of the heuristics, grouped to classes with \(JJL \le 10\,000, 20\,000, \ldots {}, 50\,000\) and then in step size of \(20\,000\) until \(150\,000\). Note that \(\%nOpt\) represents the percentage of replications per class where GUR has not been able to find an optimal solution within ten minutes. SEA and RDA shall help to get a better insight which subroutine of Fig. 2 is especially important to obtain good solutions. Average computation times aSec are again omitted for ISM because they still range below 500 milliseconds.

Table 10 Comparison of Gurobi, SDA, SEA, RDA and ISM for big problems grouped with respect to the number of binary variables JJL (no entry means: \(< 1\); \({\text {R}}=10\), \({\text {HET}} = 0.5\), \({\text {CR}} = 0.5\))
Full size table

GUR is always able to find a feasible solution, but only seldom to find the optimal one. Only for 38 percent of the smallest instances with \(JJL \le 10\,000\), a proven optimum can be reached within ten minutes.Footnote 1 In terms of solution quality, obviously SDA is the first choice for these large instances. It does in all other cases not only reliably generate feasible solutions, but also the respective benchmark solution. The average percentage deviation \(\% GUR/Best\) of Gurobi from the best solution increases from 2 percent for \(JJL \le 10\,000\) up to 212 percent for \(130\,000 < JJL \le 150\,000\).

Contrary to the results of the base instances given in Table  5, SEA shows better solutions than RDA for these big instances. The average percentage deviation \(\% SEA/Best\) of SEA from the best solution is always smaller than the average percentage deviation \(\% RDA/Best\) of RDA, while computation times aSec SEA usually are also faster. Apparently, for large problem instances, finding a good sequence of sorts is more important than partitioning this sequence. A rather “dumb” partitioning algorithm can outperform another similarly “dumb” sorting algorithm, because the number of \(J- \left\lceil J/L \right\rceil + 1\) partitionings to be checked by SEA does not grow as fast as the number J! of potential, randomly selected sequences of RDA.

Nevertheless, the results also show that the demand-oriented sequencing of Sect. 4.3.1, the shortest-path-like partitioning of Sect. 4.2.1 and the single run algorithm of Ekici et al. (2010) are not only again the best combination of subroutines I–III of Fig. 2, but moreover the best way at all to solve large problem instances. ISM as well reliably and quickly generates feasible solutions. However, its quality is by far worse than the one of SDA. The deviation is around 50 percent in the best case and more than 200 percent in the worst case. This deviation seems to grow when problem sizes grow.

6 Summary and outlook

A real-world planning problem of a printing company, called the “Block Building Problem” (BBP), has been presented where different sorts of a consumer goods’ label are printed in parallel lanes on a roll of paper with sufficient length. Printing plates have to be designed to set up the printer for a certain combination of sorts. Each sort can only be printed with a single plate. Waste may be produced and has to be disposed as scrap if the demands of a printing plate’s sorts do not match each other. Decisions shall be made how to build “printing blocks”, i.e., how many and which plates to design and how long to run the printer with a certain plate so that the fixed costs for designing the plates and setting up the printer and the variable costs of waste are minimized.

To model this practical situation, a mixed integer program (MIP) has been formulated, which is an extension of the so-called the “job splitting problem” where empty lanes are not allowed and where a single sort cannot be printed in several blocks.

A heuristic solution approach has been developed, which decomposes the BBP into the three subroutines “determining a sequence”, “partitioning the sequence into printing blocks” and “scheduling each potential printing block”. These are executed successively and iteratively. Five different decomposition heuristics are proposed and tested by combining different solution alternatives for each subroutine. The two most successful decomposition heuristics are called SDD and SDA. Both of them determine the sequence of sorts to be produced by re-sorting them with respect to varying demand. And both of them partition sequences into printing blocks by solving a dynamic program that takes advantage of BBP’s proprietary constraint that a single sort can be printed in one block only. They differ in the way how the third subroutine is executed: whereas SDD relies on another dynamic program, SDA uses the so-called single run algorithm of Ekici et al. (2010). Both solve the corresponding planning problem differently, but optimally. For benchmark purposes, an additional heuristic has been introduced which combines some rather intuitive solution ideas. The heuristic SDD has been for some years and still is in use by the printing company.

From an academic point of view, the performance of these different solution heuristics compared with each other and with standard MIP solvers appears of interest. Thus a numerical study with artificially generated test instances has been executed. Small instances up to 10 sorts and 10 lanes and large instances up to 100 sorts and 15 lanes have been generated which show similar characteristics as can be found in the label printing company.

Using Gurobi as an MIP solver reveals that all small instances can be solved to optimality in less than 20 s. Large problems, however, can—within a time limit of 600 s—only optimally be solved if they do not comprise more than 20–30 different sorts. With respect to industrial practice does this mean that instances of practically relevant size can exactly be solved in many cases, but not in all.

Thus heuristics are necessary for larger instances. Besides the already described heuristics, of course, the MIP solver can also be applied heuristically when aborting after a certain time limit like the above ten minutes. Among these heuristics SDD and SDA perform best because they generate sequences problem-oriented and solve both other sub-problems, generating printing blocks and scheduling each printing block, optimally. SDD and SDA show identical solution quality. However, SDA runs faster and thus should be preferred. The intuitive methods would even be quicker, but their solution quality is not satisfying at all. For small problems, which can still be solved exactly, usually the average deviation of SDA’s and SDD’s solutions from the optimal ones is below three percent. For bigger problems with more than 10 sorts, the MIP heuristic is 16–212 % worse than SDA which needs 1-2 minutes in the worst case in contrast to the MIP solver’s 10 minutes.

Apparently, the BBP is harder to solve to optimality if the number of sorts increase than if the number of lanes grow. That means it is easier to plan for smaller labels than for more sorts per customer order. Hardly surprising, also homogeneous demands within a customer order can easier be dealt with than heterogeneous demands. The higher the influence of the scrap costs is, the more difficult it seems to find a proven optimum. The heuristic SDA shows a similar behavior like the MIP solver, but less pronounced.

The company is satisfied with SDD in terms of both solution quality and time. Nevertheless, it can be recommended to solve small problem instances to optimality instead and to replace SDD with SDA for larger instances. That means, computation times could be decreased by substituting the currently used dynamic program with the single run algorithm. These advices seem generally valid for all companies who face a planning problem like BBP.

Two directions of future research appear promising: If optimal solutions are desired, the MIP formulation might still be improved, e.g., by additional symmetry breaking constraints and valid inequalities. If heuristic solutions are sufficient, the performance of SDA could tried to be improved, for instance, by introducing more sophisticated local search principles in subroutine I of the decomposition approach. Then, the question needs to be answered whether the expected improvements in solution quality are not overcompensated by the probable increase of computation times.