Abstract
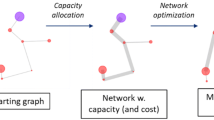
In commodity transport networks such as natural gas, hydrogen and water networks, flows arise from nonlinear potential differences between the nodes, which can be represented by so-called potential-driven network models. When operators of these networks face increasing demand or the need to handle more diverse transport situations, they regularly seek to expand the capacity of their network by building new pipelines parallel to existing ones (“looping”). The paper introduces a new mixed-integer nonlinear programming model and a new nonlinear programming model and compares these with existing models for the looping problem and related problems in the literature, both theoretically and experimentally. On this basis, we give recommendations to practitioners about the circumstances under which a certain model should be used. In particular, it turns out that one of our novel models outperforms the existing models with respect to computational time, the number of solutions found, the number of instances solved and cost savings. Moreover, the paper extends the models for optimizing over multiple demand scenarios and is the first to include the practically relevant option that a particular pipeline may be looped several times.
Similar content being viewed by others
1 Introduction
Operators of commodity transport networks such as natural gas, hydrogen and water networks regularly have to face both increasing demand and the need to handle more diverse transport situations. To deal with these challenges without having to resort to the expensive options of setting up new pipeline corridors or of demolishing pipelines and replacing them by larger ones, they must expand the capacity of the existing network. Without using compressor stations to increase the pressure in the pipelines, this can only be achieved by building pipelines parallel to existing ones, a process that is referred to as “looping” in the terminology of the industry. Due to the high costs involved, there has long been research about finding the cost minimal way of looping an existing network, i.e. of determining both the pipelines that are to be looped and the diameters of the pipelines to be built.
Commodity flows such as flows in gas and water networks arise from friction-induced potential differences between the nodes in the network, which leads to a type of nonlinear network model that is referred to as potential-driven network in the literature (Birkhoff and Diaz 1956; Raghunathan 2013; Robinius et al. 2018). Apart from the nonlinear character of potential-driven networks, a specific difficulty in finding optimal loops arises from the fact that the diameters of the pipelines typically have to be selected from a discrete set of commercially available diameters (André et al. 2009; Hansen et al. 1991; Fasold 1999), which additionally imparts to the problem a combinatorial flavour. For these reasons, the problem of capacity expansion in potential-driven networks belongs to the family of mixed-integer nonlinear programming (MINLP) problems.
As a consequence, a large body of the literature on the topic is concerned with developing sophisticated special-purpose algorithms geared at finding locally optimal solutions or approximating a global optimum, partly based on novel ways of modelling the capacity expansion problem. While this research focus has certainly advanced our ability to solve this problem, it has also led to a variety of mathematical models for the looping problem that remain unconnected in the literature. In view of the recent advances in the development of general-purpose solvers for NLP and MINLP problems that allow for an efficient implementation of models that is significantly faster than implementing one of the special-purpose algorithms developed, it seems to be useful for practitioners involved in the design of networks to shift the research focus to the modelling stage. In fact, despite the algorithmic advances in the previous decades, practitioners tackling the capacity expansion problem often find it more convenient to resort to simulation studies instead of implementing the complex special-purpose optimization models proposed in the literature, thereby not realizing the potential that an optimization-based approach has to offer. For this reason, the present paper discusses various models for finding optimal loops in potential-driven networks that can be implemented easily by using state-of-the-art MINLP solvers.
In particular, this paper brings together, for the first time, the diversity of existing models in the literature and compares these, both theoretically and experimentally. For this comparison, we choose a comprehensive approach that includes two different, rather unconnected strands of research on the problem that are referred to as the discrete approach and the split-pipe approach (see below), and also takes into account literature that does not explicitly focus on the looping problem, but addresses closely related problems. Moreover, the present paper also introduces two novel models for the looping problem, one of which has turned out to outperform the existing models in the literature with respect to computational time, the number of solutions found, the number of instances solved and cost savings. Additionally, we extend our models to include the case of optimizing capacity expansion across multiple demand scenarios. Finally, in discussing these models, the paper goes beyond the existing literature by including, throughout the paper, the practically highly relevant case that a particular pipeline may be looped several times.
Altogether, by focussing on the modelling aspect in conjunction with state-of-the-art MINLP solvers, the present paper should provide a useful guide for practitioners who look for an optimization-based alternative to simulation studies, but do not have the option to implement the special-purpose algorithms suggested in the literature. Additionally, our overview and comparison of modelling approaches in the literature, as well as our new models, may be interesting for researchers who seek to develop new special-purpose algorithms for the capacity expansion problem.
In line with our aim to bring together the diversity of existing approaches in the literature, the remainder of this section discusses the literature on the topic rather comprehensively before presenting an outline of the structure of the paper.
During the past 40 years of research on capacity problems in potential-driven networks, three different modelling approaches have been considered for the looping problem (cf. Shiono and Suzuki 2016): (1) a direct approach where the optimal diameters for the loops are chosen from the set of commercially available diameters (discrete approach), (2) a continuous approach where continuous diameters are typically used to approximate the problem and (3) an extended approach where the entire length of the pipeline to be looped is split into several segments of variable lengths each of which may have its own diameter from the discrete set of available diameters (split-pipe approach).
In the following discussion of the literature about these three approaches, we will not only look at papers addressing the looping problem (in fact, to the best of our knowledge, there are so far, apart from the present paper, only two papers, namely André et al. (2009) and Pietrasz et al. (2008), that solely focus on the looping problem), but will also consider papers about two closely related problems: the network design problem, which looks for the optimal diameters of pipelines between given unconnected nodes or determines both the location of nodes and the optimal pipelines between these, and the network expansion problem, which is about the optimal placement of new network elements of different types (such as pipelines, compressors and valves) at pre-defined (previously connected or unconnected) locations in the network.
(1) Discrete diameters One of the first solution approaches using mathematical optimization techniques for this NP-hard problem (Yates et al. 1984) has been proposed by Jacoby (1968). The author solves a nonlinear model using a gradient approximation method where the resulting continuous diameters are finally rounded to the nearest discrete-valued pipe diameters. The approach was tested on a small water network that contains seven pipelines and two cycles. Other early work where the discrete approach is used for networks with a simple structure include Liang (1971), who solved a gunbarrel system using dynamic programming, and Rothfarb et al. (1970), who used a serial and parallel merge algorithm to design tree shaped networks. Later, Gessler (1985) applied selective enumeration techniques to tackle a small sized network with two cycles. In the 1990s, a class of approaches was developed that relies on meta-heuristics, such as genetic algorithms, see, e.g. Simpson et al. (1994) and Savic and Walters (1997) for water networks, and Boyd et al. (1994) and Castillo and González (1998) for gas networks.
In the past decade, different papers applied a MINLP formulation to determine discrete pipe sizes, e.g. André et al. (2009), Bragalli et al. (2012) and Robinius et al. (2018). While André et al. (2009) solve the problem heuristically in two stages, where a first step identifies pipes to be looped by solving the continuous relaxation and a second step determines discrete-valued diameters for these selected pipes using Branch and Bound, Bragalli et al. (2012) solve the model directly with an MINLP solver using a continuous reformulation of the cost function. Robinius et al. (2018) determine discrete arc sizes in the context of tree shaped networks, which allows flows on arcs to be fixed and thus simplifying the MINLP model to an Mixed Integer Programming model.
The nonlinear nature of the problem has led to a number of different MINLP models and approaches: Raghunathan (2013) presents a disjunctive program together with a convex relaxation, which is then solved to global optimality and Borraz-Sánchez et al. (2016) propose a new solution approach by presenting a new model together with a second-order cone relaxation. Humpola (2014) formulates a model that is solved to global optimality using convex reformulation techniques, special tailored cuts.
In this paper, we investigate different existing MINLP approaches and propose a new model for the discrete looping problem.
(2) Continuous diameters have been considered e.g. by Bhaskaran and Salzborn (1979a), Rowell and Barnes (1982), Bhave (1985), De Wolf and Smeers (1996), De Wolf and Bakhouya (2012), Babonneau et al. (2012) and André et al. (2013). Continuous diameters typically have been used in the literature to approximate the discrete diameters that are commercially available. Hansen et al. (1991), for example, use successive linear programming with a trust region strategy, where the algorithm adjusts the continuous diameters in each iteration to elements in the set of available discrete diameters. Osiadacz and Górecki (1995) apply sequential quadratic programming to the continuous relaxation of a gas network design problem and round the solution to the closest available diameter size. Shiono and Suzuki (2016) introduce an analytic approach that calculates the optimal diameter costs for the pipe-sizing problem of a tree-shaped gas network with continuous diameters, which are then heuristically converted to discrete pipe diameters. As the present paper is concerned with models that lead to exact solutions, we will not further consider this line of research here.
(3) Split-pipe approach This approach, where the pipes can be split into several segments with different diameters each, combines features of both the discrete and the continuous approaches: while the diameters are chosen from the discrete set of available diameters, the option to split pipes at arbitrary points into sections of different diameters leads, as we will see in the next section, to a situation that is equivalent to choosing diameters from a continuous set. This concept was first used in designing networks with a tree structure, which allows the flows in the pipelines to be treated as constants and leads to a linear programming model (e.g. Karmeli et al. (1968) and Gupta et al. (1972) for water networks, and, independently, Bhaskaran and Salzborn (1979b) for gas networks). The first paper to attempt the split-pipe version of the capacity expansion problem as a nonlinear problem for general networks was Alperovits and Shamir (1977), who introduced the linear programming gradient (LPG) method, a two-stage heuristic that alternates between solving the linear program with fixed flows from Karmeli et al. (1968) for obtaining the pipeline diameters and modifying these flows on the basis of a sensitivity analysis of the solution of the first stage. This idea stimulated a number of subsequent papers (e.g. Quindry et al. 1981; Fujiwara and Khang 1990; Kessler and Shamir 1989) that improved on the method. Starting with Eiger et al. (1994), a strand of genuinely NLP-based global solution methods emerged, with further contributions by Zhang and Zhu (1996) and Sherali et al. (2001), for example. Surprisingly, despite 50 years of research on the split-pipe approach, all these contributions proceed from the very same basic model that goes back to the linear model by Karmeli et al. (1968). For this reason, the present paper presents a novel, alternative model for the split-pipe approach and compares it to the split-pipe model in the literature.
We have now sketched the history of research on the three different approaches to our looping problem and closely related problems. In the light of the variety of models and optimization methods for these problems, it is astonishing that there is nearly no research that brings together the discrete and the split-pipe approaches and compares the models proposed in the literature. In fact, to the best of our knowledge, the very early paper by Bhaskaran and Salzborn (1979b) with its linear model for a tree-shaped network is the only paper to compare the split-pipe approach with the discrete approach, albeit for very small trees with 9 and 14 nodes. The present paper addresses this gap and presents comparisons of all models discussed in the literature.
Another important aspect of the looping problem that has not been addressed in the literature is multiple looping, where each pipeline may be reinforced with several parallel pipelines of different diameters. This is a practically highly relevant problem as multiple looping can first replace large diameters that are commercially not available; may second lead to cost savings by substituting several parallel pipelines with smaller diameters for one pipeline with a large diameter; may third, as we will see in Sect. 2.3, allow for pipe characteristics that cannot be realized with single loops; and can finally provide a tool for strategic planning where several stages of successively looping a given network are to be considered. For these reasons, we will take into account multiple looping throughout the paper.
The remainder of the paper is organized as follows: In the next section, we formalize the looping problem in potential-driven networks, show some of its basic properties and explain our approach of dealing with multiple loops. In Sect. 3, we present a new model for the discrete looping problem and contrast it with the existing models in the literature. The subsequent Sect. 4 turns to the split-pipe approach of the looping problem. Again we present a new model and address its relationship with the split-pipe model that can be found in the literature. Moreover, we discuss the way in which the feasible regions of all models presented so far are related to each other. Section 5 extends the models to the case of multi-scenarios. In Sect. 6, we carry out extensive computational experiments on instances of both natural gas and water networks that allows us to compare the performance of all models and give recommendations regarding their use. The paper ends with some concluding remarks in Sect. 7.
2 The expansion planning problem
Let us begin by formally defining the planning problem that this paper discusses.
2.1 Problem statement
Let \({\mathcal {G}} = \left( {\mathcal {V}},{\mathcal {A}}, r \right)\) be a directed multigraph with node set \({\mathcal {V}}\), arc set \({\mathcal {A}}\) and a function \(r :{\mathcal {A}} \rightarrow {\mathcal {V}} \times {\mathcal {V}}\) that maps each arc to its end points. The nodes can be partitioned into supply nodes (sources), consumption nodes (sinks) and transshipment nodes. In this paper, we restrict to passive and connected networks, where the only arc type are pipes that are needed to transport the commodities. We are given a demand vector \(b \in {\mathbb {R}}^{|{\mathcal {V}}|}\) where \(b_{v} > 0\) denotes injection into the network at source \(v \in {\mathcal {V}}\) and \(b_{v} < 0\) withdrawal at sink \(v \in {\mathcal {V}}\). Since we work with stationary and isothermal models, the demand vector is balanced, i.e. \(\sum _{v \in {\mathcal {V}}} b_{v} = 0\). With each arc \(a \in {\mathcal {A}}\), flow variables \(x_a \in [{\underline{x}}_a, {\overline{x}}_a]\) are associated. Positive values of \(x_a\) indicate flow along the arc \(a = (v,w)\) from v to w, whereas negative values indicate flow in the reversed direction. As in classical network flow problems, flow conservation is required at every node i.e. \(\sum _{a \in \delta ^+(v)} x_{a} - \sum _{a \in \delta ^-(v)} x_{a} = b_v\) with \(\delta ^+(v) := \{(v,w) \in \mathcal{A}\}\) and \(\delta ^-(v) := \{(w,v) \in \mathcal{A}\}\). In potential-based networks, the physical state is additionally described by nonnegative potential variables \(\pi _v \in [{\underline{\pi }}_v, {\overline{\pi }}_v]\) at each node \(v \in {\mathcal {V}}\).
In applications such as water transport problems, the nodal potentials \(\pi _v\) correspond to hydraulic heads, i.e. the sum of the elevation head, velocity head and pressure head (Walski et al. 2001), while they represent squared pressure variables in gas transport problems (Koch et al. 2015).
The flow along a pipe \(a = (v,w)\) depends on the potential difference at its adjacent nodes, the pipe length \(L_a > 0\), a physical parameter \(R_a > 0\) representing phenomena such as friction and density and the diameter \(d_a > 0\). The potential difference
is given by a function \(\Phi (d_a, .) : {\mathbb {R}} \rightarrow {\mathbb {R}}\) that is strictly increasing, \(\Phi (d_a, .) \in {\mathcal {C}}^1\) and anti-symmetrical, i.e. \(\Phi (d_a, -x_a) = - \Phi (d_a, x_a)\), and typically takes the form
with \(\alpha , \beta > 0\). In line with most authors in the literature, we model \(R_a\) as a constant and assume the pipes to have zero slope, i.e. there is no influence of gravity on the potential drop \(\pi _v - \pi _w\) (e.g. Zhang and Zhu 1996; André et al. 2009; Babonneau et al. 2012). The value of \(\alpha\) depends on the commodity and the type of approximation used for modelling the commodity flow. In water transport problems, the potential loss function is typically given by the equations of Darcy–Weisbach with \(\alpha = 2\) or Hazen–Williams with \(\alpha = 1.852\) (Walski et al. 2001), whereas in gas transport problems Eq. (2) takes the shape of the Weymouth equation with \(\alpha = 2\) ( Weymouth (1912)). In the approximations proposed by Darcy–Weisbach and Weymouth, the exponent of the diameter is \(\beta = 5\), while it is \(\beta = 4.87\) in the case of the approximation by Hazen–Williams.
The solution of the capacity expansion problem involves two decisions: (a) which pipelines \(a \in \mathcal{A}\) should be looped? and (b) what pipeline diameters \(d_a\) should be used for the loops? As we wish to solve the problem to global optimality and any pre-selection of certain pipes are looping candidates would be a heuristic procedure, we will allow all pipes to be looped.
For the diameters \(d_a\), we have in the discrete case \(d_a \in {\mathcal {D}}_a := \{D_{a,0}, D_{a,1}, ... ,\) \(D_{a,k_a }\}\), where \(d_{a,0}\) refers to the diameter of the already existing pipe and \(d_{a,k_a }\) denotes the maximal possible diameter when looping. In the continuous case the domain of the diameter is given by \(d_a \in {\mathcal {D}}_a := [D_{a,0}, D_{a,k_a } ]\). While the present paper is not concerned with the continuous looping problem due to its approximative nature, we will see in Sect. 2.3 that a continuous interval of diameters can also be interpreted as representing diameters in the split-pipe problem.
The general looping problem then reads
Note that even when no particular bounds \({\underline{x}}_a\) and \({{\overline{x}}}_a\) on the flow variables \(x_a\) are given, flow bounds are implied by the bounds on \(\pi _v\) and \(d_a\) by virtue of Eq. (1).
To provide the reader with some intuition for the problem statement of the expansion planning problem, let us briefly demonstrate that we can always find a solution to the problem provided that there is no flow bound (3e), that the intersection of the bounds of the potential variables is non-empty, i.e. \(\cap _{v \in \mathcal{V}} \, [\underline{\pi }_v, \overline{\pi }_v] = [\underline{\pi }, \overline{\pi }]\) with \(\underline{\pi } \le \overline{\pi }\) and that we can choose sufficiently large pipeline diameters.
Let \({{\overline{b}}}\) the overall network inflow, i.e. the sum of all flows that enter the network at the entry nodes, which is clearly an upper bound on any flow along any arc in the network. We now select for each arc \(a \in \mathcal{A}\) a diameter \({\tilde{d}}_a\) such that \(L_a R_a / {\tilde{d}}_a^{\beta } {{\,\mathrm{sgn}\,}}({\overline{b}}) {|}{{\overline{b}}}{|}^{\alpha } \le ({\overline{\pi }} - {\underline{\pi }}) / |\mathcal{A}|\).
Let \((\pi _v, x_a)_{v \in \mathcal{V}, a \in \mathcal{A}}\) be a corresponding solution of Problem (3a–c) where the values for \({\tilde{d}}_a\) are fixed. The solution has unique flow values and the potential values are uniquely determined up to a constant shift (cf. Collins et al. 1978; Humpola 2014 for the existence of such a solution), which obviously satisfies
Summing up these inequalities along any path \(\overrightarrow{v_0v_k}\) between two connected nodes \(v_0\) and \(v_k\) yields:
We now choose a node \(v_0\) with the highest potential in our solution and shift this node’s potential by a constant \(r \in {\mathbb {R}}\) such that it is equal to the upper bound \(\overline{\pi }\), i.e. such that we have \({{\tilde{\pi }}}_{v_0} := \pi _{v_0} + r = \overline{\pi }\) for the new potential of the node \(v_0\). If we shift the potentials \(\pi _v\) of all other nodes by the same constant r, all our potentials are guaranteed to satisfy (3d).
2.2 Convexity analysis
In the previous section, we have seen that we can model the expansion planning problem as a Mixed-Integer Nonlinear Program (MINLP) for discrete looping decisions and we will see in Sect. 2.3 that the split-pipe approach leads to a Nonlinear Program (NLP). We will now show that the feasible regions of the discrete and continuous (or split-pipe) capacity expansion planning problem are non-convex.
When neglecting loop expansions, i.e. \(d_a = d_{a,0}\) for all pipes \(a \in {\mathcal {A}}\), the continuous and the discrete problems (3) reduce to the same existence problem of validating a given demand scenario for feasibility. The feasible region of the resulting problem is convex (Maugis 1977; Collins et al. 1978), even though it comprises nonlinear nonconvex constraints of type (3b). However, the following proposition shows that this property does not hold for the feasible region of the expansion planning problem.
Proposition 1
There exist instances, such that the continuous and discrete expansion planning problems are nonconvex.
Proof
The discrete expansion planning problem is trivially nonconvex. Regarding the continuous (and split-pipe) problem, we consider a network of two pipes \(a_1, a_2\) in parallel with adjacent nodes v and w. For given \(\alpha = 2\) and \(\beta = 5\), let a demand situation \(b_v = 10 = - b_w\), pipe properties \(L_a, R_a = 1\) and diameters \(d_{a} \in [1,2]\) for both pipes \(a \in \{a_1, a_2\}\) be given. Then, the flow distribution among the parallel pipes is unique, where both pipes have the same flow direction, i.e. \({{\,\mathrm{sgn}\,}}(x_{a_1}) = {{\,\mathrm{sgn}\,}}(x_{a_2})\), and thus (2) reduces to \(\pi _v - \pi _w = L_{a} R_{a} / d^5_{a_1} x_{a_1}^{2} = L_{a} R_{a} / d^5_{a_2} x_{a_2}^{2}\). Then, \(s := (x_{a_1}, x_{a_2}, d_{a_1}, d_{a_2}, \pi _v, \pi _w)\) \(\approx (10/31 (4 \sqrt{2} - 1), -40/31(\sqrt{2} -8), 1, 2, 100, 97.743362)\) is a solution of problem (3), and by symmetry another solution exits when swapping the diameters of both pipes, i.e. \({\tilde{s}} := ({\tilde{x}}_{a_1}, {\tilde{x}}_{a_2}, {\tilde{d}}_{a_1}, {\tilde{d}}_{a_2}, {\tilde{\pi }}_v, {\tilde{\pi }}_w)\) \(\approx (-40/31(\sqrt{2} -8),10/31 (4 \sqrt{2} - 1), 2, 1, 100, 97.743362)\). But there exists an infeasible convex combination of both solutions, namely \(s^* := 0.5 (s + {\tilde{s}}) = (x_{a_1}^*, x_{a_2}^*, d_{a_1}^*, d_{a_2}^*, \pi _v^*, \pi _w^*) \approx (5, 5, 1.5, 1.5, 100, 97.743362)\), because \(s^*\) violates Eq. (3b), i.e.
\(\square\)
2.3 Loop diameters
After our general outline of the extension planning problem and some of its basic characteristics, we will now describe how the diameters used for looping pipelines are represented in the discrete and the split-pipe models to be discussed in the present paper. In doing so, we will go beyond the existing literature and allow that each pipeline a may be looped several times. Our starting point is a finite set \(\{ d_1, \dots , d_n\}\) of commercially available diameters for looping. These diameters are associated with costs \(c_1< \cdots < c_n\) per unit of pipeline length, see left Fig. 1.
It is well known in the literature (see Katz 1959; André et al. 2009 for the case of gas networks and Bragalli et al. (2012) for the case of water networks, for example) that two parallel pipelines with diameters \(d_1\) and \(d_2\) can be replaced, without changing any physical properties of the network, by a single pipeline with diameter \(D_{d_1,d_2}\) (called equivalent diameter) by virtue of
It is easy to see that for looping an arc a of length L with existing diameter \(d_a\) multiple (k) times with (not necessarily distinct) diameters \(d_{i_1}, d_{i_2}, ..., d_{i_k} \in D\), this relationship can be extended to
where this multiple loop is associated with costs
This equation implies that when allowing for multiple loops, we cannot only choose among the discrete set of commercially available diameters, but we have at our disposal the much larger discrete set of equivalent diameters that result from all possible combinations of available loops. This is the approach that we choose in our discrete models.
Available diameters \(\{d_1, \dots , d_n\}\) with cost factors (left). On the right: construction of the efficient frontier of dominating equivalent diameters. Note that the cost components of the points \((d_i, c_i)\) on the left side correspond with those of the points \((D_{d_a , d_i}^{-\beta }, c_{i})\) on the right side
A type of equivalent diameter also exists for the case of two serial pipelines with no source or sink inbetween. Assume we have two pipelines, one from node v to node w and the other one from w to z, with diameters \(d_1\) and \(d_2\), the same physical parameter \(R := R_1 = R_2\), a total length of L from v to z, and with \(\lambda L\) being the length of the first pipeline from v to w, where \(0< \lambda < 1\). Then, due to (1) and (2), the total potential loss along the flow x from v to z is given by
The same potential loss can be achieved with a single pipeline of length L when its diameter D is given by \(\pi _v - \pi _z = L R / D^{\beta } {{\,\mathrm{sgn}\,}}(x) {|}{x}{|}^{\alpha }.\) This and the previous equation imply that the equivalent diameter satisfies \(D^{-\beta } = \lambda d_1 ^{-\beta } + (1 - \lambda ) d_2^{-\beta }.\) Analogously, we have for the case of k serial pipeline segments with diameters \(d_1, d_2, \dots , d_k\) and lengths \(\lambda _1 L, \lambda _2 L, \dots , \lambda _k L\), where \(\sum _{i=1}^{k} \lambda _i = 1\) with \(\lambda _i \ge 0\):
For practical purposes, relationship (6) implies that, when looping pipelines, we are not restricted to the discrete set of equivalent diameters that results from multiple loops with the commercially available diameters according to (4). Instead, we can decide to split a pipeline into several segments of lengths \(\lambda _i L\) and have different, possibly multiple loops, i.e. loops with different equivalent diameters, on all segments. In this way, (6) allows us to realize in the network all diameters in the (continuous) interval between the smallest and the largest possible equivalent diameters. This is the approach that our split-pipe models use and it enables us to benefit, despite the limited number of commercially available pipeline diameters, from having the flexibility of a continuous set of equivalent diameters at our disposal.
We will allow a single pipe a to be looped up to r times, i.e. in the capacity expansion problem we have to pick up to r diameters for each existing pipeline of the network. With \(\left( {\begin{array}{c}n+k-1\\ {}k\end{array}}\right)\) being the number of k-combinations with repetitions from the diameter set \({\mathcal {D}}\), we obtain \(\sum _{k=0}^{r} \left( {\begin{array}{c}n+k-1\\ k\end{array}}\right)\) equivalent diameters for each pipe. To avoid a factorial growth of the number of variables in our models, we apply a model reduction technique to our split-pipe models that has been introduced in the literature for the case of single looping several times (e.g. Bhaskaran and Salzborn 1979b; Fujiwara and Dey 1987; Zhang and Zhu 1996). We will briefly outline this method for the general case of multiple loops.
Our aim is to compare all potential equivalent diameters resulting from both parallel pipelines (multiple loops) and serial pipelines (split-pipe setting) with respect to their costs and to incorporate into our models only those equivalent diameters that are not dominated by equivalent diameters with lower costs. To this end, we place all pairs of equivalent diameters D generated according to (4) and their corresponding costs per unit of pipeline length \(c_D\) according to (5) into a coordinate system where the horizontal axis depicts the exponentiated equivalent diameter \(D^{-\beta }\) and the vertical axis the cost \(c_D\), i.e. we consider the points \((D^{-\beta }, c_D)\). In this coordinate system, the \(D^{-\beta }\) coordinate of each convex combination of points \((D_i^{-\beta }, c_{D_i})\) represents, due to (6), an equivalent diameter that results from splitting a looped pipe into several sections with equivalent diameters \(D_i\) each, while the \(c_D\) coordinate of such a convex combination indicates, also due to (6), the corresponding cost of such a split-pipe arrangement. This is illustrated on the right side of Fig. 1. It shows for an arbitrary pipeline the original diameter \(d_a ^{-\beta }\) of the pipeline, which has zero cost (solid circle); all equivalent diameters \(D_{d_a , d_{i}}^{-\beta }\) that result from looping the existing pipeline once at cost \(c_{i}\) (dots in our diagram); all equivalent diameters \(D_{d_a , d_{i_1},d_{i_2}}^{-\beta }\) that result from looping the existing pipeline twice at cost \(c_{i_1} + c_{i_2}\) (plus signs in the diagram); and finally, all equivalent diameters \(D_{d_a , d_{i_1},d_{i_2}, d_{i_3}}^{-\beta }\) that result from triple looping at cost \(c_{i_1} + c_{i_2} + c_{i_3}\), which are represented by crosses in the diagram.
This setting allows us to identify those equivalent diameters among the equivalent diameters generated by (4) that are crucial for our models, namely those equivalent diameters that are represented by the extreme points of the “efficient frontier” on the right side of Fig. 1 (circled in the diagram). All points on the line that represent the efficient frontier in our figure correspond to convex combinations of two equivalent diameters, i.e. a split-pipe setting where the pipeline is split into two segments, and these points represent the cost minimal ways of equipping a particular arc of the network with a certain equivalent diameter. As a consequence, for finding an optimal solution to the capacity extension problem, it suffices to incorporate into our split-pipe models only the equivalent diameters that correspond to the extreme points of the efficient frontier and to discard all others. As we will see when introducing the models, this will greatly reduce the number of variables.
In the case of the discrete capacity extension problem, we cannot use convex combinations of equivalent diameters and have to get along with the equivalent diameters given by (4). Unfortunately, however, we cannot possibly use all equivalent diameters depicted on the right of Fig. 1 for all arcs of the network as this would make the problem computationally intractable. For this reason, in our computational experiments in Sect. 6 we will restrict our models to the equivalent diameters that result from looping an existing pipeline once and, additionally, to those equivalent diameters that result from looping an existing pipeline several times and are extreme points of the efficient frontier described above. In this way, we may have to do without some potentially cost-minimal diameters, but will keep our models at a reasonable size and will, due to having incorporated the option of multiple looping, still achieve better results than the approaches presented in the literature.
In the following, we denote the set of equivalent extension diameters of pipe a that we use in our models by \(\{D_{a,0}, ..., D_{a,k_a}\}\) (sorted in ascending order), where \(D_{a,0}\) represents the (unlooped) original diameter \(d_a\) of the existing pipe, and the corresponding cost factors by \(c_{a,0}< \cdots < c_{a,k_a}\). Moreover, for the sake of convenience we write \([k_a] := \{0, 1, ... , k_a \}\).
3 Discrete loop expansions
In this section, we present different approaches to model discrete loop expansions. We will begin with the model that is closest to our generic formulation of the capacity expansion problem (3).
3.1 Discrete looping with potential function constraints (model A)
To formulate a MINLP on the basis of our generic formulation (3) of the looping problem, which can be found, in its discrete version, in several recent papers (e.g. André et al. (2009); Bragalli et al. (2012); Robinius et al. (2018)), we have to specify the way in which the discrete values of the diameter variables are selected. Here this happens in a straight-forward way by means of binary variables \(\lambda _{a,i}\) each of which represents one diameter \(D_{a,i} \in \{D_{a,0}, \dots , D_{a,k_a}\}\). Constraint (7c) ensures that exactly one diameter is chosen for each arc \(a \in {\mathcal {A}}\), and in constraint (7b) the potential function has been rewritten in a way such that the chosen diameter is used for modelling the potential loss. With these variables \(\lambda _{a,i}\), the objective function is a direct consequence of (5) in conjunction with the generic objective function (3a), while all other constraints are identical with the generic model.
3.2 Discrete looping with flow direction variables (model B)
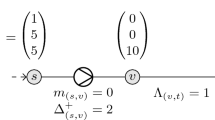
This model is based on an approach by Raghunathan (2013) to tackle the network design problem. The main difference to the previous model is that we split the flow variable \(x_a\) into two sets of variables \(x_{a, i}^+\) and \(x_{a, i}^-\), which represent the flow on arc a with diameter \(D_{a,i}\) in forward and backward direction, respectively (see constraint (8e)), and correspondingly, variables \(\Delta _{a}^+, \Delta _{a}^-\) that describe the potential drop along the arcs according to the flow direction (see constraints (8b) and (8c)). The idea behind this formulation is that constraint (7b) uses two nonlinear functions, namely the power function and the sign function, and by splitting the variable \(x_a\) into a part for a forward flow and a part for a backward flow, we are able to do without the latter function. This comes at a price, however, as we have to introduce additional binary variables \(z_a\) to choose between the two flow directions (8g, h).
In his paper, Raghunathan (2013) develops his own solution algorithm to the network design problem, where he uses a convex relaxation of the problem by relaxing the potential constraint function (1) to \(\Delta _{a}^+ \le \Phi (D_{a,i}, x_{a,i}^+)\) and \(\Delta _{a}^- \le \Phi (D_{a,i}, x_{a,i}^-)\) for all \(a \in \mathcal {A}, i \in [k_a]\). In our context here, to model the expansion problem in an exact way, our aim is to enforce these equations with equality. In general, this can be done in different ways, such as using big-M constraints for modelling the disjunctions \(\vee _{i=0}^{k_a} \Delta _{a}^+ = \Phi (D_{a,i}, x_{a,i}^+)\) and \(\vee _{i=0}^{k_a} \Delta _{a}^- = \Phi (D_{a,i}, x_{a,i}^-)\) or introducing the following constraints: \(\Delta _{a}^+ = \sum _{i = 0}^{k_a} \Phi (D_{a,i}, x_{a,i}^+)\) and \(\Delta _{a}^- = \sum _{i = 0}^{k_a} \Phi (D_{a,i}, x_{a,i}^-)\) for all \(a \in {\mathcal {A}}\). Preliminary computational tests by the authors of the present paper revealed that the best performance is achieved with Balas’s convex hull formulation (Balas 1985), i.e. when resolving these disjunctions by explicitly modelling the potential drop along arc a for diameter \(D_{a,i}\) with the variables \(\Delta _{a,i}^+, \Delta _{a,i}^-\). The model then reads as follows:
with \(\overline{\Delta }_{a}^+ := \overline{\pi }_{v} -\underline{\pi }_w\) and \(\overline{\Delta }_{a}^- := \overline{\pi }_{w} -\underline{\pi }_v\). Equations (8f–h) model that a non-negative flow of arc a takes only place along a given direction for the selected diameter \(D_{a,i}\) inducing the corresponding potential drop. To provide another upper bound on the potential loss on the arcs, Raghunathan (2013) introduces further constraints, which in our case read \(\Delta _{a,i}^- \le L_{a} R_{a} / D_{a,i}^\beta {({\overline{x}}_{a,i})}^{\alpha -1} x_{a,i}^-\) and \(\Delta _{a,i}^+ \le L_{a} R_{a} / D_{a,i}^\beta {({\overline{x}}_{a,i})}^{\alpha -1} x_{a,i}^+\).
3.3 Discrete looping with potential difference variables (model C)
The model presented in this section is a novel approach to tackle the nonlinearities of the problem. Instead of introducing variables for the flow direction as in the previous model, the idea here is to reduce the two-dimensional function \(\Phi (d_a, x_a)\) to a one-dimensional function \(\phi (x_a)\). This is achieved by shifting the loop diameters from the term that represents the flow towards the potential loss term (see Eq. 9b). To this end, we introduce variables \(\Delta _{a,i}\) to model the potential loss that corresponds to the loop diameter chosen (constraint 9c) and use the binary variables \(\lambda _{a,i}\) not to choose the diameters, but to select the potential loss. As a trade-off we have to introduce big-M constraints (9d) to determine the potential loss variables \(\Delta _{a,i}\).
where \(M_{a,i}^{(1)} := \Phi (D_{a,i}, {\underline{x}}_a), M_{a,i}^{(2)} := \Phi (D_{a,i}, {\overline{x}}_a)\).
3.4 Further approaches for discrete looping in the literature
There are two further models in the literature for the network design problem, both of which are not intended as “stand-alone models”, but as starting points for solution algorithms. While we will not go into the details of the models here because preliminary computational experiments have demonstrated that they do not perform particularly well (see Sect. 6.2), the approaches still deserve mentioning.
Borraz-Sánchez et al. (2016) present an MINLP formulation that is similar to the model developed by Raghunathan (2013) (Sect. 3.2) in the sense that it distinguishes between forward and backward flow directions. Here, however, this is achieved by binary variables \(z_a^{+}, z_a^{-}\) that are then used to model the potential loss function in product form \(\lambda _{a,i} (z_a^{+} -z_a^{-}) (\pi _v -\pi _w) = L_a R_a / D_{a,i}^{\beta } x^\alpha\).
Humpola (2014) uses indicator constraints to select arcs a in the network design problem (or diameters \(D_{a,i}\) in the context of our expansion problem), i.e. constraints of the form \(\lambda _{a,i} = 1 \, \Rightarrow \, \pi _v - \pi _w = \Phi (d_{a,i}, x_a)\) and \(\lambda _{a,i} = 0 \, \Rightarrow \, x_{a,i} = 0\), which may be represented by big-M constraints in a MINLP model.
3.5 Equivalence of the discrete models
To finish our section on discrete models for the capacity expansion problem, we show that the three models presented so far are equivalent. More precisely, we show that for each solution to one of the models, there exist solutions to the other two models such that all of them represent the (1) same physical network state in terms of flow and pressure, (2) same decisions on loop extensions, and (3) same objective function values. To this end, we use the standard projection to map the feasible regions of the discrete models onto the space of their common variables, i.e. onto the \(\left( (\pi _v, \lambda _{a,i})_{v \in V, a \in A, i \in [k_a]} \right)\)-space: In this context we denote the feasible regions of the discrete models as: \(X_{A}\) for Model A, \(X_{B}\) for Model B and \(X_{C}\) for Model C.
Proposition 2
The discrete Models A, B and C are equivalent, i.e.
Proof
“\(\underline{X_{A} \subseteq X_{C}}\)”: Let \(({\tilde{x}}_a, {\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i} )_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) be a solution of Model A, i.e. \(( {\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i} )_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]} \in X_{A}\). Then (9e–g) and (9i,j) follow right away with \(({\tilde{x}}_a, {\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i} )_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\). For pipe a, let \({\check{i}}_a \in [k_a]\) be such that \({\tilde{\lambda }}_{a,{\check{i}}_a} = 1\) and define
Then Eq. (9b) follows by construction, (9c) equals (7b) and (9d) holds by virtue of \(M_{a,i}^{(1)} = \Phi (D_{a,{\check{i}}_a}, {\underline{x}}_a), M_{a,i}^{(2)} = \Phi (D_{a,{\check{i}}_a}, {\overline{x}}_a)\) and (9h) follows from (9c) and (9g). Thus, \(({\tilde{x}}_a, {\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i}, \Delta _{a,i} )_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) is a solution of Model C, and \(( {\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i} )_{v \in \mathcal{V}, a \in \mathcal{A}, i \in [k_a]} \in X_{C}\).
“\(\underline{X_{C} \subseteq X_{A}}\)”: Let \(\left( x_a, \pi _v, \lambda _{a,i}, \Delta _{a,i} \right) _{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) be a solution of Model C, i.e. \(\left( \pi _v, \lambda _{a,i} \right) _{v \in \mathcal{V}, a \in \mathcal{A}, i \in [k_a]} \in X_{C}\). With \(\left( x_a, \pi _v, \lambda _{a,i}, \Delta _{a,i} \right) _{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\), Eq. (7b) follows from (9b–d) and (7c–g) equals (9e–g), (9j–i). Hence, \(\left( \pi _v, \lambda _{a,i} \right) _{v \in \mathcal{V}, a \in \mathcal{A}, i \in [k_a]} \in X_A\).
“\(\underline{X_{A} \subseteq X_{B}}\)”: Let \(({\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i}, {\tilde{x}}_a)_{v \in \mathcal{V}, a \in \mathcal{A}, i \in [k_a]}\) be a solution of Model A, that is, \(({\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i})_{v \in \mathcal{V}, a \in \mathcal{A}, i \in [k_a]} \in X_{A}\). For pipe a let \({\check{i}}_a \in [k_a]\) be such that \({\tilde{\lambda }}_{a,{\check{i}}_a} = 1\). We set \(x_{a,i}^+, x_{a,i}^-, \Delta _{a,i}^{+}, \Delta _{a,i}^{-} := 0\) for all \(i \in [k_a]\setminus \{{\check{i}}_a\}\).
- Case 1::
-
if \({\tilde{x}}_a \ge 0\), define \(x_{a,{\check{i}}_a }^+ := {\tilde{x}}_a, \; x_{a,{\check{i}}_a }^- = 0\) and \(\Delta _{a,{\check{i}}_a}^{+} := {\tilde{\pi }}_v - {\tilde{\pi }}_w\) and \(z_a := 1\).
- Case 2::
-
if \({\tilde{x}}_a < 0\), define \(x_{a,{\check{i}}_a }^+ = 0 ,\; x_{a,{\check{i}}_a }^- := -{\tilde{x}}_a\) and \(\Delta _{a,{\check{i}}_a}^{-} := {\tilde{\pi }}_w - {\tilde{\pi }}_v\) and \(z_a := 0\). Then in both cases (8b) – (8k) hold. Hence, \(({\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i})_{v \in \mathcal{V}, a \in \mathcal{A}, i \in [k_a]} \in X_B\).
“\(\underline{X_{B} \subseteq X_{A}}\)”:
Let \(\left( x_{a,i}^+, x_{a,i}^-, z_a, \pi _v, \lambda _{a,i}, \Delta _{a,i}^+, \Delta _{a,i}^-\right) _{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) be a solution of Model B, i.e. \((\pi _v, \lambda _{a,i})_{v \in \mathcal{V}, a \in \mathcal{A}, i \in [k_a]} \in X_{B}\). Set \({\tilde{x}}_a := \sum _{i \in k_a} (x_{a,i}^+ - x_{a,i}^-)\) for all \(a \in \mathcal{A}\), then the equations of Model A are satisfied. Hence, \((\pi _v, \lambda _{a,i} )_{v \in \mathcal{V}, a \in \mathcal{A}, i \in [k_a]} \in X_A\). \(\square\)
4 Split-pipe loop expansions
In this section, we present two equivalent modelling approaches for continuous loop expansions. The first one is a model common in the literature (e.g. Alperovits and Shamir 1977; Zhang and Zhu 1996), while the second one is a novel approach.
4.1 Split-pipe looping with length variables (Model D)
This split-pipe model is identical to the first discrete Model A, except that the indicator variables \(\lambda _{a,i} \in \{0,1\}\) have been relaxed to continuous length variables \(\lambda _{a,i} \in [0,1]\) here, turning the MINLP of Sect. 3.1 into a NLP. As explained in Sect. 2.3, these length variables denote the proportion of pipe a that is looped with diameter \(D_{a,i}\), i.e. for each arc a, the pipeline consists of segments of those equivalent diameters \(D_{a,i}\) for which \(\lambda _{a,i} > 0\).
4.2 Split-pipe looping with efficient frontier constraints (Model E)
In the previous section, we modelled the efficient frontier of equivalent diameters using length variables \(\lambda _{a,i}\) to express convex combinations of the equivalent diameters \(D_{a,i}\) that are the extreme points of the frontier. In the present section, the efficient frontier is modelled explicitly by using linear constraints.
As the efficient frontier consists of points \((D^{-\beta }, c)\) (cf. Sect. 2.3), we introduce new continuous variables \(y_a\) to model the exponentiated diameter (see constraints(11b, g) and variables \(c_{a}\) that represent the costs per unit length of pipe a for the equivalent diameters (see (11h) and the objective function). On this basis, the efficient frontier can be represented by linear constraints (11d), each of which models the frontier between a pair of adjacent extreme points (cf. the right side of Fig. 1). The parameters \(s_{a,i}\) and \(t_{a,i}\) can be calculated in advance as \(s_{a,i} = (c_{a,i} - c_{a,i+1}) / (D_{a,i}^{-\beta } - D_{a,i+1}^{-\beta })\) and \(t_{a,i} = -s_{a,i} D_{a,i+1}^{-\beta } + c_{a,i+1}\).
Note that the bounds in (11g) can be calculated as \({\underline{y}}_a = D_{a,k_a}^{-\beta }\) and \({\overline{y}}_a = D_{a,0}^{-\beta }\).
4.3 Equivalence of the split-pipe models
To compare the feasible regions of the split-pipe Models D and E, we use the standard projection to map their feasible regions onto the space of their common variables, i.e. onto the \(\left( (\pi _v, x_{a})_{v \in \mathcal{V}, a \in \mathcal{A}} \right)\)-space:
The feasible region of Model D is a subset of the feasible region of Model E due to the inequality constraints (11d), i.e. \(X_D \subseteq X_E\). But since the objective is to minimize the cost for building loops, solutions of both models are forced to be on the efficient frontier. The proof of the following proposition formalizes this argument.
Proposition 3
Each optimal solution to Model D is an optimal solution to Model E, and vice versa.
Proof
(i) Let \(( x_a^{*}, \pi _v^{*}, \lambda _{a,i}^{*} ) _{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) be an optimal solution of Model D, i.e. \(\left( x_a^{*}, \pi _v^{*} \right) _{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]} \in X_D\). According to Fujiwara and Dey (1987), an optimal solution has the property that each arc consists of at most two pipe segments, where the corresponding equivalent diameters correspond to adjacent extreme points of the efficient-frontier \(\{(D_{a,0}^{-\beta }, c_{a,0}), \ldots, (D_{a,k_a}^{-\beta }, c_{a,k_a}) \}\). Hence, for all \(a \in {\mathcal {A}}\) there exists a unique \(i_0 \in [k_a -1]\) such that \(0 \le \lambda _{a, i_0}^{*}, \lambda _{a, i_0 +1}^{*} \le 1\) with \(\lambda _{a, i_{0}}^{*} + \lambda _{a, i_{0} +1}^{*} = 1\) and \(\lambda _{a, i}^{*} = 0 \; \forall i \in [k_a] \, \setminus \, \{i_0, i_0 + 1 \}\). Define
Then, \((x_a^*, \pi _v^*, {\tilde{y}}_a, {\tilde{c}}_a)_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) obviously fulfils the variable bounds (11e–g) and Eq. (11c). From (10b) and the definition of \({\tilde{y}}\) follows (11b). We now show that (11d) holds: From our definition of \({\tilde{y}}_a\), we obtain
Since the objective is to minimize and the slopes \(s_{a,i}\) in (11d) are decreasing for increasing i, we have \({\tilde{c}}_a = s_{a,i_0} {\tilde{y}}_a + t_{a, i_0} \, = \, \max _{i \in [k_a -1]} s_{a,i} {\tilde{y}}_a + t_{a, i}\) which implies \({\tilde{c}}_a \ge s_{a,i} {\tilde{y}}_a + t_{a, i}\) for all \(a \in \mathcal{A}\) and for all \(i \in [k_a -1]\), and hence, the solution of Model D satisfies (11d). Therefore, all optimal solutions of Model D are feasible for Model E, i.e. \(\left( x_a^{*}, \pi _v^{*} \right) _{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]} \in X_E\). The optimal objective function value of Model D is \(\sum _{a \in {\mathcal {A}}} L_a (\lambda _{a,i_0}^{*} c_{a, i_0} + \lambda _{a,i_0 + 1}^{*} c_{a, i_0 +1})\) and equals \(\sum _{a \in {\mathcal {A}}} L_a {\tilde{c}}_{a}\) by construction.
(ii) Let \(\left( x_a^{*}, \pi _v^{*}, y_a^{*}, c_a^{*} \right) _{a \in \mathcal{A}, v \in \mathcal{V}}\) be an optimal solution of Model E, that is, \(\left( x_a^{*}, \pi _v^{*} \right) _{a \in A, v \in V} \in X_E\). Consider \(i_0 \in [k_a - 1]\) such that \(D_{a,i_0 +1}^{-\beta } \le y_a^{*} \le D_{a,i_0}^{-\beta }\). Then, there exist unique \(0 \le \lambda _{a, i_0}, \lambda _{a, i_0 + 1} \le 1\) with \(\lambda _{a, i_0} + \lambda _{a, i_0 +1} = 1\) such that \(y_a^{*} = \lambda _{a,i_0} D_{a,i_0}^{- \beta } + \lambda _{a,i_0 +1} D_{a, i_0 +1}^{- \beta }\) for all \(a \in {\mathcal {A}}\). We set \(\lambda _{a, i} := 0\) for all \(i \in [k_a] \, \setminus \, \{i_0, i_0 + 1 \}\); then, \((x_a^*, \pi _v^*, \lambda _a)_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) fulfils (10b–g). Hence, \(\left( x_a^{*}, \pi _v^{*} \right) _{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]} \in X_D\). Therefore, all optimal solutions of Model E are feasible for Model D, i.e. \(\left( x_a^{*}, \pi _v^{*} \right) _{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]} \in X_D\).
From (11d), we have \(c_a^* = s_{a,i_0} y_a^* + t_{a, i_0}\). However, rearranging \(y_a^{*} = \lambda _{a,i_0} D_{a,i_0}^{- \beta } + \lambda _{a,i_0 +1} D_{a, i_0 +1}^{- \beta }\) as in (12) to (14) yields \(\lambda _{a,i_0} c_{a,i_0} + \lambda _{a,i_0+1} c_{a,i_0+1} = s_{a,i_0} y_a^* + t_{a, i_0}\); hence, \(\sum _{a \in {\mathcal {A}}} L_a \ (\lambda _{a,i_0} c_{a, i_0} + \lambda _{a,i_0 + 1} c_{a, i_0 +1}) = \sum _{a \in {\mathcal {A}}} L_a c^*_{a}\). \(\square\)
4.4 Comparison of relaxations
In this section, we consider the continuous relaxations of the discrete models. As solvers relax the combinatorial part during the solution procedure, the tightness of the continuous relaxation plays a major role for the performance of the models. To this end, we use the standard projection to map their feasible regions onto the space of their common variables, i.e. onto the \(\left( (\pi _v, x_{a})_{v \in \mathcal{V}, a \in \mathcal{A}} \right)\)-space: In the following, we denote the feasible regions of the continuous relaxations of the discrete Models A, B and C by \(X_{\text {A, rel}}\) , \(X_{\text {B, rel}}\) and \(X_{\text {C, rel}}\), respectively (Fig. 2).
Relation of feasible regions. The highlighted relations in grey are proved as propositions. The other relations \(X_{A} \subseteq X_{A,rel}\), \(X_{C} \subseteq X_{\text {C, rel}}\) and \(X_{B} \subseteq X_{\text {B, rel}}\) are the canonical continuous relaxations of the corresponding discrete models. Proposition 2 also implies \(X_{C}, X_{B} \subseteq X_{A,rel}\). Since \(X_D = X_{A,rel}\), the split-pipe model can be seen as a relaxation of Models A, B and C
Proposition 4
Let \(\alpha \ne 1\). Then, the following relationships hold for the continuous relaxation of Models A, B and C:
-
1.
\(X_{A,rel} \subseteq X_{\text {C, rel}}\) but \(X_{\text {C, rel}} \ne X_{A,rel}\),
-
2.
\(X_{A,rel} \nsubseteq X_{\text {B, rel}}\) and \(X_{\text {B, rel}} \nsubseteq X_{A,rel}\),
-
3.
\(X_{\text {C,rel}} \nsubseteq X_{\text {B, rel}}\) and \(X_{\text {B, rel}} \nsubseteq X_{\text {C,rel}}\).
Proof
“\(\underline{X_{A,rel} \subseteq X_{\text {C, rel}}}\)”:
Let \(({\tilde{x}}_a, {\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i} )_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) be a solution to the continuous relaxation of Model A, i.e. \(({\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i} )_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]} \in X_{A,rel}\). We show that it can be transformed to a point in \(X_{\text {C, rel}}\). First, \(({\tilde{x}}_a, {\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i} )_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) satisfy Eqs. (9e–g) and (9i). By defining
the potential loss constraint (9c) and the bounds of \(\Delta _{a,i}\) (9h) are satisfied. With \(M_{a,i}^{(1)} = \Phi (D_{a,i}, {\underline{x}}_a)\), \(M_{a,i}^{(2)} = \Phi (D_{a,i}, {\overline{x}}_a)\), the big M-formulation (9d) holds by construction. Equation (9b) also holds, since
hence, \(({\tilde{x}}_a, {\tilde{\pi }}_v, {\tilde{\lambda }}_{a,i}, \Delta _{a,i} )_{a \in \mathcal{A}, v \in \mathcal{V}, i \in [k_a]}\) is a solution of the continuous relaxation of Model C, i.e. \(X_{A,rel} \subseteq X_{\text {C, rel}}\).
The remaining relations between the continuous relaxations of the discrete models are shown by counter examples. Throughout we consider a single pipe \(a = (v,w)\) with \(L_a R_a = 1, D_{a,0}^\beta = 1, D_{a,1}^\beta = 2\) for given \(\alpha > 0\) and \(\beta > 0\).
“\(\underline{X_{\text {C, rel}} \nsubseteq X_{A,rel} \; \text {and} \; X_{\text {B, rel}} \nsubseteq X_{A,rel}}\)”:
Let \(b_v = \root \alpha \of {100}\), \(b_w = -\root \alpha \of {100}\) and \(\pi _v, \pi _w \in [0, 3600]\) be given. Then, \((\lambda _{a,0},\lambda _{a,1}\), \(\pi _v, \pi _w) := (0.5, 0.5, 3600, 3500) \in X_{B,rel}, X_{C,rel}\), where the the remaining variables of Model B are given by e.g. \(x_{a,0}^+ = \root \alpha \of {100}, x_{a,1}^+ = 0, x_{a,0}^- = 0, x_{a,1}^- = 0, z_a = 1\), \(\Delta _{a,0}^+ = 100, \Delta _{a,1}^+ = 0, \Delta _{a,0}^- = 0, \Delta _{a,1}^- = 0\), and of Model C by \(x_{a} = \root \alpha \of {100}\) and \(\Delta _{a,0} = 100, \Delta _{a,1} = 0\). However, \((\lambda _{a,0},\lambda _{a,1}, \pi _v, \pi _w) := (0.5, 0.5, 3600, 3500) \notin X_D\), where the remaining variable \(x_{a} = \root \alpha \of {100}\) is uniquely determined by Eq. (7d), which contradicts Eq. (7b), i.e.
\(\pi _v - \pi _w = 100 \ne 0.75 \left(\root \alpha \of {100}\right)^{\alpha } = \sum _{i=0}^{k_a} (\lambda _{a,i} / D_{a,i}^\beta ) {{\,\mathrm{sgn}\,}}(x_a) {|}{x_a}{|}^{\alpha }\).
“\(\underline{X_{A,rel} \nsubseteq X_{\text {B, rel}} \; \text {and} \; X_{\text {C, rel}} \nsubseteq X_{\text {B, rel}}}\)”:
Now slightly change the above example to \(b_v = 1000 = - b_w\). Moreover, we set \({\overline{x}}_a = 1000\). Then \((\lambda _{a,0},\lambda _{a,1},\) \(\pi _v, \pi _w) := (0.5, 0.5, 3/4 \times 1000^{\alpha }, 0) \in X_{A,rel}, X_{C,rel}\), where the remaining variables of the continuous relaxation of Model A are given by \(x_{a} = 1000\) and of the continuous relaxation of Model C by \(\Delta _{a,0} = 1/2 \times 1000^{\alpha }\), \(\Delta _{a,1} = 1/4 \times 1000^{\alpha }\) and \(x_{a} = 1000\). However, \((\lambda_{a,0},\lambda_{a,1},\pi_v, \pi_w) = (0.5, 0.5, 0.75 \times 1000^{\alpha}, 0) \notin X_{\text{B, rel}}\), because it follows from Eqs. (8e–f) that \(x_{a,0}^+ = x_{a,1}^+ = 500 = 0.5 \, \overline{x}_a\) and \(x_{a,0}^- = x_{a,1}^- =0\), and from (8c, g) it follows that \(z_a = 0.5\) and \(\Delta_{a,0}^+ = 500^{\alpha}\) and \(\Delta_{a,1}^+ = 0.5 \times 500^{\alpha}\) and \(\Delta_{a,0}^-, \Delta_{a,1}^- = 0\). With these values, (8b) implies \(\sum \nolimits _{{i}\in{[k_a]}} (\Delta_{a,i}^+ - \Delta_{a,i}^-) = 3/2 \times 500^{\alpha} \ne 3/4 \times 1000^{\alpha } = \pi _v - \pi _w \,\text {for} \,\alpha \ne 1.\)
“\(\underline{X_{\text {B, rel}} \nsubseteq X_{\text {C, rel}}}\)”:
We now choose \(b_v = \root \alpha \of {75} = - b_w\) and set \(\underline{x}_a > 0\). Then \((\lambda _{a,0}, \lambda _{a,1}, \pi _v, \pi _w,\) \(x_{a,0}^+, x_{a,1}^+, x_{a,0}^-, x_{a,1}^-, z_a,\) \(\Delta _{a,0}^+ , \Delta _{a,1}^+, \Delta _{a,0}^-, \Delta _{a,1}^-):= (0.75,0.25, 3600, 3525, \root \alpha \of {75}, 0, 0, 0, 1,\) \(75, 0, 0, 0) \in X_{\text {B, rel}}\). However, \((\lambda_{a,0}, \lambda_{a,1}, \pi_v, \pi_w) = (0.75,0.25, 3600, 3525) \notin X_{\text{C, rel}}\), since \(x_a = \root \alpha \of {75}\) follows uniquely from (9f), which together with Eq. (9b) leads to \(\Delta_{a,0} + 2 \Delta_{a,1} = 75\). Moreover, from Eq. (9d) it follows that \(\Delta_{a,0}, \Delta_{a,1} > 0\), since \(\lambda_{a,0}, \lambda_{a,1} > 0\) and \(M_{a,i}^{(1)} = \Phi (D_{a,i}, \underline{x}_a) > 0\) holds by virtue of \(\underline{x}_a > 0\). But then, Eqs. (9b) and (9c) cannot be satisfied simultaneously, because (9c) yields \(\Delta_{a,0} + \Delta_{a,1} = 75\).
5 Multi-scenario modelling
Expansion planning is a long-lasting process that involves high investment costs. Hence, practitioners seek network extensions that enable feasible operations even for different possible future demand scenarios. In practice, this process is typically approached as follows: Firstly operators typically identify multiple “bottleneck scenarios” that stress the network. Afterwards, they run simulations in order to decide on network expansions that ideally resolve all bottlenecks at once.
For the problem of finding optimal gas network extensions for multiple demand scenarios, a model formulation and an algorithmic solution approach based on scenario decomposition has already been developed in the literature, see e.g. Schweiger (2016); Schweiger and Liers (2018). While these authors consider general new pipelines as extension candidates, we focus on loops in this paper. More precisely, we extend the formulations of the Models A, D and E from Sects. 3 and 4 to the case of multiple scenarios, which we simply denote as Models A-MS, D-MS and E-MS. These three models have been chosen on the basis of our computational results in the single-scenario case (see Sects. 6.2–6.4).
It is well known that network expansions might worsen the flow situation and might allow for less network throughput or might render previously feasible instances as infeasible. This phenomenon is known as Braess’s paradox (Braess 1968) and has been shown to appear in nonlinear potential-driven networks, too, see Calvert and Keady (1993). To prevent the Braess phenomenon, most authors in the literature equip pipeline extensions with valves to allow for the flow and pressure patterns that were possible prior to the extension. Similarly, our modelling approaches in the following are equipped with binary variables that enable the model to switch off loops in individual scenarios.
5.1 Discrete looping with length variables (model A-MS)
The expansion planning problem for multiple demand scenarios \(\omega \in \Omega\) concerns the cost-minimal selection of pipes to be looped such that the corresponding network enables feasible operation for each single scenario involved. For this purpose, we present a two-stage stochastic program, where the first-stage variables \(\lambda _{a,i}\) denote whether extensions are built. All remaining variables of the original model A have become scenario-dependent recourse variables. As we would like to allow the model to switch off loops in individual scenarios, we modify the potential loss function to \(\pi _{v,\omega } - \pi _{w,\omega } = L_{a} R_a \left( \lambda _{a,\omega } \sum _{i=0}^{k_a} \lambda _{a,i} D_{a,i}^{-\beta } + (1- \lambda _{a,\omega } )D_{a,0}^{-\beta } \right) {{\,\mathrm{sgn}\,}}(x_{a,\omega }) {|}{x_{a,\omega } }{|}^{\alpha }\), where the newly introduced binary variable \(\lambda _{a,\omega }\) indicates whether a loop extension of pipe \(a \in {\mathcal {A}}\) is used in scenario \(\omega \in \Omega\). This happens if \(\lambda _{a,\omega } = 1\) and \(\lambda _{a,i} > 0\) for some \(i \in [k_a] \setminus \{0\}\) is satisfied. In the case that an extension is not used, i.e. \(\lambda _{a,\omega } = 0\), the potential loss function reduces to its original form as given in Eq. (7b). Moreover, to avoid the resulting nonlinear product of binary variables, we introduce a continuous variable \(\gamma _{a,\omega } = \lambda _{a,\omega } \sum _{i=0}^{k_a} \lambda _{a,i} D_{a,i}^{-\beta }\) and linearize the product by virtue of Constraints (17–f).
5.2 Split-pipe looping with length variables (model D-MS)
As it is the case with Models A and D, the following split-pipe looping model D-MS is identical to the discrete Model A-MS with the only difference being that the variables \(\lambda _{a,i} \in \{0,1 \}\) are relaxed to continuous variables \(\lambda _{a,i} \in [0,1]\).
5.3 Split-pipe looping with efficient-frontier constraints (model E-MS)
In our extension of Model E to a two-stage stochastic program, the first-stage variables are given by the \(y_{a}\)-variables, whereas the remaining variables are scenario-dependent second-stage variables. To indicate whether a loop extension of pipe \(a \in {\mathcal {A}}\) is used in scenario \(\omega \in \Omega\) and to represent the corresponding impact of the loop extension on the pressure loss, we introduce a binary variable \(\lambda _{a,\omega }\) and a continuous variable \(y_{a,\omega }\). Then, Constraints (19j–m) guarantee that \(y_{a,\omega } = y_a\) holds if the loop extension of pipe a is used, i.e. if \(\lambda _{a,\omega } = 1\). Accordingly, if the loop extension is not used, i.e. \(\lambda _{a,\omega } = 0\), then \(y_{a,\omega } = {\overline{y}}_a\) is satisfied, which guarantees that the pressure loss Constraint (19b) reduces to the original form as given in (11b).
The model then reads as follows:
6 Computational study
In this computational study, we first investigate the performance of the discrete models and then compare the split-pipe models. In a third step, we analyse the difference in the performance of the discrete versus the split-pipe models. Especially from the point of view of practical applications, it is important to see whether the split-pipe approach can lead to significant cost-savings when compared to the discrete looping approach. Finally, we evaluate the models in multiple-scenario cases. As this paper is primarily focussed on providing useful results for practitioners, all test instances used in the following have been designed to be as close to real-world scenarios as possible. This includes, for example, the network data, the cost function for loops and the number of parallel loops and scenarios considered.
6.1 Experimental setup
The experiments were conducted on a cluster of 64-bit Intel Xeon CPU E5-2670 v2 CPUs at 2.5GHz with 25MB cache and 128GB main memory. In order to safeguard against a potential mutual slowdown of parallel processes, we bind the processes to specific cores and run at most 4 jobs per node. We solve the split-pipe and discrete expansion planning problems to global optimality using the nonconvex MINLP solver SCIP version 5.0.1 with CPLEX 12.7.1 as LP solver and Ipopt 3.12.6 as NLP solver. In all experiments, we ran SCIP with default settings and set a time limit of four hours. This time limit seems reasonable for practical purposes since expansion planning is carried out with a long-term perspective and decisions on short notice are not required as in daily operations. We solve the instances to \(\epsilon\)-global optimality with a gap limit of \(\epsilon = 10^{-4}\). As performance measure, we use the number of solved instances, the runtime and the number of Branch-and-Bound nodes. In order to reduce the impact of very easy or hard instances in the mean values, we report the shifted geometric mean \((\root n \of { \prod (t_i + s) } -s)\) for values \(t_1, ..., t_n\) with a shift of \(s = 10\) for the runtime in [sec] and \(s = 100\) for the number of branch and bound nodes. Additionally, we report the arithmetic mean of the computation time to indicate the time required for applications in practice.
The computational study was carried out on different data sets that vary in size and structure and are based on two major types of potential-driven networks: gas networks and water networks. As the starting point, we used the Belgian gas network from the GAMS model library, which has a simple, almost tree-shaped structure (with the only exception being 5 arcs that have 2 parallel pipelines) and is of a rather smaller size. We continued our computational experiments on the GasLib-40 network (Schmidt et al. 2017), to test the models on a network that is considerably larger and more complex. As the basis for our water instances, the well-known New York network (library of instances at the operations research group in Bologna) was employed. Finally, to focus not only on computational difficulties that arise from the size of the network, we systematically investigate the impact of cycles on the model performance and generated extended versions of the Belgian networks by adding 2 to 10 additional arcs. The details about different networks are found in Table 1 and Fig. 3. We note that originally the Belgian and the GasLib-40 network contain a small number of compressor stations the treatment of which is outside the scope of this paper. In the case of the Belgian network, we used data available in the GAMS model library to model these as normal pipelines, while arcs representing compressor stations had to be contracted in the case of the GasLib-40 network due to lack of available data.
For each network, we generated instances that cover a wide range of possible network demands. It is known in practice that increasing the overall network demand typically results in more complex transport situations that stress the networks. Practitioners therefore use the so-called transport moment to detect severe demand situations by approximating the transport load in the network (cf. Hiller et al. 2018). It can even be observed in many computational experiments that higher network demands tend to slow down the model performance, provided that the transport situations are not trivially infeasible. Hence, to test the performance of the models in diverse and severe situations, we consider different demand loads that represent the whole spectrum from “easier” instances with lower demands up to “harder” instances with higher demands for each network.
Throughout, we randomly generated scenarios for each given total network demand \({{\,\mathrm{{\mathcal {B}}}\,}}\) according to a random uniform distribution of the demand at sources and sinks. More precisely speaking, for all sources and for all sinks we generated uniformly distributed independent random numbers \(r_v \in [0,1)\) and then normalized the source and sink flows to calculate the demand as \({\mathcal {X}}_v = {{\,\mathrm{{\mathcal {B}}}\,}}r_v / \sum _{v \in W} r_v\). For each given total demand and for each network, we generated 500 scenarios because preliminary tests indicated that this sample size leads to sufficiently stable results for the given distribution with respect to model performances. Including preliminary tests, we calculated about 300000 instances. Due to this large number and variety of instances, we can assume that the results provide us with a representative picture for model comparisons. Here, we present a selection of 5500 different demand scenarios and a total of 40000 instances that represent the major effects observed (for further results see Lenz 2021).
Throughout the data sets, the expansion capacities of all instances are given by the diameter candidates \(\{D_{a,0}, \ldots, D_{a,k_a}\}\) resulting from at most triple loops, i.e. in the discrete case each arc of the network may consist of up to three pipelines in parallel, while in the split-pipe case up to three parallel pipelines are possible for each arc segment.
In our experiments, we use a quadratic cost function as this is the most common form in practical applications, (see e.g. De Wolf and Smeers 1996; Parker 2005). The data points for the cost function used for the gas related instances are shown on the left in Fig. 1 and were provided to us by practitioners, and for the water instances, it was part of the New York network data. (Cost functions from linear to cubic can also be found in the literature, see Osiadacz and Górecki (1995) and Babonneau et al. (2012), for example, and were used as part of our preliminary tests.)
Summarizing, with the maximum number of parallel loops fixed to 3 and the quadratic cost function being given, one instance is characterized by the choice of network and demand scenario.
The computational results for the comparison of the discrete models are found in Tables 2, 3, 4 and 5 and for the comparison of the split-pipe models in Tables 6, 7 and 8. The tables are structured as follows: each column contains the results of 500 instances with the only variable parameter being the total network demand \({{\,\mathrm{{\mathcal {B}}}\,}}\). The computational results within a column are grouped into three categories: (1) In the section All instances, we provide a summary of the results of all 500 instances and indicate the number of solved instances (\(\sum\) # solved), which includes the optimal solved instances (# opt) and the instances that were detected as infeasible (# infeas). Moreover, we state the number of instances, where at least one feasible solution was found within the time limit (# sol found), no matter whether optimality was shown for this solution. For all remaining instances, no feasible solution was found within the time limit nor was infeasibility proved. (2) The section All opt reports data for all instances for which all models under comparison have found an optimal solution. (3) In the section Only opt by, we compare the models with respect to the instances that they alone were able to solve to global optimality.
In all three cases, we report computational time by means of the shifted geometric mean (sgm) and the arithmetic mean (amm). For instances that are solved to optimality by all models, we additionally present the sgm of the number of Branch-and-Bound nodes.
6.2 Comparison of discrete models (Models A, B and C)
We begin our computational experiments with the Belgian gas network, which has frequently been used as a tool in research about network optimization (see e.g. De Wolf and Smeers (1996), De Wolf and Smeers (2000) and Babonneau et al. (2012)). Our computational results for the network are found in Table 2. Demands are given in \(10^6 \; m^3 / day\) and computational time in seconds. We first consider the performance of our models as depending on the demand. For the lowest demand \({{\,\mathrm{{\mathcal {B}}}\,}}= 100\) about all instances are solved to optimality within a couple of minutes. With increasing demand, computational time increases and the number of instances solved to optimality decreases. However, at a demand of \({{\,\mathrm{{\mathcal {B}}}\,}}= 1000\), we have reached a point where an optimum has been found for less than a quarter of the instances and more of 60 % of the instances are detected as infeasible. As a consequence of the high number of infeasibilities, the number of solved instances has increased and computational time decreased. This pattern suggests that the range of demand used here is sufficient to obtain an overview of the general behaviour of the models and that it is not necessary to test the models for a demand of less than \({{\,\mathrm{{\mathcal {B}}}\,}}= 100\) and greater than \({{\,\mathrm{{\mathcal {B}}}\,}}= 1000\). Due to this typical pattern, which was frequently observed also during our preliminary computational experiments, we will generally use a test range from a low demand to a high demand with a large number of infeasibilities.
We observe that, with respect to the sgm, Model A is the fastest model throughout, up to a factor 4.3 faster than Model B for a demand of \({{\,\mathrm{{\mathcal {B}}}\,}}= 100\), while B is the fastest with respect to the amm. This is due to the fact that Model B has a high number of instances that were solved fast (see e.g. those instances that were only solved by B). Model B also solves the largest number of instances. We note though that here Model B does not stand out with respect to the infeasible instances discovered and instances for which a feasible solution has been found.
Let us remark in passing that during our preliminary tests of the two models mentioned in Sect. 3.4, which were carried out on the rather simple Belgian network, the model in Humpola (2014) ran into the time limit at a demand of \({{\,\mathrm{{\mathcal {B}}}\,}}= 200\) with about 2/3 of all instances, while the model in Borraz-Sánchez et al. (2016) exceeded the time limit in all cases for the same demand. (In contrast with this, the three models considered here ran into the time limit only with 0.8% to 6.6% of the same instances.)
We now turn our attention to GasLib-40 (see Table 3). Again we can see that Model A is the fastest model, with B only having an advantage at a demand of \({{\,\mathrm{{\mathcal {B}}}\,}}= 1000\) with respect to the amm. This time Model A also tends to be better with respect to the number of instances solved. Finally note, that a demand of \({{\,\mathrm{{\mathcal {B}}}\,}}= 500\) is too difficult for all three models, i.e. for unfavourable demand situations we have reached the limits of what is computational tractable. (But obviously, this does not impply that expansion problems on more complex networks cannot be solved for favourable demand situations.)
The famous New York network is of particular interest for the capacity expansion problem as it is the only network in the water library where the arcs are already laid out with given diameters. Introduced by Schaake and Lai (1969), this instances has been used extensively (see e.g. Quindry et al. (1981), Bhave (1985), Bragalli et al. (2012)). On this network, Model B clearly performs best, both regarding the number of instances solved and the runtime (Table 4). We note that we have instances here where Model C performs better than Model A in terms of both solved instances and runtime (\({{\,\mathrm{{\mathcal {B}}}\,}}= 200 \; m^3/s\)).
It is well known that optimization problems on potential-driven networks get more difficult to solve the more cycles they contain because the existence of cycles leads to more complex patterns of flow directions (cf. the literature review in Shiono and Suzuki (2016)). To systematically test our models also with respect to this type of difficulty, we successively increase the circuit rank by adding up to ten new pipelines to the Belgian network, which results in five new networks Belgium + (2, 4, 6, 8, 10) arcs, see Fig. 3. Here, the intention was to add arcs that connect different regions of the network and have a high impact on the network topology. For the new pipelines we use in our data set an original diameter \(D_{a,0}\) that is equal to the average diameter of the existing pipelines in the network and use moderate demand scenarios with \({{\,\mathrm{{\mathcal {B}}}\,}}= 200\).
We observe (see Table 5) that for increasing circuit rank the number of instances solved to optimality at first decreases and then increases again for Models A and C, while it continues to decrease for Model B. A similar pattern applies with respect to computational time, where the runtime at first increases for Models A and C and then decreases for the instances with 6 or more additional arcs, while the runtime of Model B increases nearly throughout. This leads to a situation where Model A turns out to have the best sgm runtime for all circuit ranks, B solves the most instances for smaller circuit ranks, and A solves the most instances for larger circuit ranks. Finally, while Model C shows poor results for small circuit ranks, it gains ground with increasing circuit ranks and performs second best for the instances with Belgium + 10 arcs.
In sum, we can state that overall Models A and B perform better than Model C, with Model A clearly outperforming Model B on problems with a higher circuit rank (including GasLib-40). The performance of Model C may partly be a consequence of the fact that Model A, as we have shown in Sect. 4.4, has a tighter relaxation than Model C, even though there are a smaller number of entire data sets and a larger number of individual instances where Model C outperforms both Model A and Model B, in particular instances with a higher circuit rank. Model C is therefore a valuable alternative in cases where Models A and B require too much computational time to prove infeasibility or solve an instance to optimality.
6.3 Comparison of split-pipe models (models D and E)
Again we start with the Belgian network (Table 6) and proceed from easily solved instances to scenarios with a large number of infeasible instances. It turns out that both models solve a comparable number of instances, with the new Model E being somewhat faster. It is worth noting that for a demand of \({{\,\mathrm{{\mathcal {B}}}\,}}= 500\), i.e. for more difficult instances, 10% of the instances are solved to optimality by only one of the two models, i.e. in this case both models complement each other well.
To compare the performance on gas networks of larger sizes with a more complex cyclic structure, we turn to the GasLib-40 network (Table 7 on the left). Here, Model E performs clearly better: it solves up to 11 % more instances (demand \({{\,\mathrm{{\mathcal {B}}}\,}}= 100, 1000\)) and requires less runtime (up to a factor of 2.5 in the case of \({{\,\mathrm{{\mathcal {B}}}\,}}= 50\)). To further test the performance of the split-pipe models, we consider the New York water network again (Table 7 on the right). Here the results are balanced: both models solve the majority of instances in at most 3 s (sgm).
Finally, we investigate the performance of the models for increasing circuit rank. We observe (Table 8) that our novel Model E consistently outperforms D, with the ratio of the runtimes of the model becoming the more favourable for E the higher the circuit rank, up to a factor of 13.9 for 10 additional arcs. Similarly, Model E performs significantly better with respect to the number of solved instances, with the best ratios of solved instances reached at 16.2 for Belgium + 8 arcs and 10.0 for Belgium + 10 arcs.
On the basis of our computational experiments for the split-pipe case, we can clearly recommend the use of our novel model instead of the model from the literature, particularly for networks with a more complex cyclic structure, even though one will, of course, encounter instances where the other model is more successful.
6.4 Comparison of discrete and split-pipe models
Let us now compare the discrete with the split-pipe approaches. As mentioned in the introduction, this is the first time that such a comparison is carried out for networks of a practically relevant size and complexity. Of course, one may expect that the split-pipe model will perform better on average, but as our computational experiments show (compare the results for Belgium +4, +6, and +8 arcs in Tables 5 and 8, for example), there are data sets where the discrete approach yields more optimal solutions within the time limit of 4 hours than the split-pipe approach. For this reason it is unclear what size the performance gap may actually take.
In the following, we will look at two criteria: (a) potential cost savings and (b) computational time.
Concerning cost savings, Table 9 shows the average gain of the best known solutions of the split-pipe models over the discrete models. Here, we consider only those instances where an expansion actually takes place and where either at least one split-pipe and at least one discrete model have been solved to optimality (column Optimal) or where both approaches provide at least one solution (column Feasible). For these instances, we then consider the average gain of the best known split-pipe over the best-known discrete one. The column Feasible additionally shows the percentage of instances where the best-known solution is provided by the split-pipe models.
As Table 9 demonstrates, the split-pipe approach yields cost savings on all data sets. While the results for the comparably simple networks of Belgium and New York are rather low, the benefit of realizing a split-pipe solution can be considerable for networks with a complex cyclical structure. Moreover, Fig. 4 shows that for all feasible instances with non-zero objective function value, the best solutions were practically always found by the split-pipe models, with our novel Model E delivering the best results. Even more, further analysis of the data presented in Tables 2, 3, 4, 5, 6, 7 and 8 reveals that the split-pipe models optimally solve or detect (in)feasibility in all cases except 1 (Model E) or 2 (Model D) instances, whereas the number of instances with unknown status is much higher for the discrete models, namely 318 (Model A), 578 (Model B) and 348 (Model C) out of the 8000 instances we have calculated per model. Therefore, in view of the much larger number of feasible solutions by the split-pipe models, the economic benefit of these models goes well beyond the cost savings and the percentage of instances depicted in Table 9 and Fig. 4.
To compare the overall runtime performance of all discrete and split-pipe models, we use a performance profile (Dolan and Moré (2002)). It is based on the performance ratio, i.e. the runtime of a particular data set with the model under consideration divided by the best runtime for that data set with any of the five models. The performance profile describes on the y-axis the fraction of instances among all solved (i.e. optimal or infeasible) instances that the model could solve with a performance ratio of up to the corresponding number on the x-axis. Clearly, models are to be preferred when their profile shows higher y-values for fixed x-values and lower x-values for fixed y-values. To exclude trivial cases, we disregard instances that were not solved by any model and those that were solved by all models in less than 1 s CPU time.
As we can see, the runtime of Model E dominates the runtime of all other models across the spectrum of performance ratios (Fig. 5). Further insights about the model performances for different data sets are gathered from Fig. 6, which depicts the sgm of the runtime of all instances for different network types and confirms the dominance of the split-pipe models. Again Model E turns out to perform best.
6.5 Outlook: comparison of multi-scenario models
To conclude our computational experiments and provide an outlook on potential future applications, we study the behaviour of Models A, D and E in the multiple-scenario case (Models A-MS, D-MS and E-MS). Models B and C have been left out here due to their comparably weak performance as seen in Sect. 6.2, 6.4. In particular, we present the test results of the multiple-scenario models on the (original) Belgian network and on its extended versions with additional arcs (circuit rank). These networks have been chosen because we have seen in the previous sections that on these networks all three models were able to find feasible solutions for a similar number of instances and the networks are sufficiently small to suggest that the models may be able to deal with the additional complexity resulting from the multiple-scenario setting.
When evaluating potential pipeline expansions, practitioners typically look at about 5–10 scenarios. For this reason, all instances considered here will consist of 10 scenarios each. Each instance was constructed by combining 10 of the demand scenarios previously used in the single-scenario case in Sects. 6.2, 6.3. More precisely, for the Belgian network each of the 125 instances used here has been composed of two scenarios with a total demand of \({{\,\mathrm{{\mathcal {B}}}\,}}= 100\), three scenarios with \({{\,\mathrm{{\mathcal {B}}}\,}}=200\), three scenarios with \({{\,\mathrm{{\mathcal {B}}}\,}}=500\), and two scenarios with \({{\,\mathrm{{\mathcal {B}}}\,}}=1000\). In the circuit rank experiment, the previously 500 demand scenarios with \({{\,\mathrm{{\mathcal {B}}}\,}}=200\) in Sects. 6.2–6.3 were grouped into 50 multiple-scenario instances with 10 demand scenarios each. As preliminary computational tests showed that the additional complexity of the multiple-scenario setting led to a rather small number of instances for which the models could find feasible solutions, we will provide in the following the results of computational experiments where the demand data from Sects. 6.2–6.3 was scaled down by a factor of 0.4 for all instances. (Note though that this does not mean that our demand sets are just scaled versions of each other. The data sets used in the previous sections and here were generated independently for each given total network demand \({{\,\mathrm{{\mathcal {B}}}\,}}\).)
Let us first look at the instances on the Belgian network. As shown in Table 10 none of the models was able to solve any of the 125 instances to optimality or prove infeasibility. Clearly, the additional complexity of the multiple-scenario setting is taking its toll and we can only evaluate the models by looking at the instances for which feasible solutions have been found. Here Model E-MS takes the lead by finding solutions for 119 out of 125 instances, with 68 of these being better than the solutions found by the other two models. Model D-MS has found the best solution for another 60 instances, while the discrete Model A-MS can only offer best solutions for 3 instances.
A similar pattern can be observed in the case of the circuit rank experiment (Table 11) where Model E-MS was able to provide solutions for all but 2 instances of the 300 \(=\) 6 \(\times\) 50 instances, while the next best Model D did so for all but 22 instances. Moreover, again Model E turns out to have found the largest number of best solutions among the three models, namely for 245 out of the 300 instances. This time, however, in contrast with the situation in the previous experiment (Table 10), optimal solutions were found, and interestingly so mainly by Model A. It should be noted though that there are only 3 out of 300 instances for which Model A has found a better solution than the two split-pipe models, which again demonstrates the superiority of the split-pipe approach.
Even though the split-pipe models cannot be solved to proven optimality, the authors of the present paper strongly assume on the basis of their experience with solving capacity expansion models that a considerable number of instances is actually solved to optimality by both D-MS and E-MS. This assumption rests on the observations that (a) we know from the discrete model in the case of several instances that the optimal solution to the split-pipe models must include network extensions and (b) when trying to solve the split-pipe models the solver often makes no progress on the dual bound, while showing strong performance on the primal side of the algorithm that (c) frequently results in solutions to the split-pipe models that are identical. Accordingly, the feasible solutions found by D-MS and E-MS may very well be highly relevant to practitioners.
Summing up, our computational experiments in this section show that the multiple-scenario case reaches the limits of what can currently be achieved by solving models with general-purpose solvers. In view of both the algorithmic and the hardware progress made in the previous decades, however, these limits are not unlikely to be overcome in the near future, in particular as we have reasons to assume, as explained above, that the solutions provided by Models E and D are often not too far from optimality. Further, our results suggest that for finding feasible solutions the split-pipe model E-MS should be used in conjunction with D-MS.
6.6 Recommendations
To conclude this section, our computational experiments suggest the following recommendations for practitioners:
-
1.
In view of the advantages of the split-pipe approach discussed in the previous subsection, practitioners should use the split-pipe approach whenever possible.
-
2.
Our novel Model E should be the model of choice as it leads to more instances that are solved, to more instances for which feasible solutions are found, to a higher percentage of instances with a better objective function value and cost savings, and performs better with respect to computational time.
-
3.
When the split-pipe approach is not possible, Models A or B are likely to be the most useful.
-
4.
Among these two models, Model A should be tried out first on networks with a more complex cyclical structure.
-
5.
Models C and D may be useful complements when dealing with instances that happen to be particularly hard for the other models.
-
6.
The case of optimizing over multiple scenarios reaches the limits of what is currently achievable with state-of-the-art solvers, but Model E in conjunction with Model D may be useful for finding reasonably good feasible solutions in some applications.
7 Conclusion
We studied the problem of capacity expansion of potential-driven networks using loops. We showed properties of the looping problem, such as its nonconvexity in the general case, and, building on an existing method of selecting cost-minimal loop diameters a priori, we presented a model reduction approach for multiple loops. On this basis, we introduced new models for both discrete and split-pipe looping and contrasted these with existing models for the looping problem and related problems in the literature, both theoretically and empirically. This was also the first time that discrete and split-pipe approaches were compared for networks of a practically relevant size and complexity. The performance of the models was analysed in an extensive computational study with a large set of demand vectors and diverse networks of different sizes and topologies, including network variations for different circuit ranks, and led to recommendations regarding the use of different models. In particular, our experiments showed that overall our novel Model E outperforms the existing models with respect to computational time, the number of solutions found, the number of instances solved and cost savings. We also provided an outlook for the case of multiple scenarios, thereby reaching the limits of what can currently be achieved with state-of-the art solvers, but further future improvements on both the solver and the hardware side may well overcome these limits.
An interesting avenue for further research would be to improve our split-pipe Model E by generating the efficient frontier dynamically. Instead of adding all constraints for the frontier globally to the model, they could be generated dynamically during the solving process whenever the frontier is violated by the current LP solution. This could drastically reduce the model size, depending on the number of arcs and extreme points of the efficient frontier.
Moreover, while we allowed all arcs to be looped, we could reduce the model size by a heuristic pre-selection of the arcs that are most likely to be looped. Such an approach could gather the pipes that have a higher expected potential loss along the pipe, which could be determined by simple auxiliary models.
Finally, further work could also include loop expansion planning in the context of time-dynamic commodity transport.
References
Alperovits E, Shamir U (1977) Design of optimal water distribution systems. Water Resour Res 13(6):885–900
André J, Bonnans F, Cornibert L (2009) Optimization of capacity expansion planning for gas transportation networks. Eur J Oper Res 197(3):1019–1027
André J, Auray S, Brac J, De Wolf D, Maisonnier G, Ould-Sidi MM, Simonnet A (2013) Design and dimensioning of hydrogen transmission pipeline networks. Eur J Oper Res 229(1):239–251
Babonneau F, Nesterov Y, Vial JP (2012) Design and operations of gas transmission networks. Oper Res 60(1):34–47
Balas E (1985) Disjunctive programming and a hierarchy of relaxations for discrete optimization problems. SIAM J Algebraic Discrete Methods 6(3):466–486
Bhaskaran S, Salzborn FJ (1979a) Optimal design of gas pipeline networks. J Oper Res Soc 30(12):1047–1060
Bhaskaran S, Salzborn FJ (1979b) Optimal diameter assignment for gas pipeline networks. ANZIAM J 21(2):129–144
Bhave PR (1985) Optimal expansion of water distribution systems. J Environ Eng 111(2):177–197
Birkhoff G, Diaz JB (1956) Non-linear network problems. Q Appl Math 13(4):431–443
Borraz-Sánchez C, Bent R, Backhaus S, Hijazi H, Hentenryck PV (2016) Convex relaxations for gas expansion planning. INFORMS J Comput 28(4):645–656
Boyd ID, Surry PD, Radcliffe NJ (1994) Constrained gas network pipe sizing with genetic algorithms. Tech. Rep. EPCC-TR94-11, Edinburgh Parallel Computing Centre
Braess D (1968) Über ein Paradoxon aus der Verkehrsplanung. Unternehmensforschung 12(1):258–268
Bragalli C, DAmbrosio C, Lee J, Lodi A, Toth P (2012) On the optimal design of water distribution networks: a practical minlp approach. Optim Eng 13(2):219–246
Calvert B, Keady G (1993) Braesss paradox and power-law nonlinearities in networks. The ANZIAM J 35(1):1–22. https://doi.org/10.1017/S0334270000007256
Castillo L, González A (1998) Distribution network optimization: finding the most economic solution by using genetic algorithms. Eur J Oper Res 108(3):527–537
Collins M, Cooper L, Helgason R, Kennington LeBlan L (1978) Solving the pipe network analysis problem using optimization techniques. Manag Sci 24(7):747–760
De Wolf D, Smeers Y (1996) Optimal dimensioning of pipe networks with application to gas transmission networks. Oper Res 44(4):596–608
De Wolf D, Smeers Y (2000) The gas transmission problem solved by an extension of the simplex algorithm. Manag Sci 46(11):1454–1465
De Wolf D, Bakhouya B (2012) Optimal dimensioning of pipe networks: the new situation when the distribution and the transportation functions are disconnected. In: Operations Research Proceedings 2011, Springer, pp 369–374
Dolan ED, Moré JJ (2002) Benchmarking optimization software with performance profiles. Math Program 91(2):201–213
Eiger G, Shamir U, Ben-Tal A (1994) Optimal design of water distribution networks. Water Resour Res 30(9):2637–2646
Fasold HG (1999) Technisch/wirtschaftliche Gesichtspunkte bei der Leitungsparallelisierung. Das Gas-und Wasserfach / Gas, Erdgas 140(12):871–876
Fujiwara O, Dey D (1987) Two adjacent pipe diameters at the optimal solution in the water distribution network models. Water Resour Res 23(8):1457–1460
Fujiwara O, Khang DB (1990) A two-phase decomposition method for optimal design of looped water distribution networks. Water Resour Res 26(4):539–549
Gessler J (1985) Pipe network optimization by enumeration. Comput Appl Water Resour. pp 572–581
Gupta I, Hassan MZ, Cook J (1972) Linear programming analysis of a water supply system with multiple supply points. AIIE Trans 4(3):200–204
Hansen CT, Madsen K, Nielsen HB (1991) Optimization of pipe networks. Math Prog 52(1–3):45–58
Hiller B, Koch T, Schewe L, Schwarz R, Schweiger J (2018) A system to evaluate gas network capacities: concepts and implementation. Eur J Oper Res 270(3):797–808
Humpola J (2014) Gas network optimization by minlp. PhD thesis, Technische Universität zu Berlin, https://doi.org/10.14279/depositonce-4255
Jacoby SL (1968) Design of optimal hydraulic networks. J Hydraul Div 94(3):641–662
Karmeli D, Gadish Y, Meyers S (1968) Design of optimal water distribution networks. J Pipeline Division 94(1):1–10
Katz DLV (1959) Handbook of natural gas engineering. McGraw-Hill, New York City
Kessler A, Shamir U (1989) Analysis of the linear programming gradient method for optimal design of water supply networks. Water Resour Res 25(7):1469–1480
Koch T, Hiller B, Pfetsch ME, Schewe (eds) L (2015) Evaluating Gas Network Capacities. SIAM-MOS Series on Optimization. https://doi.org/10.1137/1.9781611973693
Lenz R (2021) Optimization of stationary expansion planning and transient network control by mixed-integer nonlinear programming. PhD thesis, TU Berlin
Liang T (1971) Design conduit system by dynamic programming. J Hydraul Div 97(3):383–393
Maugis J (1977) Etude de réseaux de transport et de distribution de fluide. RAIRO Oper Res Recherche Opérationnelle 11(2):243–248
Osiadacz A, Górecki M (1995) Optimization of pipe sizes for distribution gas network design. In: PSIG Conference, 27th Annual Meeting, Pipeline Simulation Interest Group
Parker N (2005) Using natural gas transmission pipeline costs to estimate hydrogen pipeline costs. Tech. Rep. UCD-ITS-RR-04-3, Institute of Transportation Studies, University of California, Davis
Pietrasz S, Antunes M, Cornibert L (2008) The problem of reinforcing regional gas transmission networks: a performance study of three optimization methods. In: EngOpt 2008: International conference on engineering optimization, pp 1–10
Quindry GE, Liebman JC, Brill ED (1981) Optimization of looped water distribution systems. J Environ Eng Div 107(4):665–679
Raghunathan AU (2013) Global optimization of nonlinear network design. SIAM J Optim 23(1):268–295
Robinius M, Schewe L, Schmidt M, Stolten D, Thürauf J, Welder L (2019) Robust optimal discrete arc sizing for tree-shaped potential networks. Comput Optim Appl 73(3):791–819
Rothfarb B, Frank H, Rosenbaum D, Steiglitz K, Kleitman DJ (1970) Optimal design of offshore natural-gas pipeline systems. Oper Res 18(6):992–1020
Rowell WF, Barnes J (1982) Obtaining the layout of water distribution systems. J Hydraul Div 108(1):137–148
Savic DA, Walters GA (1997) Genetic algorithms for least-cost design of water distribution networks. J Water Resour Plan Manag 123(2):67–77
Schaake JC, Lai FH (1969) Linear programming and dynamic programming application to water distribution network design. MIT Hydrodynamics Laboratory, Department of Civil Engineering, Report No. 116
Schmidt M, Aßmann D, Burlacu R, Humpola J, Joormann I, Kanelakis N, Koch T, Oucherif D, Pfetsch ME, Schewe L, Schwarz R, Sirvent M (2017) Gaslib: a library of gas network instances. Data. https://doi.org/10.3390/data2040040
Schweiger J (2016) Gas network extension planning for multiple demand scenarios. In: Operations Research Proceedings 2014, Springer, pp 539–544
Schweiger J, Liers F (2018) A decomposition approach for optimal gas network extension with a finite set of demand scenarios. Optim Eng 19(2):297–326
Sherali HD, Subramanian S, Loganathan G (2001) Effective relaxations and partitioning schemes for solving water distribution network design problems to global optimality. J Global Optim 19(1):1–26
Shiono N, Suzuki H (2016) Optimal pipe-sizing problem of tree-shaped gas distribution networks. Eur J Oper Res 252(2):550–560
Simpson AR, Dandy GC, Murphy LJ (1994) Genetic algorithms compared to other techniques for pipe optimization. J Water Resour Plan Manag 120(4):423–443
Walski TM, Chase DV, Savic DA (2001) Water distribution modeling. Tech. rep., University of Dayton, Civil and Environmental Engineering and Engineering Mechanics Faculty Publications, Paper 17
Weymouth TR (1912) Problems in natural gas engineering. Trans Am Soc Mech Eng 34(1349):185–231
Yates D, Templeman A, Boffey T (1984) The computational complexity of the problem of determining least capital cost designs for water supply networks. Eng Optim 7(2):143–155
Zhang J, Zhu D (1996) A bilevel programming method for pipe network optimization. SIAM J Optim 6(3):838–857
Acknowledgements
This work was supported by the Research Campus Modal funded by the German Federal Ministry of Education and Research (Fund Number 05M14ZAM) and was carried out within the framework of MATHEON supported by the Einstein Center for Mathematics Berlin (ECMath project MI10 “Acyclic Network Flows“).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lenz, R., Becker, K.H. Optimization of capacity expansion in potential-driven networks including multiple looping: a comparison of modelling approaches. OR Spectrum 44, 179–224 (2022). https://doi.org/10.1007/s00291-021-00648-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00291-021-00648-7