Time-based service constraints for inventory systems with commitment lead time

Abstract

We consider a firm which targets a certain level of customer responsiveness with a minimum operational cost. The firm employs a preorder strategy, in which customers place their orders before their actual need based on a predefined time window called commitment lead time and, in turn, they receive a bonus. The firm aims to determine the optimal control policy, which consists of the optimal commitment lead time and the optimal base-stock level, such that the total operational cost is minimized subject to a time-based service level target. We formulate two time-based service criteria to measure the firm’s responsiveness in terms of average customer waiting time and individual customer waiting time in two constraint optimization models called ACO and CCO, respectively. We derive the exact probability distribution of customer waiting time, and we propose exact and heuristic optimization algorithms to solve the ACO and CCO models. We show that the commitment lead time not only increases the firm’s responsiveness level but also decreases the customers’ maximum waiting time. We find that when the firm targets a high level of responsiveness, the value of commitment lead time is more highlighted. We study multiple interesting extensions with two customer classes, random replenishment lead times and a combined model with two time-based service level targets.

1 Introduction

In competitive markets, good customer service is a crucial factor that helps firms with not only protecting their market positions but also increasing their market shares (Stadtler and Kilger 2008). In the inventory and service management literature, scholars have often studied inventory-related service measures, i.e., they have restricted themselves to service criteria that are related to stock-out probability, e.g., replenishment cycle service level, fill rate, and ready rate. We refer the reader to Silver et al. (2016) for more details on the inventory-related service criteria. In contrast, in management-oriented textbooks on supply chain management, time-based service measures are emphasized (Tempelmeier and Fischer (2010)).

A time-based service measure enables firms to control their inventory levels such that response to customers’ demand within a desired time window is guaranteed. For example, the time-based service measure might be responding to 97% of the customer orders within 2 days. We refer to the length of the response-time window as maximum waiting threshold and the percentage as service level. The maximum waiting threshold is determined based on customers’ waiting tolerance, and the minimum service level is determined by considering other players in the market and inventory-related costs. Shang and Liu (2011) indicate that the minimum service levels for electronics, personal care, and pharmaceutical products are 91%, 88.7%, and 90.2%, respectively.

Considering different parameter settings, scholars have contributed to the literature of time-based service management by finding either the probability distribution of the customer waiting time or the optimal control policies subject to a time-based service constraint. Kruse (1980) is the first to derive the customer waiting time distribution of an inventory system with compound renewal customer demand and constant lead time. For the (R, S) policy, van der Heijden and de Kok (1992) are the first to derive the exact expression for the waiting time distribution assuming compound Poisson demand. Tempelmeier and Fischer (2010) present an approximations for the waiting time in an inventory system with (R, s, Q) control policy. Kiesmüller and de Kok (2006) and de Kok (1993) formulate the lead time shift theorem under very general conditions. These studies assume a certain inventory control policy and determine the customer waiting time. Different from them, we investigate the benefit of having more accurate demand information on customer waiting time.

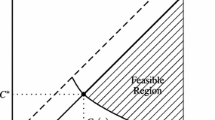
We consider a firm that relies on a preorder strategy. This strategy brings Advance Demand Information (ADI). According to the preorder strategy, customers place orders ahead of their actual need. Hence, they make an implicit agreement with the firm on on-time delivery date. As it is illustrated in Fig. 1, the preorder strategy implies two distinguished due dates: the agreed and actual delivery dates. The former indicates on-time fulfillment date and the latter indicates the date when the customer actually receives the product. The time that elapses between the moment an order is communicated by the customer and the moment the order must be delivered, i.e., agreed delivery date, is called a commitment lead time. The customer starts waiting if the firm is not able to fulfill the order at the agreed delivery date. Hence, if the actual delivery date is later than the agreed delivery date, the customer experiences a late delivery and the customer waiting time is the difference between the actual and agreed delivery dates. In Fig. 1, the customer waiting time is $t_3-t_2$. Notice that under the preorder strategy, the actual delivery date cannot be smaller than the agreed delivery date ($t_2\le t_3$).

Fig. 1

An illustration of agreed and actual delivery dates under the preorder strategy

Reducing the mismatch between demand and supply helps firms to reduce the customer waiting time and increase customer satisfaction. In this paper, we investigate the profitability of the preorder strategy in a single-location inventory system with time-based service constraints. Under the proposed preorder strategy, the firm can use the commitment lead time not only to decrease its inventory holding cost but also to reduce customer waiting time. The firm uses a base-stock policy to replenish its inventory from an outside supplier with infinite capacity. The firm aims to determine the optimal control policy as a combination of the base-stock level and the commitment lead time such that the long-run average inventory holding and commitment costs subject to a time-based service level target is minimized. We distinguish two time-based service measures in terms of average customer waiting time and individual customer waiting time. For the first measure, we require the average customer waiting time to be no more than a maximum waiting threshold, $\omega$. We refer to the corresponding model as the Average Constraint Optimization (ACO) model. For the second, we require the fraction of the customers, who experiences a waiting time no more than $\omega$ to be at least a certain fraction $\eta$. Hence, we formulate this time-based measure as a chance constraint and refer to it as the Chance Constraint Optimization (CCO) model. Using the ACO and CCO models, we answer the following research questions:

• 1. When should the firm use a preorder strategy?

  We find that the commitment lead time plays a significant role in the determination of the optimal control policy when the maximum waiting threshold is small or the minimum service level requirement is high. In other words, when the firm wants to provide a high level of responsiveness (i.e., $\omega \rightarrow 0$) to a high percentage of its customers (i.e., $\eta \rightarrow 1$), the value of the commitment lead time in terms of cost reduction is more highlighted.

• 2. What is the optimal control policy, i.e., optimal bases-stock level and optimal commitment lead time?

  Since for the above-mentioned settings, we are dealing with constraint optimization problems, to the best of our knowledge, finding closed-form solutions is difficult and, to some extent, impossible. We develop exact and heuristic optimization algorithms for solving the ACO and CCO models.

• 3. What is the impact of the commitment lead time on the customer waiting time and optimal cost?

  We derive the exact probability distribution of the customer waiting time in terms of system and control policy parameters. We show that the commitment lead time not only increases the service level, i.e., the fraction of the customers who experience waiting up to a maximum waiting threshold, but also decreases the maximum waiting time that each customer might experience. We prove that for any arbitrary maximum waiting threshold and minimum service level, the optimal cost value of the both models is bounded above.

• 4. What is the impact of commitment lead time on the equivalent unit backordering cost to maximum waiting threshold?

  We consider an unconstraint optimization model with backordering cost and its equivalent constraint optimization model with the average waiting time constraint. We find the equivalent unit backordering cost and maximum waiting threshold such that both models have the same optimal cost. We find that when the commitment lead time is taken into account, the equivalent unit backordering cost is always bounded above.

• 5. What is the impact of commitment lead time if some customers are not willing to order in advance?

  We study an extension with two customer classes. Customers in the first class accept the preorder strategy and expect to receive the product after the commitment lead time while customers in the second class reject the preorder strategy and expect to receive the product immediately after placing their orders. We find that for a given level of responsiveness, the more customers accept the preorder strategy, the lower the firm’s operational costs is. Hence, it is important to incentive the customers to preorder.

The businesses that require advance orders/reservations before realizations of customer demands can benefit from this study. Different from all the studies on this topic, we study the impact of the commitment lead time on the customer waiting time and provide service level-type constraints. In practice, compared to the backordering costs, these constraints are much easier to use and understand. Using our algorithms practitioners can optimize the commitment lead time and more importantly, they can benefit from customer commitments by reducing their operational costs. In addition, the companies that do not require advance orders/reservation can evaluate the profitability of this option for their businesses.

Responsiveness, as an indicator of how fast companies respond to their customer demands, plays an essential role in creating a competitive advantage. Using emerging technologies, such as Internet-of-things (IoT), customers can easily share their advance demand information with the suppliers if they have an incentive. Giving a bonus as an incentive allows companies to employ a preorder strategy with commitment lead time. Hence, our results and findings are useful for companies with customers who agree upon sharing ADI.

The remainder of the paper is organized as follows. In Sect. 2, we provide a brief review of the relevant literature. In Sect. 3, we describe the problem. We present the problem formulation and analyses in Sect. 4. We propose exact and heuristic solution algorithms in Sect. 5. In Sect. 6, we compare the ACO and CCO models and provide insights into when to use them. In Sect. 7, we study multiple extensions with two customer classes, random replenishment lead time and a model that combines ACO and CCO constraints. Our concluding remarks are in Sect. 8. We defer all the proofs and algorithms to "Appendix 1".

2 Literature review

In the literature of inventory management, supplier-oriented measures such as fill rate and ready-rate have been studied broadly. This work is related to a customer-oriented measure in the form of customer waiting time. We divide the relevant literature of inventory management on customer waiting time into two categories. In the first category, we review studies that focus on deriving the probability distribution of customer waiting time for a given inventory control policy. We provide a summary of the most relevant literature on this category in Table 1.

Table 1 Literature on customer waiting time distribution

In the second category, the customer waiting time constraint is incorporated into an optimization problem. Mostly, an expected cost with multiple components including inventory holding and transportation costs subject to a waiting time constraint is minimized. We summarize the relevant literature associated with this category in Table 2.

Table 2 Literature on service-constraint optimization

Commitment lead time and ADI concepts can be viewed interchangeably. The ADI can be either perfect or imperfect based on the accuracy of demand information available ahead of the realization of actual demand. Since our study is related to the perfect ADI, we restrict the review to this type of ADI. When a firm has perfect ADI, customers place orders ahead of time in specific quantities to be delivered at specified due dates. Hariharan and Zipkin (1995) are the first to study the perfect ADI situation in a continuous-review setting. After this seminal work, many researchers assume perfect ADI and study different problems. We provide a summary of the most relevant literature on perfect ADI in Table 3.

Table 3 Literature on perfect ADI

To the best of our knowledge, the impact of commitment lead time on customer waiting time has not been addressed in the literature. Ahmadi et al. (2019a, b) study the concept of the commitment lead time in single-location and assemble-to-order (ATO) systems, respectively. Both studies find the optimal control policies based on minimizing the total cost as the system performance indicator. They prove that the optimal policy for commitment lead time is a bang-bang policy.

In this paper, different from Ahmadi et al. (2019a, b), we study the impact of the commitment lead time from a customer-oriented perspective by taking time-based customer service level constraints into consideration. We show that the optimal control policy is not necessarily a bang-bang policy. We contribute to the literature by investigating the impact of the commitment lead time on the customer waiting time and firm’s responsiveness. We provide exact and heuristic methods to determine the optimal control policy.

3 Problem formulation

We consider a firm managing the inventory of a single item. The firm uses a base-stock policy with a base-stock level $s\in \left\{ 0,1,\dots \right\}$ to replenish its inventory from an uncapacitated supplier. The replenishment lead time, l, is constant. Customer orders describe a Poisson process with a rate $\lambda$. Each customer orders a single unit. The firm uses a preorder strategy, which requires that customers place their orders $\psi$ time units before their actual need. We say that the customer demand occurs $\psi$ time units after the corresponding customer order. We call $\psi \ge 0$ the commitment lead time. It is a continuous variable. The preorder strategy dictates two delivery dates: agreed delivery date and actual delivery date. We benefit from Fig. 2 to define these dates. Suppose that the customer needs a unit of product at time $t_1$. Then, according to the preorder strategy, the order should be placed at time $t_1-\psi$. The customer demand occurs at time $t_1$. Depending on inventory availability at time t, this demand might be satisfied at time $t_1$ or later, say time $t_2>t_1$. The agreed delivery date is $t_1$ and the actual delivery date is $t_2$. If $t_2=t_1$, the customer demand is satisfied at the agreed delivery date and if $t_2>t_1$, the customer experiences a waiting time of $t_2-t_1$ time units.

Fig. 2

An illustration of the commitment lead time and customer waiting time

The firm encourages orders to be placed before the actual demand by paying a commitment cost $K(\psi )$ per customer order. We assume that $K(0)=0$ and $K(\psi )$ is strictly increasing and convex in the length of the commitment lead time $\psi$. The convexity of the commitment cost makes longer commitment lead times more attractive to the customers. In addition to the commitment cost, the firm pays an inventory holding cost of h per unit per time unit. The firm aims to find the optimal control policy as a combination of the base-stock level and commitment lead time such that the long-run average total cost consisting of holding and commitment costs is minimized and a time-based service level is achieved.

We distinguish two time-based service measures in terms of average customer waiting time and individual customer waiting time. For the first measure, we define that the average customer waiting time should be less than or equal to a maximum waiting threshold, $\omega$. We refer to the corresponding constraint optimization as the Average Constraint Optimization (ACO) model. For the second, we define that the fraction of the customers experience a waiting time less than or equal to $\omega$ should be greater than or equal to a minimum service level, $\eta$. We refer to the corresponding constraint optimization as Chance Constraint Optimization (CCO) model.

The customer waiting time $W(s,\psi )$ is a nonnegative random variable. It is a function of the control policy, i.e., the base-stock level s and the commitment lead time $\psi$. We define ${\overline{W}}(s,\psi )$ as the average customer waiting time and $F_{W(s,\psi )}(\omega )=P\{W(s,\psi )\le \omega \}$ as the cumulative distribution function of the customer waiting time. Hence, the constraints for the ACO and CCO models can be written as follows:

• 1. The average waiting time constraint for the ACO model: ${\overline{W}}(s,\psi )\le \omega$.

• 2. The chance constraint for the CCO model: $F_{W(s,\psi )}(\omega )\ge \eta$.

Note that the chance constraint with $\omega =0$ reduces to a fill-rate constraint with a fill-rate $\eta$.

4 Analysis

In this section, we derive the exact probability distribution of the customer waiting time, formulate the expression for the long-run average total cost and analyze the properties of the ACO and CCO models.

In order to find out how the commitment lead time affects the waiting time and the long-run average total cost, we need to define the following notation:

$D^{-}(t_1,t_2{]}$::

cumulative customer orders from $t_1$ to $t_2$, $t_1<t_2$,

$D(t_1, t_2{]}$::

cumulative customer demand from $t_1$ to $t_2$, $t_1<t_2$,

IO(t)::

number of outstanding orders at time t,

IN(t)::

net inventory level of the firm at time t,

IP(t)::

inventory position of the firm at time t.

For a standard single-location inventory system (i.e., without the commitment lead time), the net inventory level follows the simple conservation-of-flow law;

$$\begin{aligned} IN(t+l)& = IN(t)+IO(t)-D(t,t+l]\\ & = IP(t)-D(t,t+l]. \end{aligned}$$

(1)

When the system operates under a base-stock policy with base-stock level s every customer demand triggers a replenishment order and IP(t) has a stationary behavior over time, i.e., $\forall t>0, IP(t)=s$. Then, $IN(t+l)=s-D(t,t+l]$. For an inventory system with commitment lead time $\psi$, the control policy is based on the customer order. We call this policy an order-base-stock policy. According to the order-base-stock policy every customer order triggers a replenishment order. Under the order-base-stock policy with base-stock level s, $IP(t)=IN(t)+IO(t)$ is non-stationary over time. It means that the equality $IP(t)= s$ does not hold $\forall t>0$. We define a modified inventory position $IP^-(t)$ as $IP^-(t)=IP(t)-D(t,t+\psi ]$. The modified inventory position depends on known demand during a time period with a length of the commitment lead time. $IP^-(t)$ has a stationary behavior over time, i.e., $\forall t>0, IP^-(t)= s$. If the firm starts with $IP^{-}(0^-)\le s$, the difference is ordered immediately so that $IP^{-}(0)$ equals s. If $IP^{-}(0^-)> s$, the firm orders nothing until demand depletes $IP^{-}(t)$ to s. Once $IP^{-}(t)$ hits s, it remains there from then on. Hence, Eq. (1) can be customized for an inventory system with commitment lead time $\psi$ as follows:

$$\begin{aligned} IN(t+l)&=IP(t)-D[t,t+l]\\&=IP(t)-(D(t,t+\psi ]+D(t+\psi ,t+l])\\&=(IP(t)-D(t,t+\psi ])-D(t+\psi ,t+l]\\&=IP^{-}(t)-D(t+\psi ,t+l]\\&=s-D(t+\psi ,t+l]. \end{aligned}$$

(2)

Since each customer order after $\psi$ time unites becomes a customer demand, for $0\le \psi \le t_1<t_2$, we have ${D}(t_1,t_2]={D}^-(t_1-\psi ,t_2-\psi ]$ and $IN(t+l)$ becomes

$$\begin{aligned} IN(t+l)=s-D^-(t,t+l-\psi ], \end{aligned}$$

(3)

where ${D}^-(t,t+l-\psi ]$ presents the number of customer orders during an interval of length $l-\psi$. We define IN and $X(\psi )$ as the variables representing the steady-state behaviour of IN(t) and ${D}^-(t,t+l-\psi ]$, respectively. Then, $IN=s-X(\psi )$, where $X(\psi )$ has a Poisson distribution with mean $\mu _{X(\psi )}=\lambda (l-\psi )$. We use ${P}_{X(\psi )}(x)$ to represent the probability mass function of $X(\psi )$. The dependency on $\psi$ is made explicit since this helps in subsequent analysis.

4.1 Probability distribution of the customer waiting time

Since the customer order arrival process is stochastic and the amount of available inventory is limited, the firm might not be able to meet all the customer demand immediately. When a customer demand arrives and no inventory is available, the firm is not able to satisfy the demand. Consequently, the customer has to wait until the arrival of replenishment order, which can be used to satisfy the corresponding demand. The waiting time of each customer depends on the status of the system at the customer’s arrival time. Since the status of the system is changing over time, the waiting time of the customer is a random variable. Since the firm operates under the preorder strategy, it receives ADI from the customers and it can use this information to make more cost-efficient decisions while reducing the customer waiting time.

Note that if the commitment lead time is longer than the replenishment lead time, i.e., $\psi > l$, the firm can provide on-time delivery without holding inventory by placing a replenishment order $\psi -l$ time units after a customer order occurs. This results in zero holding cost and zero customer waiting time. Since the firm pays for the commitment lead time, this strategy can be a costly and undesirable. In this study, we consider the commitment lead times in the range [0, l], i.e., $0\le \psi \le l$. As a result we have $W(s,\psi )\in [0,l-\psi ]$.

In Theorem 1, we consider $W(s,\psi )$ and specify its probability mass at zero ${P}_{W(s,\psi )}(0)$, probability density function $f_{W(s,\psi )}(\tau )$ and cumulative distribution function ${F}_{W(s,\psi )}(\tau )$.

Theorem 1

In a single-location inventory system, for given$s\in {\mathbb {N}}_0$, and$\psi \in [0,l]$,

• 1. the probability mass of the customer waiting time at zero is

  $$\begin{aligned} {P}_{W(s,\psi )}(0)=\sum \limits _{k=0}^{s-1} \frac{\mu _{X(\psi )}^k}{k!}e^{-\mu _{X(\psi )}}, \end{aligned}$$

• 2. the probability density function of the customer waiting time is

  $$\begin{aligned} f_{W(s,\psi )}(\tau )= {\left\{ \begin{array}{ll} \lambda \frac{\left( \mu _{X(\psi )}-\lambda \tau \right) ^{s-1}}{(s-1)!} e^{-\left( \mu _{X(\psi )}-\lambda \tau \right) } & \quad 0<\tau < l-\psi ,\\ 0 & \quad \tau \ge l-\psi ,\\ \end{array}\right. } \end{aligned}$$

• 3. the cumulative distribution function of the customer waiting time is

  $$\begin{aligned} {F}_{W(s,\psi )}(\tau )= {\left\{ \begin{array}{ll} \sum \limits _{k=0}^{s-1} \frac{\left( \mu _{X(\psi )}-\lambda \tau \right) ^{k}}{k!}e^{-\left( \mu _{X(\psi )} -\lambda \tau \right) } & \quad 0\le \tau < l-\psi ,\\ 1 & \quad \tau \ge l-\psi .\\ \end{array}\right. } \end{aligned}$$

We refer to "Proof of Theorem 1" in Appendix for the proof. Note that the commitment lead time decreases the possible maximum waiting time from l to $l-\psi$. Hence, the possible maximum waiting time is decreasing in the ADI. It is obvious that with complete ADI, i.e., $\psi =l$, the customer waiting time is zero. However, with incomplete ADI, i.e., $\psi <l$, the analysis is no longer intuitive. Next, we explore the impact of the incomplete ADI on the total cost and customer waiting time.

The cumulative distribution function ${F}_{W(s,\psi )}(\tau )$ plays a crucial role in our subsequent analysis. It is a mixed bivariate function: continuous and discrete with respect to $\psi$ and s, respectively. In Lemma 1, we analyze the behavior of ${F}_{W(s,\psi )}(\tau )$ with respect to these two variables.

Lemma 1

For all$s\in {\mathbb {N}}_0$, ${F}_{W(s,\psi )}(\tau )$is an increasing function of$\psi$and for all$\psi \in [0,l]$, ${F}_{W(s,\psi )}(\tau )$is a non-decreasing function ins.

We refer to "Proof of Lemma 1" in Appendix for the proof. According to Lemma 1, the commitment lead time not only decreases the possible maximum waiting time, but also increases the service level measured as the likelihood of meeting a customer demand before a given waiting time threshold. Having a higher base-stock level is another alternative choice to increase this service level; however, it does not decrease the possible maximum waiting time.

To have better understanding of the commitment lead time and base-stock level impacts on the service level, we consider an example with parameters setting: $\lambda =2$, $l=10$ and $\psi =2$. The behavior of ${F}_{W(s,2)}(\tau )$ for different base-stock levels is illustrated in Fig. 3a. As it can be seen, higher base-stock levels provide higher service levels. For instance, when the base-stock levels are 10 and 15, the likelihoods of meeting customer demand within a 3-unit time window are $45.79\%$ and $91.65\%$, respectively, i.e., ${F}_{W(10,2)}(3)=0.4579$ and ${F}_{W(15,2)}(3)=0.9165$. Hence, having a higher base-stock level results in substantial improvement in the service level. Note that the waiting time range remains at $[0,l-\psi ]$ independent of the base-stock level.

Fig. 3

The behavior of ${F}_{W(s,\psi )}(\tau )$ for different values of s and $\psi$

The behavior of ${F}_{W(s,2)}(\tau )$ for different values of commitment lead times is illustrated in Fig. 3b. The figure suggests that longer commitment lead times result in higher service levels. For example, when the firm uses preorder strategies with $\psi =5$ and $\psi =10$ (complete ADI), the likelihoods of meeting customer demand within a 3-unit time window are $23.81\%$ and $100\%$, respectively, i.e., ${F}_{W(3,5)}(3)=0.2381$ and ${F}_{W(3,10)}(3)=1$. Note that the waiting time range $[0,l-\psi ]$ depends on $\psi$ and it gets shorter with the longer commitment lead time.

4.2 Long-run average cost function

Based on the derivations at the beginning of this section, we have $IN=s-X(\psi )$, where $X(\psi )$ is the cumulative demand during $l-\psi$. $X(\psi )$ is a Poisson process with mean $\mu _{X(\psi )}=\lambda (l-\psi )$. Using this definition for IN, we define $C(s,\psi )$ as the long-run average total cost when the base-stock level and commitment lead time are s and $\psi$, respectively. Then, we can write the expression for $C(s,\psi )$ as follows;

$$\begin{aligned} C(s,\psi )& = h{\mathbb {E}}\left\{ \max (0,IN)\right\} +\lambda K(\psi )\\ & = h\left( s{F}_{X(\psi )}(s)-\mu _{X(\psi )} {F}_{X(\psi )}(s-1)\right) +\lambda K(\psi ), \end{aligned}$$

(4)

where ${F}_{X(\psi )}(x)$ is the cumulative distribution function of $X(\psi )$. Expression (4) represents the expected holding and commitment costs. The last expression can easily be obtained by using the definitions of IN, ${F}_{X(\psi )}$ and $\mu _{X(\psi )}$ (Ahmadi et al. 2019a). It is worth emphasizing that our analysis and results hold for any form of $K(\psi )$ as long as it is increasing and convex in $\psi$ and $K(0)=0$.

$C(s,\psi )$ is a discrete function with respect to s and a continuous function with respect to $\psi$. We analyze the behavior of $C(s,\psi )$ with respect to s and $\psi$ in Lemma 2.

Lemma 2

$C(s,\psi )$has the following properties with respect to$\psi$ands:

• 1. for all$s\in {\mathbb {N}}$, $C(s,\psi )$is increasing and convex in$\psi$,

• 2. for all$\psi \in [0,l]$, $C(s,\psi )$is increasing and convex ins.

We defer the proofs to "Proof of Lemma 2" in Appendix. According to Lemma 2, for a given commitment lead time $\psi$, increasing the base-stock level s results in higher average holding cost. This is an intuitive result. For a given base-stock level s, increasing $\psi$ results in a higher average cost.

4.3 Constraints on the customer waiting time

In this section, the ACO and CCO models are analyzed. We use subscripts a and c to refer to the ACO and CCO models, respectively.

4.3.1 The ACO model

The time between a customer order and the corresponding demand is exactly equal to the commitment lead time. The customer arrives after the commitment lead time and if there is no inventory starts waiting. As it is shown in Fig. 2, the customer order lead time is the summation of the commitment lead time and the customer waiting time. Since the commitment lead time is deterministic, the customer waiting time ${\overline{W}}(s,\psi )$ is a proper representative of the customer order lead time. Using Theorem 1, we derive the expression for the average customer waiting time in Proposition 1.

Proposition 1

In a single-location inventory system, for all$s\in {\mathbb {N}}_0$and$\psi \in [0,l]$, the average customer waiting time${\overline{W}}(s,\psi )$is given by

$$\begin{aligned} {\overline{W}}(s,\psi )=\frac{1}{\lambda }\left( s{F}_{X(\psi )}(s)-\mu _{X(\psi )} {F}_{X(\psi )}(s-1)+\mu _{X(\psi )}-s \right) \end{aligned}$$

See "Proof of Proposition 1" Appendix for the proof. ${\overline{W}}(s,\psi )$ is a nonlinear and discrete function of s, and it is a nonlinear and continuous function of $\psi$. In Lemma 3, we specify the behavior of ${\overline{W}}(s,\psi )$ with respect to s and $\psi$.

Lemma 3

In a single-location inventory system,

• 1. for all$s\in {\mathbb {N}}_0$, the average customer waiting time${\overline{W}}(s,\psi )$is non-increasing in$\psi$,

• 2. for all$\psi \in [0,l]$, the average customer waiting time${\overline{W}}(s,\psi )$is non-increasing ins.

Refer to "Proof of Lemma 3" in Appendix for the proof. According to Lemma 3, the average waiting time can be reduced by increasing the base-stock level s and/or increasing the commitment lead time $\psi$. The decision on which one of these two is more beneficial and cost-efficient depends on the cost parameters and amount of reduction in the average waiting time. For the aforementioned parameter setting in Sect. 4.1, we plot ${\overline{W}}(s,\psi )$ with respect to commitment lead time $\psi$ for different base-stock levels. As seen in Fig. 4, when $s=0$, ${\overline{W}}(s,\psi )$ is a decreasing linear function of $\psi$. For positive base-stock levels, the function is not linear anymore. For all $s\in {\mathbb {N}}_0$, the reduction in average waiting time is non-increasing in $\psi$.

Fig. 4

The behavior of ${\overline{W}}(s,\psi )$ with respect to commitment lead time $\psi$

Using Proposition 1 and Eq. (4), we write the ACO model as follows:

$$\begin{aligned} \hbox {(ACO)}: \quad \min _{s,\psi } \quad&C(s,\psi ) =h\left( s{F}_{X(\psi )}(s)-\mu _{X(\psi )} {F}_{X(\psi )}(s-1)\right) + \lambda K(\psi ), \quad \\ \hbox {subject to:} \quad&\phi _{a}(s,\psi ) \le 0,\\&s\in {\mathbb {N}}_0,\psi \in [0,l], \end{aligned}$$

(5)

where $\phi _a(s,\psi )=s{F}_{X(\psi )}(s)-\mu _{X(\psi )} {F}_{X(\psi )}(s-1)+\mu _{X(\psi )}-s-\lambda \omega$. The ACO model is a Constraint Mixed-Integer Nonlinear Program (C-MINLP). To the best of our knowledge, finding closed-form expressions for the decision variables is not possible. We tackle the problem by initially fixing the value of commitment lead time and analyzing the problem as if the base-stock level is the only decision variable. We solve the following optimization problem:

$$\begin{aligned} C_a(s^\psi ,\psi )=\min _{s\in {\mathbb {N}}_0} \quad&C(s,\psi ), \\ \hbox {subject to:} \quad&\phi _{a}(s,\psi ) \le 0. \end{aligned}$$

(6)

We define $s^{\psi }$ as the optimal base-stock level for a given $\psi$ and $C_a(s^\psi ,\psi )$ as the long-run average cost when the commitment lead time is $\psi$ and the base-stock level is $s^\psi$. Proposition 2 describes the behavior of $s^\psi$ with respect to $\psi$.

Proposition 2

$s^\psi$is non-increasing in$\psi$.

Refer to "Proof of Proposition 2" in Appendix for the proof. Given that the base-stock level is an integer, when we increase the value of $\psi$ the same base-stock level remains optimal for an interval of $\psi$ values. According to Proposition 2, for a long enough commitment lead time, the optimal base-stock level is zero. By solving the optimization problem (6), the interval [0, l] as domain of the univariate function $C_a(s^\psi ,\psi )$ is divided into $s^0+1$ subintervals such that

$$\begin{aligned} {[}0,l]= & \Psi _{s^0}\cup \Psi _{s^0-1}\cup \cdots \cup \Psi _{1}\cup \Psi _{0}. \end{aligned}$$

Here $\Psi _{s^\psi }$ is a subinterval of [0, l] such that $\forall \psi \in \Psi _{s^\psi }$, the base-stock level $s^\psi$ is the optimal base-stock level. Hence, $C_a(s^\psi ,\psi )$ is a discontinuous piecewise-convex function with continuous and convex pieces in each subinterval $\Psi _{s^\psi }$. We refer to Fig. 5 for an example.

Fig. 5

The discontinuous piecewise nonlinear function $C_a(s^\psi ,\psi )$ on [0, l]

We further define $\psi _{s^{\psi }}$ as the smallest $\psi \in \Psi _{s^\psi }$ for which $s^\psi$ is the optimal solution of the optimization problem (6). According to this definition, we have $\psi _{s^0}=0$ and $\psi _{0}=l-\omega$. There is only one point $\psi _{s^{\psi }}$ for each subinterval. We call these points breakpoints and define $\Theta _{a}$ as the set of all breakpoints of the ACO model. We have $|\Theta _{a}|=s^0+1$ and the following inequalities for the breakpoints hold: $\psi _{s^{0}}<\psi _{s^{0}-1}<\cdots<\psi _{1}<\psi _{0}$. For instance, in Fig. 5, we have $s_a^0=7$ and $\Theta _{a}=\{0,1.16,2.65,4.11,5.54,6.92,8.22,9.40\}$. These definitions help us in our further analysis. The dependency of the decision variables s and $\psi$ makes the optimization problem (5) difficult. In fact, different values of the maximum waiting threshold $\omega$ provide different feasible regions. It means that maximum waiting threshold $\omega$ can change the optimal control policy. To illustrate the impact of $\omega$ on the behavior of $C_a(s^\psi ,\psi )$ and optimal control policy, consider two settings with different values of $\omega$ and common parameters $\lambda =3, h=15, K(\psi )=2.2\psi$, and $l=10$. As it is shown in Fig. 6, when the waiting time threshold $\omega$ is changed from 0.35 to 0.10, the optimal control policy $(s^*,\psi ^*)$, which is shown as a dot in the figures, is changed from (32, 0.28) to (0, 9.90). In the setting with $\omega =0.1$, the effect of commitment lead time on the optimal control policy is more substantial.

Fig. 6

Behavior of $C_a(s^\psi ,\psi )$ in terms of $\psi$ for different values of $\omega$

As shown in Fig. 6, the optimal control policy and the corresponding average cost depend on $\omega$. With the next proposition, we provide an upper bound for the optimal cost.

Proposition 3

In the ACO model, for all$\psi \in [0,l]$, $\omega \in [0,l]$, and $s\in {\mathbb {N}}_0$, the optimal cost$C_a(s^*,\psi ^*)$is bounded above by$\lambda K(l-\omega )$.

We refer to "Proof of Proposition 3" in Appendix for the proof. According to Proposition 3, the optimal average cost, subject to a constraint any threshold value $\omega$ on the average waiting time, is bounded. When the firm targets a high level of responsiveness (i.e., a very quick response at the agreed delivery date, i.e., $\omega$ is close to zero), the firm should entice the customers to provide almost complete ADI, i.e., $\psi =l-\omega$. In this situation, the firm does not hold inventory and incurs commitment cost only. This cost is equal to $K(l-\omega )$.

4.3.2 The CCO model

In the ACO model, we have considered a threshold on the average customer waiting time. In this section, we consider a chance constraint to ensure that at least $\eta \in [0,1]$ fraction of the customers experience a waiting time less than the threshold $\omega$. Our objective is to find the optimal control policy such that a desired percentage of the customers receives service within a time frame target. This type of service measure is recommended when customer waiting time variability is high. We refer to corresponding optimization model as the chance constraint optimization (CCO) model.

For a given $\omega \in [0,l]$, $\eta \in [0,1]$ and using Theorem 1, the chance constraint can be written in terms of the cumulative distribution function of Poisson distribution as follows:

$$\begin{aligned} {F}_{W(s,\psi )}(\omega )={P}\{W(s,\psi )\le \omega \}=\sum \limits _{k=0}^{s-1} \frac{\left( \mu _{X(\psi )}-\omega \lambda \right) ^{k}}{k!}e^{-\left( \mu _{X(\psi )} -\omega \lambda \right) }. \end{aligned}$$

(7)

As it seen from Eq. (7), ${F}_{W(s,\psi )}(\omega )$ can be rewritten as the cumulative distribution function of the Poisson random variable $Y(\omega ,\psi )$ at $s-1$ with mean $\mu _{Y(\omega ,\psi )}=\mu _{X(\psi )}-\omega \lambda$. Hence, ${F}_{W(s,\psi )}(\omega )={F}_{Y(\omega ,\psi )}(s-1)$. Therefore, the CCO model can be formulated as follows:

$$\begin{aligned} \hbox {(CCO)}: \quad \min _{s,\psi } \quad&C(s,\psi )=h\left( s{F}_{X(\psi )}(s)-\mu _{X(\psi )} {F}_{X(\psi )}(s-1)\right) +\lambda K(\psi )\quad \\ \hbox {subject to:} \quad&\phi _{c}(s,\psi )\le 0\\&s\in {\mathbb {N}}_0,\psi \in [0,l], \end{aligned}$$

(8)

where $\phi _{c}(s,\psi )=\eta -{F}_{Y(\omega ,\psi )}(s-1)$. Recall that ${F}_{X(\psi )}(s)$ and ${F}_{Y(\omega ,\psi )}(s-1)$ are the cumulative distribution function of the Poisson distribution with mean $\mu _{X(\psi )}=\lambda (l-\psi )$ and $\mu _{Y(\omega ,\psi )}=\mu _{X(\psi )}-\omega \lambda$, respectively. Similar to the ACO model, the CCO model is C-MINLP and finding a closed-form solution to this problem is difficult and to some extent impossible.

Following the approach applied to the ACO model, we can get a tight lower bound by obtaining the univariate function $C_c(s^\psi ,\psi )$ by solving

$$\begin{aligned} C_c(s^\psi ,\psi )=\min _{s\in {\mathbb {N}}_0} \quad&C(s,\psi ), \quad \\ \hbox {subject to:} \quad&\phi _{c}(s,\psi ) \le 0. \end{aligned}$$

(9)

Similar to the ACO model, $s^\psi$ is defined as the optimal base-stock level for a given $\psi$ and $C_c(s^\psi ,\psi )$ is the long-run average cost when the commitment lead time is $\psi$ and the base-stock level is $s^\psi$. For a parameter setting with $\lambda =0.5, h=10$, $K(\psi )=2\psi , \omega =2$, and $\eta =0.5$, $C_c(s^\psi ,\psi )$ is depicted in Fig. 7. This function behaves similar to $C_a(s^\psi ,\psi )$; it is a discontinuous piecewise-convex function.

Fig. 7

The discontinuous piecewise-convex function $C_c(s^\psi ,\psi )$ on [0, l]

By solving the optimization problem (9), we divide the interval [0, l] into $s^0+1$ subintervals such that

$$\begin{aligned}[0,l]= & \Psi _{s^0}\cup \Psi _{s^0-1}\cup \cdots \cup \Psi _{0}. \end{aligned}$$

$\psi _{s^{\psi }}$ is the smallest $\psi \in \Psi _{s^\psi }$ for which $s^\psi$ is the optimal solution of the optimization problem (9). There is only one point $\psi _{s^{\psi }}$ for each subinterval. We define $\Theta _{c}$ as the set of all breakpoints of the CCO model. We have $|\Theta _{c}|=s^0+1$ and $\psi _{s^{0}}<\psi _{s^{0}-1}<\cdots <\psi _{0}$, where $\psi _{s^{0}}=0$ and $\psi _{0}=l-\omega$.

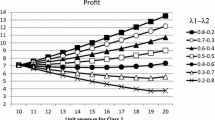
In order to show how the optimal control policy depends on the service level $\eta$ and the waiting time threshold $\omega$, we solve multiple problems and depict our findings in Fig. 8.

Fig. 8

Behavior of $C_c(s^\psi ,\psi )$ in terms of $\psi$

In Fig. 8a, we observe that increasing $\eta$ from 0.90 to 0.95 results in an significant change in the control policy. When $\eta$ is 0.90, the optimal policy suggests keeping almost no inventory and having a long commitment lead time. On the other hand, when the service level requirement is slightly increased to 0.95, the optimal policy changes to keeping a lot of inventory and having almost zero commitment lead time. These results suggest that for the CCO model, the idea of commitment lead time would work when the service level requirements are not extremely high. We observe a similar behaviour with respect to the maximum waiting time threshold $\omega$. According to Fig. 8b, when the threshold increases the optimal control policy changes from low base-stock level and long commitment lead time to low base-stock level and short commitment lead time. Hence, for a given service level requirement, if customers are not willing to wait for long, i.e., $\omega$ is small, having long commitment lead times is preferable to keeping a lot of inventory.

As shown in Fig. 8, the optimal control policy and the corresponding average cost depend on both $\eta$ and $\omega$. The following proposition presents an upper bound for the optimal cost in terms of these and other system parameters.

Proposition 4

In the CCO model, for all$\omega \in [0,l]$and$\eta \in [0,1]$, the optimal cost$C_c(s^*,\psi ^*)$, is bounded above by$\lambda K(l-\omega )$.

We refer to "Proof of Proposition 4" in Appendix for the proof. When the firm targets a very quick response, i.e., $\omega$ close to zero, or a very high service level, i.e., $\eta$ close to one, the firm should entice the customers to provide complete ADI, i.e., $\psi =l-\omega$. In this situation, the holding cost is zero and the firm incurs a commitment cost, which is equal to $K(l-\omega )$.

Under the preorder strategy, the immediate fill rate refers to the fraction of the customers who receive an on-time fulfillment. In other words, it is the fraction of the customers who receives the product at the moment it is needed. Setting $\omega =0$ in the chance constraint, we define the immediate fill rate as ${F}_{W(s,\psi )}(0)\ge \eta$. Since the customer demand is a pure Poisson process and fulfillment of demand is based on a First-Come, First-Served (FCFS) allocation rule, as an equivalence of zero waiting time, we can write $P\{W(s,\psi )= 0\}=P\{IN>0\}$. Using this definition, we conjecture the following result on the optimal commitment lead time.

Conjecture 1

In the CCO model with$\omega =0$, $(s^*,\psi ^*)$is either$(s^0,0)$or (0, l).

According to Conjecture 1, the optimal commitment lead time is either 0 or l, i.e., it follows a bang-bang policy. In Section 5.3, we rely on a comprehensive numerical experiment to confirm the correctness of the conjecture.

5 Solution methodology

In this section, we develop exact and heuristic algorithms for each constraint optimization model. Then, we evaluate the accuracy of the heuristic algorithms using numerical experiments.

5.1 Exact optimization algorithms

In Lemma 2, we prove that $C(s,\psi )$ is increasing in $\psi$ over the interval [0, l]. This means that $C(s^\psi ,\psi )$ is strictly increasing in $\psi$ over the subinterval $\Psi _s$. In this case, we can claim that the global minimum happens at one of the breakpoints. The number of breakpoints is finite and equal to $|\Theta _a|$ and $|\Theta _c|$ for the ACO and CCO models, respectively. Once the breakpoints are known, we can evaluate the average cost at these points and by comparing the average costs, we can identify the optimal solution. We use Newton’s and bisection methods to find the breakpoints of the ACO and CCO models, respectively. We refer to "Exact optimization algorithm for ACO model" and "Exact optimization algorithm for CCO model" in Appendix for the exact algorithms (i.e., Procedures 1 and 2). We refer to these exact algorithms as ACO and CCO exact algorithms, respectively. We would like to note that the cost function in Ahmadi et al. (2019a) is equivalent to the Lagrangian of the ACO model when $\omega =0$. In this case, we can claim that the optimal solution of Ahmadi et al. (2019a) and the ACO model are the same (van Houtum and Zijm (2000)). However, when $\omega \ne 0$, these two models are not equivalent and they might have different optimal solutions.

5.2 Heuristic algorithms

The exact optimization algorithms find the global minimums of the average cost functions. However, they are computationally intensive procedures since we need to find all the breakpoints and evaluate the cost function at these points. This is why we propose heuristic algorithms. A closer look at the ACO and CCO optimization problems reveals the fact that if the structure of average cost function obtained by evaluating the cost only at the breakpoints $\Theta _a\backslash \{0\}$ and $\Theta _c\backslash \{0\}$ can have one of the following forms: concave (or linear), convex (or linear) and concave–convex. For the ACO model, these forms are depicted in Fig. 9 as an example.

Fig. 9

Different behaviors of $C_a(s^\psi ,\psi )$

Our comprehensive numeral experiments show that, for both the ACO and CCO models, in most cases for all $\psi \in \Theta \backslash \{0\}$ and the corresponding optimal base-stock level $s^\psi$, $C(s^\psi ,\psi )$ exhibits a concave (on linear) behavior in terms of $\psi$. This means that the minimum of $C(s^\psi ,\psi )$ occurs at the end points. Instead of finding all the breakpoints of $\Theta \backslash \{0\}$, we just look at the smallest and biggest elements of $\Theta \backslash \{0\}$ as well as $\psi _{s^0}=0$. Therefore, in total, we need to evaluate cost function at three points. Based on the evaluation of these three points, we propose two heuristic algorithms. We refer to "Heuristic algorithm for ACO model" and "Heuristic algorithm for CCO model" in Appendix for these heuristic algorithms (i.e., Procedures 3 and 4). We refer to these heuristics as ACO and CCO heuristics, respectively.

5.3 Performance evaluation of the heuristic algorithms

We rely on numerical analysis for evaluating the accuracy of the ACO and CCO heuristics. We use 500,000 different parameter combinations. The parameter values are randomly generated from uniform distributions; we have $\lambda \sim U[0.1,10]$, $h\sim U[0.1,50]$, $c\sim U[0,h]$, $l\sim U[0.5,30]$, $\omega \sim U[0,l]$, and $\eta \sim U[0.01,0.99]$, where $x\sim U[a,b]$ means that the values of parameter x are chosen from a Uniform distribution in interval [a, b].

For both ACO and CCO models, for each parameter combination, we calculate $s^*$ and $\psi ^*$ using the exact algorithms and ${\hat{s}}^*$ and ${\hat{\psi }}^*$ using the heuristic algorithms. Then, we calculate the percentage gap between the optimal cost and heuristic cost values. We define $E_i$ as the percentage gap for parameter combination i. Then, we have

$$\begin{aligned} E_i=\frac{C(s^*,\psi ^*)-C({\hat{s}}^*,{\hat{\psi }}^*)}{C(s^*,\psi ^*)}\times 100. \quad i=1,2,\ldots ,500{,}000 \end{aligned}$$

(10)

The CDF of $E_i$ for the ACO and CCO heuristic algorithms are plotted in Fig. 10a, b, respectively. These figures suggest that both heuristic algorithms perform quite well. In fact, both heuristic algorithms provide the optimal solution in 99.5% of the parameter combinations.

Fig. 10

The CDF of the error for the heuristic algorithms

We also run the above-mentioned numerical experiment for evaluating the accuracy of Conjecture 1. Hence, we solve the CCO model with $\omega =0$ for 500,000 parameter combinations. The results of all 500,000 instances are consistent with Conjecture 1. Hence, the correctness of the conjecture is confirmed.

6 Model comparisons

In this section, we initially elaborate on which time-based service measure to use. Then, we compare the ACO model with its equivalent unconstrained problem with backordering cost.

6.1 Comparison of the ACO and CCO models

In the ACO model, the service measure is based on the average waiting time of all the customers. In the CCO model, the waiting time of each customer is considered and on average, only a certain percentage of customers is allowed to experience long waiting times. Depending on the characteristics of the firm, one of these two measures can be chosen. For instance, when the variability of the customer waiting time is high, the CCO model is recommended and when the variability is low, the ACO model is advised.

Instead of considering only of the constraints, one might think of consider a model with both service criteria. This results in a combined model that is difficult to analyze analytically. However, we are able to provide numerical results. In Table 4, we report the solutions of the combined model and also the solutions of the ACO and CCO models. We also report the active constraints. According to our results if the constraint of ACO (CCO) model is active, the optimal solution of ACO (CCO) model is also the optimal solution of combined model. Note that there are cases where both or none of the constraints are active.

Table 4 $\lambda =2,h=10,K(\psi )=3\psi , l=10, \eta \in \{0.85,0.95\}, \omega _a,\omega _c\in \{0,5,10\}$

6.2 Comparison of the ACO and unconstrained backordering models

In this section, we consider two optimization models. We first consider an unconstraint optimization (UCO) model with the average cost function consisting of the holding, backordering, and commitment costs. We refer to this model as UCO model and use $C_u(s_u,\psi _u)$ to represent its average cost function.

$$\begin{aligned} \hbox {(UCO)}\quad \min \limits _{s_u\in {\mathbb {N}}_0, \psi _u\in [0,l]} \quad C_u(s_u,\psi _u) & = (h+p)\left( s_u{F}_{X(\psi _u)}(s_u)-\mu _{X(\psi _u)}{F}_{X(\psi _u)}(s_u-1)\right) \\&+p\left( \mu _{X(\psi _u)}-s_u\right) +\lambda K(\psi _u),\\ \end{aligned}$$

(11)

where $C_u(s_u,\psi _u)$ is the same as the cost function derived in Ahmadi et al. (2019a). Then, we consider the equivalent ACO model, in which the backordering cost is replaced by the average customer waiting time constraint with maximum waiting threshold $\omega$. We use $C_a(s_a,\psi _a)$ to represent the average cost function of the ACO model.

$$\begin{aligned} \hbox {(ACO):} \quad \min \limits _{s_a\in {\mathbb {N}}_0, \psi _a\in [0,l]} \quad&C_a(s_a,\psi _a)=h\left( s_a{F}_{X(\psi _a)}(s_a)-\mu _{X(\psi _a)} {F}_{X(\psi _a)}(s_a-1)\right) + \lambda K(\psi _a), \quad \\ \hbox {subject to:} \quad&\phi _{a}(s_a,\psi _a) \le 0 \end{aligned}$$

(12)

Using these two models, we find the unit backordering cost $p\ge 0$, under which both optimization problems have the same optimal average cost values. The following proposition summarizes our findings.

Proposition 5

For any arbitrary maximum waiting threshold$\omega \in [0,l]$,

• 1. there exists a nonnegativepsuch that$C_u(s_u^*,\psi _u^*)=C_a(s^*_a,\psi ^*_a)$,

• 2. pis bounded and can be calculated as

  $$\begin{aligned} p=\frac{C_a(s_a^*,\psi ^*_a)-h{\overline{I}}(s_u^0,0)}{\lambda {\overline{W}}(s_u^0,0)}, \end{aligned}$$

  where${\overline{I}}(s_u^0,0)$and${\overline{W}}(s_u^0,0)$ are the average inventory and customer waiting time under control policy$(s^0_u,0)$.

We refer to "Proof of Proposition 5" in Appendix for the proof. From Sect. 4.3.1, we know that when the maximum waiting threshold is small enough or close to zero, we have $s_a^*=0$ and $\psi _a^*=l-\omega$. Consequently, $C_a(s_a^*,\psi ^*_a)=\lambda K(l-\omega )$. In this case, p can be calculated as follows:

$$\begin{aligned} p=\frac{\lambda K(l-\omega )-h{\overline{I}}(s_u^0,0)}{\lambda {\overline{W}}(s_u^0,0)}. \end{aligned}$$

(13)

Since $K(\psi )$ is a strictly increasing function in $\psi$, p is decreasing in $\omega$. For two parameter settings, we plot the behavior of p as a function of $\omega$ in Fig. 11. In both settings, a negative nonlinear relationship between p and $\omega$ is observed.

Fig. 11

The equivalent unit backordering cost p to the waiting time threshold $\omega$

Notice that by considering commitment lead time, it is always possible to find an equivalent unit backordering cost such that a desired maximum waiting threshold on average customer waiting time is guaranteed.

We would like to note that we do not observe any fundamental differences in the system behavior when backordering cost instead of the service level constraint is considered. Although not practical, unconstrained models are easier to analyze analytically. Hence, the results in this section are beneficial for researchers who would like to (1) study the commitment lead time concept for other supply chain structures and (2) benefit from the practical relevance of constrained models and the analytical tractability of unconstrained models.

7 Extensions

In the previous sections, we make multiple simplifying assumptions which enable us to provide concrete analytical results and building blocks for more complicated problems. Two of the assumptions that drive our analytical results are the deterministic replenishment lead time and all customers accepting to follow the preorder strategy. These assumptions drive and impact on our findings. In this section, we relax these two assumptions and calculate the resulting optimal control policies. We would like to note these relaxations do not allow for analytical derivations. This is why we rely on simulation-based optimization models for obtaining the subsequent results.

7.1 Committed and uncommitted customers

In the previous sections, we assume that all customers accept to preorder. In this section, we relax this assumption and consider two classes of customers. Customers in the first (committed) class accept the preorder strategy and they expect to receive their products at the agreed delivery date, which is commitment lead time away from the ordering moment. Customers in the second (uncommitted) class reject the preorder strategy, and they expect to receive their products immediately after placing their orders.

Similar to Arda and Hennet (2006), we split the customer arrival process $\{N(t); t > 0\}$ using a switch based on a Bernoulli process, which is independent of the arrival process. Each customer arrival is switched to an arrival process of $\{N_1(t); t > 0\}$ with probability $p_s$; otherwise, it is switched to an arrival process of $\{N_2(t); t > 0\}$. We refer to $p_s$ as the switching probability. Ross (2014) proves that processes $\{N_1(t); t > 0\}$ and $\{N_2(t); t > 0\}$ are mutually independent.

$\{N_1(t); t > 0\}$ represents the arrival process of the first class (i.e., committed customers) and $\{N_2(t); t > 0\}$ represents the arrival process of the second class (i.e., uncommitted customers). The switching probability represents the percentage of the customers who follow the preorder strategy. Both processes originate from the Poisson process $\{N(t); t > 0\}$ with mean $\lambda$. Then, given their mutual independence, the processes $\{N _1(t); t > 0\}$ and $\{N_2(t); t > 0\}$ follow Poisson processes with means $\lambda _1=p_s\lambda$ and $\lambda _2=(1-p_s)\lambda$, respectively.

In this setting, the waiting time of uncommitted customers starts immediately after placing their orders, whereas for the committed customers, it starts after the commitment lead time. Therefore, the overall waiting time depends on switching probability $p_s$ as well as the commitment lead time and the base-stock level. For a given base-stock level, Fig. 12 represents the behavior of the average waiting time with respect to the commitment lead time and the switching probability.

Fig. 12

The impact of switching probability and commitment lead time on the average waiting time

According to this figure, for a given base-stock level, the average waiting time is non-increasing in both commitment lead time and switching probability. Hence, for a fixed base-stock level, a higher value of the switching probability, the commitment lead time can result in more customers’ waiting time reduction.

We obtain the optimal policies for the ACO and CCO models assuming the following parameters: $\lambda =0.5, h=15, K(\psi )=5\psi , l=10, \omega =0.5$, and $\eta =0.98$. Our results are in Table 5. As a general observation for both models, the optimal base-stock level and optimal cost are non-increasing in switching probability. This can be explained by looking at breakpoints set $\Theta _a$ and $\Theta _c$. The number of the breakpoints is non-increasing in switching probability. Hence, a higher switching probability adds more degree of freedom to the optimization problem and, in turn, leads to a lower optimal cost. Higher switching probability means that more customers accept the preorder strategy. Since advance demand information is beneficial, the firm enjoys lower cost.

Table 5 The behaviour of the optimal control policy and optimal cost in terms of $p_s$

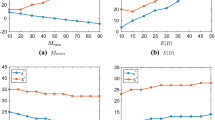
In addition to the results in Table 5, we analyze the behavior of both ACO and CCO models for many different settings. In general, we find that for a given level of responsiveness (i.e., for given $\eta$ and $\omega _c$ in CCO model and $\omega _a$ in the ACO model), the more customers accept the preorder strategy, the lower the firm’s optimal cost is. Hence, a setting with $p_s=1$ provides a lower bound while a setting with $p_s=0$ provides an upper bound on the cost. For the ACO model, the lower and upper bound costs correspond to $C_a(s^*,\psi ^*)$ and $C_a(s^*,0)$, respectively. In Fig. 13, we compare these bounds for different waiting time threshold values.

Fig. 13

The value of the commitment lead time in the ACO model

According to Fig. 13, the difference between the upper and lower bound is decreasing in $\omega$. Hence, when the threshold becomes very large any probability $p_s$ results in similar optimal costs.

7.2 Replenishment lead time uncertainty

In this section, we investigate the impact of replenishment lead time uncertainty on the optimal control policy and system performance. For this purpose, we consider exponential replenishment lead time, l, with mean $\mu >0$, (i.e., $l\sim \hbox {Exp} (\mu ^{-1})$). We consider the following data set $\lambda =1$, $h=15$, $K(\psi )=5\psi$, $\mu \in \{1, 5, 10\}$, $\omega \in \{0.1, 3, 7\}$, and $\mu \in \{0.1, 0.5, 0.9\}$.

For the ACO model, varying $\mu$ and $\omega$ leads to 6 different parameter combinations since we remove all the combinations in which $\omega >\mu$ as the corresponding optimal policy and optimal cost are zero. Our results are presented in Table 6.

Table 6 Optimal control policy and system performance of the ACO model

For the CCO model, varying $\mu$, $\omega$, and $\eta$ leads to 18 different parameter combinations. The corresponding results from simulation-based optimization are presented in Table 7.

Table 7 Optimal control policy and system performance of the CCO model

For both ACO and CCO models, as the mean $\mu$ increases the optimal cost increases. The optimal policy, i.e., the optimal base-stock level and the optimal commitment lead time depend on the system parameters. In general, we observe that the optimal base-stock level is non-decreasing in $\mu$, but the optimal commitment lead time does not exhibit a monotone behaviour.

8 Conclusions

In this section, we provide our concluding remarks and explain the insights generated by our findings. We also discuss multiple possible directions for further research.

8.1 Concluding remarks

In this paper, we consider a firm that faces a Poisson customer demand and uses a base-stock policy to replenish its inventories from an outside source with a deterministic lead time. The system operates under a preorder strategy, in which customers place their orders ahead of their actual need based on a predetermined time window called commitment lead time. In turn, the firm pays each customer a bonus based on the length of the commitment lead time. This cost is called commitment cost. The firm aims to find the optimal control policy as a combination of the base-stock level and commitment lead time such that a long-run average total cost consisting of holding and commitment costs is minimized subject to achieving a time-based service target. We study the responsiveness of the firm based on two time-based service level criteria: average customer waiting time and individual customer waiting time. For the first criterion, we consider a threshold on the average customer waiting time. For the second criterion, we consider a chance constraint which aims at having at least a certain percentage of customers waiting no longer that a given threshold. Corresponding to the first and second service criteria, we formulate two models: ACO and CCO models, respectively. We prove several analytical properties of these models and propose exact and heuristic optimization algorithms to solve them. Using a comprehensive numerical experiment, we show that the heuristic algorithms perform quite well.

We observe that when commitment lead time and time-based service criteria with a positive maximum waiting threshold are taken into account, the policy governing the optimal commitment lead time is not a bang-bang policy. However, for an immediate response setting in the CCO model, the optimal commitment lead time takes a bang-bang form; it is either equal to zero or l. We derive the exact probability distribution of customer waiting time in terms of system parameters and control policy. We show that the commitment lead time not only increases the firm’s responsiveness but also decreases the customers’ maximum waiting time. We show that the optimal cost is bounded and non-increasing in the maximum waiting threshold. We find that the commitment lead time plays a significant role in the determination of the optimal control policy when the firm targets a high level of responsiveness, i.e., either the maximum waiting threshold is small enough (e.g., close to zero) or the service level is high enough (e.g., close to one). In other words, when the firm wants to provide a quicker response to a higher percentage of the customers, the value of commitment lead time in terms of cost reduction is more highlighted.

Moreover, we consider an unconstraint optimization model with backordering cost and its equivalent constraint optimization model with the average waiting time constraint. We calculate equivalent unit backordering cost such that both models have the same optimal cost. We find a negative relationship between unit backordering cost and maximum waiting threshold. When commitment lead time is taken into account, the equivalent unit backordering cost is always bounded above.

We relax the assumption that all customers accept to preorder and consider a setting with two customer classes. Customers in the first class accept the preorder strategy, while customers in the second class reject the preorder strategy. We test many different parameter settings for both ACO and CCO models using simulation-based optimization approach. We conclude that the more customers accept the preorder strategy, the lower the firm’s operational cost is. As another variant, we consider stochastic replenishment lead time and study the effect of random lead time on the optimal control policy.

8.2 Practical relevance

In today’s highly competitive global marketplace, companies need to have competitive advantages to increase or maintain their position in the market. Responsiveness as an indicator of how fast a firm responds to its customer demands plays an essential role in determining whether the firm can have a competitive advantage in the market. Using emerging technologies such as Internet-of-things (IoT), customers can easily share their advance demand information with companies if they receive a bonus in return. Our research is inspired by this need of following new strategies that can benefit not only companies but also customers. Having advance demand information provides the companies with more time to react to their customer demands while customers get compensation in terms of bonus and better service.

Our results and findings can be useful for any type of business that plans to monitor and improve its responsiveness by benefiting from advance demand information. We provide multiple examples from both manufacturing and service sectors.

• Firms that are selling their products in the Construction Industry fit into our settings. When the sketch of construction is ready, the exact number of required items such as the number of windows, doors, lamps, etc., is known. However, they are not needed before the completion of the construction. It is sensible that the constructors (customers) preorder the items with the suppliers if they get a price reduction (i.e., commitment cost) in return. This is also beneficial for the suppliers as they can use this ADI to manage and guarantee the availability of the items with lower operational costs.

• Companies that manufacture products with a short life cycle can also benefit from our research. For example, cell-phone manufacturers, like Apple, can accept orders in advance and use this information to provide a fast response to their customers while reducing the operational costs and potential obsolescence risk.

• Restaurants can implement the idea of commitment lead time by offering a price reduction to customers who place their orders in advance of their arrivals. The commitment lead time enables the restaurants not only to increase their responsiveness by reducing customers’ waiting time, but also to increase the customer satisfaction. Given that preordering results in lower inventory levels, restaurants might end up wasting less if they implement the preordering strategy.

8.3 Future research directions

In this paper, we investigated the impact of commitment lead time on the responsiveness of a single-location inventory system. Future research might consider more complex supply chain structures. Considering supply uncertainty in the form of supply disruptions (Atan and Snyder 2012a, b; Atan and Rousseau 2016; Atan and Snyder 2014) with commitment lead time can be another possible extension of this research. It would be interesting to see how this form of supply uncertainty affects the optimal preorder strategy.

Another extension is to utilize the distribution of customers’ waiting time to investigate the impact of the commitment lead time on customers’ risk behavior. This can be done by considering nonlinear waiting cost functions or measure such as the conditional expected waiting beyond a target value in the spirit of Value-at-Risk (VaR) or Conditional Value at Risk (CVaR).

Appendices

Appendix 1: Proofs

1.1 Proof of Theorem 1

We use the same approach presented in Kruse (1980). A customer who arrives at time t will wait less than or equal to $\tau$, if and only if he or she receives one of the outstanding orders at $t+\tau -l$. The customer gets an item from $IP(t+\tau -l)$ only if the previous demands $D[t+\tau -l,t)$ are less than $IP(t+\tau -l)$. Then,

$$\begin{aligned} {F}_{W(s,\psi )}(\tau )&=P(W(s,\psi )\le \tau )\\&=P(IP(t+\tau -l)-D[t+\tau -l,t)> 0)\\&=P\left( IP(t+\tau -l)-(D[t+\tau -l,t+\tau -l+\psi )+D[t+\tau -l+\psi ,t))> 0\right) \\&=P\left( (IP(t+\tau -l)-D[t+\tau -l,t+\tau -l+\psi ))-D[t+\tau -l+\psi ,t)> 0\right) \\&=P\left( IP^{-}(t+\tau -l)-D[t+\tau -l+\psi ,t)> 0\right) .\\ \end{aligned}$$

Under the preorder strategy, we know that $\forall t>0,IP^{-}(t)=s$. Then, $IP^{-}(t+\tau -l)=s$ and

$$\begin{aligned} {F}_{W(s,\psi )}(\tau )&=P\left( s-D[t+\tau -l+\psi ,t)> 0\right) \\&=P\left( D[t+\tau -l+\psi ,t)<s\right) \\&=P\left( D[t+\tau -l+\psi ,t)\le s-1\right) .\\ \end{aligned}$$

Since each customer order after $\psi$ time unites becomes a customer demand, then $D[t+\tau -l+\psi ,t)=D^{-}[t+\tau -l,t-\psi )$.

$$\begin{aligned} {F}_{W(s,\psi )}(\tau )&=P\left( D^{-}[t+\tau -l,t-\psi )\le s-1\right) \\&=P\left( X'(\psi )\le s-1\right) ,\\ \end{aligned}$$

where $X'(\psi )$ presents the number of customer orders during an interval of length $l-\psi -\tau$. Then, $X'(\psi )$ has a Poisson distribution with mean $\mu _{X'(\psi )}=\mu _{X(\psi )}-\lambda \tau$. Hence, for all $\psi \in [0,l], \tau \in [0,l-\psi ]$,

$$\begin{aligned} {F}_{W(s,\psi )}(\tau )&=\sum \limits _{k=0}^{s-1} \frac{\left( \mu _{X(\psi )}-\lambda \tau \right) ^{k}}{k!}e^{-\left( \mu _{X(\psi )} -\lambda \tau \right) }, \end{aligned}$$

and for $\tau \le l-\psi$, ${F}_{W(s,\psi )}(\tau )=1$. Therefore, the probability distribution function of $W(s,\psi )$ can be summarized as follows.

$$\begin{aligned} {F}_{W(s,\psi )}(\tau )= {\left\{ \begin{array}{ll} \sum \limits _{k=0}^{s-1} \frac{\left( \mu _{X(\psi )}-\lambda \tau \right) ^{k}}{k!} e^{-\left( \mu _{X(\psi )}-\lambda \tau \right) } & \quad 0\le \tau < l-\psi ,\\ 1& \quad \tau \ge l-\psi .\\ \end{array}\right. } \end{aligned}$$

For the probability mass of the customer waiting time at zero, we can write

$$\begin{aligned} {P}_{W(s,\psi )}(0)={F}_{W(s,\psi )}(0)=\sum \limits _{k=0}^{s-1} \frac{\left( \mu _{X(\psi )}\right) ^{k}}{k!}e^{-\mu _{X(\psi )}}. \end{aligned}$$

Let $f_{W(s,\psi )}(\tau )$ be the probability density function of $W(s,\psi )$. Then, for all $0<\tau <l-\psi$, $f_{W(s,\psi )}(\tau )=\frac{\hbox {d}}{\hbox {d}\tau }{F}_{W(s,\psi )}(\tau )$. For ease of calculation, let us introduce Poisson random variable $Y(\tau ,\psi )$ with mean $\mu _{X(\psi )}-\lambda \tau$. Then, for all $0<\tau <l-\psi$, ${F}_{W(s,\psi )}(\tau )={F}_{Y(\tau ,\psi )}(s-1)$. Similar to Ahmadi et al. (2019a), we can prove that $\frac{\hbox {d}{F}_{Y(\tau ,\psi )}(s-1)}{\hbox {d}\tau }=\lambda {P}_{Y(\tau ,\psi )}(s-1)$. Hence, for all $0<\tau <l-\psi$, $f_{W(s,\psi )}(\tau )=\lambda {P}_{Y(\tau ,\psi )}(s-1)$; otherwise, $f_{W(s,\psi )}(\tau )=0$. Therefore, the probability density function of $W(s,\psi )$ can be summarized as follows.

$$\begin{aligned} f_{W(s,\psi )}(\tau )= {\left\{ \begin{array}{ll} \lambda \frac{\left( \mu _{X(\psi )}-\lambda \tau \right) ^{s-1}}{(s-1)!} e^{-\left( \mu _{X(\psi )}-\lambda \tau \right) }& \quad 0<\tau < l-\psi ,\\ 0 & \quad \hbox {otherwise}.\\ \end{array}\right. } \end{aligned}$$

1.2 Proof of Lemma 1

We first show that for all $s\in {\mathbb {N}}_0$, $\frac{\hbox {d} {F}_{W(s,\psi )}(\tau )}{\hbox {d} \psi }\ge 0$. Based on "Proof of Theorem 1" in Appendix, for all $\tau \in (0,l-\psi )$, ${F}_{W(s,\psi )}(\tau )={F}_{Y(\tau ,\psi )}(s-1)$, where ${F}_{Y(\tau ,\psi )}(s-1)$ is the cumulative distribution of Poisson at $s-1$ with mean $\mu _{Y(\tau ,\psi )}=\mu _{X(\psi )}-\lambda \tau$. Also, from Ahmadi et al. (2019a), we know that $\frac{\hbox {d} {F}_{Y(\tau ,\psi )}(s-1)}{\hbox {d} \psi }=\lambda {P}_{Y(\tau ,\psi )}(s-1) \ge 0$. Then, for all $\tau \in (0,L)$,

$$\begin{aligned} \frac{\hbox {d} {F}_{W(s,\psi )}(\tau )}{\hbox {d} \psi }=\frac{\hbox {d} {F}_{Y(\tau ,\psi )}(s-1)}{\hbox {d} \psi }=\lambda {P}_{Y(\tau ,\psi )}(s-1)\ge 0. \end{aligned}$$

Then, for all $\psi \in [0,l]$, we show that $\Delta _s {F}_{W(s,\psi )}(\tau ) \ge 0$. To do so, we show that $\Delta _s {F}_{Y(\tau ,\psi )}(s-1)\ge 0$. By calculating ${F}_{Y(\tau ,\psi )}(s)={F}_{Y(\tau ,\psi )}(s-1)+{P}_{Y(\tau ,\psi )}(s)$, we can write $\Delta _s {F}_{W(s,\psi )}(\tau )=\Delta _s {F}_{Y(\tau ,\psi )}(s-1)={F}_{Y(\tau ,\psi )}(s)-{F}_{Y(\tau ,\psi )}(s-1)={P}_{Y(\tau ,\psi )}(s) \ge 0$.

1.3 Proof of Lemma 2

For all $s\in {\mathbb {N}}_0$, $C(s,\psi )$ is a continuous function with respect to $\psi$ and for all $\psi \in [0,l]$, it is a discrete function with respect to s.

First, we show that for an arbitrary $s\in {\mathbb {N}}_0$, the first derivative of $C(s,\psi )$ is positive.

$$\begin{aligned} \frac{\hbox {d} C(s,\psi )}{\hbox {d} \psi }&=h\left( s\left( \frac{\hbox {d} {F}_{X(\psi )}(s)}{\hbox {d} \psi } \right) -\left( \frac{\hbox {d} \mu _X}{\hbox {d} \psi } \right) {F}_{X(\psi )}(s-1)\right. \\&\quad \left. -\mu _X\left( \frac{\hbox {d} {F}_{X(\psi )}(s-1)}{\hbox {d} \psi } \right) \right) +\lambda c\left( \frac{\hbox {d} \psi }{\hbox {d} \psi } \right) \\&\quad \hbox {knowing }\,\frac{\hbox {d} {F}_{X(\psi )}(s)}{\hbox {d} \psi }=\lambda {P}_X(s,\psi ) \hbox { and }\frac{\hbox {d} \mu _X}{\hbox {d} \psi }=-\lambda ,\\&=h\left( s\lambda {P}_X(s,\psi ) +\lambda {F}_{X(\psi )}(s-1)-\mu _X\lambda {P}_X(s-1,\psi ) \right) +\lambda c \\&=\lambda \left( h\left( s {P}_X(s,\psi ) + {F}_{X(\psi )}(s-1)-\mu _X {P}_X(s-1,\psi ) \right) + c\right) \\&\quad \hbox {from MPF of Poisson }, s {P}_X(s,\psi )=\mu _X {P}_X(s-1,\psi ),\\&=\lambda (h{F}_{X(\psi )}(s-1)+ c)\ge 0. \\ \end{aligned}$$

Second, we show that for an arbitrary $s\in {\mathbb {N}}_0$, the second derivative of $C(s,\psi )$ is positive, too.

$$\begin{aligned} \frac{\hbox {d}^2 C(s,\psi )}{\hbox {d} \psi ^2}& = \frac{\hbox {d}}{\hbox {d} \psi } \left( \frac{\hbox {d} C(s,\psi )}{\hbox {d} \psi }\right) =\lambda h\frac{\hbox {d} {F}_{X(\psi )}(s-1)}{\hbox {d} \psi }=\lambda ^2 h {P}_{X(\psi )}(s-1)\ge 0. \end{aligned}$$

Therefore, for an arbitrary $s\in {\mathbb {N}}_0$, $C(s,\psi )$ is increasing and convex in $\psi$.

Now, we show that for an arbitrary $\psi \in [0,l]$, the first and second forward differences of $C(s,\psi )$ are positive.

First, we show that for an arbitrary $\psi \in [0,l]$, the first forward difference of $C(s,\psi )$ is positive (i.e., $\Delta _sC(s,\psi )=C(s+1,\psi )-C(s,\psi )>0$).

$$\begin{aligned} C(s+1,\psi )&=h((s+1){F}_X(s+1,\psi )-\mu _X {F}_{X(\psi )}(s))+\lambda K(\psi )\\&=h((s+1)({F}_{X(\psi )}(s)+{P}_X(s+1,\psi ))-\mu _X ({F}_{X(\psi )}(s-1)\\&\quad +{P}_X(s,\psi )))+\lambda K(\psi )\\&=h((s+1){F}_{X(\psi )}(s)+(s+1){P}_X(s+1,\psi )-\mu _X {F}_{X(\psi )}(s-1)\\&\quad -\mu _X {P}_X(s,\psi ))+\lambda K(\psi )\\&=h(s{F}_{X(\psi )}(s)+{F}_{X(\psi )}(s)+(s+1){P}_X(s+1,\psi )-\mu _X {F}_{X(\psi )}(s-1)\\&\quad -\mu _X {P}_X(s,\psi ))+\lambda K(\psi )\\&=C(s,\psi )+h({F}_{X(\psi )}(s)+(s+1){P}_X(s+1,\psi )-\mu _X {P}_X(s,\psi ))\\&=C(s,\psi )+h{F}_{X(\psi )}(s).\\ \end{aligned}$$

So, $\Delta _sC(s,\psi )=C(s+1,\psi )-C(s,\psi )=h{F}_{X(\psi )}(s)>0$.

Second, we show that for an arbitrary $\psi \in [0,l]$, the second forward difference of $C(s,\psi )$ is positive (i.e., $\Delta _s^2C(s,\psi )=\Delta _sC(s+1,\psi )-\Delta _sC(s,\psi )\ge 0$). Using our last result for $C(s+1,\psi )$, we can calculate $C(s+2,\psi )=C(s+1,\psi )+h{F}_{X(\psi )}(s+1)=C(s,\psi )+2h{F}_{X(\psi )}(s) +h{P}_{X(\psi )}(s+1)$. Then,

$$\begin{aligned} \Delta _s^2C(s,\psi )&=\Delta _sC(s+1,\psi )-\Delta _sC(s,\psi )=C(s+2,\psi ) -2C(s+1,\psi )+C(s,\psi )\\&=C(s,\psi )+2h{F}_{X(\psi )}(s)+h{P}_{X(\psi )}(s+1)-2(C(s,\psi ) +h{F}_{X(\psi )}(s))+C(s,\psi )\\&=h{P}_{X(\psi )}(s+1)\ge 0. \end{aligned}$$

Therefore, for an arbitrary $\psi \in [0,l]$, $C(s,\psi )$ is increasing and convex in s.

1.4 Proof of Proposition 1

Based on Theorem 1, the expected waiting time is calculated as follows.

$$\begin{aligned} {\overline{W}}(s,\psi )&={\mathbb {E}}\{W(s,\psi )\}=\int _{0}^{L} \tau f_{W(s,\psi )}(\tau )\hbox {d}\tau =\int _{0}^{l-\psi } \tau \lambda \frac{\left( \mu _{X(\psi )}-\lambda \tau \right) ^{s-1}}{(s-1)!}e^{-\left( \mu _{X(\psi )}-\lambda \tau \right) }\hbox {d}\tau \\&=\int _{0}^{l-\psi } \tau \lambda ^s\frac{\left( l-\psi -\tau \right) ^{s-1}}{(s-1)!}e^{-\lambda \left( l-\psi -\tau \right) }\hbox {d}\tau \\&=\frac{\lambda ^s}{(s-1)!}\int _{0}^{l-\psi } \tau (l-\psi -\tau )^{s-1} e^{-\lambda (l-\psi -\tau )} \hbox {d}\tau \end{aligned}$$

By substituting $l-\psi -\tau =x$, then $\tau =l-\psi -x$ and $\hbox {d}\tau =-\hbox {d}x$.

$$\begin{aligned} &=\frac{\lambda ^s}{(s-1)!}\int _{0}^{l-\psi } (l-\psi -x)x^{s-1} e^{-\lambda x} \hbox {d}x. \end{aligned}$$

By substituting $\lambda x=y$, then $x=\frac{1}{\lambda }y$ and $\hbox {d}x=\frac{1}{\lambda }\hbox {d}y$.

$$\begin{aligned} &=\frac{\lambda ^s}{(s-1)!}\int _{0}^{\mu _{X(\psi )}} \left( l-\psi -\frac{y}{\lambda }\right) \left( \frac{y}{\lambda }\right) ^{s-1} e^{-y} \frac{1}{\lambda }dy=\frac{1}{\lambda (s-1)!}\int _{0}^{\mu _{X(\psi )}} \left( \mu _{X(\psi )}-y\right) y^{s-1}e^{-y}\hbox {d}y\\&=\frac{1}{\lambda (s-1)!} \left( \mu _{X(\psi )}\int _{0}^{\mu _{X(\psi )}}y^{s-1}e^{-y}\hbox {d}y -\int _{0}^{\mu _{X(\psi )}}y^se^{-y}\hbox {d}y \right) ,\\ \end{aligned}$$

(14)

where $\mu _{X(\psi )}=\lambda (l-\psi )$. Based on the definition of the upper incomplete gamma function $\Gamma (s,\mu _{X(\psi )})$ for positive integer s;

$$\begin{aligned} \Gamma (s,\mu _{X(\psi )})=(s-1)!e^{-\mu _{X(\psi )}}\sum _{k=0}^{s-1} \frac{\left( \mu _{X(\psi )}\right) ^k}{k!}, \end{aligned}$$

the lower incomplete gamma function $\gamma (s,\mu _{X(\psi )})$

$$\begin{aligned} \gamma (s,\mu _{X(\psi )})=\int _0^{\mu _{X(\psi )}}y^{s-1}e^{-y}\hbox {d}y, \end{aligned}$$

the ordinary gamma function $\Gamma (s)=(s-1)!$, and their relationship as $\gamma (s,\mu _{X(\psi )})=\Gamma (s)-\Gamma (s,\mu _{X(\psi )})$, we can write

$$\begin{aligned} \int _0^{\mu _{X(\psi )}}y^{s-1}e^{-y}dy=(s-1)!\left( 1-e^{-\mu _{X(\psi )}} \sum _{k=0}^{s-1}\frac{\left( \mu _{X(\psi )}\right) ^k}{k!}\right) \end{aligned}$$

(15)

Then, based on Eq. (15), we can calculate Expression (14) as follows.

$$\begin{aligned} {\overline{W}}(s,\psi )&=\frac{1}{\lambda (s-1)!} \left( \mu _{X(\psi )}(s-1)! \left( 1-e^{-\mu _{X(\psi )}}\sum _{k=0}^{s-1}\frac{\left( \mu _{X(\psi )} \right) ^k}{k!}\right) \right. \\&\quad \left. -s!\left( 1-e^{-\mu _{X(\psi )}}\sum _{k=0}^{s} \frac{\left( \mu _{X(\psi )}\right) ^k}{k!}\right) \right) \\&=\frac{1}{\lambda } \left( \mu _{X(\psi )}\left( 1-\sum _{k=0}^{s-1} \frac{\left( \mu _{X(\psi )}\right) ^k}{k!}e^{-\mu _{X(\psi )}}\right) -s\left( 1-\sum _{k=0}^{s}\frac{\left( \mu _{X(\psi )}\right) ^k}{k!} e^{-\mu _{X(\psi )}}\right) \right) \\&=\frac{1}{\lambda } \left( \mu _{X(\psi )}\left( 1-{F}_{X(\psi )}(s-1) \right) -s\left( 1-{F}_{X(\psi )}(s)\right) \right) \\&=\frac{1}{\lambda }\left( s{F}_{X(\psi )}(s)-\mu _{X(\psi )} {F}_{X(\psi )}(s-1)+\mu _{X(\psi )}-s \right) , \end{aligned}$$

where ${F}_{X(\psi )}(s)$ is the cumulative distribution function of Poisson with mean $\mu _{X(\psi )}$.

1.5 Proof of Lemma 3

We first prove ${\overline{W}}(s,\psi )$ is non-increasing in $\psi$. For this purpose, we show that the first derivative of ${\overline{W}}(s,\psi )$ with respect to $\psi$ is non-positive. From Proposition 1, we have

$$\begin{aligned} {\overline{W}}(s,\psi )=\frac{1}{\lambda }\left( s{F}_{X(\psi )}(s)-\mu _{X(\psi )} {F}_{X(\psi )}(s-1)+\mu _{X(\psi )}-s \right) . \end{aligned}$$

Then

$$\begin{aligned} \frac{\hbox {d} {\overline{W}}(s,\psi )}{\hbox {d} \psi }&=\frac{1}{\lambda }\left( s\left( \frac{\hbox {d} {F}_{X(\psi )}(s)}{\hbox {d} \psi }\right) -\left( \left( \frac{\hbox {d} \mu _{X(\psi )}}{\hbox {d} \psi }\right) {F}_{X(\psi )}(s-1)+ \mu _{X(\psi )}\left( \frac{\hbox {d} {F}_{X(\psi )}(s-1)}{\hbox {d} \psi }\right) \right) \right) \\&\quad +\frac{1}{\lambda }\left( \frac{\hbox {d} \mu _{X(\psi )}}{\hbox {d} \psi }\right) \end{aligned}$$

From Ahmadi et al. (2019a), we know $\frac{\hbox {d} {F}_{X(\psi )}(n)}{\hbox {d} \psi }=\lambda {P}_{X(\psi )}(n)$ and $\frac{\hbox {d} \mu _{X(\psi )}}{\hbox {d} \psi }=-\lambda$. Then,

$$\begin{aligned} \frac{\hbox {d} {\overline{W}}(s,\psi )}{\hbox {d} \psi }&=\frac{1}{\lambda }\left( s\lambda {P}_{X(\psi )}(s)-\left( -\lambda {F}_{X(\psi )}(s-1)+ \mu _{X(\psi )} {P}_{X(\psi )}(s-1)\right) -\lambda \right) \\ \end{aligned}$$

From the probability mass function of Poisson, $\mu _{X(\psi )} {P}_{X(\psi )}(s-1)=s {P}_{X(\psi )}(s)$. Then, $\frac{\hbox {d} {\overline{W}}(s,\psi )}{\hbox {d} \psi }={F}_{X(\psi )}(s-1)-1\le 0.$

Next, we prove that ${\overline{W}}(s,\psi )$ is non-increasing in s. For this purpose, we show that for all $\psi \in [0,l]$, $\Delta _s{\overline{W}}(s,\psi )={\overline{W}}(s+1,\psi )-{\overline{W}}(s,\psi )\le 0$. First, we calculate ${\overline{W}}(s+1,\psi )$ as follows.

$$\begin{aligned} {\overline{W}}(s+1,\psi )&=\frac{1}{\lambda }\left( (s+1){F}_X(s+1,\psi ) -\mu _{X(\psi )} {F}_{X(\psi )}(s)+\mu _{X(\psi )}-s-1 \right) \\&=\frac{1}{\lambda }\left( s{F}_{X(\psi )}(s)+{F}_{X(\psi )}(s)+(s+1) {P}_{X(\psi )}(s+1)-\mu _{X(\psi )} {F}_{X(\psi )}(s-1) \right) \\&\quad +\frac{1}{\lambda }\left( -\mu _{X(\psi )} {P}_{X(\psi )}(s)+\mu _{X(\psi )} -s-1\right) \\&={\overline{W}}(s,\psi )+\frac{1}{\lambda }\left( {F}_{X(\psi )}(s) +(s+1){P}_{X(\psi )}(s+1)-\mu _{X(\psi )} {P}_{X(\psi )}(s)-1 \right) \end{aligned}$$

From the probability mass function of Poisson, $\mu _{X(\psi )} {P}_{X(\psi )}(s)=(s+1) {P}_{X(\psi )}(s+1)$. Then, ${\overline{W}}(s+1,\psi )={\overline{W}}(s,\psi )+\frac{1}{\lambda }\left( {F}_{X(\psi )}(s)-1 \right)$. Hence, $\Delta _s{\overline{W}}(s,\psi )=\frac{1}{\lambda }\left( {F}_{X(\psi )}(s)-1 \right) \le 0$.

1.6 Proof of Proposition 2

First, we show that for all $s\in {\mathbb {N}}_0$, $\phi _a(s,\psi )$ is non-increasing in $\psi$, and for all $\psi \in [0,l]$, $\phi _a(s,\psi )$ is non-increasing in s. For this purpose, we show that for all $\psi \in [0,l]$, the first-order difference of $\phi _a(s,\psi )$ is non-positive. By rewriting $\phi _a(s,\psi )$ as $\phi _a(s,\psi )=\lambda ({\overline{W}}(s,\psi )-\omega )$ and using proof of Lemma 3 in A.5, we have

$$\begin{aligned} \Delta _s\phi _a(s,\psi )= \lambda (\Delta _s{\overline{W}}(s,\psi )-\omega ) =\lambda \left( \frac{1}{\lambda }({F}_{X(\psi )}(s)-1)\right) ={F}_{X(\psi )}(s)-1 \end{aligned}$$

Since for all $s\in {\mathbb {N}}_0$ and $\psi \in [0,l]$ we have $\Delta _s\phi _a(s,\psi )={F}_{X(\psi )}(s)-1\le 0$, then $\phi _a(s,\psi )$ is non-increasing in s. Then, we show that for all $s\in {\mathbb {N}}_0$, the first derivative of $\phi _a(s,\psi )$ is non-positive. Using proof of Lemma 3 in A.5, we can write

$$\begin{aligned} \frac{\hbox {d} }{\hbox {d} \psi }\phi _a(s,\psi )& = \lambda \left( \frac{\hbox {d} }{\hbox {d} \psi } {\overline{W}}(s,\psi )-\omega \right) =\lambda ({F}_{X(\psi )}(s-1)-1) \end{aligned}$$

Since for all $s\in {\mathbb {N}}_0$, $\psi \in [0,l]$ and $\lambda >0$, we have $\frac{\hbox {d} }{\hbox {d} \psi }\phi _a(s,\psi )\le 0$, then $\phi _a(s,\psi )$ is non-increasing in $\psi$.

For $\psi =l$, we have $\phi _a(s,l)=s\left( {F}_{X(l)}(s)-1\right) -\lambda \omega$. Knowing that $\phi _a(0,l)=-\lambda \omega \le 0$ and for a given $\psi$, $C(s,\psi )$ is non-decreasing in s, then for given $\psi =l$, $s=0$ is optimal. Hence, $s^l=0$.

Since for a given s, $\phi _a(s,\psi )$ is non-increasing in $\psi$, by decreasing $\psi$ from l we can reach $\psi _0$, $0\le \psi _0<l$, such that $\phi _a(0,\psi _0)=0$. Hence, for all $\psi \in [\psi _0,l]$, $\phi _a(0,\psi )\le 0$. We denote $\Psi _0=[\psi _0,l]$.

Since for a given $\psi$, $\phi _a(s,\psi )$ is non-increasing in s, then for $\psi =\psi _0$, $\phi _a(1,\psi )\le 0$. Again, by deceasing $\psi$ from $\psi _0$ we reach a point $\psi _1$, $0\le \psi _1<\psi _0$, such that $\phi _a(1,\psi _1)=0$. Hence, for all $\psi \in [\psi _1,\psi _0)$, $\phi _a(1,\psi )\le 0$. We denote $\Psi _1=[\psi _1,\psi _0)$.

By continuing this procedure and reducing $\psi$, we finally reach $\psi =0$. Let $s^0$ be smallest $s\in {\mathbb {N}}_0$, such that $\phi _a(s^0,0)\le 0$. Then $\Psi _{s^0}=[\psi _{s^0},\psi _{s^0-1})=[0,\psi _{s^0-1})$. As a result, by decreasing $\psi$ from l to 0 the corresponding optimal s increases from 0 to $s^0$.

1.7 Proof of Proposition 3

Let $C_a(s^*,\psi ^*)$ be the optimal cost value of the ACO model. Then, for all the breakpoints $\psi _s\in \Theta _{a}$, we have $C_a(s^*,\psi ^*)\le C_a(s,\psi _s)$. Also, in the ACO model, ${\psi _0}=l-\omega \in \Theta _{a}$. Then, $C_a(s^*,\psi ^*)\le C_a(0,l-\omega )=\lambda K(l-\omega )$.

1.8 Proof of Proposition 4

Let $C_c(s^*,\psi ^*)$ be the optimal cost value of the CCO model. Then, for all the breakpoints $\psi _s\in \Theta _{c}$, we have $C_c(s^*,\psi ^*)\le C_c(s,\psi _s)$. Also, in the CCO model, ${\psi _0}=l-\omega \in \Theta _{c}$. Then,

$$\begin{aligned} C_c(s^*,\psi ^*)\le C_c(0,l-\omega )=\lambda K(l-\omega ) \end{aligned}$$

.

1.9 Proof of Proposition 5

• 1. From Proposition 3, we know that $C_a(s_a^*,\psi _a^*)\le \lambda K(l-\omega )$. Also, from Ahmadi et al. (2019a), we know that the optimal cost of the UCO model happens at either $(s^0,0)$ or (0, l). Hence, $C_u(s^*_u,\psi ^*_u)=C_u(0,l)=\lambda K(l)$ or $C_u(s^*,\psi ^*_u)=C_u(s^0,0)$. Since for all $\psi \in [0,l]$, $K(\psi )$ is an increasing convex function in $\psi$, for all $\omega \in (0,l]$,

  $$\begin{aligned} C_a(s_a^*,\psi _a^*)\le K(l-\omega )< \lambda K(l)=C_u(0,l). \end{aligned}$$

  From Ahmadi et al. (2019a), we also know that there is a threshold $K_0(\psi )$ for commitment cost $K(\psi )$ such that if $K(\psi )\ge K_0(\psi )$, then $C_u(s^*,\psi ^*_u)=C_u(s^0,0)$, where $K_0(\psi )$ is increasing in p. For a given $K(\psi )$, by increasing p from zero, we reach a $p_0>0$ such that $K(\psi )=K_0(\psi )$. Hence, for all $p\in (0,p_0]$, $C_u(s^*_u,\psi ^*_u)=C_u(s^0,0)$ and at $p=p_0$, $C_u(s^*,\psi ^*_u)=C_u(s^0,0)=C_u(0,l)=\lambda K(l)$. As a result, for all $p\in (0,p_0]$, $C_u(s^*_u,\psi ^*_u)$ varies from 0 to $\lambda K(l)$. Since $C_u(s^0,0)$ is a continuous function in terms of p over the range of [0, K(l)], then there exists a $p\in (0,p_0]$ for which $C_u(s_u^*,\psi _u^*)=C_a(s_a^*,\psi _a^*)$.

• 2. Based on the first part of the proposition, the equivalent optimal cost value in the UCO model always happens at $(s^0,0)$. Then, $C_u(s_u^*,\psi _u^*)=C_u(s^0_u,0)=h{\overline{I}}(s^0,0)+p\lambda {\overline{W}}(s^0,0)$ which is a continuous function in p. By putting $C_u(s^0_u,0)=C_a(s^*_a,\psi ^*_a)$, we have

  $$\begin{aligned} p=\frac{C_a(s_a^0,\psi ^*_a)-h{\overline{I}}(s_u^0,0)}{\lambda {\overline{W}}(s_u^0,0)}. \end{aligned}$$

  From Proposition 3, we know that $C_a(s_a^*,\psi _a^*)\le \lambda K(l-\omega )$. Hence,

  $$\begin{aligned} p\le \frac{ \lambda K(l-\omega )-h{\overline{I}}(s^0,0)}{\lambda {\overline{W}}(s^0,0)} \end{aligned}$$

  Therefore, p is bounded.

Appendix 2: Algorithms

1.1 Exact optimization algorithm for ACO model

1.2 Exact optimization algorithm for CCO model

1.3 Heuristic algorithm for ACO model

1.4 Heuristic algorithm for CCO model