Inventory optimization for perishables subject to supply disruptions

Abstract

We study a retailer selling perishable products with fixed lifetime. The retailer’s supply system is subject to random disruptions. Assuming a base-stock policy, deterministic demand and stationary cost parameters, we determine the expression for the optimal base-stock level. We show that if the retailer manages to make the system safer, it is possible to operate with the same expected cost even with products with shorter lifetimes. We conclude that the retailer should concentrate on reducing disruptions’ durations instead of their occurrence rate.

1 Introduction

Alan T. Cooley, founding partner of NewDawn Partnership, an Ascot, UK supply chain consultancy, says that “If you are into perishables, you really have got to have a slick supply chain, from farm to fork. There is no room for messing about.” However, even well-managed supply chains can suffer from events resulting in supply disruptions. In [11] supply disruptions are defined as “random events that cause a supplier or other elements of the supply chain to stop functioning either completely or partially, for a typically random amount of time.” It is evident that supply disruptions can be extremely costly for chains carrying perishable products since long disruptions might result in obsolescence of products. Conventional strategies for managing supply chains are inappropriate for these chains. Therefore, modified or different strategies need to be developed.

There are many high profile events showing the effects that supply disruptions can have on perishable-product supply chains. Such an event happened in 2010, when a volcanic eruption in Iceland resulted in shut-down of European air space, causing cancellations of around 100,000 flights. The eruption resulted in widespread transport and supply chain chaos and it especially hurt companies with extended supply chains. East African nations were hit particularly hard. Kenya’s growers had to dump around 65 tons of vegetables and 3,000 tons of roses. The loss per day to Kenyan growers is estimated at $1.2 to $2 million. Not only growers but buyers like FloraHolland, the Netherlands, got affected since they could not receive the flowers they planned to receive and sell. Both parties of the floral supply chain suffered costly losses.

It is obvious that events causing supply disruptions cannot be totally avoided. However, some strategies can be developed to reduce their drastic impact. There are multiple strategies that a company can choose from [13]. The best strategy depends on the company’s objective and the nature of disruptions. Different strategies can perform better for frequent but short disruptions and for rare but long disruptions.

Standard inventory theory does not take product lifetime into account; in theory products can be stored for an infinite amount of time. However, food, blood, pharmaceuticals and many other supply chains carry products with limited lifetime. Only recently, the supply disruption risks embedded in such crucial and globally dispersed supply chains has gained attention. However, only few works in the literature have considered the effects of disruptions on supply chains transporting perishable products. In fact, this is the first study to quantify the benefits of exercising the inventory mitigation strategy for a company carrying perishable products.

In this paper, we consider a single retailer selling products with fixed and limited lifetime. Assuming an infinite-horizon periodic review with supply disruptions, deterministic customer demands and linear unit holding, backordering and perishing costs, we derive an expression for the expected cost per period. The optimum stocking policy for this system is unknown, so we assume a base-stock policy. Our simplifying assumptions enable us to get some insights on benefits of having a strategy to protect against disruptions. We analyze the influence of several different parameters, including the limited lifetime, on the optimal base-stock level and the corresponding cost. The main goal is to obtain insights on inventory optimization for perishables subject to supply disruptions. Other goals are: showing the importance of taking perishability and supply disruptions into account when making replenishment decisions and providing a basis for further research in this field.

Our analysis suggests that the optimal base-stock level depends on the lifetime but not on the unit perishing cost. We show that, for items with short lifetimes, the choice of the base-stock level has a bigger impact on the cost than for items with longer lifetimes. We also show that if the retailer can manage to make the system safer, it is possible to operate with the same expected cost even with products with shorter lifetimes. When it comes to the disruption management, we conclude that companies should concentrate more on reducing the duration of supply disruptions instead of trying to prevent them. Finally, we show how to use our model for systems with stochastic demand and non-stationary parameters.

An extensive body of literature has been written and is emerging on inventory control of perishable items. This literature is nicely summarized in [5, 8] and recently in [2, 9]. Most of the papers cited at these review articles try to either determine the best inventory replenishment policy or the parameters of a given replenishment policy under different assumptions on demand, transportation and cost structures. These inventory models are classified on the basis of products’ lifetimes as fixed lifetime and random lifetime models. Our model fits into the fixed lifetime category and for a given policy, which is the base-stock policy, we determine the optimal expression for the base-stock level. We make the assumption of fixed lifetime since we want to see the effects of only one type of an uncertainty, which is supply disruptions. Although the optimal replenishment policy for the problem under consideration is not known, we assume the base-stock policy since it is commonly employed in practice and widely used in the perishable-product literature. In fact, under similar assumptions as ours (zero leadtime, no lot sizing, stationary demand, fixed lifetime), the base-stock policy is close to the optimal [3].

The literature on supply disruptions has been growing during the past decade. A very recent article [11] summarizes this literature by organizing it into six categories: evaluating disruptions; strategic decisions; sourcing decisions; contracts and incentives; inventory; and facility location. The literature on inventory mitigation is also reviewed in [1].

Disruptions can happen due to many different reasons like natural disasters and transportation problems [11]. In this paper, we do not make any assumptions regarding their type but we assume that disruptions halt the transportation process between the retailer and its supplier. It has been shown that the impact of transportation disruptions on supply chain performance can be huge [14]. This impact can be even bigger for supply chains carrying perishable products. As many researchers point out, strategic and tactical responses are needed to mitigate the effects of disruptions on perishable-item supply chains. Managing the suppliers [7], investing on rescheduling activities [6], and reorganizing the production processes [4] are some of them. Another solution, recognized and widely utilized by many companies, is to increase the amount of capital tied up in inventories. This paper contributes to the perishable-item and disruption literature, by being the first study to consider inventory mitigation strategies for perishable-item systems subject to supply disruptions.

The structure of this paper is as follows. In Sect. 2, we derive the expression for the expected cost function and analyze its properties. We present the results of our numerical analysis in Sect. 3. We conclude and provide directions for future work in Sect. 4.

2 Model and analysis

2.1 Assumptions

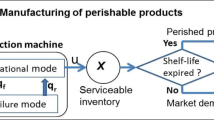
We consider a single retailer, carrying perishable products with fixed lifetime of $x$ periods. The retailer observes its inventory level and places orders with an outside supplier, which is assumed to have an infinite capacity. The inventory level is reviewed periodically and a base-stock policy with parameter $S$ is used for replenishments. The leadtime is zero, which means that, under normal circumstances, if an order is placed at the end period of $t$, the products arrive at the beginning of period $t+1$. We consider an infinite horizon.

Demand is deterministic and equal to $d$ at each period. We make this assumption not only to have a more tractable model but also to concentrate only on uncertainties in the supply side. We consider an extension in Sect. 3.3 with stochastic demand.

We assume that the customers are indifferent between products with different ages. Therefore, at the beginning of every period, if there is enough inventory, the retailer places $d$ units of the oldest products on the shelf and the customers, independent of the products’ age, buy these products. With this strategy the retailer makes sure that the oldest products are consumed first. In addition, regardless of their age, inventories are treated as equivalent units and the order size is related to satisfied demand only. Hence, the base-stock level $S$ does not depend on products’ age composition.

A holding cost of $h$ per unit per period is incurred over all products that remain in inventory at the end of each period. Unmet demands are backordered and a penalty cost of $b$ per unit per period is incurred. When products remain in inventory for $x$ periods they perish and the retailer incurs a cost of $p$ per perished unit. There is no fixed cost per order.

Supply process of the retailer is subject to random disruptions. During disruptions the retailer cannot receive any items from its supplier. The probability that the supplier is disrupted in the next period depends only on its state in the current period. We define $\alpha$ as the disruption probability and $\beta$ as the recovery probability. More specifically, $\alpha$ is the probability that the supplier is disrupted (down) in the next period given that it functions normally (up) in the current period and $\beta$ is the probability that the supplier recovers from the disruption in the next period given that it is disrupted in the current period. The up and down periods both constitute geometric processes [12].

Using $\alpha$ and $\beta$, we can model the disruption process as a two-state discrete-time Markov chain (DTMC) with an up and down state but, similar to [10, 12], we choose to model the disruptions using an infinite-state DTMC that gives more information regarding the duration of the disruptions. State $i$ represents being in a disruption that has lasted for $i$ consecutive periods. If $i=0$, the supplier is in an up period, and therefore functions normally. We define $\pi _{i}$ as the steady-state probability that the supply system is in a disruption that has lasted $i$ periods. Note that $\pi _{0}$ is the probability that the supplier is functioning normally, i.e. without any disruptions, and $1-\pi _{0}$ is the probability that the supplier is disrupted for at least one period. We define $F(j)=\sum ^{j}_{i=0}\pi _{i}$ and $F^{-1}(y)=\text{ min }\left\{ j: F(j)\ge y\right\}$ as the corresponding cumulative and inverse cumulative distribution functions. $F(j)$ represents the probability that the supplier is in a disruption that lasted $j$ periods or fewer [12]. Given these definitions, the long-run distribution of being in state $i$, i.e. $\pi _{i}$ values, are given in the following lemma:

Lemma 1

For a single location subject to supply disruptions with disruption probability $\alpha$ and recovery probability $\beta$, the steady state probabilities are

$$\begin{aligned} \pi _{0}&= \frac{\beta }{\alpha +\beta }\\ \pi _{i}&= \frac{\alpha \beta }{\alpha +\beta }(1-\beta )^{i-1}, \quad i\ge 1 \end{aligned}$$

Proof

Refer to [12]. $\square$

We assume that disruptions are independent over time and they are long enough to clear all the inventories at the retailer. Disruptions happen one at a time implying that the system cannot face another disruption during the recovery phase. The supplier is able to deliver all the outstanding orders immediately after disruptions are over, i.e. the inventory level at the beginning of the first non-disrupted period is $S$. This, in fact, is a direct consequence of the zero leadtime assumption.

Our objective is to find the optimal base-stock level $S^{*}$, i.e. $S$ that minimizes the expected cost per period $C(S)$. Using this model as a base, in Sect. 3 we study a number of interesting questions, which provide significant managerial insights.

A summary of the notation is given in Table 1.

Table 1 Notation

Before proceeding with the expression for the expected cost per period, we describe the sequence of events in each period. At the beginning of a period, if the supplier is disruption-free, the replenishment order arrives and inventory level is raised to $S$. If the supplier is disrupted, the inventory level is the same as the inventory level at the end of the previous period. During the period demand occurs. The demand is satisfied to the extend possible, and excess demands are backordered. At the end of the period all items left in inventory mature by one period, i.e., the products are marked one period older than in the prior period. If the age of a product exceeds its stipulated lifetime, the product perishes and is disposed. Finally, the holding, backordering and perishing costs are calculated and a new order is placed.

As stated before, in our model, orders are not delivered during disruptions but customers keep arriving. This results in a decreasing stock level, which might lead to backorders. We argue that when products are not perishable, i.e. $x\rightarrow \infty$; the effect of disruptions can be minimized by holding more inventory. However, when products are perishable, holding more inventory as a buffer results in high perishing cost, which might lead to a higher total cost than in a situation without buffering.

Next, we determine the expression for $C(S)$; with and without disruptions.

2.2 Expected cost functions

2.2.1 Without disruptions

Initially, we derive an expression for the average cost function for the case with a completely reliable, i.e., disruption-free, supply system. Before a general expression, we give an example with $x=3$. We need to determine the inventory and backorder levels and the number of perished products at end of each period. Table 2 helps in recognizing a cycle in development of these costs.

Table 2 Evolution of the performance measures for different base-stock levels when $x=3$

Note that when $S\le 2d$ all periods end with the same inventory and backorder levels. In addition, the number of perished units is the same in all periods. When $S\ge 3d$, the first period is a warm-up period and after it we observe cycles each with a length of three periods. In fact, these observations can be generalized for any fixed lifetime. If the lifetime is $x$ periods, when $S\le (x-1)d$, all periods end with the same inventory and backorder levels and the same number of perished products. When $S\ge xd$, warm-up periods are followed by cycles each with a length of $x$ periods. The ending inventory level is $(S-d)$ for $x-1$ of the periods in the cycle and it is $\bigl (S-d-(S-xd)^{+}\bigr )^{+}$ for one period. Perishability occurs only in one of the periods and the number of perished items is $(S-xd)$. Backorders happen only if $S=0$. Based on these observations, we can write the expected cost per period as a function of $S$ as follows:

$$\begin{aligned} C(S)&= \frac{1}{x}\biggl (h\bigl [\left( x-1\right) \left( S-d\right) ^++\left( S-d-\left( S-xd\right) ^+\right) ^+\bigr ]\\&+p\left( S-xd\right) ^++xb\left( d-S\right) ^+\biggr ) \end{aligned}$$

Theorem 1

When the supply system is disruption-free, the optimal base-stock level, $S^{*}$, is $d$ and the corresponding expected cost is 0.

Proof

Trivial. $\square$

2.2.2 With disruptions

Next, we consider the possibility of disruptions and derive the expression for the expected cost function per period. As elaborated in the previous analysis without disruptions, when the lifetime is $x$ periods the system reaches a steady state that evolves in cycles each having a length of $x$ periods. We assume that disruptions happen one at a time and the system recovers before another disruption happens. The system is said to be “recovered” from a disruption only when it starts to evolve in cycles again. Therefore, we know for sure that a new disruption can only happen when the system is evolving in cycles of length $x$.

As explained in Sect. 2.1 we model the disruptions using an infinite-horizon DTMC by defining $\alpha$ as the probability of having a disruption in the next period given that the system is disruption-free in the current period. This probability does not depend on the number of disruption-free periods before a disruption happens, i.e. the process is memoryless. In fact, the up and down periods both constitute geometric processes. Hence, when the lifetime is $x$ periods and the system evolves in cycles consisting of $x$ periods, the probability of having a disruption in one of these $x$ periods is $1/x$.

The expression of the cost function depends on when disruptions start. When the system is disrupted, the customers keep arriving and the retailer places replenishment orders but it cannot receive anything from its supplier. In addition to customer demands, the inventory level can also be reduced by perishability. In order to clarify the derivation of the general cost function, we give an example with $x=3$ and $S\ge 3d$. Similar examples can be provided for any $x$ and $S$. Initially, we assume that a disruption happens during a period which looks like period $t$ in Table 2 ($S\ge 3d$). Table 3 shows the evolution of the system.

Table 3 A disruption happens during period $t$ (see Table 2)

The expected cost function for the case described in Table 3 is as follows:

$$\begin{aligned} C^{t}(S)&= \pi _{0}h(S-d)+\pi _{1}\biggl (hd+p(S-xd)\biggr )+\sum ^{\infty }_{i=2}\pi _{i}b\biggl ((i+1)-x\biggr )d \end{aligned}$$

Next, we assume that a disruption happens during a period which looks like period $t+1$ in Table 2. Table 4 shows the evolution of the system.

Table 4 A disruption happens during period $t+1$ (see Table 2)

The expected cost function for the case described in Table 4 is as follows:

$$\begin{aligned} C^{t+1}(S)&= \pi _{0}\biggl (h2d+p(S-xd)\biggr )+\pi _{1}hd+\sum ^{\infty }_{i=2}\pi _{i}b\biggl ((i+1)-x\biggr )d \end{aligned}$$

Finally, we assume that a disruption happens during a period which looks like period $t+2$ in Table 2. Table 5 shows the evolution of the system.

Table 5 A disruption happens during period $t+2$ (see Table 2)

The expected cost function for the case described in Table 5 is as follows:

$$\begin{aligned} C^{t+2}(S)&= \pi _{0}h(S-d)+\pi _{1}h(S-2d)+\pi _{2}p(S-xd)+\sum ^{\infty }_{i=2}\pi _{i}b\biggl ((i+1)-x\biggr )d \end{aligned}$$

Given that disruptions are equally likely to happen during the periods $t$, $t+1$ and $t+2$, the overall expected cost function for this example can be written as

$$\begin{aligned} C(S)&= \frac{1}{x}\biggl (C^{t}(S)+C^{t+1}(S)+C^{t+2}(S)\biggr )\\&= \frac{1}{x}\Biggl (\pi _{0}h\biggl (2(S-d)+2d\biggr )+\pi _{1}h\biggl ((S-2d)+2d\biggr )+p(S-xd)\sum ^{2}_{i=0}\pi _{i}\\&+x\sum ^{\infty }_{i=2}\pi _{i}b\biggl ((i+1)-x\biggr )d\Biggr ) \end{aligned}$$

This example shows that during a disruption, cost evolve in a specific way. For inventory holding cost, the amount over which the cost is calculated decreases by demand, i.e. $d$, in every period and by perishing, i.e. $(S-xd)^{+}$, only in one period. The timing of perishing depends on conditions of the first disrupted period. Backordering only occurs when the system is disrupted for $x$ or more consecutive periods. Since perishing already occurs before $x$ disrupted periods, the backordering cost only increases by $bd$ when $i\ge x$.

Using the same reasoning, we write the general expected cost function, which holds for any $x$ and $S$ as follows:

$$\begin{aligned} C(S)&= \frac{1}{x}\sum _{i=0}^{\infty }{\pi _{i}} h\left( \left( x-\left( i+1\right) \right) ^+\left( S-\left( i+1\right) d\right) ^+\right. \\&\left. +\left( x-\left( x-\left( i+1\right) \right) ^+\right) \left( S-\left( i+1\right) d-\left( S-xd\right) ^+\right) ^+\right) \\&+\frac{1}{x}\sum _{i=0}^{\infty }\pi _i b\left( \left( x-(i+1)\right) ^+\left( (i+1)d-S\right) ^+\right. \\&\left. +\left( x-\left( x-(i+1)\right) ^+\right) \left( \left( S-xd\right) ^++(i+1)d-S\right) ^+\right) \\&+\sum _{i=0}^{x-1}\pi _i p \left( S-xd\right) ^+ \end{aligned}$$

When the system is not disrupted, the amount over which holding cost needs to be paid is equal to the starting inventory at the beginning of the period, $S$, minus the demand during that period, $d$, and minus the possible number of perished products, $(S-xd)^+$. However, perishing only occurs in one out of $x$ periods per cycle. Therefore, when the system is not disrupted, $i=0$, $x-1$ times we have an ending inventory of $(S-d)^{+}$, and only once we have an ending inventory of $\bigl (S-d-(S-xd)^{+}\bigr )^{+}$. When the system is disrupted for 1 period, $i=1$, the ending inventory over which holding cost needs to be paid, is equal to the starting inventory minus demand during that period and minus possible perished products. Again this perishing can only take place in 1 out of $x$ periods per cycle. However, it might be the case that the perishing of products already took place one period earlier (when the system was still up), the starting inventory in this case is $\bigl (S-d-(S-xd)^+\bigr )^+$, leading to a similar ending inventory as would be when the disruption would take place in this period (in which the system is disrupted for 1 period). So, when $i=1$, there are $x-2$ times ending inventories of $(S-2d)^+$, and 2 times ending inventories of $\bigl (S-2d-(S-xd)^+\bigr )^+$. When we set this reasoning forth, we end up with the expected holding cost, which is in the first line of the general cost function. The reasoning is similar for the backordering cost. Perishing might take place when the system is not disrupted, or disrupted for a time shorter than the lifetime of the products. This explains the last line of the general cost function.

Next, we analyze the expected cost function with an objective of finding the optimal base-stock level. The following theorem clarifies the shape of the expected cost function.

Theorem 2

$C(S)$ is a piece-wise linear function in $S$ with breakpoints at integer multiples of $d$.

Proof

As $S$ changes, $C(S)$ changes linearly until $S$ equals a multiple of $d$. This result is obvious for all the three components of $C(S)$. A more formal and straightforward proof can be provided by showing that the second order difference, $\Delta ^{2}C(S)$, is zero for the values of $0\le z<d$, where $\Delta ^{2}C(S)$ is defined as

$$\begin{aligned} \Delta ^{2}C(S)&= \Delta C(S+z)-\Delta C(S) \end{aligned}$$

where $\Delta C(S)$, the first order difference, is defined as

$$\begin{aligned} \Delta C(S)&= C(S+1)-C(S). \end{aligned}$$

$\square$

As an example, we draw Fig. 1, which shows how the components, i.e., the holding, backordering and perishability costs and the total expected cost change as $S$ is varied.

Fig. 1

$C(S)$ and the cost components vs. $S$, $d=2, x=4, h=1, b=5, p=3, \alpha =0.5$ and $\beta =0.5$

As expected, Fig. 1 suggests that the expected holding cost increases with $S$. The rate of this increase is higher when $S\le xd$. The decrease in the rate when $S>xd$ can be explained by the reduction of inventory due to perishing. In fact perishing only occurs when $S>xd$ and the expected perishing cost is linear in $S$ with a slope $pF(x-1)$. The expected backordering cost function has three different slopes. When $S<d$, we have fixed backorders each period, no matter what state the system is in. As we increase the base-stock level, backordering only occurs during disruptions, so the backordering cost decreases. When $S>dx$, the backordering cost does not depend on $S$ anymore, which results in a horizontal line. The slope of the expected cost function changes up to $S=xd$ and it is constant afterwards.

Using Theorem 2 we obtain the following result.

Corollary 1

The optimal base-stock level is an integer multiple of $d$.

Proof

The result follows directly from Theorem 2. Since the expected cost function is piece-wise linear, the optimal base-stock level can only be at one of the corner points, which are integer multiples of $d$. $\square$

Using the results in Theorem 2 and Corollary 1, we determine the exact shape of the cost function and obtain an expression for $S^{*}$. The following theorems summarize the results.

Theorem 3

The cost function $C(S)$ is

• 1. convex in $S$ for $S\le xd$,

• 2. linear and increasing $S$ for $S>xd$.

Proof

In order to understand the shape of the cost function, we derive the expressions for $\Delta C(S)$ and $\Delta ^{2} C(S)$. We initially assume $S<xd$. Based on this assumption, we can write $C(S)$, $\Delta C(S)$ and $\Delta ^{2} C(S)$ as follows:

$$\begin{aligned} C(S)&= h\sum ^{\frac{S}{d}-1}_{i=0}\pi _{i}\left( S-(i+1)d\right) +b\sum _{i=\frac{S}{d}}^{\infty }\pi _{i}\left( (i+1)d-S\right) \\ \Delta C(S)&= hdF(\frac{S}{d}-1)-bd\left( 1-F(\frac{S}{d}-1)\right) \nonumber \\ \Delta ^{2} C(S)&= hd\pi _{\frac{S}{d}}+bd\pi _{\frac{S}{d}} \nonumber \end{aligned}$$

(1)

Since $\Delta ^{2} C(S)\ge 0$, $C(S)$ is convex in $S$ if $S<xd$. If $S\ge xd$, we have

$$\begin{aligned} C(S)&= \frac{1}{x}h\sum ^{x-1}_{i=0}\pi _{i}(x-i-1)S+bd\sum ^{\infty }_{i=x}\pi _{i}(i+1-x)+p\sum ^{x-1}_{i=0}\pi _{i}(S-xd)\\ \Delta C(S)&= \frac{1}{x}h\sum ^{x-1}_{i=0}\pi _{i}(x-i-1)d+pd\sum ^{x-1}_{i=0}\pi _{i}\Delta ^{2} C(S)=0 \end{aligned}$$

These functions imply that $C(S)$ is linear and increasing in $S$ for $S\ge xd$. $\square$

According to this theorem, the cost function is convex up to a point and linearly increasing afterward. Therefore, if the convex part attains its minimum before $xd$, the optimal base-stock level is the minimum of the convex part. If, on the other hand, the minimum of this part of the function is greater than $xd$, the optimal base-stock level equals $xd$. We state the optimal base-stock level in Theorem 4.

Theorem 4

The optimal base-stock level, $S^{*}$, is $\text{ min } \biggl \{dF^{-1}(\frac{b}{h+b})+d,xd\biggr \}$.

Proof

Theorem 3 suggests that $C(S)$ is convex up to $xd$ and linearly increasing afterward. Therefore, the minimizer of this function is either the minimizer of the convex part or the cut-off point $xd$. The minimizer of the convex part can be found by solving the equation $\Delta C(S)=0$ and this results in $S^{*}=dF^{-1}(\frac{b}{h+b})+d$. Hence, in overall, we have $S^{*}=\text{ min } \left\{ dF^{-1}\left( \frac{b}{h+b}\right) +d,xd\right\}$.

3 Numerical analysis

In this section, we investigate the effects of disruptions and perishability on the expected cost function and the optimal base-stock level. In addition, we question the applicability of our method to a setting with stochastic demand. Finally, we elaborate on how to adapt our model to a case where certain system parameters are time-dependent.

3.1 Sensitivity of the cost function to disruption parameters

In this section, we analyze the effects of having long versus short disruptions, depending on recovery probability $\beta$, and also the effects of frequent and rare disruptions, depending on the disruption probability $\alpha$. As the base case, we use the following parameters: $d=2, x=4, h=1, b=5, p=3, \alpha =0.5$ and $\beta =0.5$ and we vary $\alpha$ from 0 to 0.8 and $\beta$ from 0.2 to 1 with 0.2 increments. The corresponding expected cost functions are depicted in Fig. 2a and b, respectively.

Fig. 2

Sensitivity of $C(S)$ to disruption parameters

The higher $\alpha$, the more frequent disruptions occur. During disruptions a high base-stock level helps to fulfill demand from stock. On the other hand, the higher $\beta$, the faster recoveries from disruptions. Hence, low base-stock level can be enough to avoid costly customer losses. These expectations are confirmed by Fig. 2a and b, respectively. More importantly, we observe that the effect of $\beta$ is more prominent than that of $\alpha$. For $\beta =0.5$, if we decrease $\alpha$ from 0.8 to 0.2, the optimal cost decreases by $21.92\,\%$ while for $\alpha =0.5$, if we increase $\beta$ from 0.2 to 0.8, the optimal cost decreases by $89.47\,\%$. This is an important observation which might help company managers in making decisions regarding their disruption management strategies. We suggest company managers to concentrate more on reducing the duration of disruptions, i.e., increasing $\beta$, instead of trying to avoid them.

3.2 Sensitivity of the cost function to lifetime

Next, we vary the lifetime $x$ and discuss the influence of the perishability on the total expected cost and optimal base-stock level. First, we show that as the lifetime goes to infinity, our model converges to the model in [10] adapted for deterministic demand.

Theorem 5

As $x\rightarrow \infty$,

• 1. $C(S)$ converges to $\sum ^{\infty }_{i=0}\pi _{i}\left( h\left( S-\left( i+1\right) d\right) ^+ +b\left( (i+1)d-S\right) ^+\right)$,

• 2. $S^{*}$ converges to $k^{*}d$ where $k^{*}$ is the smallest integer $k$ such that $F(k-1)\ge \frac{b}{h+b}$.

Proof

For all $x>\frac{S}{d}$, $C(S)$ is the same as in the Eq. (1). Refer to [10] for the proof of the second result. $\square$

This theorem suggests that, for given $\alpha$ and $\beta$ values, after a certain lifetime the optimal base-stock level converges. In fact, when the lifetime is short, it plays a more dominant role than the unit costs and the disruption distribution in determination of the optimal base-stock level. On the other hand, when the lifetime is long enough, it does not influence the choice of the optimal base-stock level. In fact the cut-off lifetime can be found by $\bar{x}=F^{-1}(\frac{b}{h+b})+1$. For any $x< \bar{x}$, $S^{*}=xd$ and for any $x\ge \bar{x}$, $S^{*}$ depends on the unit holding and backordering costs and the disruption distribution. As a result, our model converges to the one in [10] if $x\ge \bar{x}$.

Next, we use the same base case data as in Sect. 3.1, i.e., $d=2, x=4, h=1, b=5, p=3, \alpha =0.5$ and $\beta =0.5$, and analyze the sensitivity of the cost function and the optimal base-stock level to changes in the lifetime $x$. The first graph in Fig. 3 depicts the expected cost as a function of $S$ for different $x$ values. $\bar{x}$ is 3. For the products with short lifetimes the cost function is steeper around the optimal base-stock level. For these items the choice of the base-stock level has a bigger impact on the cost than for items with longer lifetimes. This observation emphasizes the importance of our study. More specifically, the adverse impact of using the models which assume infinite lifetime is more dominant when the actual lifetime is short.

Fig. 3

Sensitivity to lifetime

With the second graph in Fig. 3, we analyze the change in the optimal cost with respect to $x$ for multiple $\alpha$ and $\beta$ combinations. It shows that $\bar{x}$ is bigger for systems with frequent disruptions. Hence, if the retailer can manage to make his system safer, he can operate with the same expected cost even with products with shorter lifetimes. This figure also confirms our previous conclusion regarding the importance of concentrating more on increasing $\beta$ than decreasing $\alpha$.

3.3 Applicability of the model to stochastic demand case

Our model relies on some simplifying assumptions which enable us to write the expected cost function, find the closed form expression for the optimal base-stock level and get some insights on behavior of the system under specific circumstances. One of these assumptions is the deterministic demand. In fact, this assumption can be viewed as a stochastic demand being replaced by its mean. Therefore, up to this point our analysis ignores the deviation from the mean.

Next, we rely on a Monte Carlo simulation to compare the behavior of the expected cost functions under deterministic and stochastic demands. We use the same base case data as in Sect. 3.1. For the deterministic demand case, we have $d=20$ and for the stochastic demand case we have $E[d]=20$, where $E[\cdot ]$ stands for expectation. Assuming normally distributed demand, we use four different values, more specifically; $0,2,4$ and 6, for the standard deviation $\sigma$. We study 9 disruption profiles, i.e., $(\alpha , \beta )$ combinations, which are $(0.3,0.3)$, $(0.3,0.6)$, $(0.3,0.9)$, $(0.6,0.3)$, $(0.6,0.6)$, $(0.6,0.9)$, $(0.9,0.3)$, $(0.9,0.6)$ and $(0.9,0.9)$. Therefore, in total we have 36 different parameter combinations. We construct the expected cost functions for these combinations by running Monte Carlo simulations for base-stock values between 0 and 100. For each base-stock level, we simulate the system for 5,000 periods and determine the average cost per period, say $C_{i}(S)$. We run each simulation 50 times, i.e., $i\in \left\{ 1,2,\ldots ,50\right\}$. Then, we calculate the mean and standard deviation of the average costs per period. These are $C_{mean}(S)=\sum ^{50}_{i=1}C_{i}(S)$ and $C_{StDev}(S)=\sqrt{\frac{1}{49}\sum ^{50}_{i=1}(C_{i}(S)-C_{mean}(S))^{2}}$. We evaluate the accuracy of the estimated costs by building the following confidence intervals for each base-stock value in each parameter combination: $\Big (C_{mean}(S)-\frac{t_{49,1-\gamma /2}C_{StDev}(S)}{\sqrt{50}}, C_{mean}(S)+\frac{t_{49,1-\gamma /2}C_{StDev}(S)}{\sqrt{50}}\Big )$. We use $\gamma =0.95$ and $t_{49,0.025}=1.96$, where $t_{(49, 0.025)}$ is the critical value of a t-distribution with a significance level 0.95 and 49 degrees of freedom. We observe that the confidence intervals are very narrow especially for $(\alpha ,\beta )$ combinations with $\beta =0.6$ and $\beta =0.9$. Therefore, our sample size of 50 is enough to get accurate estimations for the average cost $C(S)$. The average cost functions for nine different disruption profiles are depicted in Figs. 4, 5 and 6. Note that the functions are very smooth for $\beta =0.6$ and $\beta =0.9$ but we have some fluctuations when $\beta =0.3$. However, these fluctuations do not influence the conclusions we draw from our analysis. This is why, we prefer not to increase our sample size. It is obvious that a bigger sample size would result in smoother graphs but the following conclusions would remain.

Fig. 4

Comparison of deterministic and stochastic demand cost functions, $\alpha =0.3$

Fig. 5

Comparison of deterministic and stochastic demand cost functions, $\alpha =0.6$

Fig. 6

Comparison of deterministic and stochastic demand cost functions, $\alpha =0.9$

Figures 4, 5 and 6 suggest that the shapes of the expected cost functions are quite similar for the deterministic and stochastic demand cases. The optimal base-stock levels are the same when disruptions are rather rare and short. When disruptions happen very often and long time is required to recover from them, stochastic demand case suggest keeping less inventory then deterministic demand (but still more than the case with rare and short disruptions). The difference is negative safety stock. Keeping more inventory than demand might result in high perishing costs. Hence, negative safety stocks can provide better solutions in terms of expected cost. Finally, Figs. 4, 5 and 6 suggest that the difference between the deterministic and stochastic cost functions slightly increases with $\sigma$.

3.4 Time dependency of the disruption distribution

Another simplifying assumption we made to get closed-from expressions is that the system parameters are time-independent. No matter what the state of the world is, the values of the parameters are always the same. However, in real life, the parameter values might change over time. For example, when we know that farmers will go on a strike; the disruption probability of milk supply might increase. By fast agreements, the recovery probability can be increased.

Next, we show, via a simple example, how our model can be used to handle situations like this with time-dependent parameter values. We adapt the idea of Markov Modulated Process (MMP) in such a way that an arbitrarily chosen probability distribution determines the state of the world. For simplicity, we assume a two-state world with states $0$ and $1$. The system parameters in state $0$ are different from the ones in state $1$. With a certain probability $P_{s}$, the world is in state $s\in \left\{ 0,1\right\}$. The idea can easily be extended to a world with more than two states. Representing $C_{s}(S)$ to be the expected cost function for a given base-stock level $S$ when the system is in state $s$, we can calculate the expected cost as

$$\begin{aligned} C(S)=P_{0}C_{0}(S)+P_{1}C_{1}(S) \end{aligned}$$

Using this idea, we analyze the effect of the disruption length on $S^{*}$, by assuming that, it is exactly $L_{s}$ if the system is in state $s\in \left\{ 0,1\right\}$. We choose $L_{s}$ so that $L_{0}<x$ and $L_{1}>x$. In order to make the system even more realistic, we also assume the cost of the first backorder is more expensive than the next backorders. A very extreme example of this is when a patient needs blood transplantation every period. If a backorder occurs in the very first period, the patient might not survive. This leads to the needlessness of the future deliveries and makes the first backorder much more expensive than the next ones.

Representing the unit cost of the first backordering situation with $b_{1}$, we use the following parameters $h=1, b=5, b_{1}=100, p=3, d=2, x=4, L_{0}=1$ and $L_{1}=6$ and calculate $S^{*}$ and $C(S^{*})$ for multiple $(P_{0},P_{1})$ combinations and two different $\alpha$ values. Table 6 summarizes the results.

Table 6 Analysis of the state-dependent disruption lengths and different unit backordering costs

Here we see that when $b_{1}>>b$, the optimal base-stock level goes up for those cases in which the relative number of short disruptions is high. Note that the optimal base-stock level goes up to 4 (for $\alpha =0.05$), since this amount is needed to keep fulfilling the demand from inventory when a disruption lasts only one period. However, as the frequency of disruptions increases ($\alpha =0.5$), having $b_{1}>>b$ does not effect the optimal base-stock level. Independent of the first backorder’s cost, the system needs more inventory to protect against frequent disruptions.

4 Conclusions

In this paper, we study a retailer carrying perishable products with fixed lifetime. Retailer’s supply process is subject to random disruptions. Assuming a base-stock policy, deterministic demand and stationary parameters, we derive the expression for the expected cost function which consists of holding, backordering and perishing costs. After determining the exact shape of the expected cost function, we obtain the closed form expression for the optimal base-stock level. Via numerical analysis we study sensitivity of the cost and the optimal base-stock level to changes in the system parameters.

We show that perishability influences the optimal base-stock level by putting a limit on it. We argue that for products with short lifetimes the choice of the optimal base-stock level is more important than for products with long lifetimes, since in the former case the cost function is much steeper. In fact, our analysis can be used as a supporting tool for decision making on investing in an afford of increasing the lifetime.

We show how our model with deterministic demand can be used for systems with stochastic demand. In addition, we adapt our model to handle the cases with non-stationary system parameters. This adapted model enables us to find more precise insights about the influence of the duration of a disruption on the optimal base-stock level for perishables.

Our model relies on multiple simplifying assumptions. These enable us to obtain some basic insights, which can greatly help retailers carrying perishable products in making inventory related decisions. Although we show how to use our model for the stochastic demand case, the proposed solution might not be optimal. In addition, our solution is numerical. Further research is needed to obtain analytical results for a system with stochastic demands and random lifetimes.

We assume that regardless of their age, inventories are treated as equivalent units and the order size is related to satisfied demand only. In a more realistic setting, one can consider a base-stock policy with increasing orders as the age increases. This extension would necessitate optimization of multiple base-stock levels.

Another future research direction, which can help in mimicking the real-world systems more closely, is to consider supply systems with multiple overlapping disruption profiles. It is obvious that these extensions require more complicated analysis. However, this paper can serve as a base and our results can be used as a starting point in developing exact or approximate models.