1 Introduction

The short-term unit commitment (UC) problem is one of the critical tasks that is daily performed by different actors in the electricity sector. Depending on the purpose, the UC is solved under centralized or competitive environments, from self-scheduling to centralized auction-based market clearing, over a time horizon ranging from one day to one week.

In general, the UC main objective is to meet demand at minimum cost while operating the system and units within secure technical limits [4, 11, 22]. The UC problem can then be defined as:

$$\begin{aligned} \min _{\varvec{x},\varvec{p}}\quad&\mathbf {b}^{\top }\varvec{x}+\mathbf {c}^{\top }\varvec{p} \end{aligned}$$
$$\begin{aligned} \mathrm {s.t.}\quad&\mathbf {F}\varvec{x}\le \mathbf {f},\;\varvec{x} \text{ is } \text{ binary }\end{aligned}$$
(1)
$$\begin{aligned}&\mathbf {H}\varvec{p}\le \mathbf {h}\end{aligned}$$
(2)
$$\begin{aligned}&\mathbf {A}\varvec{x}+\mathbf {B}\varvec{p}\le \mathbf {g}, \end{aligned}$$
(3)

where \(\varvec{x}\) and \(\varvec{p}\) are decision variables. The binary variable \(\varvec{x}\) is a vector of commitment-related decisions (e.g., on/off and startup/shutdown) of each generation unit for each time interval over the planning horizon. The continuous variable \(\varvec{p}\) is a vector of each unit dispatch decision for each time interval.

The objective function is to minimize the sum of the commitment cost \(\mathbf {b}^{\top }\varvec{x}\) (including non-load, startup and shutdown costs) and dispatch cost \(\mathbf {c}^{\top }\varvec{p}\) over the planning horizon. Constraint (1) involves only commitment-related variables, e.g., minimum up and down times, startup and shutdown constraints, and variable startup costs. Constraint (2) contains dispatch-related constraints, e.g., energy balance (equality can always be written as two opposite inequalities), reserve requirements, transmission limits and ramping constraints. Constraint (3) couples the commitment and dispatch decisions. e.g., minimum and maximum generation capacity constraints. The reader is referred to [11, 14, 16, 18, 19, 21–23, 26] and references therein for further details.

Conventional UC formulations, based on energy scheduling [11, 19, 21, 22, 26], do not represent the unit operation adequately, because they fail to guarantee that the resulting energy schedules can be delivered [10, 15]. To illustrate this problem, consider the following scheduling example for one generating unit. This example assumes that the minimum and maximum generation outputs of the unit are 100 and 300 MW, respectively, and that the unit can ramp up from the minimum to the maximum output in 1 h, i.e., 200 MW/h of ramp rate. As shown in Fig. 1a, if the unit has been producing 100 MW during the first hour, then the unit can produce at its maximum output (300 MW) for the next hour. This would be a natural energy schedule resulting from the traditional UC formulations, which are based on the energy scheduling approach. However, the unit is just physically capable of reaching its maximum output before the end of the second hour due to its limited ramp rate, as shown in Fig. 1b. Consequently, the solution obtained in Fig. 1a is not feasible. In fact, the unit requires an infinite ramping capability to be able to reproduce the energy schedule presented in Fig. 1a. More examples about this energy infeasibility problem can be found in [10, 14, 15] and references therein.

Fig. 1
figure 1

Scheduling versus deployment

Full size image

Another drawback of conventional UC formulations is that generating units are assumed to start/end their production at their minimum output. That is, their intrinsic startup and shutdown power trajectories are ignored. As a consequence, there is a high amount of energy that is not allocated by UC, but it is inherently present in real time, thus causing a negative economic impact [17] and also demanding a larger quantity of operating reserves to the system [14]. Although some recent works are aware of the importance of including the startup and shutdown processes in UC problems, these power trajectories continue being ignored because the resulting model is considered to largely increase the complexity of the UC problem and hence its computational intensity [3, 8, 13]. For further details of the drawbacks of conventional UC scheduling approaches, the reader is referred to [15, 18] and references therein.

Developing more accurate models would be pointless if they cannot be solved fast enough. Under the mixed integer programming (MIP) approach, it is important to develop tight formulations to reduce the UC computational burden. This allows the implementation of more advanced and computationally demanding problems. A different set of constraints has been proposed to tighten the UC problem [2, 9, 12, 16, 17, 20] . The work in [12, 20] formulates the convex hull of the minimum up and down times. Cuts to tighten ramping limits are presented in [2]. A tighter approximation for quadratic generation costs is proposed [7]. Simultaneously tight and compact MIP formulations for thermal units operation are devised in [9, 16, 17].

To overcome the drawbacks of conventional UC formulations, the model proposed in this paper draws a clear difference between power and energy, and it also takes into account the normally neglected power trajectories that occur during the startup and shutdown processes. Thus, this model adequately represents the operation of generating units to efficiently exploit their flexibility and to avoid infeasible energy delivery. This paper further improves the work in [17] by including the operation of quick-start units and providing the convex hull description for the following set of constraints: generation limits, minimum up and down times, startup and shutdown power trajectories for slow-start units, and startup and shutdown capabilities for quick-start units. Although these convex hulls do not consider some crucial constraints such as ramping, the proposed constraints can be used as the core of any power-based UC formulation, thus tightening the final UC model. In addition, two sets of case studies are carried out: (1) different case studies for a self-UC problem where we only take into account the constraints proposed in this paper, and hence the proposed convex hulls allow solving these self-UC (MIP) instances as linear programs (LP); (2) different case studies for a network-constrained UC problem, where other common constraints are taken into account, such as demand balance, reserves, ramping and transmission limits. These numerical experiments show that the proposed power-based UC formulations solve the MIP problems significantly faster when compared with two other (energy-based) UC formulations commonly known in the literature.

The remainder of this paper is organized as follows. Section 2 introduces the main nomenclature used in this paper. Section 3 details the operating constraints of a single slow- and quick-start unit. In Sect. 4, we provide a convex hull proof for the power-based UC including the constraints mentioned above. Section 5 provides and discusses results from several case studies, where a computational performance comparison with two other traditional UC formulations is made. Finally, some relevant conclusions are drawn in Sect. 6.

2 Nomenclature

Here, we introduce the main notation used in this paper. Lowercase letters are used to denote variables and indexes. Uppercase letters denote parameters.

2.1 Definitions

In this paper, we use the terminology introduced in [17] to refer to the different unit operation states; see Fig. 2.

online :

the unit is synchronized with the system.

offline :

the unit is not synchronized with the system.

up :

the unit is producing above its minimum output. During the up state, the unit output is controllable.

down :

the unit is producing below its minimum output: when offline, starting up or shutting down.

Fig. 2
figure 2

Operating states including startup and shutdown power trajectories for slow-start units

Full size image

2.2 Indexes

\(t\) :

Time periods, running from 1 to \(T\) hours.

2.3 Unit’s technical parameters

\(C^{\mathrm {LV}}\) :

Linear variable cost [$/MWh].

\(C^{\mathrm {NL}}\) :

No-load cost [$/h].

\(C^{\mathrm {SD}}\) :

Shutdown cost [$].

\(C^{\mathrm {SU}}\) :

Startup cost [$].

\(\overline{P}\) :

Maximum power output [MW].

\(\underline{P}\) :

Minimum power output [MW].

\(P_{i}^{\mathrm {SD}}\) :

Power output at the beginning of the \({i}\)th interval of the shutdown ramp process [MW]; see Fig. 2.

\(P_{i}^{\mathrm {SU}}\) :

Power output at the beginning of the \({i}\)th interval of the startup ramp process [MW]; see Fig. 2.

SD:

Shutdown capability [MW]; see Fig. 3.

SU:

Startup capability [MW]; see Fig. 3.

\(\mathrm{SD}^{\mathrm {D}}\) :

Duration of the shutdown process [h]; see Fig. 2.

\(\mathrm{SU}^{\mathrm {D}}\) :

Duration of the startup process [h]; see Fig. 2.

TD:

Minimum down time [h].

TU:

Minimum up time [h].

2.4 Continuous decision variables

\(e_{t}\) :

Total energy production during period \(t\) [MWh].

\(p_{t}\) :

Power output at the end of period \(t\), and production above the minimum output \(\underline{P}\) [MW].

\(\widehat{p}_{t}\) :

Total power output at the end of period \(t\), including startup and shutdown power trajectories [MW].

Fig. 3
figure 3

Startup and shutdown capabilities for quick-start units

Full size image

2.5 Binary decision variables

\(u_{t}\) :

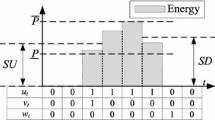
Commitment status of the unit for period \(t\), which is equal to 1 if the unit is up, and 0 if it is down; see Fig. 2.

\(v_{t}\) :

Startup status of the unit, which takes the value of 1 if the unit starts up in period \(t\) and 0 otherwise; see Fig. 2.

\(w_{t}\) :

Shutdown status of the unit, which takes the value of 1 if the unit shuts down in period \(t\) and 0 otherwise; see Fig. 2.

3 Modeling the unit’s operation

The constraints presented here are a further extension of our previous work in [17]. Here, we generalize the formulation by considering quick-start units.

The quick-start units are defined as those that can ramp up from 0 to any value between \(\underline{P}\) and SU within one period, typically 1 h, as shown in Fig. 3. Similarly, they can also ramp down from any value between SD and \(\underline{P}\) to 0 within one period. On the other hand, the slow-start units are defined as those units that require more than one period to ramp up (down) from 0 (\(\underline{P}\)) to \(\underline{P}\) (0); see Fig. 2.

The up and down states are distinguished from the online and offline states. Figure 2 shows the different operation states of a thermal unit, as defined in Sect. 2. During the up period (\(u_{t}=1\)), the unit has the flexibility to follow any power trajectory being bounded between the maximum and minimum output. On the other hand, for slow-start units, the power output follows a predefined power trajectory when the unit is starting up or shutting down. The startup and shutdown power trajectories for quick-start units are defined by the startup and shutdown capabilities; see Fig. 3.

This section first presents the basic operating constraints that applies for both slow- and quick-start units. However, the total unit’s production output is different for each of them. Sections 3.2 and 3.3 show how to obtain the total production, power and energy for slow- and quick-start generating units, respectively.

3.1 Basic operating constraints

The unit’s generation limits taking into account startup SU and shutdown SD capabilities, which are SU, SD \(\ge \underline{P}\) by definition, are set as follows; see Fig. 3:

$$\begin{aligned} p_{t}\le&\left( \overline{P}-\underline{P}\right) u_{t}-\left( \overline{P}-\text {SD}\right) w_{t+1}+\left( \text {SU}-\underline{P}\right) v_{t+1}\quad t\in \left[ 1,T-1\right] \end{aligned}$$
(4)
$$\begin{aligned} p_{T}\le&\left( \overline{P}-\underline{P}\right) u_{T}\end{aligned}$$
(5)
$$\begin{aligned} p_{t}\ge&0\quad \forall t \end{aligned}$$
(6)

and the logical relationship between the decision variables \(u_{t}\), \(v_{t}\) and \(w_{t}\); and the minimum uptime TU and downtime TD limits are ensured with

$$\begin{aligned} u_{t}-u_{t-1}&=v_{t}-w_{t}\quad \forall t\in \left[ 2,T\right] \end{aligned}$$
(7)
$$\begin{aligned} \sum _{i=t-TU+1}^{t}\quad v_{i}&\le u_{t}\quad \forall t\in \left[ TU+1,T\right] \end{aligned}$$
(8)
$$\begin{aligned} \sum _{i=t-TD+1}^{t}\quad w_{i}&\le 1-u_{t}\quad \forall t\in \left[ TD+1,T\right] \end{aligned}$$
(9)
$$\begin{aligned} 0&\le u_{t}\le 1\quad \forall t\end{aligned}$$
(10)
$$\begin{aligned} 0\le v_{t}\le 1,\quad 0&\le w_{t}\le 1\quad \forall t\in \left[ 2,T\right] , \end{aligned}$$
(11)

where (7)–(9) describe the convex hull formulation of the minimum up and down time constraints proposed in [20].

3.2 Slow-start units

The slow-start units are assumed to produce \(\underline{P}\) at the beginning and at the end of the up state; see Fig. 2. At those points, the startup and shutdown power trajectories are as shown in Fig. 2. Consequently, constraints (4)–(11) describe the operation of slow-start units during the up state when SU, SD \(= \underline{P}\).

The minimum down time TD is a function of the minimum offline time, i.e., TD is equal to the startup and shutdown duration processes \((\mathrm{SU}^\mathrm{D}+\mathrm{SD}^\mathrm{{D}}\)) plus the minimum offline time of the unit. This then avoids the possible overlapping between the startup and shutdown trajectories. That is, constraint (9) ensures that the unit is down (\(u_{t}=0\)) for enough time to fit the unit’s startup and shutdown power trajectories.

As presented in [17], the total power output including the startup and shutdown power trajectories for slow-start units is obtained with

$$\begin{aligned} \widehat{p}_{t}= \underbrace{\underline{P}\left( u_{t}+v_{t+1}\right) +p_{t}}_{\text{(i) } \text{ Output } \text{ when } \text{ being }\,{up}}+\underbrace{\sum _{i=1}^\mathrm{{SU}^\mathrm{{D}}}P_{i}^\mathrm{{SU}}v_{t-i+\text {SU}^\mathrm{{D}}+2}}_\mathrm{{(iii)~\mathrm {SU}\, trajectory}}+\underbrace{\sum _{i=2}^{\text {SD}^\mathrm{{D}}+1}P_{i}^{\text {SD}}w_{t-i+2}}_\mathrm{{(ii)~SD\, trajectory}}\quad \forall t. \end{aligned}$$
(12)

For a better understanding of (12), we can analyze how the power trajectory example in Fig. 2 is obtained from the three different parts in (12):

  1. (i)

    Output when the unit is up: Although the unit is up for five consecutive hours, there are six total power values that are greater than or equal to \(\underline{P}\), from \(\widehat{p}_{4}\) to \(\widehat{p}_{9}\) (see the squares in Fig. 2). When \(t=4\), the term \(v_{t+1}\) in (i) becomes \(v_{5}\) ensuring (the first) \(\underline{P}\) at the beginning of the \(up\) period, and the term \(u_{t}\) adds (the remaining five) \(\underline{P}\) for \(t=5\ldots 9\). In addition, \(p_{t}\) adds the power production above \(\underline{P}\).

  2. (ii)

    Shutdown power trajectory: This process lasts for 2 h, \(\mathrm{SD}^{\mathrm {D}}=2\); then, the summation term (ii) becomes \(P_{2}^{\mathrm {SD}}w_{t}+ P_{3}^{\mathrm {SD}}w_{t-1}\), which is equal to \(P_{2}^{\mathrm {SD}}\) for \(t=10\) and \(P_{3}^{\mathrm {SD}}\) for \(t=11\), being zero otherwise. This provides the shutdown power trajectory (see the circles in Fig. 2).

  3. (iii)

    Startup power trajectory: The startup power trajectory can be obtained using a procedure similar to that used in (ii) (see the triangles in Fig. 2).

Similarly to (12), the total energy production for slow-start units is given by

$$\begin{aligned} e_{t}\!=\! \underline{P}\cdot u_{t}\!+\!\frac{p_{t}\!+\!p_{t-1}}{2}+\sum _{i=1}^{\text {SD}^{\mathrm {D}}}\!\frac{P_{i+1}^{\text {SD}}\!+\!P_{i}^{\text {SD}}}{2}w_{t-i+1}+\sum _{i=1}^{\text {SU}^{\text {D}}}\frac{P_{i+1}^{\text {SU}}\!+\!P_{i}^{\text {SU}}}{2}v_{t-i+\text {SU}^{\mathrm {D}}+1}\quad \forall t \end{aligned}$$
(13)

3.3 Quick-start units

The total power for a quick-start unit is given by

$$\begin{aligned} \widehat{p}_{t}= \underline{P}\left( u_{t}+v_{t+1}\right) +p_{t}\quad \forall t \end{aligned}$$
(14)

and the total energy production is

$$\begin{aligned} e_{t}= \frac{\underline{P}\left( 2u_{t}+v_{t+1}+w_{t}\right) +p_{t-1}+p_{t}}{2}\quad \forall t. \end{aligned}$$
(15)

It is interesting to note that even though SU, SD \(\ge \underline{P}\) (by definition), the resulting energy from (15) may take values below \(\underline{P}\) during the startup and shutdown processes; see Fig. 3.

The energy for slow- and quick-start units can also be obtained as a function of the total power output \(\widehat{p}_{t}\), \(e_{t}=\frac{\widehat{p}_{t}+\widehat{p}_{t-1}}{2}\) for all \(t\). However sometimes only the total power, (12) and (14), or the total energy, (13) and (15), production is needed as a function of \(p,u,v,w\).

Notice that (12)–(15) are defined for all \(t\) and use variables that are outside the scheduling horizon \(\left[ 1,T\right] \). Those variables are considered to be equal to zero when their subindex is \(t<1\) or \(t>T\).

In summary, constraints (4)–(11), when SU, SD\(=\underline{P}\), together with (12) and (13) describe the technical operation of slow-start units. Constraints (4)–(11) together with (14) and (15) describe the technical operation of quick-start units.

3.4 Total unit operation cost

The objective function of any UC problem involves the total unit operation costs of each generating unit \(c_{t}\), which is defined as follows:

$$\begin{aligned} c_{t}=C^{\mathrm {NL}}u_{t}+C^{\mathrm {LV}}e_{t}+C^{\mathrm {SU}^{\prime }}v_{t}+C^{\mathrm {SD}^{\prime }}w_{t}. \end{aligned}$$
(16)

Note that the no-load cost (\(C^{\mathrm {NL}}\)) considered in (16) ignores the startup and shutdown periods. This is because the \(C^{\mathrm {NL}}\) only multiplies the commitment during the up state \(u_{t}\). To consider the no-load cost during the startup and shutdown periods, \(C^{\mathrm {SU}^{\prime }}\) and \(C^{\mathrm {SD}^{\prime }}\) are introduced in (16) and defined as:

$$\begin{aligned} C^{\mathrm {SU}^{\prime }}= & {} C^{\mathrm {SU}}+C^{\mathrm {NL}}SU^{\mathrm {D}}\end{aligned}$$
(16a)
$$\begin{aligned} C^{\mathrm {SD}^{\prime }}= & {} C^{\mathrm {SD}}+C^{\mathrm {NL}}SD^{\mathrm {D}}, \end{aligned}$$
(16b)

where \(\mathrm{SU}^{\mathrm {D}},\mathrm{SD}^{\mathrm {D}}=1\) for quick-start units; see Fig. 3.

4 Convex hull proof

In this section, we first prove that inequalities (4)–(6) are facet defining and then that inequalities (4)–(11) define an integral polytope. Finally, we also prove that inequalities describing the operation of slow-start units, (4)–(11) together with equalities (12)–(13), define an integral polytope. Similarly, inequalities describing the operation of quick-start units, (4)–(11) together with equalities (14)–(15), also define an integral polytope.

Note that the variables \(w_{t}\) are completely determined in terms of \(u_{t}\) and \(v_{t}\) using (7). Therefore, in the following we eliminate variables \(w_{t}\) and assume that constraints (4), (9), and (11) are reformulated accordingly.

Fig. 4
figure 4

\(3T\) Affinely independent points for \(g_{t},g^{T}=0\), \(g_{t}^{y}=P\) and \(g_{t}^{z}=U\), where \(U=SU-\underline{P}\), \(D=SD-\underline{P}\) and \(P=\overline{P}-\underline{P}\)

Full size image

Definition 1

Let \(\overline{D}_{T}\left( \mathrm{TU, TD},\overline{P},\underline{P},\mathrm{SU, SD}\right) =\{ \left( u,v,p\right) \in \mathbb {R}_{+}^{3T-1}|\left( u,v,p\right) \) satisfy (4)–(11)}. Let \(\overline{C}_{T}\left( \mathrm{TU, TD},\overline{P},\underline{P},\mathrm{SU, SD}\right) \) be the convex hull of the points in \(\overline{D}_{T}\left( \mathrm{TU,TD}, \overline{P},\underline{P},\mathrm{SU, SD}\right) \) such that \(u\in \left\{ 0,1\right\} ^{T}\), \(v\in \left\{ 0,1\right\} ^{T-1}\).

For short, we denote \(\overline{C}_{T}\left( \mathrm{TU,TD},\overline{P},\underline{P},\mathrm{SU,SD} \right) \) by \(\overline{C}_{T}\) and \(\overline{D}_{T}\left( \mathrm{TU,TD},\overline{P},\underline{P},\mathrm{SU,SD}\right) \) by \(\overline{D}_{T}\).

To facilitate the proofs, we introduce the points \(x^{i},y^{i},z^{i}\in \overline{C}_{T}\), as shown in Fig. 4. We also introduce the parameters \(U,D\) and \(P\) which are equivalent to \(U=\mathrm{SU}-\underline{P}\), \(D=\mathrm{SD}-\underline{P}\) and \(P=\overline{P}-\underline{P}\), respectively.

Proposition 1

\(\overline{C}_{T}\) is full dimensional in terms of \(u,v\) and \(p\).

Proof

From Fig. 4, it can be easily shown that the \(3T\) points \(x^{i},y^{i}\) and \(z^{i}\) for \(i\in \left[ 1,T\right] \) are affinely independent when \(g_{t},g^{T}=0\), \(g_{t}^{y}=P\) and \(g_{t}^{z}=U\). Note that in case \(D=0,\) the point \(y^{\left( 1\right) }\) must be removed and the point \(y^{\left( T+1\right) }\) added, thus keeping the \(3T\) affinely independent points. This applies for all the following proofs; but for the sake of brevity, we assume from now on that \(D\ne 0\). \(\square \)

Theorem 1

The inequalities in (4) describe facets of the polytope \(\overline{C}_{T}\).

Proof

We show that (4) describe facets of \(\overline{C}_{T}\) by the direct method [25]. We do so by presenting \(3T-1\) affinely independent points in \(\overline{C}_{T}\) that are tight (satisfying as an equality) for the given inequality. Note in Fig. 4 that the point \(z^{T}\) (the origin) satisfies (4)–(6) as equality. Therefore, to get \(3T-1\) affinely independent points, we need only \(3T-2\) other linearly independent points.

The following \(3T-2\) points are linearly independent and tight for (4) when \(g^{T}=0\), \(g_{t},g_{t}^{y}=P\) and \(g_{t}^{z}=U\): \(T-1\) points \(x^{i}\) for \(i\in \left[ 1,t-1\right] \cup \left[ t+1,T\right] \), \(T\) points \(y^{i}\) for \(i\in \left[ 1,T\right] \), and \(T-1\) points \(z^{i}\) for \(i\in \left[ 1,T-1\right] \). \(\square \)

Theorem 2

The inequality (5) describes a facet of the polytope \(\overline{C}_{T}\).

Proof

As mentioned before, it suffices to show \(3T-2\) linearly independent points that are tight for (5). The following \(3T-2\) points are linearly independent and tight for (5) when \(g_{t}=0\), \(g^{T},g_{t}^{y}=P\) and \(g_{t}^{z}=U\): \(T\) points \(x^{i}\) for \(i\in \left[ 1,T\right] \), \(T-1\) points \(y^{i}\) for \(i\in \left[ 1,T-1\right] \), and \(T-1\) points \(z^{i}\) for \(i\in \left[ 1,T-1\right] \). \(\square \)

Theorem 3

The inequalities in (6) describe facets of the polytope \(\overline{C}_{T}\).

Proof

The following \(3T-2\) points are linearly independent and tight for (6) when \(g_{t},g_{t}^{y},g_{t}^{z},g^{T}=0\): \(T\) points \(x^{i}\) for \(i\in \left[ 1,T\right] \), \(T-1\) points \(y^{i}\) for \(i\in \left[ 1,t-1\right] \cup \left[ t+1,T\right] \), and \(T-1\) points \(z^{i}\) for \(i\in \left[ 1,T-1\right] \). \(\square \)

We may conclude that (4)–(6) describe facets of \(\overline{C}_{T}\).

Now, we prove that the inequalities (4)–(11) are sufficient to describe the convex hull of the feasible solutions.

We need a preliminary lemma.

Lemma 1

Let \(P=\{x\in \mathbb {R}^{n}|Ax\le b\}\) be an integral polyhedron, i.e, \(P=conv(P\cap \mathbb {Z}^{n})\). Define \(Q=\{(x,y)\in \mathbb {R}^{n}\times \mathbb {R}^{m}|x\in P,0\le y_{i}\le c_{i}x,i=1,\ldots ,k\), \(y_{i}=d_{i}x,i=k+1,\ldots ,m\}\), where \(1\le k\le m\), \(c_{i},d_{i}\in \mathbb {R}^{n}\), and \(c_{i}x\ge 0\), \(d_{i}x\ge 0\) for \(i=1,\ldots ,m\) and for each \(x\in P\). Then every vertex \((\tilde{x},\tilde{y})\) of \(Q\) has the property that \(\tilde{x}\) is integral.

Proof

Suppose by contradiction that there exists a vertex \((\tilde{x},\tilde{y})\) of \(Q,\) such that \(\tilde{x}\) is not integral. Then, \(\tilde{x}\) is not a vertex of \(P\) and therefore there exist \(\bar{x}^{1},\bar{x}^{2}\in P,\) such that \(\tilde{x}=\frac{1}{2}\bar{x}^{1}+\frac{1}{2}\bar{x}^{2}\). Moreover, \(\tilde{y}_{i}=c_{i}\tilde{x}\) for \(i=1,\ldots ,k\); indeed, if there exists \(r\), \(1\le r\le k\), such that \(0\le \tilde{y}_{r}<c_{r}\tilde{x}\), then \((\tilde{x},\tilde{y})\) is a convex combination of the point \((\tilde{x},\hat{y})\) and the point \((\tilde{x},\check{y})\), where \(\hat{y}_{r}=c_{r}\tilde{x}\), \(\check{y}_{r}=0\), and \(\hat{y}_{i}=\check{y}_{i}=\tilde{y}_{i}\) for \(1\le i\le m\), \(i\ne r\).

For \(j=1,2\), let \(\bar{y}_{i}^{j}=c_{i}\bar{x}^{j}\) for \(i=1,\ldots ,k\) and \(\bar{y}_{i}^{j}=d_{i}\bar{x}^{j}\) for \(i=k+1,\ldots ,m\). Then \((\tilde{x},\tilde{y})=\frac{1}{2}(\bar{x}^{1},\bar{y}^{1})+\frac{1}{2}(\bar{x}^{2},\bar{y}^{2})\), i.e., \((\tilde{x},\tilde{y})\) is a convex combination of \((\bar{x}^{1},\bar{y}^{1})\) and \((\bar{x}^{2},\bar{y}^{2})\). Contradiction. \(\square \)

Theorem 4

The polytopes \(\overline{C}_{T}\) and \(\overline{D}_{T}\) are equal.

Proof

The thesis can be proved by showing that \(\overline{D}_{T}\) defines an integral polytope. This easily follows by applying Lemma 1, considering \(P\) as the integer polytope defined by inequalities (8)–(11) (see [20]), \(p_{t}\) as the additional variables and (4)–(6) as the new inequalities.

Finally, we prove that inequalities describing the operation of slow- and quick-start units to define integral polytopes. \(\square \)

Definition 2

Let the polytope that describes the operation of slow-start units be \(\overline{S}_{T}(\mathrm{TU,TD},\overline{P},\underline{P},\mathrm{SU}^{\mathrm {D}},\mathrm{SD}^{\mathrm {D}},P_{i}^{\mathrm {SU}},P_{i}^{\mathrm {SD}})=\{ (u,v,p,\widehat{p},e)\in \mathbb {R}_{+}^{5T-1}|(u,v,p)\) satisfying inequalities (4)–(13) for SU, SD \(=\underline{P}\)}, for short denoted as \(\overline{S}_{T}\). Let the polytope that describes the operation of quick-start units be \(\overline{Q}_{T}(\mathrm{TU,TD},\overline{P},\underline{P}, \mathrm{SU,SD},)\) \(=\{ (u,v,p,\widehat{p},e)\in \mathbb {R}_{+}^{5T-1}|(u,v,p)\) satisfying inequalities (4)–(11)} and (14)–(15)\(\} \), for short denoted as \(\overline{Q}_{T}\).

Theorem 5

The polytopes \(\overline{S}_{T}\) and \(\overline{Q}_{T}\) define integer polytopes on variables \(u,v\).

Proof

This easily follows by applying Lemma 1. For the polytope describing the operation of slow-start units \(\overline{S}_{T}\), \(P\) is the integer polytope \(\overline{D}_{T}\) (see Theorem 4), \(\widehat{p}_{t},e_{t}\) are the additional variables, and (12)–(13) the new equalities. Similarly, for the polytope describing the operation of quick-start units \(\overline{Q}_{T}\), \(P\) is the integer polytope \(\overline{D}_{T}\), \(\widehat{p}_{t},e_{t}\) are the additional variables, and (14)–(15) the new equalities. \(\square \)

Concluding, the constraints describing the technical operation of both slow- and quick-start units are convex hulls. These constraints are (4)–(11), when SU, SD \(=\underline{P}\), together with (12) and (13) for slow-start units; and (4)–(11) together with (14) and (15) for quick-start units.

In short, the entire formulation (4)–(15) defines an integral polytope.

5 Numerical results

To illustrate the computational performance of the formulation proposed in this paper, two sets of case studies are carried out: one for a self-UC problem and another for a network-constrained UC problem. This section compares the computational performance of the proposed power-based formulation with two energy-based formulations, [1] and [4], which have been recognized as computationally efficient in the literature [14, 18, 23].

The following three formulations are then implemented:

  • Pw: This is the complete formulation proposed in this paper. For the network-constrained UC, we include other common constraints such as demand balance, reserves, ramping and transmission limits. The complete network-constrained power-based UC is presented in Appendix .

  • 1bin: This formulation is presented in [1] and requires a single set of binary variables (per unit and per period), i.e., the startup and shutdown decisions are expressed as a function of the commitment decision variables.

  • 3bin: The convex hull of the minimum up/down time constraints proposed in [20] [see (8) and (9)] are implemented with the three-binary equivalent formulation of 1bin. This formulation is presented in [4].

Notice that a different set of constraints is used for the self-UC and for the network-constrained UC problems. For the self-UC problems, 1bin and 3bin are modeled only considering (1) generation limits, (2) minimum up and down times, and (3) startup and shutdown capabilities: the same set of constraints presented in Sect. 3. For the network-constrained UC problems, 1bin and 3bin are modeled taking into account the full set of constraints presented in [1] and its 3-bin equivalent [4], respectively; in addition, these formulations are further extended by introducing downward reserve (which is modeled in the same fashion as the upward reserve; see [1, 14, 16]), transmission limits [see (22) in Appendix ] and wind generation [which is taken into account in the demand balance (19) and transmission-limit constraints (22)].

It is important to highlight that the energy-based UC formulations 1bin and 3bin represent the same mixed-integer optimization problem. The difference between them is how the constraints are formulated. In other words, for a given case study, 1bin and 3bin obtain the same optimal results, e.g., commitments, generating outputs and operation costs. On the other hand, the power-based formulation obtains different optimal results, since the constraints are based on power-production variables rather than energy-output variables. The reader is referred to [14, 18] for further and detailed discussions about the differences between the optimal power-based and energy-based scheduling.

All tests were carried out using CPLEX 12.5 on an Intel-i7 3.4-GHz personal computer with 8 GB of RAM memory. The problems are solved until they hit the time limit of 10,000 s or until they reach optimality (more precisely to \(10^{-6}\) of relative optimality gap).

5.1 Self-UC

Here, a self-UC problem for a price-taker producer is solved for different time spans. The goal is then to optimally schedule the generating units to maximize profits (difference between the revenue and the total operating cost [5, 17]) during the planning horizon:

$$\begin{aligned} \max \sum _{t=1}^{N}\sum _{g=1}^{G}\left[ \pi _{t}e_{gt}-c_{gt}\left( u_{gt},v_{gt},w_{gt},e_{gt}\right) \right] \end{aligned}$$
(17)

where subindex \(g\) stands for generating units and G is the total quantity of units; \(\pi _{t}\) refers to the energy prices, which for these case studies are shown in Table 2; and \(c_{gt}\) is the total operating cost per unit \(g\) at period \(t\), which is defined in (16) for the proposed power-based UC formulation. The self-UC problem also arises when solving UC with decomposition methods such as Lagrangian relaxation [6].

Two different ten-unit system data are considered, one containing only quick-start units and another containing both quick- and slow-start units. The ten-unit system data for quick-start units are presented in Table 1. The power system data are based on information presented in [1, 16]. For this system of ten quick-start units, we also include a power-based formulation that only models quick-start units (see Sect. 3), labeled as PwQ.

Table 1 Generator data for quick-start units
Full size table

Another 10-unit system data set including slow-start units is created to observe the computational performance of the formulation for slow-start units. We create this new case study by replacing the first seven quick-start units from Table 1 by slow-start units. The data for these seven slow-start units are provided in Table 3. For these slow-start units, the power outputs for the startup (shutdown) power trajectories are obtained as an hourly linear change from 0 (\(\underline{P}\)) to \(\underline{P}\) (0) for a duration of \(\mathrm{SU}^{\mathrm {D}}\) (\(\mathrm{SD}^{\mathrm {D}}\) ) hours. 1bin and 3bin are modeled only for quick-start units because: (1) those traditional UC formulations ignore the units’ startup and shutdown power trajectories and including these trajectories will considerably increase the models’ computing complexity [17]; and (2) the main purpose of these case studies is to compare the computational performance of the proposed formulations with the traditional UC formulations (which ignore the startup and shutdown trajectories).

Table 2 Energy price ($/MWh)
Full size table

In short, two different case studies are carried out for the self-UC problem, the first case study models ten quick-start units (see Table 1) for formulations 3bin, 1bin and PwQ. The second case study also models ten units, seven slow-start (see Table 3) and three quick-start units (units 8 to 10 in Table 1). This case study is solved using the proposed power-based formulation for both slow- and quick-start units, which is labeled as Pw.

Table 3 Generator data for slow-start units
Full size table

Table 4 shows the computational performance of the self-UC problem (17) subject to the different UC formulations for different time spans (up to 512 days to consider large case studies). The tightness of each formulation is measured with the integrality gap (IntGap) and the integrality gap in the root node (RootIGap). The IntGap is defined as the relative distance between the MIP and LP optima [16, 24], where the MIP optimum corresponds to the best integer solution that could be found, and the LP optimum corresponds to the LP relaxation of the MIP formulation. The RootIGap is obtained as the relative difference between the upper and lower bounds before the branching process (after the solver applies initial cuts and heuristics at the root node). Beware that the IntGap of two formulations which are not modeling exactly the same problem should not be directly compared. Therefore, IntGap together with RootIGap provide a better indication of the strength of each formulation.

Table 4 Computational performance of the UC formulations for different time spans (in days)
Full size table

Note that the MIP optima of PwQ and Pw were achieved by just solving the LP problem, \(\mathrm {IntGap}=0\) (thus \(\mathrm {RootIGap}=0\)), hence solving the MIP problems in LP time. On the other hand, as usual, the branch-and-cut method was needed to solve the MIP for 3bin and 1bin. Table 4 also shows the MIP time and the branch-and-bound nodes (B&B nodes) that were explored for the different formulations.

Table 5 shows the dimensions for all formulations for the different time spans. Note that PwQ and Pw are more compact, in terms of quantity of constraints, than 3bin and 1bin. The formulations PwQ and Pw present the same quantity of binary variables of 3bin, but twice continuous variables. This is because PwQ and Pw model power and energy as two different variables. The formulation 1bin presents a third of binary variables in comparison with the other formulations, but it is the formulation presenting the largest quantity of continuous variables, constraints and nonzero elements in the constraint matrix. This is the result of reformulating the MIP model to avoid the startup and shutdown binary variables. The work in [1] claims that this would reduce the node enumeration in the branch-and-bound process. Note however that this reformulation is the least tight, see IntGap and RootIGap in Table 4, and it is also the largest, hence presenting the worst computational performance; similar results are obtained in [16].

Table 5 Problem size comparison of the UC formulations for different time spans (in days)
Full size table

5.2 Network-constrained UC

Here, the modified IEEE 118-bus test system is used for different time spans, from 24 to 60 h. All system data can be found in [14]. The IEEE-118 bus system has 118 buses; 186 transmission lines; 54 thermal units (both quick- and slow-start units); 91 loads, with average and maximum levels of 3991 MW and 5592 MW, respectively; and three wind units, with aggregated average and maximum production of 867 MW and 1333 MW, respectively, for the nominal wind case. Finally, the upward and downward reserve requirement are set as the 5% of the total nominal wind production for each hour. The network-constrained UC problem is considerably more complex than the self-UC problem described in Sect. 5.1, due to the new complicating constraints that are now included (into all the formulations), such as demand balance, reserves, ramping and transmission limits (see Appendix).

Table 6 shows the computational performance of the network-constrained UC problem for all formulations and different time spans (up to 60  h). On the one hand, the IntGap of Pw is always lower than that of 1bin, but higher than that of 3bin. However, as mentioned above, the IntGap of Pw and 3Bin (or 1bin) cannot be compared directly because they do not represent the same problem (3bin and 1bin which are equivalent, thus providing the same optimal results). Hence, based on the IntGap, 3bin seems the tightest formulation. On the other hand, based on the RootIGap, Pw seems the tightest, up to 18x and 35x tighter than 3bin a 1bin, respectively. Notice that Pw was the only formulation that solved all the cases within the time limit (10,000 s), 3bin could only solve the smallest case and 1bin none of them. For the cases where 3bin and 1bin could not be solved (time spans equal and above 36 h), Pw could achieve a lower initial optimality gap (RootIGap) than the final optimality gap achieved by 3bin and 1bin (in 10,000 s). Furthermore, Pw could achieve this initial optimality gap in a few seconds: 3.82, 10.14, 16.80, 27.87 s for the cases with time spans of 24, 36, 48 and 60 h, respectively. These times are similar to (and even lower than) the times required by 1bin and 3bin to solve their LP relaxation. We can then conclude that Pw is the tightest formulation due to its superiority in solving the MIP problems.

Table 6 IEEE 118-bus system results: computational performance of the UC formulations for different time spans (in hours)
Full size table

Table 5 shows the problem size for all formulations for different time spans. Similarly to the self-UC case study (Sect. 5.1), Pw is more compact than the others, in terms of quantity of constraints and nonzeros, but Pw has more continuous variables. Also, although 1bin has a third of binary variables in comparison with the others, it has the largest quantity of constraints and it is the least tight (see IntGap and RootIGap in Table 4), consequently presenting the worst computational performance, as also discussed in Sect. 5.1.

In conclusion, from both self-UC and network-constrained UC case studies, the proposed formulation presented a dramatic improvement in computation in comparison with 3bin and 1bin due to its tightness (speedups above 85x and 8200x, respectively) and it also presents a lower LP burden due to its compactness (see Table 5 and Table 7).

Table 7 IEEE 118-bus system results: problem size comparison of the UC formulations for different time spans (in hours)
Full size table

6 Conclusion

This paper presented the convex hull description of the basic constraints of slow- and quick-start generating units for power-based unit commitment (UC) problems. These constraints are: generation limits, and minimum up and down times, startup and shutdown power trajectories for slow-start units, and startup and shutdown capabilities for quick-start units. Although the model does not include some crucial constraints, such as ramping, it can be used as the core of any UC formulation and thus help to tighten the final UC model. Finally, two different sets of case studies were carried out, for a self-UC and for a network-constrained UC, where the proposed formulation was simultaneously tighter and more compact when compared with two other UC formulations commonly known in the literature, consequently, solving both UC problems significantly faster.