Approximations for the waiting-time distribution in an $M/PH/c$ priority queue

Abstract

We investigate the use of priority mechanisms when assigning service engineers to customers as a tool for service differentiation. To this end, we analyze a non-preemptive $M/PH/c$ priority queue with various customer classes. For this queue, we present various accurate and fast methods to estimate the first two moments of the waiting time per class given that all servers are occupied. These waiting time moments allow us to approximate the overall waiting time distribution per class. We subsequently apply these methods to real-life data in a case study.

1 Introduction

In the current business environment, the availability of key assets may be crucial for a company’s operations. Examples of such assets are radar systems on frigates and CT-scanners in hospitals. Because of the impact of asset downtime, users require services for the keeping up of the system during its lifetime. Increasingly, such services are provided by the equipment manufacturer, with agreements on the services provided being specified in so-called service contracts. In particular, service contracts often contain service level agreements (SLAs) on performance measures such as reaction times in case of failures (for instance, the time for an engineer to arrive at a customer’s site, or the time for the system to function again) and system availability (e.g., the overall fraction of time that the system should be functioning properly). Unavailability arises, e.g., from diagnosis, repair, and waiting time for spare parts and service engineers. A key challenge is that these SLAs often differ among customers, with some customers requiring very high service levels, while others are satisfied with lower service levels. In practice, service providers often handle differentiated service levels by providing all customers with more or less uniform service: a so-called one-size-fits-all approach (Cohen et al. 2006). This approach is very costly, as the service provider then needs to design the service process to provide the highest service levels. Also, customers with standard contracts have no incentive to switch to premium contracts. Therefore, we focus on applying service differentiation in the process.

Commonly, system maintenance is performed by service engineers, who travel to a customer’s site, diagnose the cause of the failure and repair the system. A key performance indicator is the response time, i.e., the time between the reporting of a failure and the arrival of the engineer at the customer’s site. Naturally, the response time is influenced by the way in which engineers are assigned to customers. In this paper, we focus on priority assignment, i.e., an available engineer is assigned to the customer with the highest priority as opposed to the customer that has been waiting longest. As a result, customers with high service level requirements exhibit short response times at the expense of other customers. We aim to accurately estimate the waiting times for the various classes of customers, with the customer’s class indicating the required level of service. As we aim for a high probability that service level targets are met, mean waiting times alone are insufficient. We need the waiting time distribution per customer class. Then, combined with the travel time to customers, we have an estimate of the response times per customer class, and hence of the service provider’s performance on his response time target.

We model the system as a multi-class, non-preemptive $M/Ph/c$ priority queue with identical service time distributions over the classes. Poisson arrivals are often a valid assumption in practice: complex systems seem to have a constant hazard function, since failures arise from various causes, thus appearing completely random. We have observed such behavior in printing and copying equipment amongst others, and Jardine and Tsang (2006) give additional cases where the Poisson assumption is reasonable, see Section 3.5.5 in the book. We consider non-preemptive priorities, since an engineer will complete service at one customer before proceeding to another, even if a higher-priority customer appears in the meantime. Finally, we consider the setting where all customers have similar types of systems. As a result, the failure behavior of the system, and hence the distribution of the time to repair the system, will be the same at all customers. It is worth noting that the non-preemptive $M/Ph/c$ priority queue has also other possible applications such as in call centers, ICT support systems, and telecommunication networks.

In the remainder of the paper, we first give an overview of the literature on multi-class multi-server systems (Sect. 2). There, we also state our main contribution. In Sect. 3, we describe our multi-class model and globally describe the analysis approach for this model. A key building block of the approach is the analysis of a single-class system, which we give in Sect. 4. We give extensions for speeding up the computations in Sect. 5. In Sect. 6, we evaluate our analysis methods and extension options in an extensive numerical experiment. In Sect. 7, we apply the best variant to a case study. Finally, we draw our main conclusions in Sect. 8.

2 Literature overview and main contribution

Our model contributes to the literature on multi-class, multi-server priority queues with a variety of priority disciplines (non-preemption, preemptive resume or preemptive repeat). Due to the constraints of our practical application, we emphasize that in this paper the research scope is focused on cases where the number of servers is not very large, e.g., it is between 1 and 10, and the traffic load is not necessarily very high, e.g., less than 95 %. As a result, the literature on heavy traffic approximations, see, e.g., Kimura (1983), and extremely large number of servers, see Whitt (1992), is not applicable. In the following, we first discuss $M/M/c$ priority queues (i.e., with exponential service times). Then, we consider multi-server priority queues with non-exponential service times, with a special focus on $M/Ph/c$ non-preemptive priority queues.

Most literature on multi-server priority queues deals with $M/M/c$ queues. For a preemptive-resume setting with multiple classes, Buzen and Bondi (1983) derive exact expressions for the mean waiting time per class when service times are identically distributed over classes, and provide approximate expressions when service times differ between classes. For non-preemptive priorities and identical service time distributions, Kella and Yechiali (1985) derive the Laplace–Stieltjes transforms (LSTs) of the waiting times per class. Sleptchenko et al. (2005) consider a system with two classes, i.e., a high and a low priority class, where each class may consist of multiple customer types, each with a distinct arrival and service rate. High-priority customers have preemptive priority over low-priority customers. The authors give an exact method to find per class the steady-state probabilities of the queue length and the number of customers in service. Zeltyn et al. (2009) consider a setting with $K$ classes, where classes 1 up to $P$ ($P<K)$ have preemptive priority over the other (lower priority) classes. The authors give explicit expressions for the LSTs of the waiting times per class.

Regarding priority queues with non-exponential service times, Tijms (1988) derives approximations for the mean waiting times per class in an $M/G/c$ non-preemptive priority queue. Moreover, Tijms (1988) proposes to approximate the distribution of the highest priority customers with an exponential distribution. Altinkemer et al. (1998) derive approximations for the mean waiting times per class in an $M/D/c$ non-preemptive priority queue. Harchol-Balter et al. (2005) consider a preemptive resume priority queue where service times have a phase-type distribution ($M/PH/c$ queue). The authors provide an approximate analysis for the distribution of the number of customers per class in the system, where they use the distribution of the busy period pertaining to high-priority classes to analyze the next lower priority class. Wagner (1997) considers a multi-server, non-preemptive priority queue model with a generalized Markovian arrival process, and a phase-type service distribution that is identical over all classes. Wagner (1997) uses matrix-geometric methods to mainly find the mean waiting times per class.

Williams (1980) derives approximations for the first two moments of the waiting times in a two-class, $M/G/c$ non-preemptive priority queue. Jagerman and Melamed (2003) consider a similar model with multiple classes and different service time distributions per class. Jagerman and Melamed (2003) and Williams (1980) use two approximations that are common in the literature:

• The delay probability, i.e., the steady-state probability that all servers are occupied, in an $M/G/c$ queue is approximated by the same probability in an $M/M/c$ queue with equal arrival rates and service rate; numerical experiments have revealed that the delay probability is not very sensitive to the service time distribution (Tijms 2003)

• If at a service completion epoch, $k$ customers are left behind in the system with $k\ge c$, then the time until the next service completion is distributed as $S/c$, where $S$ denotes the original service time of a customer.

From the second approximation, it follows that the waiting time in an $M/G/c$ queue with $\tilde{G}(s)$ as the LST of the service time can be approximated by the waiting time in an $M/G/1$ queue with a service time LST equal to $\tilde{G}(s/c)$. The latter holds for the busy period in both queues, with the busy period defined as the time that all servers are occupied. From these findings, the waiting time distributions per class are deduced. Williams (1980) states that the approximations are exact both for the single server $M/G/1$ and the multi-server $M/M/c$ queue. Hence, it follows that the mean waiting time for a class-$k$ customer satisfies the following well-known scaling approximation, which can easily be derived by conditioning on the waiting time when all servers are occupied, see, e.g., Buzen and Bondi (1983):

$$\begin{aligned} \frac{{\mathbb {E}}\left[ {W_k ( {M/G/c})} \right] }{{\mathbb {E}}\left[ {W_k ( {M/M/c})} \right] }=\frac{{\mathbb {E}}\left[ {W_k ( {M/G/1})} \right] }{{\mathbb {E}}\left[ {W_k ( {M/M/1})} \right] }, \end{aligned}$$

where the server in the single-server queues works $c$ times as fast as in their multi-server counterparts. The latter equation can be also written for the second moment of the waiting time.

Williams (1980) nor Jagerman and Melamed (2003) validate the quality of their methods. We will see that Williams’ method can be inaccurate, especially for the waiting time moments of classes with high priority and with many servers, e.g., $c\in \{3,6,9\}$ (see Tables 3, 4 in Sect. 6.2.2). Our main contributions in this paper are:

• (i) We refine the approximation assumption of Williams (1980) and Jagerman and Melamed (2003), and from that we obtain very accurate methods to estimate the waiting time distribution per class in a system with multiple priority classes.

• (ii) We present options to speed-up the numerical analysis for systems with large state space (e.g., for cases with six to ten servers and a phase-type service time distribution with three or four phases), see Sect. 5. This is done with a limited decrease in accuracy, see Sect. 6.3.

• (iii) We apply our methods to determine service-level performance in a practical setting.

We emphasize that among some side results for the $M/D/c$ queue, all the results developed for the second moment of the conditional waiting times per customer class in a non-preemptive $M/Ph/c$ priority queue are new. This is a key step to propose an accurate approximation of the distribution of the conditional waiting times. In a computational experiment, we show that our methods generally outperform Williams’ method, especially for the highest priority classes.

3 Model description and main analysis steps

We introduce our model with notation in Sect. 3.1, and provide the analysis in Sect. 3.2.

3.1 Model description

We consider a non-preemptive $M/Ph/c$ priority queue with $K$ classes. Customers of class $k$ have priority over those of classes $j\ge k+1$. Class $k$ customers arrive according to a Poisson process with rate $\lambda _k$, and are served according to the first-come-first-served (FCFS) discipline. The total arrival rate of customers is equal to $\lambda =\sum _{k=1}^K \lambda _k$. All customers have the same service time distribution, with ${\mathbb {E}}[S]$ denoting its mean, $cv_S^2$ its squared coefficient of variation, $S(t)$ the cumulative distribution, and $\tilde{S}(s)$ the Laplace–Stieltjes transform (LST). The utilization rate per class is denoted by $\rho _k=\frac{\lambda _k{\mathbb {E}}[S]}{c}$, with $\rho =\sum _{k=1}^K \rho _k$. We assume that the queue is stable $(\rho <1)$ and that all moments of the service time are finite.

We aim to estimate the first two moments of the conditional waiting time $\hbox {CW}_k$ per class $k$ given that all servers are occupied. Combined with the delay probability $\pi _w$, the probability that an arriving customer sees all the servers are occupied, we can then fit a reasonable class of distributions to estimate the waiting time distribution per class. A distribution on which data is commonly—and accurately—fitted is the gamma distribution, see, e.g., Appendix C in Al Hanbali et al. (2013) for further details. Munnik (2011) we conclude that the approximation of the conditional waiting times distribution with a gamma distribution is fairly accurate. Recall that a fairly accurate approximation for $\pi _w$ is the delay probability in an $M/M/c$ queue, i.e., Erlang’s $C$ formula, see, e.g., Tijms (2003, pp. 388).

3.2 Approximating the moments of the conditional waiting times

To find ${\mathbb {E}}[{\hbox {CW}_1}]$ and ${\mathbb {E}}[{\hbox {CW}_1^2}]$ we use the following arguments. Given the non-preemptive service discipline, it does not matter what type of customers are being served when a class 1 customer arrives to find all servers busy. Also, new arrivals from classes 2 up to $K$ have no impact on the waiting time for class 1. Therefore, we obtain ${\mathbb {E}}[{\hbox {CW}_1}]$ and ${\mathbb {E}}[{\hbox {CW}_1^2}]$ as the first two moments of the conditional waiting time, i.e., the waiting time given it is strictly positive, in a single-class $M/G/c$ queue with arrival rate $\lambda _1$.

To obtain ${\mathbb {E}}[{\hbox {CW}_k}]$ and ${\mathbb {E}}[{\hbox {CW}_k^2}]$ for classes $k\ge 2$, we use an argument similar to Williams (1980) and Cohen (1969). We first sketch what happens when a tagged customer of class $k$ arrives at the system when all servers are occupied. Upon arrival, he will see $N_1$ customers of classes $i\le k$ that are already waiting to be served. The waiting time of the tagged customer will thus at least consist of the time needed to clear these $N_1$ customers from the queue, which we denote by $T_1$. During $T_1$, new customers of classes $i<k$ may arrive that have priority over the tagged customer. Let $N_2$ denote the number of higher priority customers that arrive in the time that the first $N_1$ customers are cleared from the queue. While these $N_2$ customers are being cleared, new higher priority customers may arrive, and so forth. Overall, the waiting time for the tagged class $k$ customer thus consists of two elements: (i) the time $T_1$ to clear all $N_1$ customers of classes $i\le k$ that were already present in the queue and (ii) the time $T_2$ to clear those customers of classes $i<k$ that arrive while the tagged customer is waiting, starting with the $N_2$ customers that have arrived while the first $N_1$ are being cleared. Note that $T_1$ and $T_2$ are not strictly consecutive, as the higher priority customers that arrive while the tagged customer is waiting may also have priority over some of the $N_1$ customers that were already present. The values $T_1$ and $T_2$ simply denote the workloads associated with clearing the initial $N_1$ customers and clearing all higher priority customers that arrive after the tagged customer, respectively. Clearly, $T_2$ and $T_1$ are strongly correlated: If $T_1$ is large, $N_2$ (and thus $T_2 )$ will be large.

We compute $T_1$ as the conditional waiting time in a single-class $M/G/c$ queue with arrival rate $\lambda _k^*=\sum _{i=1}^k\lambda _i$. By conditioning on $T_1$, we can evaluate the distribution of $N_2$, and then approximate $T_2$ as the residual busy period in a single-class $M/G/c$ queue with arrival rate $\lambda _{k-1}^*$. Here we define the residual busy period as the period until all higher priority customers have left the queue, starting with $N_2$ higher priority customers of class $i<k$ in the queue, one server just starting with service, and the other $c-1$ servers busy with servicing a customer for some unknown time. We approximate the distribution of the residual service time of those $c-1$ customers in service by the equilibrium distribution of the service time as it is known from renewal theory. That is, we assume that the customer starting to receive service observes the state of the $c-1$ busy servers as if at an arbitrarily chosen point in time when these servers have been continuously busy serving customers for a very long time. In other words, assuming that the newly starting customer in service has no information about the past history of the $c-1$ busy servers, the best prediction this customer can give about the residual service time of those $c-1$ customers in service is according to the equilibrium distribution (Tijms 2003). Furthermore, we approximate the residual busy period length by the sum of $N_2$ independent and identically distributed busy periods that each start with an arrival of one customer to the queue. This approximation is exact for $M/G/1$ and $M/M/c$ queues, see, e.g., Riordan (1967) and Tijms (2003). Let $Z_k$ be the random variable that denotes the conditional waiting time in an $M/G/c$ queue with arrival rate $\lambda _k^*$, with $\tilde{Z}_k (s)$ being the corresponding LST. Similarly, let $B_{k-1}$ and $\tilde{B}_{k-1} (s)$ be the random variable and LST of the busy period of an $M/G/c$ queue with arrival rate $\lambda _{k-1}^*$. Note that $Z_k$ corresponds to $T_1$, while $T_2 =\sum _{i=0}^{N_2 } B_{k-1,i}$, where $B_{k-1,i}$ are i.i.d. copies of $B_{k-1}$. As an approximation, we can now express the conditional waiting time for a class $k$ customer as $\hbox {CW}_k =Z_k +\sum _{i=0}^{N_2 } B_{k-1,i}$ with the corresponding LST $\widetilde{\hbox {CW}}_k ( s)$ as follows, see, e.g., Williams (1980):

$$\begin{aligned} \widetilde{\hbox {CW}}_k (s)=\tilde{Z}_k\left( {s+\lambda _{k-1}^*\left( {1-\tilde{B}_{k-1} (s)}\right) }\right) . \end{aligned}$$

(1)

By taking the first two derivatives at point zero, we find the first two moments of $\hbox {CW}_k$, $k\ge 2$:

$$\begin{aligned}&\qquad \quad {\mathbb {E}}[{\hbox {CW}_k }]=({1+\lambda _{k-1}^*{\mathbb {E}}[{B_{k-1} }]}){\mathbb {E}}[{Z_k}],\end{aligned}$$

(2)

$$\begin{aligned}&{\mathbb {E}}[{\hbox {CW}_k^2 }]=\lambda _{k-1}^*\mathbb {E}[ {B_{k-1}^2 } ]\mathbb {E}[{Z_k }]+( {1+\lambda _{k-1}^*\mathbb {E}[{B_{k-1} }]})^2\mathbb {E}[{Z_k^2 }]. \end{aligned}$$

(3)

Note that the length of the residual busy period is indeed influenced by the time needed to clear all $i\le k$ customers that were initially present in the queue. In expression (2), for instance, $\lambda _{k-1}^*{\mathbb {E}}[{Z_k}]$ is the expected number of higher priority customers $N_2$ that arrive while the first $N_1$ customers are being cleared. Note that ${\mathbb {E}}[{Z_k}]$ and ${\mathbb {E}}[{Z_k^2}]$ denote the first two moments of the conditional waiting time in a single-class $M/G/c$ queue with arrival rate $\lambda _k^*$, $k\ge 2$. Similarly, ${\mathbb {E}}[{B_k}]$ and ${\mathbb {E}}[{B_k^2}]$ denote the first two moments of the busy period in a single-class $M/G/c$ queue with arrival rate $\lambda _k^*$, $k\le K-1$. Hence, we obtain the first two moments of the conditional waiting time for each customer class—including class 1—from the analysis of a single-class $M/G/c$ queue, see Sect. 4 for details.

4 Detailed analysis of a single class $M/G/c$ system

We now discuss the analysis of a single-class $M/G/c$ queue with arrival rate $\lambda$ (note that we omit class index $k$ in this section). In Sect. 4.1, we compute the first two moments of the conditional waiting time CW. In Sect. 4.2, we estimate the first two moments of the busy period $B$, i.e., the period in which all servers are occupied.

4.1 Computation of ${\mathbb {E}}[{\hbox {CW}}]$ and ${\mathbb {E}}[{\hbox {CW}^2}]$

We consider two approximate methods to obtain ${\mathbb {E}}[{\hbox {CW}}]$ and ${\mathbb {E}}[{\hbox {CW}^2}]$, which are both based on Section 9.6.2 in Tijms (2003). The first method, which we denote by AVA1,¹ is discussed in Sect. 4.1.1, whereas the second, denoted by AVA2, is discussed in Sect. 4.1.2. In both AVA1 and AVA2, we obtain performance measures for the $M/G/c$ queue from those for other queues, specifically the $M/M/c$ and $M/D/c$ queues. We denote a performance measure $V$ for the $M/M/c$ queue and the $M/D/c$ queue by $V(\hbox {exp})$ and $V({\hbox {det}})$, respectively.

4.1.1 AVA1

We can find the first two moments of the waiting time (both conditional and unconditional) using the distributional form of Little’s law (see Bertsimas and Nakazato 1995, Theorem 1), i.e.,

$$\begin{aligned}&\qquad {\mathbb {E}}[{\hbox {CW}}]=\frac{{\mathbb {E}}\left[ {\hbox {CL}_q } \right] }{\lambda },\end{aligned}$$

(4)

$$\begin{aligned}&{\mathbb {E}}[ {\hbox {CW}^2}]=\frac{{\mathbb {E}}\left[ {\hbox {CL}_q ( {\hbox {CL}_q -1})} \right] }{\lambda ^2}. \end{aligned}$$

(5)

In (4) and (5), $\hbox {CL}_q$ denotes the number of customers waiting in the queue given that all servers are occupied. Note that the distributional form of Little’s law does not hold for the sojourn times of the customers in the system, i.e., the sum of the customer’s waiting time and service time: in an $M/G/c$ queue, customers may overtake each other during service, ensuring that assumption 2 in Theorem 1 (Bertsimas and Nakazato 1995) is not necessarily satisfied.

For the $M/G/c$ queue, Tijms (2003) proposes an approximation for the generating function $P_q ( z)$ of the unconditional number of customers waiting in the queue $L_q$, see equation (9.6.22) in Tijms (2003). The approximation is based on the following assumptions: (i) if fewer than $c$ servers are occupied in the $M/G/c$ queue, that queue may be treated as an $M/G/\infty$ queue, and (ii) if all servers are occupied, the $M/G/c$ queue may be treated as an $M/G/1$ queue where the server works $c$ times as fast as the servers in the original system. For both the $M/G/\infty$ and the $M/G/1$ queue, the remaining service time of any busy server is distributed as the equilibrium excess time in a renewal process with the service times as interoccurrence times, see Section 9.6.2 in Tijms (2003).

By taking the first derivative of $P_q ( z)$ at $z=1$, Tijms (2003) finds, without giving the derivation, an expression for ${\mathbb {E}}[{L_q}]$ as linear function of ${\mathbb {E}}[{L_q({\hbox {exp}})}]$. Note that it is nontrivial to find this function. Therefore, we describe how this can be done in Appendix, where we also give the derivation for ${\mathbb {E}}[{\hbox {CL}_q (\hbox {CL}_q -1)}]$ as a function for $\mathrm{E}[{\hbox {CL}_q ({\hbox {CL}_q-1})(\hbox {exp})}]$, i.e., Eq. (9). We now use the assumption that $\pi _w$ is the same in the $M/G/c$ and $M/M/c$ queue (cf. Sect. 2) and Little’s Law to find that $\frac{{\mathbb {E}}[{L_q}]}{{\mathbb {E}}[{L_q({{\exp }})} ]}=\frac{{\mathbb {E}}[{\hbox {CL}_q}]}{{\mathbb {E}}[{\mathrm{CL}_q ( {{\exp }})}]}=\frac{{\mathbb {E}}[{\mathrm{CW}} ]}{{\mathbb {E}}[{\mathrm{CW}({{\exp }})}]}$. For additional discussion on the quality of the delay probability approximation we refer to Tijms (2003). We thus obtain the following linear relation between ${\mathbb {E}}[{\hbox {CW}}]$ and ${\mathbb {E}}[{\hbox {CW}({\hbox {exp}})}]$:

$$\begin{aligned} \frac{{\mathbb {E}}[{\hbox {CW}}]}{{\mathbb {E}}[{\hbox {CW}( {\hbox {exp}})}]}=({1-\rho })\gamma _1\frac{c}{{\mathbb {E}}[S]} +\frac{\rho }{2}({1+cv_S^2}), \end{aligned}$$

(6)

where $\gamma _1$ is given by:

$$\begin{aligned} \gamma _1=\int _0^\infty ({1-S_e(t)})^c\mathrm{d}t, \end{aligned}$$

(7)

with $S_e (t)$ denoting the equilibrium excess distribution function of the service time, i.e.,

$$\begin{aligned} S_e (t)=\frac{1}{{\mathbb {E}}[S]}\int _0^t ({1-S(u)})\mathrm{d}u. \end{aligned}$$

(8)

Note that $\gamma _1$ can be interpreted as the expectation of $\min ({S_e^1,\ldots ,S_e^c})$, where $S_e^i$, $i=1,\ldots ,c$, are i.i.d random variables with common probability distribution $S_e(t)$.

Similarly, we find a linear relation between ${\mathbb {E}}[{\hbox {CL}_q (\hbox {CL}_q -1)}]$ and ${\mathbb {E}}[\hbox {CL}_q ( {\hbox {CL}_q -1})(\hbox {exp})]$, and hence between ${\mathbb {E}}[{\hbox {CW}^2}]$ and ${\mathbb {E}}[{\hbox {CW}({\hbox {exp}})^2}]$:

$$\begin{aligned} \frac{{\mathbb {E}}[{\mathrm{CW}^2}]}{{\mathbb {E}} [{\mathrm{CW}({\exp })^2}]}&= \frac{\lambda ^2( {1-\rho })^2}{\rho ^2} \gamma _2 +\frac{\lambda ( {1-\rho })}{2}( {cv_S^2 +1})\gamma _1 +\frac{\rho ^2}{4}( {cv_S^2 +1})^2\nonumber \\&+\frac{\rho ( {1-\rho })}{6}\frac{{\mathbb {E}}[{S^3}]}{{\mathbb {E}}[S]^3}, \end{aligned}$$

(9)

where $\gamma _2$ is given by:

$$\begin{aligned} \gamma _2=\int _0^\infty t( {1-S_e ( t)})^c\mathrm{d}t. \end{aligned}$$

(10)

Similar to $\gamma _1,2\gamma _2$ can be interpreted as the second moment of $\min ({S_e^1,\ldots ,S_e^c})$. This can easily be verified via partial integration of the right-hand side of (10), see, e.g., Tijms (2003, Sect. 9.6.2). We note that Eq. (9) is new and was not found in the previous literature.

Expressions for ${\mathbb {E}}[{\hbox {CW}({\exp })}]$ and ${\mathbb {E}}[{\hbox {CW}({\exp })^2}]$ can be found, e.g., in Sect. 5.1.2 in Tijms (2003):

$$\begin{aligned} {\mathbb {E}}\left[ {\hbox {CW}( {\exp })} \right] =\frac{{\mathbb {E}}\left[ S \right] }{c( {1-\rho })},\quad {\mathbb {E}}\left[ {\hbox {CW}( {\exp })^2} \right] =\frac{2{\mathbb {E}}\left[ S \right] ^2}{c^2( {1-\rho })^2} . \end{aligned}$$

(11)

4.1.2 AVA2

We now estimate both ${\mathbb {E}}[{\hbox {CW}}]$ and ${\mathbb {E}}[{\hbox {CW}^2}]$ as weighted averages of the waiting time moments in an $M/D/c$ and an $M/M/c$ queue, with the mean service time in the latter queues equal to ${\mathbb {E}}[S]$. We use the squared coefficient of variation of the service time $cv_S^2$ as weight when computing ${\mathbb {E}}[{\hbox {CW}}]$ and $\alpha$, defined by (15) below, as weight when computing ${\mathbb {E}}[{\hbox {CW}^2}]$. We find:

$$\begin{aligned} {\mathbb {E}}[{\hbox {CW}}]&= \left( {1-cv_S^2}\right) {\mathbb {E}}\left[ {\hbox {CW}(\hbox {det})}\right] +cv_S^2 {\mathbb {E}}\left[ {\hbox {CW}(\hbox {exp})} \right] ,\end{aligned}$$

(12)

$$\begin{aligned} {\mathbb {E}}\left[ {\hbox {CW}^2}\right]&= ({1-\alpha }) {\mathbb {E}}\left[ {\hbox {CW}(\hbox {det})^2}\right] +\alpha {\mathbb {E}}\left[ {\hbox {CW}(\hbox {exp})^2}\right] . \end{aligned}$$

(13)

We propose (13) based on a similar expression for the mean waiting time in Tijms (2003, Eq. (9.6.24)). Tijms (2003) emphasizes that the approximation in (12) is accurate when $0\le cv_S^2 \le 2$. In contrast, we develop (14) ourselves, where we determine the expression for $\alpha$ such that it is exact for $c=1$. When $c=1$, we obtain expressions for ${\mathbb {E}}[\hbox {CW}]$ and ${\mathbb {E}}[{\hbox {CW}^2}]$ under any service time distribution using the Pollaczek–Khintchine formula. Note that the expression for $\alpha$ is exact for both the $M/M/c$ and the $M/D/c$ queue, with $\alpha =1$ for exponential service times and $\alpha =0$ for deterministic service times.

$$\begin{aligned} \alpha =\frac{1}{10-\rho }\left( {2( {1-\rho })\frac{{\mathbb {E}}\left[ {S^3} \right] }{{\mathbb {E}}\left[ S \right] ^3}+\frac{3\rho {\mathbb {E}}\left[ {S^2} \right] ^2}{{\mathbb {E}}\left[ S \right] ^4}-2-\rho }\right) . \end{aligned}$$

(14)

The expressions for ${\mathbb {E}}[{\hbox {CW}({\exp })}]$ and ${\mathbb {E}}[{\hbox {CW}({\exp })^2}]$ are given by the Eqs. (11) and (12), respectively. We note that Eqs. (13)–(14) are new and were not found in the previous literature. We find expressions for ${\mathbb {E}}[{\hbox {CW}(\hbox {det})}]$ and ${\mathbb {E}}[{\hbox {CW}(\hbox {det})^2}]$ from the LST of the unconditional waiting time in an $M/D/c$ queue, see, e.g., Riordan (1967):

$$\begin{aligned} {\mathbb {E}}\left[ {e^{-s\mathrm{E}\left[ S \right] ^{-1}W}} \right] =\frac{( {1-\pi _w })s}{( {c\rho })^ce^{-s}-( {c\rho -s})^c}\mathop \prod \limits _{i=1}^{c-1} ( {u_i -s}), \end{aligned}$$

(15)

where $u_i =c\rho ( {1-z_i })$, and $z_i$, $i=0,\ldots ,c-1$, are the $c$ roots of $z^c=e^{c\rho (z-1)}$, with $\left| {z_i } \right| \le 1$ and $z_0 =1$. Note that (16) does not use this latter root. The roots $z_i$ ($i\ge 1)$ can easily be computed recursively: starting with $z_i^{(0)} =0$, $z_i^{(n+1)}$ can be computed as a function of $z_i^{(n)}$ until convergence occurs (see Eq. (14) in Janssen and Leeuwaarden 2008). Moreover, the roots $z_i$ are known in closed-form as an infinite sum (Janssen and Leeuwaarden 2008). In Janssen and Leeuwaarden (2008), we also find an expression for the delay probability $\pi _w$ in the $M/D/c$ queue, which we denote by $\pi _w ( \hbox {det})$:

$$\begin{aligned} \pi _w (\hbox {det})=1-\frac{c( {1-\rho })}{\prod \nolimits _{i=1}^{c-1} ( {1-z_i })}. \end{aligned}$$

By multiplying both sides of (16) by $( {c\rho })^ce^{-s}-( {c\rho -s})^c$ and taking the second and third order derivatives of the resulting expression, we find that:

$$\begin{aligned} {\mathbb {E}}\left[ {\hbox {CW}(\hbox {det})} \right]&= \frac{1}{\lambda \pi _w (\hbox {det})}\left( {\frac{c\rho ^2-c+1}{2( {1-\rho })}+\sum _{i=1}^{c-1} \frac{1}{1-z_i }}\right) ,\end{aligned}$$

(16)

$$\begin{aligned} {\mathbb {E}}\left[ {\hbox {CW}( {\hbox {det}})^2} \right]&= \frac{c^2\rho ^3-( {c-1})( {c-2})+3\lambda ( {c\rho ^2-c+1})\pi _w (\hbox {det}){\mathbb {E}}\left[ {\hbox {CW}( \hbox {det})} \right] }{3\lambda ^2\pi _w (\hbox {det})( {1-\rho })}\nonumber \\&+\frac{2}{\lambda ^2\pi _w (\hbox {det})}\sum _{i=1}^{c-2} \frac{1}{1-z_i }\sum _{l=i+1}^{c-1} \frac{1}{1-z_l }. \end{aligned}$$

(17)

We note that Eqs. (16)–(17) are new and were not found in the previous literature.

4.2 Computation of ${\mathbb {E}}\left[ B \right]$ and ${\mathbb {E}}\left[ {B^2} \right]$

We now show how to compute the first two moments of the busy period. Both in this section, and in the computational experiments, we restrict ourselves to $M/Ph_m /c$ queues, i.e., queues where the service time has a phase-type distribution with $m$ phases. A phase-type distribution characterizes the time until absorption in an absorbing Markov chain with a finite state space given that the chain starts in an initial transient (non-absorbing) state. Such a distribution is characterized by the tuple $( {\varvec{\beta },\varvec{V},V^0})$, where the $\varvec{\beta }$ is a row vector of size $m$ indicating the initial state probability vector, i.e., element $j$ in $\varvec{\beta }$ denotes the probability of starting in state $j=1,\ldots ,m$, $\varvec{V}$ is an $m$-by-$m$ matrix denoting the transition rates among transient states, and $V^0$ is a column vector of size $m$ denoting the transition from the transient to the absorbing state. The two-phased Coxian-2 distribution, for instance, can be characterized as follows:

$$\begin{aligned} ( {\varvec{\beta , R}, R^0})=\left( {\left( {{\begin{array}{ll} 1 &{} 0 \\ \end{array} }}\right) ,\left( {{\begin{array}{l@{\quad }l} {-\mu _1 } &{} {p\mu _1 } \\ 0 &{} {-\mu _2 } \\ \end{array} }}\right) ,\left( {{\begin{array}{ll} {( {1-p})\mu _1 } \\ {\mu _2 } \\ \end{array} }}\right) }\right) . \end{aligned}$$

(18)

The class of phase type distributions is dense in the sense that it allows us to cover a broad range of coefficients of variation for the service time distribution. In particular, the mixed generalized Erlang distribution, i.e., a distribution that is a generalized Erlang-$n$ distribution with probability $q_n$, $n=1,..,m$, allows us to model variables with any value for $cv_S^2$. A special case of this distribution is the Coxian distribution, where the Coxian-2 distribution, for instance, can model a distribution with $cv_S^2 \ge 0.5$, see, e.g., Marie (1980).

The busy period can be seen as the first passage time of the queue-length process from the moment there are $c$ customers in the system to that when there are $c-1$ customers in the system. Let $\varvec{Q}$ denote the generator matrix of the queue length process, which is characterized by (20) for an $M/Ph_m /c$ queue. An element $( {i,j})$ in $\varvec{Q}$ denotes the transitions from level $i$ (with a level being the set of states with a queue length size $i)$ to level $j$.

$$\begin{aligned} \varvec{Q} = \left( \begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {\varvec{A}_{1}^{0} } &{} {\varvec{A}_{0}^{0} } &{} 0 &{}{0} &{} {0 } &{} \cdots &{}&{}&{} \\ {\varvec{A}_{2}^{1} } &{} {\varvec{A}_{1}^{1} } &{} {\varvec{A}_{0}^{1} }&{}{0 } &{}{0 } &{} \cdots \\ &{} \ddots &{} \ddots &{}\ddots &{} {0 } &{} \cdots &{}&{}\\ &{} 0 &{} {\varvec{A}_{2}^{{c - 1}} } &{}{\varvec{A}_{1}^{{c - 1}} } &{} {\varvec{A}_{0}^{{c - 1}} } &{} 0&{}\cdots &{} &{} \\ &{} \cdots &{} 0 &{}{\varvec{A}_{2}^{c} } &{} {\varvec{A}_{1} } &{} {\varvec{A}_{0} }&{}0 &{} \cdots &{} \\ &{} &{} \cdots &{} {0 } &{}{ \varvec{A}_{2} } &{}{\varvec{A}_{1} } &{}{\varvec{A}_{0} } &{} 0 &{}\cdots \\ &{}&{}&{}\cdots &{} 0&{}{\varvec{A}_{2} } &{}{\varvec{A}_{1} }&{}{\varvec{A}_{0} } &{}0\\ &{}&{}&{}&{}\cdots &{} 0&{}\ddots &{} \ddots &{} \ddots \\ \end{array}\right) \end{aligned}$$

(19)

In $\varvec{Q}$, $\varvec{A}_0 =\lambda \varvec{I}$, $\varvec{A}_1 =-\lambda \varvec{I}+\oplus _{i=1}^c \varvec{V}$, and $\varvec{A}_2 =\oplus _{i=1}^c V^0\varvec{\beta }$, with $I$ being the identity matrix of size $m^c$ and $\oplus _{i=1}^c \varvec{V}=\varvec{V}\oplus \cdots \oplus \varvec{V}$, i.e., the Kronecker sum of $\varvec{V}$ by itself $c$ times, see, e.g., Neuts (1981). Note that $\varvec{Q}$ is a quasi-birth–death process that is homogeneous for levels strictly larger than $c$. This property also holds for the $M/Ph_m /1$ queue. Therefore, the busy period results of $M/Ph_m /1$ also hold for $M/Ph_m /c$ by setting $\varvec{A}_0,\varvec{A}_1 ,$ and $\varvec{A}_2$ as defined before. Neuts (1981, Sect. 3.3) studies the busy period of phase-type single server queues using an efficient matrix analytical approach. Another way to find the busy period results is using the transform-based approach, see, e.g., Al Hanbali (2011). We shall now apply Neuts’ approach to derive the first two moments of the busy period in an $M/Ph_m /c$ queue. Let $\varvec{G}$ denote an $m^{c}$-by-$m^{c}$ matrix where entry $(j,j^{\prime })$ denotes the conditional probability that the queue-length process, starting in level $i+1$ ($i\ge c)$ at state $j$ at time zero, reaches level $i$ for the first time in state $j'$. Note that the entries in $\varvec{G}$ are independent of $i$ due to the homogeneous property of $\varvec{Q}$ for levels greater than $c$. The matrix $\varvec{G}$ is the minimal solution of the following quadratic matrix equation:

$$\begin{aligned} \varvec{G}=\varvec{C}_0 +\varvec{C}_2 \varvec{G}^2, \end{aligned}$$

(20)

where $\varvec{C}_0 =-( {\varvec{A}_1 })^{-1}\varvec{A}_2$ and $\varvec{C}_2 =-( {\varvec{A}_1 })^{-1}\varvec{A}_0$. Note that $\varvec{C}_0$ is the transition probability matrix that the queue-length process jumps from level $i+1$ to $i$, $i\ge c$, and $C_2$ the transition probability matrix that the queue length process jumps from level $i$ to $i+1$, $i\ge c$. The matrix $\varvec{G}$ is stochastic, i.e., $\varvec{G}e=e$. Moreover, it is the unique solution of (21) if the queue is stable (Neuts 1981, Th. 3.3.2). We assume that the queue is stable, i.e., that $\rho <1$. Therefore, $\varvec{G}$ can be computed recursively. Let $\varvec{G}_n$ denote the estimate of $\varvec{G}$ after iteration $n$. We then find:

$$\begin{aligned} \varvec{G}_{n+1} =\varvec{C}_0 +\varvec{C}_2 ( {\varvec{G}_n })^2,\quad n\ge 1, \end{aligned}$$

where $\varvec{G}_1 =\varvec{C}_0$. The above equation is proven to converge, see Th. 3.3.1 in Neuts (1981).

From $\varvec{G}$, we are able to derive the first two moments of the busy period $B$. Let $bp_1$ denote a column vector of size $m^c$ with the $j$-th entry being equal to the mean conditional busy period given that the busy period starts in level $c$ in state $j$. Similar to the way in which Neuts derives the busy period moments from $\varvec{G}$, we find the following expression for $bp_1$ from Eq. (3.3.23) and (3.3.36) in Neuts (1981).

$$\begin{aligned} bp_1 =-( {\varvec{A}_0 +\varvec{A}_1 +\varvec{A}_0 \varvec{G}})^{-1}e. \end{aligned}$$

(21)

Note that the matrix $\varvec{A}_0 +\varvec{A}_1 +\varvec{A}_0 \varvec{G}$ is nonsingular since it can be written as a product of two nonsingular matrices, see Neuts (1981, Th. 3.3.3).

Similar to $bp_1$, let $bp_2$ also be a column vector of size $m^c$ with the $j$-th entry equal to the second moment of the conditional busy period that starts in level $c$ in state $j$. We derive $bp_2$ by simplifying Eq. (3.3.26) in Neuts (1981):

$$\begin{aligned} bp_2 =-2( {\varvec{A}_0 +\varvec{A}_1 +\varvec{A}_0 \varvec{G}})^{-1}({\varvec{A}_0 \varvec{M}_1 +\varvec{I}})bp_1, \end{aligned}$$

(22)

where the matrix $\varvec{M}_1$ is the minimal, unique and nonnegative solution of the following equation:

$$\begin{aligned} \varvec{M}_1 =-( {\varvec{A}_1 })^{-1}\varvec{G}+\varvec{C}_2 ( {\varvec{GM}_1 +\varvec{M}_1 \varvec{G}}). \end{aligned}$$

This matrix equation can be solved recursively by starting with an initial solution that is equal to the zero matrix and using an iteration procedure similar to that for computing matrix $\varvec{G}$.

We now obtain the first two moments of the busy period by multiplying $bp_1$ and $bp_2$ by the joint distribution of the remaining service times on the servers when a busy period starts. At the start of a busy period, there is exactly one server that just started service. For the other $c-1$ servers, we use the common approximation, see, e.g, Tijms (2003), that the remaining service time on each server has a distribution equal to that of the remaining service time in equilibrium, where the service times are assumed to be independent among all servers. Given that the service times are phase-type distributed, we find the equilibrium distribution of the remaining service time on any server by considering the probability of being in each phase, since the time spent in any phase is exponentially distributed. Overall, the initial distribution of the joint phases of customers in service at the start of a busy period equals $\varvec{\beta } \oplus ( {\oplus _{i=1}^{c-1} z^*})$, with $z^*$ equal to the following expression, see, e.g., Lemma 1 in Al Hanbali et al. (2012):

$$\begin{aligned} z^*=-\frac{1}{{\mathbb {E}}\left[ S \right] }\varvec{\beta } \cdot \varvec{V}^{-1}. \end{aligned}$$

5 Extensions to speed up the analysis methods

As we will show in Sect. 6.2.1, it can be time-consuming to estimate the two moments of the busy period for problem instances with many servers and service times with low values for $cv_S^2$ (corresponding to distributions with many phases). Therefore, we present three options for reducing the computation time, which we describe in Sections 5.1 through 5.3. We note that theoretically it is possible to use the approach of Nojo and Watanabe (1987) to approximate the class of distributions with a squared coefficient of variations smaller than 0.5. In the following, we will not use this approach due to its limited accuracy for small squared coefficients of variation, see, e.g., van der Heijden (1993).

5.1 Option 1: scaling the service time distribution

We scale the service time distribution based on the number of servers when estimating the first two moments of the busy period. Specifically, we replace the $M/Ph_m /c$ queue by a $M/Ph_m /3$ queue where the service rate in each phase is $\frac{c}{3}$ times as fast as in the original queue. We limit the number of servers to 3 to obtain small matrices when computing ${\mathbb {E}}\left[ {B_k } \right]$ and ${\mathbb {E}}[{B_k^2 }]$. As a result, the computation times for 3-server instances remain below 1 second for service time distributions with up to 4 phases, see Sect. 6.2.1. In contrast, the computation times explode for 6 servers or more. For the $M/M/c$ queue with service rate $\mu$, the distribution of the busy period is equal to that in an equivalent $M/M/1$ queue with service rate $c\mu$, see, e.g., Riordan (1967). As a result, scaling does not affect the solution quality for that queue. For this reason, we cannot apply a correction factor when we scale the service time distribution, such as that proposed by Buzen and Bondi (1983).

5.2 Option 2: estimating ${\mathbb {E}}[{\hbox {CW}_k}]$ and ${\mathbb {E}}[{\hbox {CW}_k^2 }]$ for class $k$ ($1<k<K)$ through interpolation from those of class 1 and class $K$ customers

Our second option is to estimate the waiting time moments for class $k$ customers, $1<k<K$, from those of class 1 and class $K$ customers. Then, we do not require values for ${\mathbb {E}}[{B_{k-1}}]$ and ${\mathbb {E}}[{B_{k-1}^2}]$ to compute ${\mathbb {E}}[{\hbox {CW}_k}]$ and ${\mathbb {E}}[{\hbox {CW}_k^2 }]$. In fact, we only need to compute $\mathrm{E}[{B_{K-1}}]$ and $\mathrm{E}[{B_{K-1}^2 }]$ to estimate the waiting time moments for the lowest priority class $K$. Clearly, this approximation can only be used if we have at least 3 classes, as we require the waiting time moments for class 1 and class $K$ to estimate the moments for the remaining classes.

We obtain ${\mathbb {E}}[{\hbox {CW}_k}]$ and ${\mathbb {E}}[{\hbox {CW}_k^2 }]$, $1<k<K$, from the moments of classes 1 and $K$ as follows:

$$\begin{aligned}&{\mathbb {E}}\left[ {\hbox {CW}_k } \right] =r_{1k} {\mathbb {E}}\left[ {\hbox {CW}_1 } \right] +( {1-r_{1k} }){\mathbb {E}}\left[ {\hbox {CW}_K } \right] ,\end{aligned}$$

(23)

$$\begin{aligned}&{\mathbb {E}}\left[ {\hbox {CW}_k^2 } \right] =r_{2k} {\mathbb {E}}\left[ {\hbox {CW}_1^2 } \right] +( {1-r_{2k} }){\mathbb {E}}\left[ {\hbox {CW}_K^2 } \right] . \end{aligned}$$

(24)

We find the factors $r_{jk}$ ($j=1,2$, $k\in \left\{ {2,\ldots ,K-1} \right\} )$ by solving (23) and (24) for the $M/M/c$ queue, using the formulas for the waiting time moments per class in Kella and Yechiali (1985), see Al Hanbali et al. (2013), Sect. 5.2 for details.

5.3 Option 3: extrapolation for service time distributions with low variability

When the service time variability is low (i.e., $cv_S^2 \le 0.2)$, the approach of Sect. 3 may result in large computation times, as the corresponding phase type distribution will have many phases. For example, the mixed Erlang distribution, a sub-class of phase-type distributions, with $k$ phases has a squared coefficient of variations which satisfies $\frac{1}{k}\le cv_S^2 \le \frac{1}{k-1}$. Therefore, the mixed Erlang distribution with $cv_S^2 \le 0.2$ has at least $5$ phases. To improve the computation efficiency when many phases are required, we may use extrapolation, i.e., we estimate the conditional waiting time moments for a distribution with a low $cv_S^2$ ($\le 0.2)$ from those of distributions with larger values for $cv_S^2 (\in \{0.25,1/3,0.5,1\})$, see Sect. 6.3.2. We use a least squares approach to fit a function on a set of support points, with a support point denoting the known waiting time moment value for a given $cv_S^2$ (and thus serving as input for the extrapolation). Given that the conditional waiting time moments increase monotonically in $cv_S^2$, it is reasonable to fit a monotonically increasing function on the support points, such as a linear or exponential function.

6 Computational experiment and results

We performed an experiment to validate our methods. Section 6.1 contains our experiment design. We validate our methods and extension options in Sects. 6.2 and 6.3, respectively.

6.1 Experimental design

We use discrete-event simulation as a benchmark for method validation. We use a replication–deletion approach with a warm-up period of 1 million arrivals and multiple runs of 1 million arrivals each. After each run, we compute as performance measures the first two moments of the conditional waiting times per class over all arrivals after the warm-up period (and not only the arrivals in the most recent run). Let ${\mathbb {E}}\left[ {X( j)} \right]$ denote the average value of a performance measure after the $j$-th run. The simulation stops once convergence occurs, i.e., $\frac{{\mathbb {E}}\left[ {X( j)} \right] -{\mathbb {E}}\left[ {X( {j-1})} \right] }{{\mathbb {E}}\left[ {X( {j-1})} \right] }<0.05~\%$ for the first two moments of the conditional waiting times of all classes. For the two-class instances, we need at least 23 runs per instance, with the average being 51. For details on the selection of the warm-up period and the individual run length we refer the reader to Law (2007). Both the simulations and the analysis using our methods have been performed on a Dell Optiplex 760 computer with Intel quad core, 2.83 GHz processor, with our methods implemented in Maple 14.

Our test bed consists of 648 problem instances, 324 with two customer classes and 324 with three classes. Table 1 shows the parameter values considered. The asterisks in the table pertain to the subset of instances on which extension option 3 (i.e., extrapolation) was tested (see Sect. 6.3.2). To obtain the class arrival rates $\lambda _k$, we compute the total arrival rate $\lambda$ as $\rho c/{\mathbb {E}}\left[ S \right]$ and disaggregate $\lambda$ over the classes using the ratios $\lambda _k /\lambda$. For the squared coefficient of variation $cv_S^2 \le 0.5,$ we fit an Erlang-$n$ distribution to ${\mathbb {E}}\left[ S \right]$ and $cv_S^2$. For $cv_S^2 =0.75$, we use a Coxian-2 distribution with $\mu _1 =\frac{2}{{\mathbb {E}}\left[ S \right] }$, $p=\frac{0.5}{cv_S^2 }$, and $\mu _2 =\mu _1 p$, see Marie (1980).

Table 1 Parameter values considered for theoretical problem instances

6.2 Method validation

We first show in Sect. 6.2.1 that we obtain good results when using a scaled service time distribution to find the first two moments of the busy period (i.e., extension option 1, see Sect. 5.1). Then, we validate AVA1 and AVA2 with scaling in Sect. 6.2.2.

6.2.1 The impact of scaling the service distribution

We show the performance of AVA1 (see Sect. 4.1) both with and without scaling (the findings are similar for AVA2), where we only consider the 108 instances with 2 classes and 6 servers. We omit the 9-server instances, because we are unable to estimate the busy period moments without scaling when $cv_S^2 =0.25$. Then, the required matrices become too large to evaluate.

Table 2 shows the average and maximum relative error to simulation (rows ‘Avg. RE’ and ‘Max. RE’, respectively) for the first two moments of $B_1$ (the busy period when there are only class 1 arrivals) and $\hbox {CW}_2$. We conclude that the mean busy period ${\mathbb {E}}\left[ {B_1 } \right]$ remains accurate under scaling. Also, although ${\mathbb {E}}[{B_1^2 }]$ is less accurate under scaling, the relative error for ${\mathbb {E}}[ {\hbox {CW}_2 }]$ is comparable under scaling and non-scaling, whereas the errors for $\mathrm{E}[{\hbox {CW}_2^2 }]$ are smallest under scaling. The estimates for ${\mathbb {E}}[{\hbox {CW}_2 }]$ remain accurate for a larger number of servers.

Table 2 Solution quality with and without scaling for method AVA1

Scaling is also very fast: the time to compute the busy period moments is at most 0.9 s. In contrast, the non-scaled variant has an average computation time of 17 min for cases with 6 servers and a $cv_S^2$ of 0.25. For the 9-server instances with $cv_S^2 =0.25$, the resulting matrices are so large that we obtain memory errors. As a result, we even cannot compute the busy period moments without scaling. We therefore use scaling from now on.

6.2.2 Validation of AVA1 and AVA2

We evaluate the accuracy of AVA1 and AVA2 by comparison to Williams’ method (Williams 1980) and to simulation. Tables 3 and 4 show the overall relative error to simulation for the mean and second moment of the conditional waiting time per class, respectively. In both tables, ‘Will’ denotes the results using Williams’ method.

Table 3 Relative error per method for the mean conditional waiting time per class

Table 4 Relative error per method for the second moment of the conditional waiting time per class

In general, AVA1 and AVA2 both clearly outperform Williams’ method. The latter method gives particularly poor results for class 1 customers, for which it always severely underestimates the first two moments of the waiting time. Still, William’s method works very well for the lowest priority class. In fact, that method is very accurate for the class 3 waiting time moments, even giving the most accurate values for ${\mathbb {E}}[{\hbox {CW}_3^2 }]$. A further investigation of the results shows that:

• AVA1 gives the most accurate results, especially on the class 1 waiting time moments. For the remaining classes, AVA1 gives comparable or better results than AVA2 and performs much better than Williams’ method, except for the lowest priority class (see below). AVA1 is most accurate when the low-priority customers are a large fraction of the total demand rate.

• For the lowest priority class, Williams’ method works very well under high loads, large fractions of class 1 customers and few servers. Then, the accuracy of Williams’ method is comparable to—and often better than—that of AVA1 and AVA2.

• In general, the accuracy of AVA2 increases as $c$ decreases. For the lower priority classes, the relative errors are then equal to, or smaller than, those with AVA1.

• AVA2 outperforms the other methods on class $K$ when $\rho$ is low. On the mean waiting time ${\mathbb {E}}[{\hbox {CW}_K}](K=2,3)$, for instance, the relative error with AVA2 is 0.5 %. The second best method is AVA1 with a relative error of 1 %.

We also find that all methods become much more accurate as $cv_S^2$ increases to 1. This is expected since Williams, AVA1, and AVA2 are exact in case of an exponentially distributed service times ($cv_S^2 =1)$, i.e., all approximation assumptions for $M/G/c$ are true in case of an $M/M/c$.

The computation times of both AVA1 and AVA2 are a fraction of a second on average, and at most a few seconds. Williams’ method even has negligible computation time, since the waiting time moments are found using analytical expressions. Therefore, this method may be beneficial for estimating the conditional waiting time moments of class $K$.

A final finding, that applies both for AVA1 and AVA2, is that the squared coefficient of variation $cv_{\hbox {CW}}^2$ of the conditional waiting time over all classes increases to 1 with the utilization rate $\rho$. The squared coefficient of variation $cv_{\hbox {CW}_K }^2$of the conditional waiting time for the lowest priority class also tends to move to 1 with the increase of $\rho$. For the remaining classes $k$, $cv_{\hbox {CW}_k }^2$ remains constant in $\rho$, see Appendix B in Al Hanbali et al. (2013) for further details.

6.3 Performance of the extension options 2 and 3

6.3.1 Performance of option 2: interpolation over customer classes

Table 5 shows the relative error of AVA1 and AVA2 in estimating ${\mathbb {E}}[{\hbox {CW}_2 }]$ and ${\mathbb {E}}[{\hbox {CW}_2^2 }]$, both under the original variant (i.e., using Eqs. (2) and (3) of Sect. 3.2, denoted by ‘Orig’) and under interpolation (i.e., Sect. 5.2, denoted by ‘IntPol’). For the mean conditional waiting time ${\mathbb {E}}[{\hbox {CW}_2 } ]$, the solution quality of both variants is similar. For the second moment ${\mathbb {E}}[{\hbox {CW}_2^2 }]$, the results are clearly worse under interpolation.

Table 5 Comparison of original analysis method to the interpolation variant for class 2 waiting time moments

6.3.2 Performance of option 3: using extrapolation when service variability is low

We use extrapolation to analyze distributions with $cv_S^2 \in \left\{ {0,0.1,0.2} \right\}$, as computation times explode when the phase-type service time distributions have more than, say, 5 phases. To this end, we use at most four distributions to construct support points, i.e., those with $cv_S^2 \in \left\{ {0.25,1/3,0.5,1} \right\}$. We consider all combinations of at least 2 support points. Overall, we thus have $\sum _{i=2}^4 \left( \begin{array}{l} 4 \\ i \\ \end{array}\right) =11$ strategies, where a strategy denotes the set of support points considered.

We test each strategy on 16 two-class problem instances, with the parameter values marked by an asterisk in Table 1. We obtain our support points using AVA1. Both the first and second moment of $\hbox {CW}_k$ ($k=1,\ldots ,K)$ are more or less a linear function of $cv_S^2$, see Fig. 1 for the first two moments of $\hbox {CW}_2$ in one problem instance (the results are similar for other instances).

Fig. 1

The first two moments of $\hbox {CW}_2$ as functions of $cv_S^2$ for one problem instance

Overall, accuracy is largest when we use support points with low squared coefficients of variation, particularly when estimating the second moment of the conditional waiting time per class. The accuracy does not necessarily increase when using additional support points. Still, the extrapolation method is not sufficiently accurate for estimating performance when $cv_S^2 =0$: the maximum relative error to simulation can amount to 20 %. For larger values of $cv_S^2$, the accuracy is reasonable, with a maximum relative error of 10 %.

7 Case study

Given our experiment findings, we choose to apply AVA1 with scaling (extension option 1) and interpolation (extension option 3) to a case at a manufacturer of printing and copying systems. We consider one service region with two customer classes that each have distinct service level requirements on the overall (i.e., unconditional) waiting time: the waiting time for the premium class should always be below 3 h, while the average waiting time for the non-premium class should remain below 3.5 h. Since the first requirement would yield an excessive amount of service engineers equal to the size of the installed base, we translated this requirement into a high probability that the 3-h limit is not exceeded (e.g., 99.9 %). The remaining parameter values are a utilization rate $\rho$ of 0.93, a mean service time ${\mathbb {E}}\left[ S \right]$ of 2.3662 h, a squared coefficient of the service time $cv_S^2$ of 0.2161, and a division over classes $( {\frac{\lambda _1 }{\lambda };\frac{\lambda _2}{\lambda }})$ of (0.15; 0.85). In general, a service region is serviced by 4 engineers. It is worth mentioning that the Poisson arrivals assumption is validated empirically using company data on the time between failures and the clicks (prints) between failures (Munnik 2011). In Sect. 7.1, we therefore first evaluate performance under that setting. We shall see that the service target for class 2 cannot be met then. In Sect. 7.2, we therefore consider two alternatives for meeting all service level targets.

7.1 Performance under the current capacity

First, we compute the first two moments of the conditional waiting time per class using linear interpolation with the waiting time moments in an Erlang-5 distribution (with $cv_S^2 =0.2)$ and an Erlang-4 distribution (with $cv_S^2 =0.25)$ as support points.² Then, we estimate the distribution of $W_1$ (the overall class 1 waiting time) by fitting a gamma distribution on the conditional waiting time moments. We also estimate the mean class 2 waiting time ${\mathbb {E}}[{W_2}]$. Our analysis shows that the target for class 1 is met in 99.9 % of the cases, while the mean waiting time for class 2 is 5.2 h, which is far larger than the target of 3.5 h.

7.2 Options for meeting the service level targets

We have two options to reduce the class 2 waiting time, while ensuring that the class 1 waiting time never exceeds 3 h. First, we can increase the number of servers. Alternatively, we may consider a dynamic priority mechanism for service engineer assignment. As class 1 customers always have priority over class 2 customers at present, it may be that the class 1 waiting times are lower than required at the expense of the class 2 waiting times. Therefore, we prefer a mechanism where a new class 1 customer does not have priority over a class 2 customer that has already been waiting for a certain amount of time. Still, system analysis quickly becomes complicated under such a priority mechanism. To get an idea of the potential impact of a dynamic allocation rule, we use as emulation a softer priority mechanism by treating an arriving class 2 customer as a class 1 customer with a probability $p$, with $p$ being any value between 0 and 1. The value of $p$ influences the waiting times of both classes: as $p$ increases, some class 2 customers experience a lower waiting time, which might reduce the overall waiting time for that class. Conversely, as class 1 customers now occasionally need to wait for an ‘upgraded’ class 2 customer, the class 1 waiting times increases. We now use the following approach to determine values for $c$ and $p$:

• 1. Set $c$ to its original value. In our case study $c$ will thus equal 4.

• 2. For the current value of $c$, compute performance both when (A) no class 2 customer is treated as a class 1 customer (corresponding to $p=0)$, and when (B) all customers are treated equally, i.e., $p=1$.

• 3. Depending on the outcome of the previous step, do the following:

  • (a) If the targets for both classes are met under either (A) or (B), STOP.

  • (b) If the target for class 1 is not met under (A), it will certainly not be met for $p>0$. Conversely, if the class 2 target is not met under (B), it will not be met for $p<1$. In both cases, increase $c$ by 1 unit and proceed to step 2.

  • (c) If the target for class 1 is met under (A), while the class 2 target is met under (B), it might be possible to meet both targets by setting $p>0$. Proceed to step 4. Otherwise, increase $c$ by 1 unit and proceed to step 2.

• 4. Use bisection to check whether a value for $p$ exists such that the service targets are satisfied for both classes. Proceed until either all targets are satisfied (we then STOP), or no value for $p$ exists such that all targets are satisfied (we then increase $c$ by 1 and go to step 2).

For our case study, we require 5 servers to meet both service level targets (see Table 6). Increasing $p$ when $c=4$ has no benefit, as we still are not able to meet the class 2 target even when $p=1$. This is because the low-priority customers comprise the bulk of the workload: reducing their waiting time has a strong impact on the waiting time of low-priority customers.

Table 6 Performance on service level targets for various control options

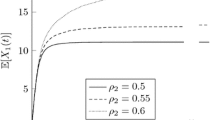
We find that the impact of $p$ depends on the type of service level considered, see Fig. 2. We base the figure mainly on the case study values, with only $cv_S^2$ adjusted to 0.2 for simplicity. In the left figure, ${\mathbb {E}}[W_2 ]$ decreases slightly with $p$, while ${\mathbb {E}}[{W_1}]$ explodes for large values of $p$. The picture is different for the waiting time percentiles (where the figure on the right denotes the 90th percentile per class, i.e., the value $X$ such that $\Pr \{{W_k \le X}\}=0.9$ for $k=1,2)$. Specifically, the percentile function for class 2 initially increases with $p$. This occurs because the variability of $W_2$ may increase with $p$, since a fraction of class 2 customers is now treated as a class 1 customer (with a corresponding low waiting time), while the remaining class 2 customers have an increasingly high waiting time.

Fig. 2

The impact of $p$ on the mean waiting time and waiting time distribution per class

Overall, our analysis methods enable a service provider to accurately estimate performance on various types of service levels. In particular, he is now able to characterize the distribution of the waiting time per class from the first and second moment of the conditional waiting time per class. The service provider can use these methods both to estimate service level performance for a given number of engineers and, conversely, to determine what service levels he can guarantee to his customers. In this case study, for instance, the service provider must consider whether it is beneficial to guarantee a mean waiting time of at most 3.5 h to his lowest priority customers, since he then requires a fifth service engineer to satisfy all targets.

8 Conclusions

We considered a non-preemptive $M/G/c$ queue with $K$ classes. For this system, we developed two main methods to obtain the first two moments of the waiting time per class given that all servers are busy. We also presented three options for reducing computation times. We applied the various approaches to an extensive set of theoretical instances and to a case study at a manufacturer of printing and copying equipment. Our main conclusions are:

• Overall, AVA1 is the most effective analysis method. AVA1 generally gives the most accurate results, especially when estimating the conditional waiting time moments of the highest priority class. Furthermore, the computation time of the method is on average a fraction of a second and at most 4 seconds for settings with two customer classes.

• In some settings, Williams’ method may be a good alternative for finding the conditional waiting time moments of the lowest priority class only. Williams’ method can be more accurate than AVA1 for the conditional waiting time moments of class $K$, for instance in systems with high loads or few servers. As Williams’ method is also very fast, it is a good alternative for class $K$ waiting times, especially when there are 3 or more customer classes.

• The scaling of the service time distribution is an effective option for reducing the analysis time. Numerical results show that the scaling of the service time distribution generally leads to promising results: under AVA1, the average relative error to simulation for any performance measure remains below 2.5 %, while the maximum relative error is 12.3 %. Scaling also greatly reduces analysis time in settings with 6 or more servers and a complex service time distribution with 4 or more phases. Indeed, scaling is even necessary for analyzing queues with 9 or more servers.

• The analysis methods allow a service provider to accurately estimate his performance on various types of service levels. Given that the methods compute both the mean and second moment of the conditional waiting time per class, a service provider is able to estimate the distribution of the overall waiting time besides the corresponding mean value. As a result, he is able to evaluate his performance on various types of service levels and, more importantly, determine what service levels he can feasibly promise to his customers.

In this paper, all customer classes have the same service time distribution. Still, it might be that the service time distribution varies per customer segment, for instance if an engineer can service multiple types of systems that each require different service times, while the system type is not evenly distributed over the customer classes. It would thus be an interesting area of further research to allow the service time distribution to vary per customer segment. Such an extension will likely result in a significant increase in complexity. For instance, the distribution of the remaining service time of any busy server will now depend on the type of customer being served by that server.

Appendix: The first two queue length moments in an \(M/G/c\) queue

We obtain ${\mathbb {E}}[{L_q}]$ and ${\mathbb {E}}[{L_q ( {L_q -1})}]$ by first taking the first two derivatives of the generating function $P_q ( z)$ given by Equation (9.6.22) in Tijms (2003) in $z=1$. We then simplify elements of the resulting expressions. After differentiating $P_q ( z)$ in $z=1$, we find:

$$\begin{aligned}&\qquad \qquad {\mathbb {E}}\left[ {L_q } \right] =\frac{c}{{\mathbb {E}}\left[ S \right] }( {1-\rho })\pi _w \left( {\frac{I_5 }{1-\lambda I_1 }+\frac{\lambda I_2 I_4 }{( {1-\lambda I_1 })^2}}\right) ,\end{aligned}$$

(25)

$$\begin{aligned}&{\mathbb {E}}\left[ {L_q ( {L_q -1})} \right] =\frac{c}{{\mathbb {E}}\left[ S \right] }( {1-\rho })\pi _w \left( {\frac{I_6 }{1-\lambda I_1 }+\frac{2\lambda I_2 I_5 }{( {1-\lambda I_1 })^2}+\frac{2\lambda ^2I_2^2 I_4 }{( {1-\lambda I_1 })^3}+\frac{\lambda I_3 I_4 }{( {1-\lambda I_1 })^2}}\right) ,\nonumber \\ \end{aligned}$$

(26)

where $I_1$ through $I_6$ pertain to the integrals in Eqs. (27) to (32). Note that each integral can be greatly simplified, as shown below. Details on the derivations are given afterwards.

$$\begin{aligned} I_1&= \int _0^\infty ( {1-S( {c\cdot t})})\mathrm{d}t=\int _0^\infty ( {1-S( u)})\frac{\mathrm{d}u}{c}=\frac{{\mathbb {E}}\left[ S \right] }{c}.\end{aligned}$$

(27)

$$\begin{aligned} I_2&= \int _0^\infty ( {1-S( {c\cdot t})})\lambda t\,\mathrm{d}t=\lambda \int _0^\infty ( {1-S(u)})\frac{u}{c}\frac{\mathrm{d}u}{c}\nonumber \\&= \frac{\lambda }{c^2} \int _0^\infty ( {1-S(u)})u\,\mathrm{d}u=\frac{\lambda {\mathbb {E}}\left[ {S^2} \right] }{2c^2}.\end{aligned}$$

(28)

$$\begin{aligned} I_3&= \int _0^\infty ( {1-S( {c\cdot t})})\lambda ^2t^2\mathrm{d}t=\frac{\lambda ^2}{c^3}\int _0^\infty (1-S( u)u^2\mathrm{d}u=\frac{\lambda ^2{\mathbb {E}}\left[ {S^3} \right] }{3c^3}.\end{aligned}$$

(29)

$$\begin{aligned} I_4&= \int _0^\infty \left( {1-\frac{\int _0^{t} ( {1-S( u)})\mathrm{d}u}{{\mathbb {E}}\left[ S \right] }}\right) ^{c-1}( {1-S( t)})\mathrm{d}t=\frac{{\mathbb {E}}\left[ S \right] }{c}.\end{aligned}$$

(30)

$$\begin{aligned} I_5&= \int _0^\infty \left( {1-\frac{\int _0^t ( {1-S( u)})\mathrm{d}u}{\mathrm{E}[S]}}\right) ^{c-1}( {1-S( t)})\lambda t\mathrm{d}t=\rho \cdot \gamma _1,\end{aligned}$$

(31)

$$\begin{aligned} I_6&= \int _0^\infty \left( {1-\frac{\int _0^t ( {1-S( u)})\mathrm{d}u}{{\mathbb {E}}\left[ S \right] }}\right) ^{c-1}( {1-S( t)})\lambda ^2t^2\mathrm{d}t=2\lambda \cdot \rho \cdot \gamma _2, \end{aligned}$$

(32)

where $\gamma _1$ and $\gamma _2$ are defined by (7) and (10), respectively. The rewriting of $I_1$ is trivial. For $I_2$, we find that $\mathop \smallint \nolimits _0^\infty ( {1-S(u)}) u\mathrm{d}u=\frac{1}{2}{\mathbb {E}}\left[ {S^2} \right]$ through integration by parts. In a similar way, we obtain $I_3$. For $I_4$, we first rewrite $1-\frac{\int _0^t ( {1-S( u)})\mathrm{d}u}{{\mathbb {E}}\left[ S \right] }$ as $Y( t)$ (i.e., $Y( t)=1-\frac{\int _0^t ( {1-S( u)})\mathrm{d}u}{{\mathbb {E}}\left[ S \right] })$. We then find:

$$\begin{aligned} I_4 =-\int _0^\infty ( {Y( t)})^{c-1}\cdot Y^{'}( t)\cdot {\mathbb {E}}\left[ S \right] \mathrm{d}t=-{\mathbb {E}}\left[ S \right] \left[ {\frac{( {Y( t)})^c}{c}} \right] _0^\infty =\frac{{\mathbb {E}}\left[ S \right] }{c}. \end{aligned}$$

Finally, to simplify $I_5$ and $I_6$, we again substitute $1-\frac{\int _0^t ( {1-S( u)})\mathrm{d}u}{{\mathbb {E}}\left[ S \right] }$ by $Y( t)$. We find for $I_5$:

$$\begin{aligned} I_5 =-\int _0^\infty ( {Y( t)})^{c-1}\cdot Y^{'}( t)\cdot {\mathbb {E}}\left[ S \right] \lambda t\,\mathrm{d}t=-\lambda {\mathbb {E}}\left[ S \right] \mathop \smallint \limits _0^\infty t\cdot ( {Y( t)})^{c-1}\cdot Y^{'}( t)\cdot \mathrm{d}t. \end{aligned}$$

By integrating the latter integral by parts, we find the simplified expression for $I_5$. In a similar way, we find the expression for $I_6$. By dividing the simple expressions for ${\mathbb {E}}[ {L_q }]$ and ${\mathbb {E}}[{L_q ( {L_q -1})} ]$ by those for ${\mathbb {E}}[ {L_q (\exp )} ]$ and ${\mathbb {E}}[ {L_q ( {L_q -1})(\exp )}]$, respectively, we obtain expressions (6) and (9) in Sect. 4.1.1.