Effect of modeling fixed cost in a serial inventory system with periodic review

Abstract

We study a two-echelon serial inventory system with stochastic demand. We assume that fixed ordering costs are charged only when an order initiates a non-zero shipment. The system is centrally controlled and ordering decisions are based on echelon base stock policies. The review period of the upper echelon is an integer multiple of the review period of the lower echelon. We derive an exact analytical expression for the objective function. From this expression, we determine optimal base stock levels and review periods. Through a numerical study we show that there may be several combinations of optimal review periods and that under high fixed ordering costs both stockpoints have the same order frequency. In addition, we identify parameter settings under which the system behaves like a PUSH-system, where the upstream stockpoint never holds any stock. Generally, in literature fixed ordering costs are charged at every review moment, even if no shipment results due to zero upstream stock. We test the impact of this simplifying assumption and illustrate when it is justified.

Appendix

1.1 Derivation of Eq. (14)

We first derive the expected cost per period attached to replenishment cycle of stage 2. In Eq. (8) this cost is given as:

$$\begin{aligned}&\frac{1}{R_2}\sum \limits _{k=0}^{R_2-1}E[C_2(t_0 + l_2 + k)] \nonumber \\&\quad =\frac{1}{R_2}\sum \limits _{k=0}^{R_2-1} E [ \delta _{2}(t_0 + l_2 + k) K_2 + h_2 X_{2}(t_0 + l_2 + k)] \nonumber \\&\quad = \frac{K_2}{R_2} P \{ D[t_0-R_2,t_0) > 0 \} + h_2 \frac{1}{R_2}\sum \limits _{k=0}^{R_2-1} ( S_2 - (l_2 + k + 1))\nonumber \\&\quad = \frac{K_2}{R_2} P \{ D[t_0-R_2,t_0) > 0 \} + h_2\left( S_2-\left( l_2+\frac{1}{2}(R_2 + 1)\right) \mu \right) . \end{aligned}$$

(19)

Similarly, the cost per period attached to replenishment cycle of stage 1 is

$$\begin{aligned}&\frac{1}{R_2}\sum \limits _{i=0}^{r-1}{\sum \limits _{j=0}^{R_1-1}E[C_1(t_0 + l_1 + l_2 +iR_1 + j)]} \nonumber \\&\quad =\frac{1}{R_2}\sum \limits _{i=0}^{r-1}\sum \limits _{j=0}^{R_1-1} E [ \delta _{1}(t_0 + l_1 + l_2 +iR_1 + j) K_1 + h_1 X_{1}(t_0 + l_1 + l_2 +iR_1 + j) \nonumber \\&\qquad + (p+h_1+h_2)X_{1}(t_0 + l_1 + l_2 +iR_1 + j)^{-}] \nonumber \\{}&\quad = h_1 ( S_1-(l_1+\frac{1}{2}(R_1+1))\mu - \frac{R_1}{R_2}\sum \limits _{i=0}^{r-1}E[B_1(t_0+l_2+i R_1)] ) \nonumber \\&\qquad +(p+h_1+h_2)\frac{1}{R_2}\sum \limits _{i=0}^{r-1}\sum \limits _{j=0}^{R_1-1}E[X_1(t_0+l_1 + l_2+i R_1+j)^-] \nonumber \\&\qquad + \frac{K_1}{R_2}\sum \limits _{i=0}^{r-1}E[\delta _{1}(t_0 + l_1 + l_2 + i R_1)]. \end{aligned}$$

(20)

The summation of (19) and (20) results in (14).

1.2 Proof of Theorem 1

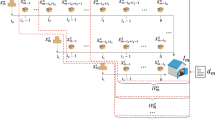
Stockpoint 1 will place an order at period $t$ if the following conditions are met:

• 1. $t$ is a review period for stockpoint 1,

• 2. Inventory position of stockpoint 1 before placing the order at the beginning of period $t$ is below $S_1$,

• 3. The physical stock level at stockpoint 2 is positive at the beginning of period $t$ before stockpoint 1 places an order.

Using these principles we prove each condition separately.

• Case 1: $i=0,\ldots ,r-1$ and $j=1,\ldots ,R_1-1$

The periods $t_0+l_2+iR_1+j$ for $i=0,\ldots ,r-1$ and $j=1,\ldots ,R_1-1$ are not review periods of stockpoint 1, so there will be no arrival of orders at the beginning of periods $t_0+l_1 + l_2 +iR_1 + j$ when $j\ne 0$. Thus, $\delta _{1}(t_0 + l_1 + l_2 + i R_1 + j) = 0$.

• Case 2: $i=1,\ldots ,r-1$ and $j=0$

The installation stock level of $2$ directly affects the decision of ordering of stockpoint $1$. It changes only when there is an order arrival from the supplier, or items are ordered from stockpoint $1$. We define the installation stock level of stockpoint $2$ as $IS_{2}(t)$ at the beginning of period $t$, after arrival of orders to stockpoint $2$ and after stockpoint $1$ places an order. It is equal to the difference between the echelon stock of stockpoint $2$ and the inventory position of stockpoint $1$ at period $t$. Throughout the review periods $t_0+l_2+iR_1$ such that $i=1,\ldots ,r-1$, there are no order arrivals to stockpoint $2$. Also, there will be no shipments from stockpoint $2$ to $1$ in between two review periods of stockpoint $1$. Thus, the installation stock level at stockpoint $2$ at period $t_0+l_2+iR_1$ before stockpoint 1 places an order will be equal to $IS_2(t_0+l_2+(i-1)R_1)$.

$$\begin{aligned}&IS_{2}(t_0+l_2+(i-1)R_1)= IL_2(t_0+l_2+(i-1)R_1)-IP_{1}(t_0+l_2+(i-1)R_1)\\&\quad \!=\! S_2 - S_1 - D[t_0,t_0\!+\!l_2\!+\!(i-1)R_1) \!+\! [D[t_0,t_0\!+\!l_2\!+\!(i-1)R_1) \!-\! (S_2 - S_1)]^-. \end{aligned}$$

There are two possible outcomes for the installation stock level depending on the amount of demand during the time interval $[t_0,t_0+l_2+(i-1)R_1)$:

• 1. If $D[t_0,t_0+l_2+(i-1)R_1) \ge S_{2}-S_{1}$, then $IS_{2}(t_0+l_2+(i-1)R_{1})=0$,

• 2. If $D[t_0,t_0+l_2+(i-1)R_1) < S_{2}-S_{1}$, then $IS_2(t_0+l_2+(i-1)R_{1})>0$.

An order can be placed by stockpoint 1 at the beginning of period $t_0+l_2+ iR_1$, only when $IS_2(t_0+l_2+(i-1)R_{1})>0$. If this is the case, it also means that stockpoint 1 has raised its inventory position up to $S_1$ at period $t_0+l_2+(i-1)R_{1}$. Then, if customer demand during last $R_1$ periods is positive, stockpoint 1 will place an order at the beginning of period $t_0+l_1 + l_2+iR_1$. Thus, the expected value of $\delta _1(t_0+l_1 + l_2+iR_1)$ for $i=1,\ldots ,r-1$ is $P\{D[t_0,t_0+l_2+(i-1)R_1) < S_{2}-S_{1}\}P\{D[t_0+l_2+(i-1)R_1,t_0+l_2+iR_1)>0\}$.

• Case 3: $i=0$ and $j=0$

The arguments we have followed for Case 2 also hold for this case. On top of that, there can be an order arrival to stockpoint 2 at the beginning of the period $t_0 + l_2$ and $IS_2(t_0 +l_2)$ can be positive. Therefore, we differentiate three situations where stockpoint 1 can place an order.

• 1. $IS_2(t_0+l_2-R_1)>0$,

• 2. $IS_2(t_0+l_2-R_1)=0$ and $IP_1(t_0+l_2-R_1) < S_1$,

• 3. $IS_2(t_0+l_2-R_1)=0$ and $IP_1(t_0+l_2-R_1) = S_1$.

At the first situation, stockpoint 1 will place an order if $D[t_0+l_2-R_1,t_0+l_2)>0$. Here, it is not important if stockpoint 2 receives a shipment at $t_0+l_2$ since it already has positive stock level. The probability for situation 1 is: $P\{D[t_0,t_0+l_2-R_1 < S_{2}-S_{1}\}P\{D[t_0+l_2-R_1,t_0+l_2)>0\}$.

At the second situation, stockpoint 2 has no physical stock left and stockpoint 1 has positive shortfall. Thus, stockpoint 1 will place an order even if there is no demand during $[t_0+l_2-R_1,t_0+l_2)$. Beware that an order can be shipped from stockpoint 2 to stockpoint 1, if there is an order arrival to stockpoint 2 at the beginning of period $t_0+l_2$. So, for situation 2, we have $P\{D[t_0 - R_2, t_0 + l_2 -R_1) > S_2 - S_1, D[t_0 -R_2, t_0) > 0 \}$ as the expected order frequency.

At the last situation, stockpoint 1 will be below its inventory position if $D[t_0+l_2-R_1,t_0+l_2)>0$ and it can place an order if there is an arrival to stockpoint 2 at $t_0+l_2$. The combined probability for ordering becomes $P \{ D[t_0-R_2, t_0+l_2-R_1) = S_2 - S_1, D[t_0 - R_2, t_0) > 0, D[t_0 + l_2-R_1, t_0 + l_2) > 0\}$.