A mosquito population suppression model with a saturated Wolbachia release strategy in seasonal succession

Abstract

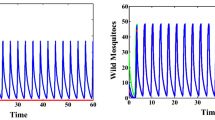
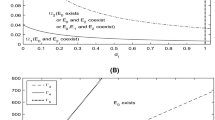
Releasing Wolbachia-infected male mosquitoes to suppress wild female mosquitoes through cytoplasmic incompatibility has shown great promise in controlling and preventing mosquito-borne diseases. To make the release logistically and economically feasible, we propose a saturated release strategy, which is only implemented during the epidemic season of mosquito-borne diseases. Under this assumption, the model becomes a seasonally switching ordinary differential equation model. The seasonal switch brings rich dynamics, including the existence of a unique periodic solution or exactly two periodic solutions, which are proved by using the qualitative property of the Poincaré map. Sufficient conditions are also obtained for determining the stability of the periodic solutions.

Appendices

Appendices

A Computing the poincaré map

The Poincaré map p(u) is bridged by ${\bar{p}}(u)$, and the relation between ${\bar{p}}(u)$ and p(u) is governed by equation (1.9) when $t\in [\phi T,T)$. Initiated from $w(\phi T)$, equation (1.9) can be solved as

$$\begin{aligned} d\left( \ln \left( \frac{w}{A-w}\right) ^{-\frac{1}{A}}\right) = -\xi dt. \end{aligned}$$

(A.1)

Integrating (A.1) from $\phi T$ to T then yields

$$\begin{aligned} p(u)=\frac{A e^{A\xi T(1-\phi )}{\bar{p}}(u)}{A+(e^{A\xi T(1-\phi )}-1){\bar{p}}(u)}. \end{aligned}$$

(A.2)

It follows from (A.2) that to compute p(u), we only need to specify ${\bar{p}}(u)$, which is governed by equation (1.8) when $t\in [0,\phi T)$. We write (1.8) as

$$\begin{aligned} \dfrac{w+1+b}{w\left( w^2+c_{1}w+c_{2}\right) }dw = -\xi dt, \end{aligned}$$

(A.3)

where

$$\begin{aligned} c_{1}=1+b-A, \ c_{2}= \frac{\mu }{\xi }\left( 1+b-\frac{a}{\mu }\right) . \end{aligned}$$

Next, we compute ${\bar{p}}(u)$ in two cases.

1.1 Case 1: $\varvec{c}_{2}={0}$

When $c_2=0$, we get $b=b^*$, and we rewrite equation (A.3) as

$$\begin{aligned} \dfrac{w+1+b^*}{w^2(w-E^*)}dw = -\xi dt, \end{aligned}$$

(A.4)

with $E^*=-c_1>0$. Equation (A.4) can be decomposed to

$$\begin{aligned} \left( \frac{\alpha _1}{w-E^*}+\frac{\beta _1}{w}+\frac{\gamma _1}{w^2}\right) dw = -\xi dt, \end{aligned}$$

(A.5)

where

$$\begin{aligned} \alpha _1= \frac{1+b^*+E^*}{E^{*2}}, \ \beta _1 = -\frac{1+b^*+E^*}{E^{*2}}<0, \ \gamma _1 = -\frac{1+b^*}{E^*}. \end{aligned}$$

From (A.5) we get

$$\begin{aligned} d\left( \ln \left( w^{\beta _1} (w-E^*)^{\alpha _1} e^{-\frac{\gamma _1}{w}}\right) \right) = -\xi dt. \end{aligned}$$

(A.6)

Integrating (A.6) from 0 to $\phi T$, we have

$$\begin{aligned} {\bar{p}}(u)=u\left( \frac{u-E^*}{{\bar{p}}(u)-E^*}\right) ^{\frac{\alpha _1}{\beta _1}} e^{\frac{\gamma _1}{\beta _1}\left( \frac{1}{{\bar{p}}(u)}-\frac{1}{u}\right) }e^\frac{-\xi \phi T}{\beta _1}. \end{aligned}$$

(A.7)

1.2 Case 2: $\varvec{c}_{2}\ne {0}$

In this case, equation (A.3) can be decomposed to

$$\begin{aligned} \left( \frac{\alpha _2}{w}+\frac{\beta _2 w+\gamma _2}{w^2+c_{1}w+c_{2}}\right) dw = -\xi dt, \end{aligned}$$

(A.8)

where

$$\begin{aligned} \alpha _2 = \frac{1+b}{c_{2}}, \ \beta _2 = -\frac{1+b}{c_{2}}, \ \gamma _2 = 1-\frac{(1+b)c_{1}}{c_{2}}. \end{aligned}$$

Elementary calculation yields

$$\begin{aligned} \int \frac{\beta _2 w+\gamma _2}{w^2+c_{1}w+c_{2}}dw = \ln G(w)+c, \end{aligned}$$

where

$$\begin{aligned} G(w)=\left\{ \begin{aligned}&(w^2+c_1w+c_2)^\frac{\beta _2}{2}\exp \left( {\frac{m}{r}\tan ^{-1}\left( \frac{w+\frac{c_{1}}{2}}{r}\right) }\right) ,&\text {if}&\quad w^2+c_1w+c_2>0, \\&|w-E^{**}|^{\beta _2} \exp \left( {-\frac{\beta _2E^{**}+\gamma _2}{w-E^{**}}}\right) ,&\text {if}&\quad w^2+c_1w+c_2=(w-E^{**})^2, \\&|w-E^-|^{\frac{\beta _2 E^-+\gamma _2}{E^--E^+}}|w-E^+|^{-\frac{\beta _2 E^++\gamma _2}{E^--E^+}},&\text {if}&\quad w^2+c_1w+c_2=(w-E^-)(w-E^+), \end{aligned}\right. \nonumber \\ \end{aligned}$$

(A.9)

with

$$\begin{aligned} \ m= \gamma _2-\frac{c_1}{2}\beta _2,\ r=\sqrt{c_{2}-\frac{c_{1}^2}{4}}. \end{aligned}$$

Hence, integrating (A.8) from 0 to $\phi T$ offers

$$\begin{aligned} {\bar{p}}(u)=u\left( \frac{G(u)}{G({\bar{p}}(u))}\right) ^{\frac{1}{\alpha _2}}e^{-\frac{\xi \phi T}{\alpha _2}}. \end{aligned}$$

(A.10)

B Computing $\varvec{p}'(0)$ for local stability of $E_0=0$

The computation of $p'(0)$ divides into two separate cases.

1.1 Case 1: $\varvec{c}_{2}=0$

Since ${\bar{p}}(0)=0$, from (A.7), we get

$$\begin{aligned} {\bar{p}}'(0)=\lim _{u \rightarrow 0}\frac{{\bar{p}}(u)}{u}= e^{\frac{\gamma _1}{\beta _1}\lim _{u \rightarrow 0}\left( \frac{1}{{\bar{p}}(u)}-\frac{1}{u}\right) }e^\frac{-\xi \phi T}{\beta _1}. \end{aligned}$$

Note that

$$\begin{aligned} \lim _{u \rightarrow 0}\left( \frac{1}{{\bar{p}}(u)}-\frac{1}{u}\right) = \lim _{u \rightarrow 0} \frac{u-{\bar{p}}(u)}{u{\bar{p}}(u)} =\lim _{u \rightarrow 0} \frac{1-{\bar{p}}'(u)}{{\bar{p}}(u)+u{\bar{p}}'(u)}, \end{aligned}$$

(B.1)

we have two cases to consider when calculating ${\bar{p}}'(0)$.

• (1) If $\lim _{u \rightarrow 0}\left( \frac{1}{{\bar{p}}(u)}-\frac{1}{u}\right)$ is finite, then (B.1) implies that ${\bar{p}}'(0)=1$.

• (2) If $\lim _{u \rightarrow 0}\left( \frac{1}{{\bar{p}}(u)}-\frac{1}{u}\right) =-\infty$, then ${\bar{p}}'(0)=0$. However, revisiting (B.1) again leads to $\lim _{u \rightarrow 0}\left( \frac{1}{{\bar{p}}(u)}-\frac{1}{u}\right) =+\infty$, a contradiction.

Combining the above two cases, we get ${\bar{p}}'(0)=1$. It follows from (A.2) that

$$\begin{aligned} \lim _{u \rightarrow 0}\frac{p(u)}{{\bar{p}}(u)} =e^{(a-\mu )T(1-\phi )}, \end{aligned}$$

and hence

$$\begin{aligned} p'(0)={\bar{p}}'(0) \lim _{u \rightarrow 0}\frac{p(u)}{{\bar{p}}(u)} =e^{(a-\mu )(T-T_{1}^{*})}, \end{aligned}$$

(B.2)

where

$$\begin{aligned} T_{1}^{*}=\phi T. \end{aligned}$$

1.2 Case 2: $\varvec{c}_{2}\ne {0}$

We obtain, from (A.10)

$$\begin{aligned} {\bar{p}}'(0)=\lim _{u \rightarrow 0}\frac{{\bar{p}}(u)}{u} = \lim _{u \rightarrow 0}\left( \frac{G(u)}{G({\bar{p}}(u))}\right) ^{\frac{1}{\alpha _2}}e^{-\frac{\xi \phi T}{\alpha _2}}=e^{-\frac{c_{2}\xi \phi T}{1+b}}. \end{aligned}$$

(B.3)

Equation (A.2) and (B.3) imply

$$\begin{aligned} p'(0)=\lim _{u \rightarrow 0}\frac{p(u)}{u} = \lim _{u \rightarrow 0}\left( \frac{p(u)}{{\bar{p}}(u)} \cdot \frac{{\bar{p}}(u)}{u}\right) =e^{(a-\mu )(T-T_{2}^{*})}, \end{aligned}$$

(B.4)

where

$$\begin{aligned} T_{2}^{*}=\frac{ab\phi T}{(a-\mu )(1+b)}. \end{aligned}$$

It’s easy to see that $c_2=0$ if and only if $b=b^*,$ under which

$$\begin{aligned} T_{2}^{*}(b^*)=\frac{ab^*\phi T}{(a-\mu )(1+b^*)}=\phi T=T_{1}^{*}. \end{aligned}$$

Hence, by defining

$$\begin{aligned} T^{*}=\frac{ab\phi T}{(a-\mu )(1+b)}, \end{aligned}$$

we have

Proposition B.1

When $T>T^*$, one has $p'(0)>1$ and hence $E_0$ is unstable. When $T<T^*$, then $p'(0)<1$ and $E_0$ is locally asymptotically stable.

Proof

From (B.2) and (B.4), we get $p'(0)>1$ if $T>T^*$, which implies that there exists a small enough $\delta >0$ such that $p(u)>u$ for $u \in \left( 0, \delta \right) .$ Together with the fact that for any $u \in \left( 0, \delta \right)$, then sequences $\{w(nT; 0,u)\}$ is strictly increasing, which means that solution w(t; 0, u) does not go to zero as $t\rightarrow \infty$, hence $E_0$ is unstable. Similarly, when $T<T^*$, we have $p'(0)<1$, then there is $\delta ^*>0$ sufficiently small such that $p(u)<u$ for $u \in \left( 0, \delta ^*\right) .$ We know that the sequences $\{w(nT; 0, u)\}$ is strictly decreasing and so there are some solutions w(t; 0, u) such that $\lim _{t \rightarrow \infty }w(t; 0,u)=0$ for $u \in \left( 0, \delta ^*\right) ,$ hence $E_0$ is locally asymptotically stable. $\square$

C Sufficient conditions for the stability of the T-periodic solution

Lemma C.1

Let $w(t; 0, {\bar{u}})$ be the unique T-periodic solution lying in $U^0({\bar{u}}, \gamma )= ({\bar{u}}-\gamma , {\bar{u}}) \cup ({\bar{u}}, {\bar{u}}+\gamma )$ with $\gamma >0$. If

$$\begin{aligned} (u-{\bar{u}})(p(u)-u)<0, \ u \in U^0({\bar{u}}, \gamma ), \end{aligned}$$

(C.1)

then $w(t; 0, {\bar{u}})$ is asymptotically stable.

Proof

First, we claim that $p(u)<u$ implies

$$\begin{aligned} w(t+T; 0, u)<w(t; 0, u), \ t\ge 0. \end{aligned}$$

(C.2)

Otherwise, we assume that $t_{0}$ is the first time point such that $w\left( t_{0}+T; 0, u\right) =w\left( t_{0}; 0, u\right)$. Write ${\bar{w}}(t)=w(t+T; 0, u)$, or, equivalently, ${\bar{w}}(t)=w(t; 0, w(T))=w(t; 0, p(u))$, which is also a solution of (1.8)-(1.9). Comparing w(t) and ${\bar{w}}(t)$ at $t_{0}$, we have

$$\begin{aligned} w\left( t_{0}\right) =w\left( t_{0}+T; 0, u\right) =w\left( t_{0}; 0, p(u)\right) ={\bar{w}}\left( t_{0}\right) , \end{aligned}$$

which contradicts the existence and uniqueness of initial value problems, proving (C.2). Similarly, we can prove that if $p(u)>u$, then

$$\begin{aligned} w(t+T; 0, u)> w(t; 0, u), \ t\ge 0, \end{aligned}$$

if $p(u)=u$, then w(t; 0, u) is a T-periodic solution.

Now, we show that $w(t; 0, {\bar{u}})$ is asymptotically stable if (C.1) holds. Without loss of generality, we only consider the case with $u \in ({\bar{u}}, {\bar{u}}+\gamma )$. For any $\varepsilon = \gamma >0$, if

$$\begin{aligned} \max _{t \in [0, T]}\{w(t; 0, {\bar{u}}+\gamma )-w(t; 0, {\bar{u}})\} \le \gamma , \end{aligned}$$

then choose $\delta =\varepsilon$, we have

$$\begin{aligned} w(t; 0, u)-w(t; 0, {\bar{u}})<\varepsilon , \ u \in ({\bar{u}}, {\bar{u}}+\delta ). \end{aligned}$$

Otherwise, if

$$\begin{aligned} \max _{t \in [0, T]}\{w(t; 0, {\bar{u}}+\gamma )-w(t; 0, {\bar{u}})\} > \gamma , \end{aligned}$$

then there must be a $\gamma _{1}<\gamma$ such that

$$\begin{aligned} \max _{t \in [0, T]}\{w(t; 0, {\bar{u}}+\gamma _1)-w(t; 0, {\bar{u}})\} \le \gamma . \end{aligned}$$

Choosing $\delta =\gamma _{1}$, we get

$$\begin{aligned} w(t; 0, u)-w(t; 0, {\bar{u}})<\max _{t \in [0, T]}\left\{ w\left( t; 0, {\bar{u}}+\gamma _{1}\right) -w(t; 0, {\bar{u}})\right\} \le \varepsilon ,\ u \in \left( {\bar{u}}, {\bar{u}}+\delta \right) , \end{aligned}$$

which completes the proof of the stability of $w(t; 0, {\bar{u}})$.

Regarding the attractivity of $w(t; 0, {\bar{u}})$, we begin with proving that for given $t_1\ge 0$,

$$\begin{aligned} \lim _{n \rightarrow \infty } w(t_{1}+nT; 0, u)= w\left( t_1; 0, {\bar{u}}\right) , \ u \in U^0({\bar{u}}, \gamma ). \end{aligned}$$

We assume by contradiction that there exists ${\hat{u}}\ne {\bar{u}}$ such that

$$\begin{aligned} \lim _{n \rightarrow \infty } w(t_{1}+nT; 0, u)= w\left( t_1; 0, {\hat{u}}\right) , \ u \in U^0({\bar{u}}, \gamma ). \end{aligned}$$

which implies that

$$\begin{aligned} w\left( t_1+T; 0, {\hat{u}}\right)= & {} \lim _{n \rightarrow \infty } w(t_{1}+T+nT; 0, u)\\= & {} \lim _{n \rightarrow \infty } w(t_{1}+nT; 0, u)= w\left( t_1; 0, {\hat{u}}\right) . \end{aligned}$$

Hence we get another T-periodic solution, which leads to a contradiction to the uniqueness of the T-periodic solutions in $u \in U^0({\bar{u}}, \gamma )$. This completes the proof of the Lemma C.1. $\square$

Lemma C.2

With $U^0({\bar{u}}, \gamma )$ defined as in Lemma C.1, if

$$\begin{aligned} (u-{\bar{u}})(p(u)-u)>0, \ u \in U^0({\bar{u}}, \gamma ), \end{aligned}$$

(C.3)

then $w(t; 0, {\bar{u}})$ is unstable.

Proof

For any $\delta \in (0, \gamma )$, it follows from (C.3) that $p(u)>u$ for $u\in ({\bar{u}}, {\bar{u}}+\delta ]$, and $p(u)<u$ for $u\in [{\bar{u}}-\delta , {\bar{u}}),$ which leads to

$$\begin{aligned} w(T; 0, {\bar{u}}+\delta )>{\bar{u}}+\delta , \ w(T; 0, {\bar{u}}-\delta )<{\bar{u}}-\delta . \end{aligned}$$

Hence

$$\begin{aligned} \mid w(T; 0, {\bar{u}}\pm \delta )-w(T; 0, {\bar{u}})\mid =\mid w(T; 0, {\bar{u}}\pm \delta )-{\bar{u}}\mid >\delta , \end{aligned}$$

proving the instability of $w(t; 0, {\bar{u}})$. $\square$

Lemma C.3

It follows from Lemmas C.1 and C.2 that if

$$\begin{aligned} (u-{\bar{u}})(p(u)-u)>0, \ u \in ({\bar{u}}- \gamma , {\bar{u}}), \end{aligned}$$

and

$$\begin{aligned} (u-{\bar{u}})(p(u)-u)<0, \ u \in ({\bar{u}}, {\bar{u}}+\gamma ), \end{aligned}$$

then $w(t; 0, {\bar{u}})$ is unstable from the left-side. However, $w(t; 0, {\bar{u}})$ is stable from the right-side.