An investigation of tuberculosis progression revealing the role of macrophages apoptosis via sensitivity and bifurcation analysis

Abstract

Mycobacterium tuberculosis infection features various disease outcomes: clearance, latency, active disease, and latent tuberculosis infection (LTBI) reactivation. Identifying the decisive factors for disease outcomes and progression is crucial to elucidate the macrophages-tuberculosis interaction and provide insights into therapeutic strategies. To achieve this goal, we first model the disease progression as a dynamical shift among different disease outcomes, which are characterized by various steady states of bacterial concentration. The causal mechanisms of steady-state transitions can be the occurrence of transcritical and saddle-node bifurcations, which are induced by slowly changing parameters. Transcritical bifurcation, occurring when the basic reproduction number equals to one, determines whether the infection clears or spreads. Saddle-node bifurcation is the key mechanism to create and destroy steady states. Based on these two steady-state transition mechanisms, we carry out two sample-based sensitivity analyses on transcritical bifurcation conditions and saddle-node bifurcation conditions. The sensitivity analysis results suggest that the macrophage apoptosis rate is the most significant factor affecting the transition in disease outcomes. This result agrees with the discovery that the programmed cell death (apoptosis) plays a unique role in the complex microorganism-host interplay. Sensitivity analysis narrows down the parameters of interest, but cannot answer how these parameters influence the model outcomes. To do this, we employ bifurcation analysis and numerical simulation to unfold various disease outcomes induced by the variation of macrophage apoptosis rate. Our findings support the hypothesis that the regulation mechanism of macrophage apoptosis affects the host immunity against tuberculosis infection and tuberculosis virulence. Moreover, our mathematical results suggest that new treatments and/or vaccines that regulate macrophage apoptosis in combination with weakening bacillary viability and/or promoting adaptive immunity could have therapeutic value.

1 Introduction

Tuberculosis (TB), a disease caused by Mycobacterium tuberculosis (Mtb), remains the deadliest infectious disease in the world (Sud et al. 2006; Lin and Flynn 2010). According to a CDC (Centers for Disease Control and Prevention) report (WHO 2019), in the United States, the reactivation of latent Tuberculosis infection was a major cause for TB incidence in 2019. A detailed understanding of the most significant driving factors for TB disease progression is crucial for the improvement of the treatment strategies to help host fight against the invader pathogen.

To serve this motivation, we adopt an established in-host tuberculosis infection model that generates various disease outcomes. Since transcritical bifurcations determine the fate of infection and saddle-node bifurcations create multiple infected equilibrium solutions, we carry out a parameter sensitivity analysis on the conditions for transcritical and saddle-node bifurcations. We then further investigate model behavior through bifurcation analysis to examine how the macrophage apoptosis rate and other statistically significant parameters impact disease progression and examine how the mathematical results relate to the complexities of the disease dynamics. Finally, we utilize a 2-dimensional bifurcation analysis to explore how combination therapies can enhance macrophage apoptosis modulation therapy to inhibit bacillary viability and promote adaptive immunity.

Before we present our methodology and results, we provide a brief introduction of tuberculosis, including the various disease outcomes, in-host Mtb life cycles, and therapeutic strategies, in Sect. 1.1 and discuss the previous in-host Mtb mathematical modeling literature in Sect. 1.2.

1.1 TB epidemiology and immunology background

Tuberculosis (TB), a disease caused by pathogenic bacterium species Mycobacterium tuberculosis (Mtb), has been spreading among humans for thousands of years (Donoghue et al. 2004). Despite the availability of effective TB treatments, TB continues claiming 1.5 million lives per year by infecting one quarter of the global population (Sud et al. 2006; Lin and Flynn 2010). A characteristic feature for Tuberculosis infection is that infected individuals experience various disease outcomes, including clearance, latent infection (LTBI), and active disease. Approximately 10% of infected individuals clear the infection and another 10% progress to primary disease, while the majority of infected individuals become latently infected with no symptoms. Individuals with LTBI carry the risk of developing TB later in life. Slow TB progression through LTBI reactivation contributes approximately $80\%$ of cases globally and threatens a TB re-emergence (Cooper 2009; Rich et al. 1951). A better understanding on TB progression, especially LTBI reactivation, can help to improve the efficacy of therapeutic strategies, and enhance both the innate and adaptive immune responses.

The life cycle of tuberculosis begins when aerosol droplets containing Mtb are inhaled by an uninfected individual. After inhalation, Mtb usually reach the alveoli of the lung, and are preferentially ingested by alveolar macrophages (Warner and Mizrahi 2007), then launch proliferation (Canetti 1955). This makes alveolar macrophages the main target cells for Mtb invasion (Gammack et al. 2005; Gideon and Flynn 2011). Even though activated macrophages can initialize phagocytosis, Mtb can also set up various strategies against macrophage killing and replicate within the host macrophages. Moreover, cytokine environment is also modified to favor the intracellular Mtb survival (BoseDasgupta and Pieters 2014; Orme et al. 2015). Innate immune responses are the crucial factor for the TB outcome (Orme et al. 2015). While the clearance of the phagocytized bacteria is also determined by the adaptive immunity, which is activated by innate immune signals (Torrado and Cooper 2013). These infected macrophages release chemotactic signals to recruit and activate migrating lymphocytes to the site of infection (Gammack et al. 2005; Gideon and Flynn 2011). The progressive immune responses lead to an aggregation of lymphocytes around mycobacteria-harboring macrophages, which is called a granuloma. Granulomas are able to isolate infected macrophages from the rest of the lung to limit the bacillary growth and spread of Mtb from intracellular Mtb replication, and so serve as an immune micro-environment to enhance the T cells and macrophages interactions (Russell et al. 2010; Gideon and Flynn 2011). On the other hand, the granuloma concealed Mtb switch to a non-replicating state, which is a typical feature to enable the bacillus persistence during the long TB latency period (Barry et al. 2009). Mtb has evolved new strategy to escape granulomas: leak into the lung and expectorate bacilli (Ehlers and Schaible 2013). The granuloma then serves as a battle ground between mycobacteria and host immune cells. The host-pathogen dynamics decide granuloma to promote or inhibit the infection and then determine the disease outcomes (Ulrichs and Kaufmann 2006; Ehlers and Schaible 2013). An imbalanced interplay between Mtb and immune cells result in the failure of controlling infection, then lead to the LTBI reactivation (O’Garra et al. 2013).

Today, TB disease can be cured with antibiotics. For the newly diagnosed pulmonary TB, four first-line anti-TB drugs isoniazid (INH), rifampin (RIF), ethambutol (EMB), and pyrazinamide (PZA) form the essence of treatment regimens (Organization 2017). The major problem of the current TB drug regimen is its duration, which requires 6 to 9 months. Incorrect TB drug treatment (the wrong length of duration or dose) could lead the remaining alive Mtb resistant to those drugs. These patients are more likely to develop drug-resistant TB, which is more difficult to treat. The goal of shortening the long treatment duration can advance treatment effectiveness by improving patients’ compliance and reducing the chance of the drug resistance and disease relapse. Mathematical models may be useful tools for, first, elucidating in-host TB progression mechanisms, and then also for suggesting crucial factors for advancing therapeutic strategies.

1.2 Mathematical modeling background

Numerous TB in-host modeling studies have been done to identify the driving factor for different TB infection outcomes. The TB host-immune modeling began with models considering HIV-1 and Mtb coinfection by Kirschner (1999) and her collaborators Bauer et al. (2008). HIV infection weakens the immune system, and make patients vulnerable to opportunistic infections, such as TB. Untreated latent TB and HIV coinfection significantly increases the possibility of developing TB disease. The study of TB infection is carried out through ODE models to capture the cellular and cytokine network (Antia et al. 1996; Abdelrazec et al. 2016; Wigginton and Kirschner 2001; Magombedze et al. 2006) and CD8+ T cells for host infection control (Sud et al. 2006; Magombedze et al. 2006), PDE models have been developed for cytokine and antibiotics molecules diffusion (Lauffenburger and Linderman 1993), agent-based models for spatial and temporal features of granuloma (Segovia-Juarez et al. 2004; Ray et al. 2009) and multiple scale models for investigating the granulomas dynamics in a smaller scale (such as a lung) and a larger scale (such as a host body) (Gong et al. 2015; Marino and Kirschner 2016). However, little work has been done to investigate the determining factors for LTBI reactivation. One of the challenges is the computational cost due to the large number of considered compartments and parameters, combined with complex nonlinear terms. In this paper, we only consider the key factors involved in the in-host Mtb dynamics, which include the infection interaction and innate immune response between macrophages and bacteria, the adaptive immune response initiated by T cells, and bacterial growth and elimination processes.

A four-dimensional within-host TB model was developed in previous modeling work by Du et al. (2017). This 4-dimensional model, presented in (1), incorporates the uninfected macrophages (the Mtb target cells), infected macrophages, Mtb bacteria and CD4 T cells. The model numerically captures various TB infection outcomes, which are clearance, latency, and active disease. In an analytical study of the same model (Zhang et al. 2020), we showed the existence of four coexisting equilibria that reflect the different disease outcomes. We also determined conditions for forward and backward bifurcations (Zhang et al. 2020). However, neither (Du et al. 2017) or (Zhang et al. 2020) has analyzed the driving factors behind the different outcomes of disease.

1.3 Overview

We provide a brief immunology and mathematical modeling background of tuberculosis infection in Sect. 1. In Sect. 2, we introduce an established in-host tuberculosis model, then identify parameters statistically significantly influencing the early stage TB infection through a sample-based sensitivity analysis on the basic reproduction number. Using identified parameters from the first sensitivity analysis, we employ a second sensitivity analysis on the single-zero eigenvalue bifurcation condition and identify that macrophage apoptosis rate is the statistically significantly parameter for disease progression, especially LTBI reactivation. In Sect. 3, using bifurcation analysis and numerical simulations, various disease outcomes are fully unfolded under the variation of the macrophage apoptosis rate. In Sect. 4, we describe how the mathematical results from the previous section reveal the complicated roles of macrophage apoptosis in the complex Mtb-macrophage dynamics. In Sect. 5, we further investigate the disease outcomes under the influence of macrophage apoptosis and one of the other four parameters to give insight into the development of new therapeutic strategies. Our findings suggest that macrophage apoptosis modulation therapy can be enhanced with combination therapies, which inhibit bacillary viability and promote adaptive immunity.

2 Investigation of the driving factors for disease progression through sensitivity analysis

Tuberculosis progression is characterized by reactivation of LTBI, which occurs when a weakened immune system is no longer capable of controlling the latent stage Mtb. The awoken bacteria become active, defeat the immune defense, and lead to the infected individual to active TB disease. In other words, the LTBI reactivation can be described as the Mtb bacterial level shifted from a lower infection steady state to a higher infection steady state. Our target in this section is to identify the important factors determining the shifting of Mtb bacterial level by evaluating the influence/sensitivity level of each involving mechanism applied on the shift.

2.1 Model

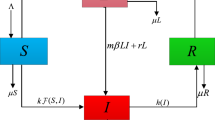
The TB model with various disease outcomes (Du et al. 2017) is written as follows:

$$\begin{aligned} \dfrac{d M_u}{dt}= & {} s_M - \mu _M M_u - \beta M_u B \nonumber \\ \dfrac{d M_i}{dt}= & {} \beta M_u B - b M_i - \gamma M_i \dfrac{T/M_i}{T/M_i + c} \nonumber \\ \dfrac{dB}{dt}= & {} \delta B \left( 1-\dfrac{B}{K}\right) + M_i \left( N_1 b + N_2 \gamma \dfrac{T/M_i}{T/M_i +c} \right) - M_u B (\eta + N_3 \beta ) \nonumber \\ \dfrac{dT}{dt}= & {} s_T + \dfrac{c_M M_i T}{e_M T + 1} + \dfrac{c_B B T}{e_B T + 1} - \mu _T T. \end{aligned}$$

(1)

Here, uninfected macrophages $M_u$ are generated and die naturally at constant rates $s_M$ and $\mu _M$. Moreover, they become infected through the engulfment of Mtb at a rate of $\beta M_u B$. The internalized Mtb reproduction can kill infected macrophages at a rate b and produce $N_1$ intracellular Mtb bacteria per cell, on average. Infected macrophages can also be eliminated through T cell-mediated cytotoxicity. Both CD4 and CD8 T cells account for the cytotoxic process. The rate of the cytotoxic effect, which T lymphocytes (E) act on Mtb-stimulated monocytes (T), depends on the E:T ratio, $T/M_i$ (Lewinsohn et al. 1998; Wigginton and Kirschner 2001). This ratio has a maximum rate $\gamma$ and saturating factor c. During the cytotoxic process, infected macrophages die and release on average $N_2$ intracellular Mtb bacteria to the extracellular compartment B. Extracellular bacteria can divide, modeled as a logistic term $B(1-B/K)$. The infection in macrophages can lead to a loss of extracellular Mtb. This is modeled using the term $N_3\beta M_u B$. On the other hand, uninfected macrophages phogocytize Mtb bacteria, then initiate phagosome maturation, which causes microbicidal and degrading effects on phogocytized pathogens. The Mtb killing rate by this process is denoted as $\eta B M_u$ (Kinchen and Ravichandran 2008; Upadhyay et al. 2018). Host adaptive immune responses are signaled by CD4 T cells, which are assumed to have constant production and death rates $s_T$ and $\mu _T$. CD4 T cells can proliferate in the presence of Mtb bacteria ($\frac{c_B B T}{e_B T + 1}$) or/and infected macrophages ($\frac{c_M M_i T}{e_M T + 1}$). More detailed model assumptions are explained in Du et al. (2017) and parameters values are stored in Table 1.

2.2 Basic model properties

A detailed analytical investigation on the property of model (1) is carried out in Zhang et al. (2020). For convenience, we change the notation as

$$\begin{aligned} \begin{array}{c} y_1=M_u,\; y_2=M_i,\; y_3=B,\; y_4=T;\\ [2.0ex] f_1=\dfrac{d M_u}{dt},\; f_2=\dfrac{d M_i}{dt},\; f_3 = \dfrac{d B}{dt},\; f_4=\dfrac{d T}{dt}. \end{array}\nonumber \\ \end{aligned}$$

(2)

The solutions of model (1) are well-posed and bounded and include a disease free equilibrium ($E_0$) and infected equilibriums ($E^{*}$) as follows (Zhang et al. 2020)

$$\begin{aligned} \begin{array}{ll} E_0&{}=(\frac{s_M}{\mu _M},\,0,\,0,\frac{s_T}{\mu _T}), \quad \text {and} \quad E^{*}=(\bar{y}_1,\,\bar{y}_2,\,\bar{y}_3,\,\bar{y}_4), \quad \text {where,}\\ [2.0ex] \bar{y}_1(y_3)&{}=\dfrac{s_M}{\beta y_3+\mu _M}, \\ [2.0ex] \bar{y}_2(y_3) &{}= \left( \dfrac{y_3\delta }{K}-\dfrac{\delta +s_M(N_2-N_3)\beta -s_M\eta }{\beta y_3+\mu _M}\right) \dfrac{y_3}{b(N1-N2)}, \\ [2.0ex] &{}\qquad \text {if} \quad \dfrac{y_3 \delta }{K}>\dfrac{\delta +s_M(N_2-N_3)\beta -s_M\eta }{\beta y_3+\mu _M}\quad \text {and} \quad N_1>N_2, \\ [2.0ex] \bar{y_4}(y_3)&{}= \dfrac{[\beta s_M y_3-(\beta y_3+ \mu _M) b y_2]c y_2}{\beta s_M y_3-(b+\gamma )(\beta y_3+\mu _M) y_2}, \quad \text {and} \quad \\ [2.0ex] F(y_3)&{}=-e_B e_M \mu _T \bar{y}_4^3+ [(c_M \bar{y}_2 + e_M s_T - \mu _T) e_B + e_M (c_B y_3 - \mu _T)] \bar{y}_4^2 \\ [2.0ex] &{}\quad + [c_B y_3 + c_M \bar{y}_2(y_3) + e_B s_T + e_M s_T - \mu _T] \bar{y}_4(y_3) + s_T=0. \end{array}\nonumber \\ \end{aligned}$$

(3)

Furthermore, equilibrium solutions $E_0$ and $E_*$ intersect and exchange local stability at a transcritical bifurcation as

$$\begin{aligned} \beta = \frac{(-\delta \mu _M + \eta s_M) (b + \gamma )}{s_M \gamma (N_2 - N_3) \gamma + s_M b (N_1 - N_3)}:=\beta _T. \end{aligned}$$

(4)

Moreover, at the transcritical bifurcation the basic reproduction number equals to unit (Du et al. 2017), i.e. $R_0=1$, where

$$\begin{aligned} R_0&=\dfrac{ [\gamma (N_2 - N_3) + b (N_1 - N_3)]\beta }{(-\delta \mu _M/s_M + \eta ) (b + \gamma )}\nonumber \\&=\left[ (N_2-N_3)(1-\dfrac{b}{b+\gamma })+(N_1-N_3)\dfrac{b}{b+\gamma }\right] \dfrac{\beta }{\eta - \dfrac{\mu _M}{s_M}\delta }. \end{aligned}$$

(5)

2.3 Sensitivity analysis of $R_0$ for the early stage of TB infection

After the exposure of TB disease, the critical value to determine the fate of the infection is the basic reproduction number $R_0$. Starting from one infectious pathogen, the infection will be able to spread to the whole body if $R_0>1$, but will be eliminated if $R_0<1$. Because $R_0$ is not a constant number for any given disease, in the case of in-host TB dynamics, $R_0$ is affected by in-host immunological factors and Mtb behaviors. We first investigate $R_0$ in (5) for all model parameters in the experimental and/or estimated ranges from Table 1. We then choose $R_0$ in (5) as the first sensitivity/output function of the model parameters (or input factors) to identify which parameters significantly affect the uncertainty on disease spread and elimination in the early stage of the TB infection. The analytical formulation (5) indicates that $R_0$ is linear on the parameters $\beta$, $N_1$, $N_2$, and $N_3$, along with the ratio $\frac{b}{b+\gamma }$. $R_0$ also depends on the term $\frac{ \mu _M}{s_M}\delta$.

Table 1 Parameter descriptions and values (Du et al. 2017; Zhang et al. 2020)

To show the uncertainty on $R_0$ due to the uncertainties in model parameters, we perform uncertainty analysis. Because a priori knowledge of the Mtb-host relationship between the model parameter and $R_0$ is unavailable, we choose the most popular sampling-based approach, i.e. Latin Hypercube sampling (LHS) (McKay et al. 1979). LHS belongs to the Monte Carlo class of sampling procedures for the propagation of uncertainty. LHS performs a full stratification over each sampled-parameter range to allow every parameter get equally sampled, and returns unbiased estimates for the sample mean and distribution function over each sampled-parameter range. Moreover, when necessary, a log scale can be applied on the parameter range for LHS to prevent under-sampling (McKay et al. 1979; Marino et al. 2008). Furthermore, LHS nearly eliminates confounding in estimating parameter effects by ensuring that exactly one parameter is sampled from each stratum in a given sample. That is, if there are 3 parameters, then each parameter range is partitioned into 3 strata and one parameter is sampled from the lowest stratum, another from the middle stratum, and the last from the highest stratum. This is repeated many times to ensure that all parameters are sampled from each of their sampling strata. This results in the main effects of each parameter being confounded only with high-order interactions of other parameters, which are classically considered negligible in experimental design. This also makes LHS a computationally inexpensive approach, especially compared to full factorial sampling designs, and allows LHS to perform robustly for even a relatively small sample size, i.e. sample size$_{LHS}=50$ to 200, which is used in Iman and Helton (1988); Kleijnen and Helton (1999); Helton and Davis (2003). As such, this sampling design facilitates a measurement of parameter’s corresponding impact on the value of the sensitivity functions $R_0$ in (5) and $a_4(E^{*},\,p_v)$ in (12).

Due to the multi-variable property of sensitivity functions, standard correlation coefficients (CCs) are not sufficient for measuring the influence of parameter values on sensitivity functions because CCs are restricted to quantify relationships between just two variables and, as such, cannot account for the impact of the other parameters on the variation in sensitivity functions. Instead, we can calculate partial correlation coefficients (PCCs), which quantify the relationship between each parameter on the portion of the variation in sensitivity functions that is unexplained by the variation in the values of the other parameters and thusly, provide a more appropriate measure of influence. However, PCCs only reflect the linear relationships between the output of sensitivity functions and the input variables/parameters. To capture the nonlinear relationships between sensitivity functions and the model parameters, we can instead apply the rank transformation to all quantities (Conover and Iman 1981; Saltelli and Sobol 1995). Calculating the correlations between these provided us with the Spearman correlation coefficients, which measure the strength and direction of monotonic relationships. PCCs for the ranked quantities yields partial rank correlation coefficients (PRCC), which provide a robust sensitivity measure for quantifying potentially nonlinear, but monotonic, relationships between the output and each of the model parameters in the presence of the other parameters (Marino et al. 2008; Saltelli and Annoni 2011).

Fig. 1

PRCC values for $R_0$ under the variations of all model parameters. n.s. denotes statistically not significant, that is p value$>0.05$

Using the MATLAB LHS and PRCC code provided in Marino et al. (2008), we run an LHS uncertainty analysis on a sample of 1000 parameter sets, and set the baseline value/mean, lower bound, and upper bound for each parameter in its range from Table 1. Scatter plots showing the relationships between residuals of the output $R_0$ and input parameters, along with their PRCCs and associated p-values, are shown in Figure 1 in Appendix (see supplementary material). From these figures, it is readily apparent that all of the pairs with near-zero PRCCs display no evidence of non-monotonic relationships, so PRCCs appropriately describe the relationships. A summary of the PRCC values is shown as a bar graph in Fig. 1. Following traditional use, p-values below 0.05 designate pairs of parameters whose partial rank correlations are statistically significantly different than 0. The negative or positive sign of PRCC indicate the negative or positive correlation between $R_0$ and the specific parameter.

The PRCC between $R_0$ and each parameters in Fig. 1a indicate that the expected number of bacteria, $R_0$, generated by one single bacterium after exposure to Mtb has

• a significantly positive relation with $N_1$, $N_2$, and $N_3$;

• a significantly negative relation with $\beta$ because the infection process involves the loss of extracellular Mtb by macrophages phagocytosis;

• a significantly negative relation with $\eta$;

• a significant relation with the whole term $\frac{b}{b+\gamma }$, indicating that more intracellular Mtb are released from apoptosis than necrosis (Lee et al. 2009);

• a positive relation with the whole term $\frac{\mu _M}{s_M}\delta$.

There is an identifiablility issue with the parameters $\delta$, $s_M$ and $\mu _M$, because they only appear in (5) together as the term $\frac{\mu _M}{s_M}\delta$. While each of these parameters should be expected to have a non-zero rank correlation with $R_0$,since partial correlation accounts for the effects of the other parameters, only one of these three can have a high PRCC value. In this case, the effect appeared present for $\delta$ rather than the other two. Since the uninfected macrophages level in a healthy host is relatively constant, the Mtb proliferation rate $\delta$ is chosen to represent the significantly positive influence on $R_0$. Also note that the other non-influential parameters are $s_T$, $\mu _T$, c, K, $c_M$, $c_B$, $e_M$, $e_B$, which do not show in the analytical formula of $R_0$ in (5).

2.4 Sensitivity analysis of saddle-node bifurcations for LTBI reactivation

LTBI reactivation is characterized by an in-host Mtb outbreak. The Mtb level shifts from a low-level latent infection stage to a high-level active disease stage by the slowly weakening immune system, which may be caused by AIDS, chemotherapy, aging, and diabetes. In our mathematical model, the LTBI reactivation can be captured by the bacteria level traveling from a low steady state to a high steady state due to slowly changing parameter values. The prerequisite condition is the existence of co-existing steady states. The fundamental mechanism for the generation and destruction of steady states is the occurrence of saddle-node bifurcation. Therefore, the parameter influence on the shifting of the infection steady states is replaced by the parameter influence on the occurrence of saddle-node bifurcation. The sensitivity analysis of the LTBI reactivation is taken over by the sensitivity analysis of the saddle-node bifurcation conditions.

In general, we consider an n-dimensional nonlinear system

$$\begin{aligned} \dfrac{d x}{d t} = f(x, p), \quad x \in R^n,\quad p \in R^m, \quad f: R^{n+m}\rightarrow R^n, \end{aligned}$$

(6)

with m parameter values and equilibrium solutions $x_e=x_e(p)$ derived from the equilibrium condition

$$\begin{aligned} f(x_e(p), p)=0, \quad x \in R^n,\quad p \in R^m. \end{aligned}$$

(7)

The local stability of the equilibrium points $x_e(p)$ is determined by the eigenvalues of the Jacobian $J(p)=[\partial f_i(x_e(p), p)/\partial x_j]$, which are the roots of the corresponding characteristic polynomial equation

$$\begin{aligned} P_n(\lambda )=\det [\lambda I - J(p)] = \lambda + a_1(p) \lambda ^{n-1} + a_2(p) \lambda ^{n-2} + \cdots + a_{n-1}(p) \lambda + a_n(p). \end{aligned}$$

(8)

The necessary and sufficient conditions for zero singularities are given in Yu (2005).

Theorem 1

Yu (2005) The necessary and sufficient conditions for system (6) to have a k-zero singularity at a fixed point (equilibrium), $x=x_e(p)$, of the system are given by

$$\begin{aligned} a_n(p) = a_{n-1}(p) = \cdots = a_{n+1-k}(p)=0, \end{aligned}$$

(9)

which $a_i(p)$’s are the coefficients of the characteristic polynomial (8). Further, if the remaining coefficients $a_1,\; a_2,\; \dots \; a_{n-k}$ still obey the Hurwitz conditions for order $n-k$, then all the remaining eigenvalues of the Jacobian have negative real parts.

For the current case, we only need to study single zero bifurcations, that is $k=1$. The corresponding necessary condition becomes $a_4(p)=0$, since the dimension of model (1) is 4. Single zero bifurcations include saddle-node/turning bifurcation, which creates or destroys steady states, transcritical bifurcation (at $R_0=1$), which serves as the intersection between infection-free and infected steady states (Zhang et al. 2020), and pitchfork bifurcation, which is not common in within-host infectious disease model, due to the symmetric property.

Fig. 2

PRCC values for single zero-eigenvalue bifurcations $a(y_3,p_v)$ in (12) on the influential parameters for disease outcomes $p_v$

The sensitivity function on LTBI reaction for model (1) is represented by the sensitivity function of the necessary condition of single zero bifurcation (denoted by $a_4(p)=0$) in terms of the parameters (denoted by $p_v$) significantly affecting the transcritical bifurcation condition ($R_0=1$). The sensitivity analysis in Sect. 2.3 identified the significant parameters affecting $R_0$ to be

$$\begin{aligned} p_v=(b, \gamma , \beta , \delta , \eta , N_1, N_2, N_3). \end{aligned}$$

(10)

We fix the parameters, which are not significantly affecting $R_0$ or the fate of disease as the corresponding mean values in Table 1. There parameters are denoted as

$$\begin{aligned} p_f= (s_T, s_M \mu _M, \mu _T, c, K, c_M, c_B, e_M, e_B). \end{aligned}$$

(11)

Due to the uncertainties of the input parameters $p_v$, we run Latin Hypercube sampling for 10, 000 sampled parameter set. The sensitivity function/output is set as

$$\begin{aligned} a_4(E^{*}, p_v) = a_4(y_3, b, \gamma , \beta , \delta , \eta , N_1, N_2, N_3), \end{aligned}$$

(12)

where $E^{*}$ denotes the infected steady state and $y_3$ satisfies $F(y_3)=0$ in (3). Moreover, the non-influential parameters $p_f$ in terms of disease outcomes are fixed. Scatter plots showing the relationships between the disease-outcome influential parameters $p_v$ and the sensitivity function $a_4(E^{*}, p_v)$ in (12) are shown in Fig. 2. As in the preceding sensitivity analysis, these plots show no evidence of non-monotonicity, which again suggests that PRCC scores are appropriate to use. The PRCC scores for these are shown in bar graph form in Fig. 2. The sensitivity analysis identifies that

• b has the largest magnitude PRCC value with the sensitivity function $a_4(E^{*}, p_v)$;

• $N_2$ is non-influential to the LTBI reactivation;

• the other parameters in $p_v$ are statistically significant but have a moderate absolute PRCC value with the sensitivity function/output $a_4(E^{*}, p_v)$.

To further investigate how the identified significant parameter affects disease progression and what disease outcome will show up, we set b as a bifurcation parameter of interest for a one-parameter bifurcation analysis in the next section. More two-dimensional bifurcation diagrams are provided in the later section on the identified influential parameters to provide insight on TB treatment strategies.

3 Bifurcation analysis of the macrophages programmed cell death rate

3.1 Investigation of the single-zero eigenvalue bifurcation

The single-zero eigenvalue bifurcations are derived according to Theorem 1. Leaving the most influential parameter b as the bifurcation parameter, fixing the other influential parameters in $p_v$ and non-influential parameters in $p_f$ as the corresponding mean value in Table 1, we rewrite model (1) using the new notation in (2) as

$$\begin{aligned} \dot{y}=f(y)=[f_1(y,b),f_2(y,b),f_3(y,b),f_4(y,b)]^T, \quad y=(y_1,y_2,y_3,y_4) \in \mathbb {R}^4. \end{aligned}$$

(13)

Suppose the steady state/equilibrium is given in the form

$$\begin{aligned} \bar{y}=\bar{y}(b)= (\bar{y}_1(b),\bar{y}_2(b),\bar{y}_3(b),\bar{y}_4(b)), \end{aligned}$$

which could represent multiple co-existing equilibrium solutions. Then the Jacobian matrix of (13) at the infected equilibrium $E^{*}$ in (3) is

$$\begin{aligned} J(b)=D_yf|_{y=\bar{y}(b)}=\dfrac{\partial f_i(\bar{y}(b),b)}{\partial y_j}, \end{aligned}$$

(14)

where $\bar{y}(b)$ satisfies the equilibrium conditions in (3). We denote the fourth-degree characteristic polynomial in terms of L at the infected equilibrium $E^{*}$ in (3) as

$$\begin{aligned} P_4(L;\, y_3,\,b)= L^4 + a_1( y_3,\,b) L^3 + a_2(y_3,\,b) L^2 +a_3(y_3,\,b) L + a_4(y_3,\,b), \end{aligned}$$

(15)

where $y_3$ satisfies the equilibrium condition in (3) $F(y_3, b)=0$. Evaluating this with the parameter values in Table 1, the formula of $F(y_3, b)$ and $a_i(y_3,\,b)$ $i=1,...,4$ are shown in Appendix (see supplementary material) Equations (1),(3),(4),(5), and (6). We assume

• (SN1) the Jacobian matrix $J(b)=D_yf|_{y=\bar{y}(b)}=D_yf(E^{*},b)$ has a simple zero eigenvalue, at $b=b_T$, if (1) $\Delta _1=a_1(y_3,\, b)>0$, (2) $\Delta _2=a_1(y_3,\, b)\, a_2(y_3,\, b) -a_3(y_3,\, b) >0$, (3) $\Delta _3=[a_1(y_3,\, b) \,a_2(y_3,\, b) -a_3(y_3,\, b)] \,a_3(y_3,\, b) - a_1^2(y_3,\, b)\, a_4(y_3,\, b) > 0$, and (4) $\Delta _4=\Delta _3\,a_4(y_3,\, b) = 0$ or $a_4(y_3,\, b)=0$. Then $b=b_T$ and $E^{*}=E^{*} (b_T)$ is called critical point (Yu 2005).

We obtain four single-zero bifurcation critical points:

• Single-zero 1. $b_{T1} = 0.0295$ day$^{-1}$, $E^{*} _1 = (497833,\,122,\,8.7,\,40)$ cells/ml.

• Single-zero 2. $b_{T2} = 0.2993$ day$^{-1}$, $E^{*} _2 = (21089,\,2664,\,45417,\,6952168)$ cells/ml.

• Single-zero 3. $b_{T3} = 0.1363$ day$^{-1}$, $E^{*} _3 = (20,\,3055,\,49998972,\,7575684467)$ cells/ml.

• Single-zero 4. $b_{T4} = 0.3000036$ day$^{-1}$, $E^{*} _4 = (500000,\,0,\,0,\,20)$ cells/ml.

Single-zero bifurcation include saddle-node/turning bifurcation, transcritical bifurcation, and pitchfork bifurcation, through the pitchfork bifurcation is not common in infectious disease models due to the symmetric pattern. To identify the type of the single-zero bifurcation and the local behavior of the corresponding vector field, We apply Theorem 3.4.1 in Guckenheimer and Holmes (1990). That is, for the system (13), there are three hypotheses SN1,

• (SN2) $v \; \frac{\partial f}{\partial b}(E^{*} ,b_T) \ne 0$,

• (SN2’) $v\; \left( \frac{\partial f^2}{\partial b \partial y}(E^{*} ,b_T) (w)\right) \ne 0$

• (SN3) $v \; [D_y^2f(E^{*} ,b_T)(w,\,w)] \ne 0$,

where w and v are the left and right eigenvectors corresponding to the 0 eigenvalue of the matrix $D_yf(E^{*} ,b_T)=D_yf|_{y=\bar{y}(b_T)}:=D_y f_b(y)|_{y=\bar{y}(b_T)}$. Moreover the transversality and degeneracy conditions are defined respectively as

$$\begin{aligned} \begin{array}{rl} v \left[ \dfrac{\partial f}{\partial b} \right] &{}= v \left[ \dfrac{\partial f_1}{\partial b},\, \dfrac{\partial f_2}{\partial b},\,\dfrac{\partial f_3}{\partial b},\,\dfrac{\partial f_4}{\partial b} \right] ^T \\ [3.0ex] v \left[ D_y^2 f_b (w,\,w) \right] &{}= v \left[ w^T \left( \dfrac{\partial ^2 f_1}{\partial y_j \partial y_k} \right) w ,\, \dots ,\, w^T \left( \dfrac{\partial ^2 f_4}{\partial y_j \partial y_k} \right) w \right] ^T. \end{array} \end{aligned}$$

If system (13) satisfies three hypotheses SN1, SN2, and SN3, there are no equilibriums that exist near $(E^{*} ,b_T)$ when $b<b_T$ ($b>b_T$) and two equilibria near $(E^{*} ,b_T)$ when $b>b_T$ ($b<b_T$). It implies a saddle-node bifurcation. If we replace SN2 by SN2’, then a transcritical bifurcation occurs.

For the critical point $(b_{T1},\,E^{*}_1)$, the left and right eigenvectors corresponding to the simple zero eigenvalue of $D_y f_b(y)|_{(b_{T1},E^{*} _1)}$ are chosen respectively as

$$\begin{aligned} \begin{array}{c} v_{T1}=[0.0045,\, 21.9549, 0.8369,\, -12.8169]\\ w_{T1}= [-0.9982,\,0.0564,\,0.00403,\,0.01845]^T, \end{array} \end{aligned}$$

where $<v_{T1},\,w_{T1}>=1$. The transversality and degeneracy conditions are satisfied since

$$\begin{aligned}&v_{T1} \left[ \frac{\partial f}{\partial b} \right] |_{(b_{T1},E^{*} _1)} = 2434.1057 \ne 0 \quad \text {and} \quad \\&v_{T1} \left[ w_{T1}^T (D_y^2 f_b) w_{T1} \right] |_{(b_{T1},E^{*} _1)} = -0.3579 \times 10^{-4} \ne 0. \end{aligned}$$

The signs of the transversality and degeneracy conditions indicate that no equilibrium point near $(b_{T1},E^{*} _1)$ when $b<b_{T1}$, but two equilibria are near $(b_{T1},E^{*} _1)$ when $b>b_{T1}$. Choosing $b=0.0298$, we test the stability of the two bifurcation equilibria: $E^{*+} _1=(497620,\,133,\, 9.6,\, 44)$ (associated with four negative real-part eigenvalues $-62.3025$, $-0.0864$, $-0.0096+0.0009i$, and $-0.0096-0.0009i$) and $E^{*-} _1=( 498014,\,111,\, 8,\,37)$ (associated with one positive and three negative eigenvalues $-62.3471$, $-0.1356$, $-0.0099$, and 0.0059). Given these results, a saddle-node bifurcation occurs at $(b_{T1},E^{*} _1)$ shown in Fig. 3a,b as LP$_1$. The bifurcating upper branch equilibrium is stable and the lower branch is unstable.

For the critical point $(b_{T2},\,E^{*}_2)$, the left and right eigenvectors corresponding to the simple zero eigenvalue of $D_y f_b(y)|_{(b_{T2},E^{*}_2)}$ are chosen respectively as

$$\begin{aligned} \begin{array}{c} v_{T2}=[0.001291 \,-3578.6696,\,-143.1454,\, 0.001432]\\ w_{T2}= [0.0029,\,-0.000016, -0.0066,\, -0.99997]^T, \end{array} \end{aligned}$$

where $<v_{T2},\,w_{T2}>=1$. The transversality and degeneracy conditions are satisfied since

$$\begin{aligned}&v_{T2} \left[ \frac{\partial f}{\partial b} \right] |_{(b_{T2},E^{*} _2)} = -9533936.0987 \ne 0 \quad \text {and} \quad \\&v_{T2} \left[ w_{T2}^T (D_y^2 f_b) w_{T2} \right] |_{(b_{T2},E^{*}_2)} = -0.1244 \times 10^{-9} \ne 0. \end{aligned}$$

The other three negative eigenvalues associated with $D_y f_b(y)|_{(b_{T2},E^{*} _2)}$ are $-4.5701$, $-0.3294$, and $-0.0987$. Since both the transversality and degeneracy conditions are positive, there is no equilibrium near $(b_{T2},E^{*} _2)$ when $b>b_{T2}$, but there are two equilibria near $(b_{T2},E^{*} _2)$ when $b<b_{T2}$. To test the stability of the bifurcating equilibria, we choose $b=0.29$ and obtain an unstable upper equilibrium $E^{*+} _2=(705,\,2789,\,1415628,\,214563623)$ (associated with four eigenvalues $-7.2051$, $-1.7611$, $-0.32998$, and 0.00048) and a stable lower equilibrium $E^{*-} _2=(468905,\,179,\,133,\,15543)$ (associated with four eigenvalues $-60.3205$, $-0.1793$, $-0.0083+ 0.0026 i$, and $-0.0083 - 0.0026 i$). There also exist an unstable positive equilibrium $E_{T2l}=(499959,\,0.2307,\,0.1606,\,20.0627)$ (associated with four eigenvalues $-64.1962$, $-0.3289$, $-0.01$, and 0.0094) and a stable positive equilibrium $E_{T2h}=(10,\,2793,\,98580761,\,14936553571)$ (associated with four eigenvalues $-492.9151$, $-1.78999$, $-0.3299$, and $-0.00048$). The dynamics are summarized in Fig. 3a near the point LP$_2$.

For the critical point $(b_{T3},E^{*} _3)$, The left and right eigenvectors corresponding to the simple zero eigenvalue of $D_y f_b(y)|_{(b_{T3},E^{*}_3)}$ are chosen respectively as

$$\begin{aligned} \begin{array}{c} v_{T3}=[-0.1103,\,0.9929,\,0.04412,\,-0.2447\times 10^{-12} ]\\ w_{T3}= [-0.9064\times 10^{-5},\,0.5385\times 10^{-7}, \, 22.6606,\, 3433.4342 ]^T, \end{array} \end{aligned}$$

where $<v_{T3},\,w_{T3}>=1$. The transversality and degeneracy conditions are satisfied since

$$\begin{aligned}&v_{T3} \left[ \frac{\partial f}{\partial b} \right] |_{(b_{T3},E^{*} _3)} = 3707.9009 \ne 0 \quad \text {and} \quad \\&v_{T3} \left[ w_{T3}^T (D_y^2 f_b) w_{T3} \right] |_{(b_{T3},E^{*} _3)} = -0.2266\times 10^{-9} \ne 0. \end{aligned}$$

The rest of the three negative eigenvalues associated with $f_b(y)|_{(b_{T3},E^{*}_3)}$ are $-250$, $-1.6363$, and $-0.3299$). The signs of the transversality and degeneracy conditions indicate no equilibrium near $(b_{T3},E^{*} _3)$ when $b<b_{T3}$, and two equilibria near $(b_{T3},E^{*} _3)$ when $b>b_{T3}$. Choosing $b=0.163$ we test the stability of the bifurcating branches and observe that there are two equilibria near $(b_{T3},E^{*} _3)$, a stable $E^{*+} _3=(14,\, 3006,\,70982833,\,10755055859)$ (associated with four eigenvalues $-354.9259$, $-1.6629$, $-0.3299$, and $-0.0002$) and an unstable $E^{*-} _3=(34,\,3006,\,29015090,$ 4396306898) (associated with four eigenvalues $-145.0898$, $-1.6629$, $-0.3299$, and 0.0002). The other two unstable positive equilibria located further away from $(b_{T3},E^{*} _3)$ are $E_{T3h}=(489397,\,108,\,43,\,386)$ (associated with four eigenvalues $-61.9168$, $-0.0102$, $0.0537+0.1342 i$, and $0.0537-0.1342 i$) and $E_{T3l}=(499421,\,6,\,2,\,21)$ (associated with four eigenvalues $-63.1107$, $-0.0099$, $-0.3064$, and 0.0709). The dynamics are summarized in Fig. 3a near the point LP$_3$.

At $(b_{T4},E_{T4})$, the disease free equilibrium $E_0$ and infected equilibrium $E^{*}$ intersect and exchange stability. The qualitative behavior of the model (1) at $(b_{T4},E_{T4})$ is determined by its corresponding center manifold governed by $\dot{c}= \mathscr {A} c^2 + \mathscr {B} \phi c$. The formula of the coefficients $\mathscr {A}$ and $\mathscr {B}$ are derived in our previous work (Zhang et al. 2020). Using the parameter values in Table 1, we have $\mathscr {A}|_{(b_{T4},E_{T4})}=4.3403$ and $\mathscr {B}|_{(b_{T4},E_{T4})}=24.9999$. Therefore, the model (1) undergoes a transcritical bifurcation at $(b_{T4},E_{T4})$. Furthermore it shows a backward bifurcation due to the positiveness of the coefficients $\mathscr {A}$ and $\mathscr {B}$ in the quadratic terms. The dynamics are summarized in Fig. 3b near the point BP.

Note that the magnitudes of transversality and degeneracy conditions depend on the normalization of the corresponding left and right eigenvalues $v_{T1}$ and $w_{T1}$ (or $v_{T2}$ and $w_{T2}$ and $v_{T3}$ and $w_{T3}$). While the signs of transversality and degeneracy conditions (which are related to the opening direction of the saddle node bifurcation) are invariant under the scaling of the left and right eigenvectors. Therefore, we choose the left and right eigenvectors such that their dot product equals to one. Furthermore, the signs of transversality and degeneracy conditions for $E^{*}_1$, $E^{*}_2$, and $E^{*}_3$ show that the opening direction of the saddle node bifurcation LP$_2$ is different with LP$_1$ and LP$_3$ (see Fig. 3).

3.2 Investigation of the Hopf bifurcations

The necessary and sufficient conditions (Wm 1994; Yu 2005; Yu and Wang 2019) for Hopf bifurcation $E^{*}$ require

• Condition Hopf 1. $\Delta _3(y_3,\,b)=0$,

• Condition Hopf 2. $\Delta _{1,2}(y_3,\,b)>0$,

• Condition Hopf 3. $\det (J(y_3,\,b))>0$ (positive determinant of the corresponding Jacobian matrix),

• Condition Hopf 4. $\frac{d \Delta _3(y_3,\,b)}{d b} =\frac{\partial \Delta _3(y_3,\,b)}{\partial b} + \frac{\partial \Delta _3(y_3,\,b)}{\partial B} \frac{d y_3}{db}= \frac{\partial \Delta _3(y_3,\,b)}{\partial b} - \frac{\partial \Delta _3(y_3,\,b)}{\partial y_3} \frac{\partial F/\partial b}{\partial F/\partial y_3} \ne 0$.

Here, $\Delta _i(y_3,\,b)$, $i=1,\dots ,4$ are Hurwitz arguments and the function $F(y_3)=0$ is the equilibrium condition. The above four criteria yield two Hopf bifurcation points:

• Hopf 1. $b_{H1} = 0.0419$ day$^{-1}$, $E_{H1} = (495822.4505,\,166.2001,\,16.8509,\,80.9264)$ cells/ml, with $\Delta _1|_{(E_{H1}, b_{H1})}= 62.1427$, $\Delta _2|_{(E_{H1}, b_{H1})}=38.7987$, and $\frac{d \Delta _3(B,\,b)}{d b}|_{(E_{H1}, b_{H1})}= -5907.7516$, and $\det (J(E_{H1},b_{H1}))=0.003699$. The corresponding eigenvalues are $( -62.1326,\,-0.0100,\,0.07697 i,\, -0.07697 i)$ with $i^2=-1$.

• Hopf 2. $b_{H2} = 0.2611$ day$^{-1}$, $E_{H2} = (485669.6896,\,91.4745,\,59.0125,\,1841.8417)$ cells/ml, with $\Delta _1|_{(E_{H2}, b_{H2})}=62.1708$, and $\Delta _2|_{(E_{H2}, b_{H2})}=39.7038,\; \frac{d \Delta _3(B,\,b)}{d b}|_{(E_{H2}, b_{H2})}= 5475.2113$, $\det (J(E_{H2},b_{H2}))=0.005743$. The corresponding eigenvalues are $(-0.1605,\, -0.01027,\, 0.09483 i,\, -0.09483 i)$.

We further study the post-critical behavior of the Hopf bifurcations to determine the stability of the bifurcating limit cycles. The corresponding Hopf bifurcation normal forms up to third order terms are derived through center manifold and normal form reductions. Due to the high non-linearity and stiffness of the model equations, we employ an established Maple program (Yu 1998) for the model analysis.

3.2.1 The Hopf bifurcation at $b_{H1}$

We first apply a parameter-dependent shift of coordinate on the equilibrium condition in Eq. 3, that is

$$\begin{aligned} F(y_{3|E_{H1}}+\varepsilon ,\,b)=0. \end{aligned}$$

Solving the preceding equation obtains

$$\begin{aligned} b(\varepsilon )= b_{H1} + 0.0023 \, \varepsilon + O(\varepsilon ^2). \end{aligned}$$

Taking only the linear approximation of $b(\varepsilon )$, we assume that $b(\varepsilon )=b_{H1}+\mu$, where $\mu =0.0023 \, varepsilon$, $\mu$ and $\epsilon$ are small perturbation parameters. It follows that $E^{*}_{H1}(\epsilon )= E_{H1}+[ - 245.8399 \epsilon ,\, 0.7032 \epsilon ,\, \epsilon ,\, 5.4797\epsilon ]^T +O(\epsilon ^2)$. We introduce the transformation

$$\begin{aligned} \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}= E^{*}_{H1}(\epsilon ) + T_{H1} \begin{bmatrix} u_{11}\\ u_{12}\\ u_{13}\\ u_{14}\end{bmatrix}, \quad T_{H1}= \begin{bmatrix} 0.9581 &{} 0. &{} -0.0398 &{} -0.9999\\ 0.1293 &{} -0.1352 &{} 0.0399 &{} -0.0002\\ -0.0039 &{} -0.0297 &{} -0.9984 &{} 0.00001\\ -0.0789 &{} -0.2002 &{} 0.0064 &{} -0.0001 \end{bmatrix},\nonumber \\ \end{aligned}$$

(16)

into (1) and obtain

$$\begin{aligned} \frac{du_{1i}}{dt}=g_{1i}(u_{11},\,u_{12},\,u_{13},\,u_{14};\,\epsilon ), \qquad \text {for}\quad i = 1,\,2,\,3,\,4, \end{aligned}$$

where $g_{1i}$ for $i=1...4$ are stored in Appendix (see supplementary material) (7)–(10). The corresponding Jacobian matrix of equations evaluated at the equilibrium $u_{1i}=0$, $i=1,\,2,\,3,\,4$ takes the Jordan canonical form as

$$\begin{aligned} J_{H1} = \begin{bmatrix} 0&{} \omega _{10} &{} 0&{}0\\ -\omega _{10} &{} 0 &{}0&{}0\\ 0&{}0&{}-62.1326&{}0\\ 0&{}0&{}0&{}-0.01005 \end{bmatrix}, \end{aligned}$$

where $\omega _{10}= 0.07697$. The corresponding Hopf bifurcation normal form up to third order term is

$$\begin{aligned} \dfrac{dr_1}{d t_1} = r_1(v_{10} \epsilon + v_{11} r_1^2), \qquad \dfrac{d \theta _1}{d t_1} = \omega _{10} + \tau _{10} \epsilon + \tau _{11} r_1^2 , \end{aligned}$$

where $v_{10}$ and $\tau _{10}$ are derived from linear analysis as follows

$$\begin{aligned} \begin{array}{lll} v_{10} &{}= \dfrac{1}{2} \left( \dfrac{\partial ^2 g_{11}}{\partial u_{11} \partial \epsilon }+ \dfrac{\partial ^2 g_{12}}{\partial u_{12} \partial \epsilon } \right) |_{u_{1i}=0, \epsilon =0}&{}= 0.0046752,\\ [2.0ex] \tau _{10} &{}= \dfrac{1}{2} \left( \dfrac{\partial ^2 g_{11}}{\partial u_{12} \partial \epsilon } - \dfrac{\partial ^2 g_{12}}{\partial u_{11} \partial \epsilon } \right) |_{u_{1i}=0, \epsilon =0}&{}= 0.0042939. \end{array} \end{aligned}$$

The first focus value $v_{11}$ and the coefficient $\tau _{11}$ are derived from the Maple program (Yu 1998) taking $\epsilon =0$ as input. We obtain

$$\begin{aligned} v_{11}= -0.1195 \times 10^{-6}, \qquad \tau _{11} = -0.1632 \times 10^{-7}. \end{aligned}$$

The trivial equilibrium $\bar{r}_{10}=0$ indicates the equilibrium $E_{H1}$ for model (1). While the nontrivial equilibrium $\bar{r}_{11}=-\frac{v_{10}\epsilon }{v_{11}}$ exists if $\epsilon >0$ and represents the amplitude of the bifurcating limit cycle. Since

$$\begin{aligned} \dfrac{d (v_{10} \epsilon r_1 + v_{11} r_1^3)}{d r_1}|_{\bar{r}_1} = \left\{ \begin{array}{rl} v_{10}\epsilon , &{} \bar{r}_1=\bar{r}_{10},\\ -2 v_{10}\epsilon , &{} \bar{r}_1=\bar{r}_{11}. \end{array} \right. \end{aligned}$$

The trivial equilibrium $\bar{r}_{10}=0$ is stable when $\epsilon <0$. When $\epsilon >0$, $\bar{r}_{10}=0$ becomes unstable, then a stable limit cycle merged with an amplitude of $\bar{r}_{11}$.

3.2.2 The Hopf bifurcation at $b_{H2}$

Employing the similar approach as shown in the previous subsection, we first take the linear approximation of $b(\epsilon )$ solved from $F(y_{3|E_{H2}}+\epsilon ,\,b)=0$. That is, $b(\epsilon )=b_{H2}+\mu$ with $\mu =0.0027 \epsilon$ ( $\mu$ and $\epsilon$ are small perturbations). Then we introduce the following transformation

$$\begin{aligned} \begin{array}{c} \begin{bmatrix} y_1\\ y_2\\ y_3\\ y_4 \end{bmatrix}= E^{*}_{H2}(\epsilon ) + T_{H2} \begin{bmatrix} u_{21}\\ u_{22}\\ u_{23}\\ u_{24}\end{bmatrix},\quad T_{H1}= \begin{bmatrix} 0.2376 &{} -0.1206 &{} 0.0387 &{} -0.9999\\ -0.0051 &{} -0.0149 &{} -0.0396 &{} -0.0002\\ -0.0057 &{} -0.0087 &{} 0.9908 &{} 0.8749 \times 10^{-5}\\ -0.9637 &{} 0. &{} -0.1231 &{} -0.0045 \end{bmatrix},\\ [5.0ex] E^{*}_{H2}(\epsilon )= E_{H2}+ \left[ - 235.8751\,\epsilon ,\, 0.5539\, \epsilon ,\, \epsilon ,\, 158.9314\,\epsilon \right] ^T +O(\epsilon ^2), \end{array}\qquad \end{aligned}$$

(17)

into (1). It yields $\frac{du_{2i}}{dt}=g_{2i}(u_{21},\,u_{22},\,u_{23},\,u_{24};\,\epsilon )$, for $i = 1,\,2,\,3,\,4$, where $g_{2i}$ are stored in (11)-(14) in the Appendix (see supplementary material). The expression of functions $g_{1i}(u_{11},\,u_{12},\,u_{13},\,u_{14};\,\epsilon )$ are omitted for brevity. The corresponding Jacobian matrix of equations evaluated at the equilibrium $u_{2i}=0$ ($i=1,\,2,\,3,\,4$) is in the Jordan canonical form $J_{H2}=diag[\begin{bmatrix} 0 &{} \omega _{20} \\ -\omega _{20} &{} 0\end{bmatrix},\, -0.1605,\, -0.0103 ]$, where $\omega _{20}= 0.0948$. The corresponding Hopf bifurcation normal form up to third order term is written as $\frac{dr_2}{d t_2} = r_2(v_{10} \epsilon + v_{21} r_2^2)$ and $\frac{d \theta _2}{d t_2} = \omega _{20} + \tau _{20} \epsilon + \tau _{21} r_2^2$, where $v_{20}= -0.0034$, $\tau _{20}= -0.0034$, $v_{21} = -0.1238 \times 10^{-8}$, and $\tau _{21}= -0.1584 \times 10^{-9}$. The trivial equilibrium $\bar{r}_{20}=0$ indicating $E_{H2}$ is stable if $\epsilon >0$ and unstable if $\epsilon <0$, while the non-trivial equilibrium $\bar{r}_{21}=-\frac{v_{20}\epsilon }{v_{21}}$ exists and is stable if $\epsilon <0$. A stable limit cycle is generated from this Hopf bifurcation.

Fig. 3

Bifurcation diagram of Mtb concentration B ($y_3$ ) vs macrophage apoptosis rate b. Infected ($E^*$) equilibriums are plotted according to Equation 1 in Appendix (see supplementary material) as $F(y_3,b)=0$ in blue lines (see (a) and (b)). The disease-free ($E_0$) is in red. The solid and broken line styles distinguish stable and unstable equilibriums. Oscillating bacterial load are due to two supercritical Hopf bifurcations. Two oscillation regions are separated because periodic solutions merge with the lowest branch of $E^*$ (see (b)) and generate blow-up periods (see (c)) (color figure online)

4 Demonstrating roles of macrophage programmed cell death through numerical simulations

The bifurcation diagrams in Fig. 3 demonstrate the diverse Mtb levels B with regard to the infected macrophage programmed cell death (apoptosis) rate b. Disease-free equilibrium $E_0$ (red line in Fig. 3b) and infected equilibrium $E^*$ (blue curve in Fig. 3a, b) intersect and exchange stability at a transcritical bifurcation (marked as point BP at $b=b_{T4}$). In the first branch from the bottom of the infected equilibrium, $E^*$ is unstable and undergoes two neutral saddle points (marked as NS), then bifurcates to a stable equilibrium solution in the second branch from the bottom at a saddle-node bifurcation (marked as LP$_1$ at $b=b_{T1}$). The stable $E^*$ loses its stability at a supercritical Hopf bifurcation at $b=b_{H1}$ (marked as H$_1$). The stable bifurcating limit cycles disappear when the periodic solution merges with the lowest branch of $E^*$ (see Fig. 3b) and induces a blow up in the period (see Fig. 3c top). $E^*$ keeps being unstable until reaching to a second supercritical Hopf bifurcation at $b=b_{H2}$ (marked as H$_2$). The corresponding bifurcating stable limit cycles also vanish when the cycles merge with the lowest branch of $E^*$ (see Fig. 3b), and induce a blow up in the period (see Fig. 3c bottom). This leaves a window in the branch at the second from the bottom of $E^*$ (approximately $b\in (0.052,\,0.163$ day$^{-1}$), where solutions converge to the stable disease-free equilibrium $E_0$ (red line). Bistability is possible if $b\in (b_{T3},\,0.163)$ day$^{-1}$. The stable branch at the second from the bottom of $E^*$ after H$_2$ bifurcates an unstable branch (at the second from the top) at another saddle node bifurcation (marked as LP$_2$) at $b=b_{H2}$. Then $E^*$ gains back stability at the third saddle node bifurcation (marked as LP$_3$) at $b=b_{H3}$. It yields the top stable branch for the infected equilibrium $E^*$. Overall, the model (1) admits various disease outcomes (clearance, latent infection (LTBI), and active infection Cadena et al. 2017) through the occurrence of three saddle node bifurcations (LP$_1$ at $b=b_{T1}$, LP$_2$ at $b=b_{T2}$, LP$_3$ at $b=b_{T3}$ and BP at $b=b_{T4}$). Interestingly, in the second $E^{*}$ branch from the bottom, where Mtb level B is in latent stage ($b\in (PL_1,\,LP_2)$), the Mtb level first stabilizes at a low level ($b\in (LP_1,\, H_1)$), then oscillates $b\in (H_1,\,0.052)$, then vanished ($b\in (0.052,\,0.163)$ day$^{-1}$), and oscillate again ($b\in (0.163,\,b_{H2})$ day$^{-1}$), then gain back stability ($b\in (H_1,\,LP_2)$). These surprisingly complex dynamical behaviors motivate us to investigate the macrophage-Mtb interaction model 1 regarding the macrophage apoptosis against Mtb.

4.1 Macrophage programmed cell death in TB infection

Before interpreting the complex macrophage-Mtb interplay shown in the bifurcation diagrams in Fig. 3 and the simulations in Figs. 4 and 5, it may be helpful to review macrophage apoptosis as a defense strategy against Mtb infection. Host immune responses to tuberculosis infection start from the inhalation of air droplets containing Mtb pathogens. These bacilli first manage to enter into resident alveolar macrophages through the phagocytosis process. A phagolysosome is then formed by the fusion of lysosomes with phagosomes containing engulfed Mtb pathogens. In the phagolysosome, internalized bacilli are degraded by reactive oxygen species and the acidification. However, Mtb pathogens evolve to survive from this cell anti-bacterial mechanism and to reproduce inside the macrophage. At this point, infected macrophages prohibit the extracellular Mtb pathogens, but facilitate intracellular bacterial replication at least until the activation of the adaptive immune responses (Sturgill-Koszycki et al. 1994), and provide an intracellular environment in favor of bacterial latency (Kornfeld et al. 1999). To defend against intracellular parasitic Mtb pathogens, a common strategy is to initiate host cell apoptosis. It destroys the protected intracellular environment, which promote intracellular bacterial reproduction and latency (Lee et al. 2009). However, to confront the elimination through host cell apoptosis, Mtb pathogens (especially virulent Mtb strains) evolve to interrupt tumor necrosis factor-$\alpha$ (TNF-$\alpha$) signaling (Spira et al. 2003) and promote anti-apoptotic Mcl-1 (Sly et al. 2003). These signals suppress the infected macrophage apoptosis. On the other hand, after maintaining the suitable intracellular environment, virulent strain Mtb pathogens manage to replicate, but still need a mean to spread the newly replicated pathogens. Host cell death is then triggered by heavy load of intracellular bacteria to spread the infection to other host cells. This heavily infected macrophage apoptosis process progresses rapidly and ends up in macrophage necrosis. It is found that the intracellular Mtb pathogens released from this process are not killed by host immune cells and able to replicate as extracellular bacteria (Lee et al. 2006). The macrophage necrosis caused by heavy load of intracellular Mtb benefits the TB progression to active TB disease.

4.2 TB outcomes with a small bacterial load

Pathogen clearance is possible if $b<b_{T4}$, due to the local stability of the disease free equilibrium $E_0$. To represent the low bacterial level due to low inhaled bacterial load or antibiotic drug treatments, we choose a low initial bacterial load $(M_u(0),\,M_i(0),\,B(0),\,T(0))=(10,\,1,\,1,\,100)$ cells/ml for the simulations in Fig. 4. The simulated Mtb infection clearance are shown in Fig. 4 panel (a) for six different macrophage apoptosis rates satisfying $b<b_{T4}$ day$^{-1}$. Simulations in Fig. 4a also demonstrate a positive relation between infection clearance time (and the Mtb peak magnitude) and infected macrophage apoptosis rate b. It is probably because the release of intracellular Mtb pathogens during the Mtb-containing macrophage apoptosis process causes the increase of the total bacterial load, which takes the immune system longer time to eliminate.

Fig. 4

Clearance and development of infection with different speeds

Increasing the Mtb-containing macrophage apoptosis rate passing $b>b_{T4}$ day$^{-1}$ indicates the occurrence of heavily infected macrophage necrosis. In this scenario, the host immune system loses control of the growth of the invading pathogen. Either a small amount of inhaled Mtb pathogens or a small load of latent Mtb bacteria will eventually progress to active TB disease (see Fig. 4b). A positive relation between the speed (and magnitude) and infected macrophages apoptosis rate b is also observed in Fig. 4b. This result supports the experimental finding that the release of Mtb pathogens through necrosis induces the high Mtb bacterial burden (Lee et al. 2011).

Overall, simulation results confirm the experimental findings that the infected macrophage undergoing apoptosis promotes the clearance of Mtb infection (Keane et al. 1997, 2000; Lee et al. 2009) even though the released Mtb pathogens increase the total bacterial burden and result in longer clearance time. Moreover, the apoptosis for heavily infected macrophages culminates in necrosis, which releases more intracellular Mtb pathogens (Lee et al. 2009). The uncontrolled infection prolongs clearance time and facilitates infection progression to active TB disease.

4.3 The tug of war between macrophage apoptosis and TB infection in LTBI state

Latent tuberculosis infection (LTBI) describes an Mtb-infected individual who does not develop active disease and is not contagious. In this stage, the Mtb-infected macrophages provide a suitable environment for the latency and persistence of intracellular bacteria. However, diseases impairing the immune system (such as AIDS), treatments causing immune system suppression (such as chemotherapy for cancer), or advanced age can trigger LTBI reactivation. The LTBI status is demonstrated as low levels of Mtb pathogen load in Fig. 3 when the macrophage apoptosis rate is between LP$_1$ and LP$_2$. Low levels of Mtb load can be both persistent (b between LP$_1$ and $H_1$ or between $H_2$ and LP$_2$) and oscillatory (generated from two Hopf bifurcations $H_1$ and $H_2$). Interestingly, the oscillations won’t persist in the whole parameter interval of ($H_1$, $H_2$), but disappear when oscillations starting from $H_1$ and starting from $H_2$ merge with the lower branch of the infected equilibrium $E^*$ (see Fig. 3b). It follows blowing-up oscillation periods (see Fig. 3c), where the coexisting unstable branches of infected equilibrium $E^*$ repel nearby solutions to the locally asymptotically stable disease free equilibrium $E_0$. A macrophage apoptosis rate window (approximately $(0.052,\,0.163$ day$^{-1}$) between two Hopf bifurcations $H_1$ and $H_2$ are generated, where oscillations disappear. Moreover, the risk to progress to active disease is possible if the macrophage apoptosis rate b is between LP$_3$ and LP$_2$, and if large load of Mtb pathogens is released due to the weakened immune system.

Fig. 5

Simulated Mtb concentration as the result of the interplay between the host defense mechanism (macrophage apoptosis) and virulent Mtb strains counteract strategies (inhibition of macrophage apoptosis and trigger macrophage necrosis)

The role of macrophage apoptosis on the Mtb pathogen dynamics can be demonstrated by time-history simulations (see Fig. 5) based on the analytical predictions in bifurcation diagrams in Fig. 3. The clearance of internalized Mtb pathogens after phagocytosis by the acidification is demonstrated (see Fig. 5a) by a low level of macrophage apoptosis rate b near LP$_1$ ($b<b_{T1}$ and $b=0.0294$ day$^{-1}$) and a low initial Mtb concentration in LTBI state. To confront the parasite pathogen after the infection establishment, Mtb-containing macrophages adopt a defense strategy to activate the host cell programmed death (macrophage apoptosis). This host defense mechanism is demonstrated by increasing the macrophage apoptosis rate b to the window (approximately $(0.052,\,0.163$ day$^{-1}$). Disease clearance is shown in both LTBI case (with low initial Mtb load) for $b=0.131$ day$^{-1}$ and $b=0.1317$ day$^{-1}$) (see Fig. 5b) and high initial Mtb load case for $b_{T3}>b=0.134$ day$^{-1}$ (see Fig. 5c). Infected macrophage apoptosis effectively inhibits intracellular Mtb reproduction. To counteract this survival disadvantage, Mtb pathogens evolve virulent strains, which are capable of suppressing Mtb-containing macrophage apoptosis and continuing intracellular replication. The reduced macrophage apoptosis rate by virulent Mtb strains is between $b_{T1}=0.0295$ day$^{-1}$ (LP$_1$) and 0.163 day$^{-1}$. The low level persistent and oscillatory Mtb levels are shown in Fig. 5a for $b_{T1}<b=0.02952$ day$^{-1}$ and 0.043 day$^{-1}$). Virulent Mtb strains manage to suppress macrophage apoptosis for the intracellular replication, but also provoke host macrophage necrosis when the intracellular pathogen load passes a threshold or the host cell resources are depleted. The rapid macrophage apoptosis progresses to macrophage necrosis, which induces a large amount of intracellular pathogen release and benefits the infection. Figure 5b and c show that the low-level oscillatory Mtb level for $b=0.165$ day$^{-1}$ and $b=0.2$ day$^{-1}$ ($\in (0.043,\,H_2)$ day$^{-1}$) and an active disease case for $b=0.15$ day$^{-1}$ ($\in (b_{T3}, 0.043)$ day$^{-1}$) if the patient is exposed with high level Mtb pathogen. Even undergoing host cell necrosis, the immune system can still manage to control the growth of Mtb pathogens (shown in Fig. 5 for $b=0.26$ day$^{-1}$ and $b=0.29$ day$^{-1}$), but fails if the infected macrophage loss rate passes through the threshold $b_{T4}$ (BP) (shown in Fig. 5 for $b=0.32$ day$^{-1}$).

Our analytical and numerical results confirm the mechanism that the host immune system employs programmed cell death (apoptosis) as a strategy to defend against intracellular Mtb parasitism (Lee et al. 2009). However, Mtb pathogens counteract macrophage apoptosis by evolving virulent Mtb strains. Virulent Mtb strains can both inhibit macrophage apoptosis to facilitate intracellular Mtb replication and trigger heavily-infected macrophage necrosis to release intracellular pathogens (Zychlinsky 1993; McCormick 2008; Lee et al. 2009). This complex parasitic relationship determines the various TB disease outcomes. Moreover, a comprehensive understanding of the interplay between macrophage apoptosis and Mtb pathogens is fundamental for the TB treatment design.

Fig. 6

2-dimensional bifurcation diagrams of b vs $\beta$, $\delta$, $\gamma$ and $N_1$

5 New treatments suggested by the new insights of macrophages programmed cell death

The current standard treatment of TB involves four first-line antibiotics (WHO 2019). Effective treatment for curing TB, however, can be hampered by the development of drug resistance, which can occur when treatment is not properly completed or adhered to. Host directed therapy (HDT), which includes small molecule therapies that can modulate the host immune response, can be used to augment treatment regimens to better control TB infection of both antibiotic sensitive and resistant TB strains (Kolloli and Subbian 2017). Antibiotic and HDT treatment can increase bacterial elimination ($\eta$), infected macrophage loss (b, $\gamma$), T-cell generation ($s_T$, $c_m$, $c_b$), and decrease macrophage infection ($\beta$), and intracellular and extracellular bacterial proliferation ($\delta$, $N_1$, $N_2$). Sensitivity analysis has shown that $\eta$, $s_T$, $c_m$, $c_b$, and $N_2$ do not significantly affect the reproduction number (Fig. 1) or LTBI reactivation (Fig. 2). These parameters are therefore ignored, and we proceed with an analysis of b, $\beta$, $\delta$, and $\gamma$ and $N_1$, which significantly affect the reproduction number and LTBI reactivation.

Figure 6 plots two parameter bifurcation diagrams that consider parameter b with $\beta$, $\delta$, $\gamma$, and $N_1$. For convenience in the bifurcation analyses, we denote the TB model (1) as $\frac{dx}{dt}=f(x,p)$, where $x=(M_u,M_i, B,T)\in R^4$, $p=(p_b,p_f) \in R^{18}$, and $f:R^{4+18}\rightarrow R^4$. Here, $p_b \in R^{2}$ denotes the two chosen bifurcation parameters, which are one of the following pairs: $(b,\beta )$, $(b, \delta )$, $(b, \gamma )$, and $(b,N_1)$. $p_f$ represents the remaining 16 parameters, which take the corresponding fixed values from Table 1. We represent equilibrium solutions as $x_e=x_e(p_b)$. Single-zero eigenvalue bifurcation happens if $\det (J(x_e(p_b),p_b))=0$ with positive Hurwitz conditions $\Delta _i>0$, for $i=1,2,3$. Hopf bifurcation occurs when (1) $\Delta _3(x_e(p_b),p_b))=0$, (2) $\Delta _{1,2}(x_e(p_b),p_b)>0$, (3) $\det (J(x_e(p_b),p_b))>0$ (positive determinant of the corresponding Jacobian matrix), and (4) $\frac{d \Delta _3(x_e(p_b),p_b)}{d p_b} \ne 0$. Single-zero (saddle-node) bifurcation curves are denoted as LP in blue. Transcritical bifurcation satisfying (4) are denoted as BP in green. Hopf bifurcation curves are plotted in red. Here, LP$_1$, LP$_2$, and LP$_3$ correspond to the three limit point (saddle-node) bifurcations in Fig. 3a. BP is consistent with the branching point (transcritical) bifurcation and Hopf matches with the two Hopf bifurcations. Note that LP$_1$ and LP$_3$ denote two different branches of equilibrium solutions in Fig. 3a. Therefore, even though the parameter curves for LP$_1$ and LP$_3$ intersect (see Fig. 6) in the corresponding 2-dimensional parameter space, the corresponding equilibrium solutions are different. Therefore, there is no intersection in the parameter-state space. It follows that no higher-codimension bifurcation occurs. We note that Bogdanov-Takens, generalized Hopf, and zero-Hopf bifurcations are detected for the bifurcation analyses b vs $\gamma$ and b vs $\delta$. However, the bifurcation critical points lie outside of biologically feasible regions from Table 1, and therefore, are not considered.

Figure 6 first shows that with a fixed value for $\beta$, $\delta$, $\gamma$, and $N_1$, the order of bifurcation occurrence matches the order shown in Fig. 3a – as b increases, we have LP$_1$, Hopf$_1$, LP$_3$, Hopf$_2$, LP$_3$, and BP. Panels (a) and (b) also show that as b changes, the infection outcome does not vary widely, given change in $\beta$ and $\delta$. Therefore, if drug therapy moderates the macrophage apoptosis rate b, very large changes in Mtb infection rate $\beta$ or Mtb proliferation rate $\delta$ are needed to see a change from a current stable equilibrium or periodic cycle. Additionally, to achieve bacteria elimination and prevent reactivation of LTBI, for a given $\beta$ or $\delta$, b must be decreased to a value smaller than LP$_2$. As the macrophage apoptosis rate b changes, changes in cell-mediated immunity rate $\gamma$ and average number of released bacteria $N_1$ can also have an effect. Here, we identify the disease clearance region (in Fig. 6 above LP$_1$ in (c) or below LP$_1$ in (d)) and LTBI controllable region (in Fig. 6 above LP$_2$ in (c) or below LP$_2$ in (d)). To enlarge the disease clearance and LTBI controllable regions, we need to increase b and increase $\gamma$ or decrease $N_1$. It means that a drug therapy that moderates the macrophage apoptosis works better with the combination of an increased killing rate of infected cells by the immune system $\gamma$ or a decreased Mtb released number $N_1$ during programmed cell death.

In drug development, research on apoptosis modulation indicates therapeutic value in cancer (Reed 2004), cardiovascular disease, and other diseases (Cotter et al. 2003). Our findings enhance the idea that a drug therapy promoting macrophage apoptosis, but inhibiting the progression to necrosis induced by heavily-infected cell death, could benefit host defense against Mtb. In the mean time, we should consider the pathogen anti-apoptosis strategies, which could increase bacillary viability, then increase the number of released intracellular Mtb $N_1$. For example, Mtb virulent strains are capable of inhibiting host macrophage apoptosis for intracellular reproduction by hindering the tumor necrosis factor$\alpha$ (TNF$\alpha$). A negative therapeutic effect is associated with treating TB with infliximab, a TNF$\alpha$-neutralizing agent (Keane et al. 2001). Moreover, adaptive immunity is promoted by the effect of the efferocytosis process, in which Mtb-infected apoptotic corpses are removed by phagocytic cells. These phagocytic cells then present Mtb antigen and active CD8+ T cells. This phenomenon not only explains the positive effect of macrophage apoptosis on host, but also inspires vaccine development to promote adaptive immunity (Lee et al. 2009).

In conclusion, to prevent LTBI reactivation and to eliminate TB disease, the development of apoptosis modulation drugs must take the Mtb survival strategies into account. Furthermore, an understanding of the enhanced cell-mediated immunity gives new insight into vaccine development.

6 Conclusion

In this paper, we investigate the macrophage and Mycobacterium tuberculosis (Mtb) dynamics through an established 4-dimensional host-pathogen model. We pay particular attention to identify the determining mechanisms for Mtb elimination, LTBI reactivation prevention, and active TB treatment.

The first goal is to identify the determining factors for various disease outcomes that are unique features for TB infection. These include clearance, LTBI, active disease, and LTBI reactivation. Various disease outcomes in the mathematical model indicate the co-existing Mtb steady states levels (equilibriums). The basic mathematical mechanism for the creation and emergence of steady states is the occurrence of saddle-node bifurcation. Additionally, the fundamental mathematical mechanism for the disease clearance and persistence is the occurrence of transcritical bifurcation. Both saddle-node and transcritical bifurcations are single zero-eigenvalue bifurcation. The problem of identifying parameter sensitivity for TB elimination and LTBI reactivation is replaced by the problem of identifying parameter sensitivity for the occurrence of single zero-eigenvalue bifurcation. Note that pitchfork bifurcation is the other single zero-eigenvalue bifurcation, but is not common in infectious disease models due to its symmetric nature. It is therefore left out of our consideration.

We then perform a sample-based sensitivity analysis for the condition of transcritical bifurcation (the basic reproduction number) on all eleven model parameters. Our results demonstrate that eight of the eleven parameters significantly influence the basic reproduction number ($R_0$). The eight parameters are the infection rate $\beta$, T cell-mediated immunity rate $\gamma$, extracellular bacterium proliferation rate $\delta$, infected macrophages apoptotic rate b, uninfected macrophages bacterial killing rate $\eta$, and average number of bacterium engulfed by uninfected macrophages $N_3$ or released through the death of infected macrophage induced by apoptosis $N_1$ and cell-mediated immunity $N_2$. Fixing the parameters that do not statistically significantly affect the basic reproduction number, another sensitivity analysis is carried out for the conditions of saddle node bifurcation on the eight parameters that significantly influence $R_0$. These two steps of sensitivity analyses find that the infected macrophage cell death rate b is the most influential factor on both $R_0$ and the occurrence of saddle-node bifurcation, which determines the occurrence of various disease outcomes and, in turn, rules the fate of the disease. Biologically, the host cell death in the form of apoptosis is considered to inhibits Mtb replication and to produce bacterial antigens to activate adaptive immune responses (Behar et al. 2011; Queval et al. 2017). On the other hand, cell death in the form of necrosis is associated with spreading infection (Behar et al. 2011; Queval et al. 2017). Other proposed host factors and Mtb invading strategies, which contribute to the disease progression, include genetic diversity (Gagneux 2013), T-cell mediated immune responses (Verrall et al. 2014; Flynn and Chan 2001), the responses of two pivotal cytokines gamma interferon (IFN-$\gamma$) and tumor necrosis factor alpha (TNF-$\alpha$) (Flynn and Chan 2001), Mtb inhibiting the elimination of phagocytized bacteria Queval et al. (2017), and Mtb controlling host cell death to escape from kaltilling Queval et al. 2017. One limitation of our mathematical results is the choice of parameter values. The parameter ranges in Table 1 are based on current experimental and clinical literature, but still inherit their restrictions. Nevertheless, our mathematical results confirm the crucial and controversial role in the host immune defense against invading Mtb pathogens (Queval et al. 2017).

Sensitivity analysis dramatically narrows down parameters of interest for understanding model behaviors (including infection elimination and LTBI progression), but it can not tell how the identified parameters affect the model behaviors, or what model dynamics can be unfolded from the change of the identified parameters. Answering these two questions serves as our second goal. We employ bifurcation analysis to tackle these questions. Considering the macrophage apoptosis rate b as a bifurcation parameter, we explore the role of macrophage apoptosis in TB infection through bifurcation analyses. A spectrum of disease outcomes are verified by numerical simulations. We carry out bifurcation analyses on single-zero eigenvalues bifurcations and derive Hopf bifurcation normal forms. Our analytical results are consistent with the numerical bifurcation output from MatCont (Dhooge et al. 2003).

Regarding TB pathobiology, our findings of the mathematical model dynamics agree with the clinical and experimental macrophage-Mtb interaction outcomes (Lee et al. 2009), which consider the complex roles of macrophage apoptosis in the host defense against TB infection. Our mathematical model (1) demonstrates the following: (1) the clearance of low level Mtb load during phagocytosis is associated with low macrophage apoptosis rate (Verrall et al. 2014); (2) the TNF$\alpha$-induced macrophage apoptosis facilitates the host defense against intracellular Mtb proliferation (Lee et al. 2009); (3) macrophage apoptosis is suppressed by virulent Mtb strains interfering with TNF$\alpha$ signaling pathways. Virulent Mtb then gain an intracellular reproduction environment (Kornfeld et al. 1999); and (4) heavily infected macrophage apoptosis induces macrophage necrosis, which releases a large amount of intracellular bacteria and benefits the spread of the pathogen (Lee et al. 2009; Behar et al. 2011).

Elucidating the complex roles of macrophage apoptosis played in Mtb in-host dynamics could give new insights into the treatments aiming at TB elimination and LTBI reactivation prevention. Treatment strategies regulate macrophage apoptosis in combination with the control of bacillary viability is recommended. Mtb antigen presentation after the efferocytosis of Mtb-containing apoptotic remaining enhance adaptive immunity by activating CD8+ T cells. The adaptive immunity promoting mechanism can help the development of the new vaccine and new treatments.