Canard-induced complex oscillations in an excitatory network

Abstract

In Neuroscience, mathematical modelling involving multiple spatial and temporal scales can unveil complex oscillatory activity such as excitable responses to an input current, subthreshold oscillations, spiking or bursting. While the number of slow and fast variables and the geometry of the system determine the type of the complex oscillations, canard structures define boundaries between them. In this study, we use geometric singular perturbation theory to identify and characterise boundaries between different dynamical regimes in multiple-timescale firing rate models of the developing spinal cord. These rate models are either three or four dimensional with state variables chosen within an overall group of two slow and two fast variables. The fast subsystem corresponds to a recurrent excitatory network with fast activity-dependent synaptic depression, and the slow variables represent the cell firing threshold and slow activity-dependent synaptic depression, respectively. We start by demonstrating canard-induced bursting and mixed-mode oscillations in two different three-dimensional rate models. Then, in the full four-dimensional model we show that a canard-mediated slow passage creates dynamics that combine these complex oscillations and give rise to mixed-mode bursting oscillations (MMBOs). We unveil complicated isolas along which MMBOs exist in parameter space. The profile of solutions along each isola undergoes canard-mediated transitions between the sub-threshold regime and the bursting regime; these explosive transitions change the number of oscillations in each regime. Finally, we relate the MMBO dynamics to experimental recordings and discuss their effects on the silent phases of bursting patterns as well as their potential role in creating subthreshold fluctuations that are often interpreted as noise. The mathematical framework used in this paper is relevant for modelling multiple timescale dynamics in excitable systems.

Appendices

Canard-mediated transitions to burst and spike-adding in the $(a,d,\theta )$-model

Here we study canards and spike-adding transitions in the $(a,d,\theta )$-model keeping s as the bifurcation parameter. Note that similar study in the (a, d, s)-model with the parameter $\theta$ will give qualitatively similar slow-fast transitions. We use the same parameter set for which MMBO solutions exists in (4) (see Fig. 3 and Sect. 3), but change $\tau _{\theta }=5000$ for a clear visualisation of transitions.

The $(a, d, \theta )$-model reads:

$$\begin{aligned} \begin{aligned} \tau _a{\dot{a}}&= a_{\infty }(w\,d\,s\,a- \theta - \theta _0) - a,\\ \tau _d{\dot{d}}&= d_{\infty }(a) - d,\\ {\dot{\theta }}&= \varepsilon (\theta _{\infty }(a) - \theta ), \end{aligned} \end{aligned}$$

(10)

where $\varepsilon =1/\tau _{\theta }$ being the small parameter (given that $\tau _a=1$ and $\tau _d=2$). System (10) undergoes a supercritical Hopf bifurcation at $s_{Hopf} \approx 0.95657$. As in the canard explosion scenario in planar systems, the canard solutions of (10) lie along a quasi-vertical segment of the solution branch in the bifurcation diagram in terms of s. This quasi-vertical segment is located at an $O(1/\tau _\theta )$-distance of the Hopf point at $s_{Hopf}$, that is, near the canard value at $s_c \approx 0.95704$. Next, we explain how canard orbits are formed from the early stages of the canard explosion until the formation of the first spike (Fig. 4), as well as for the second and third spikes (Fig. 12).

In order to understand the canard trajectories structuring these periodic orbits, we need to examine the bifurcation diagram of the (a, d) fast subsystem with respect to $\theta$ for $s \approx s_c$. The $\theta$-dependent family of equilibrium points $(a^*, d^*)= (a^*, d_\infty (a^*))$ of the fast subsystem is defined by

$$\begin{aligned} \left\{ a_{\infty }(w\,d\,s\,a-\theta -\theta _0)-a=0\right\} \cap \left\{ d_{\infty }(a) - d=0\right\} \end{aligned}$$

that is,

$$\begin{aligned} \left\{ \theta = k_a{\mathrm {ln}}\left( \frac{1}{a}-1\right) +w\, d_\infty (a)\,s\,a-\theta _0 \right\} , \end{aligned}$$

(11)

and forms a Z-shaped curve for $a \in (0, 1)$ (blue curve in Fig. 11) with twofold points, $\theta _{f}^{l}$ and $\theta _{f}^{r}$. The lower branch consists of stable nodes for $\theta > \theta _{f}^{l}$. Saddle equilibria, whose invariant manifolds are weaker in the stable direction than in the unstable direction, lie along the middle branch between $\theta _{f}^{l}$ and $\theta _{f}^{r}$. The upper branch has stable foci until the supercritical Hopf bifurcation at $\theta _{H}$, which gives a narrow paraboloid of limit cycles. This paraboloid folds back at $\theta _{FC}$ towards the middle branch of saddles and makes a saddle-homoclinic connection at $\theta _{HC}$. The bursting behaviour resulting from this bifurcation structure in the (a, d) fast subsystem is classified as a “Hopf/ fold cycle” bursting by Izhikevich (2000). The homoclinic connection at $\theta _{HC}$ is one of the main ingredients of the spike-adding phenomena explained below.

Fig. 11

a Bifurcation diagram of the (a, d) fast subsystem upon variation of $\theta$ (blue), together with an example canard cycle of the $(a, d, \theta )$ system for $s_c \approx 0.95704$ (black). The purple line represents the $\theta$-nullcline of the $(a, d, \theta )$ system. Panel (a1) corresponds to a zoom of panel a in the dashed rectangle. In both upper panels, H denotes a Hopf bifurcation, LP limit point bifurcations (folds) of equilibria, HC a homoclinic bifurcation and FC a fold bifurcation of cycles. The equilibrium points on the Z-shaped (blue) curve are stable nodes along the lower branch for $\theta > \theta _{f}^{l}$ and saddles between the fold bifurcation values $\theta _{f}^{l} = 0.18326$ and $\theta _{f}^{r} =0.2432$. The stable focus type equilibria along the upper branch undergo a supercritical Hopf bifurcation at $\theta _{H} \approx 0.21335$, which gives a narrow paraboloid of limit cycles. The inner cycles, between $\theta _{H}$ and $\theta _{FC}\approx 0.21423$, are stable, while the outer cycles, between $\theta _{FC}$ and $\theta _{HC}\approx 0.21343$, are unstable. The upper branch hosts unstable equilibria of focus type between $\theta _{H}$ and $\theta \approx 0.241448$, then unstable nodes until $\theta _{f}^{r}$ (color figure online)

After having dissected the (a, d) subsystem with respect to $\theta$, we can focus on the slow-fast transitions in (10). Equation (11) defines the critical manifold $S^{0, (a, d, \theta )}$ of (10) where the only slow variable is $\theta$. Therefore, the slow flow lies along the 1D critical manifold, whose discrete fold set is defined by:

$$\begin{aligned} F^{(a, d, \theta )} =\left\{ \frac{-k_a}{a(1-a)} + w\, s\left( a\,d'_{\infty }(a)+d_{\infty }(a)\right) = 0\right\} \end{aligned}$$

with $d'_{\infty }(a) = \displaystyle \frac{d}{da}(d_{\infty }(a))=-\displaystyle \frac{e^{(a-\theta _d)/k_d}}{k_d (1+e^{(a-\theta _d)/k_d})^2}$. The two fold points are located at $\theta _{f}^{l}$ and $\theta _{f}^{r}$. The passage of the slow nullcline $\{\theta = \theta _\infty (a)\}$ through $\theta _{f}^{l}$ in the 3D phase space as s slowly varies gives the transition from resting to spiking, then adds the spikes successively via canard trajectories until the bursting regime is reached.

The upper panels of Fig. 4 show the first canard cycles induced by the Hopf bifurcation at $s_{Hopf}$ in a similar analogy to that of VDP-type planar systems: the trajectories move along the lower branch of stable nodes, pass through $\theta _f^l$ and follow 1D saddle-type slow manifolds before jumping back to the branch of stable nodes (Fig. 4-(1, 2)). As s varies along the canard explosion $s \approx s_c$, the canard cycles grow in amplitude up to the maximal canard while moving towards $\theta _f^r$. These spikeless cycles are analogous to the canard without head trajectories in planar systems and the maximal canard is the excitability threshold of the $(a, d, \theta )$-system.

When the limit cycle passes near $\theta _f^r$, the (un)stable manifolds of the equilibria shape the cycle. The invariant set of the saddle at $\theta _f^r$ expands the cycle in the a-direction, then brings it back towards the branch of the stable nodes (a similar expansion-contraction mechanism is shown in Guckenheimer and Kuehn (2009), Figure 6). This expansion and contraction at $\theta _f^r$ gives birth to the first spike (Fig. 4-(4)). As s varies, the trajectory is repelled in the a-direction by the unstable manifolds of saddle points of the middle branch then attracted by the stable lower branch of $S^{0,{(a,d,\theta )}}$. This behaviour is similar to the canard with head cycles in planar systems where a trajectory follows both attracting branches of the critical manifold. However, in the $(a,d,\theta )$-system, the critical manifold contains repelling equilibria along the upper branch between $\theta _f^l$ and $\theta _{H}$. Thus, the trajectory returns to the lower branch after it has left the vicinity of the middle branch.

The formation of a cycle with one spike is completed once the spike is located to the left of $\theta _{H}$. Note that it is still a canard cycle since a certain part of it lies along the unstable middle branch: it follows the stable branch as $\theta$ decreases towards $\theta _{f}^l$, passes through $\theta _{f}^l$, continues along the unstable middle branch before departing in the direction of the unstable manifold of the middle-branch saddle equilibrium of the fast subsystem towards the upper-branch attracting focus. Since the (a, d) subsystem does not possess any cycle for $\theta <\theta _{H}$ and the stable foci are weakly attracting, the trajectory does not necessarily follow the upper branch of equilibria of the fast subsystem.

As s varies, the trajectory can follow again the 1D saddle-type slow manifold provided the trajectory comes back exponentially close to it after a spike. This can only happen in the vicinity of the homoclinic bifurcation of the fast subsystem (for small enough $\varepsilon >0$). Hence, as the trajectory comes close to the homoclinic point after the spike, it can grow a new canard segment and this initiates the formation of the next spike (Guckenheimer and Kuehn 2009); see Fig. 12. After the first spike, the second canard segment of the trajectory expands from $\theta _{HC}$ to $\theta _{f}^r$: the limit cycle with one spike grows in the $\theta$-direction, gains the second spike at $\theta _{f}^r$ and then shrinks towards $\theta _{f}^l$. Different from the first spike, the second one follows the stable limit cycles of the (a, d) subsystem – which gives the fast oscillations of the burst episode. Note that the speed of the drift in $\theta$ may not allow the second spike to follow closely the narrow paraboloid of stable limit cycles (between $\theta _{H}$ and $\theta _{FC}$). As for the third and subsequent spikes, fast oscillations drift inside the paraboloid of limit cycles of the fast subsystem after passing near $\theta _{H}$, remain closer to the stable objects in that region Fig. 12-(15). These fast oscillations terminate near $\theta _{FC}$. The transition from the first orbit in Fig. 4 to the fifteenth orbit in Fig. 12 occurs within an exponentially small range of s, that is $s \in [0.9570404035, 0.9570404037]$, approximately.

Fig. 12

Formation of the second (panels (7)–(11)) and third (panels (12)–(15)) spikes in system (10) upon exponentially small variations of $s \approx s_c$. Each up-down pair shows a solution superimposed on the bifurcation diagram of the (a, d) fast subsystem versus $\theta$ (upper panel) and the time course of the solution for variable a (lower panel). Panels (11) and (15) display zoomed views so as to better visualize the interaction between the spikes and the bifurcation diagram of the fast subsystem. Arrows in panel (8) represent the direction of the flow, valid in all panels: single (resp. double) arrows correspond to slow (resp. fast) flow

Folded node and MMOs in the $(a,\theta ,s)$-model

In this section we analyse in detail the $(a,\theta ,s)$-model and unveil its canard dynamics. The model equations read

$$\begin{aligned} \begin{aligned} \tau _a{\dot{a}}&= a_{\infty }({\tilde{w}} \, s \,a-\theta - \theta _0) - a,\\ {\dot{\theta }}&= \varepsilon (\theta _{\infty }(a) - \theta ),\\ {\dot{s}}&= \varepsilon {\tilde{\tau }}_s (s_{\infty }(a) - s). \end{aligned} \end{aligned}$$

(12)

The $(a,\theta ,s)$-model does not account for the fast kinetics of the activity-dependent synaptic depression, thus its effective network connectivity coefficient, ${\tilde{w}}$, takes different values than w of the $(a, d, \theta ,s)$-model. The number of slow variables determines the dimension of the critical manifold and, hence, that of the slow flow on it. With the usual parameter set ($\tau _a=1, \tau _\theta =1000, {\tilde{\tau }}_s=\tau _{\theta }/\tau _s =2$), the $(a,\theta , s)$-model has one fast (a) and two slow variables ($s, \theta$), therefore the a-nullsurface in (12) defines the critical manifold:

$$\begin{aligned} S^{0, (a, \theta , s)}:= & {} \left\{ a_{\infty }({\tilde{w}} \, s \,a-\theta - \theta _0) - a =0\right\} \nonumber \\:= & {} \left\{ k_a{\mathrm {ln}}\left( \frac{1}{a}-1\right) +{\tilde{w}}sa-\theta -\theta _0 = 0\right\} . \end{aligned}$$

(13)

Fig. 5 shows $S^{0, (a, \theta , s)}$ with the fold curve (blue), that is

$$\begin{aligned} F^{(a, \theta , s)} =\left\{ \frac{-k_a}{a(1-a)}+{\tilde{w}}s=0\right\} . \end{aligned}$$

The black curve shown in Fig. 5 is an example of MMO-type periodic orbit of (12), with SAOs along $F^{(a, \theta , s)}$. Here the limiting slow dynamics near $F^{(a, \theta , s)}$ are investigated using the DRS approach. Note that system (12) is expressed in the fast-time parametrisation. A time rescaling by $\varepsilon$ brings it to the slow-time formulation and setting $\varepsilon$ to 0 gives the following reduced system:

$$\begin{aligned} \begin{aligned} 0&= a_{\infty }({\tilde{w}}sa-\theta _0 - \theta ) - a ,\\ {\dot{\theta }}&= \theta _{\infty }(a) - \theta ,\\ {\dot{s}}&= {\tilde{\tau }}_s(s_{\infty }(a) - s), \end{aligned} \end{aligned}$$

(14)

where the dot represents now the derivative with respect to the slow time. The algebraic condition in (14) defines the critical manifold $S^{0, (a, \theta , s)}$ given in (13). Differentiating $S^{0, (a, \theta , s)}$ with respect to time, and projecting onto the (a, s)-space leads to the following system of differential equations:

$$\begin{aligned} -\left( \frac{-k_a}{a(1-a)}+{\tilde{w}}s\right) {\dot{a}}= & {} -{\dot{\theta }} + {\tilde{w}}a{\dot{s}}\;=\;-(\theta _{\infty }(a) - \theta )+{\tilde{w}}a{\tilde{\tau }}_s(s_{\infty }(a) - s)\nonumber \\ {\dot{s}}= & {} {\tilde{\tau }}_s(s_{\infty }(a) - s), \end{aligned}$$

(15)

with $\theta$ constrained to be on $S^{0, (a, \theta , s)}$, that is

$$\begin{aligned} \theta = k_a {\mathrm {ln}}\left( \frac{1}{a}-1\right) + {\tilde{w}}sa - \theta _0 = \theta (a,s). \end{aligned}$$

The singularities of Eq. (15) along the fold curve $F^{(a, \theta , s)}$ can be resolve through desingularization by applying a time rescaling of factor $\frac{k_a}{a(1-a)}-{\tilde{w}}s$, which gives the DRS:

$$\begin{aligned} \begin{aligned} {{\dot{a}}}&= -\theta _\infty (a)+\theta (a,s)+{\tilde{w}}a{\tilde{\tau }}_s(s_{\infty }(a) - s),\\ {{\dot{s}}}&= \bigg (\frac{k_a}{a(1-a)} - {\tilde{w}}s\bigg ){\tilde{\tau }}_s(s_{\infty }(a) - s). \end{aligned} \end{aligned}$$

(16)

Note that desingularization reverses the direction of flow on the repelling sheet of $S^{0, (a, \theta ,s)}$ where $\frac{k_a}{a(1-a)}-{\tilde{w}}s<0$. Hence, the phase portrait of the reduced system is obtained by changing the direction of the flow in the phase portrait of the DRS where for $\frac{k_a}{a(1-a)}-{\tilde{w}}s<0$.

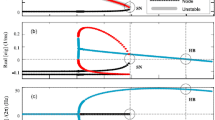
The bifurcation diagram of (16) with respect to ${\tilde{w}}$ is presented in Fig. 13a. Similar to the one of (9), two sets of equilibria of saddle- and node-type (black and red curves) undergo a transcritical bifurcation at ${\tilde{w}}_T \approx 0.754644$ (a FSNII event). For ${\tilde{w}}<{\tilde{w}}_T$, the nodes of (16) are the true equilibria of (12) and the saddles are folded saddles, hence the solutions of (12) are not affected by the folded saddles in this region because trajectories are attracted to the node equilibria.On the other hand, the nodes of (16) become folded nodes when ${\tilde{w}} > {\tilde{w}}_T$ because they are on $F^{(a, \theta , s)}$ (see Fig. 13b), while the saddles on the curve $\{s = s_{\infty }(a)\}$ turn into saddle-foci of the 3D system, with complex eigenvalues with positive real parts and one negative real eigenvalue. In this region of parameter space (i.e. ${\tilde{w}}>{\tilde{w}}_T$) and for big enough time-scale difference between the fast and slow components of the system, the orbits approach the folded node, around which there is as funnel structure (Desroches et al. 2012; Krupa and Wechselberger 2010) that first attracts the orbits with a inward spiralling motion, and then repels them towards the 2D invariant manifold of the saddle of the full 3D system. Finally, the 2D unstable manifold of the saddle (associated with its complex eigenvalues) provokes additional small oscillations just before the orbit leaves the vicinity of the critical manifold.

Fig. 13

a Bifurcation diagram of (16) with respect to ${\tilde{w}}$. Solid (resp. dashed) lines correspond to stable (resp. unstable) equilibria, and both branches cross at ${\tilde{w}}_{T} \approx 0.754644$, where they exchange stability via a transcritical bifurcation (marked by a red dot); note that the branch plotted in red corresponds to the projection of the fold curve onto the (a, s)-plane. b Nullclines of (16) for ${\tilde{w}}=0.7625$. The node equilibrium $\mathrm {n}$ of the DRS corresponds to a folded node for the reduced system, with coordinates $(a_{\mathrm {fn}}, s_{\mathrm {fn}})\approx (0.074695, 0.94877)$; it lies at the intersection between the a-nullcline (blue) and the projection $\varPi (F^{(a, \theta , s)})$ of the fold curve onto the (a, s)-plane (red). The saddle equilibrium $\mathrm {s}$, with coordinates $(a_{\mathrm {s}}, s_{\mathrm {s}})\approx (0.074424, 0.96385)$, lies at the intersection between the a-nullcline (blue) and the $\{s=s_{\infty }\}$-component of the s-nullcline (yellow) (color figure online)

1.1 MMOs and behaviour along isolas

Figure 14a shows the ${{\tilde{w}}}$-dependent bifurcation diagram of the $(a,\theta ,s)$-model. The system undergoes a supercritical Hopf bifurcation at ${\tilde{w}}_{Hopf} \approx 0.755319$. The periodic solutions lying along the red branch starting at ${\tilde{w}}_{Hopf}$ grow in amplitude until $a_{max}=1$, which corresponds to the relaxation type solutions studied in Tabak et al. (2006) (Fig.  14d).

The periodic solutions along the Hopf branch are unstable between two PD bifurcations at ${\tilde{w}} \approx 0.758948$ and ${\tilde{w}} \approx 0.771919$. These unstable solutions are canard orbits that follow the unstable middle sheet of $S^{0, (a, \theta , s)}$. The stable solutions for ${\tilde{w}}$ approximately in [0.758948, 0.771919] are MMO-type periodic orbits: n-number of SAOs near the folded node of $S^{0, (a, \theta , s)}$ followed by a LAO of relaxation type (Fig. 5a). All solutions with the same number of SAOs belong to the same isolated closed curve of periodic orbits in parameter space, a so-called isola. Stable solutions lie on the top of each isola between two PD bifurcations. It is possible to pass from one isola to the next as ${\tilde{w}}$ changes within the approximate interval [0.758948, 0.771919]. Transitions between neighbouring isolas corresponds to a $\pm 1$ change in the number of SAOs. The time course of some of these periodic orbits are given in Fig. 14c. See also Fig. 7b for a comparison with the MMBO orbits appearing in the 4D model.

Fig. 14

a Bifurcation diagram of the $(a,\theta ,s)$-model with isolas of MMO solutions. b Zoom of panel a near the 9-SAO-isola. The inset panel offers a further zoom into the upper region of the isola. Bold lines correspond to stable solutions, dashed lines represent unstable ones. In all panels, red dots indicate PD bifurcations and the black dot corresponds to the Hopf (H) bifurcation. In panel b and its inset, marked solutions are shown in Figs 15 and 16. c Example of MMO-type periodic solutions of the $(a,\theta ,s)$-model for ${\tilde{w}} \in [0.758948, 0.771919]$. Each single orbit is shown during its corresponding period. d A relaxation-type solution of the $(a,\theta ,s)$-model for ${\tilde{w}} = 0.78$ (color figure online)

Fig. 15

Upward behaviour of the orbits when w moves along the left quasi-vertical segment of the isola on panel (b) of Fig. 14. A canard explosion connects in parameter space a SAO periodic orbit (upper left) to a MMO periodic orbit (bottom right). The green surface is the critical manifold $S^{0, (a, \theta , s)}$, the blue lines on $S^{0, (a, \theta , s)}$ correspond to the single fold curve $S^{0, (a, \theta , s)}$ (the critical manifold is in fact a cusp surface). Each panel below the $(a, \theta , s)$-space projection shows the time course for a of the periodic orbit shown above

Fig. 16

Downward behaviour of the orbits when w moves along the right quasi-vertical segment of the isola on panel (b) of Fig. 14. A canard implosion connects in parameter space the MMO periodic orbit (upper left) to SAO periodic orbit (bottom right). The green surface is the critical manifold $S^{0, (a, \theta , s)}$, the blue lines on $S^{0, (a, \theta , s)}$ correspond to the single fold curve $S^{0, (a, \theta , s)}$ (the critical manifold is in fact a cusp surface). Each panel below the $(a, \theta , s)$-space projection shows the time course for a of the periodic orbit shown above

The 9-SAO isola is displayed in Fig. 14b as an example. Observe that, the isolas present two high-slope segments between the bottom right corner (points 2 and 11) and the plateau on the top (see points 6 and 8 in the inset plot). We keep referring to them as the quasi-vertical segments of the solution branches. They connect the small-amplitude orbits to MMO-type orbits via canard explosions. Example periodic orbits on the left and right quasi-vertical segments are given in Figs 15 and 16, respectively. The orbit at the bottom left of the isola is in Fig. 15-(1). This subthreshold orbit has the shortest segment along the repelling surface and it has 9 SAOs plus one last oscillation slightly larger than the others. When moving ${\tilde{w}}$ on the left quasi-vertical segment, the associated cycle extends the part of its last oscillation along the repelling middle sheet of $S^{0, (a, \theta , s)}$ (the orbits on panels (1)–(3) are similar to the canard-without-head cycles in planar systems). The maximal canard trajectory (the third orbit) is the solution that stretches out from the lower side of the fold curve all the way to the upper side. As ${\tilde{w}}$ changes, the solution follows the repelling sheet of the critical manifold, before jumping up to the upper attracting sheet, then jumping down to the lower attracting branch and finally funnels into the folded-node region (the fourth and fifth orbits are similar to the canard-with-head cycles in planar systems). The formation of the relaxation segment of the periodic solution (the LAO) is completed when ${\tilde{w}}$ passes the first PD bifurcation point (Fig. 15-(6)), where the solutions become stable.

As ${\tilde{w}}$ continues to move along the isola, periodic orbits lose their stability at the second PD point, then they shrink in amplitude while the parameter goes down along the right quasi-vertical segment. Here we observe a second canard explosion, which happens in the opposite direction as the usual one (in a sense, a canard implosion), connecting the MMOs to the small-amplitude periodic orbits (Fig. 16). We see that the only difference between the solutions on the left and right quasi-vertical segments is the amplitude of the 9th SAO, which is slightly larger than the ones along the left quasi-vertical segment.

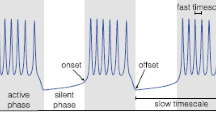
We also observe that the silent phase duration increases with the number of SAOs, i.e. when decreasing the value of ${{\tilde{w}}}$ (Fig. 14c). The silent phase can take up to 12 times longer than the active phase for the MMOs, whereas the maximum ratio for the relaxation type orbits (Fig. 14-d) is around 5. This provides a new hypothesis to explain the large silent to active phase duration ratio observed experimentally.

The bifurcation structure of this model, in particular the family of isolas of MMOs, their shape and organization in parameter space, is very much exemplary of excitable systems with one fast and two slow variables near a folded node. Indeed, such bifurcation structure has been found in various single neuron models (e.g. in the reduced Hodgkin–Huxley model) and also in models of chemical reactions such as the Koper model; see Desroches et al. (2012) for details and further examples.