Interactions between a locally separating stable manifold and a bursting periodic orbit

Abstract

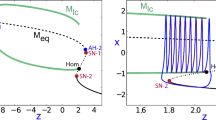
Multi-spike bursting of the membrane potential is understood to be a key mechanism for cell signalling in neurons. During the active phase of a burst, the voltage potential across the cell membrane exhibits a series of spikes. This is followed by a silent (recovery) phase during which there is relatively little change in the potential. Mathematical models of this behaviour are frequently based on Hodgkin–Huxley formalism; the dynamics of the voltage is expressed in terms of ionic currents that lead to a system of ordinary differential equations in which some variables (voltage, in particular) are fast and others are slow. The bursting patterns observed in such slow-fast models are often explained in terms of transitions between different coexisting attracting states associated with the so-called fast subsystem, for which the slow variables are viewed as parameters. In particular, the threshold that determines when the voltage starts to burst is identified with the basin boundary between two attractors associated with the active and silent phases. In reality, however, the bursting threshold is a more complicated object. Numerical methods recently developed by the authors approximate the bursting threshold as a locally separating stable manifold of the full slow-fast system. Here, we use these numerical techniques to investigate how a bursting periodic orbit interacts with this stable manifold. We focus on a Morris–Lecar model, which is three dimensional with one slow and two fast variables, as a representative example. We show how the locally separating stable manifold organises the number of spikes in a bursting periodic orbit, and illustrate its role in a spike-adding transition as a parameter is varied.