Modeling a SI epidemic with stochastic transmission: hyperbolic incidence rate

Abstract

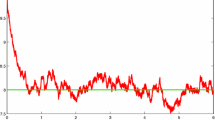
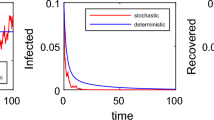
In this paper a stochastic susceptible-infectious (SI) epidemic model is analysed, which is based on the model proposed by Roberts and Saha (Appl Math Lett 12: 37–41, 1999), considering a hyperbolic type nonlinear incidence rate. Assuming the proportion of infected population varies with time, our new model is described by an ordinary differential equation, which is analogous to the equation that describes the double Allee effect. The limit of the solution of this equation (deterministic model) is found when time tends to infinity. Then, the asymptotic behaviour of a stochastic fluctuation due to the environmental variation in the coefficient of disease transmission is studied. Thus a stochastic differential equation (SDE) is obtained and the existence of a unique solution is proved. Moreover, the SDE is analysed through the associated Fokker–Planck equation to obtain the invariant measure when the proportion of the infected population reaches steady state. An explicit expression for invariant measure is found and we study some of its properties. The long time behaviour of deterministic and stochastic models are compared by simulations. According to our knowledge this incidence rate has not been previously used for this type of epidemic models.

Appendix

1.1 Expression for $P^{*}$

Given $Z\in [\epsilon ,1]$, $\epsilon >0$, by replacing F(Z) and G(Z) in equation for $P^{*}(Z)$ in Theorem 4.68 in Capasso and Bakstein (2012), we obtain

$$\begin{aligned} P^{*}(Z)=\frac{K' e^{\int _{\epsilon }^{Z} \frac{-\left( 1-p\right) By+\left( \frac{q_0y}{y+a}C-\alpha \right) \left( 1-y\right) y }{\left( \frac{\rho C}{y+a} y^2 (1-y)\right) ^2}dy}}{\left( \frac{\rho C}{Z+a} Z^2 (1-Z)\right) ^2} , \end{aligned}$$

(16)

where $K'$ is the normalizing constant, that is, $\int \nolimits _{0}^{1} P^{*}(Z) dZ=1$, if $P^{*}(Z)$ is integrable in [0, 1]. By splitting the integral in the exponent we can rewrite $P^{*}(Z)$ by

$$\begin{aligned} P^{*}(Z)=\frac{K' e^{I_1+I_2+I_3}}{\left( \frac{\rho C}{Z+a} Z^2 (1-Z)\right) ^2} , \end{aligned}$$

(17)

where $I_1=\frac{-2(1-p)B}{\rho ^2 C^2} \int \nolimits _{\epsilon }^{Z} \frac{(y+a)^2}{y^3 (1-y)^2} dy$, $I_2=\frac{2q_0}{\rho ^2 C} \int \nolimits _{\epsilon }^{Z} \frac{(y+a)}{y^2 (1-y)} dy$ and $I_3=\frac{-2\alpha }{\rho ^2 C^2} \int \nolimits _{\epsilon }^{Z} \frac{(y+a)^2}{y^3 (1-y)} dy$.

After solving the three integrals, we set

$$\begin{aligned} I_1= & {} \frac{-2(1-p)B}{\rho ^2 C^2}\\&. \left[ (1+4a+3a^2) \log \left( \frac{Z}{1-Z}\right) -\frac{2a(1+a)}{Z}-\frac{a^2}{2Z^2}+\frac{(1+a)^2}{1-Z} +\tilde{C}_1\right] ,\\ I_2= & {} \frac{2q_0}{\rho ^2 C} \int \limits _{\epsilon }^{Z} \frac{(y+a)}{ (1-y)^2} dy=\frac{2q_0}{\rho ^2 C} \left[ (1+a) \log \left( \frac{Z}{1-Z}\right) -\frac{a}{Z}+\tilde{C}_2\right] ,\\ I_3= & {} \frac{-2\alpha }{\rho ^2 C^2} \left[ (1+a)^2 \log \left( \frac{Z}{1-Z}\right) -\frac{a(2+a)}{Z}-\frac{a^2}{2Z^2}+\tilde{C}_3\right] . \end{aligned}$$

With algebraic manipulation over (17) and putting $L=e^{\tilde{C}_1 +\tilde{C}_2 -\tilde{C}_3} K'$, we obtain (15).